ORIGINAL ARTICLE
PEREIRA, Olavo de Carvalho [1]
PEREIRA, Olavo de Carvalho. Limit calculation of a function without using ![]() and
and ![]() . Revista Científica Multidisciplinar Núcleo do Conhecimento. Year. 06, Ed. 08, Vol. 04, p. 05-31. August 2021. ISSN: 2448-0959, Access link: https://www.nucleodoconhecimento.com.br/mathematical-olympiads/limit-calculation, DOI: 10.32749/nucleodoconhecimento.com.br/mathematical-olympiads/limit-calculation
. Revista Científica Multidisciplinar Núcleo do Conhecimento. Year. 06, Ed. 08, Vol. 04, p. 05-31. August 2021. ISSN: 2448-0959, Access link: https://www.nucleodoconhecimento.com.br/mathematical-olympiads/limit-calculation, DOI: 10.32749/nucleodoconhecimento.com.br/mathematical-olympiads/limit-calculation
ABSTRACT
The consulted bibliography does not present, in any of the analyzed cases, a calculation of the limit of a function, but only “shows” that the values presented as the “limit” satisfy the definition of limit of a function expressed through inequalities involving ![]() and
and ![]() , there is, therefore, a gap in this theme, which the present article comes to fill by fundamentally using the concept of defined function, as well as by identifying the expression ”
, there is, therefore, a gap in this theme, which the present article comes to fill by fundamentally using the concept of defined function, as well as by identifying the expression ” ![]() tends to a certain number” with a corresponding equality.
tends to a certain number” with a corresponding equality.
Keywords: Limit Of A Function, Limit Calculus, Lateral Limits, Infinite Limits, Limits At Infinity.
1. INTRODUCTION
This article presents the “calculation of limit of a function” in order to fill an existing gap in this subject.
The presentation of the calculation mentioned in the solution of several limits is the main objective of the article.
In a supplementary way, we intend to clarify the real need to calculate, or not, the limit of a function.
We will also discuss, in a very simple way, the case in which a simple function, defined at a certain number, is continuous at that number.
Although the geometric interpretation is always important, here we will only take an algebraic approach to the “limit calculus” presented.
1.1 CALCULATION OF LIMIT OF A FUNCTION
The definition of a function’s limit is presented in math textbooks as an estimate.
For example: Leithold (1994) presents the definition of a function’s limit as follows:
Seja ![]() uma função definida para todo número em algum intervalo aberto contendo
uma função definida para todo número em algum intervalo aberto contendo ![]() , exceto possivelmente no próprio número
, exceto possivelmente no próprio número ![]() O limite de
O limite de ![]() quando
quando ![]() tende a
tende a ![]() será
será ![]() , escrito como
, escrito como ![]() se a seguinte afirmativa for verdadeira:
se a seguinte afirmativa for verdadeira:
Dado ![]() qualquer, existe um
qualquer, existe um ![]() , tal que, se
, tal que, se ![]() então
então ![]() .‘‘
.‘‘
A definição acima afirma que os valores de ![]() tendem a um limite
tendem a um limite ![]() quando
quando ![]() tende a um número
tende a um número ![]() , se o valor absoluto da diferença entre
, se o valor absoluto da diferença entre ![]() e
e ![]() puder se tornar tão pequeno quanto desejarmos, tomando
puder se tornar tão pequeno quanto desejarmos, tomando![]() suficientemente próximo de
suficientemente próximo de ![]() , mas não igual a
, mas não igual a ![]() .
.
Lezzi, Murakami and Machado (1991) express themselves as follows about the same definition:
Seja ![]() um intervalo aberto ao qual pertence o número real
um intervalo aberto ao qual pertence o número real ![]() . Seja
. Seja ![]() uma função definida para
uma função definida para ![]() Dizemos que o limite de
Dizemos que o limite de ![]() , quando
, quando ![]() tende a
tende a ![]() , é
, é ![]() , e escrevemos
, e escrevemos ![]() se para todo
se para todo ![]() , existir
, existir ![]() tal que se
tal que se
![]() então
então ![]() .
.
Munem and Foulis (1982) use the following definition:
Se ![]() é uma função e
é uma função e ![]() é um número, entende-se a notação
é um número, entende-se a notação ![]() como “o limite de
como “o limite de ![]() ” quando
” quando![]() tende a
tende a ![]() é
é ![]() isto é,
isto é, ![]() se aproxima do número
se aproxima do número ![]() quando
quando ![]() se aproxima de
se aproxima de ![]() .
.
As can be seen from the above definitions, a limit is presented ![]() just to satisfy the definition itself.
just to satisfy the definition itself.
No calculation of this limit is presented at any time.
This article presents the “limit calculation” of a function that can be used in all cases where it is necessary to perform such an operation.
Now, on to the argument.
For some functions, not defined in a certain number, in order to know, with the maximum possible precision, what would be their value in that number, it is customary to evaluate them in values close to that number for which they are not defined.
Example: 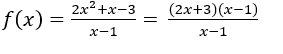 set to all
set to all ![]() except
except ![]() .
.
If we replace the ![]() by 1, we have the indeterminacy
by 1, we have the indeterminacy ![]() .
.
As the function is not defined, that is, it does not exist for the value 1, we evaluate, so, its value close to 1, since our objective is to know the value of the function, at least, close to 1, since it does not exist for ![]() .
.
For values of ![]() , different from 1, greater or less than 1, but very close to 1,
, different from 1, greater or less than 1, but very close to 1, ![]() , so
, so![]() will be equal to 1, and will have values close to 5, as we will see below:
will be equal to 1, and will have values close to 5, as we will see below:
Let’s assign to ![]() the values
the values ![]() , that is, we are taking values of increasingly closer to 1, but smaller than 1. The values of
, that is, we are taking values of increasingly closer to 1, but smaller than 1. The values of ![]() found are:
found are: 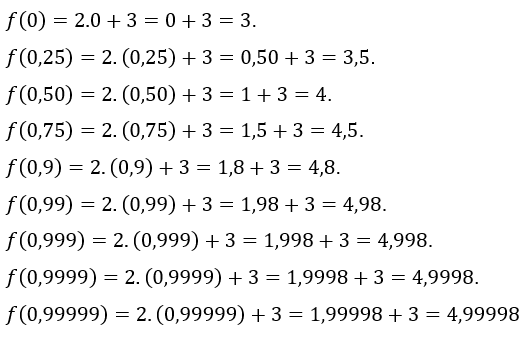 Now let’s assign the
Now let’s assign the ![]() the values
the values ![]() , that is, we are taking values of increasingly closer to 1, but greater than 1. The values of
, that is, we are taking values of increasingly closer to 1, but greater than 1. The values of ![]() found are:
found are: 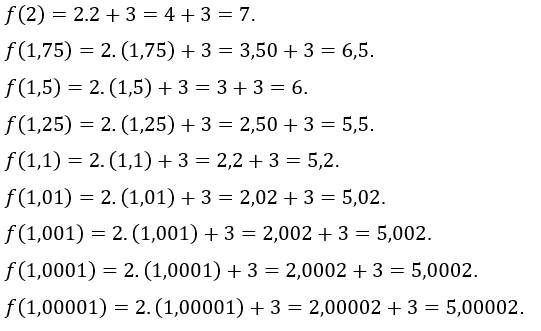
As can be seen, in both cases, as ![]() approaches 1,
approaches 1, ![]() approaches 5, leading us to believe that this is the limit of
approaches 5, leading us to believe that this is the limit of ![]() .
.
However, no limit “calculation” was made here, but only an evaluation of ![]() , when
, when ![]() takes values very close to 1.
takes values very close to 1.
So the value 5 is “candidate” to be the limit that we still need to calculate.
The consulted authors structure the definition of limit in terms of inequalities from examples like this and assume the estimated value, in this case 5, as really the limit of the function.
In this regard, they claim that ![]() , because for any
, because for any ![]() , no matter how small it is, there is a
, no matter how small it is, there is a ![]() , such that if
, such that if ![]() so
so![]() .
.
The limit definition given at the beginning, which has no limit calculation, is used to “prove” that given numbers, with no indication of where they were taken, are limits of functions.
We will show that the definition of limit does not prove, does not demonstrate, that a given number is the limit of a function, but only “shows” that the given number is the limit.
Let’s use an example to make the difference between a “show” and a “demonstration” clear.
- Show that 2 is the root of the equation
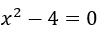 .
.
This means that if we replace the ![]() by 2, we will have zero as a result of the equation.
by 2, we will have zero as a result of the equation.
let’s see ![]() .
.
This was an example of “demonstration”, that is, only something was shown, nothing was demonstrated, nothing was calculated, only the value provided was replaced.
It is different when you say: prove that 2 is a root, it is a solution of the equation ![]() .
.
In that case, we have to calculate, solve the equation, and see if we get ![]() .
.
Well, solving, we have: ![]() , soon
, soon ![]() , and extracting the square root on both sides we have:
, and extracting the square root on both sides we have: ![]() , that is,
, that is, ![]() or
or ![]() .
.
Then one of the values of ![]() it really is 2.
it really is 2.
With this, it was “demonstrated” that 2 is really the root of the equation ![]() .
.
We will see, in the examples given below, that there is no proof, but only a “show” that the given number is the limit of the given function.
Example. Use the limit definition to “prove” that ![]() .
.
Here it is not said how the conclusion that the limit is 5 was reached, nor does it say where that number was taken from.
We will discuss, in general terms, the solution presented in the consulted books:
The first requirement of the definition is that ![]() be defined on every number of some open interval containing 3, except possibly on 3. As
be defined on every number of some open interval containing 3, except possibly on 3. As ![]() is defined for all real numbers, any open interval containing 3 will satisfy this requirement. We need to show now that for all
is defined for all real numbers, any open interval containing 3 will satisfy this requirement. We need to show now that for all ![]() there is one
there is one ![]() , tal que se
, tal que se ![]() so
so![]() we have to
we have to![]()
We have, so, ![]() and
and ![]()
This statement indicates that ![]() é um delta satisfatório.
é um delta satisfatório.
With this choice of ![]() we have the following argument:
we have the following argument:![]() , so
, so![]() , so
, so![]() , so
, so![]() , so
, so ![]() so
so ![]()
This just “shows”, from the definition of limit, that ![]()
As we have seen, there was no proof, but only a “show”, since, given the number 5, we simply substituted it and the given function, in the definition of a function’s limit.
Let’s go to one more example: use the definition to “prove” that ![]() .
.
Again a number is given, in this case 4, as the limit, but it is not said where this number was taken from.
Here’s the solution, in general terms:
Like ![]()
is defined for all real numbers, any open interval containing 2 will satisfy the first requirement of the definition.
We need to show that for all ![]() , there is one
, there is one ![]() , such that
, such that
If ![]() so
so ![]()
Soon ![]() so
so ![]()
We need to put a constraint on ![]() that gives us an inequality involving
that gives us an inequality involving ![]() . Such a restriction is made to select the open interval required by the definition. We choose the range
. Such a restriction is made to select the open interval required by the definition. We choose the range ![]() and this implies that
and this implies that ![]() .
.
So ![]() and
and ![]() , so
, so ![]() so
so ![]() so
so ![]() so.
so.
Now we have ![]() and
and ![]() , so
, so ![]() as our goal is to get
as our goal is to get ![]() , we must require
, we must require ![]() With this
With this ![]()
Using this ![]() we have completed the so-called “proof”.
we have completed the so-called “proof”.
As we saw above, again nothing was proved, but only that the number given as the limit, in this case 4, satisfies the definition of limit.
There was no calculation to show that the number 4 is really the limit.
From this point on, we will present the limit calculus of a function.
Before presenting the “calculus” itself, let us evaluate ![]() in the same values of
in the same values of ![]() given above, but considering them to be compounds of number 1.
given above, but considering them to be compounds of number 1.
This will show, in general terms, the reasoning used to calculate the limit of the function.
The function is ![]() , valid for all
, valid for all ![]() .
.
For ![]() or
or ![]() we have to
we have to 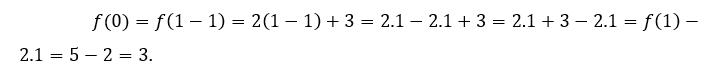
For ![]() or
or ![]() , we have to
, we have to 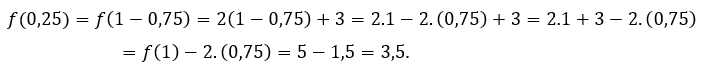
For ![]() or
or ![]() we have to
we have to 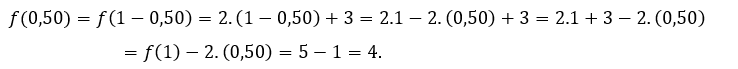
For ![]() or
or ![]() , we have to
, we have to 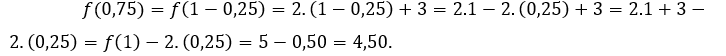
For ![]() or
or ![]() , we have to
, we have to 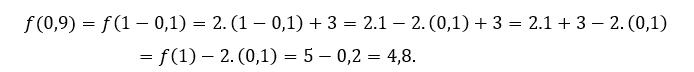
For ![]() or
or ![]() we have to
we have to 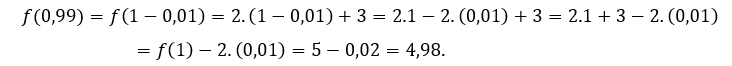
For ![]() or
or ![]() we have to
we have to 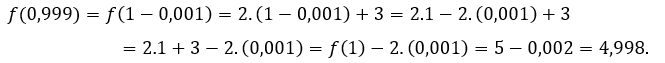
For ![]() or
or ![]() , we have to
, we have to 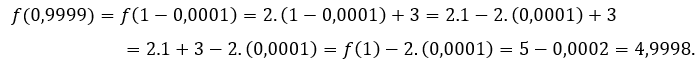
For ![]() or
or ![]() we have to
we have to
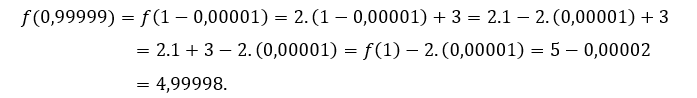
We tested some values of ![]() less than 1.
less than 1.
Now we will evaluate ![]() at values greater than 1 but close to 1.
at values greater than 1 but close to 1.
For ![]() or
or ![]() , we have to
, we have to 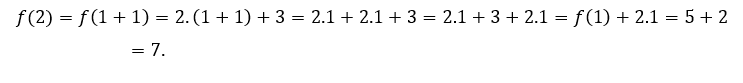
For![]() or
or![]() we have to
we have to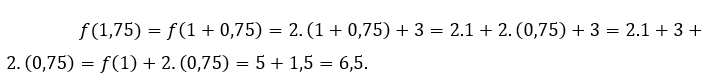
For![]() or
or![]() we have to
we have to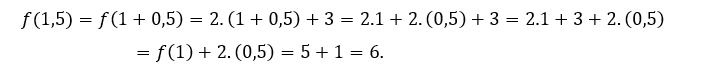
For![]() or
or![]() , we have to
, we have to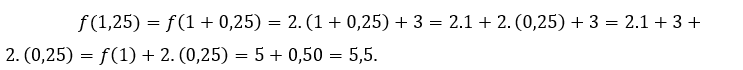
For ![]() or
or ![]() , we have to
, we have to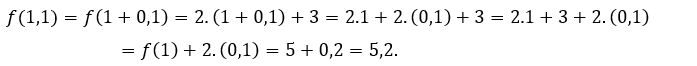
For ![]() or
or![]() we have to
we have to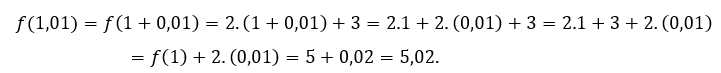
For ![]() or
or![]() , we have to
, we have to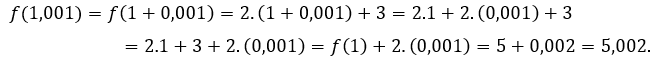
For ![]() or
or![]() , we have to
, we have to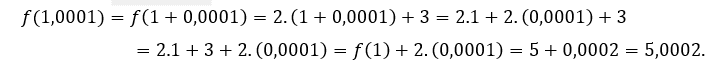
For ![]() or
or![]() , we have to
, we have to
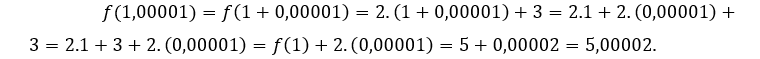
From the above, we realize that the more![]() approaches 1, the more
approaches 1, the more![]() approaches 5, that is, when
approaches 5, that is, when ![]() tends to 1,
tends to 1, ![]() tends to 5.
tends to 5.
We observed in the calculations above, in all the values assigned to![]() , the appearance of a constant
, the appearance of a constant![]() to which a value was added or subtracted, which tended to zero, as
to which a value was added or subtracted, which tended to zero, as ![]() was approaching 1.
was approaching 1.
This constant is, therefore, a “candidate” to be the “limit” mentioned above, that is, there is an indication that we may have ![]() .
.
We will now express the situation above in a semi-generic way to present the “limit calculation” itself.
The expression “![]() tends to 1″, represented by
tends to 1″, represented by![]() , it’s equivalent to
, it’s equivalent to![]() , ou
, ou ![]() , when
, when![]() tends to zero,
tends to zero, ![]() , e
, e ![]() .
.
With this, the expression![]() , replacing
, replacing ![]() per
per![]() or
or![]() , it’s equivalent to
, it’s equivalent to![]() , or
, or ![]() , that is,
, that is, ![]() , or
, or ![]() .
.
From the above equality, it is possible to “calculate” the value of the limit of![]() when
when ![]() tends to 1, since it is enough to calculate the value of
tends to 1, since it is enough to calculate the value of ![]() , or
, or ![]() .
.
We will now do, using the same function as before, the calculation for![]() , when
, when ![]() .
.
In this way, we are left with:
![]() then
then![]() regardless of
regardless of ![]() , and
, and ![]() tends to zero when
tends to zero when![]() , that is, it is so small that it approaches zero as far as we like.
, that is, it is so small that it approaches zero as far as we like.
The calculation for ![]() , that is,
, that is,![]() , is analogous and produces the same result.
, is analogous and produces the same result.
let’s see:![]()
We will now calculate a series of limits of functions, to exemplify the application of the mentioned “calculus”.
- Let’s calculate
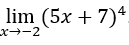 .
.
Like![]() , we can do, for example,
, we can do, for example, ![]() ,
, ![]() and
and ![]() .
.
Stay with ![]()
![]() termos em
termos em ![]() que tendem todos a zero.
que tendem todos a zero.
Then the result will be ![]()
- Let’s calculate
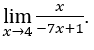
Like ![]() , we can do, for example,
, we can do, for example,![]() ,
, ![]() e
e ![]() .
.
Stay with
![]() ,because the numerator tends to 4 and the denominator tends to
,because the numerator tends to 4 and the denominator tends to![]() .
.
- Let’s calculate
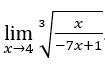 .
.
As we saw above, in the end we will be left with
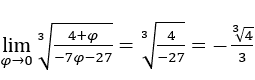
- Let’s calculate
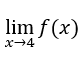 as below.
as below.
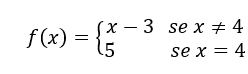 .
.
We must calculate ![]() , because no matter what happens to
, because no matter what happens to![]() when
when ![]() .
.
Like ![]() , we can do, for example,
, we can do, for example, ![]()
![]() e
e ![]() .
.
Stay with
![]() , then
, then![]() .
.
Be![]() , set to all
, set to all![]() , except
, except ![]() .
.
Let’s consider ![]() that is,
that is, ![]() , for which
, for which![]() reduces to
reduces to![]() .
.
- Let’s calculate the
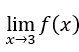 . We have to
. We have to 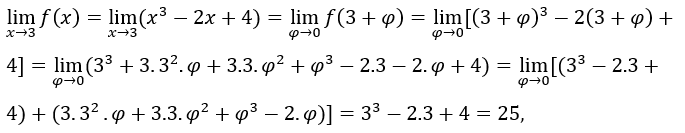 , uma vez que, quando
, uma vez que, quando 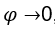 the expression
the expression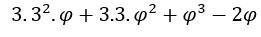 tends to zero.
tends to zero.
So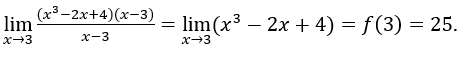
Now consider the following example: ![]() , set to all
, set to all ![]() ,and calculate its limit when
,and calculate its limit when![]() tends to 2.
tends to 2.
For![]() condition of existence of the function,
condition of existence of the function, ![]() , and when
, and when ![]() we can do, for example,
we can do, for example, ![]() , with
, with![]()
![]() and we will have to calculate the limit
and we will have to calculate the limit![]() .
.
Like ![]() , the expression
, the expression ![]() tende a
tende a ![]() , and the limit will then be
, and the limit will then be ![]() .
.
In conclusion, we are left with: ![]() .
.
Observation.
We could have applied “calculus” directly to the function, without first dividing the factor common to the numerator and denominator.
let’s see![]()
In fact, we can apply the “calculus” directly on the function, without first making a “preparation” on it.
We will now give some examples of limit calculation involving trigonometric and exponential functions in order to exemplify the consolidated above.
Let’s consider the function![]() , set to all
, set to all ![]() , except
, except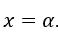
Remembering: ![]() means, for example, that
means, for example, that![]() , where
, where![]() ,
, ![]() .
.
Substituting this value for x In the original equation above, we have: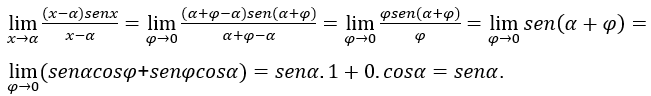
Then, ![]() and
and ![]() are independent of
are independent of ![]() it’s the
it’s the ![]() , while the
, while the![]() .
.
Another example: consider the function ![]() set to all
set to all ![]() , except
, except![]() .
.
- Let’s calculate the
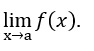
- Making the substitution
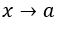 for, for example,
for, for example, 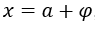 , with
, with 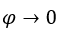 ,
, 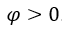 . We have:
. We have: 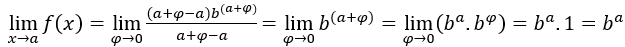 , because the
, because the 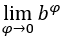 is 1 and
is 1 and 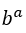 regardless of
regardless of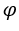 .
.
Now let’s calculate the limit of the functions given at the beginning to confirm the values of the limits given.
- Let’s calculate
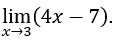
Like ![]() , we can do, for example,
, we can do, for example,![]() ,
, ![]() and
and![]() and we are left with
and we are left with![]()
- Let’s calculate
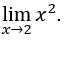
Like![]() , we can do, for example,
, we can do, for example,![]() ,
, ![]() and
and ![]() and we are left with
and we are left with![]()
As can be seen from the “calculations” above, the limits given in the previous examples were correct.
We will demonstrate just one theorem about limits to exemplify the calculus shown here.
Theorem if ![]() and
and ![]() are any constants, then
are any constants, then![]() .
.
Just calculate the limit by doing, for example, ![]()
![]() and
and![]()
Stay with:![]() , then
, then ![]() tends to zero, since
tends to zero, since ![]() tends to zero.
tends to zero.
There is an immense simplicity in the “calculation” presented.
In this case, there is no doubt that the limit is![]() .
.
We will now use the presented “limit calculus” to compute limits of functions in various circumstances.
- Let’s calculate
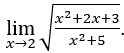
Like![]() , so we can do, for example,
, so we can do, for example, ![]() ,
, ![]() and
and ![]()
Stay with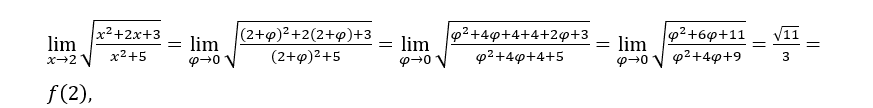 since
since ![]() tends to 11 and
tends to 11 and![]() tends to 9.
tends to 9.
- Let’s calculate
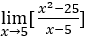 .
.
Like x → 5, so we can do, for example,![]() ,
, ![]() and
and![]()
Stay with ![]()
It is observed that it was not necessary to “prepare” the function to apply the “calculus”, that is, it was not necessary to write the function as ![]() and finally how
and finally how ![]()
- Calculemos
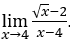 .
.
In cases involving radicals, to which a real number is added or subtracted, when the direct substitution of the value of ![]() leads to indeterminacy
leads to indeterminacy![]()
we have to prepare the equation, because the direct application of the “calculus” does not undo the indeterminacy, as we will see below.
What happens in this case is that there is a factor common to both the numerator and the denominator, but that is only expressed when we divide, either the numerator by the denominator, or the denominator by the numerator.
This currently translates into mathematics as rationalization.
Let’s see in the example above: if we divide the denominator by the numerator, since the exponent of ![]() in the denominator is 1 and the exponent of
in the denominator is 1 and the exponent of ![]() in the numerator is smaller, that is, it is worth
in the numerator is smaller, that is, it is worth ![]() we will have:
we will have: ![]() and substituting, we will have
and substituting, we will have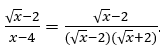 .
.
We are thus able to express the factor common to the numerator and denominator.
The other way is to divide the numerator by the denominator, but in this case, we must do the same thing is the rationalization, since the exponent of ![]() in the numerator is less than the exponent of
in the numerator is less than the exponent of ![]() denominator, and therefore needs to be multiplied by a factor in
denominator, and therefore needs to be multiplied by a factor in ![]() to make its exponent at least equal to the exponent of the denominator.
to make its exponent at least equal to the exponent of the denominator.
This is the famous rationalization that we do.
We will do the calculation first, without preparation.
Like ![]() , we can do, for example,
, we can do, for example, ![]() ,
,![]() and
and ![]() .
.
Stay with ![]() We observe the need to rationalize, as the limit is still undetermined when
We observe the need to rationalize, as the limit is still undetermined when ![]() in the numerator and denominator, tending to
in the numerator and denominator, tending to ![]()
We will then multiply and divide by ![]() , and we will be with
, and we will be with![]()
Now we will do the calculation, preparing the function before applying it.
![]() .
.
How direct substitution of 4 leads to indeterminacy ![]() , means that the numerator and denominator have as a common factor
, means that the numerator and denominator have as a common factor ![]() or
or ![]()
In this case, as it is a radical minus a real number, the way used to “release” the common factor is through rationalization.
Before computing the limit, we will multiply and divide the numerator and denominator of the function by ![]()
Stay with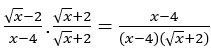 . In this function, we can already apply the calculus. let’s see:
. In this function, we can already apply the calculus. let’s see: ![]()
Like![]() we can do, for example,
we can do, for example,![]() ,
, ![]() and
and ![]()
Stay with 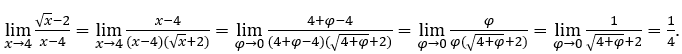
1.2 SIDE LIMITS
In cases where a function is defined for every real number except a real number![]() , when we calculate its limit with the independent variable tending to
, when we calculate its limit with the independent variable tending to![]() , as in the examples given above, it does not matter whether we use
, as in the examples given above, it does not matter whether we use![]() how much
how much ![]() ,
, ![]() e
e ![]() , since it is set to all numbers to the left and right of
, since it is set to all numbers to the left and right of ![]() .
.
And of course, this is not a sentence function.
When a function is not defined to the left or right of a number
![]() and we have to calculate its limit with
and we have to calculate its limit with ![]() tending to, we must use the value of
tending to, we must use the value of![]() as the case may be.
as the case may be.
When ![]() and we do
and we do ![]() or
or ![]() ,
, ![]() and
and ![]() , so
, so ![]() indicates that
indicates that![]() is approaching
is approaching ![]() for values greater than
for values greater than ![]() ,and therefore is approaching
,and therefore is approaching ![]() on the right.
on the right.
The calculation made with ![]() is, therefore, the limit when
is, therefore, the limit when ![]() tends to
tends to ![]() on the right.
on the right.
It is, therefore, the right-hand limit.
We use ![]() to calculate the left-hand limit.
to calculate the left-hand limit.
We know that the limit exists only when the one-sided limits exist and are equal.
- Let’s calculate
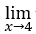 √x – 4.
√x – 4.
We know that the function exists only for ![]() , that is,
, that is, ![]()
Therefore, there is no left-hand limit and, therefore, the limit in question does not exist.
But there is the right-hand limit which can be calculated by substituting ![]() per
per![]() ,
, ![]() e
e ![]()
![]()
Be![]()
- We calculate the side limits.
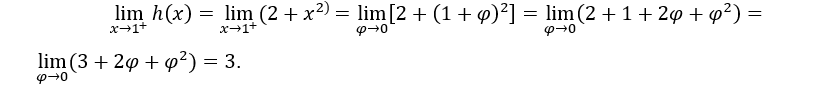
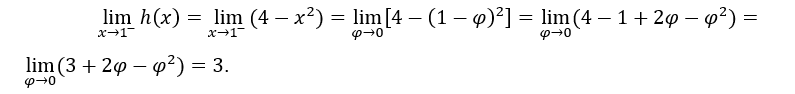
How are they the same,![]()
In the above calculation, we made ![]() , to calculate the right-hand limit and
, to calculate the right-hand limit and ![]() to calculate the left-hand limit.
to calculate the left-hand limit.
We calculate the limit of ![]() defined by
defined by
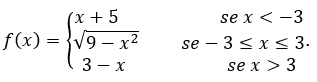
- Let’s calculate
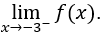
We must then calculate![]()
We will then do ![]() ,
, ![]() and
and ![]()
- Let’s calculate
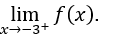
We must then calculate,![]()
We will do it then, ![]() ,
, ![]() e
e ![]()
Stay with
![]()
- Let’s calculate
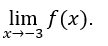
Like![]() then the
then the ![]() does not exist.
does not exist.
- Let’s calculate
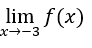 .
.
We must then calculate,![]()
We will then do![]() ,
, ![]() And
And ![]()
Stay with
![]()
- Let’s calculate
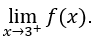
We must then calculate ![]()
We will then do ![]() ,
, ![]() and
and ![]()
Stay with
![]()
Let’s calculate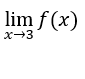
Like ![]() , so
, so 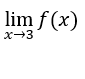 exists and is equal to zero.
exists and is equal to zero.
1.3 INFINITE LIMITS
Those whose functional values increase or decrease without limitation, when the independent variable gets closer and closer to a fixed number, can be solved equally by the limit “calculation” presented here, with the advantage of not having to worry about theorems.
Before applying the “calculation”, let us remember the following situations:
![]()
- Let’s calculate the following limit
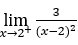 .
.
Like![]() , we must do
, we must do ![]() ,
, ![]() and
and![]()
Stay with ![]() .
.
- Let’s calculate now
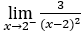 .
.
Like![]() , we must do
, we must do![]() ,
, ![]() and
and ![]()
Stay with ![]() .
.
- Let’s calculate
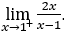 .
.
Like ![]() , we must do
, we must do ![]() ,
, ![]() and
and ![]()
Stay with ![]() , because the numerator tends to 2, while the denominator tends to zero through positive values.
, because the numerator tends to 2, while the denominator tends to zero through positive values.
- Let’s calculate now
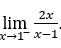 .
.
Like![]() , we must do
, we must do![]() ,
, ![]() and
and ![]()
Stay with 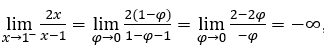 , because the numerator tends to 2 and the denominator tends to zero through negative values.
, because the numerator tends to 2 and the denominator tends to zero through negative values.
- Let’s calculate
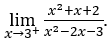
Like![]() ,we must do
,we must do ![]() ,
, ![]() and
and![]()
Stay with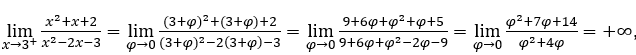 because the numerator tends to 14, while the denominator tends to zero for positive values.
because the numerator tends to 14, while the denominator tends to zero for positive values.
- Let’s calculate now
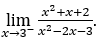
Like ![]() , we must do
, we must do ![]() ,
, ![]() and
and![]()
Stay with![]() , since the numerator tends to 14, while the denominator tends to zero for negative values, since
, since the numerator tends to 14, while the denominator tends to zero for negative values, since ![]() tends to zero always for positive values.
tends to zero always for positive values.
In this case the denominator is ![]() whenever
whenever ![]() , It is like
, It is like ![]() , the denominator is always negative.
, the denominator is always negative.
- Let’s calculate
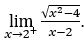 .
.
Like ![]() , we must do
, we must do ![]() ,
, ![]() and
and ![]()
We are like
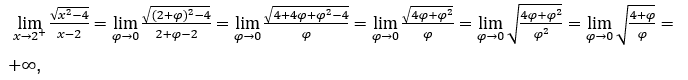 because the numerator tends to 2 and the denominator tends to zero for positive values.
because the numerator tends to 2 and the denominator tends to zero for positive values.
- Let’s calculate
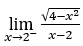
Like ![]() , we must do
, we must do ![]() ,
, ![]() and
and ![]()
Stay with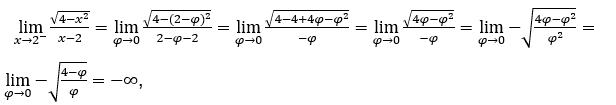 , because the numerator tends to -2 and the denominator tends to zero for positive values.
, because the numerator tends to -2 and the denominator tends to zero for positive values.
In these two cases, we were able to![]() into the radical because it is always positive.
into the radical because it is always positive.
- Let’s calculate
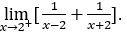 .
.
Like![]() , we must do
, we must do ![]() ,
, ![]() and
and ![]()
Stay with ![]() because the numerator tends to 4, while the denominator tends to zero for positive values.
because the numerator tends to 4, while the denominator tends to zero for positive values.
Note We could have directly substituted the value of in the original equation.
- Let’s calculate
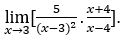
Like![]() , we must do
, we must do![]() ,
, ![]() and
and![]()
Stay with![]() , because the numerator tends to 35, while the denominator tends to zero for negative values, since is negative for < 1.
, because the numerator tends to 35, while the denominator tends to zero for negative values, since is negative for < 1.
- Let’s calculate
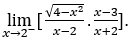 .
.
Like ![]() , we will do
, we will do ![]() ,
, ![]() and
and ![]()
Stay with 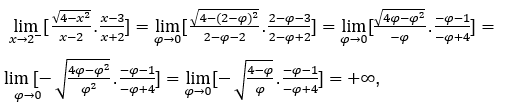 , because the numerator tends to
, because the numerator tends to![]() and the denominator tends to
and the denominator tends to ![]() by positive values.
by positive values.
1.4 LIMITES NO INFINITO
In the same way as for the limits mentioned so far, the literature consulted also does not present a calculation of limits at infinity, but only evaluates the function when the independent variable increases or decreases indefinitely.
The evaluation result is used as the threshold.
Let’s see.
Given the function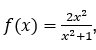 , we attribute to
, we attribute to![]() the values
the values![]() and so on, allowing it to grow indefinitely. The corresponding functional values will be
and so on, allowing it to grow indefinitely. The corresponding functional values will be
![]()
We observe that when ![]() grows, taking positive values, the functional values approach 2.
grows, taking positive values, the functional values approach 2.
When an independent variable ![]() grows indefinitely, through positive values, we write
grows indefinitely, through positive values, we write![]() the example given, the conclusion was drawn that
the example given, the conclusion was drawn that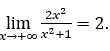
As seen above, from the given example, no limit calculation of the function was presented, but it was only observed that, as![]()
increased, by positive values, the function approached 2.
This value 2 was then used as the limit of the function.
We will present, below, the “calculation” of limit of functions when the independent variable tends to![]() or the
or the ![]()
In cases where ![]() , we will do
, we will do 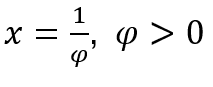 and
and![]() , because, as we saw above, when
, because, as we saw above, when ![]() tends to zero for positive values,
tends to zero for positive values, ![]() tends to
tends to![]() ,and with that,
,and with that,![]() tends to
tends to![]()
In cases where ![]() , we will do
, we will do 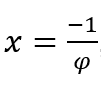
![]() and
and![]() , because, as we saw above, when φ tends to zero for positive values
, because, as we saw above, when φ tends to zero for positive values![]() ,
,![]() tends to, and with that,
tends to, and with that, ![]() tends to
tends to![]() .
.
- Let’s calculate
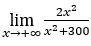 .
.
Like ![]() , we will do
, we will do 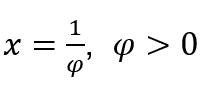 e
e ![]()
Stay with
![]() because the numerator tends to 2 and the denominator tends to 1.
because the numerator tends to 2 and the denominator tends to 1.
- Let’s calculate
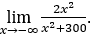 .
.
Like ![]() , we will do
, we will do ![]() and
and ![]()
Stay with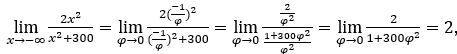 because the numerator tends to 2 and the denominator tends to 1.
because the numerator tends to 2 and the denominator tends to 1.
- Let’s calculate
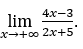
Like ![]() , we will do
, we will do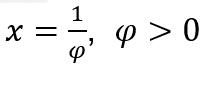 and
and![]()
Stay with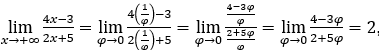 , because the numerator tends to 4 and the denominator tends to 2.
, because the numerator tends to 4 and the denominator tends to 2.
- Let’s calculate
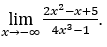
Like![]() , we will do
, we will do![]()
![]() and
and ![]()
Stay with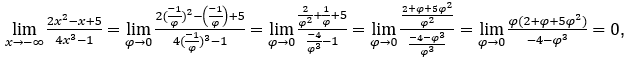 because the numerator tends to zero and the denominator tends to -4.
because the numerator tends to zero and the denominator tends to -4.
- Let’s calculate
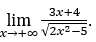
Like ![]() , we will do
, we will do ![]() e
e ![]()
Stay with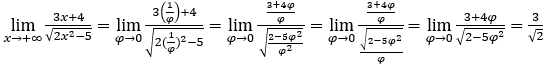 , because the numerator tends to 3 and the denominator tends to
, because the numerator tends to 3 and the denominator tends to![]()
- Let’s calculate
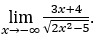
Like![]() , we will do
, we will do![]()
![]() and
and ![]()
Stay with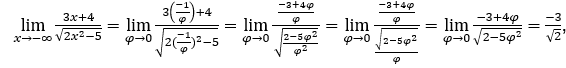 ,because the numerator tends to -3 and the denominator tends to √2.
,because the numerator tends to -3 and the denominator tends to √2.
- Let’s calculate
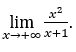
Like![]() , we will do
, we will do ![]() and
and ![]()
Stay with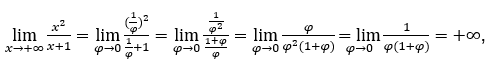 because the numerator is 1 and the denominator tends to zero for positive values.
because the numerator is 1 and the denominator tends to zero for positive values.
- Let’s calculate
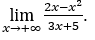
Like ![]() , we will do
, we will do ![]() =
= ![]() φ > 0 and φ → 0.
φ > 0 and φ → 0.
Stay with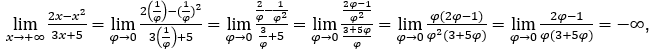 because the numerator tends to -1 and the denominator tends to zero for positive values.
because the numerator tends to -1 and the denominator tends to zero for positive values.
- Let’s calculate
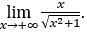
Like![]() , we will do
, we will do ![]() and
and ![]()
Stay with 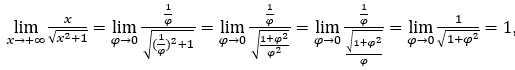 because the numerator is 1 and the denominator tends to 1.
because the numerator is 1 and the denominator tends to 1.
- Let’s calculate now
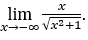
Like ![]() , we will do
, we will do![]() and
and![]()
Stay with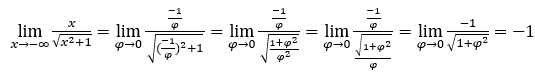 , because the numerator is -1 and the denominator tends to 1.
, because the numerator is -1 and the denominator tends to 1.
- Let’s calculate
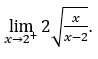
Like ![]() , we must do
, we must do![]() ,
, ![]()
Stay with 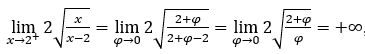 , because the numerator tends to
, because the numerator tends to![]() and the denominator tends to zero for positive values.
and the denominator tends to zero for positive values.
- Let’s calculate now
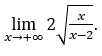
Like![]() , we will do
, we will do ![]() and
and ![]()
Stay with 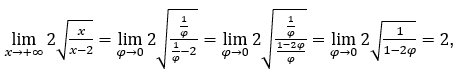 because the numerator tends to 2 and the denominator tends to 1.
because the numerator tends to 2 and the denominator tends to 1.
Observation.
Calculation of limits at infinity cannot be applied, for example, to trigonometric functions, since some of them vary in a certain interval, and others increase or decrease indefinitely, depending on the value considered.
For example, if we tried to calculate the![]() , we would go through all the values of the range infinite times
, we would go through all the values of the range infinite times ![]() , because, for all
, because, for all ![]() ,
, ![]() , that is, we would not arrive at any definite value.
, that is, we would not arrive at any definite value.
Indeed, polynomial functions, or functions expressed by ratios between polynomials, are the most suitable for applying limits.
2. OBSERVATIONS
1) The limit calculation presented arose from the identification of the expression![]() tends to a certain number
tends to a certain number ![]() with equality
with equality ![]() , or
, or ![]() , with
, with ![]() and
and![]() ,since, really, when
,since, really, when![]() ,
, 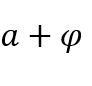 e
e ![]() tend to
tend to![]() and with that,
and with that,![]() tends to
tends to![]()
In the case of limits at infinity, the substitution for the expression ![]() tends to
tends to ![]() was
was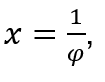 , and a replacement for an expression
, and a replacement for an expression ![]() tends to
tends to ![]() was
was ![]() , with
, with![]() and
and ![]()
The substitution makes the most sense, because, really, when ![]() , always for positive values,
, always for positive values,![]() tend
tend![]() e
e ![]() tends to
tends to![]() , making
, making ![]() really tend to
really tend to ![]() or the
or the ![]() , as the case may be.
, as the case may be.
If we substitute, in the case where ![]() tends to
tends to![]() or the
or the ![]() the
the ![]() per,
per, ![]() or
or![]() and
and![]() , the result would be the same.
, the result would be the same.
An example.
- Let’s calculate
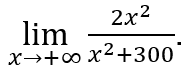
we will do ![]() e
e ![]()
Stay with
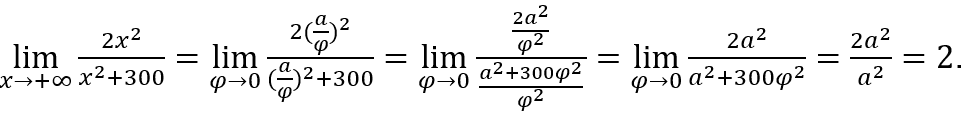
2. As seen in the various examples, the “limit calculus” presented is quite “fluent” and of direct application, without the need to consult theorems or to “organize” the function before performing the calculation, except when we have to rationalize.
This fact brings a lot of tranquility when calculating the limit of a function, as the “calculation” presented is a true synthesis of this subject.
For example, “calculation” can be used directly over the function
![]() , without the need to organize it, that is, to express it as
, without the need to organize it, that is, to express it as 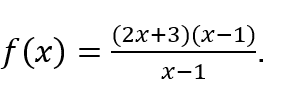
Let’s see 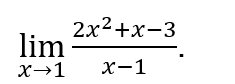
Like![]() , we can do, for example,
, we can do, for example, ![]() and
and ![]()
Stay with
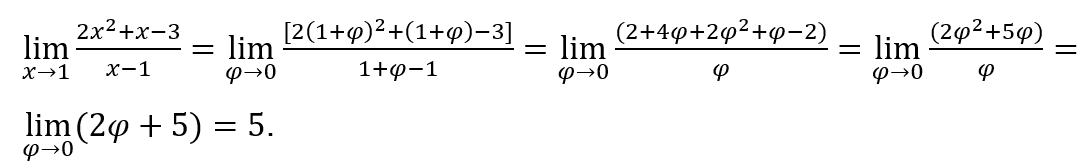
This brings an enormous advantage over the current presentation of this subject, which, in addition to not presenting any limit calculation, is shown to be quite “stuck” by the immense amount of theorems that must be considered in the “evaluations” of limits, as well as of the “organizations” , that must be done on the functions before “estimating” their limit.
3) I would like to add, to the “limit calculation” presented, some evaluations of a practical nature.
a) It only makes sense to calculate the limit of a function close to a value for which it is not defined.
If the function is defined for a certain value, that is, if the function exists for a certain value, it makes no sense to calculate the limit near that value, since we know how much the function is worth at that value.
For example, be![]()
This function is defined for all ![]() , it exists for everyone
, it exists for everyone![]()
Therefore, it would be unreasonable to calculate, for example,![]() , since the function exists for
, since the function exists for![]() , that is, why calculate this limit if we can simply substitute
, that is, why calculate this limit if we can simply substitute ![]() by 3 in
by 3 in ![]() and we get the value of the function at 3, that is,
and we get the value of the function at 3, that is, ![]()
With this, hundreds of exercises no longer have a reason to exist.
Obviously the functions considered in this article are of ![]()
b) By using the concept of limit, we will make an observation here about continuity of a function.
According to Lethold’s calculus book (1994), the definition of a continuous function at a point translates as follows:
Dizemos que a função ![]() é contínua no número a se e somente se as seguintes condições forem satisfeitas:
é contínua no número a se e somente se as seguintes condições forem satisfeitas:
(i) ![]() existe;
existe;
(ii) ![]() existe;
existe;
(iii) ![]()
Se uma ou mais de uma dessas condições não forem verificadas em ![]() , a função
, a função![]() será descontínua em
será descontínua em ![]()
So Lima (1978) defines continuity of a function:
Uma função ![]() diz-se contínua no ponto
diz-se contínua no ponto ![]() quando é possível tornar
quando é possível tornar ![]() arbitrariamente próximo de
arbitrariamente próximo de ![]() desde que se tome
desde que se tome ![]() suficientemente próximo de
suficientemente próximo de ![]()
Em termos precisos, diremos que ![]() é contínua no ponto
é contínua no ponto ![]() quando, para todo
quando, para todo ![]() dado arbitrariamente, pudermos achar
dado arbitrariamente, pudermos achar ![]() tal que
tal que ![]() e
e ![]() impliquem
impliquem ![]()
We know that if a function is defined on a certain interval, that is, if it exists for every number contained in a certain interval, then there is no point in computing the limit of that function for some number in that interval, since we can simply evaluate the function on every number in that range.
In simpler terms: if a function, represented by just one expression, by just one sentence, exists for a certain number ![]() then it is totally unnecessary to calculate the limit of the function for
then it is totally unnecessary to calculate the limit of the function for ![]() , since, simply, we can calculate the value of the function in
, since, simply, we can calculate the value of the function in![]()
Of course, if we were to calculate this limit, as we did above, it would be ![]()
As stated above, it only makes sense to calculate the limit of a function around a number for which it is not defined.
Therefore, if we are analyzing functions represented by only one expression, saying that a function exists for a certain number ![]() , means that there is a limit of this function in
, means that there is a limit of this function in ![]() this limit being the value of the function in
this limit being the value of the function in ![]() , and with that we don’t need to calculate the limit of this function in that number
, and with that we don’t need to calculate the limit of this function in that number![]()
Applying this to the above definition of a continuous function, items (ii) and (iii) of the definition will become unnecessary, since in item (i) it is stated that![]() exist.
exist.
Therefore, for functions represented by “just one expression”, the simple statement that it, the function ![]() , is defined in a number
, is defined in a number ![]() that is, the simple statement that
that is, the simple statement that ![]() exists is enough to conclude that the function is continuous at that number
exists is enough to conclude that the function is continuous at that number![]()
Likewise, with this observation about continuous functions, hundreds of exercises lose their raison d’être.
Example: let the function ![]() which is defined for every real number, that is, it exists for every
which is defined for every real number, that is, it exists for every ![]() real.
real.
Thus, there is no need to calculate the limit of![]() for no value of
for no value of ![]() , because in this case, be defined in
, because in this case, be defined in ![]() is synonymous with having a limit in
is synonymous with having a limit in ![]() and that this limit is equal to the value of the function in
and that this limit is equal to the value of the function in ![]() considered.
considered.
Then the function ![]() is continuous for all
is continuous for all ![]()
3. CONCLUSION
In the above, we show that, in fact, the theory of limits is deficient in relation to a calculation of limit and, therefore, it surrounds itself with a series of arguments based on the definition of limit in order to fill this gap.
We then present the “calculation of the limit of a function” and show that it synthesizes all the mentioned subject, having, therefore, direct application.
We hope to be contributing to a better understanding of such a fundamental subject in mathematics.
REFERENCES
IEZZI, Gelson; MURAKAMI, Carlos et all. Fundamentos de Matemática Elementar, vol. 8, 1991.
LEITHOLD, Louis. O Cálculo com Geometria Analítica, vol. 1, 1994.
LIMA, Elon Lages. Curso de Análise, vol. 1, 1978.
MUNEM, Mustafa A. e FOULIS, David J. Cálculo, vol. 1, 1982.
[1] Graduate, bachelor’s degree in mathematics, from the University of Brasília.
Sent: June, 2021.
Approved: August, 2021.