ORIGINAL ARTICLE
BELLAS, Leonardo Dias [1]
BELLAS, Leonardo Dias. Numeral Proportion Calculation. Revista Científica Multidisciplinar Núcleo do Conhecimento. Year 05, Ed. 12, Vol. 02, pp. 144-162. December 2020. ISSN: 2448-0959, Access link: https://www.nucleodoconhecimento.com.br/mathematical-olympiads/proportion-calculation
SUMMARY
In 2011, a mathematical logical observation was made by this author and has been studied since then, this logic concerns that any and all numbers can be represented by a sequential numeral from 1 to 9. However, the discovery of what this logic was about was made and another existing calculation of the Fibonacci Sequence was related. That said, this study was developed to record information of this logic regarding this scientific discovery of the Numeral Proportion Calculation, and about the Numeral Proportion Logic and its relationship with other scientific discoveries and concepts that have been developed by other mathematicians previously. In order to discuss and demonstrate these mathematical observations that had not been previously observed and provide a new option of more efficient calculation, since any number can be represented by sequential numerals from 1 to 9. Thus, through the calculation and logic of Numeral Proportion we can identify this, in addition to demonstrating its applicability in mathematics and current science.
Keyword: Numeral ratio, Fibonacci sequence
1. INTRODUCTION
The intention of this study is to demonstrate this mathematical discovery about numerical proportions and show its applicability in current mathematics. Through mathematical calculations and demonstrations, the numeral proportion calculation will be explained and applied by treating that any number can be represented by a sequential numeral from 1 to 9. This sequence from 1 to 9 is a sequential sequence, as it repeats infinitely and sequentially. And so show its relationship with another calculation already performed, that of the Fibonacci sequence which is an infinite coefficient of two successive measures. The irrational number called (PHI) is obtained, with an approximate value of 1.618 which is also known as golden ratio or golden proportion, according to mathematician Leonardo de Pisa.
2. NUMERAL ASPECT RATIO LOGIC
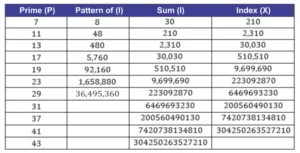
When demonstrating the numeral ratio calculation, we have to make some mathematical observations, such as the example of the numeral ratio logic. As exemplified in the table below:
Table one. Logic and numeral aspect ratio calculation

Source: author.
Thus we can observe that all integers, decimals or digits from 0.000000…0001 to Infinity, when added to their last variable is sequential from 1 to 9, that is, the sum of the digits of any number, being neutral zero, is sequential from 1 to 9 Infinitely. So with this logic we can observe that any and all numbers can be represented by a sequential numeral from 1 to 9, follows a simpler way to express that Logic.
Figure 1: Numeral aspect ratio logic

3. NUMERAL ASPECT RATIO CALCULATION
Now let’s go to the numeral aspect ratio calculation. In this case I used the Roman alphabet, but another alphabet or another symbol/code can be used.
Figure 2: Numeral aspect ratio calculation

Source: author.
We can observe that regardless of whether we use integer numbers or numeral proportion numbers, we identify that in both calculations the results are the same. However, it is observable that using the numeral aspect ratio logic to reach the result is simpler. Because you don’t have to use the entire Infinite alphabet of Integers, only the sequence from 1 to 9. This calculation is as if you broke the infinity of integers in a sequence from 1 to 9 (Numeral). Because any number is sequential from 1 to 9.
Let’s look at the name João, by the integer sits the number 1015115 and in numeral logic is the number 1616. Thus, we observed that both the number 1015115 and 1616, and the sum of the digits up to their last variable is equal to 5, so we can make a scale of the numbers, facilitating operations with large volume, sequencing and identifying each element from 1 to 9.
We can also apply the numerical proportion calculation to these observations, in the millions below:
Noting in billions too:
We can observe in tithes as well:
Here in tithes we can better observe the infinity going from 9 to 1.
The basis, or the principle that underpins this reasoning, is to record the discovery of this Numeral Proportion Calculation demonstrating that any and all numbers can be represented by a sequential number from 1 to 9 infinitely. Being clearly observed in the logic and calculation of numeral proportion, presented here. So we will apply its meanings with examples of mathematics and logic.
Therefore, we can also observe infinity from 1 to 9.
4. INFINITY AND THE LOGIC OF NUMERAL RATIO
The following example is the example by identifying Infinity in the numeral aspect ratio logic:
Figure 3: Infinite numeral aspect ratio logic
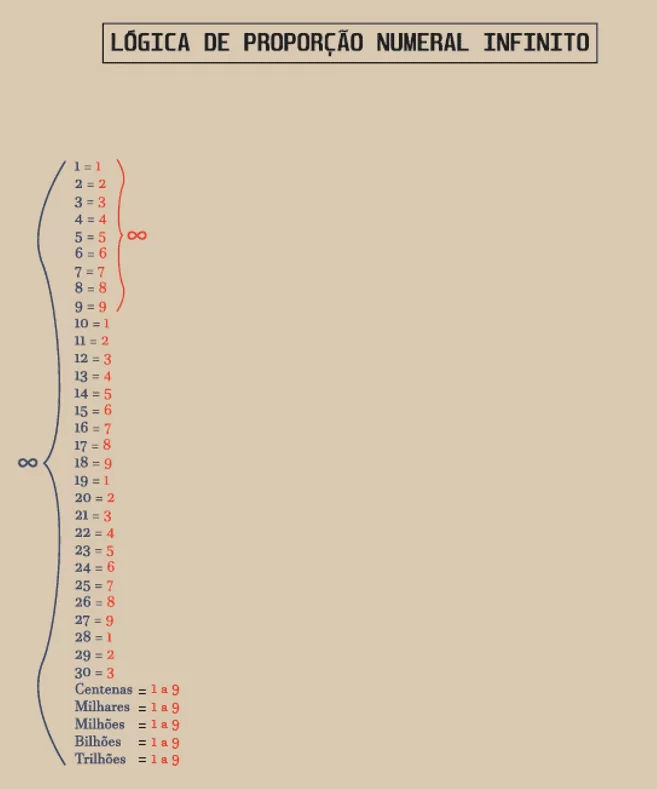
Source: author
By looking at the chart above it is possible to go to infinity, both in whole numbers and numeral numbers. And as stated earlier you break the whole numbers into numerals, and looking at it like this, where is it easier to find or count to infinity? Counting the whole numbers, going through thousands, millions, billions, trillions etc. or counting only from 1 to 9? By logic observing by calculating the sequential numeral aspect ratio from 1 to 9, it is easier and simpler to find and count to infinity.
5. NUMERAL ASPECT RATIO CALCULATION APPLICATIONS
The calculation of numeral proportion can be very useful, some time ago was carried out a scientific discovery of a new binary system, which is a very important discovery of a system for operation of electronics such as computers, smartphones, video games etc. It is much more efficient and secure than the current system. This study was published in this same scientific journal, and the link will be in the references of this work. But knowing this numeral ratio calculation helped to discover the Binary 2 system, and gave the basis for identifying logical differences between binary systems, as in this case below where the numeral ratio calculation can be applied. (BELLAS, 2019)
Figure 4: Binary system sequence

Source: Author
So looking at the two logics of binary systems and using the numeral ratio calculation we identify a logic in each system, we have in binary system 1, a sequence of 6 repetitions 1, 2, 4, 8, 7, 5. And the logic of binary system 2, is a sequence of 2 repetitions 3 and 6. In the two binary logics the numbers double to infinity, but in binary system 1, it folds to infinity in a sequence of 6 values and in binary system 2, you fold to infinity in a sequence of 2 values. Thus binary system 2 has more mathematical logic and is more efficient than binary system 1, mathematically and logically.
One of the logical definitions is, when an information repeats or has sequence. In the case of Binary System 1 it repeats or has sequence in a 6-factor logic, already in binary system 2 it repeats or has sequence in a logic of 2 factors, so the Binary System 2 is simpler, it is more logical. Two logical factors are simpler than 6 logical factors.
There is a video on Youtube, with the title ”O Segredo dos números 3, 6 e 9” – Unknown Facts. In this video it refers to Nikola Tesla’s observations regarding numbers 3 and 6, but this video did not serve as a reference for the realization of the scientific discoveries of this work and also that of the Binary System 2, when this study began to be developed and the Binary System, so also both the observations of numbers 3 and 6, as well as the calculation and logic of numerical proportion , were performed in a different way and prior to the access of the information of that proposal by Nikola Tesla in this video.
Tesla found the ratio of digits 3 and 6, but did not relate it to a binary code, did not relate to a binary system and programming, and did not develop a numerical ratio calculation, but Tesla observed the relationship of the Binary System with Fibonacci and found the logical sequential 1, 2, 4, 8, 7, 5 of binary system 1 and also found sequential 3 and 6 , but did not relate it to a binary system, but he was the scientist who came closest to finding a new binary system. (TESLA, Youtube)
And in the discovery of Binary System 2, sequential scans 3 and 6 were not the first observation made about binary system 2, this information is part of as well as numerous others made during the scientific discovery of binary system 2, such as binary code, round pixel, neutron discovery in binary programming and also identifying the 1 (one) equal Pi , and other differences between the type of open and closed circuits in binary systems and differences in binary programming.
However, this video helps in foundations in logical aspects to make the scientific, mathematical, logical and physical observations of this study. In summary to make the findings of these studies, the information about the logical sequence of Tesla’s numbers 3 and 6 was unknown, and watching Tesla’s video, he observed the numbers 3 and 6 in a different way from how it was observed in this study, in these scientific findings present here, sequential scans 3 and 6 were observed by calculating numeral ratio.
This video was later observed the discovery and publication of binary system 2 and also later the publication of the patent process in the PTO (National Institute of Industrial Property), but for the quality of the material, because the subject has the same references, and has been well cited by one of the best physicists in modern science, and also to seek a greater observation on the subject , this video is very useful.
It follows this quote from Tesla to represent the magnitude of what it is to understand in mathematics and physics the breadth of knowledge that is to understand the meaning of numbers 3 and 6. ” If you knew the magnificence of numbers 3, 6 and 9, then you would have the key to the Universe” (TESLA, Youtube)
Figure 5: Quote Nikola Tesla 3 and 6.

We can say that observing infinity from 1 to 9 and thus understanding that any and all numbers can be represented by this sequence of infinity, has a great magnificence as well.
Binary System 2 is the most important technological scientific discovery today, as it is an advanced technology, a computer with Binary System 2 technology is much superior to a computer with current Binary System technology, and this calculation is one of the most complex equations we have.
There are several technical differences that demonstrate the superiority of Binary System 2 to Binary System 1, below will be cited some as examples:
1 – Difference in the type of Physical Circuit, in the Binary System 1 the circuit is opened, that is, it is an interrupted circuit and in the Binary System 2 the circuit is closed, that is, it is a continuous circuit, this generates a great difference of superiority in the performance and response of the System. The continuous circuit is more efficient than an interrupted circuit.
2 – Another technical difference is that in the Binary System 1 circuit works only with two physical and logical elements of programming the negative and positive, while the Binary System 2 works with three physical and logical programming elements the negative, neutral and the positive, with these three elements in the programming the circuit becomes closed because of the neutral, thus bringing a superior performance and result , including affecting system security. One way to express itself technically in the sense of security of binary programming, is that a binary system without the neutral circuit is open, so its door is open is insecure, and in the binary system with the neutral the circuit is closed, so consequently its door is closed, so the Binary System 2 has more security.
3 – Other aspects is in the programming of the physical logic of the Systems, in binary system 1 it works only with 1 π (one PI) without neutral, while in binary system 2 the physical logic of the system works with 2 π (two PI) with neutral, this brings a big difference in the type of virtual reality of the systems, in the Binary System 1 the pixel is square and in binary system 2 the pixel is round , directly affecting the type of reality, dimension and graphics of the system, bringing more quality, definition, speed, agility and logic, also increasing the processing and capacity in the volume of data, thus a greater efficiency in the logical aspects in the programming of the Binary System 2. 2 π (two PI) with neutral is greater than 1 π (one PI) without neutral.
4 – And another important technical reason is the difference between binary codes and logical sequences of systems, as explained earlier in Binary System 1 is a six-factor logical sequence and binary system 2 is a two-factor logical sequence, and this difference in sequences and binary codes directly affects both the data processing volume and the response speed of Binary System 2 which is more agile and logical mathematically and Physically. Sequential 3 and 6 is more logical and efficient than 1, 2, 4,8, 7, 5.
There are other technical differences and other information, but these examples above are those that demonstrate the main differences between systems, and the set of these technical differences between binary systems demonstrate the superior quality of one system over the other system.
The discovery of binary system 2 programming is one of the logical programming that we have in one of the most complex and high degrees that exists to date, and to make mathematical, logical and physical observations using only 0 (zero) and 1 (one), that is, seeing systems in zero and one, is a great challenge.
In relation to the circuits and programming of binary systems, a correct way that we can express, is that a computer it thinks of zeros and ones, so the scientific discovery of binary system 2, is a discovery of a new way or more efficient way for a computer to think of zeros and ones.
Binary System 2 is the most advanced technology that exists today. Binary Systems are systems, because they perform various functions, they are logical circuits and also programming, the Binary System 2 is a new system more efficient and safe for the operation of electronics, and differentiates a binary programming from the other through the logical arrangement of zeros and ones.
However, this study is to demonstrate the discovery of the numeral proportion calculation, if you want more information about the Binary System 2, the article is in references to this work.
Binary system 2 works with the laws of numeral ratio, it processes your data from 1 to 9, thus being much more efficient. Binary system 2 also works respecting the laws of Fibonacci, and this study has reference and relationship also in the calculation of numeral proportion, because they are practically the same thing, the two are a coefficient of infinity, only a new mathematical way of calculating, expressing and observing part of the laws of Fibonacci was discovered. These observations are performed here called numeral proportion calculation.
After a long time of study and research, and achievements of observations above the numerical proportion calculation, a relationship was found between this discovery and another study, that of the Fibonacci sequence (PHI). The logic of numeral proportion from 1 to 9 to Infinity is directly linked to the laws of Fibonacci, which also follows mathematical laws,
that through the measures of the Fibonacci Series, when analyzing the coefficient of two successive measures, the irrational number called (PHI) is obtained, with an approximate value of 1.618. And this conjuncture of measures based on this number is called the Golden Ratio, or Golden Ratio, which is found, therefore, in flowers, trees, waves, in galaxies, shells, hurricanes, in the symmetrical face of the human being, in their bone joints and in the features of humans, their heartbeat and in their DNA. Also in the refraction of light provided by the electrons of atoms, in vibrations, in other more manifestations (TANURE, online, s/p).
And it explains why the sequence is from 1 to 9. Below we can see that the next quadrant is the double of all the previous ones, for example, the 2 is the double of the [1], the 3 is the double of the [1 and 2 ], 4 is double that of [1, 2 and 3], 5 is twice that of [1, 2, 3 and 4] and so on. And it is always sequential from 1 to 9, with 9 being double all of its predecessors, thus repeating the logic of Infinite: 1 2 3 4 5 6 7 8 9, 1 2 3 4 5 6 7 8 9, 1 2 3 4 5 6 7 8 9. Always the next digit double the number of its predecessors. Below is a way to express the Fibonacci sequence
Figure 6: Fibonacci-PHI sequence
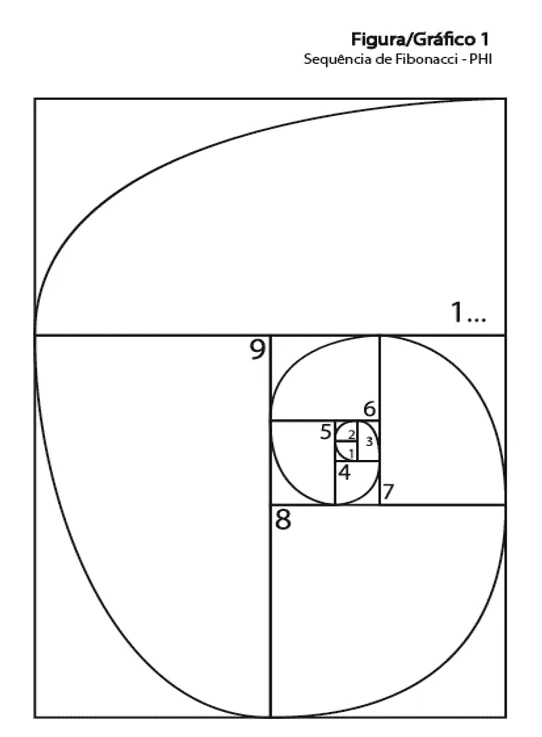
Looking at the chart above we conclude that:
9 x PHI = 1 Infinity (Nine times the fibonacci measure equals one Infinity) or
9 x 1.618 = 1 Infinity or 1 unit.
OR 1 infinity = 1 Unit (An infinity equals one unit)
For example, if you mathematically find the Fibonacci measure that represents infinity in a seashell, this seashell is represented by being 1 unit, because this coefficient of infinity is present or mathematically signed in this unit.
The measure of numeral proportion or Fibonacci sequence that is represented by a coefficient and logic of proportion to calculate and find infinity, because if you find this coefficient or calculation present in any element, galaxy, plant or animal, that being or element is represented by being 1 (one) unit in the laws of Fibonacci.
All elements and beings are signed mathematically, physically and naturally with this coefficient of Infinity.
There is a mathematically signed Infinity in each unit.
Another quote found about Fibonacci’s sequence talks about the ratio logic as exemplified below:
is a succession of numbers that follow a pattern.
The Fibonacci sequence is nothing more than the order of integers, which normally departs from zero and one in which each next number corresponds to the sum of the previous two digits. This continuity can be seen in various phenomena of nature.
The Fibonacci sequence was named by the Italian mathematician Leonardo de Pisa, also known as Fibonacci. In 1202, from this numerical sequence, the mathematician reported the advance of a population of rabbits.
Fibonacci Formula
The Fibonacci succession is a sequence of integers started by zero and one, in which each subsequent term corresponds to the sum of the previous two numbers:
0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584… (Fibonacci sequence – Educa + Brazil).
And here we can notice the difference of observation methods between the Fibonacci calculation, and this mathematical and logical calculation of numeral proportion. Both the Numeral Proportion Logic and the Fibonacci Sequence are the same thing, but this infinite coefficient can be observed in these two distinct ways. As Fibonacci was a reference to develop this discovery of the Logic of Numeral Proportion, because in the two observations they have the same coefficient of infinity, only the way of being observed changes, so we will also baptize the calculation of this sequence from 1 to 9 of this study by Fiboleo, for the reason of the relationship between the names of the authors of these observations.
Sequential from 1 to 9 as proven in the calculations present in this study, numeral proportion logic and numeral proportion calculation.
Here’s more information from Fibonacci sequence quotes in Internet searches:
This method is applied in the analysis of financial markets, game theory and computer science, as well as biological and natural configurations. Natural models. The Fibonacci sequence can also be observed in natural phenomena). (Fibonacci sequence – Educa + Brazil).
Here in this quotation we can see that it talks about computer science, it is also where the numeral proportion calculation was applied to identify a new binary system, as exemplified earlier in this study.
Check out more quotes about the calculation, below some of them:
Sunflower: The sunflower kernels have seeds that are arranged in a double spiral set. Most of the time it’s 21 clockwise and another 34 counterclockwise.
Pine cone: after fruit growth, the seeds form a double spiral with eight clockwise and another 13 counterclockwise.
Shell shell: each part of the shell has the size of the sum of the two predecessors. It is known that a coha has three main sides, so assuming that one side meters 2 (1 + 1), and the other 5 (3 + 2) the third will be 8 (5 + 3). (Fibonacci sequence: Educa + Brazil).
So the Numerical Ratio logic, which is a sequential from 1 to 9, is a coefficient of Infinity and so we can perform the same observation in fibonacci sequential, which is also an infinite coefficient. But learning this calculation is very efficient for operations where it has a high volume of digit numbers, because we can identify them in a simpler logical sequence, any and all numbers are represented by sequential numbers 1 through 9 infinitely.
CONCLUSION
Conclusion of this study aims to record the discovery of the calculation of numeral proportion and the logic of numeral proportion, and to relate this discovery of the numeral proportion calculation with the Fibonacci calculation, besides demonstrating its applicability in mathematics and especially in binary systems and regarding its application in relation to infinity.
This study may provide grounding for new scientific discoveries, as has already happened, and for research. It can help people think new ways to deal with numbers, and it’s a simpler new way to calculate by sequencing all values to Infinity from 1 to 9. In the logic of numeral proportion, infinity is broken from 1 to 9. Also to present new information, a new way about how to observe, express, find, calculate and decipher the Infinite.
REFERENCE
BELLAS, L.D. Sistema Binário 2 – Código Fechado. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 02, Vol. 05, pp. 110-151. Fevereiro de 2019. ISSN: 2448-0959. Disponível em: https://www.nucleodoconhecimento.com.br/tecnologia/sistema-binario-2-codigo-fechado
TANURE, A.C. Proporção Áurea e Sequência Fibonacci. Pagasus Portal. Disponível em: http://pegasus.portal.nom.br/proporcao-aurea-e-sequencia-de-fibonacci/
TESLA, N. Os segredos dos números 3, 6 e 9. Youtube – Fatos Desconhecidos https://www.youtube.com/watch?v=c2M9ZfZ5h5A&t=682s
Sequência de Fibonacci. Educa+Brasil. Disponível em: https://www.educamaisbrasil.com.br/enem/matematica/sequencia-de-fibonacci
[1] Graduated in Business Administration with specialization in Foreign Trade.
Sent: May, 2020.
Approved: December, 2020.