ORIGINALER ARTIKEL
PEREIRA, Olavo de Carvalho [1]
PEREIRA, Olavo de Carvalho. Grenzberechnung einer funktion ohne verwendung von ![]() und
und ![]() . Revista Científica Multidisciplinar Núcleo do Conhecimento. Jahr. 06, Hrsg. 08, Bd. 04, p. 05-31. August 2021. ISSN: 2448-0959, Zugangslink: https://www.nucleodoconhecimento.com.br/mathematischen-olympiaden/grenzberechnung, DOI: 10.32749/nucleodoconhecimento.com.br/mathematischen-olympiaden/grenzberechnung
. Revista Científica Multidisciplinar Núcleo do Conhecimento. Jahr. 06, Hrsg. 08, Bd. 04, p. 05-31. August 2021. ISSN: 2448-0959, Zugangslink: https://www.nucleodoconhecimento.com.br/mathematischen-olympiaden/grenzberechnung, DOI: 10.32749/nucleodoconhecimento.com.br/mathematischen-olympiaden/grenzberechnung
ZUSAMMENFASSUNG
Die konsultierte Bibliographie enthält in keinem der analysierten Fälle eine Berechnung der Grenze einer Funktion, sondern „zeigt“ nur, dass die als „Grenze“ dargestellten Werte die durch Ungleichungen ausgedrückte Definition der Grenze einer Funktion erfüllen einbeziehen![]() und
und ![]() , es gibt also eine lücke in diesem thema, die der vorliegende artikel zu füllen versucht, indem er den begriff der definierten funktion grundsätzlich verwendet und den ausdruck identifiziert“
, es gibt also eine lücke in diesem thema, die der vorliegende artikel zu füllen versucht, indem er den begriff der definierten funktion grundsätzlich verwendet und den ausdruck identifiziert“ ![]() tendiert zu einer bestimmten Zahl“ mit entsprechender Gleichheit.
tendiert zu einer bestimmten Zahl“ mit entsprechender Gleichheit.
Stichworte: Grenzwert einer Funktion, Grenzwertrechnung, Laterale Grenzwerte, Unendliche Grenzwerte, Grenzwerte im Unendlichen.
1. EINLEITUNG
Dieser Artikel stellt die „Grenzwertberechnung einer Funktion“ vor, um eine bestehende Lücke in diesem Fachgebiet zu schließen.
Die Darstellung der in der Berechnung erwähnten Lösung mehrerer Grenzwerte ist das Hauptziel des Artikels.
Ergänzend wollen wir klären, ob es wirklich notwendig ist, den Grenzwert einer Funktion zu berechnen oder nicht.
Wir werden auch auf sehr einfache Weise den Fall diskutieren, in dem eine einfache Funktion, die bei einer bestimmten Zahl definiert ist, bei dieser Zahl stetig ist.
Obwohl die geometrische Interpretation immer wichtig ist, werden wir uns hier nur algebraisch mit dem vorgestellten „Grenzwertkalkül“ befassen.
1.1 GRENZBERECHNUNG EINER FUNKTION
Die Definition des Grenzwerts einer Funktion wird in Mathematiklehrbüchern als Schätzung angegeben.
Zum Beispiel: Leithold (1994) präsentiert die Definition der Grenze einer Funktion wie folgt:
Seja ![]() uma função definida para todo número em algum intervalo aberto contendo
uma função definida para todo número em algum intervalo aberto contendo ![]() , exceto possivelmente no próprio número
, exceto possivelmente no próprio número ![]() O limite de
O limite de ![]() quando
quando ![]() tende a
tende a ![]() será
será ![]() , escrito como
, escrito como ![]() se a seguinte afirmativa for verdadeira:
se a seguinte afirmativa for verdadeira:
Dado ![]() qualquer, existe um
qualquer, existe um ![]() , tal que, se
, tal que, se ![]() então
então ![]() .‘‘
.‘‘
A definição acima afirma que os valores de ![]() tendem a um limite
tendem a um limite ![]() quando
quando ![]() tende a um número
tende a um número ![]() , se o valor absoluto da diferença entre
, se o valor absoluto da diferença entre ![]() e
e ![]() puder se tornar tão pequeno quanto desejarmos, tomando
puder se tornar tão pequeno quanto desejarmos, tomando![]() suficientemente próximo de
suficientemente próximo de ![]() , mas não igual a
, mas não igual a ![]() .
.
Andererseits äußern sich Lezzi, Murakami und Machado (1991) zu derselben Definition:
Seja ![]() um intervalo aberto ao qual pertence o número real
um intervalo aberto ao qual pertence o número real ![]() . Seja
. Seja ![]() uma função definida para
uma função definida para ![]() Dizemos que o limite de
Dizemos que o limite de ![]() , quando
, quando ![]() tende a
tende a ![]() , é
, é ![]() , e escrevemos
, e escrevemos ![]() se para todo
se para todo ![]() , existir
, existir ![]() tal que se
tal que se
![]() então
então ![]() .
.
Munem und Foulis (1982) verwenden die folgende Definition:
Se ![]() é uma função e
é uma função e ![]() é um número, entende-se a notação
é um número, entende-se a notação ![]() como “o limite de
como “o limite de ![]() ” quando
” quando![]() tende a
tende a ![]() é
é ![]() isto é,
isto é, ![]() se aproxima do número
se aproxima do número ![]() quando
quando ![]() se aproxima de
se aproxima de ![]() .
.
Wie aus den obigen Definitionen ersichtlich ist, wird eine Grenze präsentiert![]() nur um die Definition selbst zu erfüllen.
nur um die Definition selbst zu erfüllen.
Eine Berechnung dieser Grenze wird zu keinem Zeitpunkt vorgelegt.
Dieser Artikel stellt die „Grenzwertberechnung“ einer Funktion vor, die in allen Fällen verwendet werden kann, in denen es notwendig ist, eine solche Operation durchzuführen.
Nun zur Argumentation.
Für einige Funktionen, die nicht in einer bestimmten Zahl definiert sind, ist es üblich, sie in Werten zu bewerten, die in der Nähe dieser Zahl liegen, für die sie es nicht sind, um mit der größtmöglichen Genauigkeit zu wissen, was ihr Wert in dieser Zahl wäre definiert.
Beispiel: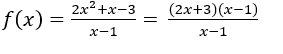 auf alle setzen
auf alle setzen ![]() außer
außer 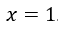 .
.
Wenn wir die ersetzen![]() mit 1 haben wir die Unbestimmtheit
mit 1 haben wir die Unbestimmtheit ![]() .
.
Da die Funktion nicht definiert ist, das heißt, sie existiert nicht für den Wert 1, bewerten wir dann ihren Wert nahe 1, da unser Ziel darin besteht, den Wert der Funktion zu kennen, der mindestens nahe 1 liegt es existiert nicht![]() .
.
Für Werte von ![]() , anders als 1, größer oder kleiner als 1, aber sehr nahe bei 1,
, anders als 1, größer oder kleiner als 1, aber sehr nahe bei 1, ![]() , dann
, dann![]() gleich 1 sein und Werte nahe 5 haben, wie wir unten sehen werden:
gleich 1 sein und Werte nahe 5 haben, wie wir unten sehen werden:
Lassen Sie uns zuweisen![]() die Werte
die Werte![]() , das heißt, wir nehmen Werte von
, das heißt, wir nehmen Werte von ![]() immer näher an 1, aber kleiner als 1. Die Werte von
immer näher an 1, aber kleiner als 1. Die Werte von ![]() gefunden sind:
gefunden sind:
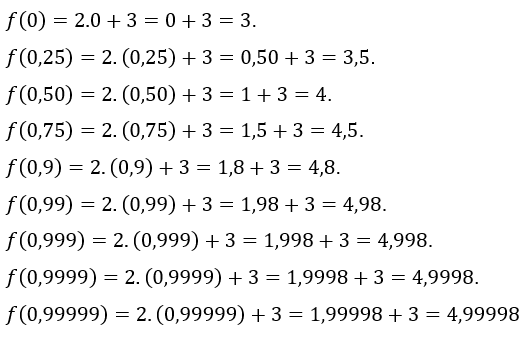
Lassen Sie uns nun die zuweisen![]() die Werte
die Werte ![]() , das heißt, wir nehmen Werte von
, das heißt, wir nehmen Werte von ![]() immer näher an 1, aber größer als 1. Die Werte von
immer näher an 1, aber größer als 1. Die Werte von ![]() gefunden sind:
gefunden sind: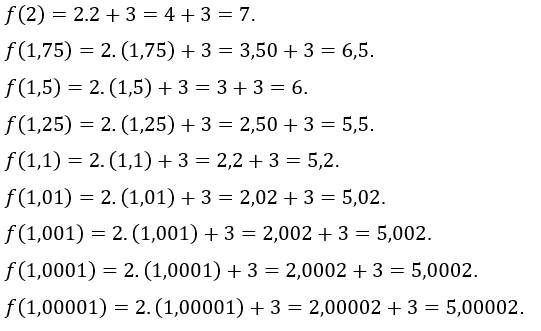
Wie ersichtlich, in beiden Fällen, wie![]() Ansätze 1,
Ansätze 1, ![]() nähert sich 5, was uns glauben lässt, dass dies die Grenze von ist
nähert sich 5, was uns glauben lässt, dass dies die Grenze von ist ![]() .
.
Allerdings wurde hier keine Grenzwert-„Berechnung“ vorgenommen, sondern nur eine Bewertung![]() , Wann
, Wann![]() nimmt Werte sehr nahe bei 1 an.
nimmt Werte sehr nahe bei 1 an.
Der Wert 5 ist also „Kandidat“, um die Grenze zu sein, die wir noch berechnen müssen.
Die konsultierten Autoren strukturieren die Definition des Grenzwerts in Bezug auf Ungleichungen aus Beispielen wie diesem und nehmen den geschätzten Wert, in diesem Fall 5, als wirklichen Grenzwert der Funktion an.
Diesbezüglich behaupten sie das ![]() , denn für jeden
, denn für jeden ![]() , Egal wie klein es ist, es gibt eine
, Egal wie klein es ist, es gibt eine ![]() , so dass wenn
, so dass wenn ![]() dann
dann ![]() .
.
Die eingangs gegebene Grenzwertdefinition ohne Grenzwertrechnung dient dem „Beweis“, dass gegebene Zahlen ohne Hinweis darauf, wo sie genommen wurden, Grenzwerte von Funktionen sind.
Wir werden zeigen, dass die Definition von Grenzwert nicht beweist, nicht demonstriert, dass eine gegebene Zahl der Grenzwert einer Funktion ist, sondern nur „zeigt“, dass die gegebene Zahl der Grenzwert ist.
Lassen Sie uns anhand eines Beispiels den Unterschied zwischen einer „Show“ und einer „Demonstration“ verdeutlichen.
- Zeigen Sie, dass 2 die Wurzel der Gleichung ist
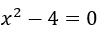 .
.
Das heißt, wenn wir die ersetzen![]() Pelz 2,Wir werden Null als Ergebnis der Gleichung haben.
Pelz 2,Wir werden Null als Ergebnis der Gleichung haben.
Mal schauen![]() .
.
Dies war ein Beispiel für „Demonstration“, dh es wurde nur etwas gezeigt, nichts demonstriert, nichts berechnet, nur der gelieferte Wert ersetzt.
Anders ist es, wenn Sie sagen: Beweisen Sie, dass 2 eine Wurzel ist, es ist eine Lösung der Gleichung ![]() .
.
In diesem Fall müssen wir rechnen, die Gleichung lösen und sehen, ob wir sie bekommen ![]() .
.
Nun, wir haben es gelöst: ![]() , logo
, logo ![]() , und auf beiden Seiten die Quadratwurzel ziehen, erhalten wir:
, und auf beiden Seiten die Quadratwurzel ziehen, erhalten wir: ![]() , das ist,
, das ist, ![]() oder
oder ![]() .
.
Dann einer der Werte von![]() wirklich ist 2.
wirklich ist 2.
Damit wurde „bewiesen“, dass 2 wirklich die Wurzel der Gleichung ist ![]() .
.
Wir werden in den unten angegebenen Beispielen sehen, dass es keinen Beweis gibt, sondern nur einen „Zeigen“, dass die gegebene Zahl der Grenzwert der gegebenen Funktion ist.
Beispiel. Verwenden Sie die Grenzwertdefinition, um das zu „beweisen“.![]() .
.
Hier wird nicht gesagt, wie der Schluss gezogen wurde, dass die Grenze 5 ist, noch wird gesagt, woher diese Zahl genommen wurde.
Wir werden allgemein die in den konsultierten Büchern vorgestellte Lösung diskutieren:
Die erste Anforderung der Definition ist die![]() auf jeder Zahl eines offenen Intervalls definiert werden, das 3 enthält, außer möglicherweise auf 3. As
auf jeder Zahl eines offenen Intervalls definiert werden, das 3 enthält, außer möglicherweise auf 3. As ![]() für alle reellen Zahlen definiert ist, erfüllt jedes offene Intervall, das 3 enthält, diese Anforderung. Das müssen wir jetzt allen zeigen
für alle reellen Zahlen definiert ist, erfüllt jedes offene Intervall, das 3 enthält, diese Anforderung. Das müssen wir jetzt allen zeigen ![]() da ist einer
da ist einer ![]() , so dass wenn
, so dass wenn ![]() dann
dann![]() Wir müssen
Wir müssen
![]()
, demnächst ![]() e
e ![]()
Wir haben dann, ![]() und
und ![]()
Darauf weist diese Aussage hin![]() ist ein zufriedenstellendes Delta.
ist ein zufriedenstellendes Delta.
Mit dieser Wahl von ![]() wir haben folgende Argumentation:
wir haben folgende Argumentation:![]() , dann
, dann![]() , dann
, dann![]() , dann
, dann![]() dann
dann![]() , dann
, dann![]()
Dies „zeigt“ nur, von der Definition der Grenze, dass![]()
Wie wir gesehen haben, gab es keinen Beweis, sondern nur eine „Show“, da wir bei der gegebenen Zahl 5 einfach diese und die gegebene Funktion in der Definition des Grenzwerts einer Funktion eingesetzt haben.
Gehen wir zu einem weiteren Beispiel: Verwenden Sie die Definition, um das zu „beweisen“ ![]() .
.
Als Grenze wird wieder eine Zahl angegeben, in diesem Fall 4, aber es wird nicht gesagt, woher diese Zahl stammt.
Hier ist die Lösung, allgemein ausgedrückt:
Wie ![]() für alle reellen Zahlen definiert ist, erfüllt jedes offene Intervall, das 2 enthält, die erste Anforderung der Definition.
für alle reellen Zahlen definiert ist, erfüllt jedes offene Intervall, das 2 enthält, die erste Anforderung der Definition.
Das müssen wir allen zeigen![]() , da ist einer
, da ist einer ![]() , so dass
, so dass
Wenn![]() dann
dann![]()
Demnächst![]() dann
dann![]()
Wir müssen eine Einschränkung auferlegen![]() das gibt uns eine Ungleichheit mit
das gibt uns eine Ungleichheit mit ![]() . Eine solche Beschränkung wird vorgenommen, um das von der Definition geforderte offene Intervall auszuwählen. Wir wählen das Sortiment
. Eine solche Beschränkung wird vorgenommen, um das von der Definition geforderte offene Intervall auszuwählen. Wir wählen das Sortiment ![]() und das impliziert das
und das impliziert das ![]() . Dann
. Dann![]() und
und ![]() , dann
, dann ![]() dann
dann ![]() dann
dann![]() dann
dann![]() .
.
Jetzt haben wir![]() e
e ![]() , dann
, dann ![]() Als unser Ziel ist es zu bekommen
Als unser Ziel ist es zu bekommen ![]() , wir müssen verlangen
, wir müssen verlangen ![]() Mit diesem
Mit diesem 
Mit diesem ![]() wir haben den sogenannten „Beweis“ abgeschlossen.
wir haben den sogenannten „Beweis“ abgeschlossen.
Wie wir oben gesehen haben, wurde wieder nichts bewiesen, sondern nur, dass die als Grenze angegebene Zahl, in diesem Fall 4, der Definition von Grenze genügt.
Es gab keine Berechnung, um zu zeigen, dass die Zahl 4 wirklich die Grenze ist.
Ab hier stellen wir die Grenzwertrechnung einer Funktion vor.
Bevor wir die “Berechnung” selbst präsentieren, lassen Sie uns bewerten![]() in den gleichen Werten von
in den gleichen Werten von ![]() oben angegeben, aber als Verbindungen der Nummer 1 betrachtet.
oben angegeben, aber als Verbindungen der Nummer 1 betrachtet.
Dies wird allgemein die Argumentation zeigen, die zur Berechnung des Grenzwerts der Funktion verwendet wurde.
Die Funktion ist![]() , gültig für alle
, gültig für alle ![]() .
.
Zum ![]() oder
oder ![]() , Wir müssen
, Wir müssen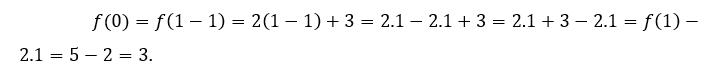
Zum ![]() oder
oder ![]() , Wir müssen
, Wir müssen 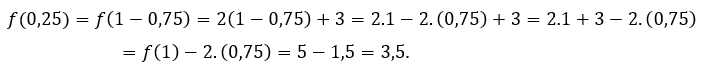 Zum
Zum ![]() oder
oder ![]() Wir müssen
Wir müssen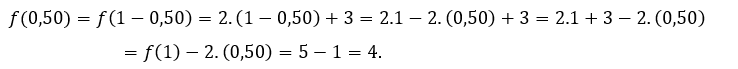
Zum ![]() oder
oder ![]() Wir müssen
Wir müssen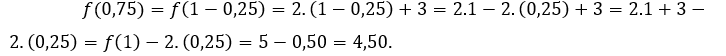 Zum
Zum ![]() oder
oder ![]() , Wir müssen
, Wir müssen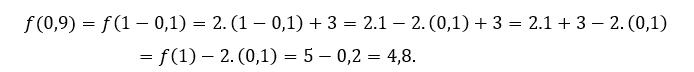
Zum ![]() ou
ou ![]() , Wir müssen
, Wir müssen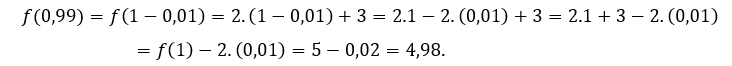
Zum ![]() oder
oder ![]() Wir müssen
Wir müssen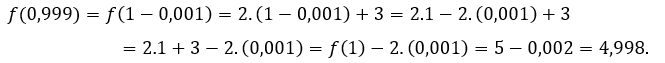
Zum ![]() oder
oder ![]() , Wir müssen
, Wir müssen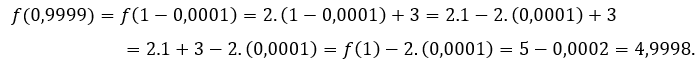
Zum ![]() oder
oder ![]() , Wir müssen
, Wir müssen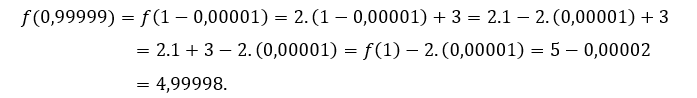
Wir haben einige Werte von getestet ![]() weniger als 1.
weniger als 1.
Jetzt werten wir aus ![]() bei Werten größer als 1, aber nahe 1.
bei Werten größer als 1, aber nahe 1.
Zum ![]() oder
oder ![]() , Wir müssen
, Wir müssen 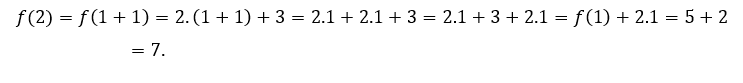
Zum![]() oder
oder ![]() Wir müssen
Wir müssen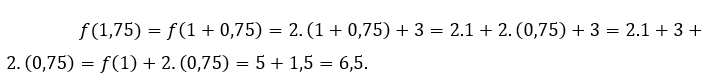
Zum ![]() oder
oder ![]() Wir müssen
Wir müssen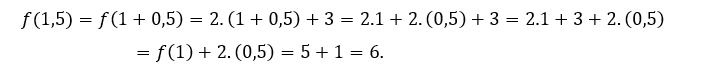
Zum ![]() oder
oder ![]() , Wir müssen
, Wir müssen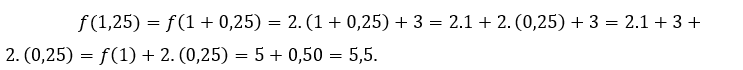
Zum ![]() oder
oder ![]() , Wir müssen
, Wir müssen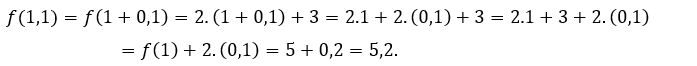
Zum ![]() oder
oder ![]() Wir müssen
Wir müssen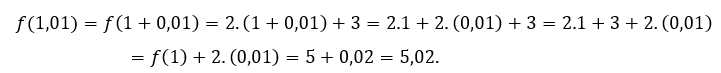
Zum![]() oder
oder ![]() , Wir müssen
, Wir müssen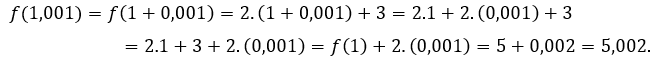
Zum![]() oder
oder ![]() , Wir müssen
, Wir müssen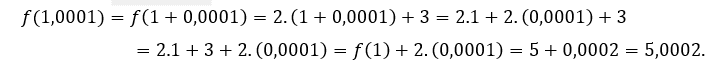
Zum![]() oder
oder ![]() , Wir müssen
, Wir müssen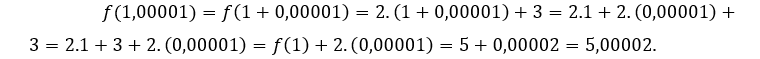
Aus dem oben Gesagten erkennen wir das umso mehr ![]() nähert sich 1, desto mehr
nähert sich 1, desto mehr ![]() nähert sich 5, das heißt, wenn
nähert sich 5, das heißt, wenn ![]() tendiert zu 1,
tendiert zu 1, ![]() tendiert zu 5.
tendiert zu 5.
Wir beobachteten in den Berechnungen oben, in allen zugewiesenen Werten![]() , das Auftreten einer Konstante
, das Auftreten einer Konstante ![]() zu dem ein Wert addiert oder subtrahiert wurde, der gegen Null tendierte, als
zu dem ein Wert addiert oder subtrahiert wurde, der gegen Null tendierte, als ![]() näherte sich dem 1.
näherte sich dem 1.
Diese Konstante ist daher ein „Kandidat“ für die oben erwähnte „Grenze“, das heißt, es gibt einen Hinweis, den wir möglicherweise haben ![]() .
.
Wir werden die obige Situation nun halb allgemein ausdrücken, um die „Grenzwertberechnung“ selbst darzustellen.
Der Ausdruck “![]() tendiert zu 1″, dargestellt durch
tendiert zu 1″, dargestellt durch ![]() , es ist äquivalent zu
, es ist äquivalent zu ![]() , oder
, oder ![]() , Wann
, Wann ![]() tendiert gegen null,
tendiert gegen null, ![]() , und
, und ![]() .
.
Damit der Ausdruck![]() , ersetzen
, ersetzen![]() pro
pro![]() oder
oder ![]() , es ist äquivalent zu
, es ist äquivalent zu ![]() , oder
, oder![]() , das ist,
, das ist, ![]() , oder
, oder ![]() .
.
Aus der obigen Gleichheit ist es möglich, den Wert der Grenze von zu „berechnen“![]() Wann
Wann ![]() gegen 1 tendiert, da es ausreicht, den Wert von zu berechnen
gegen 1 tendiert, da es ausreicht, den Wert von zu berechnen ![]() , oder
, oder ![]() .
.
Wir werden nun mit der gleichen Funktion wie zuvor die Berechnung für durchführen![]() , Wann
, Wann ![]() .
.
Auf diese Weise bleiben wir übrig:
![]() dann
dann![]() Egal ob
Egal ob ![]() , und
, und ![]() tendiert gegen Null, wenn
tendiert gegen Null, wenn ![]() , das heißt, sie ist so klein, dass sie sich beliebig weit Null nähert.
, das heißt, sie ist so klein, dass sie sich beliebig weit Null nähert.
Die Berechnung für ![]() , das ist,
, das ist, ![]() , ist analog und liefert das gleiche Ergebnis.
, ist analog und liefert das gleiche Ergebnis.
Mal schauen: ![]()
Wir werden nun eine Reihe von Grenzwerten von Funktionen berechnen, um die Anwendung des erwähnten „Kalküls“ zu veranschaulichen.
- Lassen Sie uns rechnen
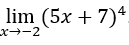 .
.
Wie![]() , können wir zB,
, können wir zB, ![]() ,
, ![]() und
und ![]() .
.
Bleib bei![]()
![]() Bedingungen ein
Bedingungen ein ![]() die alle gegen Null gehen.
die alle gegen Null gehen.
Dann wird das Ergebnis sein ![]()
- Lassen Sie uns rechnen
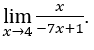
Wie ![]() , können wir zB,
, können wir zB, ![]() ,
, ![]() und
und ![]() .
.
Bleib bei
![]() , weil der Zähler gegen 4 tendiert und der Nenner gegen 4
, weil der Zähler gegen 4 tendiert und der Nenner gegen 4 ![]() .
.
- Lassen Sie uns rechnen
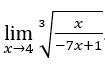 .
.
Wie wir oben gesehen haben, werden wir am Ende bei uns bleiben
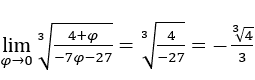
- Lassen Sie uns rechnen
 wie nachstehend.
wie nachstehend.
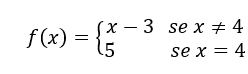 .
.
Wir müssen rechnen![]() , denn egal was passiert
, denn egal was passiert ![]() Wann
Wann ![]() .
.
Wie ![]() , können wir zB,
, können wir zB, ![]()
![]() und
und ![]() .
.
Bleib bei ![]() , dann
, dann![]() .
.
Sei![]() , auf alle setzen
, auf alle setzen ![]() , außer
, außer ![]() .
.
Lassen Sie uns überlegen ![]() das ist,
das ist, ![]() , wofür
, wofür ![]() reduziert zu
reduziert zu ![]() .
.
- Lassen Sie uns die berechnen
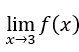 . Wir müssen
. Wir müssen 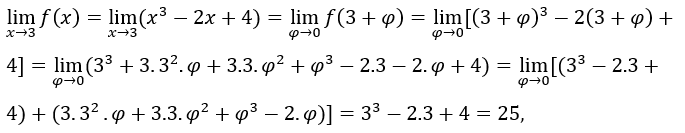 , einmal als
, einmal als 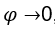 , der Ausdruck
, der Ausdruck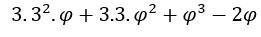 tendiert gegen null.
tendiert gegen null.
Dann
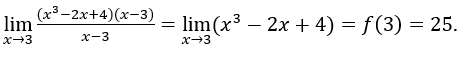
Betrachten wir nun das folgende Beispiel: ![]() , auf alle setzen
, auf alle setzen ![]() , und berechnen Sie seine Grenze wann
, und berechnen Sie seine Grenze wann ![]() tendiert zu 2.
tendiert zu 2.
Zum![]() Existenzbedingung der Funktion,
Existenzbedingung der Funktion, ![]() , und wann
, und wann ![]() können wir zB,
können wir zB, ![]() , mit
, mit ![]()
![]() und wir müssen die Grenze berechnen
und wir müssen die Grenze berechnen![]() .
.
Wie![]() , der Ausdruck
, der Ausdruck ![]() neigt dazu
neigt dazu ![]() , und die Grenze wird dann sein
, und die Grenze wird dann sein ![]() .
.
Als Fazit bleibt uns:![]() .
.
Überwachung.
Wir hätten „Kalkül“ direkt auf die Funktion anwenden können, ohne zuerst den gemeinsamen Faktor von Zähler und Nenner zu dividieren.
Mal schauen![]()
Tatsächlich können wir den „Kalkül“ direkt auf die Funktion anwenden, ohne zuerst eine „Vorbereitung“ darauf zu treffen.
Wir werden nun einige Beispiele für die Berechnung von Grenzwerten mit trigonometrischen und Exponentialfunktionen geben, um das Obige zu veranschaulichen.
Betrachten wir die Funktion ![]() , auf alle setzen
, auf alle setzen ![]() , außer
, außer 
Erinnern: ![]() bedeutet zum Beispiel das
bedeutet zum Beispiel das![]() , Wo
, Wo ![]() ,
, ![]() .
.
Setzen wir diesen Wert von x in die obige ursprüngliche Gleichung ein, erhalten wir: 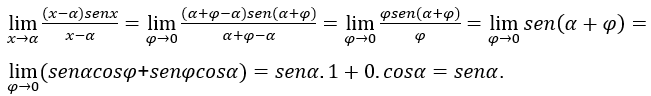
Dann, ![]() und
und ![]() sind unabhängig von
sind unabhängig von ![]() es ist das
es ist das![]() , während
, während ![]() .
.
Ein weiteres Beispiel: Betrachten Sie die Funktion![]() auf alle setzen
auf alle setzen ![]() , außer
, außer ![]() .
.
- Lassen Sie uns die berechnen
- Die Substitution vornehmen
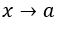 für zum Beispiel,
für zum Beispiel, 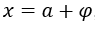 , mit
, mit 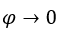 ,
, 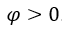 . Wir haben:
. Wir haben: 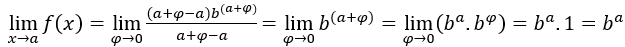 , weil die
, weil die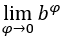 ist 1 und
ist 1 und 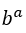 Egal ob
Egal ob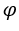 .
.
Lassen Sie uns nun die Grenze der zu Beginn angegebenen Funktionen berechnen, um die Werte der angegebenen Grenzen zu bestätigen.
- Lassen Sie uns rechnen
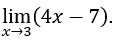
Wie![]() , können wir zB,
, können wir zB, ![]() ,
, ![]() und
und ![]() und wir bleiben übrig
und wir bleiben übrig![]()
- Lassen Sie uns rechnen
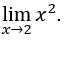
Wie![]() , können wir zB,
, können wir zB, ![]() ,
, ![]() und
und ![]() und wir bleiben übrig
und wir bleiben übrig![]()
Wie aus den obigen “Berechnungen” ersichtlich ist, waren die in den vorherigen Beispielen angegebenen Grenzen korrekt.
Wir werden nur einen Satz über Grenzen demonstrieren, um den hier gezeigten Kalkül zu veranschaulichen.
Satz. Wenn ![]() und
und ![]() sind dann irgendwelche Konstanten
sind dann irgendwelche Konstanten ![]() .
.
Berechnen Sie einfach die Grenze, indem Sie zum Beispiel tun, ![]()
![]() und
und ![]()
Bleib bei: ![]() , dann
, dann ![]() gegen Null tendiert, da
gegen Null tendiert, da ![]() tendiert gegen null.
tendiert gegen null.
Die dargestellte „Rechnung“ ist von ungeheurer Einfachheit.
In diesem Fall gibt es keinen Zweifel, dass die Grenze ist![]() .
.
Wir werden nun den vorgestellten „Grenzwertkalkül“ verwenden, um Grenzwerte von Funktionen unter verschiedenen Umständen zu berechnen.
- Lassen Sie uns rechnen
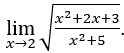
Wie ![]() , so können wir zb,
, so können wir zb, ![]() ,
, ![]() und
und ![]()
Bleib bei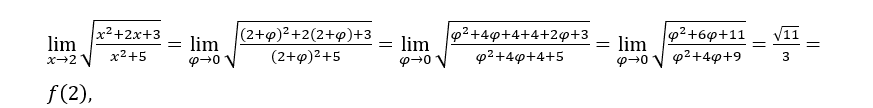 , einmal
, einmal ![]() neigt zu 11 und
neigt zu 11 und![]() tendiert zu 9.
tendiert zu 9.
- Lassen Sie uns rechnen
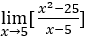 .
.
Wie x → 5, so können wir zb, ![]() ,
, ![]() und
und ![]()
Bleib bei 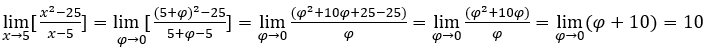
Es wird beobachtet, dass es nicht notwendig war, die Funktion „vorzubereiten“, um den „Kalkül“ anzuwenden, das heißt, es war nicht notwendig, die Funktion als zu schreiben ![]() und, schließlich, wie
und, schließlich, wie ![]()
- Lassen Sie uns rechnen
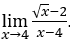 .
.
In Fällen mit Radikalen, zu denen eine reelle Zahl addiert oder subtrahiert wird, wenn die direkte Substitution des Werts von ![]() führt zu Unbestimmtheit
führt zu Unbestimmtheit ![]() wir müssen die Gleichung aufstellen, denn die direkte Anwendung des „Kalküls“ hebt die Unbestimmtheit nicht auf, wie wir weiter unten sehen werden.
wir müssen die Gleichung aufstellen, denn die direkte Anwendung des „Kalküls“ hebt die Unbestimmtheit nicht auf, wie wir weiter unten sehen werden.
Was in diesem Fall passiert ist, dass Zähler und Nenner einen gemeinsamen Faktor haben, der aber nur ausgedrückt wird, wenn wir entweder den Zähler durch den Nenner oder den Nenner durch den Zähler dividieren.
Dies wird derzeit in der Mathematik als Rationalisierung übersetzt.
Sehen wir uns das obige Beispiel an: Wenn wir den Nenner durch den Zähler dividieren, da der Exponent von ![]() im Nenner ist 1 und der Exponent von
im Nenner ist 1 und der Exponent von ![]() im Zähler ist kleiner, das heißt, es ist wert
im Zähler ist kleiner, das heißt, es ist wert ![]() wir werden haben:
wir werden haben: ![]() und ersetzen, werden wir haben
und ersetzen, werden wir haben 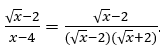 .
.
Damit können wir den gemeinsamen Faktor von Zähler und Nenner ausdrücken.
Die andere Möglichkeit besteht darin, den Zähler durch den Nenner zu dividieren, aber in diesem Fall müssen wir das Gleiche tun, da der Exponent von ![]() im Zähler ist kleiner als der Exponent von
im Zähler ist kleiner als der Exponent von ![]() Nenner und muss daher mit einem Faktor in multipliziert werden
Nenner und muss daher mit einem Faktor in multipliziert werden ![]() seinen Exponenten mindestens gleich dem Exponenten des Nenners zu machen.
seinen Exponenten mindestens gleich dem Exponenten des Nenners zu machen.
Das ist die berühmte Rationalisierung, die wir machen.
Wir werden zuerst die Berechnung durchführen, ohne Vorbereitung.
Wie ![]() , können wir zB,
, können wir zB, ![]() ,
,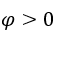 und
und ![]() .
.
Bleib bei![]() Wir beobachten die Notwendigkeit, zu rationalisieren, da die Grenze noch unbestimmt ist, wann
Wir beobachten die Notwendigkeit, zu rationalisieren, da die Grenze noch unbestimmt ist, wann ![]() im Zähler und Nenner, tendenziell
im Zähler und Nenner, tendenziell ![]()
Wir werden dann multiplizieren und dividieren durch![]() , und wir werden mit sein
, und wir werden mit sein ![]()
Jetzt führen wir die Berechnung durch und bereiten die Funktion vor, bevor wir sie anwenden.
![]() .
.
Wie die direkte Substitution von 4 zu Unbestimmtheit führto ![]() bedeutet, dass Zähler und Nenner einen gemeinsamen Teiler haben
bedeutet, dass Zähler und Nenner einen gemeinsamen Teiler haben ![]() oder
oder ![]()
Da es sich in diesem Fall um eine Wurzel minus einer reellen Zahl handelt, wird der gemeinsame Faktor durch Rationalisierung „freigegeben“.
Bevor wir den Grenzwert berechnen, multiplizieren und dividieren wir Zähler und Nenner der Funktion mit![]()
Bleib bei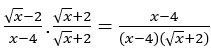 . In dieser Funktion können wir den Kalkül bereits anwenden. Mal schauen:
. In dieser Funktion können wir den Kalkül bereits anwenden. Mal schauen: 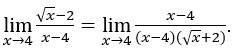
Wie ![]() wir können zb,
wir können zb,![]() ,
, ![]() und
und ![]()
Bleib bei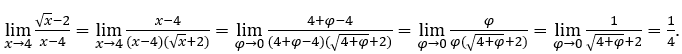
1.2 SEITLICHE GRENZEN
In Fällen, in denen eine Funktion für jede reelle Zahl außer einer reellen Zahl definiert ist![]() , wenn wir seine Grenze berechnen, wobei die unabhängige Variable dazu tendiert
, wenn wir seine Grenze berechnen, wobei die unabhängige Variable dazu tendiert![]() , Wie in den oben angegebenen Beispielen spielt es keine Rolle, ob wir verwenden
, Wie in den oben angegebenen Beispielen spielt es keine Rolle, ob wir verwenden ![]() wie viel
wie viel ![]() ,
, ![]() und
und ![]() , da es auf alle Nummern links und rechts davon eingestellt ist
, da es auf alle Nummern links und rechts davon eingestellt ist ![]() .
.
Und natürlich ist dies keine Satzfunktion.
Wenn links oder rechts von einer Zahl keine Funktion definiert ist ![]() und wir müssen seine Grenze mit berechnen
und wir müssen seine Grenze mit berechnen ![]() pflegen
pflegen ![]() , wir müssen den Wert von verwenden
, wir müssen den Wert von verwenden ![]() wie es der Fall sein mag.
wie es der Fall sein mag.
Wann ![]() und das tun wir
und das tun wir ![]() , oder
, oder ![]() ,
, ![]() und
und ![]() , dann
, dann![]() zeigt an, dass
zeigt an, dass ![]() auf etwas oder jemanden zukommen
auf etwas oder jemanden zukommen ![]() für Werte größer als
für Werte größer als ![]() , und, daher nähert es sich
, und, daher nähert es sich ![]() Nach rechts.
Nach rechts.
Die Berechnung erfolgte mit![]() ist daher die Grenze, wann
ist daher die Grenze, wann ![]() neigt dazu
neigt dazu ![]() Nach rechts.
Nach rechts.
Es handelt sich also um die rechte Grenze.
Wir gebrauchen ![]() um die linke Grenze zu berechnen.
um die linke Grenze zu berechnen.
Wir wissen, dass die Grenze nur existiert, wenn die einseitigen Grenzen existieren und gleich sind.
- Lassen Sie uns rechnen
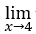 √x – 4.
√x – 4.
Wir wissen, dass die Funktion nur für existiert![]() , das ist,
, das ist, ![]()
Daher gibt es keine linke Grenze und daher existiert die betreffende Grenze nicht.
Aber es gibt die rechte Grenze, die durch Einsetzen berechnet werden kann ![]() pro
pro ![]() ,
, ![]() und
und ![]()
![]()
![]()
- Lassen Sie uns die einseitigen Grenzen berechnen.
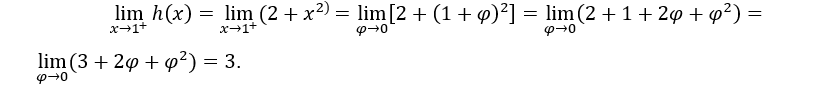
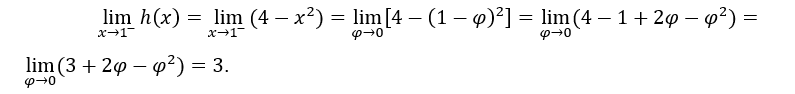
Wie sind sie gleich,![]()
In der obigen Berechnung haben wir gemacht ![]() , die rechte Grenze zu berechnen und
, die rechte Grenze zu berechnen und ![]() um die linke Grenze zu berechnen.
um die linke Grenze zu berechnen.
Wir berechnen die Grenze von ![]() definiert von
definiert von
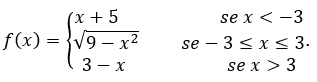
- Lassen Sie uns rechnen
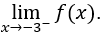
Wir müssen dann rechnen,![]()
Dann machen wir das, ![]() ,
, ![]() und
und ![]()
- Lassen Sie uns rechnen
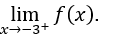
Wir müssen dann rechnen,![]()
Dann machen wir das, ![]() ,
, ![]() und
und ![]()
Bleib bei
![]()
- Lassen Sie uns rechnen
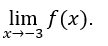
Wie ![]() dann ist die
dann ist die ![]() ist nicht vorhanden.
ist nicht vorhanden.
- Lassen Sie uns rechnen
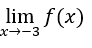 .
.
Wir müssen dann rechnen,![]()
Dann machen wir das, ![]() ,
, ![]() und
und ![]()
Bleib bei
![]()
- Lassen Sie uns rechnen
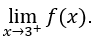
Wir müssen dann rechnen, ![]()
Wir werden dann tun,![]() ,
, ![]() und
und ![]()
Bleib bei
![]() Lassen Sie uns rechnen
Lassen Sie uns rechnen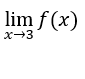
Wie![]() , dann
, dann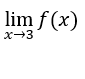 existiert und gleich Null ist.
existiert und gleich Null ist.
1.3 UNENDLICHE GRENZEN
Diejenigen, deren Funktionswerte ohne Begrenzung steigen oder fallen, wenn die unabhängige Variable immer näher an eine feste Zahl herankommt, können durch die hier vorgestellte Grenzwert-„Berechnung“ gleichermaßen gelöst werden, mit dem Vorteil, sich nicht um Theoreme kümmern zu müssen.
Bevor wir die „Berechnung“ anwenden, erinnern wir uns an die folgenden Situationen:
![]()
- Lassen Sie uns die folgende Grenze berechnen
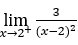 .
.
Wie![]() , wir müssen tun
, wir müssen tun ![]() ,
, ![]() und
und ![]()
Bleib bei ![]() .
.
- Rechnen wir jetzt
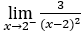 .
.
Wie![]() , wir müssen tun
, wir müssen tun ![]() ,
, ![]() und
und ![]()
Bleib bei![]() .
.
- Lassen Sie uns rechnen
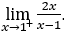 .
.
Wie ![]() , wir müssen tun
, wir müssen tun ![]() ,
, ![]() und
und ![]()
Bleib bei ![]() , weil der Zähler gegen 2 tendiert, während der Nenner durch positive Werte gegen Null tendiert.
, weil der Zähler gegen 2 tendiert, während der Nenner durch positive Werte gegen Null tendiert.
- Rechnen wir jetzt
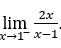 .
.
Wie ![]() , wir müssen tun
, wir müssen tun ![]() ,
, ![]() und
und ![]()
Bleib bei ![]() , weil durch negative Werte der Zähler gegen 2 und der Nenner gegen null strebt.
, weil durch negative Werte der Zähler gegen 2 und der Nenner gegen null strebt.
- Lassen Sie uns rechnen
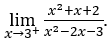
Wie![]() , wir müssen tun
, wir müssen tun ![]() ,
, ![]() und
und ![]()
Bleib bei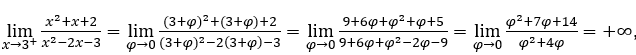 weil der Zähler bei positiven Werten gegen 14 tendiert, während der Nenner gegen Null tendiert.
weil der Zähler bei positiven Werten gegen 14 tendiert, während der Nenner gegen Null tendiert.
- Rechnen wir jetzt
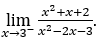
Wie ![]() , wir müssen tun
, wir müssen tun ![]() ,
, ![]() und
und ![]()
Bleib bei![]() , da der Zähler bei negativen Werten gegen 14 tendiert, während der Nenner bei negativen Werten gegen Null tendiert, da
, da der Zähler bei negativen Werten gegen 14 tendiert, während der Nenner bei negativen Werten gegen Null tendiert, da ![]() geht bei positiven Werten immer gegen Null.
geht bei positiven Werten immer gegen Null.
In diesem Fall ist der Nenner ![]() wann immer
wann immer ![]() , Es ist wie
, Es ist wie ![]() , der Nenner ist immer negativ.
, der Nenner ist immer negativ.
- Lassen Sie uns rechnen
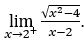
Wie ![]() , wir müssen tun
, wir müssen tun ![]() ,
, ![]() und
und ![]()
Wir sind wie
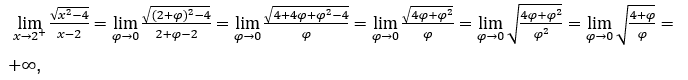 weil der Zähler bei positiven Werten gegen 2 und der Nenner gegen null tendiert.
weil der Zähler bei positiven Werten gegen 2 und der Nenner gegen null tendiert.
- Lassen Sie uns rechnen
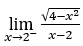
Wie ![]() , wir müssen tun
, wir müssen tun ![]() ,
, ![]() und
und ![]()
Bleib bei 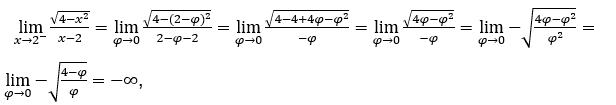 , weil der Zähler bei positiven Werten gegen -2 und der Nenner gegen Null tendiert.
, weil der Zähler bei positiven Werten gegen -2 und der Nenner gegen Null tendiert.
In diesen beiden Fällen konnten wir das![]() ins Radikal, weil es immer positiv ist.
ins Radikal, weil es immer positiv ist.
- Lassen Sie uns rechnen
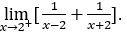
Wie![]() , wir müssen tun
, wir müssen tun ![]() ,
, ![]() und
und ![]()
Bleib bei![]() weil der Zähler bei positiven Werten gegen 4 tendiert, während der Nenner gegen Null tendiert.
weil der Zähler bei positiven Werten gegen 4 tendiert, während der Nenner gegen Null tendiert.
Notiz Wir hätten den Wert von direkt ersetzen können![]() in der ursprünglichen Gleichung.
in der ursprünglichen Gleichung.
- Lassen Sie uns rechnen
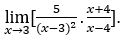
Wie![]() , wir müssen tun
, wir müssen tun ![]() ,
, ![]() und
und ![]()
Bleib bei ![]() , weil der Zähler bei negativen Werten gegen 35 tendiert, während der Nenner bei negativen Werten gegen null tendiert, da negativ für ist < 1.
, weil der Zähler bei negativen Werten gegen 35 tendiert, während der Nenner bei negativen Werten gegen null tendiert, da negativ für ist < 1.
- Lassen Sie uns rechnen
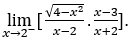
Wie ![]() , wir werden das machen
, wir werden das machen ![]() ,
, ![]() und
und ![]()
Bleib bei 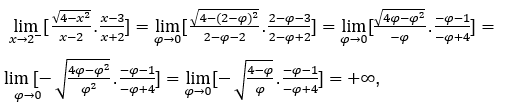 , weil der Zähler dazu tendiert
, weil der Zähler dazu tendiert![]() und der Nenner tendiert dazu
und der Nenner tendiert dazu![]() durch positive Werte.
durch positive Werte.
1.4 GRENZEN IN DER UNENDLICHKEIT
Ebenso wie bei den bisher erwähnten Grenzen stellt auch die herangezogene Literatur keine Berechnung von Grenzen im Unendlichen dar, sondern wertet die Funktion nur dann aus, wenn die unabhängige Variable unendlich zunimmt oder abnimmt.
Das Bewertungsergebnis wird als Schwellenwert verwendet.
Mal schauen.
Die Funktion gegeben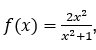 , wir schreiben zu
, wir schreiben zu ![]() die werte
die werte![]() und so weiter, wodurch es unbegrenzt wachsen kann. Die entsprechenden Funktionswerte werden
und so weiter, wodurch es unbegrenzt wachsen kann. Die entsprechenden Funktionswerte werden
![]()
Wir beobachten das wann ![]() wächst und positive Werte annimmt, nähern sich die Funktionswerte 2.
wächst und positive Werte annimmt, nähern sich die Funktionswerte 2.
Wenn eine unabhängige Variable ![]() wächst unendlich, durch positive Werte schreiben wir
wächst unendlich, durch positive Werte schreiben wir ![]() dem gegebenen Beispiel wurde der Schluss gezogen, dass
dem gegebenen Beispiel wurde der Schluss gezogen, dass 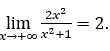
Wie oben zu sehen ist, wurde aus dem gegebenen Beispiel keine Grenzberechnung der Funktion präsentiert, sondern es wurde nur beobachtet, dass, as ![]() erhöht, um positive Werte näherte sich die Funktion 2.
erhöht, um positive Werte näherte sich die Funktion 2.
Dieser Wert 2 wurde dann als Grenzwert der Funktion verwendet.
Wir werden im Folgenden die „Berechnung“ der Funktionsgrenze vorstellen, wenn die unabhängige Variable dazu tendiert![]() oder der
oder der ![]()
In Fällen wo ![]() , wir werden das machen
, wir werden das machen ![]() und
und ![]() , denn, wie wir oben gesehen haben, wann
, denn, wie wir oben gesehen haben, wann ![]() geht bei positiven Werten gegen Null,
geht bei positiven Werten gegen Null, ![]() neigt dazu
neigt dazu ![]() , und damit,
, und damit, ![]() neigt dazu
neigt dazu ![]()
In Fällen wo ![]() , wir werden das machen
, wir werden das machen 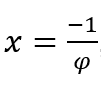
![]() und
und ![]() , denn, wie wir oben gesehen haben, wenn φ bei positiven Werten gegen Null geht
, denn, wie wir oben gesehen haben, wenn φ bei positiven Werten gegen Null geht![]() ,
,![]() dazu neigt, und damit,
dazu neigt, und damit,![]() neigt dazu
neigt dazu ![]() .
.
- Lassen Sie uns rechnen
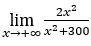 .
.
Wie 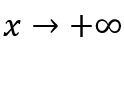 , wir werden das machen
, wir werden das machen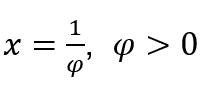 und
und ![]()
Bleib bei ![]() weil der Zähler gegen 2 tendiert und der Nenner gegen 1.
weil der Zähler gegen 2 tendiert und der Nenner gegen 1.
- Lassen Sie uns rechnen
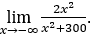
Wie ![]() , wir werden das machen
, wir werden das machen ![]() und
und ![]()
Bleib bei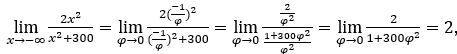 , weil der Zähler gegen 2 tendiert und der Nenner gegen 1.
, weil der Zähler gegen 2 tendiert und der Nenner gegen 1.
- Lassen Sie uns rechnen
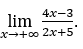
Wie ![]() , wir werden das machen
, wir werden das machen![]() und
und ![]()
Bleib bei![]() , weil der Zähler gegen 4 tendiert und der Nenner gegen 2.
, weil der Zähler gegen 4 tendiert und der Nenner gegen 2.
- Lassen Sie uns rechnen
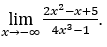
Wie ![]() , wir werden das machen
, wir werden das machen![]()
![]() und
und ![]()
Bleib bei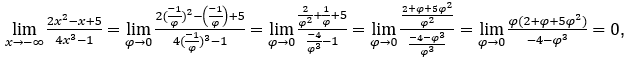 weil der Zähler gegen Null tendiert und der Nenner gegen -4 tendiert.
weil der Zähler gegen Null tendiert und der Nenner gegen -4 tendiert.
- Lassen Sie uns rechnen
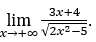
Wie ![]() , wir werden das machen
, wir werden das machen ![]() und
und ![]()
Bleib bei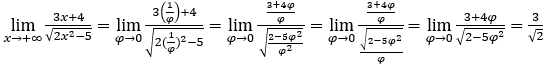 , weil der Zähler gegen 3 tendiert und der Nenner gegen √2 tendiert.
, weil der Zähler gegen 3 tendiert und der Nenner gegen √2 tendiert.
- Lassen Sie uns rechnen
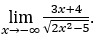
Wie ![]() , wir werden das machen
, wir werden das machen![]()
![]() und
und ![]()
Bleib bei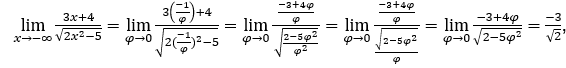 , weil der Zähler gegen -3 tendiert und der Nenner gegen √2 tendiert.
, weil der Zähler gegen -3 tendiert und der Nenner gegen √2 tendiert.
- Lassen Sie uns rechnen
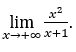
Wie ![]() , wir werden das machen
, wir werden das machen![]() und
und ![]()
Bleib bei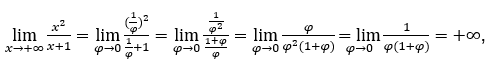 weil der Zähler 1 ist und der Nenner bei positiven Werten gegen Null geht.
weil der Zähler 1 ist und der Nenner bei positiven Werten gegen Null geht.
- Lassen Sie uns rechnen
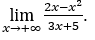
Wie ![]() , wir werden das machen
, wir werden das machen ![]() =
= ![]() φ > 0 und φ → 0.
φ > 0 und φ → 0.
Bleib bei 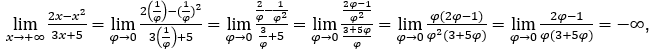 weil der Zähler bei positiven Werten gegen -1 und der Nenner gegen Null tendiert.
weil der Zähler bei positiven Werten gegen -1 und der Nenner gegen Null tendiert.
- Lassen Sie uns rechnen
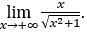
Wie ![]() , wir werden das machen
, wir werden das machen![]() und
und ![]()
Bleib bei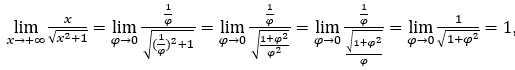 weil der Zähler 1 ist und der Nenner gegen 1 geht.
weil der Zähler 1 ist und der Nenner gegen 1 geht.
- Rechnen wir jetzt
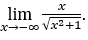
Wie![]() , wir werden das machen
, wir werden das machen![]() und
und ![]()
Bleib bei 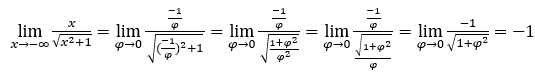 , weil der Zähler -1 ist und der Nenner gegen 1 tendiert.
, weil der Zähler -1 ist und der Nenner gegen 1 tendiert.
- Lassen Sie uns rechnen
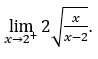
Wie ![]() , wir müssen tun
, wir müssen tun ![]() ,
, ![]()
Bleib bei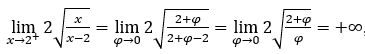 , weil der Zähler dazu tendiert
, weil der Zähler dazu tendiert ![]() und der Nenner geht für positive Werte gegen Null.
und der Nenner geht für positive Werte gegen Null.
- Rechnen wir jetzt
Wie ![]() , wir werden das machen
, wir werden das machen ![]() und
und ![]()
Bleib bei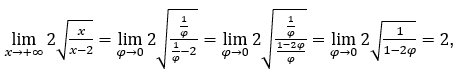 weil der Zähler gegen 2 tendiert und der Nenner gegen 1.
weil der Zähler gegen 2 tendiert und der Nenner gegen 1.
Überwachung.
Die Berechnung von Grenzen im Unendlichen kann beispielsweise nicht auf trigonometrische Funktionen angewendet werden, da einige von ihnen in einem bestimmten Intervall variieren und andere je nach betrachtetem Wert unbegrenzt zunehmen oder abnehmen.
Wenn wir zum Beispiel versuchten, die zu berechnen![]() , wir würden alle Werte des Bereichs unendlich oft durchlaufen
, wir würden alle Werte des Bereichs unendlich oft durchlaufen ![]() , denn für alle
, denn für alle ![]() ,
, ![]() , das heißt, wir würden zu keinem bestimmten Wert gelangen.
, das heißt, wir würden zu keinem bestimmten Wert gelangen.
Tatsächlich sind Polynomfunktionen oder Funktionen, die durch Verhältnisse zwischen Polynomen ausgedrückt werden, am besten zum Anwenden von Grenzen geeignet.
2. KOMMENTARE
1) Die vorgestellte Grenzwertberechnung ergab sich aus der Identifikation des Ausdrucks ![]() tendiert zu einer bestimmten Zahl
tendiert zu einer bestimmten Zahl ![]() mit Gleichberechtigung
mit Gleichberechtigung ![]() , oder
, oder ![]() , mit
, mit![]() e
e ![]() , seit, wirklich, wann
, seit, wirklich, wann ![]() ,
, ![]() und
und ![]() dazu neigen
dazu neigen ![]() und damit,
und damit, ![]() neigt dazu
neigt dazu ![]()
Bei Grenzen im Unendlichen die Substitution für den Ausdruck![]() neigt dazu
neigt dazu ![]() er war
er war ![]() , und die Substitution für den Ausdruck
, und die Substitution für den Ausdruck ![]() neigt dazu
neigt dazu ![]() er war
er war ![]() , mit
, mit ![]() und
und ![]()
Die Substitution macht am meisten Sinn, denn eigentlich wann![]() , immer für positive Werte,
, immer für positive Werte,![]() neigen
neigen![]() und
und ![]() neigt dazu
neigt dazu ![]() , verursacht
, verursacht ![]() wirklich dazu neigen
wirklich dazu neigen ![]() Oder der
Oder der ![]() , wie es der Fall sein mag.
, wie es der Fall sein mag.
Wenn wir ersetzen, in dem Fall, wo![]() neigt dazu
neigt dazu![]() Oder der
Oder der ![]() die
die ![]() por,
por, ![]() oder
oder ![]() und
und ![]() , das Ergebnis wäre das gleiche.
, das Ergebnis wäre das gleiche.
Ein Beispiel.
- Lassen Sie uns rechnen
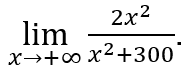
Wir werden das machen ![]() und
und ![]()
Bleib bei
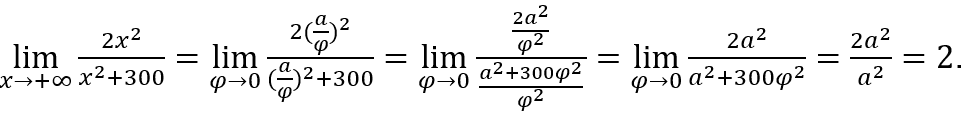
2. Wie in den verschiedenen Beispielen zu sehen ist, ist der vorgestellte „Grenzwertkalkül“ ziemlich „fließend“ und direkt anwendbar, ohne dass die Notwendigkeit besteht, Theoreme zu konsultieren oder die Funktion vor der Durchführung der Berechnung zu „organisieren“, außer wenn wir rationalisieren müssen.
Diese Tatsache bringt viel Ruhe bei der Berechnung des Grenzwertes einer Funktion, denn die vorgestellte „Berechnung“ ist eine wahre Synthese dieses Themas.
Beispielsweise kann „Berechnung“ direkt über der Funktion verwendet werden![]() , ohne die Notwendigkeit, es zu organisieren, das heißt, es auszudrücken als
, ohne die Notwendigkeit, es zu organisieren, das heißt, es auszudrücken als 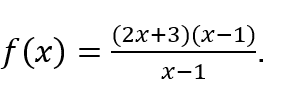
Mal schauen ![]()
Wie![]() , können wir zB,
, können wir zB, ![]() und
und ![]()
Bleib bei
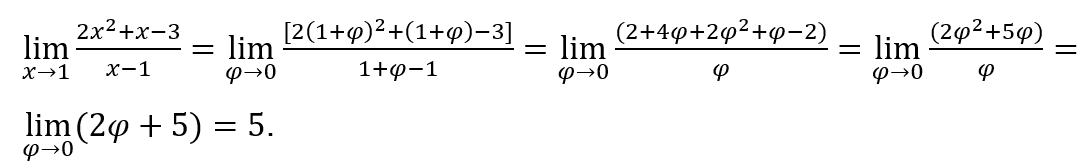
Dies bringt einen enormen Vorteil gegenüber der derzeitigen Darstellung dieses Themas, das, abgesehen davon, dass es keine Grenzwertberechnung präsentiert, an der immensen Menge an Theoremen, die bei der „Auswertung“ von Grenzwerten berücksichtigt werden müssen, ziemlich „festgefahren“ ist, wie z sowie der „Organisationen“, die an den Funktionen durchgeführt werden müssen, bevor ihre Grenze „abgeschätzt“ wird.
3) Ich möchte der vorgestellten „Grenzwertrechnung“ einige Wertungen praktischer Natur hinzufügen.
a) Es ist nur sinnvoll, den Grenzwert einer Funktion in der Nähe eines Wertes zu berechnen, für den sie nicht definiert ist.
Wenn die Funktion für einen bestimmten Wert definiert ist, das heißt, wenn die Funktion für einen bestimmten Wert existiert, macht es keinen Sinn, die Grenze in der Nähe dieses Werts zu berechnen, da wir wissen, wie viel die Funktion bei diesem Wert wert ist.
Zum Beispiel sein![]()
Diese Funktion ist für alle definiert ![]() , es existiert für alle
, es existiert für alle ![]()
Daher wäre es unangemessen, beispielsweise zu berechnen,, ![]() , da die Funktion existiert für
, da die Funktion existiert für ![]() , das heißt, warum diese Grenze berechnen, wenn wir einfach ersetzen können
, das heißt, warum diese Grenze berechnen, wenn wir einfach ersetzen können ![]() um 3 Zoll
um 3 Zoll ![]() und wir erhalten den Wert der Funktion bei 3, das heißt,
und wir erhalten den Wert der Funktion bei 3, das heißt, ![]()
Damit haben Hunderte von Übungen keine Daseinsberechtigung mehr.
Offensichtlich sind die in diesem Artikel betrachteten Funktionen von ![]()
b) Unter Verwendung des Grenzwertbegriffs machen wir hier eine Beobachtung über die Stetigkeit einer Funktion.
Nach Letholds Kalkülbuch (1994) wird die Definition einer stetigen Funktion an einem Punkt wie folgt übersetzt:
Dizemos que a função ![]() é contínua no número a se e somente se as seguintes condições forem satisfeitas:
é contínua no número a se e somente se as seguintes condições forem satisfeitas:
(i) ![]() existe;
existe;
(ii) ![]() existe;
existe;
(iii) ![]()
Se uma ou mais de uma dessas condições não forem verificadas em ![]() , a função
, a função![]() será descontínua em
será descontínua em ![]()
So definiert Lima (1978) die Kontinuität einer Funktion:
Uma função ![]() diz-se contínua no ponto
diz-se contínua no ponto ![]() quando é possível tornar
quando é possível tornar ![]() arbitrariamente próximo de
arbitrariamente próximo de ![]() desde que se tome
desde que se tome ![]() suficientemente próximo de
suficientemente próximo de ![]()
Em termos precisos, diremos que ![]() é contínua no ponto
é contínua no ponto ![]() quando, para todo
quando, para todo ![]() dado arbitrariamente, pudermos achar
dado arbitrariamente, pudermos achar ![]() tal que
tal que ![]() e
e ![]() impliquem
impliquem ![]()
Wir wissen, dass, wenn eine Funktion in einem bestimmten Intervall definiert ist, das heißt, wenn sie für jede Zahl in einem bestimmten Intervall existiert, es keinen Sinn macht, den Grenzwert dieser Funktion für eine Zahl in diesem Intervall zu berechnen, da wir dies können werten Sie einfach die Funktion für jede Zahl in diesem Bereich aus.
Einfacher ausgedrückt: wenn eine Funktion, repräsentiert durch nur einen Ausdruck, durch nur einen Satz, für eine bestimmte Zahl existiert ![]() dann ist es völlig unnötig, den Grenzwert der Funktion für zu berechnen
dann ist es völlig unnötig, den Grenzwert der Funktion für zu berechnen ![]() , da wir einfach den Wert der Funktion in berechnen können
, da wir einfach den Wert der Funktion in berechnen können ![]()
Wenn wir diese Grenze berechnen würden, wie wir es oben getan haben, wäre es natürlich so![]()
Wie oben erwähnt, ist es nur sinnvoll, den Grenzwert einer Funktion um eine Zahl herum zu berechnen, für die sie nicht definiert ist.
Wenn wir also Funktionen analysieren, die nur durch einen Ausdruck repräsentiert werden, sagen wir, dass eine Funktion für eine bestimmte Zahl existiert ![]() , bedeutet, dass diese Funktion in begrenzt ist
, bedeutet, dass diese Funktion in begrenzt ist ![]() diese Grenze ist der Wert der Funktion in
diese Grenze ist der Wert der Funktion in ![]() , und damit brauchen wir den Grenzwert dieser Funktion nicht in dieser Zahl zu berechnen
, und damit brauchen wir den Grenzwert dieser Funktion nicht in dieser Zahl zu berechnen ![]()
Wendet man dies auf die obige Definition einer kontinuierlichen Funktion an, werden die Punkte (ii) und (iii) der Definition unnötig, da in Punkt (i) angegeben ist, dass![]() existiert.
existiert.
Daher gilt für Funktionen, die durch „nur einen Ausdruck“ repräsentiert werden, die einfache Aussage, dass es sich um die Funktion handelt![]() , ist in einer Zahl definiert
, ist in einer Zahl definiert ![]() das heißt, die einfache Aussage, dass
das heißt, die einfache Aussage, dass ![]() existiert, reicht aus, um zu schließen, dass die Funktion bei dieser Zahl stetig ist
existiert, reicht aus, um zu schließen, dass die Funktion bei dieser Zahl stetig ist![]()
Ebenso verlieren mit dieser Beobachtung über stetige Funktionen Hunderte von Übungen ihre Daseinsberechtigung.
Beispiel: let die Funktion ![]() die für jede reelle Zahl definiert ist, also für jede existiert
die für jede reelle Zahl definiert ist, also für jede existiert ![]() real.
real.
Daher ist es nicht erforderlich, die Grenze von zu berechnen![]() für keinen Wert von
für keinen Wert von ![]() , weil in diesem Fall in definiert werden
, weil in diesem Fall in definiert werden ![]() ist gleichbedeutend mit einer Begrenzung
ist gleichbedeutend mit einer Begrenzung ![]() und dass diese Grenze gleich dem Wert der Funktion in ist
und dass diese Grenze gleich dem Wert der Funktion in ist ![]() betrachtet.
betrachtet.
Dann die Funktion ![]() ist für alle stetig
ist für alle stetig![]()
3. FAZIT
Oben haben wir gezeigt, dass die Grenzentheorie in der Tat in Bezug auf eine Grenzenberechnung defizient ist und sich daher mit einer Reihe von Argumenten umgibt, die auf der Definition von Grenzen basieren, um diese Lücke zu füllen.
Wir stellen dann die „Berechnung des Grenzwerts einer Funktion“ vor und zeigen, dass sie alle genannten Themen synthetisiert und daher direkt anwendbar ist.
Wir hoffen, zu einem besseren Verständnis eines so grundlegenden Themas der Mathematik beizutragen.
VERWEISE
IEZZI, Gelson; MURAKAMI, Carlos et all. Fundamentos de Matemática Elementar, vol. 8, 1991.
LEITHOLD, Louis. O Cálculo com Geometria Analítica, vol. 1, 1994.
LIMA, Elon Lages. Curso de Análise, vol. 1, 1978.
MUNEM, Mustafa A. e FOULIS, David J. Cálculo, vol. 1, 1982.
[1] Bachelor-Abschluss in Mathematik von der Universität Brasília.
Gesendet: Juni 2021.
Genehmigt: August 2021.