ORIGINAL ARTICLE
SOUZA JÚNIOR, Elias Pereira De [1]
SOUZA JÚNIOR, Elias Pereira De. “Difference between squares” in the Pythagorean Theorem. Revista Científica Multidisciplinar Núcleo do Conhecimento. Year 05, Ed. 10, Vol. 06, pp. 05-13. October 2020. ISSN: 2448-0959, Access link: https://www.nucleodoconhecimento.com.br/mathematical-olympiads/pythagorean-theorem
ABSTRACT
This article aims to show applications of the content of the Pythagorean Theorem in the construction of knowledge in the classroom, focusing on an algebraic technique for the “difference between squares”. First, the paper explores the introduction and application of the Pythagorean Theorem as new classroom content within a contextualized example. Therefore, the Theorem was demonstrated by the teacher, and students are led to question and reason alternative methods of obtaining results in addition to the classic Pythagorean Theorem demonstrated. Soon, some methods began to emerge, possibilities of resolutions for the initial example, one of these forms was the geometric notion of Theorem, however, the students continued their investigations. The crucial part of the class was the reasoning of the algebraic procedure that drew attention in a different way during the students’ investigations, it was the “difference between squares” as a solution to the Theorem within the set of natural numbers, since, not all sets numerical values met the relation. And at this point, reflections are created for students on how to explore mathematics and investigate it in different ways, as the intention was to explore the diversity of mathematics and sharpen students’ sensitivity to make new discoveries. The Pythagorean Theorem is well known and applied, it can be easily found in several mathematical literature, but to make students transcend formulas and procedures is to teach how to think.
Keywords: Education, modeling, teaching, Pythagoras, learning.
1. INTRODUCTION
The theme presented in this article was chosen due to an experience developed in the classroom, which aimed to explore the ways of relating and applying the Pythagorean Theorem in its algebraic and geometric form according to the study of triangles with an emphasis on the right triangle, exploring the idea of the Pythagorean Theorem in the student’s view, thus managing to form various possibilities for solving problems related to the Theorem, among them the “difference between squares.
However, this article also sought to report an experience lived at school, through the collection of information and observed calculations, seeking to understand the importance of the construction of knowledge by the student, thus making a difference in the teaching-learning process. Because, in the formation of students’ knowledge, it becomes indispensable to direct, investigative or even ludic practice in the classroom, in which it is believed that challenges, doubts or certainties arise from this practice if this is the path that the student wants to follow , how to do and what not to do to proceed, thus seeking the ideal understanding in problem solving. In this class 36 students from the first grade of high school participated in class “A” of Colégio Sagrada Família, Brasília DF
Therefore, several study perspectives are applied to the Pythagorean Theorem. Then, a simple proposal will be shown in which the Theorem is interpreted, relating it to the difference between squares. Thus, resulting in an interesting fact to be shown, including from the point of view of education.
1.1 THE LESSON PROPOSAL AND THE PYTHAGORAS THEOREM
To instigate the student to seek the solution of a problem or even to encourage research in the classroom, in different ways and possibilities, is to use a different methodology, that is, it is to apply Mathematical modeling. Consequently, it makes the classroom a field of research and practice soon, a more interesting and attractive place for students, and makes all the difference.
Mathematics Education goes beyond the traditional, it is to innovate by the diversity of actions allowing countless methods of teaching and learning. Because, to challenge the student to find solutions to problems alone is to open possibilities for new discoveries, like a thread in which mathematics is being discovered in various applicable contexts, D’ambrosio (1998), spoke about the ideas mentioned above.
So, the proposal made to the students was based on the following problem, a ladder of 12 meters in length is supported under a wall. The base of the stairs is 8 meters away from the wall as shown in the figure below. The students were then asked to determine the height of the wall.
Figure 1: application of the right triangle

Intuitively, students were instructed to try to find the value of the wall measurement using the fundamental definition for any triangle, a content that had already been studied in previous years, serving as a basis for introducing other contents. In general, to build a triangle it is possible to check the condition of the existence of triangles, which is the measure of either side is less than the sum of the measures of the other two and greater than the absolute value of the difference between these measures, applying a geometric pattern. The following pattern is observed:
Figure 2: Condition of existence of a triangle
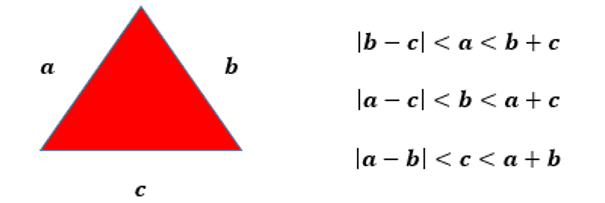
The students arrived at some possible and pertinent values to calculate the stair measure, as one side of the triangle. However, to apply the Pythagorean Theorem, it is necessary that the triangle has at least one of its angles measuring 90º. Therefore, the next step was to demonstrate the Pythagorean theorem.
1.2 DEMONSTRATION OF THE PYTHAGORAS THEOREM
In the learning process after the initial investigation of triangles and their existence, the next step was to sharpen the students’ curiosity to formalize some curiosities and initial conclusions. So, in this part of the class the students related several squares with their respective areas trying to find patterns with the mediation of the teacher. Soon, the students began to see the properties that Pythagoras used for the theorem, which is based on the sum of the areas of the polygons that form a figure constructed of congruent right triangles, that is, to compare the areas as shown in the following figures.
Figure 3 Demonstration of the Pythagorean Theorem
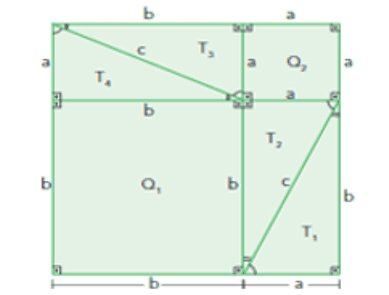
Figure 4 Demonstration of the Pythagorean Theorem
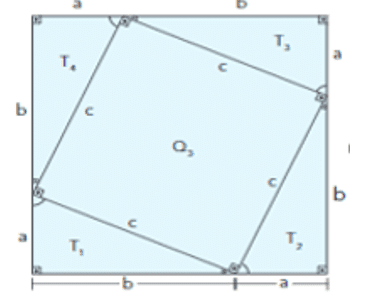
Consider that the 2 smallest sides of a triangle are called collectors and the longest side of a right triangle is the hypotenuse. Note that the figures were constructed using four congruent right-angled triangles equal to “a” and “b” and hypotenuse “c” forming larger squares with sides equal to (a + b). If the four congruent right triangles of the two figures are removed, the remaining figures have the same area. Therefore, there is
In figure 3:
- Sum of the areas of the four right triangles = (T1 + T2 + T3 + T4)
- Remaining area Q1 + Q2 = a2 + b2
In figure 4:
- Sum of the areas of the four right triangles = (T1 + T2 + T3 + T4)
- Remaining area = Q3 = c2
So, c2 = a2 + b2
This relationship can be applied to any right triangle. “C” being the largest side of the triangle called the hypotenuse, “a” and “b” the side of the triangle as shown above.
1.3 RESUMING THE INITIAL EXAMPLE
It became clear to students after the Theorem was demonstrated that the question is an application of the Pythagorean theorem, in which the sides are called catheters and the largest side of the triangle that is opposite the angle of is called the hypotenuse. Thus, the Pythagorean relationship can be written in this way:
(Hypotenuse) ² = (Cateto 1) ² + (cateto 2) ²
Figure 5: right triangle
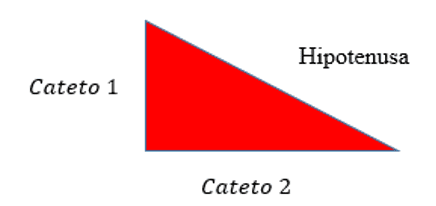
Therefore:
The students applied the above list as follows:
- The hypotenuse is equivalent to the ladder (12 m)
- The distance between the ladder and the wall is a leg (8 m)
- The height of the wall is the other side, in this case “x”
applying the theorem:
![]()
Subtracting 8² from both sides of the equality
![]()
![]()
At this point, a student asked a question about the subtraction of squares: – “can we only solve this subtraction after solving the squares?”
Hence, investigations of other ways of subtracting squares began.
1st solution:
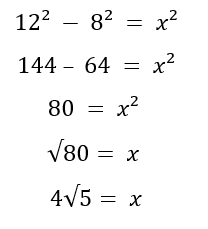
2nd solution:
A pattern was observed by the teacher along with the students. See below:
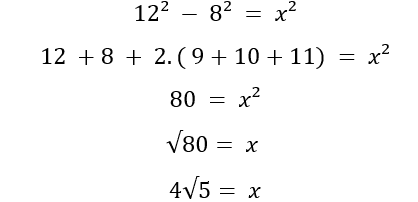
At this point, a pattern was noticed for the difference between squares, in which the numbers belong to the set of natural numbers, in the form
![]()
Example:
a = 23 and b = 19, applying …
Taking the test:
![]()
Equality is true for numbers
![]()
After testing the operations on the set of natural numbers, it was also applied to some other sets, such as the set of integers that also worked and for the real ones, which in the latter case some numbers failed to establish true equality, thus fixing this application for natural numbers.
2. PROOFING THE RELATIONSHIP
Ratio for difference between squares:
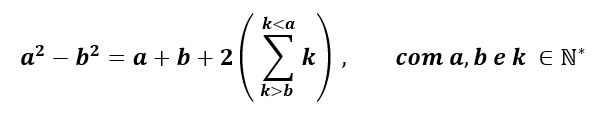
Consider
a2 + b2 with a and b belonging to natural numbers greater than zero, considering a> b, we have the following proposition for a and b:
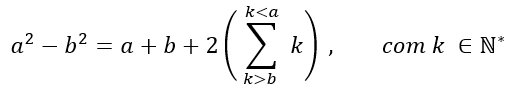
Soon if
![]()
Then
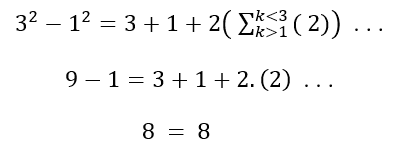
Now, considering m as any natural number.
If a and b are true, for a and b, ∈
![]()
, then a = b + m, will also be true, for m ∈
![]()
Taking m = 1, for
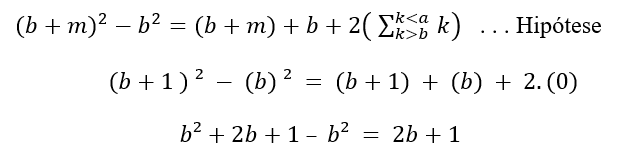
Soon,
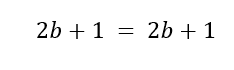
Therefore, the relationship
![]()
, is valid for any
![]()
How I wanted to demonstrate!
This demonstration was promptly shown to students who were surprised by the application they had come up with, thus finding a different relationship to the Pythagorean Theorem in the “difference between squares”.
3. CONCLUSION
The aim of instigating students to find different ways to solve problems is to build knowledge using the competences and skills already acquired, providing the basis for new learning and discoveries. This article is an example of this, since basic instructions were given by the teacher, and the students were investigating ways to solve the problem.
What makes it more interesting, is that in the midst of investigations, there may be several ways to reach a result. Seeing these ways and guiding them makes mathematics education different and pleasant for students, thus justifying mathematical modeling.
Then, following the applications of the Pythagorean Theorem in the initial example, the teacher together with the students discussed the ways to solve the difference between squares, always making it clear that the construction of knowledge is the fundamental part of the class, the teacher is the mediator and students make discoveries.
In one of the processes in which the student raised the question about the calculation of the difference between squares in solving the problem, the class with the teacher was able to state that the observed method for subtracting squares is valid on some relevant points.
Therefore, the teacher demonstrated the applicability of the operation discovered within the set of natural numbers, solving the question of the applicability of the operation, making the method clear to the student and the class. Soon, we ended the question and solved other examples with the discovered method. The student’s return to the class was the following line “we have discovered a new formula, which is cool”, for a teacher of exact words there is no way that a line can be more striking like this.
The student asked for guidance to study summation and demonstrations. That a boy from the first grade of high school, the future development of this student I leave in the imagination of those who read this article.
4. REFERENCES
DANTE, Luiz Roberto. MATEMÁTICA: Contexto e Aplicações volume único / Luiz Roberto Dante, Fernando Viana – – 4. Edição – – São Paulo: Ática, 2018.
HEFEZ, Abramo. Indução Matemática:\induçãofinal”. Estilo OBMEP – Rio de Janeiro – Departamento de Matemática Aplicada Universidade Federal Fluminense, 2009. Disponível em: http://www.obmep.org.br/docs/apostila4.pdf. Acesso em: 04 maio de 2020. D’Ambrósio, U.Etnomatemática. São Paulo: Ática, 1998.
SANTOS. Marconi Coelho dos. Teorema de Pitágoras: suas diversas demonstrações. Campina Grande (PB):UEPB, 2011. 42f. Monografia (Especialização em Educação Matemática para professores do Ensino Médio) {Universidade Estadual da Paraíba, Centro de Ciências e Tecnologia, Campina Grande, 2011.
VIANA, M. C. V.; SILVA, C. M. Concepções de Professores de Matemática sobre a utilização da História da Matemática no processo de Ensino-Aprendizagem. In: ENCONTRO NACIONAL DE HISTÓRIA DA MATEMÁTICA, 9., 2007, Belo Horizonte. Pôsteres… Belo Horizonte, 2007. Disponível: https://www2.unifap.br/matematicaead/_les/2016/03/TCC-REVISADO.pdf Acesso em: 04 maio de 2020.
[1] Post-graduation in Mathematics.
Submitted: September, 2020.
Approved: October, 2020.