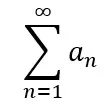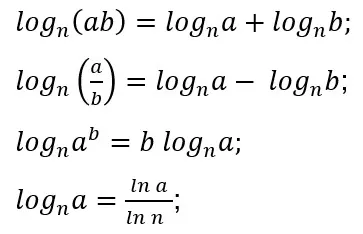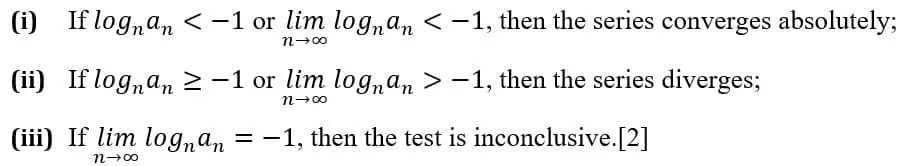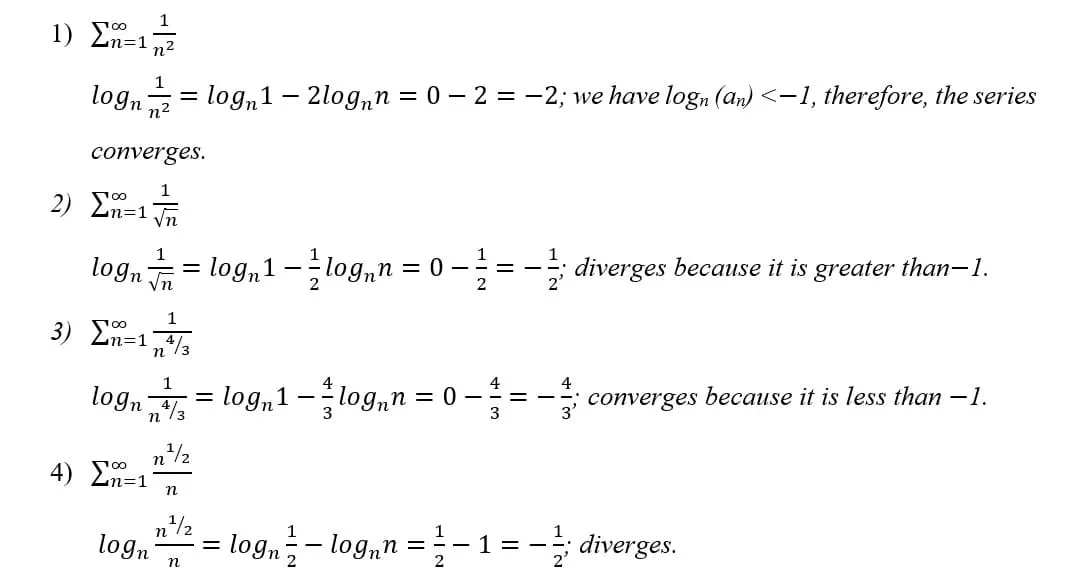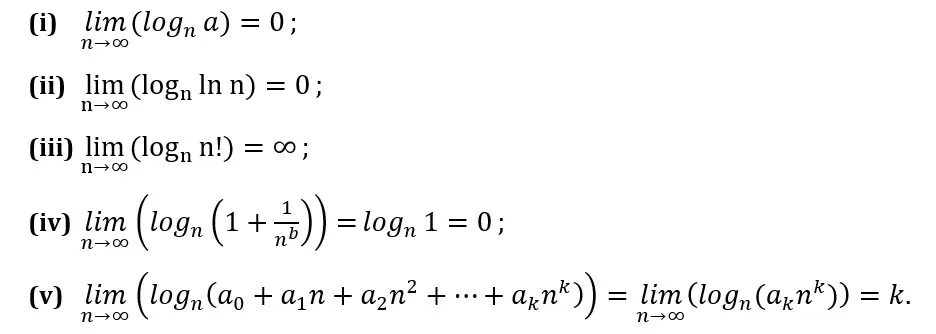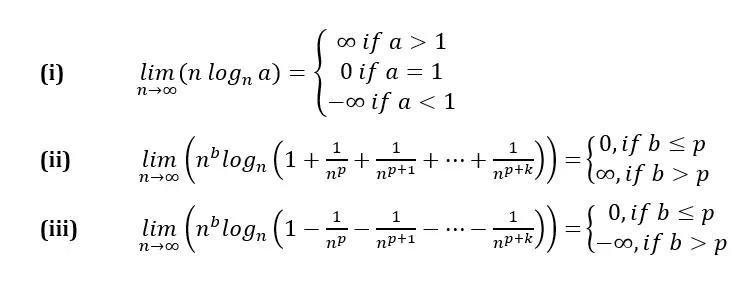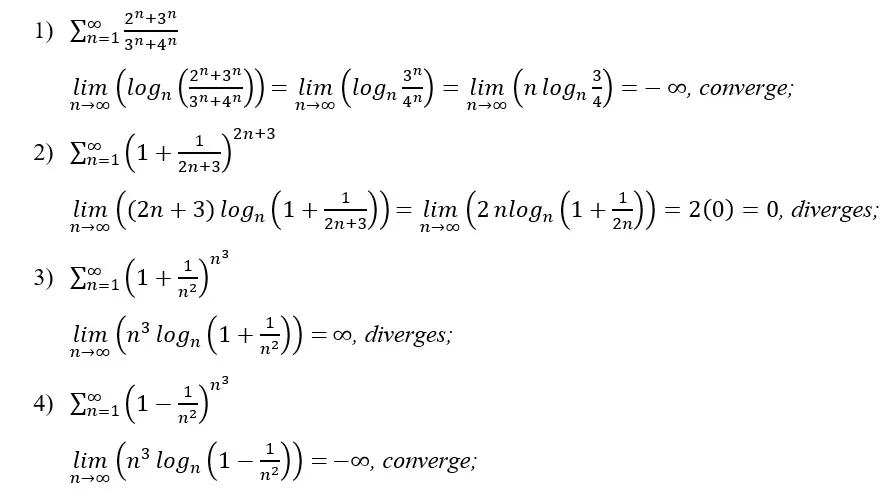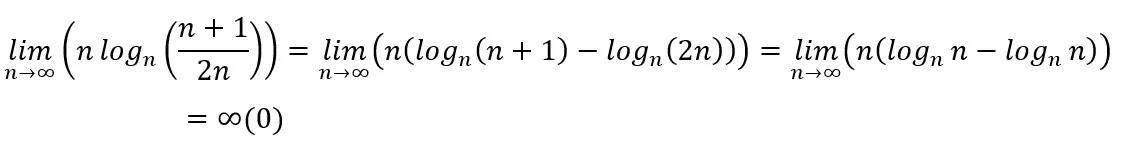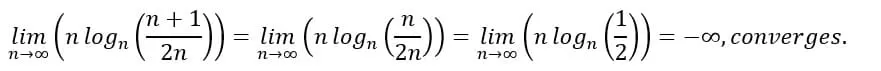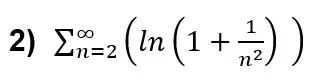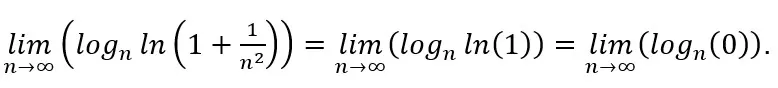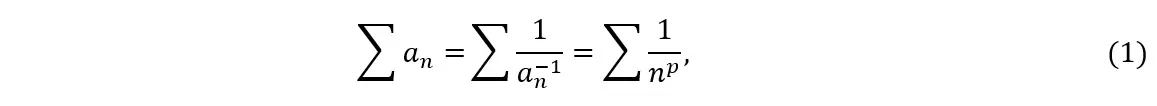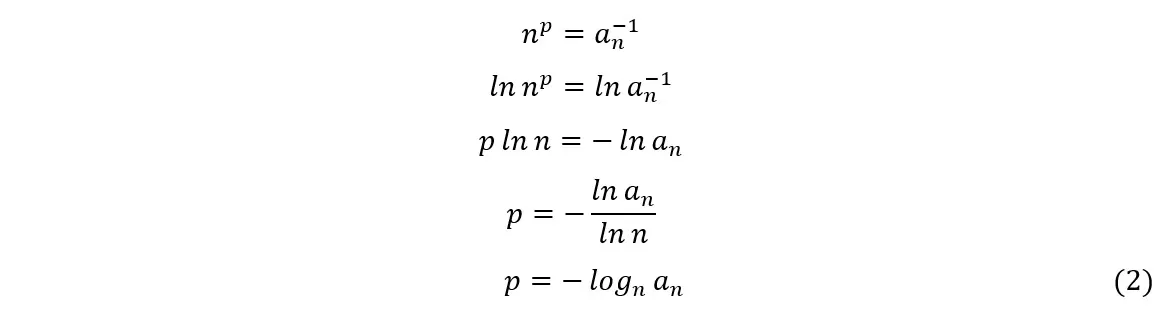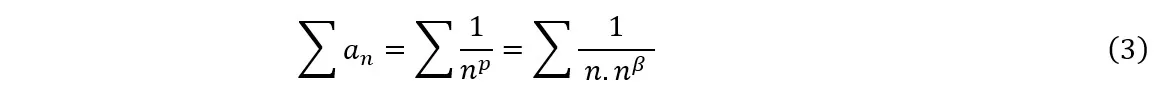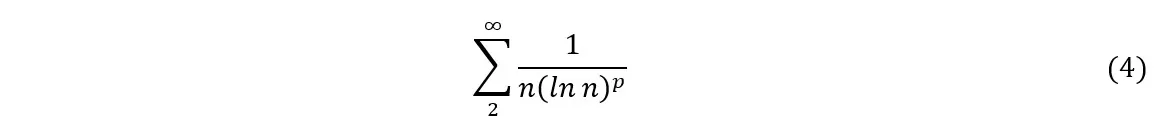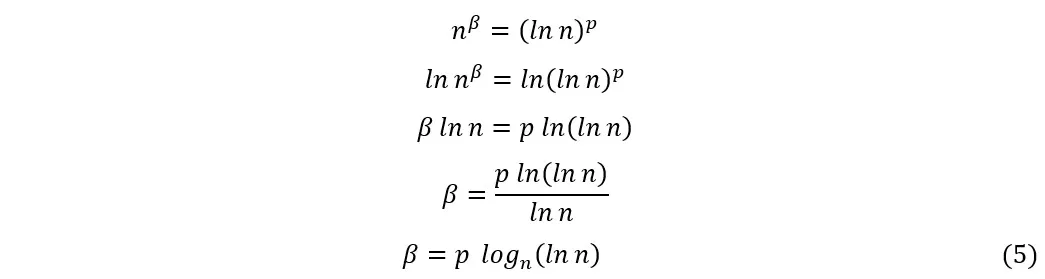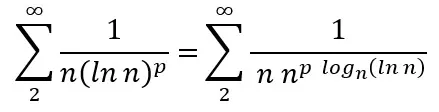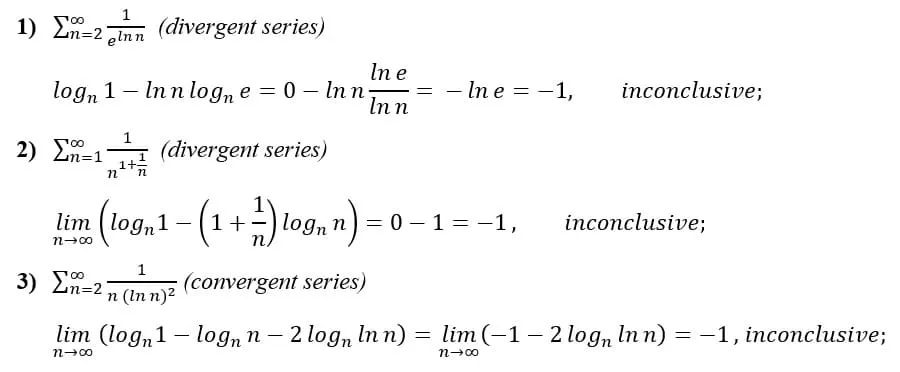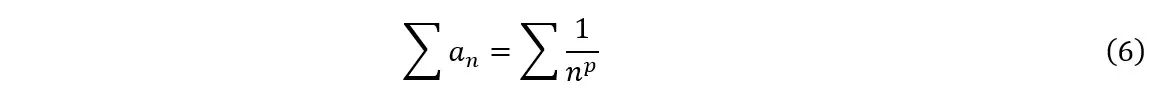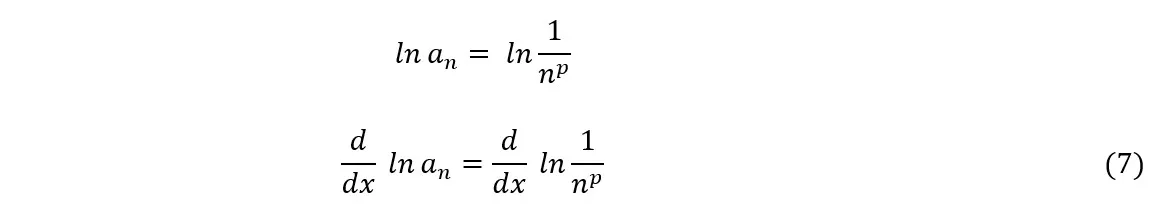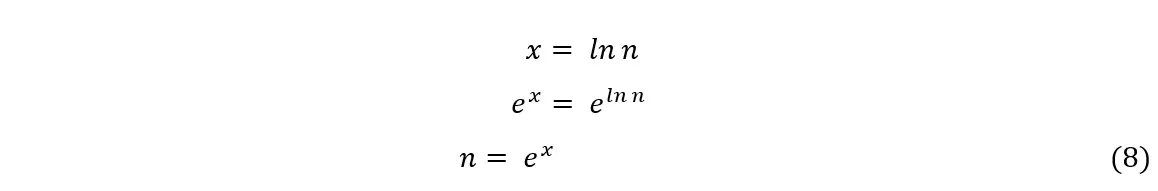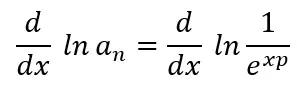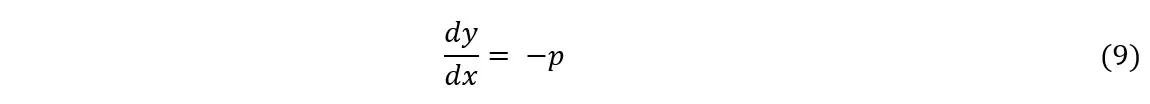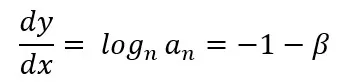MORAIS, Cláudio Marcelo [1]
MORAIS, Cláudio Marcelo. The nth logarithm test for checking the absolute convergence of series. Revista Científica Multidisciplinar Núcleo do Conhecimento. Year 08, Issue 09, Volume 01, pp. 78-97. September 2023. ISSN: 2448-0959, Access link: https://www.nucleodoconhecimento.com.br/mathematical-olympiads/nth-logarithm, DOI: 10.32749/nucleodoconhecimento.com.br/mathematical-olympiads/nth-logarithm
ABSTRACT
In this article, I present a test for absolute convergence of infinite numerical series using the concept of logarithm with base n indeterminate. Although there are cases where the current test is difficult to apply and others where inconclusive results may be obtained, it should be seen as an additional resource that mathematics students can use alongside the tests already available to verify the absolute convergence of a series.
Keywords: Convergence, Series, Test.
1. INTRODUCTION
In calculus courses, when encountering the study of infinite series, students are introduced to a variety of tests to determine whether a numerical series converges to a certain value or diverges. That is, whether the sum of its terms will tend towards a finite value (L) or towards positive or negative infinity when the number of terms (n) in the series also tends to infinity (∞).
An infinite series consists of a sequence of ordered terms, usually in decreasing order, summed together. An infinite series, or simply a series, can be expressed in the form:
Where the ellipses at the end indicate that the terms of the series continue in such a way that n tends to infinity. The series can also be expressed in a more compact manner using sigma notation:
Through the analysis of the general term 
we can determine whether the series converges or not. For this purpose, numerous convergence tests have been developed, such as the comparison test, ratio test, integral test, root test, etc. (Simmons, 1996). The purpose of this article is to present a test that serves as an additional option for mathematics students in determining the absolute convergence of an infinite numerical series.
2. LOGARITHM WITH BASE N
2.1 DEFINITION OF NTH LOGARITHM
The concept of logarithm was introduced by the Scottish mathematician John Napier in 1614 and can be considered one of the greatest scientific advancements of the 17th century, making life easier for those who needed to perform numerical calculations in a time when calculators were not yet available. In this sense, its importance is even compared to the advancement brought by the decimal number system developed by the Indians (Hobson, 1914). Although the advent of computers and electronic calculators has changed the way people perform calculations, the logarithm, studied as a function, still maintains its indispensable theoretical importance for mathematics and its applications (Simmons, 1996). The logarithmic function can be described in the form
where x is a positive real number, referred to as the argument, and
is a positive real number different from 1, referred to as the base of the logarithm. The value of
ultimately determines the type of logarithm: for 
, we have the logarithm with base two; for 
, we have the logarithm with base 3, and so on. Logarithms with base 10 and base
, iven their significance, receive special names: the logarithm with base 10 is called the common logarithm or decimal logarithm, while we refer to the base e logarithm as the natural logarithm or Napierian logarithm, to the logarithm base 
, where e is an irrational number approximately equal to 2.718281828.
We will define the logarithm with base
, or nth logarithm, of a number
, as the logarithm with an indeterminate base
. Thus, let
be a real number, we can write
Unlike logarithms with a specific base, it is not possible to obtain the value of the nth logarithm of a number, sinceis unknown. At first, this may not seem very useful; however, the intention here is to use the nth logarithm to perform operations on the general terms of the series, where n becomes the variable indexed by the sigma operator. Thus, we will attempt to implement a method to test whether a series converges or not, aiming to benefit from the operational properties of logarithms where possible.
2.2 OPERATIONS WITH NTH LOGARITHMS
The logarithm with base n follows the same operational properties as other logarithms, obeying the rules of product, quotient, power, and change of base, as follows:
3. CONVERGENCE TEST
3.1 DESCRIPTION OF THE TEST
From now on, we will propose a test for verifying the absolute convergence of series based on the use of the nth logarithm. Thus, given an infinite series of non-negative terms, we will start by finding the nth logarithm of its general term an and if the variable n still remains, we will calculate the limit of that logarithm, as n tends to infinity, if such a limit exists. That being said, the test will proceed as follows:
The application of the test without the need for limits will only occur in those rare cases where the general term of the series is composed only of powers of n with numerical exponents. In other cases, we will invariably have to resort to the use of limits. It is interesting to note that when we use the form logn(an) instead of the equivalent form ln (an)/ln n, we can often calculate the limit of the general term by applying logarithmic properties, avoiding falling into the indetermination of the type ∞/∞. However, in other instances, when calculating the nth logarithm of the general term, we may still arrive at some kind of indetermination, making it impossible to know the value of the limit. In these cases, it will be necessary to apply L’Hopital’s rule to the nth logarithm in the equivalent form ln (an)/ln n to eliminate the indetermination. However, this procedure is usually laborious and not recommended to proceed, as it is likely that one or more known tests will be more suitable for testing the convergence of the series.
3.2 SOME EXAMPLES OF TEST USAGE
3.2.1 DIRECT CALCULATION OF logn an
In simpler cases, the general term (an) is composed only of the variable n raised to some integer or fractional numerical power. Thus, it will not be necessary to calculate any limits to apply the convergence test.
3.2.2 CASES WHERE THE LIMIT OF logn an IS EASILY CALCULATED
Let’s now highlight some cases where the limits of the nth logarithm of the general term are relatively easy to calculate. i.e., we will consider cases where there is no indeterminacy in the calculation of the limits and where one of the following trivial results appears:
These results can be easily obtained by the student, since in (i) the value of the logarithm of a constant (a) tends to zero as n tends to infinity. In case (ii), where the constant is replaced by the natural logarithm of n, the value of ln n grows much slower than n, so the nth logarithm ends up also tending to zero. In case (iii), the opposite occurs, since n! grows too fast compared to n, causing the logarithm to tend to infinity. In (iv), the fraction tends to zero as n tends to infinity. Finally, in (v), the highest-degree term of the polynomial determines the final behavior of the limit as n tends to infinity. Let’s see some examples.
3.2.3 SOME REMARKABLE LIMITS
In the calculation of the limit of logn an the indetermination of the type (∞)(0). To handle this type of indetermination, below are some results that can be easily memorized and will allow us to apply the nth logarithm test to a large number of series in a straightforward manner. Let’s take a look:
In case (i), the limit is also easy to obtain since n grows asymptotically faster than
, as n tends to infinity. Thus, if a=1, which would make the logarithm equal to zero for all n, the logarithm will provide a positive or negative sign for the limit, depending on whether a is greater or less than 1. In (ii), although the behavior of the limit may not be as evident as in (i), it can be said that the exponent p is associated with how fast the limit tends to zero, while b is associated with how fast the limit tends to infinity. The same reasoning applies to case (iii). Let’s see some examples:
3.3 SOME OBSERVATIONS
(i) There are cases where a simple change in the order of operations can eliminate an indetermination. Let’s see an example
In a first attempt, we apply the logarithmic property of the quotient before calculating the limit, thus reaching an indetermination:
On another path, we first calculate the limit within the parentheses and then use the result seen in item 3.2.3 (i), and we verify that the series converges:
(ii) In some situations, when calculating the limit of 
, applying logarithmic operational properties, we may arrive at logn0 or at some indetermination, such as the difference between infinities, the product of infinity by zero, the quotient between infinities, the quotient between zeros, or the ratio between zero and infinity. However, this does not necessarily mean that the limit does not exist. It only means that the nth logarithm test is not a practical way to determine the convergence or not of the series because to do that, it would be necessary to apply L’Hopital’s rule to the nth logarithm in its form ln(an)/ln(n), including any other algebraic manipulations that may be necessary. In these cases, we will often find an existing test that is less cumbersome to apply. For example, we know that the following series converges to approximately 1.29686:
Applying the nth logarithm test, working only with logarithmic properties, we arrive at the following result:
However, after applying L’Hopital’s rule to ln(an)/ln(n) and performing some operations involving limits, we find that:
Therefore, the series converges as expected. The convergence of this series can be more easily verified by applying the comparison test with a limit.
4. DISCUSSION OF THE TEST
4.1 DEDUCTION
The present test basically consists of performing the comparison test with the series 
using the nth logarithm, therefore, it is expected to obtain a calculation ease where the operational properties of logarithms (see section 2.2) can be used, either through the direct application of those properties or in conjunction with the notion of the limit of a function. To begin our derivation, let’s consider the cases where it is possible to directly calculate the logarithm of the general term (see 3.2.1). First, let’s write the general term as the inverse of a power of n:
Where n is an integer and p is a real number. From the above equalities, we have:
Substituting (2) into (1), we have:
As we know (Simmons, 1996), if p>1, the series converges. If p≤ 1, the series diverges. Finally, substituting p for — in these inequalities and multiplying both sides by 
, we have that the series:
4.2 WHEN THE TEST IS INCONCLUSIVE
In section 3.2.1, we saw the cases in which logn an is calculated directly. However, as we saw shortly after, we often still have the variable n remaining after calculating the nth logarithm of the general term of a given series. The use of the notion of a limit allows us to extend the applicability of the test because when we calculate the limit of the logarithm as n tends to infinity, we can use the value of this limit as the result of the test to determine whether the series converges or not (see section 3.1). However, this advantage comes at a certain cost, as there are cases where this limit provides us with a result that makes the test inconclusive.
Whether a series converges or not depends on how quickly the general term tends to zero (Simmons, 1996). If we arrange the series starting from those that converge most quickly to those that converge more slowly, then moving on to the series that diverge more slowly and going towards those that diverge faster, we can delimit the range between the series
as the interval where the transition from convergent to divergent series occurs. Let’s write the series in this interval using an auxiliary exponent β, such that β be a function of n, as follows:
So, if 
, then we have p>1 and the series converges. If 
, then we have p<1 and the series diverges. However, if 
, the convergence or divergence of the series will depend on how fast β tends to zero, i.e., the series will converge as long as β tends to zero fast enough. For example, using the integral test (Simmons, 1996), it can be verified that the following series diverges for p=1 and converges for p>1:
Calculating the exponent β for this series, we have:
Substituting (5) into (3) and equating to (4), we obtain:
As 
calculated in (5) is equal to zero for all p, we conclude that
for all p. However, as we know, for certain values of p the series converges, and for others, it diverges. Thus, we can see that the nth logarithm test is inconclusive in these cases [3], as there can be both convergent and divergent series for which the test results in —1. Let’s see some examples:
5. THE NTH LOGARITHM AS A DERIVATIVE
One way that can be very interesting for students to visualize the behavior of a series is through the use of graphs with logarithmic scales. In these graphs, series whose general terms are formed by powers of n com
with exclusively numerical exponents appear as lines, and the faster a series diverges, the shallower the slope of that line will be. Thus, series that diverge rapidly give rise to lines that approach more horizontal lines when compared to lines drawn from series that diverge more slowly. On the other hand, the faster a series converges, the steeper its line will be on the graph, i.e., it will be closer to the vertical than others that converge more slowly. On the other hand, the graphs of series whose general term presents exponents that are functions of the indexed variable n, generally initially appear as exponential curves, but as n tends to infinity, the graphs approach straight lines. The graph in Figure 1 below was plotted with axes on a natural logarithmic scale and illustrates some examples of what was said. In it, convergent series are indicated with cv and divergent ones with dv. At first glance, one can see how the two series on the left with exponent n converge quickly, approaching the vertical, while at the top, we have some diverging series.
Figura 1: Figure 1: Graph of Figure 2: Graph of ln an vs. ln n for some series
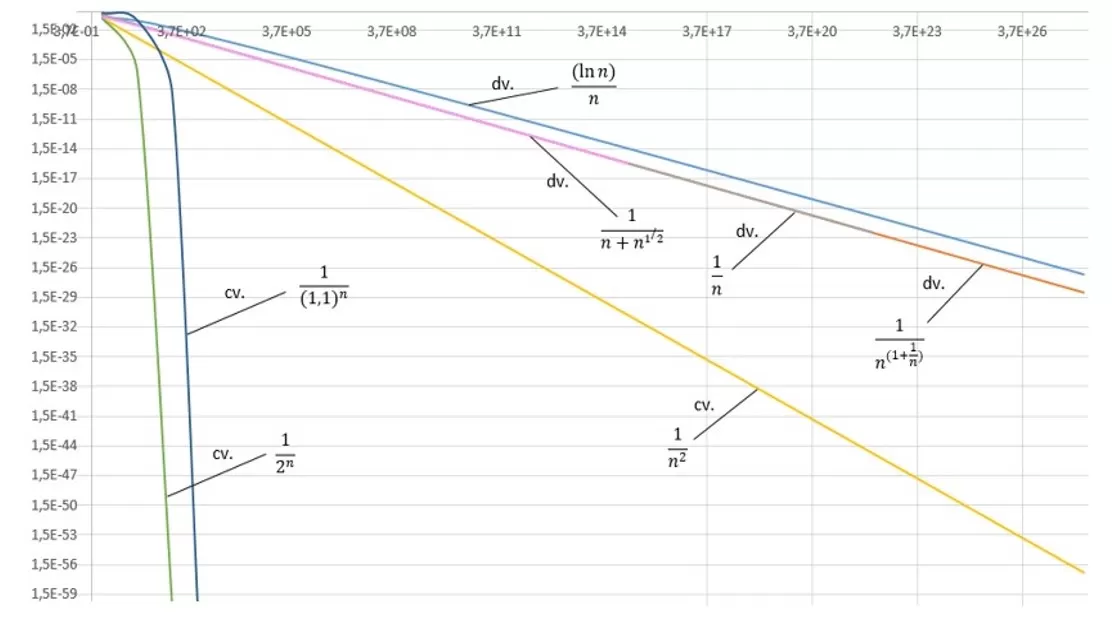
The faster the series diverges, the closer to horizontal its line will be on the graph. It can also be noted how two of the presented series, containing fractional exponents, diverge almost identically to the series with a general term of 1/n, showing how the fractional exponent influences the behavior of those series very little. I personally believe that this type of visualization can be a useful tool from an educational point of view when introducing the concept of convergence of a series. Let’s now see how the nth logarithm is related to this type of graph.
In Figure 2, we have the graph of ln an versus ln n, where the curve represents the progression of the terms of a series as n tends to infinity, and whose general form seen previously is given by:
Figure 2: Graph ln an vs. ln n
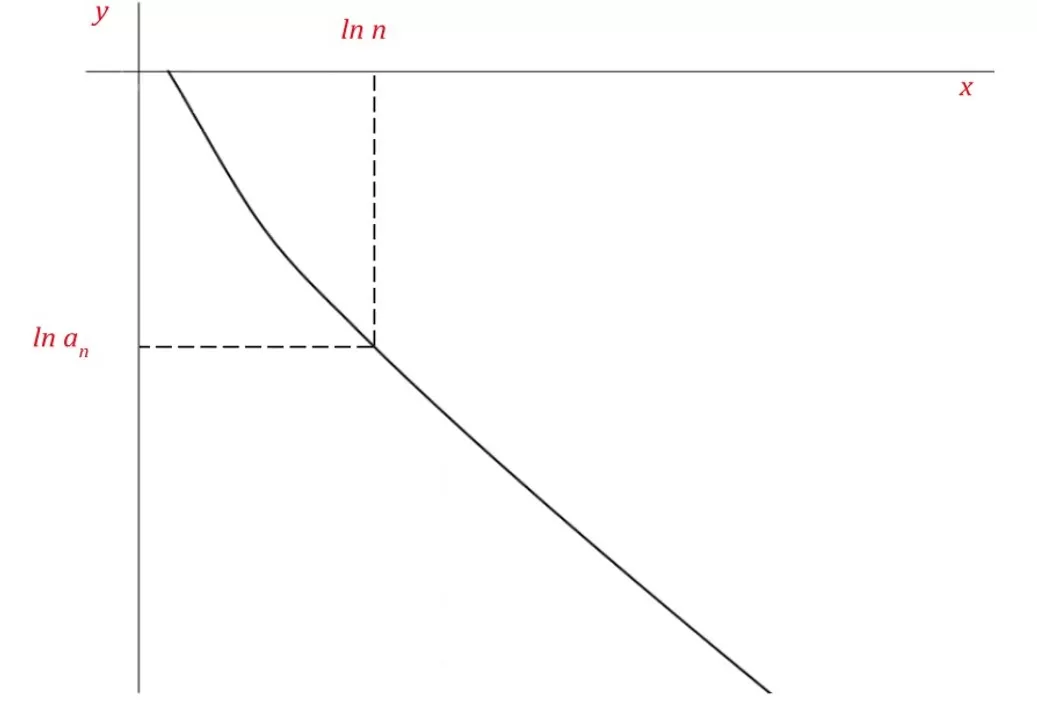
Taking the general term and calculating the derivative of the natural logarithm on each side, we have
From the graph, letting x = ln n, we have
Substituting (8) into (7), we get:
Finally, substituting ln an for y and calculating the derivative of the term on the right, we have:
However, we already know that the nth logarithm of the general term in (6) is
, so we can write:
In other words, the nth logarithm of the general term is equal to the derivative of the curve of the series on the graph of ln an x ln n. If we substitute p with 1+β, where β is a function of n, we can write:
When we calculate and find a real value δ, it means that the graph tends to a line with a slope of 
. Thus, as long
as does not tend to 
, the nth logarithm will provide us with the slope of the line that forms on the graph of ln an vs. ln n as ln n tends to infinity.
6. CONCLUSION
The use of the nth logarithm n to determine whether an infinite series converges absolutely or not can be an interesting alternative to existing methods, provided that the limit of the nth logarithm of the general term of the series, if necessary to calculate, can be obtained relatively easily. To apply the test, we can rely not only on the operational properties of logarithms but also on some basic known results. In cases where the indeterminacy persists, it can be eliminated by applying L’Hôpital’s rule to the nth logarithm of the general term in the form ln(an)/ln(n), however, in these cases, the effort usually may not be worthwhile, as there will likely be one or more known tests that can be used to determine convergence more quickly. When plotting the graph of a series with natural logarithmic scale axes, we can see that the nth logarithm of the general term at any point on the graph is nothing more than the derivative of the curve at that point.
REFERENCES
HOBSON, Ernest William. John Napier and the invention of logarithms. Cambridge: The University Press, 1914.
SIMMONS, George Finlay. Calculus with analytic geometry. 2. ed. New York: McGraw-Hill, 1996.
APPENDIX – FOOTNOTE
2.In section 4.2, we will further discuss this condition.
3. This case, although it presents only a specific family of series formed as the exponent p, varies, is sufficient to demonstrate the inconclusive nature of the test when its result obtained through the limit is, for . However, it would be interesting to show that the case n(ln n)p, with p>1, is not an exception, i.e., to show that there are other convergent series whose nth logarithm of the general term is , since finding divergent series is relatively easy.
[1] Bachelor of Physics from the Federal University of Minas Gerais (2000); Specialization in Instrumentation and Process Control by the National Service for Industrial Learning-SENAI; Professional qualification as an Electronics Technician by Instituto Monitor S/C Ltda. ORCID: 0009-0001-4633-3914. Currículo Lattes: http://lattes.cnpq.br/9333737637565760.
Submitted: July 10, 2023.
Approved: August 23, 2023.
