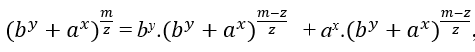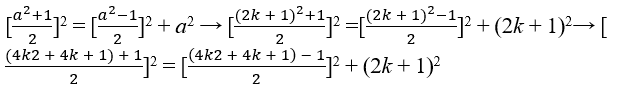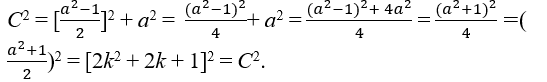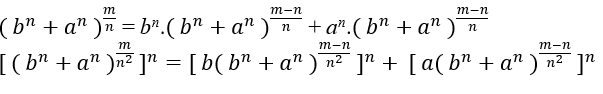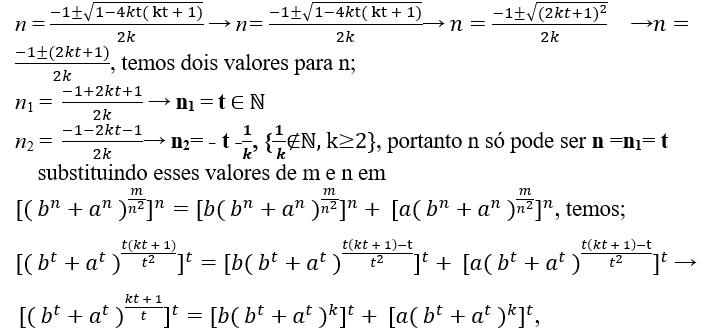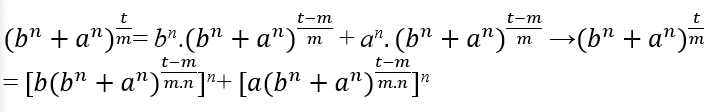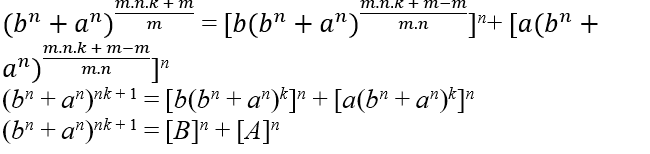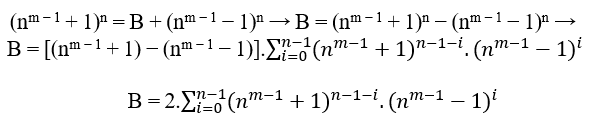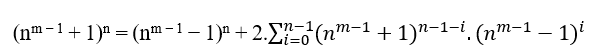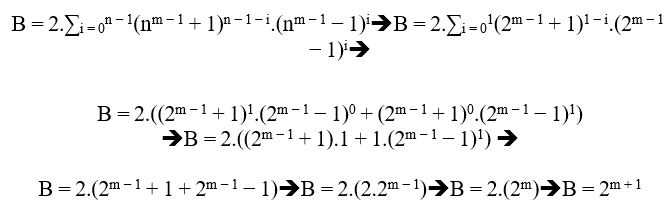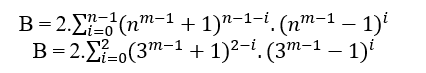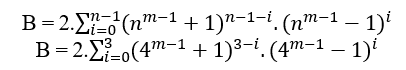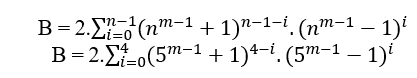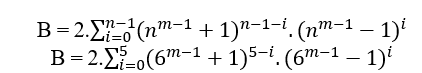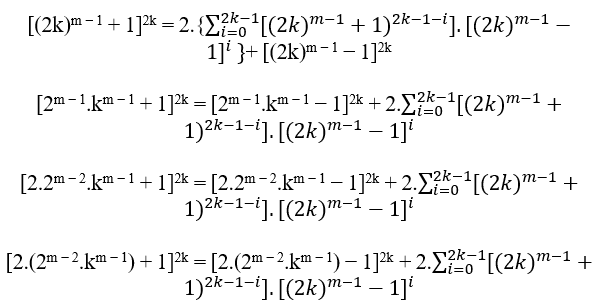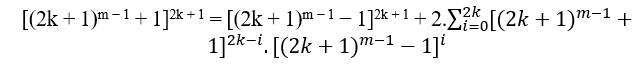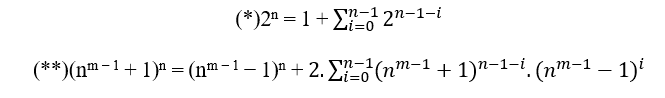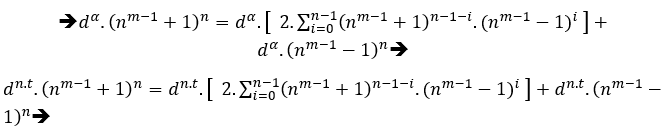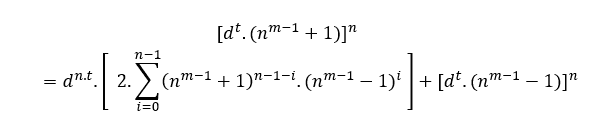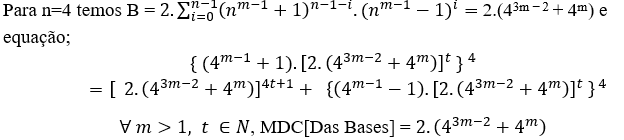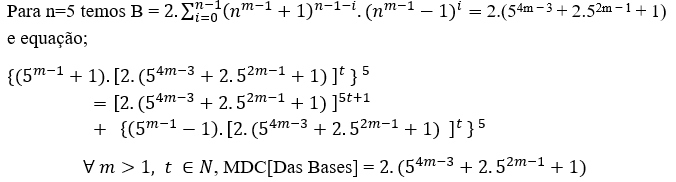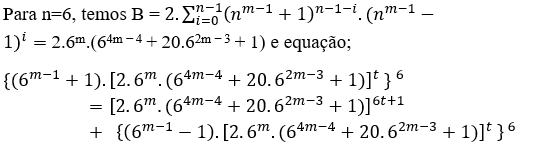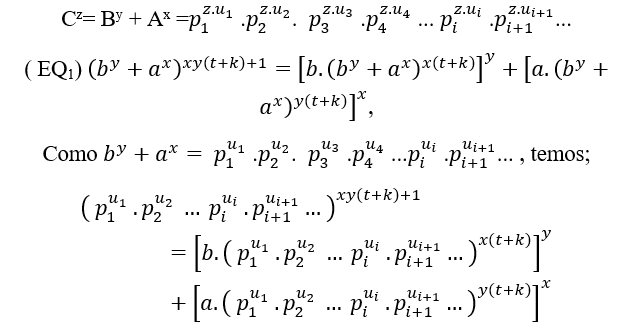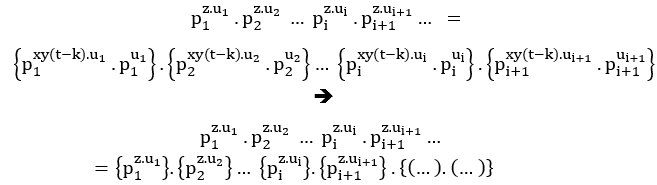Demonstration of the Beal Conjecture

ORIGINAL ARTICLE

SOUSA, Francisco Rafael Macena de ^[1]

SOUSA, Francisco Rafael Macena de. Demonstration of the Beal Conjecture. Revista Científica Multidisciplinar Núcleo do Conhecimento. 04 year, Ed. 11, Vol. 05, pp. 132-173. November 2019. ISSN: 2448-0959, Access Link: https://www.nucleodoconhecimento.com.br/mathematical-olympiads/beal-conjecture

STATEMENT OF CONJECTURE

If a^x + b^y = c^z , where a, b, c, x, y and z are positive integers and x, y, z ≥ 3, then a, b and c have a common prime factor, which means that a, b and c are divisible by the same prime number. Or, the equation a^{x +} b^{y =} c^z has no solution for positive integers with x, y, z ≥ 3 and mdc (a, b, c) = 1.

SUMMARY

This article contains demonstrations using principles of algebra and number theory, regarding the conjecture was announced by Andrew Beal a banker and enthusiast of number theory proposed a challenge for those who prove or present counterexample to such a problem that generalizes fermat’s Last Theorem, cⁿ = bⁿ + a^n, with n ≥ 3, this was demonstrated by the English mathematician Andrew Wiles using as a basis a conjecture made by mathematicians Yutaka Taniyama and Goro Shimu , this demonstration made by Wiles few mathematicians will understand by the high level or complexity, will also be used the Sebá Theorem, “Sebastião Vieira do Nascimento (Sebá)”, graduated in Economics by UFPB, master in engineering of the same, full professor of UFCG, its proven theorem is based on that c^m = bⁿ + aⁿ, with m and n prime among themselves, this is mdc (m, n) = 1 , the conjecture was proposed by Beal himself in 1993, but it was only well known even by the mathematical community in 1997 after R. D. Mauldin published the article a Generalization of Fermat’s Last Theorem: The Beal Conjecture and Prize Problem in the Journal Noticesofthe American Mathematical Society.

Keywords: Conjecture, Andrew Beal, Fermat’s Last Theorem.

1. INTRODUCTION

This article aims to prove the Conjecture of Beal, proposed by Andrew Beal a banker, entrepreneur, investor, poker player and amateur mathematician who has fascination in number theory, he challenged any mathematician in the world to prove or give a counterexample to his Conjecture that was proposed from 1993 to the present day, no demonstration was presented that generalizes the conjecture including fermat’s Last Theorem , this article contains mathematical knowledge that anyone who came to have the second grade of high school complete and has ease in mathematical properties is possible to understand the initial demonstrations, already for those who have a higher education in exact and beyond these will be easy to understand from start to finish, the conjecture is based on positive integers or solutions in natural numbers with the larger exponents equal to 3 (three) and their bases greater than or equal to 1 (one) , if so it will be demonstrated that actually the mdc (c, b , a) = C > 1, where this C is the common prime factor that divides a, b and c, with the ≤ b or a ≥ b, in such a way that it is possible to have as equation c^z = b^y + a^x, x, y, z ≥ 3,, exponents, contradictory case will possess as mdc (c, b , a ) = 1 and x, y, z ≥ 3, this is the only value that divides c, b, a is 1 (a), in other words a,b and c are primes between themselves.

To get to the demonstration it was necessary to create new theorems, but for the theorem to actually be valid as well as the conjecture must be proven in the course of the theorems are created from principles and properties in number theory, the biggest challenge in this article as any other that involves prime numbers those numbers that has only two dividers in the natural ones that is 1 (one) and himself (prime number) , because it is still something that the theory of numbers has not yet been able to find a faster way to factor giant numbers, however in number theory we have as hypothesis and also proven that any X a compound number, we can write – it X as a product of various powers of equal or distinct prime numbers, including when it has exponents 0 (zero) or 1 (one). The idea of this conjecture is simply to facilitate the encounter of prime factors.

2. BRIEF HISTORY TO CONJECTURA

2.1 FERMAT AND ITS THEOREM

It starts with Pierre Fermat who lived in 18th-century France, a civil servant in the French city of Toulouse, mathematics for him was his favorite pastime, the interesting thing is that Fermat had greater fame due to his customs of presenting to other mathematicians problems that challenged the greatest minds of the time, where they often left his contemporaries perplexed in an attempt to solve them. Fermat had the idea of creating a proposition similar to the famous Pythagoras theorem that is well known today in this century, but had no solutions in the naturals, this proposition went beyond his time and gained fame throughout the century, for not finding a solution or counterexample, because of this gained its name and for being his last challenge had as its name the Last Theorem of Fermat , the equation of his fame is cⁿ = bⁿ + aⁿ, where a, b, c and n ∈ N, with n ≥ 3, according to him had the demonstration, died without anyone knowing what was his supposed answer, because of this became known as his Last Theorem. The merit of the discovery of this proposition owed to his firstborn, he saw several notes of Fermat in a certain book of Aritmetics which belonged, for his father had a habit of making drafts or annotations in books. After the finding of the son, the notes or discoveries were published in a book Arithmetica de Diofanto containing observations of the father, in 1670 the book contained 48 observations, but along the way generations of mathematicians and physicists were giving solutions to their challenges, however had one that most thought was the last, because of this had such a challenging name. In his book he contained the following statement, “I have discovered a wonderful demonstration of this proposition which, however, does not fit in the margins of this book” (FERMAT. 1607 – 1665)².

2.2 YUTAKA TANIYAMA, GORO SHIMURA AND ANDREW WILES

In 1954, Yutaka Taniyama and Goro Shimura, young Japanese mathematicians, became friends because they took an interest in the same book, the same article and the same calculations, this Taniyama-Shimura conjecture enabled Wiles to realize his boy’s dream, employing an intellectual effort and determination that was difficult to believe as possible to a human being. The conjecture the two presented served as a path to their definitive solution to the problem, however mathematician Yutaka Taniyama took his own life in 1958, so he further delayed the development of the solution, to the development of the conjecture in whether it was not intentionally made to solve Fermat’s Last Theorem, however it was what really happened later Wiles realized that such a basis that helped the proof – there definitely this theorem , for who could imagine that the work of two students of the late twentieth century could be used in something that solved one of the greatest mysteries in the history of mathematics. But it was Andrew Wiles who ended up demonstrating Fermat’s Last Theorem, Wiles is a princeton university professor who began his interest in the problem as a child in his hometown had a public library, but it was only during 1986 that he really began to begin his work of solving the theorem of his dreams, according to Wiles that his research was done in complete secrecy , for in his being he knew he would find the solution, but it was not time to affirm such a thing to the academic community, intuition is everything to a passionate in number theory, however the intuition shows the way, but proving whether it is right or wrong takes time and dedication, perhaps fearing the pressure that would suffer in the face of such a famous problem and difficult solution was too risky to affirm such a possible initial solution , in analyzing the conjecture of the two Japanese, Andrew Wiles noted that such a theorem could be a way to solve, however the conjecture had to be proven first before demonstrating what he had sought so much since he was a child, in his mind it was so clear that Wiles could dream of the solution of the theorem all depended on the proof of the conjecture of the two students , however Wiles did not demonstrate Fermat’s Last Theorem, but rather the Taniyama-Shimura conjecture, which will imply proof – there.

Finally, on June 23, 1993, at a conference held at sir Isaac Newton Institute for Mathematical Sciences in Cambridge, Andrew Wiles, 356 years after the presentation of the theorem, made his announcement of his demonstration, but contained a small flaw in his solution, Wiles withdraws for a year in order to correct such a mistake and present his new recast demonstration , after the correction and review of the same error detected, it took a few months to assess its solution, its demonstration had 200 pages, and after a long period of anxiety, its discovery or demonstration was finally accepted, but so complex that only a few people worldwide were able to understand it, and Wiles (after receiving a prize worth 50,000.00 pounds from the Wolfskehl Foundation) , he enters as the mathematician who demonstrated the most intriguing and challenging theorem in the history of mathematics, and thus concludes one of the greatest problems not encountered or demonstrated that challenged great mathematicians before and during, so Fermat’s Last Theorem has no solutions with positive integers with n ≥ 3³.

2.3 ANDREW BEAL AND HIS CONJECTURE THAT RECEIVED HIS NAME

Andrew Beal (born November 29, 1952), banker, entrepreneur, investor, poker player and amateur mathematician and enthusiast of one of the best areas that is number theory. Beal is also known for Beal’s conjecture while investigating generalizations of Fermat’s last theorem, from 1993 to 1997, Beal offered a monetary prize for a peer-reviewed proof of this conjecture or a counter-example, because in 1993 it had a value of $5,000 the value of the prize increased several times and currently is $1,000,000.00 for the person who proves it or presents a contradictory example in other words a counter- example for those who generalize Fermat’s Last Theorem. According to the banker’s own statements, in an American Mathmatical Society press ad, the goal of millionaire value is to “inspire young minds to reflect on the issue and make them more and more interested in the study of mathematics” ⁴.

3. DEVELOPMENT TO THE CONJECTURE OF BEAL

To demonstrate it will take three new theorems (T.M, S.T.M e T.G.M), because Sebá’s Theorem is a particular case of Beal’s conjecture, this will also be shown later.

3.1 MACENA OR T.M

Given two equations Eq₁:c^z = b^y + a^x e Eq₂:c^m = c^m with positive whole solutions and has as common basis c ≠ 0, with c, b, a, z, y, x and m ∈ N, m > z it is possible to determine a new Equation Eq₃ that has both the format of Eq₁ as well as Eq₂ This means if Eq3 does not satisfy Eq_{1 i}t does not have entire positive solutions. Example₁ is the equation Eq₁ → c² = b² + a² e Eq₂ → c^m = c^m with c ≠ 0 and m ∈ N, we know that Eq₁ has entire solutions because it is pythagorean’s own theorem, just check using the pythagoric triples, just as Eq₂ also has entire solutions this will be proven ahead. That said, then it is possible to determine an Eq₃ equation that has both the Eq₁ and Eq₂ format. Like c ≠ 0 we can use the following steps in Eq₁ → c² = b² + a² → 1 = c^− 2.(b² + a²)(I) Eq₁ → c² = b² + a² →  c=(b²+a²)^1/2(II)
Next step is to use Eq₂, because we can write Eq₂ this way c^m = c^m.1 when replacing (I) we have c^m = c^m.c⁻².(b² + a²) → c^m = c^m−2.(b² + a²) → c^m = b².c^m−2 + a².c^m−2(III) Replacing (II) in (III);

= b².

+ a².

→

=

. Let m − 2 be a multiple of 4 ie m − 2 = 4.n, with n ∈ ℕ, then we have m = 4.n + 2, when replacing we have; (b² + a²)^2.n + 1 = [b(b² + a²)ⁿ]² +[a(b²+a²)ⁿ]²

(b² + a²)^2n + 1= [B]² + [A]² now we just have to check if (b² + a²)^2n + 1 it’s like C²,pelaby the Pythagorean triples this equality is soon satisfied (b² + a²)^2.n + 1 = (c²)^2.n + 1 = c^{2.(2.n + 1)}= [c^2.n + 1]² = [C]²
Therefore C² = [B]² + [A]² the same format Eq₁ to conclude must have ownership of Eq₂C² = [B]² + [A]² → (b² + a²)^2n + 1 = [b(b² + a²)ⁿ]² + [a(b²+ a²)ⁿ]² → (c²)^2n + 1= [b(c²)ⁿ]² + [a(c²)ⁿ]² →
c^4n + 2 = [b.c²ⁿ]2 + [a.c²ⁿ]2 → c^4n + 2 = b²c⁴ⁿ + a²c⁴ⁿ → c^4n + 2 = c⁴ⁿ.(b² + a²) → c⁴ⁿ⁺²=c⁴ⁿ.(c²) → c⁴ⁿ⁺²=c⁴ⁿ⁺² →c^m=c^m . Then it was verified that it is possible to find a Eq₃ that has both properties then the Eq₃ for these two equations it is; Eq₃ → (b²+a²)2ⁿ⁺¹=[b(b²+a²)ⁿ]²+[a(b²+a²)ⁿ]²

3.1.1 TASTING T.M

Seja Eq₁: c^z = b^y + a^x e Eq₂: c^m = c^m, with m > z, a, b, c, x, y, z , m ∈ ℕ e c ≠ 0.
Proving Eq₂:

In fact 1 = 1, multiplying both sides by c ∈ N* we have 1.c = 1.c, when multiplying again by the same c we have c2 = c2^, logically multiplying by m times we will have;
c^m = c^{{(1₁ + 1₂ + 1₃ + … + 1_m − 1 + 1_m) = m}} = c^m. Therefore shown to Eq₂.

As c ≠ 0, we can use the following devices:

c^z = b^y + a^x → 1 = c^− z.(b^y + a^x)( I ) neutral element of multiplication
c^z = b^y + a^x → c =(b^y+a^x)^1/z( II )

A Eq₂ pode ser escrita da seguinte maneira c^m = c^m.1 , ao substituir (I) nessa equação é obtido:

c^m = c^m.1 → c^m = c^m.c ^− z.(b^y + a^x) → c^m = c^m − z.(b^y + a^x) → c^m = b^y.c^m − z + a^x.c^m − z
Replacing (II) results in;

, putting the y and x exponents in evidence

For what

∈ ℕ o MMC( zy , zx )= zxy, so m – z must be a multiple of zxy, so m – z = zxy.k, com k ∈ ℕ. Isolating m and replacing in the equation results:

(b^y + a^x)^xyk + 1 = [b.(b^y + a^x)^xk]^y + [a.(b^y + a^x)^yk]^x

So this is the new equation;
Eq₃:(b^y + a^x)^xyk + 1 = [b.(b^y + a^x)^xk]^y + [a.(b^y + a^x)^yk]^x → C^xyk + 1 = B^y + A^x
By the principle of comparison or format C^xyk + 1 = B^y + A^x it’s equivalent to c^z = b^y + a^x, it is the very structure of Beal’s conjecture.

Soon it satisfied the Eq₁ lack shows that it also has the format of Eq₂: c^m = c^m

(b^y + a^x)^xyk + 1 = [b.(b^y + a^x)^xk]^y+ [a.(b^y + a^x)^yk]^x, como c^z = b^y + a^x we have;
(c^z)^xyk + 1 = [b.(c^z)^xk]^y + [a.(c^z)^yk]^x → c^z.^{(xyk + 1)} = [b.c^z.xk]^y + [a.c^z.yk]^x → c^zxyk + z = b^y.c^zxyk + a^x.c^zxyk →  as
m = zxyk + z
c^m = b^y.c^zxyk + a^x.c^zxyk → c^m = c^zxyk.(b^y + a^x) → c^m = c^zxyk.(c^z) → c^m = c^zxyk + z = c^m.

Therefore proven since Eq₃ satisfied Eq₁ e Eq₂.:.

Dados:

C^Z= B^y + A^x

C = b^y + a^x, B = b.(b^y + a^x)^xk, A = a.(b^y + a^x)^yk e Z = xyk + 1

MDC(C, B, A) = MDC(b^y + a^x, b.(b^y + a^x)^xk, a.(b^y + a^x)^yk) = b^y + a^x = c^z = C.

MDC(Z, y, x) = MDC(xyk + 1, y, x) = 1

OBS:

If k is zero we have;
(b^y + a^x)^xyk + 1 = [b.(b^y + a^x)^xk]^y + [a.(b^y + a^x)^yk]^x → (b^y + a^x)¹ = [b.(b^y + a^x)⁰]^y + [a.(b^y + a^x)⁰]^x, like b^y + a^x = c^z ≠ 0 therefore (b^y + a^x)⁰ = 1
(b^y + a^x)¹ = [b.1]^y + [a.1]^x → b^y + a^x = b^y + a^x

If m were equal to z the equation Eq₁ and Eq₂ would be equal, in turn would be equal to Eq₃

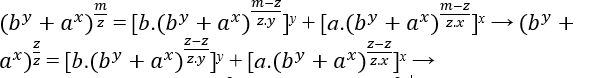
(b^y + a^x)¹ = [b.(b^y+a^x)⁰]^y + [a.(b^y+a^x)⁰]^x →  b^y + a^x = [b.1]^y + [a.1]^x.

If case x=y=k=1 we have a perfect square
(by + ax⁾x^{yk + 1} = y[b.(b^y + a^x)^xk] + x[a.(b^y + a^x)^yk] → (b1 + a1⁾1 ^{+ 1} = 1[b.(b¹ + a¹)¹] + 1[a.(b¹ + a¹)¹] →
(b + a)2 = +[b.(b + a)] → [a.(b + a)](b + a)2 = b.(b + a) + a.(b + a) = b2 + ba + ab + a2 = b2 + 2ab + a2 = (b + a)2
Example₂ Checking with numbers the equation Eq3, be b=3, a=2 and n=1 we have;

(b² + a²)^{2n + 1} = [b(b² + a²)ⁿ]² + [a(b² + a²)ⁿ]² → (3² + 2²)^{2.1 + 1} = [3(3² + 2²)¹]² + [2(3² + 2²)¹]² →
(9 + 4)³ = [3(9 + 4)]² + [2(9 + 4)]² → 13³ = [3.13]² + [2.13]² → 13³ = 39² + 26² → 2187 = 1521 + 676 → 2187 = 2187

3.2 SHOWING EACH CASE PER T.M

To show the validity of this theorem it is also necessary to show the possibilities or possible values of z, y, x and m ∈ N, if it does not contradict any theorem already demonstrated by mathematicians such as (Pythagoras theorem ” by several Mathematicians”, Sebá’s theorem ” by Sebastian ” and fermat’s Last Theorem ” by Andrew Wiles ” and so on) then the T.M is valid and will be a tool to prove the Beal Conjecture.

3.2.1 PYTHAGORAS THEME

This is when z=y=x=2
Suppose that Eq₁ → c² = b² + a² , has entire solutions, for c, a, b, m ∈ N, c ≠ 0 and Eq₂→ c^m = c^m it is possible to find an Eq3 that satisfies the two previous equations, if this occurs soon Eq₁ → c=√(b²+a² )∈ N.
This demonstration has already been shown in Example1, it is only necessary to show that actually using the pythagorean triple is satisfied the condition c=√(b²+a²) ∈ ℕ.
Hypothesis is c² = b² + a², Thesis C² = C².
Using Hypothesis c² = b² + a² adding on both sides by 2b + 1 ∈ N, a perfect square is obtained on one side, c2 + 2b + ¹ = b2 + 2b + 1 + a2 → c2 + 2b + 1 = (b + 1)2 + a2, we kⁿow that in a right triangle the hypotenuse is greater than any of the catetos in particular c > b > a, then there is the possibility of c = b + 1 , realize that this is an appropriate solution to solve equation c² + 2b + 1 = (b + 1)² + a² → c² + 2b + 1 = c² + a² → 2b + 1 = a² when isolating b, is obtained

and as ,

,realize that both b and c to be an integer suffice (a) be odd because odd odd times remains odd, therefore a = 2k + 1 condition to be odd with k ∈ , so we have;

→ [2k² + 2k + 1]² = [2k² + 2k]² + (2k + 1)², So we have C = 2k² + 2k + 1, B = 2k² + 2k and A = 2k + 1 ∈ ℕ, are the Pythagorean triples(2k² + 2k + 1, 2k² + 2k, 2k + 1), checking the thesis

3.2.2 FOR THE CASE OF FERMAT’S LAST THEOREM

This is when z=y=x=n
Suppose that Eq₁ → cⁿ = bⁿ + aⁿ , has solution for n≥3, with c, a, b, m ∈ ℕ, c ≠ 0 e Eq₂ → c^m = c^m it is possible to find an Eq₃ that satisfies the two previous equations, if this occurs soon Eq₁ → c = ⁿ√bⁿ+aⁿ ∈ ℕ.
As c ≠ 0 we can write Eq1, as follows;

Eq₁ → cⁿ = bⁿ + aⁿ → 1 = c ^− n.(bⁿ + aⁿ)(I) neutral element of multiplication
Eq₁ → cⁿ = bⁿ + aⁿ → c = ( bⁿ+aⁿ )^1/n(II)
Check that Eq₂ can be written as follows without changing its values c^m = c^m.1, ao replace (I) in Eq₂, we have;
c^m = c^m.c ^− n.(bⁿ + aⁿ) → c^m = c^m − n.(bⁿ + aⁿ) → c^m = bⁿ.c^m − n + aⁿ.c^m − n(III)

Replaced (II) in (III)

Realize that the format is the same as Eq₁, just check if m − n is multiple of n², if yes then we can write m − n = n².k with k ∈ ℕ, isolating m we have m = n².k + n this is an equation of 2ª grau;
m = n².k + n ⇒ kn² + n − m = 0, with that we can find values for m and n by Bhaskara.

, so that n is necessarily natural  -1±√1-4km must be a multiple of 2k, so;
-1±√1-4km = 2k.t, com t ∈ ℕ
-1±√1-4km = 2k.t → ±√1-4km= 2k.t + 1 raising both to the quarter we have 1 + 4km = (2k.t + 1)²→ 4km = (2k.t + 1)² − 1 realize that it is the difference of two squares then;
4km = (2k.t + 1 − 1).(2k.t + 1 + 1) → 4km = (2k.t).(2k.t + 2) → 4km = 4.(k.t).(k.t + 1) → km = k.t.(k.t + 1) →
m = t( kt + 1), then replacing this value of m in n =  -1±√1-4km we have;

soon (b^t+ a^t)^kt + 1 = B^t + A^t, realize kt + 1 is not a multiple of t, because mdc( kt + 1 , t ) = 1, that is “kt + 1” and “t” are prime between, and by Andrew Wiles it is impossible b^t + a^t = c^t (Fermat’s Last Theorem), for t > 2.
Because kt + 1 ≠ t.α, with 2 < α ∈ N, therefore does not satisfy eq₁, so Eq₁ has no solutions, as it is said in T.M.
However C =^kt+1√B^t+A^t ∈ ℕ, EQSebá, Seba’s theorem, checking equality;
C = ^kt+1√B^t+A → C = ^kt+1√[b (b^t+a^t )^k]^t+ [a( b^t+a^t )^k]^t  →C = ^kt+1√b^t( b^t+a^t )^kt + a^t ( b^t+a^t )^kt → ^kt+1√( b^t+a^t )^kt.( b^t+a^t ) → C = ^kt+1√( b^t+a^t )^kt+1 → C = b^t + a^t.

3.2.3 SEBÁ THEME

c^m = bⁿ+ aⁿ, with mdc(m,n)=1
Demonstration of Sebastião Vieira do Nascimento ( Sebá )
Theorem: The equation C^m = Aⁿ + Bⁿ admits natural solutions for m and n primes to each other.
Proof:
Be the equation;
( 1 )c^m = bⁿ + aⁿ, being a, b, c, n and m positive integers. Multiplicando ambos os membros da equação ( 1 ) por (bⁿ + aⁿ)^m
you get:
( 2 )c^m*(bⁿ + aⁿ)^m = (bⁿ + aⁿ)*(bⁿ + aⁿ)^m, Substituting the value of da (1) in (2), we obtain:
(bⁿ + aⁿ)^m + 1 = (bⁿ + aⁿ)*(bⁿ + aⁿ)^m
or
( 3 )(bⁿ + aⁿ)^m + 1 = bⁿ(bⁿ + aⁿ)^m + aⁿ(bⁿ + aⁿ)^m
If we choose values for a and b such that a ≤ b or a≥b, and substitute in (3), positive integer values are obtained for A, B and C.

Example: Be dividing a square into two cubes in several different ways. Let the equation be:
( 4 )C² = B³ + A³, Consider the equation:
c² = b³ + a³, Multiplying both members of the above equation by (b³ + a³)^m, where m and n  ∈ ℕ, we have:

c²(b³ + a³)m = (b³ + a³)(b³ + a³)^m
( 5 )(b³ + a³)^m + 1 = b³(b³ + a³)^m + a³(b³ + a³)^m

Comparing equation (5) with equation (4), we must decompose m into powers of 3 and m + 1 into powers of 2. This will only be possible if m and m + 1 are, respectively, multiples of 3 and 2. Soon:
m = 6k – 3 e m + 1 = 6k – 2, Thus, equation (5) is:

(b³ + a³)^6k − 2 = b³(b³ + a³)^6k − 3 + a³(b³ + a³)^6k − 3
[(b³ + a³)^3k − 1]² = [b(b³ + a³)^2k − 1]³ + [a(b³ + a³)^2k − 1]³, Therefore, the solutions to the given equation are obtained by doing:

C = (b³ + a³)^3k − 1, B = b(b³ + a³)^2k − 1 e A = a(b³ + a³)^2k − 1, onde k ∈ N*, a e b ∈ ℕ.
Proving Using the T.M That’s when z=m e y=x=n
Suppose that Eq₁ → c^m = bⁿ + aⁿ, has solution for m and n prime to each other this is mdc(m,n)=1, with c, a, b, t, m and n ∈ ℕ, c ≠ 0 and Eq₂ → c^t = c^t you can find one Eq₃ that satisfies the two previous equations, if this occurs soon Eq₁ → c =^m√bⁿ+aⁿ ∈ ℕ.

As c ≠ 0 we can use the following methods;
c^m = bⁿ + aⁿ → 1 = c^− m*(bⁿ + aⁿ), (I) neutral element of multiplication
c^m= bⁿ + aⁿ → c = (bⁿ+aⁿ)^1/m, (II)
We can write Eq₂ this way c^t = c^t.1, replacing ( I ) in Eq₂ we have;

c^t = c^t.c^− m.(bⁿ + aⁿ) → c^t = c^t − m.(bⁿ + aⁿ) → c^t = bⁿc^t − m + aⁿc^t − m, when replacing (II) we have;

For what

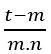
be natural t – m must be a multiple of n and m, therefore t − m = m.n.k, with k ∈ ℕ, isolating t we have t = m.n.k + m, when replacing in the equation it is obtained;

It remains to show that nk + 1 is a multiple of m, if yes it is of the form nk + 1 = m.α, with α ∈ ℕ or bⁿ + aⁿ = C^m
If any of these two occurs, if we have Cm = Bn + An then it will be shown that Eq₁ has a solution.

We have to t − m = m.n.k dividing both by m, it is obtained

-1 = n.k adding 1 on both sides

= n.k + 1, as t is multiple of m, so

∈ N, with this we can use the following steps;

As

= n.k + 1 and nk + 1 = m.α this is

= m.α → α =

, if α is natural then

it should be natural, if only if t is also multiple of m², but t is not multiple of m², because it is of the form t = m.n.k + m, even if k was equal to m, it would be of the form t = n.m² + m = m.(nk + 1) ≠ m². (nk+1), so nk+1 is not multiple of T, so mdc (NK+1,T)=1, are primes between each other.

It is only left to check whether bⁿ + aⁿ =C^m.
We know that nk + 1 is not a multiple of n, because the mdc(nk + 1, n) = 1 and how the equation equals (bⁿ + aⁿ)^nk + 1 = [b(bⁿ + aⁿ)^k]ⁿ + [a(bⁿ + aⁿ)^k]ⁿ is satisfied already shown earlier in EQ_Sebá, by the format or comparison principle we have to:

C^nk + 1= Bⁿ + Aⁿ equals a c^m = bⁿ + aⁿ, soon;

(bⁿ + aⁿ)^nk + 1 = Bⁿ + Aⁿ → (c^m)^nk + 1 = c^{m.(nk + 1)} = [c^nk + 1]^m = C^m = Bⁿ + Aⁿ

With that, the Eq₁, missing show Eq₂ → c^t = c^t, realize that:
(bⁿ + aⁿ)^nk + 1 = Bⁿ + Aⁿ → (bⁿ + aⁿ)^nk + 1 = [b(bⁿ + aⁿ)^k]ⁿ + [a(bⁿ + aⁿ)^k]ⁿ →
(c^m)^nk + 1 = [b(c^m)^k]ⁿ + [a(c^m)^k]ⁿ → c^{m.(nk + 1)} = [b(c^m)^k]ⁿ + [a(c^m)^k]ⁿ
like t= m.( nk + 1 );
c^t = bⁿ(c^m)^nk+ aⁿ(c^m)^nk → c^t = (c^m)^nk(bⁿ + aⁿ) → c^t = (c^m)^nk(c^m) → c^t = (c^m)^nk + 1 → c^t = c^{m.(nk + 1)} = c^t, So proven because Eq3 has properties of both Eq1 and Eq2.

3.2.4 IN CASE THEY ARE MULTIPLE BY T.M

Case (1): for multiple y of x this is y = xk with k ∈ N
Be _Eq1: c^z = b^xk + a^x and Eq₂ :c^m = c^m, with m > z and c ≠ 0 you can find a new Equation Eq₃, which has properties of Eq₁ and Eq₂ if Eq₃ does not have property of Eq₁ logo _Eq1, has no entire solutions.

As c ≠ 0, we have;
c^z = b^xk + a^x → 1 = c ^− z.(b^xk + a^x), (I) neutral element of multiplication
c^z = b^xk + a^x → c = (b^xk+a^x)^1/z, (II)

We can write Eq₂ in the following way using (I);
c^m = c^m.c^− z.(b^xk + a^x) → c^m = c^m − z.(b^xk + a^x) → c^m = b^xk.c^m − z + a^x.c^m − z, ao substituir (II) temos;

Putting the xk and x in evidence we have;
, note that mmc (zxk, zx) and so that

∈ ℕ, z – m must be a multiple of zxk that is m – z = zxk.α with α ∈ ℕ, with that we have;

(b^xk + a^x)^{xk.α + 1} = [b.(b^xk + a^x)^α]^xk + [a.(b^xk + a^x)^k.α]^x, note that this equation can be written as follows;

(b^xk + a^x)^{xk.α + 1} = [b^k.(b^xk + a^x)^k.α]^x + [a.(b^xk + a^x)^k.α]^x, that’s Seba’s Theorem so already proven soon C^{xk.α + 1} = B^xk + A^x equivalent to C^m = B^x + A^x pois MDC(xk.α + 1 , xk )=MDC(xk.α + 1 , x)= MDC(m,x)=1, therefore cousin to each other, equivalent to Eq1.

Checking Eq2 which is c^m = c^m
(b^xk + a^x)^{xk.α + 1} = [b.(b^xk + a^x)^α]^xk+ [a.(b^xk+ a^x)^k.α]^x, como b^xk + a^x = c^z we have; (c^z)^{xk.α + 1} = [b.(c^z)^α]^xk + [a.(c^z)^k.α]^x → c^{zxk.α + z} = [b.c^zα]^xk + [a.c^zk.α]^x como m = zxk.α + z
c^m = b^xk.c^xzkα + a^x.c^xzk.α → c^m = c^xzkα(b^xk + a^x) → c^m = c^xzkα(c^z) → c^m = c^{xzkα + z} = c^m.
Soon satisfied Eq₁ and Eq₂, therefore proven.
Case (2): for x multiple of y this is x = yk with k ∈ ℕ
This demonstration is analogous to Case (1), as Eq₃ is;
(b^y + a^yk)^{yk.α + 1} = [b.(b^y + a^yk)^k.α]^y + [a.(b^y + a^yk)^α]^yk →
(b^y + a^yk)^{yk.α + 1} = [b.(b^y + a^yk)^k.α]^y + [a.(b^y + a^yk)^kα]^y → C^{yk.α + 1} = B^y + A^y equivalent C^m = B^y + A^y equivalent in turn Eq₁: c^z = b^y + a^yk com k, α ∈ ℕ .
Case (3): for multiple z of x this is z = xk and MDC(z,x,y)=1, with k ∈ N

Be Eq₁: c^xk = b^y + a^x, we can write Eq₁ of the following format Eq₁: b^{y =} c^xk− a^x, and Eq₂ will be on the basis of b instead of c, with b ≠ 0 and c > a, soon Eq₂^: b^m = b^m, with m > y, so it is possible Eq₃ that has both Eq₁ and Eq₂ propert_y, if it does not satisfy Eq₁ then Eq1 does not have full positive solutions.

As b ≠ 0 we have;
b^y = c^xk − a^x → 1 = b ^− y(c^xk − a^x), (I) neutral element of multiplication
b^y = c^xk − a^x → b = (c^xk-a^x)^1/y, (II)
Eq₂ can be written as follows b^m = b^m.1, substituted (I) in Eq2 we have;
b^m = b^m.b^− y(c^xk − a^x) → b^m = b^m − y(c^xk − a^x) → b^m = c^xk.b^m − y− a^x.b^m − y, substituted (II)we have;

, isolating xk and x we have;
MMC( xyk , x )= xyk, so that

∈ ℕ, m – y must be a multiple of xyk, that is m – y = xyk.α, with α ∈ ℕ, with these data we have;

(c^xk − a^x)^xkα + 1 = [c.(c^xk − a^x)^α]^xk − [a.(c^xk − a^x)^k.α]^x, note that we can organize as follows;

(c^xk − a^x)^xkα + 1 = [c.(c^xk − a^x)^α]^xk − [a.(c^xk − a^x)^k.α]^x → [c.(c^xk − a^x)^α]^xk = (c^xk − a^x)^xkα + 1 + [a.(c^xk − a^x)^k.α]^x, therefore z can be a multiple of x, and its MDC( z , x , y ) = 1

As z = xk, we have;
[c.(c^z − a^x)^α]^z = (c^z − a^x)^zα + 1 + [a.(c^z − a^x)^k.α]^x, with that we have;

C = c.(c^z − a^x)^α, B = c^z − a^x e A = a.(c¹ − a^x)^k.α, soon C^z= B^zα + 1 + A^x, with z=xk, this is equivalent to Eq₁, remains to show that it is also Eq₂: b^m = b^m.

[c.(c^z − a^x)^α]^z = (c^z − a^x)^zα + 1 + [a.(c^z − a^x)^k.α]^x, like b^y = c^z − a^xez = xk, we have;

[c.(b^y)^α]^xk = (b^y)^xkα + 1 + [a.(b^y)^k.α]^x → c^xk.(b^y)^xkα = b^{xykα + y} + a^x.(b^y)^xk.α, like m = xykα + y, we have;

c^xk.b^xykα = b^m + a^x.b^xyk.α → c^xk.b^xykα − a^x.b^xyk.α = b^m → b^xykα.(c^xk − a^x) = b^m → b^xykα.(b^y) = b^m → b^{xykα + y} = b^m
→ b^m = b^m

Therefore, as Eq₃ satisfied Eq₁ and Eq₂, therefore Eq₁ has solutions on positive integers.
Case (4) for multiple z of y this is z = yk with k ∈ N
This demonstration is analogous in relation to Case (3), they reach the same format as equation Eq₃, but with b in place of a, and y in place of x;

[c.(c^yk − b^y)^α]^yk =[b.(c^yk − b^y)^k.α]^y + (c^yk − ^bx)^{ykα + 1}, with α ∈ N.
Case (5): for multiple z of x and y this is z = xyk with MDC(z, x, y) = MDC(x, y)≥1, and k ∈ N
Be Eq₁^: c^xyk = b^y + a^x and Eq₂: c^m = c^m, with c ≠ 0 and k ∈ N, you can find a new Equation Eq₃, which has properties of Eq₁ and Eq₂ if Eq₃ does not have property of Eq₁ soon Eq₁ has no entire solutions.

As c ≠ 0 we have;
c^xyk = b^y + a^x → 1 = c ^− xyk*(b^y + a^x), (I) neutral element of multiplication

We can write Eq₂ as follows using ( I );
c^m = c^m.c^− xyk.(b^y + a^x) → c^m = c^{m − xyk}.(b^y + a^x) → c^m = b^y.c^{m − xyk} + a^x.c^{m − xyk} , when replacing (II) we have;

, Putting y and x evidence we have;

The MMC(xy²k , x²yk )=x²y²k, so that

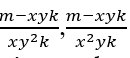
∈ ℕ, mandatorily m – xyk must be a multiple of x²y²k that is m – xyk = x²y²k.α, with α ∈ ℕ, then we have;

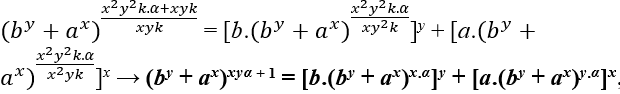Note that xyα + 1 is not a multiple of xy, because LCD (xy.α + 1, xy) = 1, so Eq₁ does not have positive integer solutions for z multiple of x and y.
For b^y + a^x by the principle of comparison shown earlier equals c^{xyk + 1 =} b^y + a^x and as z = xyk, we have c^{z + 1} = b^y + a^x. Therefore z +1 is not multiple of x and y, so Eq₁ has no solution in positive integers.
Case (6): for z multiple of x, and y multiple of x is z = xk and y = xt, with k ≥ t and MDC (z, x, y) = x, and k, t ∈ ℕ
Let Eq₁: c^xk = b^xt + a^x and Eq₂: c^m = c^m, with c ≠ 0 e k, t ∈ ℕ, it is possible to find a new equation Eq₃, which has properties of Eq₁ and Eq₂ if Eq₃ does not have Eq₁ property so Eq₁ does not has whole solutions.

As c ≠ 0 we have;
c^xk = b^xt + a^x → 1 = c^− xk*(b^xt + a^x), , (I) neutral element of multiplication
c^xk = b^xt + a^x → c = (b^xt + a^x)^1/xk (II)

We can write Eq₂ as follows using ( I );
c^m = c^m.c^− xk.(b^xt + a^x) → c^m = c^m − xk.(b^xt + a^x) → c^m = b^xt.c^m − xk + a^x.c^m − xk, when replacing (II) we have;

, isolating xt and x we have;
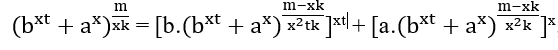, MMC(x²tk,x²k)=x²tk, so that

∈ ℕ it is necessary that m – xk is a multiple of x²tk, that is m – xk = x²tk.α, with α ∈ ℕ, substituting these values is obtained;

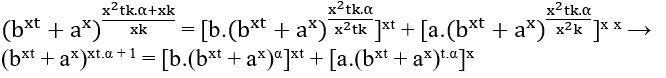as xt.α + 1 is not a multiple of x, it remains to look at b^xt + a^x, notice that initially Eq₁ is c^xk = b^xt + a^x → (c^k)^x = (b^t)^x + a^x Fermat’s last theorem.
Because Eq₃ did not satisfie Eq₁, therefore Eq₁ has no positive whole solution when z is multiple of x, and y multiple of x.

Case (7): for z multiple of y, and x multiple of y is z = yk and x = yt, with k ≥ t and MDC (z, x, y) = y, and k, t ∈ ℕ
This demonstration is analogous to Case (6), as it falls into Fermat’s Last Theorem.

Case (8): for z multiple of y e x, x or y multiple of each other, this is z = xyk and x = yt or z = xyk and y = xt, with k ≥ t and MDC (z, x, y) = y or MDC (z, x, y) = x, e k, t ∈ ℕ
This demonstration is analogous to Case (6) and (7), as it falls into Fermat’s Last Theorem.

Note: c^xyk = b^xt + a^x → (c^yk) ^x = (b^t) ^x + a^x and c^xyk = b^y + a^yt → (c^xk) ^y = b^y + (a^t) ^y, both of Fermat’s Last Theorem.

Conclusion in case the exponents are multiple:
There is no solution for positive integers, in cases (5), ( 6 ), ( 7 ) and ( 8 )

3.3 ACCORDING TO MACENA OR S.T.m

Given n ≥ 2 the degree of the first member of the equation it is always possible to determine a B=(n^{m − 1} + 1)ⁿ−(n^{m − 1} − 1)ⁿ, and if MDC(a, B, c) = 1 then n has even degree, if the MDC(a, B, c) = 2.t ≥ 2 then the n degree is odd, in both cases satisfy aⁿ = B + cⁿ , in particular for any even or odd n we have the MDC(a,B,c) = c where c is of the form 2ⁿ − 1.
To prove this theorem you will need to find a Tool before proofing it.
Tool:
To find the tool first we must analyze how newton’s binomial behaves from grade 2.

(x + y)² = 1.x² + 2.x.y + 1.y², this is 1 2 1.
(x + y)³ = 1.x³ + 3.x².y + 3.x.y² + 1.y³, this is 1 33 1.
(x + y)⁴ = 1.x⁴ + 4.x³.y + 6.x².y² + 4.x.y³ + 1.y⁴, this is 1 4 6 4 1.
(x + y)⁵ = 1.x⁵ + 5.x⁴.y + 10.x³.y² + 10.x².y³ + 5.x.y⁴ + 1.y⁵, this is 15101051.
*
*

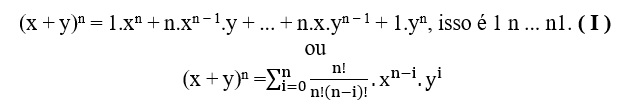
Now by subtracting xⁿ or yⁿ on both sides of (I), it is obtained;

(x + y)ⁿ − xⁿ = n.x^n − 1.y + … + n.x.y^n − 1 + yⁿ( I I)
or
(x + y)ⁿ − yⁿ = 1.xⁿ + n.x^n − 1.y + … + n.x.y^{n − 1}( I I)

By the difference of two powers of the same degree we can write (x + y)ⁿ − xⁿ, as follows;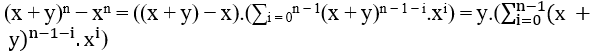

Similarly we can also write (x + y)ⁿ − yⁿ, as follows;

With this we have two new equations differentiating only in x and y.

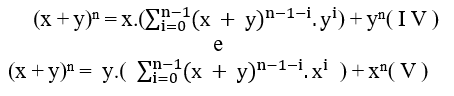
Adding ( I V ) and ( V ) we have;

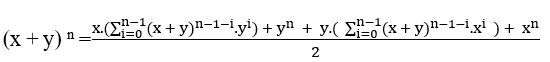
For it to , be divisible by 2, just y be equal to x this is y = x or x = y, with that we have

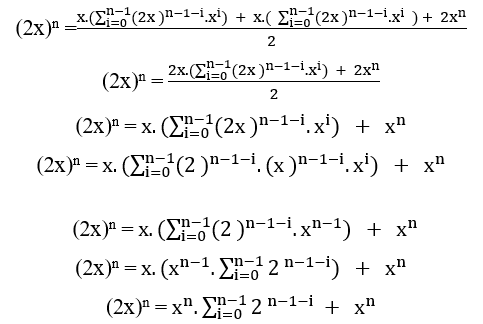
Dividing by the common factor that is xⁿ we have;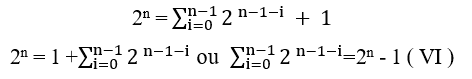

The item ( VI ) is the tool that will be used to prove the Theorem.

Proving the cases of n being odd or even:

If m ≥ 2, it is possible to obtain equations of the format cⁿ = B + aⁿ, where the MDC(c,B,a) = 1 if degree n is even, and MDC(c, B, a) = 2.t ≥ 2, with t ∈ N^*, if the degree n is odd.

Method if the base is 2, it will be used for completing squares, if it is 3 it will be completing cubes, and so on, until the base n will use completing the umpisth power.

Be b a base, with b ∈ N*, so giving initiative we have;

For b = 2 we have;

2^m = 2^m in fact this is valid, we can write as follows
2^m = 2^m.1, realize that the following equality is valid.
2^m = 2^m.(2 − 1) → 2^m = 2^m + 1 − 2^m → 2.2^m − 1 = 2^m + 1 − 2.2^m − 1, to complete the square of the first member just add on both sides2^{2 (m – 1)} + 1, this results in;

2.2^m − 1 + 2^{2(m − 1)} + 1 = 2^m + 1 − 2.2^m − 1 + 2^{2(m − 1)} + 1 → (2^{2(m − 1)} + 2.2^m − 1 + 1) = 2^m + 1 + (2^{2(m − 1)} − 2.2^m − 1 + 1) , so we have two perfect squares, and with that a new equation;

(2 ^{m – 1}+ 1 )² = 2 ^{m + 1}+ (2 ^{m – 1}– 1 )²( 1 )

Your MDC(2^m − 1 + 1, 2, 2^m − 1 − 1) = 1

See that it only depends on a variable in case m, see the examples using the numbers.

For m = 2

(2^m − 1 + 1)² = 2^m + 1 + (2^m − 1 − 1)²
(2¹ + 1)² = 2³ + (2¹ − 1)²
(2 + 1)² = 2³ + (2 − 1)²
3² = 2³ + 1²
9 = 8 + 1

For m = 3

(2^m − 1 + 1)² = 2^m + 1 + (2^m − 1 − 1)²
(2² + 1)² = 2⁴ + (2² − 1)²
(4 + 1)² = 2⁴ + (4 − 1)²
5² = 2⁴ + 3²
5² = 4² + 3²
25 = 16 + 9

For m = 4

(2^m − 1 + 1)² = 2^m + 1 + (2^m − 1 − 1)²
(2³ + 1)² = 2⁵ + (2³ − 1)²
(8 + 1)² = 2⁵ + (8 − 1)²
9² = 2⁵ + 7²
(3²)² = 2⁵ + 7²
3⁴ = 2⁵ + 7²
81 = 32 + 49

For m = 5

(2^m − 1 + 1)² = 2^m + 1 + (2^m − 1 − 1)²
(2⁴ + 1)² = 2⁶ + (2⁴ − 1)²
(16 + 1)² = 2⁶ + (16 − 1)²
17² = 2⁶ + 15²
289 = 64 + 225

For m = 6

(2^m − 1 + 1)² = 2^m + 1 + (2^m − 1 − 1)²
(2⁵ + 1)² = 2⁷ + (2⁵ − 1)²
(32 + 1)² = 2⁷ + (32 − 1)²
33² = 2⁷ + 31²
1089 = 128 + 961

And so on.

For b = 3, we have;

3^m = 3^m in fact this is valid, we can write as follows
3^m = 3^m.1, realize that the following equality is valid.
3^m = 3^m.1 → 3^m = 3^m.(3 − 2) → 3^m = 3^m + 1 − 2.3^m → 3.3^m − 1 = 3^m + 1 − 3.2.3^m − 1, to complete the cube on the first side of the equation, just add 3^{3 (m – 1)} + 3.3^{2 (m – 1)} + 1 on both sides, this results in;
3.3^m − 1 + 3^{3(m − 1)} + 3.3^{2(m − 1)} + 1 = 3^m + 1 − 2.3^m + 3^{3(m − 1)} + 3.3^{2(m − 1)} + 1 → (3^{3(m − 1)} + 3.3^{2(m − 1)} + 3.3^m − 1 + 1) = 3^m + 1 + 3^{3(m − 1)} + 3.3^{2(m − 1)} +  − 3.2.3^m − 1 + 1 → (3^m − 1 + 1)³ = 3^m + 1 + 3^{3(m − 1)} + 3.3^{2(m − 1)} − 2.3^m + 1, there must be some k ∈ ℕ, which added and subtracted to generate a perfect cube on the second side of the equality as in the previous example, so we have;
(3^m − 1 + 1)³ = [3^m + 1 + 3^{3(m − 1)} + 3.3^{2(m − 1)} − 2.3^m + 1 + k] − k, to determine k, just 3^m + 1 + 3^{3(m − 1)} + 3.3^{2(m − 1)} − 2.3^m + 1 + k = (3^m − 1 − 1)³;

3^m + 1 + 3^{3(m − 1)} + 3.3^{2(m − 1)} − 2.3^m + 1 + k = 3^{3(m − 1)} − 3.3^{2(m − 1)} + 3.3^m − 1 − 1
3^m + 1 + 3.3^{2(m − 1)} − 2.3^m + 1 + k =  − 3.3^{2(m − 1)} + 3.3^m − 1 − 1
k =  − 3^m + 1 − 3.3^{2(m − 1)} − 3.3^{2(m − 1)} + 3.3^m − 1 + 2.3^m − 1 − 1
k =  − 3^m + 1 − 6.3^{2(m − 1)} + 3.3^m − 1 + 2.3^m − 2
k =  − 3^m + 1 − 2.3.3^{2(m − 1)} + 3^m + 2.3^m − 2
k =  − 3^m + 1 − 2.3^{2(m − 1) + 1} + 3.3^m − 2
k =  − 3^m + 1 − 2.3^2m − 1 + 3.3^m − 2
k =  − 3^m + 1 − 2.(3^2m − 1 + 1) + 3.3^m
k =  − 3^m + 1 − 2.(3^2m − 1 + 1) + 3^m + 1
k =  − 2.(3^2m − 1 + 1)

Soon

− k = 2.(3^2m − 1 + 1)
With that we have another equation
(3^m − 1 + 1)³ = [3^m + 1 + 3^{3(m − 1)} + 3.3^{2(m − 1)} − 2.3^m + 1 + k] − k
(3^m − 1 + 1)³ = (3^m − 1 − 1)³ + 2.(3^2m − 1 + 1)

(3^m − 1 + 1)³ = 2.(3^2m − 1 + 1) + (3^m − 1 − 1)³( 2 )

As 3^m − 1 + 1 , 2.(3^2m − 1 + 1) and 3^m − 1 − 1, they are pairs because power of 3 is always odd adding 1 or subtracting 1 from that power to give us a pair.
So the MDC(3^m − 1 + 1, 2.(3^2m − 1 + 1), 3^m − 1 − 1) = 2.t ≥ 2, com t ∈ N^*. Example in numbers:

For m = 2 we have;

(3^m − 1 + 1)³ = 2.(3^2m − 1 + 1) + (3^m − 1 − 1)³
(3¹ + 1)³ = 2.(3³ + 1) + (3¹ − 1)³
(4)³ = 2.(28) + (2)³
4³ = 2.28 + 2³, MDC( 4 , 2.28 , 2 ) = 2
64 = 56 + 8

For m = 3 we have;

(3^m − 1 + 1)³ = 2.(3^2m − 1 + 1) + (3^m − 1 − 1)³
(3² + 1)³ = 2.(3⁵ + 1) + (3² − 1)³
(10)³ = 2.(244) + (8)³
10³ = 2.244 + 8³
1000 = 488 + 512

And so on.

The quickest method of finding these equations is using cⁿ =B +aⁿ where c = n^m − 1+1 e a = n^m − 1−1, that is;

So the general equation is;

If n is grade 2 we have;

Therefore;
(n^m − 1 + 1)ⁿ = B + (n^m − 1 − 1)ⁿ

(2^m − 1 + 1)² = 2^m + 1 + (2^m − 1 − 1)²( 1 )

MDC(2^m − 1 + 1, 2, 2^m − 1 − 1) = 1, with m ≥ 2.

If n is of grade 3 we have;

B = 2.((3^m − 1 + 1)².(3^m − 1 − 1)⁰ + (3^m − 1 + 1)¹.(3^m − 1 − 1)¹ + (3^m − 1 + 1)⁰.(3^m − 1 − 1)²)

B = 2.((3^m − 1 + 1)² + (3^m − 1 + 1).(3^m − 1 − 1) + (3^m − 1 − 1)²)

B = 2.((3^{2(m − 1)} + 2.3^m − 1 + 1) + 3^{2(m − 1)} − 1 + (3^{2(m − 1)} − 2.3^m − 1 + 1))

B = 2.(2.3^{2(m − 1)} + 1 + 3^{2(m − 1)})

B = 2.(3^{2(m − 1)}(2 + 1) + 1)

B = 2.(3^{2(m − 1)}(3) + 1)

B = 2.(3^{2(m − 1) + 1} + 1)

B = 2.(3^2m − 1 + 1)

Therefore;

(n^m − 1 + 1)ⁿ = B + (n^m − 1 − 1)ⁿ

(3^m − 1 + 1)³ = 2.(3^2m − 1 + 1) + (3^m − 1 − 1)³( 2 )

MDC(3^m − 1 + 1, 2.(3^2m − 1 + 1), 3^m − 1 − 1) = 2.t ≥ 2, with t ∈ N^* and m ≥ 2

If n is of grade 4 we have;

B = 2.((4^m − 1 + 1)³.(4^m − 1 − 1)⁰ + 4^m − 1 + 1)².(4^m − 1 − 1)¹ + 4^m − 1 + 1)¹.(4^m − 1 − 1)² + 4^m − 1 + 1)⁰.(4^m − 1 − 1)³)

B = 2.(4^3m − 2 + 4^m) or B = 2^2m + 1.(2^{4(m − 1)} + 1) or B = 2^6m − 3 + 2^2m + 1 or B = 8^2m − 1 + 2^2m + 1

Doing the calculations correctly arrived at;

B = 2.(43m − 2 + 4m) or B = 22m + 1.(24(m − 1) + 1) or B = 26m − 3 + 22m + 1 or B = 82m − 1 + 22m + 1

Therefore we have;

(n^m − 1 + 1)ⁿ = B + (n^m − 1 − 1)ⁿ
(4^m − 1 + 1)⁴ = 2.(4^3m − 2 + 4^m) + (4^m − 1 − 1)⁴( 3 )
The MDC(4^m − 1 + 1, 2.(4^3m − 2 + 4^m), 4^m − 1 − 1) = 1, with m ≥ 2

or

(2^{2(m − 1)} + 1)⁴ = 2^2m + 1.(2^{4(m − 1)} + 1) + (2^{2(m − 1)} − 1)⁴
The MDC(2^{2(m − 1)} + 1, 2^2m + 1.(2^{4(m − 1)} + 1), 2^{2(m − 1)} − 1) = 1, with m ≥ 2

or

(2^{2(m − 1)} + 1)⁴ = 2^6m − 3 + 2^2m + 1 + (2^{2(m − 1)} − 1)⁴
The MDC(2^{2(m − 1)} + 1, 2^6m − 3, 2^2m + 1, 2^{2(m − 1)} − 1) = 1, with m ≥ 2

If n is grade 5 we have;

B = 2((5^m − 1 + 1)^4 − 0.(5^m − 1 − 1)⁰ + (5^m − 1 + 1)^4 − 1.(5^m − 1 − 1)¹ + (5^m − 1 + 1)^4 − 2.(5^m − 1 − 1)² + (5^m − 1 + 1)^4 − 3.(5^m − 1 − 1)³ + (5^m − 1 + 1)^4 − 4.(5^m − 1 − 1)⁴)

B = 2((5^m − 1 + 1)⁴ + (5^m − 1 + 1)³.(5^m − 1 − 1) + (5^m − 1 + 1)².(5^m − 1 − 1)² + (5^m − 1 + 1).(5^m − 1 − 1)³ + (5^m − 1 − 1)⁴)

Making the calculations it will arrive that B is worth;

B = 2.(5^4m − 3 + 2.5^2m − 1 + 1)

So the equation for grade 5 is;

(5^m − 1 + 1)⁵ = 2.(5^4m − 3 + 2.5^2m − 1 + 1) + (5^m − 1 − 1)⁵( 4 )

MDC(5^m − 1 + 1, 2.(5^4m − 3 + 2.5^2m − 1 + 1), 5^m − 1 − 1) = 2.t ≥ 2, with t ∈ N^* and m ≥ 2.

If n is grade 6 we have;

B = 2.((6^m − 1 + 1)^5 − 0.(6^m − 1 − 1)⁰ + (6^m − 1 + 1)^5 − 1.(6^m − 1 − 1)¹ + (6^m − 1 + 1)^5 − 2.(6^m − 1 − 1)² + (6^m − 1 + 1)^5 − 3.(6^m − 1 − 1)³ + (6^m − 1 + 1)^5 − 4.(6^m − 1 − 1)⁴ + (6^m − 1 + 1)^5 − 5.(6^m − 1 − 1)⁵)

B = 2.((6^m − 1 + 1)⁵ + (6^m − 1 + 1)⁴.(6^m − 1 − 1) + (6^m − 1 + 1)³.(6^m − 1 − 1)² + (6^m − 1 + 1)².(6^m − 1 − 1)³ + (6^m − 1 + 1).(6^m − 1 − 1)⁴ + (6^m − 1 − 1)⁵)

Doing the calculations correctly will arrive at;

B = 2.(6^5m − 4 + 20.6^3m − 3 + 6^m), or B = 2.6^m.(6^4m − 4 + 20.6^2m − 3 + 1) and the equation is;

(6^m − 1 + 1)⁶ = 2.6^m.(6^4m − 4 + 20.6^2m − 3 + 1) + (6^m − 1 − 1)⁶( 5 )

With MDC(6^m − 1 + 1, 2.6^m.(6^4m − 4 + 20.6^2m − 3 + 1), 6^m − 1 − 1) = 1, with m ≥ 2

Then notice that the conditions from (1) to (5) have been satisfied for the cases where n is even and n is odd.

In order to prove this equation we must show for the general case not only from (1) to ( 5 ) but from (1) to (n).

For n pair:
Be n =2k with k ∈ N*, by the previous examples the MDC(a,B,c)=1, the Replaced in B is obtained;

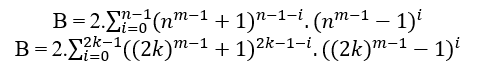
By the definition of Pair the B is already a Pair, then it is divisible by 2, it remains to check c and a. If c and a are Odd then the MDC (c,B,a) is 1, if c and b is Even then the MDC(c,B,a) is 2.t ≥ 2, with t ∈ N*.

As c = n^{m − 1} + 1 and a = n^{m − 1} − 1 of equation cⁿ = B ⁺ aⁿ when replacing the values of n and B we have;

So 2.(2^{m − 2.}k^{m − 1}) + 1 as 2.(2^{m − 2}.k^{m − 1}) − 1, are odd, so a and c are odd, with this the only value dividing a, B and c is 1.

For n Impar:
Whether n = 2k + 1 with k ∈ ^N*, by the previous examples the MDC(a,B,c)=1, the Replaced in B is obtained;

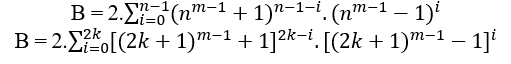
By setting pair the B is already a pair, then it is divisible by 2, it remains to check c and a. If c and a are odd then the MDC(c,B,a) is 1, if c and b is even then the MDC(c,B,a) is 2.t ≥ 2, with t ∈ N*.

As c = n^m − 1 + 1 and a = n^m − 1 − 1 of the equation cⁿ = B + aⁿ when replacing the values of n and B we have;

As 2k + 1 is odd if we square it is also odd:
(2k + 1)² = 4k² + 4k + 1 = 2.(2k² + 2k) + 1
If we add 1 on both sides or subtract 1, is that a pair?
(2k + 1)² + 1 = 2.(2k² + 2k) + 2 = 2.[2k² + 2k + 1] it’s a pair, and (2k + 1)² − 1 = 2.(2k² + 2k) − 2 = 2.[2k² + 2k − 1] it’s a pair.

As 2k + 1 is odd if we rise to the cube is also odd:
(2k + 1)³ = 8k³ + 12k² + 6k + 1 = 2.(4k³ + 6k² + 3k) + 1
If we add 1 on both sides or subtract 1, is that a pair?
(2k + 1)³ + 1 = 2.(4k³ + 6k² + 3k) + 2 = 2.[4k³ + 6k² + 3k + 1] it’s a pair, and (2k + 1)³ − 1 = 2.(4k³ + 6k² + 3k) − 2 = 2.[4k³ + 6k² + 3k − 1] it’s a pair.

As 2k + 1 is odd if we raise the fourth power is also odd:
(2k + 1)⁴ = 16k⁴ + 32k³ + 6k + 1 = 2.(8k⁴ + 16k³ + 3k²) + 1
If we add 1 on both sides or subtract 1, is that a pair?
(2k + 1)⁴ + 1 = 2.(8k⁴ + 16k³ + 3k²) + 2 = 2.[8k⁴ + 16k³ + 3k² + 1] it’s a pair, and (2k + 1)⁴ − 1 = 2.(8k⁴ + 16k³ + 3k²) − 2 = 2.[8k⁴ + 16k³ + 3k² − 1] it’s a par.

if it continues it will always be a pair so (2k + 1)^m − 1 + 1 and (2k + 1)^m − 1 − 1 is even and as B is also even, so the smallest value that divides c, B and a is 2, so MDC (a, B, c) = 2.t ≥ 2, with t ∈ N *

So we have the two main Equations:

3.3.1 TASTING S.T.m

To taste S.T.M just remains to show that regardless of the n whether it is even or odd we have MDC(a,B,c) = c where c = 2n − 1 has already been shown that (**) has different MDC if n is even as well as n is odd. But if we use the tool (*) that was generated from Newton’s binomial, when doing x = y it was reduced to the following equation;

As

by isolating

we have;

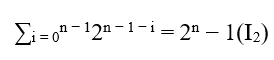
By replacing (I2) and (I1) it is obtained;

(2x)ⁿ = xⁿ.(2ⁿ− 1) + xⁿ

For the first side of the equation to be written as the sum of two powers of the second side of the equation, and as the common factor is xn, however as it has not been defined which value of x, then it is enough x to be written as 2ⁿ – 1, said this the equation will only depend on the degree n, so we have;

(2x)ⁿ = xⁿ.(2ⁿ− 1) + xⁿ
(2.(2ⁿ − 1))ⁿ = (2ⁿ − 1)ⁿ.(2ⁿ − 1) + (2ⁿ − 1)ⁿ

So another equation that only depends on one variable.

(2.(2ⁿ − 1))ⁿ = (2ⁿ − 1)^n + 1 + (2ⁿ − 1)ⁿ

Data for this new equation;
a = 2.(2ⁿ − 1), B = (2ⁿ − 1)^n + 1 and c = 2ⁿ − 1

MDC(a,B,c)=MDC(2.(2ⁿ − 1), (2ⁿ − 1)^n + 1, 2ⁿ − 1) = 2ⁿ − 1 = c

for n even
That is n=2k with k ∈ N^*

MDC(2.(2^2k − 1), (2^2k − 1)^2k + 1, 2^2k − 1) = 2^2k − 1 = c

for odd n
That is n= 2k + 1 with k ∈ N^*

MDC(2.(2^2k + 1 − 1), (2^2k + 1 − 1)^2k + 2, 2^2k + 1 − 1) = 2^2k + 1 − 1 = c

In fact, it has been proven because all the statements that the S.T.M proposed have been answered.
Test with numbers;
For n = 2 we have;

(2.(2ⁿ − 1))ⁿ = (2ⁿ − 1)^n + 1 + (2ⁿ − 1)ⁿ
(2.(2² − 1))² = (2² − 1)^2 + 1 + (2² − 1)²
(2.(3))² = 3³ + 3²
6² = 3³ + 3²
36 = 27 + 9

For n = 3 we have;

(2.(2ⁿ − 1))ⁿ = (2ⁿ − 1)^n + 1 + (2ⁿ − 1)ⁿ
(2.(2³ − 1))³ = (2³ − 1)^3 + 1 + (2² − 1)³
(2.(7))³ = 7⁴ + 7³
14³ = 7⁴ + 7³
2744 = 2401 + 343

At the moment S.T.M apparently two equations, but only one is in the Conjecture format that it is;

(2^m − 1 + 1)² = 2^m + 1 + (2^m − 1 − 1)²
MDC(2^m − 1 + 1, 2, 2^m − 1 − 1) = 1, with m ≥ 2.  “It is not, because it contains 2 as an exponent ”

and

(2.(2ⁿ − 1))ⁿ = (2ⁿ − 1)^n + 1 + (2ⁿ − 1)ⁿ
MDC(2.(2ⁿ − 1), 2ⁿ − 1, 2ⁿ − 1) = 2ⁿ − 1, with n ≥ 2. ” if n>2 then belongs to Beal Conjecture”

3.4 OTHER EQUATIONS GENERATED BY THE METHOD OF S.T.M.

F₁: ⇒  (2^m − 1 + 2^k − 1)² = 2^k(m + 1) + (2^m − 1 − 2^k − 1)²
It is the general ( 1 ).
MDC(2^m − 1 + 2^k − 1, 2, 2^m − 1 − 2^k − 1) = 1, with k = 1 and m ≥ 2.
or
MDC(2^m − 1 + 2^k − 1, 2, 2^m − 1 − 2^k − 1) = 2, with m ≥ 2 and m > k > 1.
Type if m = 4, then k can be 3.2 and 1.

F₂: ⇒  (2^m − 1.k^m + k)² = (2k)^m + 1 + (2^m − 1.k^m − k)²
This is the general equation of the previous one.
MDC(2^m − 1.k^m + k, 2k, 2^m − 1.k^m − k) = k, with m ≥ 2 and k ∈ N^*.

F₃: ⇒  (2^m + k^m + 2)² = (2k)^m + 2 + (2^m − k^m + 2)²
or
(2^m + k^m + 2)² = (2k)^m + 2 + (k^m + 2 − 2^m)²
If m = 0 and k is even we have; MDC(1 + k², 2k, |1 − k²|) = 1, with k ∈ N^*.
If m = 0 and k is odd we have; MDC(1 + k², 2k, |1 − k²|) = 2α ≥ 2, with k, α ∈ N^*.
If k is odd we have; MDC(2^m + k^m + 2, 2k, |2^m − k^m + 2|) = 1, with m ≥ 1 and k ∈ N^*.
If k is even we have; MDC(2^m + k^m + 2, 2k, |2^m − k^m + 2|) = 2α ≥ 2, with m ≥ 1 and k, α ∈ N^*.

General Format Formula C² = B + A² ⇒ C² = b^m + A²
G₁: ⇒  (a^m + 2^m − 2.t^m)² = (2.a.t)^m + (a^m − 2^m − 2.t^m)²
Dice:
C = a^m + 2^m − 2.t^m, b = 2.a.t and A = |a^m − 2^m − 2.t^m|

( i ) If a is odd and m> 2 the MDC(C,b,A)=1, ∀t ∈ N^*.

( ii ) If a is odd with m = 2 and t an Even, the MDC(C,b,A)=1 .

( iii ) If a is odd with m = 2 and t an Odd, the MDC(C, b, A) = 2α ≥ 2 with α ∈ ^N*.

( iv ) If a is pair and m > 2 the MDC (C, b, A) = 2α ≥ 2, ∀t, α ∈ ^N*.

( v ) If a is paired with m = 2 and t an Odd the MDC(C, b, A) = 1, t ∈ ^N*.

( vi ) If a is paired with m = 2 and t a Pair the MDC (C, b, A) = 2α ≥ 2, t, α ∈ ^N*.

How each Formula or Equation came about:
The idea arose due to Fermat–Catalan conjecture, because when having C^z = B^y + A^x, it only has a finite amount of solutions in which A, B, and C are positive integers without common prime factors and x, y, and z are positive integers satisfying ()/() < 1, because all solutions will have 2 as one of the exponents. Because of this it would be possible that fixing exponent 2 in the square difference would have satisfactory results in the format of the conjecture? When using the same method of S.T.M, new equations with solutions in positive integers appeared.

F₁: Be (2^r + 2^s)² = B + (2^r − 2^s)² ⇒ B = (2^r + 2^s)² − (2^r − 2^s)², with B, r, s ∈ ℕ where r > s, r and s variables not currently defined.

B = (2^r + 2^s)² − (2^r − 2^s)² → B = (2^r + 2^s − 2^r + 2^s).(2^r + 2^s + 2^r − 2^s) → B = (2^s + 2^s).(2^r + 2^r) → B = 2^s + 1.2^r + 1 → B = 2^{s + r + 2}

When adapting to be in the mek variables as STM, we have m> k subtracting 1 on both sides we have m – 1> k – 1 when comparing r> s, we have r = m – 1 and s = k – 1, with that we have B = 2^{k – 1 + m – 1 + 2} → B = 2^{m + k – 2 + 2} → B = 2^{m + k}, so the equation is;

F₁: ⇒ (2^m − 1 + 2^k − 1)² = 2^m + k + (2^m − 1 − 2^k − 1)²

If k is 1, then MDC(2^m − 1 + 2^1 − 1, 2, 2^m − 1 − 2^1 − 1) = MDC(2^m − 1 + 2⁰, 2, 2^m − 1 − 2⁰) = MDC(2^m − 1 + 1, 2, 2^m − 1 − 1) = 1, ∀m ∈ N^*

Example when using this equation that has GCD = 1, with m = 2, 3, 5, 6.; m cannot be 1 because k was 1.

For m = 2
(2^2 − 1 + 1)² = 2^2 + 1 + (2^2 − 1 − 1)² → 3² = 2³ + 1² → 9 = 8 + 1

For m = 3
(2^3 − 1 + 1)² = 2^3 + 1 + (2^3 − 1 − 1)² → 5² = 2⁴ + 3² → 25 = 16 + 9

For m = 4
(2^4 − 1 + 1)² = 2^4 + 1 + (2^4 − 1 − 1)² → 9² = 2⁵ + 7² → 3⁴ = 2⁵ + 7² → 81 = 32 + 49

For m = 5
(2^5 − 1 + 1)² = 2^5 + 1 + (2^5 − 1 − 1)² → 17² = 2⁶ + 15² → 289 = 64 + 225

For m = 6
(2^6 − 1 + 1)² = 2^6 + 1 + (2^6 − 1 − 1)² → 33² = 2⁷ + 31² → 1089 = 128 + 961

If k > 1, then MDC(2^m − 1 + 2^k − 1, 2, 2^m − 1 − 2^k − 1) = 2, ∀m, k ∈ N^*, where m > k

Example if m = 5, then k varies between 2 to 4.

(2^m − 1 + 2^k − 1)² =2^m + k + (2^m − 1 − 2^k − 1)²→ (2^5 − 1 + 2^k − 1)² =2^5 + k + (2^5 − 1 − 2^k − 1)²→ (2⁴ +2^k − 1)² =2^5 + k + (2⁴ − 2^k − 1)²

For k = 2
(2⁴ + 2^2 − 1)² = 2^5 + 2 + (2⁴ − 2^2 − 1)² → (2⁴ + 2¹)² = 2⁷ + (2⁴ − 2¹)²
→ 18² = 2⁷ + 14² → 324 = 128 + 196

For k = 3
(2⁴ + 2^3 − 1)² = 2^5 + 3 + (2⁴ − 2^3 − 1)² → (2⁴ + 2²)² = 2⁸ + (2⁴ − 2²)²
→ 20² = 2⁸ + 12² → 400 = 256 + 144

For k = 4
(2⁴ + 2^4 − 1)² = 2^5 + 4 + (2⁴ − 2^4 − 1)² → (2⁴ + 2³)² = 2⁹ + (2⁴ − 2³)²
→ 24² = 2⁹ + 8² → 24² = 2⁹ + 2⁶ → 576 = 512 + 64

F₂: Be (2^s.k^r + k)² = B + (2^s.k^r − k)² ⇒ B = (2^s.k^r + k)² − (2^s.k^r − k)², wiyh B, k, r, s ∈ ℕ where r > s, r and s variables not currently defined.

B = (2^s.k^r + k)² − (2^s.k^r − k)² → B = (2^s.k^r + k − 2^s.k^r + k).(2^s.k^r + k + 2^s.k^r − k) → B = (2k).(2^s + 1.k^r) → B = 2k.2^s + 1.k^r → B = 2^s + 2.k^r + 1, For B to be written as a power just s + 2 = r + 1, this results in B = (2k)^{r + 1} or B = (2k)^{s + 2}, However for this to be true r must be greater than s that’s r> s.

Hypothesis s + 2 = r + 1 ⇒ s = r − 1  and thesis r > s

We have to s + 1> s adding 1 on both sides s + 2> s + 1 ⇒ r + 1 = s + 2> s + 1> s ⇒ r + 1> s in turn r + 1> r therefore r > s, notice that when using the Hypothesis where s = r – 1 ⇒ r = s + 1 and substitute in r> s, the inequality s + 1> s is satisfied.

So B = (2k) ^{r + 1} = (2k) ^{s + 2} = (2k) ^{r + 1}, so the equation is;
(2^{r – 1}.k^r + k)² = (2k)^{r + 1} + (2^{r – 1}.k^r – k)², so that everything is based on the same variable m, just r be equal to m, that is r = m. With that we already have another equation;

F₂: ⇒ (2^m − 1.k^m + k)² = (2k)^m + 1 + (2^m − 1.k^m − k)²

If k is 1, this is the MDC’s own F1 equation = 1;

(2^m − 1.1^m + 1)² = (2.1)^m + 1 + (2^m − 1.1^m − 1)² → (2^m − 1 + 1)² = 2^m + 1 + (2^m − 1 − 1)²

If k > 1 has as MDC = k

MDC(2^m − 1.k^m + k, 2k, 2^m − 1.k^m − k) = k, ∀m, k ∈ N^*.

For k = 2

(2^m − 1.k^m + k)² = (2k)^m + 1 + (2^m − 1.k^m − k)²
(2^m − 1.2^m + 2)² = (4)^m + 1 + (2^m − 1.2^m − 2)²
(2^2m − 1 + 2)² = 4^m + 1 + (2^2m − 1 − 2)²
If m = 1
(2^{2.1 − 1} + 2)² = 4^1 + 1 + (2^{2.1 − 1} − 2)² → 4² = 4² + 0² → 16 = 16
If m = 2
(2^{2.2 − 1} + 2)² = 4^2 + 1 + (2^{2.2 − 1} − 2)² → (2³ + 2)² = 4³ + (2³ − 2)² → 10² = 4³ + 6² → 100 = 64 + 36
Se m = 3
(2^{2.3 − 1} + 2)² = 4^3 + 1 + (2^{2.3 − 1} − 2)² → (2⁵ + 2)² = 4⁴ + (2⁵ − 2)² → 34² = 4⁴ + 30² → 1156 = 256 + 900
*
*
*
And so on …

For k = 3
(2^m − 1.k^m + k)² = (2k)^m + 1 + (2^m − 1.k^m − k)²
(2^m − 1.3^m + 3)² = 6^m + 1 + (2^m − 1.3^m − 3)²
If m = 1
(2^1 − 1.3¹ + 3)² = 6^1 + 1 + (2^1 − 1.3¹ − 3)²
(2⁰.3 + 3)² = 6² + (2⁰.3 − 3)² → 6² = 6² + 0²
If m = 2
(2^2 − 1.3² + 3)² = 6^2 + 1 + (2^2 − 1.3² − 3)²
(2¹.9 + 3)² = 6³ + (2¹.9 − 3)² → 21² = 6³ + 15² → 441 = 216 + 225
If m = 3
(2^3 − 1.3³ + 3)² = 6^3 + 1 + (2^3 − 1.3³ − 3)^2Nn
(2².27 + 3)² = 6⁴ + (2².27 − 3)² → 111² = 6⁴ + 105² → 12321 = 1296 + 11025
*
*
*

And so on …
F₃: Be (2^s + k^r)² = B + (2^s − k^r)² ⇒ B = (2^s + k^r)² − (2^s − k^r)², with B, r, s ∈ ℕ where r > s, r and s variables not currently defined.

B = (2^s + k^r)² − (2^s − k^r)² → B = (2^s + k^r − 2^s + k^r).(2^s + k^r + 2^s − k^r) → B = 2.k^r.2^s + 1 → B = 2^s + 2.k^r, in this case for B to be a power enough r = s + 2. In fact r > s because s + 2 > r = s + 1 > s ⇒ r > s when placing the exponent as a function of m, just s = m this give us r = m + 2.

Soon B = 2^{s + 2}.k^r = (2k)^r = (2k)^{m + 2}.

So the new equation is;

F₃: ⇒ (2^m + k^m + 2)² = (2k)^m + 2 + (2^m − k^m + 2)², with k ∈ N^*and m ≥ 0.
If k is 1 for ∀m ∈ N* the MDC = 1 or If m is 0 to ∀k ∈ N^* also the MDC = 1.
If none of these cases occur F3 Has MDC = 2α ≥ 2, ∀α ∈ N *

The logic is the same for G₁, “Since it is the general”;

Because when doing B = (a^r + 2^s.t^r )² − (a^r − 2^s.t^r)² → B = (a^r + 2^s.t^r  − a^r  + 2^s.t^r).(a^r + 2^s.t^r  + a^r- 2^s.t^r) →

.Simply put, s + 2 = r or s = r – 2, as r is m doing the conversion we have s = m – 2, that is;
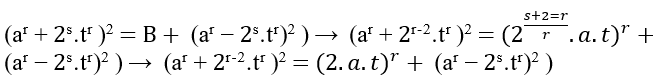G₁: ⇒  (a^m + 2^m − 2.t^m)² = (2.a.t)^m + (a^m − 2^m − 2.t^m)²
Dice:
C = a^m + 2^m − 2.t^m, B = 2.a.t e A = |a^m − 2^m − 2.t^m|

( i ) If a is odd and m> 2 the MDC (C, b, A) = 1, ∀t ∈ N *.

( ii ) If a is odd with m = 2 and t an Even, the MDC(C,b,A)=1 .

( iii ) If a is odd with m = 2 and t an Odd, the MDC(C, b, A) = 2α ≥ 2 with α ∈ ^N*.

( iv ) If a is pair and m > 2 the MDC (C, b, A) = 2α ≥ 2, ∀t, α ∈ ^N*.

( v ) If a is paired with m = 2 and t an Odd the MDC(C, b, A) = 1, t ∈ ^N*.
( vi ) If a is paired with m = 2 and t a Pair the MDC (C, b, A) = 2α ≥ 2, t, α ∈ ^N*.

4. FORMULAS GENERATED BY T.M E S.T.M WITH SOLUTIONS IN NATURAL

Basic data; a,b,c,x,y,z,A,B,C,α and k ∈ N

Formula₁: C^z = C^{xyk + 1} = B^y+ A^x, mdc(x,y,z)=1

( b^y + a^x )^xyk + 1  = [ b( b^y + a^x)^xk]^y + [ a( b^y + a^x )^yk]^x

Dice:
C =b^y+ a^x,  B =b(b^y+ a^x)^xk  e  A = a( b^y+ a^x )^yk,  MDC(C, B, A) = C.

Formula₂: C^z = C^{xk + 1} = B^x+ A^x, ouC^z = C^{yk + 1} = B^y+ A^y, mdc(z,x)= mdc(z,x) = 1

( b^x + a^x )^xk + 1  = [ b( b^x + a^x )^k ]^x + [ a( b^x + a^x )^k ]^x

OR

( b^y + a^y )^yk + 1  = [ b( b^y + a^y )^k]^y + [ a( b^y + a^y )^k ]^y

Dice:
C =b^x+ a^x, B =b(b^x+ a^x)^k e A = a(b^x+ a^x )^k, MDC(C, B, A) = C.

OR

C =b^y+ a^y, B =b(b^y+ a^y)^k e A = a( b^y+ a^y )^k, MDC(C, B, A) = C.

Formula₃: C^z = C^xk = B^{xkα+ 1}+A^x, or C^z=C^yk = B^{ykα+ 1}+A^y, mdc( z, y , x ) = 1

[ c( c^xk− a^x )^α]^xk = ( c^xk− a^x )^xkα+1 +[ a(c^xk−a^x)^kα]^x

OR

[ c( c^yk− b^y )^α]^yk = [ b( c^yk− b^y )^kα]^y + ( c^yk− b^y )^ykα+1

Dice:
C = c(c^xk − a^x), B = c^xk − a^x and A = a.(c^xk −a^x), MDC(C,B,A)= B.

OR

C = c(c^yk − b^y),  B = b(c^yk − b^y) and A = c^yk − b^y,  MDC(C,B,A)= A.

Formula₄:

(2.(2ⁿ − 1))ⁿ = (2ⁿ − 1)^n + 1 + (2ⁿ − 1)ⁿ

or

(2ⁿ⁺¹ − 2)ⁿ = (2ⁿ − 1)^n + 1 + (2ⁿ − 1)ⁿ

Dice;
a = 2.(2ⁿ − 1), B = (2ⁿ − 1)^n + 1 and c = 2ⁿ − 1, MDC(a B,c)=MDC(2.(2ⁿ − 1), (2ⁿ − 1)^n + 1, 2ⁿ − 1) = 2ⁿ − 1 = c

Formula₅:

G₁: ⇒ (a^m + 2^m − 2.t^m)² = (2.a.t)^m + (a^m − 2^m − 2.t^m)²
Dice:
C = a^m + 2^m − 2.t^m, B = 2.a.t and A = |a^m − 2^m − 2.t^m|, With t ≠ 2.a

( i ) If a is odd and m> 2 the MDC(C,b,A)=1, ∀t ∈ N^*.

( ii ) If a is odd with m = 2 and t an Even, the MDC(C,b,A)=1 .

( iii ) If a is odd with m = 2 and t an Odd, the MDC(C, b, A) = 2α ≥ 2 with α ∈ ^N*.

( iv ) If a is pair and m > 2 the MDC (C, b, A) = 2α ≥ 2, ∀t, α ∈ ^N*.

( v ) If a is paired with m = 2 and t an Odd the MDC(C, b, A) = 1, t ∈ ^N*.
( vi ) If a is paired with m = 2 and t a Pair the MDC (C, b, A) = 2α ≥ 2, t, α ∈ ^N*.

In particular

c² = 2^{m + 1} + b², MDC(a,b,c)=1

(2^m−1+1)²=2^m+1+(2^m−1−1)²
c=2^m−1+1, b=2 and a=2^m−1−1, MDC(a,b,c)=1

5. T.G.M OR GENERAL THEOREM MACENA

Given any valid equation of the positive integers in the form of power, or generated by T.M or S.T.M when multiplying by dα a power, where d is an adequate basis of transformation into the sum of two powers, and α is a multiple positive integer exponent of the exponents of the other bases or mmc of the exponents multiplied by t *, thus results in a power written in the sum of two other powers with a common factor d or multiple of d.

Exemplo:
, with B>A and m ≥ n ≥ 2, where α=mmc(1,m,n).t, t ϵ N*
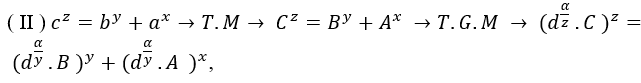, where α=mmc(z,y,x).t, t ϵ N*
, where α=mmc(n,1,n).t, t ϵ N*
( IV ) C²=B+A²→ Geralpor S.T.M→ ( a^m  +  2^m − 2.t^m )²  =  ( 2.a.t )^m  + ( a^m − 2^m − 2.t^m )²→T.G.M →
, where α =mmc(2,m,2).β, β ε N*
With this we always have a common factor in the format of the Conjecture if the exponents x,y,z≥3, regardless of the equation addressed.
“With the exception of ( IV ) which will have grade 2 always at least on one of the bases”.

5.1 PROVING T.G.M

To prove this theorem it is necessary to prove the items. ( I ), ( II ), ( III ) and ( IV ).

Proving item (I) Whether any equation of the type
,with B,

by multiplying by a power

, d not defined at the moment, however
, this is d^m.n.t, soon we have;
as d is not defined it is enough to be equal C to that is 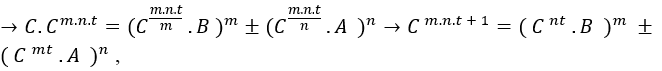, where C is the common factor of the equation, since 
Example in numbers;

C₁ = B^m+A^m→ 29 =3³ + 2², by theorem d=C₁=29 eα= mmc(1,3,2).t = 6t,  →29^6t+1 = 3³ . 29^6t + 2². 29^6t

29^6t+1 =( 3.29^2t )³ + ( 2.29^3t )² , if t=1 we have 29⁷=2523³+48778², mdc( 29 , 2523 , 48778 ) = 29 , if t = 2 we have 29¹³=2121843³+1189646642², mdc(29, 2121843 , 1189646642 ) = 29 and so on with t ≥3
C₂ = B^m-Aⁿ→ 23 =3³-2², by theoremd=C₂=23eα=mmc(1,3,2).t = 6t,→23^6t+1 =3³.23^6t-2².23^6t→
23^6t+1 =(3.23^2t)³ – (2.23^3t)²→, if t=1 we have 23⁷=1587³-24334²,mdc( 23 , 1587 , 24334 ) = 23,if t = 2 we have 23¹³=839523³-296071778², mdc(23, 839523 , 296071778 ) = 23 and so on with t ≥3.
Proving item (II) Whether any equation of type c^z = b^y + a^x with solutions on positive integers, by T.M we will arrive at an equivalent equation with the following bases;
C =b^y+a^x, B =b(b^y+a^x )^xk and A =a( b^y+a^x )^yk, with equation C^xyk+1=B^y+A^x→C^z=B^y+A^x
When multiplying by a power dα, d not defined at the moment, however α = mmc (z, y, x) .t, tϵN *, this is d^zyx.t, so we have;
d^zyx.t .C^z= d^zyx.t.B^y+d^zyx.t .A^x→(d^yx.t .C )^z= (d^zx.t .B )^y+(d^zy.t .A )^x→ As mdc( C , B , A ) = C then

MDC[(d^yx.t .C ),(d^zx.t .B ),(d^zy.t .A ) ] ≥ d^t .C , in particular if d = C we have C^z(yxt+1)= (C^zx.t .B )^y+(C^zy.t .A )^x
MDC[ C , (C^zx.t .B ), (C^zy.t .A ) ] = C. Expanding using all the data the equation is;

{ d^yx.t . b^y+a^x  }^z= {d^zx.t .b( b^y+a^x )^xk}^y+{d^zy.t .a( b^y+a^x )^yk}^x
As z= xyk + 1
{d^yx.t .( b^y+a^x ) }^xyk+1= {d^(xyk+1)x.t .b(b^y+a^x )^xk}^y+{d^(xyk+1)y.t .a( b^y+a^x )^yk}^x
Example in numbers
x=y=2, t=k=1 and b=a=3 and d=5
{5⁴ .( 3²+3² ) }⁵= {5¹⁰ .3( 3²+3² )²}²+{5¹⁰ .3( 3²+3² )²}²
{5⁴ .18 }⁵= {5¹⁰ .3.18²}²+{5¹⁰ .3.18²}²
11250⁵=9492187500²+9492187500²
MDC(11250 ,9492187500,9492187500)=11250
Proving item (III) Whether any equation of type cⁿ = B + aⁿ, with solutions on positive integers, by S.T.M, we have a vast amount of equations but B is always

, ao multiplicar a equação pela potencia d^α, d não definida no momento, com α = mmc(n,1,n).t, t ϵ N*, temos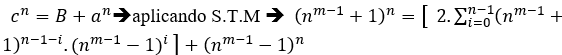

As we have;

→Since d is not defined, d = B is enough;

Or

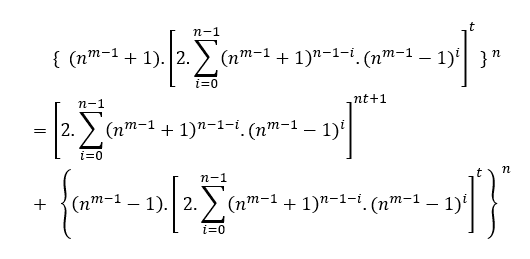
Examples;
( 1 )

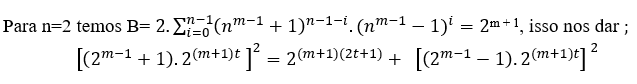
Without = 2, we have→ (3.2^3t )²=2^3(2t+1)+ 2^6t, ∀ t ∈N, MDC[(3.2^3t),2,2]=2
If m = 3, we have →(5.2^4t )²=2^4(2t+1)+(3.2^4t)², ∀ t ∈N, MDC[(5.2^4t),2,(5.2^4t)]=2
[…]
( 2 )

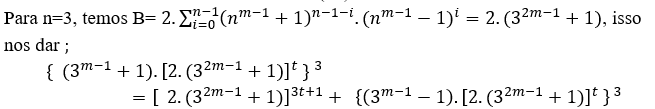Without = 2, we have →{4.56^t}³=56^3t+1+ {2.56^t } ³, ∀ t ∈N, MDC[(4.56^t),56,2.56^t]= 56
If m=3, we have →{10.488^t} ³=488^3t+1+ {8.488^t }³, ∀ t ∈N,MDC[(10.488^t),488,8.488^t] = 488
[…]
( 4 )

( 5 )

( 6 )

∀ m > 1, t ∈ N, MDC[Das Bases] = 2.6^m. (6^4m-4 + 20. 6^2m-3 +1)

( 7 )
And so on
.
.
.
( … )

NOTE: So far the items ( I ), ( II ) and ( III ) only remains ( IV )

Proving item ( IV ) Be any equation of type c²=B+a², with solutions in the positive integers, using the means of S.T.M, we have;
C²=B+C²→General by S.T.M→( a^m +  2^m − 2.t^m )²  =  ( 2.a.t )^m  + ( a^m − 2^m − 2.t^m )², ao multiplicar pela potencia d^α, com d não definido no momento, porém α = mdc(2,m,2).β , β ϵ N*, dessa vez usa β devido que a equação já possui t, dito isso temos;

d^α.(a^m  +  2^m − 2.t^m )²  =  d^α.( 2.a.t )^m  + d^α.( a^m − 2^m − 2.t^m )²
[d^mβ.( a^m  +  2^m − 2.t^m )]²  = [d^2β.( 2.a.t )]^m  + [d^mβ( a^m − 2^m − 2.t^m )]² [d^mβ .( a^m  +  2^m − 2.t^m )]² = [2at.d^2β ]^m  + [d^mβ ( a^m − 2^m − 2.t^m )]²

In this case d can be any number belonging to the positive integers except zero, (dεN*).
Example in numbers;

a=2, d=5et=m=β = 3

[5⁹ .( 2³  +  2¹.3³)]²  = [12.5⁶]3 + [5⁹ .( 2³  -  2¹.3³)]²
[ 5⁹ .( 62 )]²  = [12.5⁶]³ + [5⁹ .( -46)]²
[121093750]²  = [187500]³+ [ -89843750 ]²
121093750²  = 187500³ + (- 89843750 )²

MDC[121093750 ,187500 ,| – 89843750 |] = 31250

OBS: Já o MDC(Das Bases ) ≥ d^β, esse 31250 = 2.d^2β>d^β

The idea is the same for any equation with the sum of 2 power.

So you’re proving T.G.M

Curiosity:( 1.0 )

5 = 3 + 2 → multiplied by the base 3 → 5.3 = 3² + 2.3 → like 3 = 5 – 2 → replaces in the first member 5(5 – 2)=3² + 2.3 → 5² – 2.5 = 3² + 2.³ → isolating 5² = 3² + 2.( 3 + 5 ) →
5² = 3² + 2.( 8 ) → 5² = 3² + 2.( 23 ) → 5² = 3² + 2⁴.

( 1.1 )

5³ = 5³ → 5³ = 5.5² → we can write 5 = 2² + 1, putting in the second member →
5³ = (2² + 1).5^{2 →} 53 = 2².5² + 5² → 5³= 10² + 5².

“NOTE: This curiosity is another article that I will publish in the future, ABC Conjecture”

6. PROVING THE BEAL CONJECTURE

(1st Condition) Given the equation c^z = b^y + a^x, with solutions in the positive integers, with { z , y, x ≥ 3 / c, b , a ≠ 0 }, then a, b and c have a common prime factor, which means that a, b and c are divisible by the same prime number.

Or

(2nd Condition) Equation a ^x + b ^y = c ^z  has no solution for positive integers with x,y,z ≥ 3 and mdc(a,b,c)=1

Starting the test

A (2nd Condition ) It is impossible to obtain numbers in the positive integers with mdc(a,b,c) =1, and exponents x,y,z ≥ 3, for two reasons already shown:

1st — It has been shown that the Fermat–Catalan Conjecture only has a finite amount of solutions, currently there are only 10 equations found, in which a, b, and c are positive integers without common prime factors and x, y, and z are positive wholes satisfying ,

because all solutions will have 2 as one of the exponents, this already sticks to the hypothesis of mdc(a ,b,c) =1, and exponents x,y,z ≥ 3.

THE 10 FOUND ARE; Image taken from wikipedia site.

2nd — If you vote for part S.T.M note that where the equations have the mdc(bases)=1, it always has an exponent 2, even varying the other exponents, and as S.T.M has been proven, just as the Fermat Conjecture – Catalan states at least one of the exponents should be 2, then sticks the hypothesis for the simple reason of containing an exponent 2 in one of the bases.

So there’s only one other condition left to be proven.

The (1st Condition) is already possible through T.M, S.T.M e T.G.M, all have common factors in both bases only to show that it has a common prime factor that divides both bases with the exponents x,y,z ≥ 3.

TEST:

Dice;

Let p be a prime number, and F^p = p^u a common prime factor p, and pi ≠pi+1, i index, distinct cousins and exponents Ui ≥ Ui+1≥0, i index, different exponents or not, then C a natural number can be entered as;

C = Fp = p^u, ou C = p1^u1.p2^u2 ou C = p1^u1.p2^u2. p3^u3 .p4^u4 …pi^ui .pi+1^ui+1… Common prime factors, such as c^z = b^y + a^x, and by some method of T.M, S.T.M e T.G.M, is obtained C^z = B^y + A^x, so;

C^z =(F^p )^z = p^z.u↔B^y + A^x = p^z.u, or C^z =( p1^u1 ) .p2^u2 )^z =p1^z.u1 .p2^z.u2 ↔B^y + A^x = p1^z.u1 .p2^z.u2 or

C^z =(p1^u1.p2^u2. p3^u3 .p4^u4 … pi^ui.pi+1^ui+1…)^z =p1^z.u1 .p2^z.u2. p3^z.u3.p4^z.u4… pi^z.ui.pi^+1z.ui+1…= B^y + A^x

BUILDING C^{z →} C^z FROM Cⁿ.

In fact 1 = 1, because 1 is a neutral element of multiplication said that is c ε N*, when multiplied on both sides we have 1.c = 1.c→c = c, when multiplied again by c we have c.c =c.c→c2 = ^c2→ i^f this process continues for n times we have → cⁿ = cⁿ, note if n > z, we have cⁿ>c^z.

So cⁿ = cⁿ can be inscribed as cⁿ = c^z.c^{n – z}, the hypothesis of conjecture is that c^z= b^y+ a^x, has a common prime factor that divides the bases c,b and a, with z,y,x ≥ 3, with this we have;

cⁿ = c^z.cⁿ – z→cⁿ = ( b^y+ a^x).cn – z→cⁿ = b^y. c^{n – z} + a^x.c^{n – z}, then if c^z= b^y+ a^x  has solutions in the positive integers, with exponents greater than or equal to 3, in fact cⁿ = b^y. c^{n – z} + a^x.c^{n – z} has a factor that divides both because the mdc(cⁿ, b^y. c^{n – z}, a^x.c^{n – z}) = cⁿ> 1.

Translating is demonstrated that c^z= b^y+ a^x  has such solutions so in fact it is confirming the hypothesis and this is a thesis. But to get to that statement we have to prove equality, but this has already been shown by the T theorems.M, S.T.M e T.G.M, however, the conditions of the exponents were greater than or equal to 3 were not included, nor the conditions of the prime factors so concluding this is proven the Beal Conjecture.

Using T.M we have that equation c^z= b^y+ a^x, become;

(b^y+a^x)^xyk+1=[b.(b^y+a^x)^xk ]^y+[a.(b^y+a^x)^yk]^x, where z = xyk + 1, C = b^y+a^x ,
B= b.(b^y+a^x)^xk and A = a.(b^y+a^x)^yk , that is C^z = B^y + A^x, with mdc (C,B,A) = C >1, for
x,y,z> 2 ou x,y,(xyk+1) > 2.

So if C^z = B^y + A^x has solutions in the positive integers then c^z = c^xyk+1 = by + ^ax, simply because it has the same format or structure. Dito isso resta mostrar cⁿ, que é;
cⁿ = b^y. c^{n – z} + a^x.c^{n – z} , adapting for bases C, B and A we have;

C ⁿ = B^y. C ^{n – z} + A^x.C^{n – z}

(b^y+a^x)ⁿ=[b.(b^y+a^x)^xk ]^y.(b^y+a^x)(n-z)+[a.(b^y+a^x)(yk )]^x.(b^y+a^x)(n-z)
(b^y+a^x)ⁿ=b^y.(b^y+a^x)^{xyk + n- z}+a^x.(b^y+a^x)^{xyk + n- z} , like z = xyk+1,
(b^y+a^x)n=b^y.(b^y+a^x)^{xyk + n- xyk-1} +a^x.(b^y+a^x)^{xyk + n- xyk-1}
(b^y+a^x)ⁿ=b^y.(b^y+a^x)^n-1+a^x.(b^y+a^x)^n-1

“This is the equation in functions of the exponents n, x, y, based on the previously shown theorems we have (n – 1) is a multiple of x, y, this is n – 1 =

xyt or n = xy.t + 1, t is just to differentiate from k, already using ”

(b^y+a^x)^xy.t+1=b^y.(b^y+a^x)^xyt +a^x.(b^y+a^x) ^xyt
(b^y+a^x)^xy.t+1=[b.(b^y+a^x)^xt ]^y+[a.(b^y+a^x)^yt]^x
So, as Cⁿ>C^z→Cⁿ-C^z> 0 → (b^y+a^x )^xy.t+1-(b^y+a^x )(x^y.k+1)>0→dividing by(b^y+a^x ), we have→(b^y+a^x )^xy.t-(b^y+a^x )(x^y.k)>0→dividing (b^y+a^x )^xy, we have →
(b^y+a^x )^t-(b^y+a^x )^k>0→(b^y+a^x )^t>(b^y+a^x )^k→t > k, ∀ t,k ∈N

So the equation with all the variables can be written as follows;
( EQ₁ )(b^y+a^x)^xy(t+k)⁺¹=[b.(b^y+a^x)x^(t+k) ]^y+[a.(b^y+a^x)(^y(t+k) )]^x

Or

( EQ₂ ) (b^y+a^x)^{xy( t – k )+1)}=[b.(b^y+a^x)^{x( t – k ) ]y}+[a.(b^y+a^x)^{y(t – k)} ]x

To get to these two formulas just use T.M, with n-z=xyt→n= xyt + z, and as z=xyt, we have n = xy (t +k), and as it was shown that t > k, is also valid n = xy( t – k ) ∈N*

Like the other formulas generated by T.M and some also of S.T.M e T.G.M, which has the format C^z = B^y +A^x, has the same behavior as ( EQ1)e ₍ EQ2), then showing the conditions of prime factors as at the beginning of this test is literally proving all the conditions of the Beal Conjecture for the affirmative case that is (1st Condition ).

(#) For the case of a common prime factor in ( EQ1)e ( EQ2), this isC^z= B^y + A^x = p^z.u ;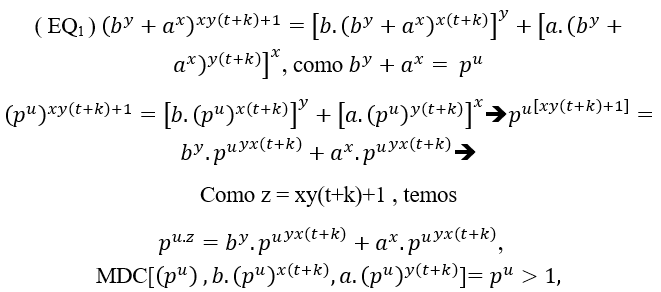

Thus a common prime factor p, because equality is satisfied if it continues,

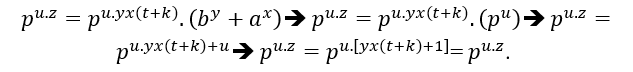Analogously to ( EQ1 ) will have the same result

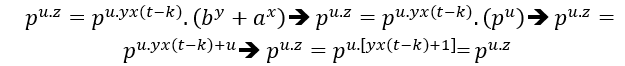(##)For the case of 2 common prime factors in (EQ1)and (EQ2), this is

, in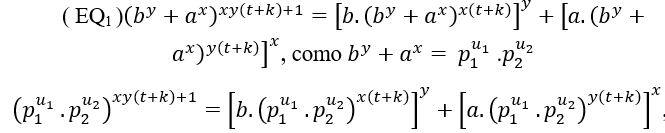 fact the mdc will be the product of two powers of distinct primes, this is
Checking equality, such as z = xy(t+k)+1, we have;

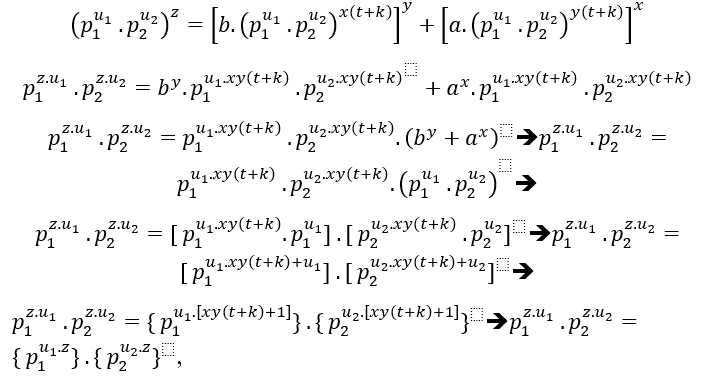when dividing by any of the common prime factors falls into the condition ( # ).
Analogously to (EQ2);

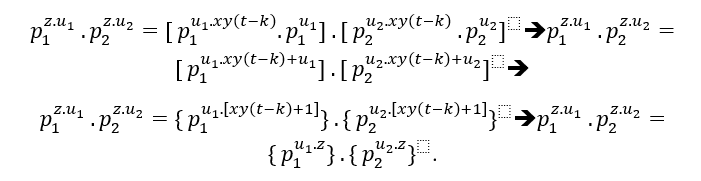 ( ###) For the case of a common prime factor in (EQ1) and (EQ2), this is;

In fact we will have an MDC with several common prime factors, or from 3 onwards, powers of distinct primes from each other, that’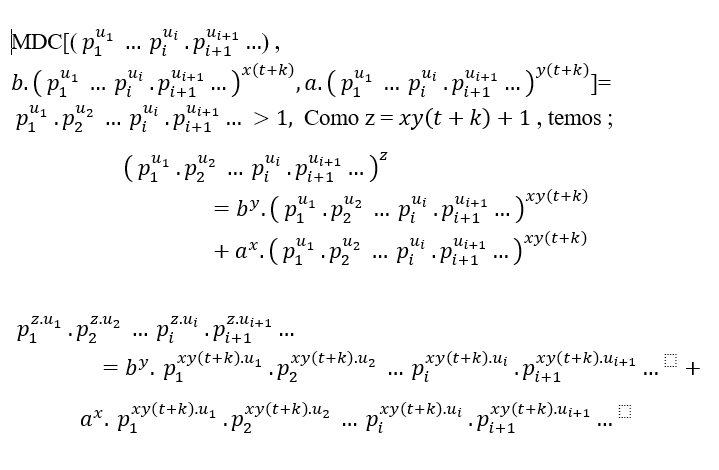
_________

_________

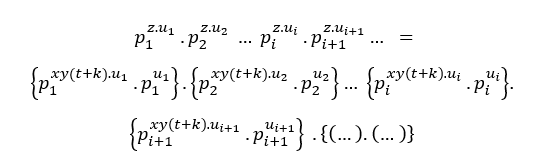
Just like the condition (## ), we have;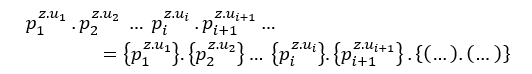

Each time it divides by a common prime factor they will reduce until it becomes only a common prime factor.
Analogously to (EQ2), _it is also satisfied;

Therefore proven conjecture!

7. FINAL CONSIDERATIONS

This article was proposed as a general objective proof – there the Beal Conjecture, when using the T theorems.M, S.T.M e T.G.M combined with applications in number theory it was actually possible to demonstrate, however it was not possible to find a con – example, however when using the means in the course of development must have noticed that each step was essential for the other anyway in relation to the theorems presented without the T.M could not use T.G.M, sem o T.G.M o S.T.M could not be used for the Beal Conjecture if it did not have T.M o S.T.M e T.G.M would be something very vague in other words did not support the demonstration of such Conjecture.
At best without the other theorems such as Pythagoras Theorem, Fermat’s Last Theorem, Sebá’s Theorem and Fermat’s Conjecture – Catalan the T.M would be something very vague and would take much longer to be proven, just by possessing such theorems the T.M is an extension and at the same time what support the theorems cited, in other words T.M was the missing piece for completion.

8. REFERENCES

BEAL, Andrew. Site: Wiki de Poker. 2008. Disponível em:<https://poker.fandom.com/wiki/Andrew_Beal> Acesso em: 03 de Junho de 2018.

FERMAT, biografias de Matemáticos. Site: Só Matemática. 1998-2019. Disponível em: <https://www.somatematica.com.br/biograf/fermat.php> Acesso em: 18 de Maio de 2018.

KILHIAN, (Sebastião Vieira do Nascimento, “Sebá”). A Conjectura de Beal – Casos Particulares. Site: O baricentro da Mente. 28/04/2012. Disponível em: <https://www.obaricentrodamente.com/2014/11/a-conjectura-de-beal-casos-particulares.html> Acesso em: 27 de Maio de 2018.

TANIYAMA e SHIMURA, Teorema de Shimura-taniyama-Wil. Editada pela última vez em 5 de setembro de 2017 Site: Wikipédia. Disponível em:<https://pt.wikipedia.org/wiki/Teorema_de_Shimura-Taniyama-Weil> Acesso em: 16 de Junho de 2018.

WILES, Biografia de matemáticos. Site: Só Matemática. 1998-2019. Disponível em: <https://www.somatematica.com.br/biograf/andrew.php > Acesso em: 15 de Maio de 2018.

9. SEARCH SOURCES

Site: O Baricentro da Mente. Título: A conjectura de Beal casos particulares. URL: <https://www.obaricentrodamente.com/2014/11/a-conjectura-de-beal-casos-particulares.html> Acesso em: 05 de Maio de 2018.
Site: O Baricentro da Mente. Título: Método de resolução das equações de Sebá. URL: <https://www.obaricentrodamente.com/2012/04/metodo-de-resolucao-das-equacoes-de.html> Acesso em: 05 de Maio de 2018.
Site: Folha de São Paulo. Título: Livro narra solução de teorema que confundiu teóricos por 358 anos. URL: <https://www1.folha.uol.com.br/fsp/ciencia/fe25109801.htm> Acesso em: 10 de Maio de 2018.
Site: Wikipedia. Título: Conjectura de Beal. URL:
<https://pt.wikipedia.org/wiki/Conjectura_de_Beal> Acesso em: 24 de Maio de 2018.
Site: ICM. Título: Detalhes do Autor “Sebastião Vieira do nascimento ( Sebá )”. URL:
<https://www.lcm.com.br/site/livros/detalhesAutor?id=A01644> Acesso em: 27 de Setembro de 2019.
Site: Morfismo. Título: Conjectura de Beal. URL:
<https://morfismo.wordpress.com/2013/11/25/conjectura-de-beal/> Acesso em: 28 de Julho de 2018.
Site: DocSity. Título: Fermat, Notas de estudos de Física. URL:
<https://www.docsity.com/pt/fermat-6-1/4705276/> Acesso em: 01 de Setembro de 2019.
Site: Wikipedia. Título: Conjectura de Fermat-Catalan. URL:
<https://pt.wikipedia.org/wiki/Conjectura_de_Fermat-Catalan> Acesso em: 23 de Setembro de 2019.

^[1] Graduation in mathematics.

Submitted: August, 2019.

Approved: November, 2019.