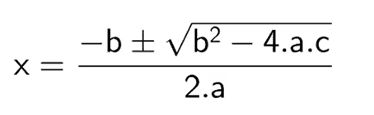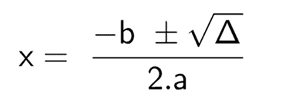ORIGINAL ARTICLE
PEDREIRA, Sinvaldo Martins [1]
PEDREIRA, Sinvaldo Martins. Bhaskara’s Failure. Revista Científica Multidisciplinar Núcleo do Conhecimento. Year. 07, Ed. 02, Vol. 02, p. 178-186. February 2022. ISSN: 2448-0959, Access link: https://www.nucleodoconhecimento.com.br/mathematical-olympiads/bhaskaras-failure
ABSTRACT
This work aims to show that due to flaws in the arithmetic system, university rules based on a wrong standard can generate incorrect results, such as the quadratic equation rule, which can propagate a false certainty of accuracy, for the simple fact of being to follow secular paradigms, without a broad contextual observance of the reality involved, because when dealing with exact sciences, we must always have a holistic view, broadly considering all the factors involved, since a present action has consequences in the future and when we base ourselves on systems flawed, we end up having a false sense of success, since we follow all pseudo precepts to the letter. However, a new system emerges, putting to the test the forcefulness of the arithmetic path to be followed.
Keywords: Failures, Accuracy, System; Holistic.
1. INTRODUÇÃO
First of all, this work is not intended to belittle Bhaskara’s genius, but to show that due to a conceptual flaw in the arithmetic system, even geniuses can make mistakes.
The quadratic equation was standardized by being presented in the following form: ax² + bx + c = 0, where its solution was an unknown, so the solution to the problem came with the formula:
But to simplify the resolution, find the delta first;
Δ = b² – 4ac
Subsequently, the result of delta is joined to the equation:
Finally, as it is a quadratic equation, X has two results:
X = X, and X = X,,
Example I:
X² + 10 X – 56 = 0 A = 1, B = 10, C = – 56
Δ = 10² – (4. 1 .- 56)
Δ = 100 – (- 224)
Δ = 324
X = -10 ± √324
2.1
X, = -10 + 18 => X, = 8 => X, = 4
2 2
X,, = -10 – 18 => X,, = – 28 => X,,= – 14
2 2
So the answers are: X, = 4 and X,, = -14
Example II :
X² – 10 X – 56 = 0 A = 1, B = -10, C = – 56
Δ = -10² – ( 4. 1 .- 56)
Δ = 100 – (- 224)
Δ = 324
X = -10 ± √324
2.1
X, = 10 + 18 => X, = 28 => X, = 14
2 2
X,, = 10 – 18 => X,, = – 8 => X,,= – 4
2 2
So the answers are: X, = 14 and X,, = – 4
2. HOLISM
2.1 HOLISM I
As mentioned earlier, let’s use a little holism; every quadratic equation comes from a distributive one, where:
1st case
(a + b)² => (a + b) . (a + b) = a² + 2ab + b² Note: both a and b are strictly positive according to the rule.
2nd case
(a – b)² => (a – b) . (a – b) = a² – 2ab + b² Note: a positive and b negative according to the rule.
2.2 HOLISM II
In the hidden term, every addition and every subtraction has a result, so
a + b = c, consequence (a + b)² = c², then; a² + 2ab + b² = c²
a – b = c, consequence (a – b)² = c², then; a² – 2ab + b² = c²
2.3 HOLISM III
Evidencing terms, let’s put the terms of the equation in evidence;
I. a = X, b = 5, c = 9
Next; (a + b)² = c² => ( X + 5)² = 9² => X² + 2 . 5X + 25 = 81 => X² + 10X + 25 – 81 = 0 => X² + 10X – 56 = 0
II. a = X, b = – 5, c = 9
Next; (a – b)² = c² => ( X – 5)² = 9² => X² – 2 . 5X + 25 = 81 => X² – 10X + 25 – 81 = 0
=>X² – 10X – 56 = 0
2.4 HOLISM IV
Correspondência:
I. X² + 10X – 56 = 0
A = X² , B = 10X, C = -56, then, A = a², B = 2 . 5X, C = 25 – 81, implies A = a², B = 2 . ab, C = b² – ( c²),
II. X² – 10X – 56 = 0
A = X², B = – 10X, C = -56, then, A = a², B = – 2 . 5X, C = 25 – 81, implies A = a², B = – 2 . ab, C = b² – ( c²),
3. RATIONALIZING
I. If in (a + b)² = c² => a² + 2ab + b²- (c²) = 0
A = a², B = 2 ab , C = b² – (c²), Note: (B = 2 ab) by rule a and b are strictly positive, in X² + 10X – 56 = 0
A = X² , B = 10X, C = -56, Note: (B = 10X) by rule X are strictly positive.
So in X² + 10X – 56 = 0 the only possible root is 4, then-14 goes against the mathematical rule.
II. If in (a – b)² = c² => a² – 2ab + b²- (c²) = 0, (a = X, b = – 5, c = 9)
A = a², B = – 2 ab, C = b² – (c²), Note: (B = – 2 ab) as a rule if b is negative, a must be strictly positive.
In X² – 10X – 56 = 0
A = X² , B = -10X, C = -56, Note: (B = – 10X) by rule X is strictly positive.
So in X² – 10X – 56 = 0, the only possible root of X is 14, then – 4 goes against the mathematical rule.
4. ORDERING
4.1 CASE I
If (X² + 10X – 56 = 0) = (a² – 2ab + b²- (c²)) then:
A = X² and A = a², implies (X = a)
B = 10X and B = 2ab, implies (10X = 2ab)
C = -56 and C = + b²- (c²), implies (- 56 = b² – ( c²))
Finding the root, first find the value of b:
If A = X and A + a, B = 10X where B = 2ab, we put b in evidence
10X = 10a, implies 10a = 2ab => b = 10a/ 2a => b = 5
According to the value of c;
If C = -56 and C = + b²- (c²), we put c in evidence
-56 = b²- (c²) implies -56 = 5²- (c²) => c² = 25 + 56 => c² = 81 => c = 9
Finally, the value of the root is found;
Therefore (a + b)² = c², implies (a + b) = c
If ((a + b)² = c² ) = ((X + b)² = c²), implies (X + b) = c, ie:
X + 5 = 9 => X = 9 – 5 => X = 4
4.2 CASE II
If (X² – 10X – 56 = 0) = (a² – 2ab + b²- (c²)) then:
A = X² and A = a², implies (X = a)
B = – 10X and B = – 2ab, implies (- 10X = 2ab)
C = -56 and C = b²- (c²), implies (- 56 = b² – ( c²))
Finding the root, first find the value of b:
If A = X and A = a, B = – 10X where B = – 2ab, we put b in evidence
– 10X = – 10a, implies – 10a = – 2ab => – b = – 10a/ 2a => – b = – 5
According to the value of c:
If C = – 56 and C = – b²- (c²), we put c in evidence
– 56 = – b²- (c²) implies – 56 = – 5²- (c²) => c² = 25 + 56 => c² = 81 => c = 9
Finally, we find the value of the root:
Therefore (a – b)² = c², implies (a – b) = c
If ((a – b)² = c² ) = ((X – b)² = c²) , implies (X – b) = c, ie:
X – 5 = 9 => X = 9 + 5 => X = 14
5. PARADOX
As demonstrated in the two examples, it was not necessary to use Bhaskara’s formula to solve any of the quadratic equations.
So much (X² + 10X – 56 = 0) as (X² – 10X – 56 = 0), were solved without the use of such a mathematical resource, emphasizing that in both there is only one possible root.
However, despite the flaw in Bhaskara’s formula having been demonstrated, there is still a flaw of a greater systemic degree, which is the rule of signs, because as seen and normalized by Pedreira (2016), a negative number squared remains negative, since geometric ratios have neutral characteristics, just multiplying or dividing something; ex.: 3 x *3 = *9 (where (*) before a number indicates that it is negative, so as not to confuse it with the sign (–)which indicates a subtraction), there is still the failure to exchange signs when the equality side is changed, which can be solved with the Basis and Components rule, where the Basis (B) is equal to the sum of the Components and the Component (C) is equal to the difference of the Base by one or more Components,
Ex.: B = 15 C = 8 and 7, 15 = 8 + 7 => 15 – 8 = 7 => 8 = 15 – 7 => 8+7 = 15 => 15 – (8 + 7) = 0
6. MAKING A COMPARISON
The equation (a + b)² = c² always ended up in an unknown in the form: a² + 2ab +b² – (c²) = 0 and this ends up demanding a second stage of arithmetic elaboration to solve the problem, as seen before. While if we use the rule of Base and Components (BC), the solution is linear and continuous;
Ex.: (a + b)² = c², by the rule BC: c (a + b) = c² => ca + cb = c²
7. IN PRACTICE:
7.1 EXAMPLE I
Current rule: ( X + 8)² = 144 => ( X + 8) . ( X + 8) = 144 => X² + 2 . 8 . X + 64 = 144 =>
X² + 16X + 64 – 144 = 0 => X² + 16X – 80 = 0 (unknown)
Base Rule and Components: (X + 8)² = 144 => 12 . X + 12 . 8 = 144 => 12X + 96 = 144 =>
12X = 144 – 96 => 12X = 48 => X = 48/12 => X = 4 (direct result)
7.2 EXAMPLE II
Current rule: ( X – 5)² = 49 => ( X – 5) . ( X – 5) = 49 => X² + 2 . – 5 . X + 25 = 49 =>
X² + 10X + 25 – 49 = 0 => X² + 10X – 14 = 0 (unknown)
Base Rule and Components: (X – 5)² = 49 => 7 . X – 7 . 5 = 49 => 7X – 35 = 49 =>
7X = 49 +35 => 7X = 84 => X = 84/7 => X = 12 (direct result)
7.3 EXAMPLE III: OTHER POSSIBILITIES
Current rule: ( X + 6)² = – 121 ( without solution): due to the rule in force in a quadratic equation in the form (a + b)² = c², c² will always be positive, because every positive or negative number, when raised to the power of an even exponent, becomes positive.
Base Rule and Components: (X + 6)² = *121 => 11X + 11 . 6 = *121 => 11X = *121 – 66 => 11X = *187 => X = *187/11 => X = *17 ( have a solution): because the Base and Components rule considers the numbers as multipliers or divisors as geometric ratios (RG) and the RGs have a neutral character, regardless of whether it is raised to any power, even or odd, if it is positive, it will continue to be positive, if it is negative (*) will continue to be negative.
8. FINAL CONSIDERATIONS
It has been proven that even within the rules currently used, the formula of the quadratic equation always gives two roots as an answer, triggering an eternal duality of exactitude, which is in itself a paradox, this failure arising from the fact that we do not consider hidden terms in its solution, that is, when we consider the distributive: (a + b)² => (a + b) . (a + b) = a² + 2ab + b² , we omit the equality (c²) and this ends up generating an obscurity in its resolution, causing a systemic lapse.
Even correcting this lapse, the current system is still limited, because when we use the rule of Base and components, we infinitely increase the possibilities of operations, since when we consider geometric ratios as neutral, equations raised to any power will have the sign of their numerator, whether positive or negative.
REFERENCES
PEDREIRA, S. M. O Valor dos Números. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 01, Vol. 08. pp. 05-16. setembro de 2016. Disponível em: https://www.nucleodoconhecimento.com.br/matematica/o-valor-dos-numeros.
PEDREIRA, S. M. Reestruturando os Números. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 09, Vol. 06, pp. 115-120. Setembro de 2019. Disponível em: https://www.nucleodoconhecimento.com.br/matematica/reestruturando-os-numeros.
SILVA, L. P. M. Fórmula de Bhaskara. Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/formula-bhaskara.htm. Acesso em 15 de dezembro de 2021.
[1] Graduated in Logistics, 4th semester in Chemistry, Amateur Mathematician.
Sent: December, 2021.
Approved: February, 2022.