ARTICLE ORIGINAL
PEREIRA, Olavo de Carvalho [1]
PEREIRA, Olavo de Carvalho. Limiter le calcul d’une fonction sans l’utilisation de ![]() et
et ![]() . Revista Científica Multidisciplinar Núcleo do Conhecimento. An. 06, éd. 08, Vol. 04, p. 05-31. Août 2021. ISSN : 2448-0959, lien d’accès : https://www.nucleodoconhecimento.com.br/olympiades-mathematiques/limiter-le-calcul, DOI: 10.32749/nucleodoconhecimento.com.br/olympiades-mathematiques/limiter-le-calcul
. Revista Científica Multidisciplinar Núcleo do Conhecimento. An. 06, éd. 08, Vol. 04, p. 05-31. Août 2021. ISSN : 2448-0959, lien d’accès : https://www.nucleodoconhecimento.com.br/olympiades-mathematiques/limiter-le-calcul, DOI: 10.32749/nucleodoconhecimento.com.br/olympiades-mathematiques/limiter-le-calcul
RÉSUMÉ
La bibliographie consultée ne présente, dans aucun des cas analysés, un calcul de la limite d’une fonction, mais seulement « montre » que les valeurs présentées comme la « limite » satisfont à la définition de limite d’une fonction exprimée par des inégalités impliquant![]() et
et ![]() , il y a donc une lacune dans ce thème, que le présent article vient combler en utilisant fondamentalement le concept de fonction définie, ainsi qu’en identifiant l’expression «
, il y a donc une lacune dans ce thème, que le présent article vient combler en utilisant fondamentalement le concept de fonction définie, ainsi qu’en identifiant l’expression « ![]() tend vers un certain nombre » avec une égalité correspondante.
tend vers un certain nombre » avec une égalité correspondante.
Mots clés : Limite D’une Fonction, Calcul Des Limites, Limites Latérales, Limites Infinies, Limites À L’infini.
1. INTRODUCTION
Cet article présente le « calcul de la limite d’une fonction » afin de combler une lacune existante dans ce sujet.
La présentation du calcul mentionné dans la solution de plusieurs limites est l’objectif principal de l’article.
De manière complémentaire, nous entendons préciser le réel besoin de calculer ou non la limite d’une fonction.
Nous aborderons aussi, de façon très simple, le cas où une fonction simple, définie à un certain nombre, est continue à ce nombre.
Bien que l’interprétation géométrique soit toujours importante, nous n’adopterons ici qu’une approche algébrique du « calcul limite » présenté.
1.1 CALCUL DE LIMITE D’UNE FONCTION
La définition de la limite d’une fonction est présentée dans les manuels de mathématiques comme une estimation.
Par exemple : Leithold (1994) présente la définition de la limite d’une fonction comme suit :
Seja ![]() uma função definida para todo número em algum intervalo aberto contendo
uma função definida para todo número em algum intervalo aberto contendo ![]() , exceto possivelmente no próprio número
, exceto possivelmente no próprio número ![]() O limite de
O limite de ![]() quando
quando ![]() tende a
tende a ![]() será
será ![]() , escrito como
, escrito como ![]() se a seguinte afirmativa for verdadeira:
se a seguinte afirmativa for verdadeira:
Dado ![]() qualquer, existe um
qualquer, existe um ![]() , tal que, se
, tal que, se ![]() então
então ![]() .‘‘
.‘‘
A definição acima afirma que os valores de ![]() tendem a um limite
tendem a um limite ![]() quando
quando ![]() tende a um número
tende a um número ![]() , se o valor absoluto da diferença entre
, se o valor absoluto da diferença entre ![]() e
e ![]() puder se tornar tão pequeno quanto desejarmos, tomando
puder se tornar tão pequeno quanto desejarmos, tomando![]() suficientemente próximo de
suficientemente próximo de ![]() , mas não igual a
, mas não igual a ![]() .
.
En revanche, Lezzi, Murakami et Machado (1991) s’expriment à peu près sur la même définition :
Seja ![]() um intervalo aberto ao qual pertence o número real
um intervalo aberto ao qual pertence o número real ![]() . Seja
. Seja ![]() uma função definida para
uma função definida para ![]() Dizemos que o limite de
Dizemos que o limite de ![]() , quando
, quando ![]() tende a
tende a ![]() , é
, é ![]() , e escrevemos
, e escrevemos ![]() se para todo
se para todo ![]() , existir
, existir ![]() tal que se
tal que se
![]() então
então ![]() .
.
Munem et Foulis (1982) utilisez la définition suivante :
Se ![]() é uma função e
é uma função e ![]() é um número, entende-se a notação
é um número, entende-se a notação ![]() como “o limite de
como “o limite de ![]() ” quando
” quando![]() tende a
tende a ![]() é
é ![]() isto é,
isto é, ![]() se aproxima do número
se aproxima do número ![]() quando
quando ![]() se aproxima de
se aproxima de ![]() .
.
Comme on peut le voir à partir des définitions ci-dessus, une limite est présentée![]() juste pour satisfaire la définition elle-même.
juste pour satisfaire la définition elle-même.
Aucun calcul de cette limite n’est présenté à aucun moment.
Cet article présente le « calcul limite » d’une fonction utilisable dans tous les cas où il est nécessaire d’effectuer une telle opération.
Maintenant, passons à l’argumentation.
Pour certaines fonctions, non définies dans un certain nombre, afin de savoir, avec le maximum de précision possible, quelle serait leur valeur dans ce nombre, il est d’usage de les évaluer dans des valeurs proches de ce nombre pour lesquelles elles ne le sont pas défini.
Exemple: 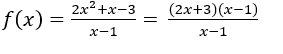 mis à tous
mis à tous ![]() à l’exception
à l’exception![]() .
.
Si nous remplaçons le ![]() par 1, on a l’indétermination
par 1, on a l’indétermination ![]() .
.
Comme la fonction n’est pas définie, c’est-à-dire qu’elle n’existe pas pour la valeur 1, nous évaluons alors sa valeur proche de 1, puisque notre objectif est de connaître la valeur de la fonction, au moins, proche de 1, puisque il n’existe pas ![]() .
.
Pour les valeurs de ![]() , différent de 1, supérieur ou inférieur à 1, mais très proche de 1,
, différent de 1, supérieur ou inférieur à 1, mais très proche de 1, ![]() , pois
, pois ![]() sera égal à 1, et aura des valeurs proche de 5, comme nous le verrons ci-dessous :
sera égal à 1, et aura des valeurs proche de 5, comme nous le verrons ci-dessous :
Attribuons à ![]() les valeurs
les valeurs![]() , c’est-à-dire que nous prenons des valeurs de
, c’est-à-dire que nous prenons des valeurs de ![]() de plus en plus proche de 1, mais inférieur à 1. Les valeurs de
de plus en plus proche de 1, mais inférieur à 1. Les valeurs de ![]() trouvés sont :
trouvés sont :
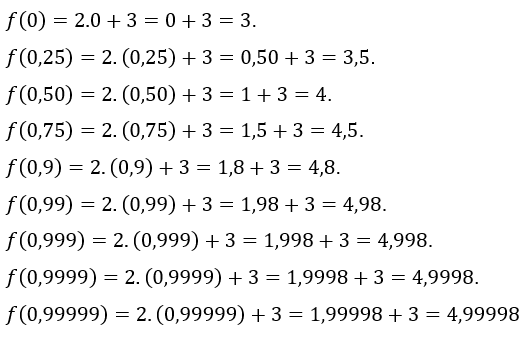
Attribuons maintenant le![]() les valeurs
les valeurs![]() , c’est-à-dire que nous prenons des valeurs de
, c’est-à-dire que nous prenons des valeurs de ![]() de plus en plus proche de 1, mais supérieur à 1. Les valeurs de
de plus en plus proche de 1, mais supérieur à 1. Les valeurs de ![]() trouvés sont :
trouvés sont :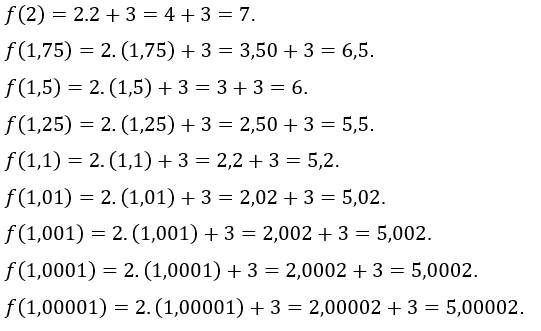
Trouvés sont : Comme on peut le voir, dans les deux cas, comme![]() approches 1,
approches 1, ![]() approches 5, nous laissant croire que c’est la limite de
approches 5, nous laissant croire que c’est la limite de ![]() .
.
Cependant, aucun « calcul » de limite n’a été effectué ici, mais seulement une évaluation de ![]() , lorsque
, lorsque ![]() prend des valeurs très proches de 1.
prend des valeurs très proches de 1.
prend des valeurs très proches de 1.
Les auteurs consultés structurent la définition de la limite en termes d’inégalités à partir d’exemples comme celui-ci et supposent la valeur estimée, dans ce cas 5, comme réellement la limite de la fonction.
À cet égard, ils prétendent que![]() , car pour tout
, car pour tout![]() , aussi petit soit-il, il y a un
, aussi petit soit-il, il y a un ![]() , telle que si
, telle que si ![]() alors
alors![]() .
.
La définition de limite donnée au début, qui n’a pas de calcul de limite, est utilisée pour « prouver » que des nombres donnés, sans indication de l’endroit où ils ont été pris, sont des limites de fonctions.
Nous allons montrer que la définition de limite ne prouve pas, ne démontre pas qu’un nombre donné est la limite d’une fonction, mais « montre » seulement que le nombre fourni est la limite.
Prenons un exemple pour bien faire la différence entre un « spectacle » et une « démonstration ».
- Montrer que 2 est la racine de l’équation
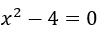 .
.
Cela signifie que si nous remplaçons le![]() par 2, nous aurons zéro comme résultat de l’équation.
par 2, nous aurons zéro comme résultat de l’équation.
Voyons voir![]() .
.
C’était un exemple de « démonstration », c’est-à-dire que seulement quelque chose était montré, rien n’était démontré, rien n’était calculé, seule la valeur fournie était remplacée.
C’est différent quand on dit : prouver que 2 est une racine, c’est une solution de l’équation ![]() .
.
Dans ce cas, nous devons calculer, résoudre l’équation et voir si nous obtenons ![]() .
.
Bon, en résolvant, on a : ![]() , bientôt
, bientôt![]() , et en prenant la racine carrée des deux côtés, nous obtenons:
, et en prenant la racine carrée des deux côtés, nous obtenons: ![]() , c’est,
, c’est, ![]() ou alors
ou alors ![]() .
.
Alors une des valeurs de![]() c’est vraiment 2.
c’est vraiment 2.
Avec cela, il a été « démontré » que 2 est vraiment la racine de l’équation![]() .
.
Nous verrons, dans les exemples donnés ci-dessous, qu’il n’y a pas de preuve, mais seulement une « démonstration » que le nombre donné est la limite de la fonction donnée.
Exemple. Utilisez la définition de la limite pour « prouver » que![]() .
.
Ici, il n’est pas dit comment la conclusion a été atteinte que la limite est de 5, ni d’où ce nombre a été tiré.
Nous aborderons, de manière générale, la solution présentée dans les ouvrages consultés :
La première exigence de la définition est que ![]() être défini sur tout nombre d’un intervalle ouvert contenant 3, sauf éventuellement sur 3. Comme
être défini sur tout nombre d’un intervalle ouvert contenant 3, sauf éventuellement sur 3. Comme ![]() est défini pour tous les nombres réels, tout intervalle ouvert contenant 3 satisfera à cette exigence. Il faut maintenant montrer que pour tout
est défini pour tous les nombres réels, tout intervalle ouvert contenant 3 satisfera à cette exigence. Il faut maintenant montrer que pour tout ![]() il existe une
il existe une![]() , telle que si
, telle que si ![]() alors
alors![]() nous devons
nous devons![]() , bientôt
, bientôt![]() et
et ![]()
Nous avons alors, ![]() et
et ![]()
Cette déclaration indique que![]() est un delta satisfaisant.
est un delta satisfaisant.
Avec ce choix de![]() on a l’argument suivant:
on a l’argument suivant:![]() ,alors
,alors ![]() , alors
, alors ![]() , alors
, alors ![]() alors
alors ![]() , alors
, alors ![]()
Cela « montre » simplement, d’après la définition de la limite, que ![]()
Comme nous l’avons vu, il n’y avait pas de preuve, mais seulement un « spectacle », puisque, étant donné le nombre 5, nous l’avons simplement substitué ainsi que la fonction donnée, dans la définition de la limite d’une fonction.
Prenons un autre exemple : utilisez la définition pour « prouver » que ![]() .
.
Encore une fois, un nombre est donné, dans ce cas 4, comme limite, mais il n’est pas dit d’où ce nombre a été tiré.
Voici la solution, en termes généraux :
Comment ![]() est défini pour tous les nombres réels, tout intervalle ouvert contenant 2 satisfera la première exigence de la définition.
est défini pour tous les nombres réels, tout intervalle ouvert contenant 2 satisfera la première exigence de la définition.
Il faut montrer que pour tout ![]() , il existe une
, il existe une ![]() ,
,
tel que
Si
![]() alors
alors ![]()
Bientôt![]() alors
alors ![]()
Nous devons mettre une contrainte sur ![]() ce qui nous donne une inégalité impliquant
ce qui nous donne une inégalité impliquant ![]() . Une telle restriction est faite pour sélectionner l’intervalle ouvert requis par la définition. Nous choisissons la gamme
. Une telle restriction est faite pour sélectionner l’intervalle ouvert requis par la définition. Nous choisissons la gamme ![]() et cela implique que
et cela implique que ![]() . Puis
. Puis![]() et
et ![]() , puis
, puis![]() puis
puis![]() puis
puis![]() puis
puis![]() .
.
Maintenant nous avons![]() et
et ![]() , puis
, puis![]() Comme notre objectif est d’obtenir
Comme notre objectif est d’obtenir![]() , nous devons exiger
, nous devons exiger![]() Avec ça
Avec ça 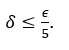
En utilisant ceci ![]() nous avons terminé la soi-disant « preuve ».
nous avons terminé la soi-disant « preuve ».
Comme nous l’avons vu plus haut, encore une fois rien n’a été prouvé, mais seulement que le nombre donné comme limite, dans ce cas 4, satisfait à la définition de limite.
Il n’y avait aucun calcul pour montrer que le nombre 4 est vraiment la limite.
A partir de ce point, nous présenterons le calcul limite d’une fonction.
Avant de présenter le « calcul » proprement dit, évaluons ![]() dans les mêmes valeurs de
dans les mêmes valeurs de ![]() données ci-dessus, mais en les considérant comme des composés du nombre 1.
données ci-dessus, mais en les considérant comme des composés du nombre 1.
Cela montrera, en termes généraux, le raisonnement utilisé pour calculer la limite de la fonction.
La fonction est![]() , valable pour tous
, valable pour tous ![]() .
.
Pour![]() ou alors
ou alors ![]() , nous devons
, nous devons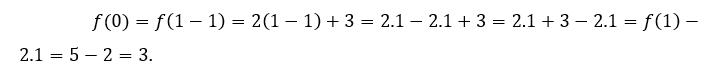
Pour![]() ou alors
ou alors ![]() , nous devons
, nous devons 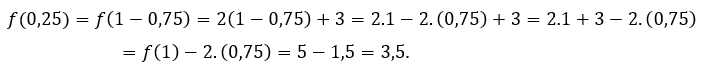 Pour
Pour ![]() ou alors
ou alors ![]() , nous devons
, nous devons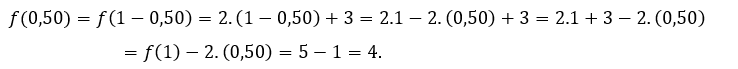
Pour ![]() ou alors
ou alors ![]() nous devons
nous devons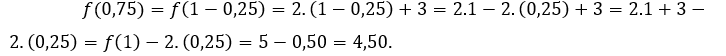 Pour
Pour ![]() ou alors
ou alors ![]() , nous devons
, nous devons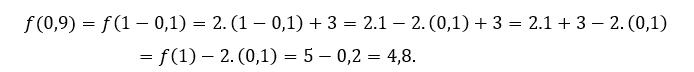
Pour ![]() ou alors
ou alors ![]() , nous devons
, nous devons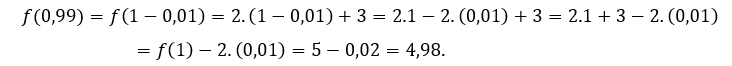
Pour ![]() ou alors
ou alors ![]() , nous devons
, nous devons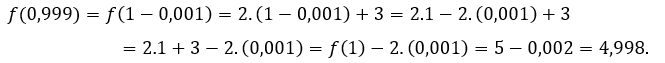
Pour ![]() ou alors
ou alors ![]() , nous devons
, nous devons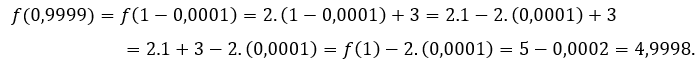
Pour![]() ou alors
ou alors ![]() , nous devons
, nous devons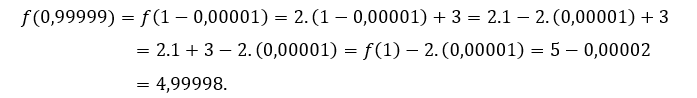
Nous avons testé quelques valeurs de ![]() moins que 1.
moins que 1.
Nous allons maintenant évaluer ![]() à des valeurs supérieures à 1 mais proches de 1.
à des valeurs supérieures à 1 mais proches de 1.
Pour![]() ou alors
ou alors ![]() , nous devons
, nous devons 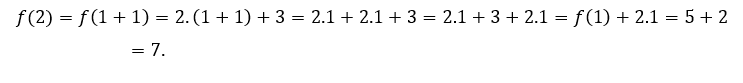
Pour![]() ou alors
ou alors ![]() nous devons
nous devons 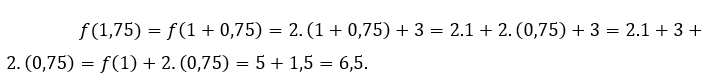
Pour![]() ou alors
ou alors ![]() nous devons
nous devons 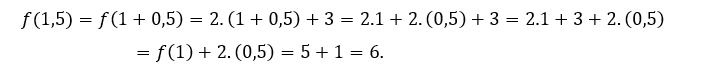
Pour![]() ou alors
ou alors ![]() , nous devons
, nous devons 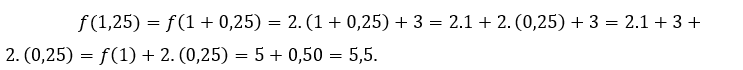
Pour![]() ou alors
ou alors ![]() , nous devons
, nous devons 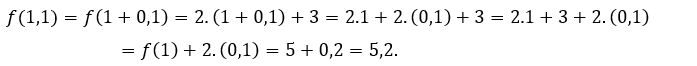
Pour![]() ou alors
ou alors ![]() nous devons
nous devons 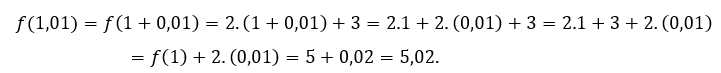
Pour![]() ou alors
ou alors ![]() , nous devons
, nous devons 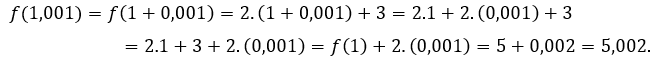
Pour![]() ou alors
ou alors ![]() , nous devons
, nous devons 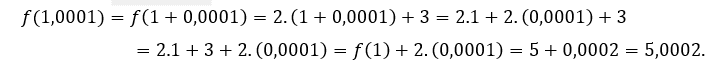
Pour![]() ou alors
ou alors ![]() , nous devons
, nous devons 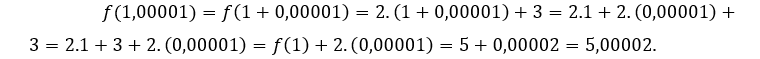
De ce qui précède, nous réalisons que plus![]() se rapproche de 1, plus
se rapproche de 1, plus![]() se rapproche de 5, c’est-à-dire lorsque
se rapproche de 5, c’est-à-dire lorsque ![]() tend vers 1,
tend vers 1, ![]() tend vers 5.
tend vers 5.
Nous avons observé dans les calculs ci-dessus, dans toutes les valeurs attribuées à![]() , l’apparition d’une constante
, l’apparition d’une constante ![]() à laquelle une valeur a été ajoutée ou soustraite, qui tendait vers zéro, comme
à laquelle une valeur a été ajoutée ou soustraite, qui tendait vers zéro, comme ![]() se rapprochait de 1.
se rapprochait de 1.
Cette constante est donc un « candidat » pour être la « limite » mentionnée ci-dessus, c’est-à-dire qu’il y a une indication que nous pouvons avoir![]() .
.
Nous allons maintenant exprimer la situation ci-dessus de manière semi-générique pour présenter le « calcul limite » lui-même.
L’expression« ![]() tend vers 1 », représenté par
tend vers 1 », représenté par ![]() , c’est équivalent à
, c’est équivalent à![]() , ou
, ou ![]() , lorsque
, lorsque![]() tend vers zéro,
tend vers zéro, ![]() , et
, et ![]() .
.
Avec cela, l’expression ![]() , remplacer
, remplacer![]() par
par![]() ou alors
ou alors![]() , c’est équivalent à
, c’est équivalent à![]() , ou alors
, ou alors![]() ,c’est,
,c’est, ![]() , ou alors
, ou alors ![]() .
.
A partir de l’égalité ci-dessus, il est possible de « calculer » la valeur de la limite de![]() lorsque
lorsque![]() tend vers 1, puisqu’il suffit de calculer la valeur de
tend vers 1, puisqu’il suffit de calculer la valeur de![]() , ou alors
, ou alors ![]() .
.
Nous allons maintenant faire, en utilisant la même fonction que précédemment, le calcul pour![]() , lorsque
, lorsque![]() .
.
De cette manière, il nous reste :
![]() alors
alors![]() outre le fait que
outre le fait que![]() , et
, et ![]() tend vers zéro quand
tend vers zéro quand![]() , c’est-à-dire qu’il est si petit qu’il s’approche de zéro autant que nous le souhaitons.
, c’est-à-dire qu’il est si petit qu’il s’approche de zéro autant que nous le souhaitons.
Le calcul pour![]() , c’est,
, c’est, ![]() , est analogue et produit le même résultat.
, est analogue et produit le même résultat.
Voyons voir:![]()
Nous allons maintenant calculer une série de limites de fonctions, pour illustrer l’application du « calcul » mentionné.
- Calculons
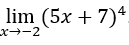 .
.
Comment![]() , nous pouvons faire, par exemple,
, nous pouvons faire, par exemple,![]() ,
, ![]() et
et ![]() .
.
Rester avec
![]()
![]() termes en
termes en ![]() qui tendent tous vers zéro. Le résultat sera alors
qui tendent tous vers zéro. Le résultat sera alors![]()
- Calculons
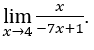
Comment ![]() , nous pouvons faire, par exemple,
, nous pouvons faire, par exemple,![]() ,
, ![]() et
et ![]() .
.
Rester avec
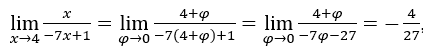 , car le numérateur tend vers 4 et le dénominateur tend vers
, car le numérateur tend vers 4 et le dénominateur tend vers ![]() .
.
- Calculons
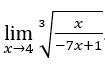 .
.
Comme nous l’avons vu plus haut, à la fin il nous restera
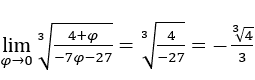
- Calculons
 comme ci-dessous.
comme ci-dessous.
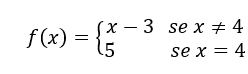 .
.
Nous devons calculer ![]() , parce que peu importe ce qui arrive à
, parce que peu importe ce qui arrive à ![]() lorsque
lorsque ![]() .
.
Comment ![]() , nous pouvons faire, par exemple,
, nous pouvons faire, par exemple, ![]()
![]() et
et ![]() .
.
Rester avec ![]() , alors
, alors![]() .
.
Être![]() , mis à tous
, mis à tous![]() , à l’exception
, à l’exception ![]() .
.
Considérons ![]() c’est,
c’est, ![]() , pour qui
, pour qui ![]() réduit à
réduit à![]() .
.
- Calculons le
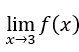 . Nous devons
. Nous devons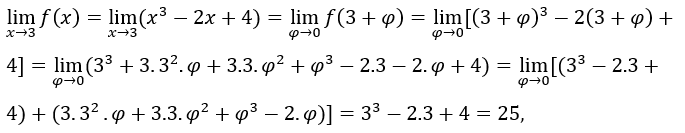 , une fois, quand
, une fois, quand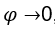 , l’expression
, l’expression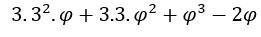 tend vers zéro.
tend vers zéro.
Puis
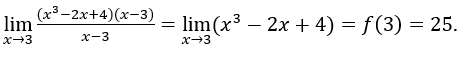
Considérons maintenant l’exemple suivant :![]() , mis à tous
, mis à tous![]() , et calculer sa limite lorsque
, et calculer sa limite lorsque![]() tend vers 2.
tend vers 2.
Pour condition d’existence de la fonction,
condition d’existence de la fonction, ![]() , et lorsque
, et lorsque ![]() nous pouvons faire, par exemple,
nous pouvons faire, par exemple, ![]() , avec
, avec![]()
![]() et nous devrons calculer la limite
et nous devrons calculer la limite![]() .
.
Comment ![]() , l’expression
, l’expression ![]() tend à
tend à![]() ,et la limite sera alors,
,et la limite sera alors, ![]() .
.
En conclusion, il nous reste:![]() .
.
Observation.
Nous aurions pu appliquer le « calcul » directement à la fonction, sans d’abord diviser le facteur commun au numérateur et au dénominateur.
Vejamos ![]()
En fait, on peut appliquer le « calcul » directement sur la fonction, sans faire au préalable une « préparation » sur celle-ci.
Nous allons maintenant donner quelques exemples de calcul de limite impliquant des fonctions trigonométriques et exponentielles afin d’illustrer la consolidation ci-dessus.
Considérons la fonction ![]() , mis à tous
, mis à tous ![]() , à l’exception
, à l’exception
Se souvenir: ![]() signifie, par exemple, que
signifie, par exemple, que![]() , où
, où![]() ,
, ![]() .
.
En remplaçant cette valeur de x dans l’équation d’origine ci-dessus, nous avons :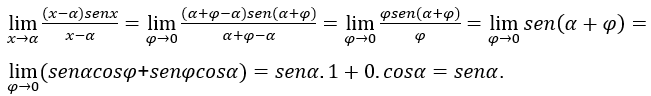
Puis, ![]() et
et ![]() sont indépendants de
sont indépendants de ![]() c’est le
c’est le ![]()
, tandis que le ![]() .
.
Autre exemple : considérons la fonction ![]() mis à tous
mis à tous ![]() , à l’exception
, à l’exception![]() .
.
- Calculons le
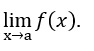
- faire le remplacement
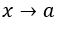 pour, par exemple,
pour, par exemple, 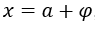 , avec
, avec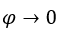 ,
, 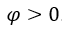 . Nous avons:
. Nous avons: 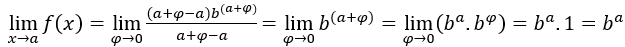 , parce que le
, parce que le 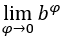 vaut 1 et
vaut 1 et 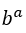 outre le fait que
outre le fait que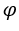 .
.
Calculons maintenant la limite des fonctions données au début pour confirmer les valeurs des limites données.
- Calculons
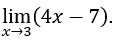
Comment![]() , nous pouvons faire, par exemple,
, nous pouvons faire, par exemple, ![]() ,
, ![]() et
et ![]() et il nous reste
et il nous reste ![]()
- Calculons
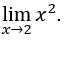
Comment![]() , nous pouvons faire, par exemple,
, nous pouvons faire, par exemple, ![]() ,
, ![]() et
et 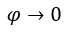 et il nous reste
et il nous reste![]()
Comme on peut le voir d’après les « calculs » ci-dessus, les limites données dans les exemples précédents étaient correctes.
Nous allons démontrer un seul théorème sur les limites pour illustrer le calcul présenté ici.
Théorème. Si ![]() et
et ![]() sont des constantes, alors
sont des constantes, alors ![]() .
.
Calculez simplement la limite en faisant, par exemple, ![]()
![]() et
et ![]()
Rester avec:![]() , alors
, alors ![]() tend vers zéro puisque
tend vers zéro puisque ![]() tend vers zéro.
tend vers zéro.
Il y a une immense simplicité dans le « calcul » présenté.
Dans ce cas, il ne fait aucun doute que la limite est![]() .
.
Nous allons maintenant utiliser le « calcul limite » présenté pour calculer les limites des fonctions dans diverses circonstances.
- Calculons
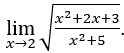
Comment![]() , donc on peut faire, par exemple,
, donc on peut faire, par exemple, ![]() ,
, ![]() et
et ![]()
Rester avec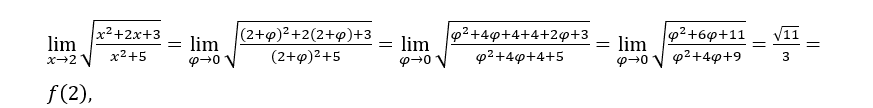 , puisque
, puisque ![]() tend vers 11 et
tend vers 11 et![]() tend vers 9.
tend vers 9.
- Calculons
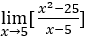 .
.
Comment x → 5, donc on peut faire par exemple, ![]() ,
, ![]() et
et ![]()
Rester avec 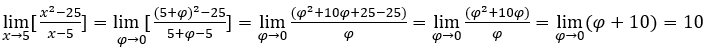
On observe qu’il n’était pas nécessaire de « préparer » la fonction pour appliquer le « calcul », c’est-à-dire qu’il n’était pas nécessaire d’écrire la fonction comme ![]() et, enfin comment
et, enfin comment ![]()
- Calculons
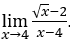 .
.
Dans les cas impliquant des radicaux, auxquels un nombre réel est ajouté ou soustrait, lorsque la substitution directe de la valeur de![]() conduit à l’indétermination
conduit à l’indétermination ![]() il faut préparer l’équation, car l’application directe du « calcul » ne défait pas l’indétermination, comme nous le verrons plus loin.
il faut préparer l’équation, car l’application directe du « calcul » ne défait pas l’indétermination, comme nous le verrons plus loin.
Ce qui se passe dans ce cas, c’est qu’il existe un facteur commun au numérateur et au dénominateur, mais qui n’est exprimé que lorsque nous divisons, soit le numérateur par le dénominateur, soit le dénominateur par le numérateur.
Cela se traduit actuellement en mathématiques par la rationalisation.
Voyons dans l’exemple ci-dessus : si on divise le dénominateur par le numérateur, puisque l’exposant de ![]() au dénominateur est 1 et l’exposant de
au dénominateur est 1 et l’exposant de ![]() au numérateur est plus petit, c’est-à-dire qu’il vaut
au numérateur est plus petit, c’est-à-dire qu’il vaut ![]() nous aurons:
nous aurons: ![]() et en remplaçant, nous aurons
et en remplaçant, nous aurons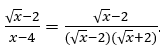 .
.
On peut ainsi exprimer le facteur commun au numérateur et au dénominateur.
L’autre façon est de diviser le numérateur par le dénominateur, mais dans ce cas, nous devons faire la même chose est la rationalisation, puisque l’exposant de ![]() au numérateur est inférieur à l’exposant de
au numérateur est inférieur à l’exposant de ![]() dénominateur, et doit donc être multiplié par un facteur dans
dénominateur, et doit donc être multiplié par un facteur dans ![]() rendre son exposant au moins égal à l’exposant du dénominateur.
rendre son exposant au moins égal à l’exposant du dénominateur.
C’est la fameuse rationalisation que nous faisons.
Nous ferons d’abord le calcul, sans préparation.
Comment![]() , nous pouvons faire, par exemple,
, nous pouvons faire, par exemple, ![]() ,
,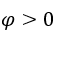 et
et ![]() .
.
Rester avec![]() On observe la nécessité de rationaliser, car la limite est encore indéterminée quand
On observe la nécessité de rationaliser, car la limite est encore indéterminée quand ![]() au numérateur et au dénominateur, tendant à
au numérateur et au dénominateur, tendant à ![]()
On va alors multiplier et diviser par ![]() , et nous serons avec
, et nous serons avec![]()
Nous allons maintenant faire le calcul, en préparant la fonction avant de l’appliquer.
![]() .
.
Comment la substitution directe de 4 conduit à l’indétermination![]() signifie que le numérateur et le dénominateur ont pour diviseur commun
signifie que le numérateur et le dénominateur ont pour diviseur commun ![]() ou alors
ou alors ![]()
Dans ce cas, comme il s’agit d’un radical moins un nombre réel, le moyen utilisé pour « libérer » le facteur commun passe par la rationalisation.
Avant de calculer la limite, nous allons multiplier et diviser le numérateur et le dénominateur de la fonction par![]()
Rester avec 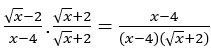 . Dans cette fonction, nous pouvons déjà appliquer le calcul. Voyons voir:
. Dans cette fonction, nous pouvons déjà appliquer le calcul. Voyons voir: 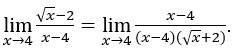
Comment 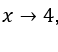 nous pouvons faire, par exemple,
nous pouvons faire, par exemple, ![]() ,
, ![]() et
et ![]()
Rester avec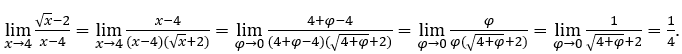
1.2 LIMITES LATÉRALES
Dans les cas où une fonction est définie pour chaque nombre réel sauf un nombre réel![]() , quand on calcule sa limite avec la variable indépendante tendant vers
, quand on calcule sa limite avec la variable indépendante tendant vers ![]() ,comme dans les exemples donnés ci-dessus, peu importe que nous utilisions
,comme dans les exemples donnés ci-dessus, peu importe que nous utilisions![]() combien
combien ![]() ,
, ![]() et
et ![]() ,puisqu’il est réglé sur tous les nombres à gauche et à droite de
,puisqu’il est réglé sur tous les nombres à gauche et à droite de ![]() .
.
Et bien sûr, ce n’est pas une fonction de phrase.
Lorsqu’une fonction n’est pas définie à gauche ou à droite d’un nombre ![]() et nous devons calculer sa limite avec
et nous devons calculer sa limite avec ![]() tendant à, nous devons utiliser la valeur de
tendant à, nous devons utiliser la valeur de ![]() selon le cas.
selon le cas.
Lorsque![]() et nous faisons
et nous faisons ![]() , ou alors
, ou alors ![]() ,
, ![]() et
et ![]() , então
, então ![]() indique que
indique que ![]() approche
approche ![]() pour des valeurs supérieures à
pour des valeurs supérieures à ![]() , et s’approche donc
, et s’approche donc ![]() sur la droite.
sur la droite.
Le calcul fait avec ![]() est donc la limite lorsque
est donc la limite lorsque ![]() tend à
tend à ![]() sur la droite.
sur la droite.
C’est donc la limite de droite.
Nous utilisons ![]() pour calculer la limite gauche.
pour calculer la limite gauche.
Nous savons que la limite n’existe que lorsque les limites unilatérales existent et sont égales.
- Calculons
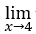 √x – 4.
√x – 4.
On sait que la fonction n’existe que pour ![]() , c’est,
, c’est, ![]()
Il n’y a donc pas de limite à gauche et donc la limite en question n’existe pas.
Mais il y a la limite de droite qui peut être calculée en remplaçant![]() par
par![]() ,
, ![]() et
et ![]()
![]()
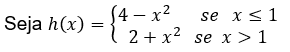
- Calculons les limites unilatérales.
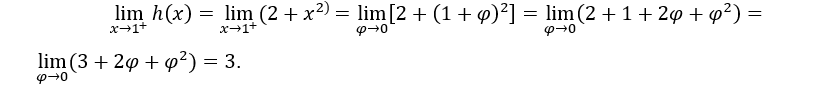
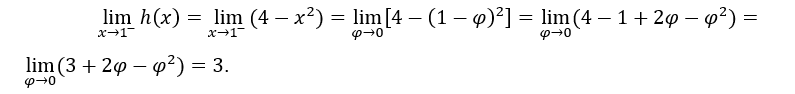
Comme ce sont les mêmes,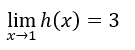
Dans le calcul ci-dessus, nous avons fait ![]() , pour calculer la limite de droite et
, pour calculer la limite de droite et ![]() pour calculer la limite gauche.
pour calculer la limite gauche.
On calcule la limite de ![]() défini par
défini par
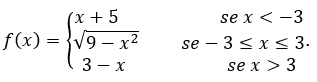
- Calculons
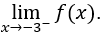
Il faut alors calculer,![]()
On va le faire alors, ![]() ,
, ![]() et
et ![]()
Rester avec
![]()
- Calculons
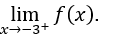
Il faut alors calculer ,![]()
On va le faire alors, ![]() ,
, ![]() et
et ![]()
Rester avec
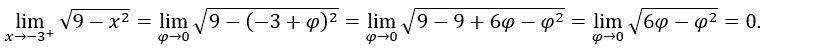
- Calculemos
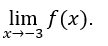
Comment![]() puis le
puis le ![]() n’existe pas.
n’existe pas.
- Calculons
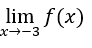 .
.
Il faut alors calculer,![]()
Nous ferons alors ![]() ,
, ![]() et
et ![]()
Rester avec
![]()
- Calculons
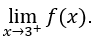
Il faut alors calculer, ![]()
Nous ferons alors, ![]() ,
, ![]() et
et ![]()
Rester avec
![]() Calculons
Calculons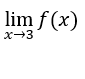
Comment![]() , alors
, alors 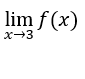 existe et est égal à zéro.
existe et est égal à zéro.
1.3 LIMITES INFINIES
Ceux dont les valeurs fonctionnelles augmentent ou diminuent sans limitation, lorsque la variable indépendante se rapproche de plus en plus d’un nombre fixe, peuvent être résolus également par le « calcul » limite présenté ici, avec l’avantage de ne pas avoir à se soucier des théorèmes.
Avant d’appliquer le « calcul », rappelons les situations suivantes :
![]()
- Calculons la limite suivante
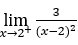 .
.
Comment![]() , nous devons faire
, nous devons faire ![]() ,
, ![]() et
et ![]()
Rester avec ![]() .
.
- Calculons maintenant
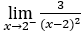 .
.
Comment ![]() , nous devons faire
, nous devons faire ![]() ,
, ![]() et
et ![]()
Rester avec ![]() .
.
- Calculons
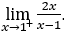 .
.
Comment![]() , nous devons faire
, nous devons faire ![]() ,
, ![]() et
et ![]()
Rester avec ![]() , car le numérateur tend vers 2, tandis que le dénominateur tend vers zéro en passant par des valeurs positives.
, car le numérateur tend vers 2, tandis que le dénominateur tend vers zéro en passant par des valeurs positives.
- Calculons maintenant
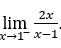 .
.
Comment![]() , nous devons faire
, nous devons faire ![]() ,
, ![]() et
et ![]()
Rester avec 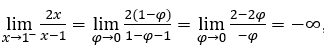 , car le numérateur tend vers 2 et le dénominateur tend vers zéro via des valeurs négatives.
, car le numérateur tend vers 2 et le dénominateur tend vers zéro via des valeurs négatives.
- Calculons
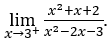
Comment![]() , nous devons faire
, nous devons faire ![]() ,
, ![]() et
et ![]()
Rester avec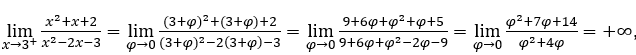 car le numérateur tend vers 14, tandis que le dénominateur tend vers zéro pour les valeurs positives.
car le numérateur tend vers 14, tandis que le dénominateur tend vers zéro pour les valeurs positives.
- Calculons maintenant
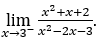
Comment ![]() , nous devons faire
, nous devons faire ![]() ,
, ![]() et
et ![]()
Rester avec ![]() , puisque le numérateur tend vers 14, tandis que le dénominateur tend vers zéro pour les valeurs négatives, puisque
, puisque le numérateur tend vers 14, tandis que le dénominateur tend vers zéro pour les valeurs négatives, puisque ![]() tend toujours vers zéro pour les valeurs positives.
tend toujours vers zéro pour les valeurs positives.
Dans ce cas, le dénominateur est ![]() chaque fois que
chaque fois que ![]() , c’est comme
, c’est comme ![]() , le dénominateur est toujours négatif.
, le dénominateur est toujours négatif.
- Calculons
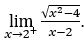
Comment ![]() , nous devons faire
, nous devons faire ![]() ,
, ![]() et
et ![]()
Nous sommes comme
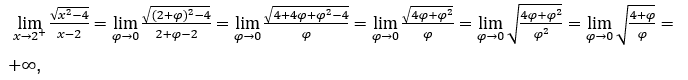 car le numérateur tend vers 2 et le dénominateur tend vers zéro pour les valeurs positives.
car le numérateur tend vers 2 et le dénominateur tend vers zéro pour les valeurs positives.
- Calculons
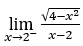
Comment ![]() , nous devons faire
, nous devons faire ![]() ,
, ![]() et
et ![]()
Rester avec 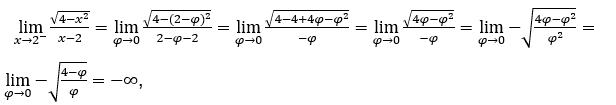 , car le numérateur tend vers -2 et le dénominateur tend vers zéro pour les valeurs positives.
, car le numérateur tend vers -2 et le dénominateur tend vers zéro pour les valeurs positives.
Dans ces deux cas, nous avons pu ![]() dans le radical parce qu’il est toujours positif.
dans le radical parce qu’il est toujours positif.
- Calculons
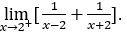
Comment ![]() , nous devons faire
, nous devons faire ![]() ,
, ![]() et
et ![]()
Rester avec ![]() car le numérateur tend vers 4, tandis que le dénominateur tend vers zéro pour les valeurs positives.
car le numérateur tend vers 4, tandis que le dénominateur tend vers zéro pour les valeurs positives.
Noter Nous aurions pu remplacer directement la valeur de dans l’équation d’origine.
- Calculons
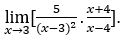
Comment![]() , nous devons faire
, nous devons faire![]() ,
, ![]() et
et ![]()
Rester avec ![]() , car le numérateur tend vers 35, tandis que le dénominateur tend vers zéro pour les valeurs négatives, puisque est négatif pour < 1.
, car le numérateur tend vers 35, tandis que le dénominateur tend vers zéro pour les valeurs négatives, puisque est négatif pour < 1.
- Calculons
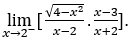
Comment ![]() , nous ferons
, nous ferons ![]() ,
, ![]() et
et ![]()
Rester avec 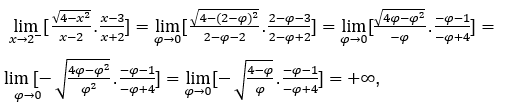 , car le numérateur tend à
, car le numérateur tend à ![]() et le dénominateur tend à
et le dénominateur tend à![]() par des valeurs positives.
par des valeurs positives.
1.4 LIMITES SUR L’INFINI
De la même manière que pour les bornes évoquées jusqu’ici, la littérature consultée ne présente pas non plus un calcul de bornes à l’infini, mais n’évalue la fonction que lorsque la variable indépendante croît ou décroît indéfiniment.
Le résultat de l’évaluation est utilisé comme seuil.
Voyons voir.
Compte tenu de la fonction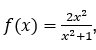 , nous attribuons à
, nous attribuons à![]() les valeurs
les valeurs![]() et ainsi de suite, lui permettant de croître indéfiniment. Les valeurs fonctionnelles correspondantes seront
et ainsi de suite, lui permettant de croître indéfiniment. Les valeurs fonctionnelles correspondantes seront
![]()
Nous observons que lorsque ![]() croît, en prenant des valeurs positives, les valeurs fonctionnelles approchent 2.
croît, en prenant des valeurs positives, les valeurs fonctionnelles approchent 2.
Lorsqu’une variable indépendante ![]() croît indéfiniment, à travers des valeurs positives, on écrit
croît indéfiniment, à travers des valeurs positives, on écrit ![]() l’exemple donné, la conclusion a été tirée que
l’exemple donné, la conclusion a été tirée que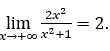
Comme vu ci-dessus, à partir de l’exemple donné, aucun calcul de limite de la fonction n’a été présenté, mais il a seulement été observé que, comme ![]() augmenté, par des valeurs positives, la fonction approchée de 2.
augmenté, par des valeurs positives, la fonction approchée de 2.
Cette valeur 2 a ensuite été utilisée comme limite de la fonction.
Nous présenterons, ci-dessous, le « calcul » de limite de fonctions lorsque la variable indépendante tend vers ![]() ou la
ou la ![]()
Dans les cas où ![]() , nous ferons
, nous ferons 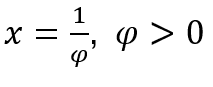 et
et ![]() , car, comme nous l’avons vu plus haut, lorsque
, car, comme nous l’avons vu plus haut, lorsque![]() tend vers zéro pour les valeurs positives,
tend vers zéro pour les valeurs positives, ![]() tend à
tend à ![]() , et avec cela,
, et avec cela, ![]() tend à
tend à![]()
Dans les cas où ![]() , nous ferons
, nous ferons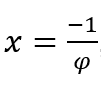
![]() et
et ![]() , car, comme nous l’avons vu plus haut, lorsque φ tend vers zéro pour les valeurs positives
, car, comme nous l’avons vu plus haut, lorsque φ tend vers zéro pour les valeurs positives![]() ,
,![]() tend à, et avec cela,
tend à, et avec cela,![]() tend à
tend à![]() .
.
- Calculons
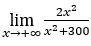 .
.
Comment 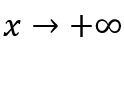 , nous ferons
, nous ferons 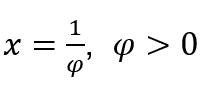 et
et ![]()
Rester avec![]() car le numérateur tend vers 2 et le dénominateur tend vers 1.
car le numérateur tend vers 2 et le dénominateur tend vers 1.
- Calculons
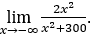
Comment ![]() , nous ferons
, nous ferons ![]() et
et ![]()
Rester avec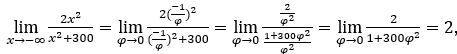 , car le numérateur tend vers 2 et le dénominateur tend vers 1.
, car le numérateur tend vers 2 et le dénominateur tend vers 1.
- Calculons
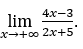
Comment ![]() , nous ferons
, nous ferons 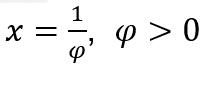 et
et ![]()
Rester avec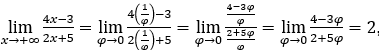 , car le numérateur tend vers 4 et le dénominateur tend vers 2.
, car le numérateur tend vers 4 et le dénominateur tend vers 2.
- Calculons
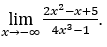
Comment ![]() , nous ferons
, nous ferons![]()
![]() et
et ![]()
Rester avec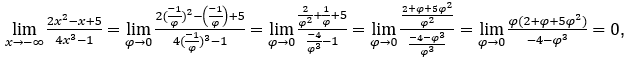 car le numérateur tend vers zéro et le dénominateur vers -4.
car le numérateur tend vers zéro et le dénominateur vers -4.
- Calculons
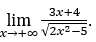
Comment ![]() , nous ferons
, nous ferons ![]() et
et ![]()
Rester avec 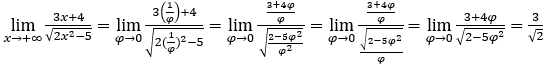 , car le numérateur tend vers 3 et le dénominateur tend vers
, car le numérateur tend vers 3 et le dénominateur tend vers![]()
- Calculons
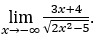
Comment ![]() , nous ferons
, nous ferons![]()
![]() et
et ![]()
Rester avec 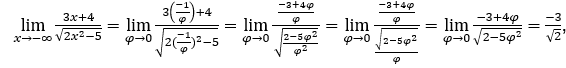 , car le numérateur tend vers -3 et le dénominateur tend vers √2.
, car le numérateur tend vers -3 et le dénominateur tend vers √2.
- Calculons
Comment ![]() , nous ferons
, nous ferons![]() et
et ![]()
Rester avec 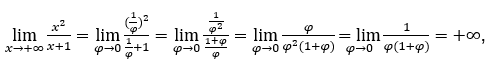 car le numérateur est 1 et le dénominateur tend vers zéro pour les valeurs positives.
car le numérateur est 1 et le dénominateur tend vers zéro pour les valeurs positives.
- Calculons
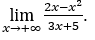
Comment ![]() , nous ferons
, nous ferons ![]() =
= ![]() φ > 0 et φ → 0.
φ > 0 et φ → 0.
Rester avec 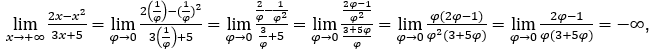 car le numérateur tend vers -1 et le dénominateur tend vers zéro pour les valeurs positives.
car le numérateur tend vers -1 et le dénominateur tend vers zéro pour les valeurs positives.
- Calculons
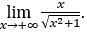
Comment ![]() , nous ferons
, nous ferons ![]() et
et ![]()
Rester avec 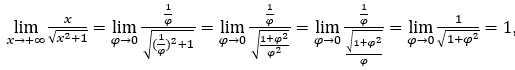 car le numérateur est 1 et le dénominateur tend vers 1.
car le numérateur est 1 et le dénominateur tend vers 1.
- Calculons maintenant
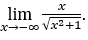
Comment ![]() , nous ferons
, nous ferons![]() et
et ![]()
Rester avec 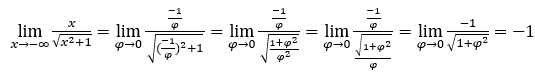 , car le numérateur est -1 et le dénominateur tend vers 1.
, car le numérateur est -1 et le dénominateur tend vers 1.
- Calculons
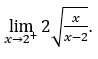
Comment ![]() , nous devons faire
, nous devons faire ![]() ,
, ![]()
Rester avec 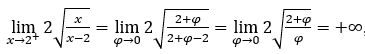 , car le numérateur tend à
, car le numérateur tend à ![]() et le dénominateur tend vers zéro pour les valeurs positives.
et le dénominateur tend vers zéro pour les valeurs positives.
- Calculons maintenant
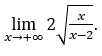
Comment![]() , nous ferons
, nous ferons ![]() e
e ![]()
Rester avec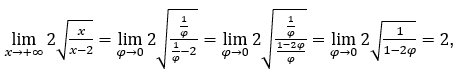 car le numérateur tend vers 2 et le dénominateur tend vers 1.
car le numérateur tend vers 2 et le dénominateur tend vers 1.
Observation.
Le calcul des limites à l’infini ne peut s’appliquer, par exemple, aux fonctions trigonométriques, puisque certaines d’entre elles varient dans un certain intervalle, et d’autres augmentent ou diminuent indéfiniment, selon la valeur considérée.
Par exemple, si nous essayons de calculer le 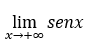 , on passerait par toutes les valeurs de la plage des temps infinis
, on passerait par toutes les valeurs de la plage des temps infinis ![]() , car, pour tout
, car, pour tout![]() ,
, ![]() , c’est-à-dire que nous n’arriverions à aucune valeur définie.
, c’est-à-dire que nous n’arriverions à aucune valeur définie.
En effet, les fonctions polynomiales, ou fonctions exprimées par des rapports entre polynômes, sont les plus adaptées pour appliquer des limites.
2. OBSERVATIONS
1) Le calcul de limite présenté est issu de l’identification de l’expression![]() tend vers un certain nombre
tend vers un certain nombre ![]() avec égalité
avec égalité ![]() , ou alors
, ou alors ![]() , com
, com![]() et
et![]() , depuis, vraiment, quand
, depuis, vraiment, quand ![]() ,
, 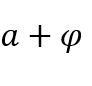 e
e ![]() avoir tendance à
avoir tendance à ![]() et avec cela,
et avec cela, ![]() tend à
tend à ![]()
Dans le cas des limites à l’infini, la substitution de l’expression ![]() tend à
tend à ![]() il était
il était ![]() et la substitution de l’expression
et la substitution de l’expression ![]() tend à
tend à ![]() il était
il était ![]() , avec
, avec![]() et
et ![]()
La substitution a le plus de sens, parce que, vraiment, quand ![]() , toujours pour des valeurs positives,
, toujours pour des valeurs positives,![]() soigner
soigner ![]() et
et ![]() tend à
tend à ![]() , fabrication
, fabrication ![]() ont vraiment tendance à
ont vraiment tendance à ![]() ou la
ou la ![]() , selon le cas.
, selon le cas.
Si on substitue, dans le cas où ![]() tend à
tend à![]() ou la
ou la ![]() le
le ![]() par,
par, ![]() ou alors
ou alors![]() e
e ![]() , le résultat serait le même.
, le résultat serait le même.
Un exemple.
- Calculons
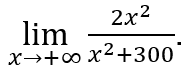
Nous ferons ![]() et
et ![]()
Rester avec
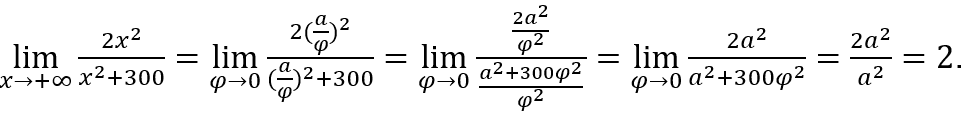
2. Comme on le voit dans les différents exemples, le « calcul limite » présenté est assez « fluide » et d’application directe, sans qu’il soit nécessaire de consulter des théorèmes ou « d’organiser » la fonction avant d’effectuer le calcul, sauf lorsqu’il faut rationaliser.
Ce fait apporte beaucoup de tranquillité lors du calcul de la limite d’une fonction, car le « calcul » présenté est une véritable synthèse de ce sujet.
Par exemple, « calcul » peut être utilisé directement sur la fonction 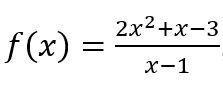 , sans avoir besoin de l’organiser, c’est-à-dire l’exprimer comme
, sans avoir besoin de l’organiser, c’est-à-dire l’exprimer comme 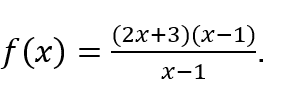
Voyons voir ![]()
Comment ![]() , nous pouvons faire, par exemple,
, nous pouvons faire, par exemple, ![]() et
et ![]()
Rester avec
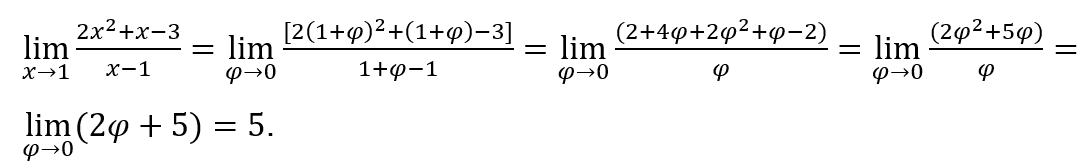
Cela apporte un énorme avantage par rapport à la présentation actuelle de ce sujet, qui, en plus de ne présenter aucun calcul de limite, se montre assez « coincée » par l’immense quantité de théorèmes qu’il faut considérer dans les « évaluations » de limites, ainsi que des « organisations » qu’il faut faire sur les fonctions avant « d’estimer » leur limite.
3) Je voudrais ajouter, au « calcul limite » présenté, quelques évaluations d’ordre pratique.
a) Cela n’a de sens que de calculer la limite d’une fonction proche d’une valeur pour laquelle elle n’est pas définie.
Si la fonction est définie pour une certaine valeur, c’est-à-dire si la fonction existe pour une certaine valeur, cela n’a aucun sens de calculer la limite près de cette valeur, puisque nous savons combien vaut la fonction à cette valeur.
Par exemple, être ![]()
Cette fonction est définie pour tous ![]() , ça existe pour tout le monde
, ça existe pour tout le monde ![]()
Par conséquent, il serait déraisonnable de calculer, par exemple,![]() , puisque la fonction existe pour
, puisque la fonction existe pour ![]() , c’est-à-dire, pourquoi calculer cette limite si nous pouvons simplement substituer
, c’est-à-dire, pourquoi calculer cette limite si nous pouvons simplement substituer![]() par 3 dans
par 3 dans ![]() et nous obtenons la valeur de la fonction en 3, c’est-à-dire
et nous obtenons la valeur de la fonction en 3, c’est-à-dire![]()
Avec cela, des centaines d’exercices n’ont plus de raison d’être.
Évidemment, les fonctions considérées dans cet article sont de ![]()
b) En utilisant la notion de limite, nous ferons ici une observation sur la continuité d’une fonction.
Selon le livre de calcul de Lethold (1994), la définition d’une fonction continue en un point se traduit comme suit :
Dizemos que a função ![]() é contínua no número a se e somente se as seguintes condições forem satisfeitas:
é contínua no número a se e somente se as seguintes condições forem satisfeitas:
(i) ![]() existe;
existe;
(ii) ![]() existe;
existe;
(iii) ![]()
Se uma ou mais de uma dessas condições não forem verificadas em ![]() , a função
, a função![]() será descontínua em
será descontínua em ![]() .
.
Ainsi Lima (1978) définit la continuité d’une fonction :
Uma função ![]() diz-se contínua no ponto
diz-se contínua no ponto ![]() quando é possível tornar
quando é possível tornar ![]() arbitrariamente próximo de
arbitrariamente próximo de ![]() desde que se tome
desde que se tome ![]() suficientemente próximo de
suficientemente próximo de ![]()
Em termos precisos, diremos que ![]() é contínua no ponto
é contínua no ponto ![]() quando, para todo
quando, para todo ![]() dado arbitrariamente, pudermos achar
dado arbitrariamente, pudermos achar ![]() tal que
tal que ![]() e
e ![]() impliquem
impliquem ![]()
Nous savons que si une fonction est définie sur un certain intervalle, c’est-à-dire si elle existe pour chaque nombre contenu dans un certain intervalle, alors il est inutile de calculer la limite de cette fonction pour un certain nombre dans cet intervalle, puisque nous pouvons évaluez simplement la fonction sur chaque nombre de cette plage.
En termes plus simples : si une fonction, représentée par une seule expression, par une seule phrase, existe pour un certain nombre ![]() alors il est totalement inutile de calculer la limite de la fonction pour
alors il est totalement inutile de calculer la limite de la fonction pour ![]() , puisque, simplement, on peut calculer la valeur de la fonction dans
, puisque, simplement, on peut calculer la valeur de la fonction dans ![]()
Bien sûr, si nous devions calculer cette limite, comme nous l’avons fait ci-dessus, ce serait ![]()
Comme indiqué ci-dessus, cela n’a de sens que de calculer la limite d’une fonction autour d’un nombre pour lequel elle n’est pas définie.
Par conséquent, si nous analysons des fonctions représentées par une seule expression, en disant qu’une fonction existe pour un certain nombre
![]() , signifie qu’il y a une limite de cette fonction dans
, signifie qu’il y a une limite de cette fonction dans ![]() cette limite étant la valeur de la fonction dans
cette limite étant la valeur de la fonction dans ![]() , et avec cela nous n’avons pas besoin de calculer la limite de cette fonction dans ce nombre
, et avec cela nous n’avons pas besoin de calculer la limite de cette fonction dans ce nombre![]()
En appliquant cela à la définition ci-dessus d’une fonction continue, les points (ii) et (iii) de la définition deviendront inutiles, car au point (i), il est indiqué que![]() exister.
exister.
Par conséquent, pour les fonctions représentées par « une seule expression », la simple déclaration qu’elle, la fonction![]() , est défini en un nombre
, est défini en un nombre ![]() c’est-à-dire la simple déclaration que
c’est-à-dire la simple déclaration que ![]() existe est suffisant pour conclure que la fonction est continue à ce nombre
existe est suffisant pour conclure que la fonction est continue à ce nombre![]()
De même, avec ce constat sur les fonctions continues, des centaines d’exercices perdent leur raison d’être.
Exemple : laisser la fonction ![]() qui est défini pour tout nombre réel, c’est-à-dire qu’il existe pour tout
qui est défini pour tout nombre réel, c’est-à-dire qu’il existe pour tout ![]() réel.
réel.
Ainsi, il n’est pas nécessaire de calculer la limite de![]() pour aucune valeur de
pour aucune valeur de ![]() , car dans ce cas, être défini dans
, car dans ce cas, être défini dans ![]() est synonyme d’avoir une limite dans
est synonyme d’avoir une limite dans ![]() et que cette limite est égale à la valeur de la fonction dans
et que cette limite est égale à la valeur de la fonction dans ![]() considéré.
considéré.
Ensuite la fonction![]() est continue pour tout
est continue pour tout![]()
3. CONCLUSION
Dans ce qui précède, nous montrons qu’en fait, la théorie des limites est déficiente par rapport à un calcul de limite et, par conséquent, elle s’entoure d’une série d’arguments basés sur la définition de la limite afin de combler cette lacune.
Nous présentons ensuite le « calcul de la limite d’une fonction » et montrons qu’il synthétise tout le sujet évoqué, ayant donc une application directe.
Nous espérons contribuer à une meilleure compréhension d’un sujet aussi fondamental en mathématiques.
RÉFÉRENCES
IEZZI, Gelson; MURAKAMI, Carlos et all. Fundamentos de Matemática Elementar, vol. 8, 1991.
LEITHOLD, Louis. O Cálculo com Geometria Analítica, vol. 1, 1994.
LIMA, Elon Lages. Curso de Análise, vol. 1, 1978.
MUNEM, Mustafa A. e FOULIS, David J. Cálculo, vol. 1, 1982.
[1] Licence en Mathématiques de l’Université de Brasilia.
Envoyé : Juin 2021.
Approuvé : Août 2021.