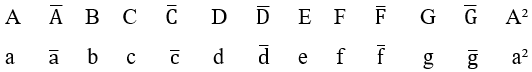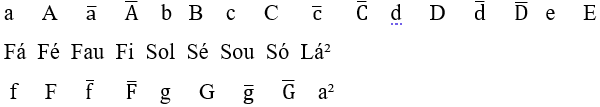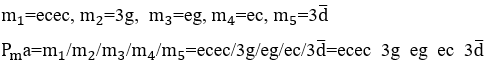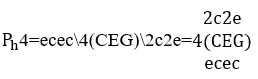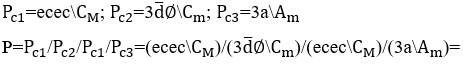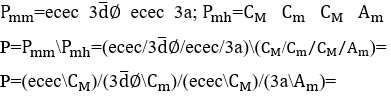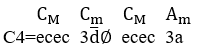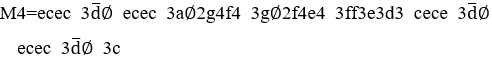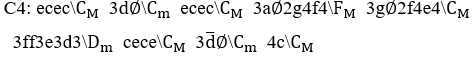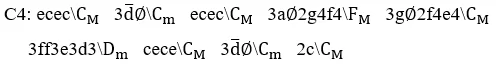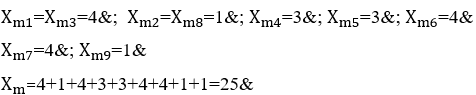The mathematical structure of music

ORIGINAL ARTICLE

VIANA, Arnóbio Araújo ^[1]

VIANA, Arnóbio Araújo. The mathematical structure of music. Revista Científica Multidisciplinar Núcleo do Conhecimento. Year. 07, Ed. 08, Vol. 02, p. 196-220. August 2022. ISSN: 2448-0959, Access link: https://www.nucleodoconhecimento.com.br/mathematical-olympiads/mathematical-structure-of-music, DOI: 10.32749/nucleodoconhecimento.com.br/mathematical-olympiads/mathematical-structure-of-music

ABSTRACT

Taking into account that musical composition is a sound mathematical structure, this article demonstrates the development of the Mathematical Structure of Music, disseminating a more understandable sound language and adapted to the current technology of scientific studies related to the Science of Music. Therefore, the objective of this research was to develop an algebraic language to mathematically structure Music, using only letters, numbers and symbols to write the sounds of musical notes in an alphanumeric way, representing its main sound characteristics, such as: frequency (f) , amplitude (a) and duration time (t), in a single expression to identify a sound wave. The developed language allows a spelling with simple reading and allows the study of musical phenomena in general on a platform with graphic representations in the Cartesian coordinate system of the structures of the melodic groupings, with the musical notes in melody and the harmonic groups with the notes in harmony, thus promoting the Mathematical Structure of Music.

Keywords: Musical Cell, Melody, Harmony, Rhythm.

1. INTRODUCTION

This research was made possible by the development of the Harmonization or H operations and its inverse Melodyation or M, established in the article “the harmonization operation (H) and its inverse melody operation (M)” (VIANA, 2022).

In the aforementioned article, it is defined that the Operation H (\), between sound waves of musical notes, form a harmonic grouping, whose harmony (h) is the sound effect of the result of a combination between them . In this case, these waves are interconnected simultaneously in space-time, that is, their initial times are equal and their final times are also equal. These waves of equal musical notes form a harmonic grouping of a single sound or a unison harmony (VIANA, 2022).

Its inverse Operation M (\), is defined between sound waves of musical notes that form a melodic grouping, whose melody is the sound effect of the result of the arrangement between them  . In this case, these waves are continuously interconnected in space-time, that is, the final time of a wave is equal to the initial time of the next wave and so on, where waves of equal musical notes form a melodic grouping of repeated sounds  . In this way, the musical groups formed and organized in space-time will constitute a musical composition, composed of melody, harmony and rhythm (VIANA, 2022).

Therefore, the objective of this research was to develop an algebraic language to mathematically structure Music, using only letters, numbers and symbols to write the sounds of musical notes in an alphanumeric way, representing its main sound characteristics, such as: frequency (f) , amplitude (a) and duration time (t), in a single expression to identify a sound wave.

2. REPRESENTATION OF A MUSICAL NOTE

 PTo represent the sound of a musical note algebraically in this research, three fundamental characteristics are necessary: the sound frequency (f); the amplitude (a); and the duration time (t), forming the expression “”, called, in this study, the Musical Cell.

This nomenclature was given because it represents any sound or non-sound wave, or even any attribute that composes the structure of a song, with the musical note being the most important sound cell to Music, and the musical pause, the most important non-sound cell to the Music. Music, considered a silent or soundless musical note, where the zero amplitude frequency  is represented by a negated zero as your cipher in this Musical Algebraic Language.

2.1 REPRESENTATION OF MUSICAL FREQUENCY

Frequency (f), in general, is the most important characteristic of any vibration and is caused by an earthquake in any medium, which will produce a series of frequencies. When in Operation H natural between them, a harmony is formed, which determines the resulting frequency of this shake  . In addition, the one with the lowest sound or the lowest oscillation between them , is the most important of all, called the Fundamental Frequency , being the characteristic responsible for the sound we hear and that allows us to distinguish a bass or low-frequency sound from a high-pitched or high-frequency sound.

Represented in Music, currently, based on the work of Guest (2020, p. 33 to 41), by the first seven letters of the Latin Alphabet A, B, C, D, E, F and G, called ciphers, respectively representing the musical notesLá, Si, Dó, Ré, Mi, Fá and Sol, where in capital letters they will indicate the harmonies of instrumental accompaniments or Musical Chords that, in this study, will also represent the musical notes grouped in harmony, result of the Operation ” H” among them . The lowercase letters will represent the musical notes grouped in melody, the result of Operation “M” between them .

The eighth musical note of the alphabet mentioned above is the repetition of the first note , twice as often, identified by a numeric index two on the upper side of its cipher and, if this index were positioned below , this note would be called the Low Octave, with its frequency halfway down the first note, meaning that its frequencies are decreasing .

Therefore, a musical note scale in octave can be represented in parentheses with its indicative index above   or low octave with its indicative index below .

Among the eight main musical notes , yet, there are five other intermediate notes, currently represented with the symbol of sharp   next to its cipher on an increasing scale in Lá , separated by frequency spaces called a semitone .

However, in this study, the word “Sharp” is replaced by the letter “u” and its symbol   by a slash over the cipher , to provide a monosyllabic or one-syllable name, which can be sung by anyone in the solfeggio study of these musical notes. Thus, the musical note Lá sharp    is also the note Lau , Dó sharp   the note Dou  , Ré sharp the note Reu , Fá sharp the note Fau and Sol sharp the note Sou .

Yet, too, there are twelve musical notes in between, between the thirteen notes of the crescent semitone scale in Lá , separated by frequency spaces called a Microtom , used, normally, by musicians from the Eastern Continent, who, in this study, present their names with their figures, originated with the first letter of the note before their position in the ascending scale in Lá , joined to a vowel (a, e, i, o, u), excluding those that repeat the names of existing notes.

For example, the first microtone note “”  between the notes Lá and Lau , have your name “Lé”, formed with the letter L of the note A (a), plus the vowel “e” of the sequence “a, (e), i, o, u”, excluding the vowel “a” of the note Lá and its cipher is the same of the note Lá (a), but in capital letter (A) when in melody, as well as the name of the next microtone note “”  between the notes Lau and Si , have your name “Li”, formed with the letter L of the note Lau , plus the vowel “i” of the sequence “a, e, (i), o, u”, excluding the vowels “a” and “e” of the notes Lá and Lé, its number being the same as the note Lau , but in capital letter and, the name of the twelfth musical note   between the note Sou and Lá octave , it is “Só” , being formed by the letter “S” in Sou and “o” from the vowel sequence “a, e, i, (o), u”, excluding the vowels “a” existing in Sá, “e” existing in Sé, “i” existing in Si, leaving the vowel “o”. Your number is the same as the note Sou , but in capital letter . This is how the musical notes microtones were called, below the semitone scale and the microtone scale in Lá.

Semitone musical scale in Lá

Lá  Lau  Si  Dó  Dou  Ré  Reu  Mi  Fá  Fau  Sol  Sou  Lá2

Microtone musical scale in Lá

Lá Lé Lau Li Si Sá Dó Dá Dou Dé Ré Rá Reu Ri Mi Má

2.2 TONE 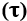, SEMITONE 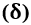AND MICROTOM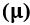

Whatever the musical scale, its musical notes are separated in melody by spaces of frequency intervals  , which can present three measurements at different frequencies, called Tone , Semitone and Microtom , being the semitone determined through its scale of thirteen musical notes ,which is a series of a GP or Geometric Progression, (SILVA, s.d.).

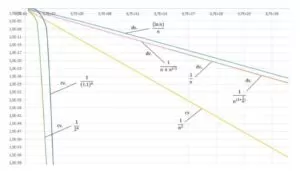
In this case, a Musical GP (MGP), where the thirteenth note is twice the first  . Therefore, one can apply the Nth Term formula of a GP   and calculate your reason , where and , resulting in the interval of a semitone  , tone being calculated by the square power of a semitone    and the microtone calculated by the square root of a semitone .

These values can also be determined by the general formula of frequency intervals where “n” equal to one results in the interval of a semitone   “n” equal to two   results in the range of a tone “n” equal to half results in the range of a microtone   In this way, the frequency of a musical note can be calculated through the formula of the General Term of a GP   where the first term   is the standard fundamental frequency of the musical note Lá   and the second term   is the frequency of the next musical note , Therefore, the fundamental frequency of the note Si is the product between the note Lá by Tom  , as well as the product between the frequency of the note Si by the semitone, results in the frequency of the note Dó and the product of the note frequency Dó by the microtone, results in the frequency of the note Dá and so on for any musical note.

However, it is worth remembering that these frequencies are approximate values, as the Tone , the Semitone   and the Microtom   are irrational or infinite numbers, like the number pi   Furthermore, for a better operational understanding of frequency intervals on a linear scale, one Semitone is considered equal to one-half Tone a Microtom is equal to a quarter of Tone and a semitone equal to half a microtone .

2.3 REPRESENTATION OF MUSICAL TIMBRE

When the fundamental frequency is taken from the set of harmonic frequencies, which make up any frequency   the remaining frequencies will form the Timbre   from Latin Timpanum, which is a secondary characteristic of the resulting frequency  , but that allows us to distinguish distinct sounds with the same fundamental frequency.

This feature is considered optional in Musical Algebraic Language, leaving it up to the performer to choose the instrument to be used in the emission of musical notes. However, the Timbre can be represented by a natural integer number accented with a tilde appended to the musical note cipher or at the beginning of the spelling   for every melody or come before a parenthesis only for some musical notes , where is the melody part indicating the instrument to be used is subtitled (= instrument).

2.4 REPRESENTATION OF MUSICAL RANGE

The amplitude (a) of a musical note   is measured by its sound intensity in decibels, which can vary from zero to an audible limit bearable by the human being (HELERBROCK, s.d.), being the characteristic that allows us to distinguish a weak sound from a strong sound.

Normally, the sound intensity range between forty to sixty decibels is used    as the normal intensity range for any musical note to be heard by human beings and, below this range , the cipher of the note is identified with a grave accent and, above this range with an acute accent . Also, if a specific intensity is needed for any value, just a circumflex accent on that value attached to the note cipher , indicating this intensity multiplied by ten, may also come before a parenthesis for several musical notes   . An arrow attached to a musical note will indicate that its sound intensity is increasing descending or increasing-decreasing and vice-versa.

2.5 REPRESENTATION OF MUSICAL DURATION TIME

the duration time of a musical cell  , note or rest, is the characteristic that allows us to distinguish a sound of short duration from a sound of long duration, being represented by a positive natural integer number  , that in a melodic arrangement before the cipher of a musical cell , represents a duration equal to or greater than one second  . In this context, the most used are those of a second , two seconds , three seconds , four seconds   and few others over that duration .

Due to the most used measures in a musical rhythm, in this study, the standard period is limited to four seconds and, when that same integer comes in a melodic arrangement after the cipher of a musical cell    it will represent a duration equal to or less than one second constituting a fractional number to Music.

Implying “n” as a denominator number of a fraction, whose numerator is the unit  , the most used durations being half a second , a third of a second  , a quarter of a second  , one sixth of a second  , an eighth of a second   and no more than a ninth of a second long  , because the sound ceases to be auditory for the human being when it is equal to or less than a tenth of a second  . Therefore, both the duration time in seconds and in fractions of a second can be represented in the same musical cell. For example,   is the note Ré three seconds long, is the note Ré one-third of a second long and is the note Ré one second, another half and another quarter of a second long.

When a duration time   come with an acute accent   or serious , means it is instantaneous or equal to one ninth of a second  , with the rest of the actual duration in musical pause. In this case, the acute accent indicates an amplitude with strong intensity and the bass accent indicates an amplitude with weak intensity. For example,   it is the note Dó with strong sound intensity in the instantaneous duration and pause for the remainder of the half-second duration.

When a duration is followed by a colon it means a brief interruption in the musical composition, allowing the musicians to interact with the audience, restarting at any time, normally in the same measure of the interruption.

When a duration is accompanied by an ellipsis   means that after its end, it extends in musical pause for another certain time, being able to end in the same measure or in another measure different. For example, it is the note Sol with a duration of one second, and can end in the same measure or in any other measure.

When a musical note starts in one measure and ends in another without losing its sound continuity, its cipher in the next measure is identified with an apostrophe. For example, the note Dó with three seconds  , being two seconds   in a measure and a second   in the next bar .

3. OPERATIONS BETWEEN MUSICAL CELLS

The operations between musical cells form groupings of notes and musical rests, called musical monomials and when a duration time come between two musical cells , it will always belong to the first cell   and the second has a later duration. In this case, it’s a second implied and only a comma before that duration will make you belong to the second cell   making the first one last for an implied second. For example,   it is the note Dó with half a second and the note Mi one second long and   it is the note Dó with a second and the note Mi two seconds long.

3.1 OPERATION “M” BETWEEN MUSICAL CELLS

When any two or more musical cells are in operation M, they form a melodic algebraic monomial m, the result of which is a melody between them  , where the final duration time of the first note   is equal to the initial duration time of the second note , as well as the final duration time of the second note   is equal to the initial duration time of the third note . For example, musical notes Dó, Mi, Sol, Mi, Dó, all one second long    in Operation M form a melodic monomial of domisolmidó melody and, any change of position of one of these notes, in this operation, will form another result with another melody .

3.2 OPERATION “H” BETWEEN MUSICAL CELLS

When two or more rhythmic musical notes or notes of equal duration   stay in operation , they form a harmonic algebraic monomial h, the result of which is a harmony between them, where their initial duration times are all equal , as well as their final duration times .

Equal musical notes, in this operation, result in a unison monomial or a single musical note and, when these notes are arrhythmic or with different durations, they will form various harmonies depending on the operation M. For example, the operation H in between  and between . In this case, the note Sol with shorter duration forms the first harmony domisol , leaving the Mi note with a shorter duration   forming the harmony domi   in melody with the domisol harmony, leaving the note Dó one second long in melody with harmony domi.

3.3 OPERATION “M” BETWEEN MUSICAL MONOMIS

When two or more musical monomials are in operation , they will form a melodic polynomial  , where their monomials are separated by white spaces, implying the operators   between them, being able to be formed: only by melodic monomials in a single melody , only by harmonic monomials in a melody of harmonies and composed of melodic and harmonic monomials  .

These monomials must be rhythmic or have equal periods  , being determined by the sum of the duration times of their musical cells  , property called in this study the Rhythm Principle, which allows any system to remain in equilibrium during its existence and, even if an eventual arrhythmia occurs in its structure or if one of these periods is different from the others, the following period will remain the same as the previous one. equilibrium period to correct the occasional imbalance. However, a sequence of arrhythmias in the rhythmic structure can cause the rhythm of this polynomial to collapse.

When the monomials of this polynomial are arrhythmic, they must be modulated in a rhythm in a binary rhythmic structure , ternary , quaternary or any other , adjusting the arrhythmic periods in rhythmics and only the first and the last monomial of a rhythm can be incomplete of musical notes, respectively, subtending musical pause before and after these notes completing the periods of these monomials, as shown in the examples below.

a) Operation with the rhythmic monomials

quaternary melodic polynomial

b) Operation with the arrhythmic monomials

arrhythmic melodic polynomial

ternary rhythmic module in

ternary melodic polynomial

3.4 OPERATION “H” BETWEEN MUSICAL MONOMIS

When two or more musical monomials are in operation , they form a harmonic polynomial . Thus, the monomials remain in the same operational form, separated by their operators    or they can be in the form of a column array 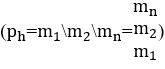, can be formed only by melodic monomials in harmony , only by harmonic monomials    and composed of melodic and harmonic monomials . Below is an example of the Operation   between three rhythmic musical monomials.

Below is an example of the Operation between three rhythmic musical monomials.

Melodic monomials

Operational Form: 

Array Shape:

The harmonic monomial   can be replaced by its chord form of Dó larger(ALMADA, 2012). In this way, its duration is implied and is equal to the duration of the melodic monomials of this operation    or it can stick to its specific duration if it is different from the duration of the melodic monomial, which determine the period of the bar. For example, if  .

3.5 OPERATION “M” BETWEEN MUSICAL POLYNOMIS

When two or more rhythmic musical polynomials are in operation M, they can form various types of new monorhythmic musical polynomials. When all the polynomials present the same rhythm, otherwise, they form polyrhythmic polynomials, being the most used in Music, those formed only by harmonic polynomials that are rhythmic compounds  , as example below.

Given the compound polynomials form: 

Operational Form:

Array Shape:

Where:

3.6 OPERATION “H” BETWEEN MUSICAL POLYNOMIS

When two or more rhythmic musical polynomials are in operation ,they can form several types of new musical polynomials, the most used in Music being those formed between melodic polynomials only with rhythmic melodic monomials, with melodic polynomials only with rhythmic harmonic monomials , in this case, the monomials of the operating polynomials   must be rhythmic with each other, as shown in the example below.

Given the melodic polynomials form

Operational Form:

Array Shape:

4. GRAPHICS OF A MUSICAL POLYNOM

Musical monomials can be plotted on a graph on the axes of Cartesian coordinates. To do this, the frequencies or figures of your musical notes must be allocated on the ordinate axis or on its vertical line, and on the abscissa axis or on its horizontal line, the duration time of these notes. Then, connecting these points with line segments for a melodic monomial, the Melodic Line graph is formed.

However, for a harmonic monomial, where their durations are simultaneous, simply plot the duration of its tonic musical note or the main note of the musical accompaniment chord on the melodic monomial line graph, just above the figure for a harmony of the major and a little lower for a harmony of the minor mode, forming the Harmonic Line graph, according to the examples listed below.

a) in

Graphic 1. Musical scale in C in binary rhythm

 

 

b)

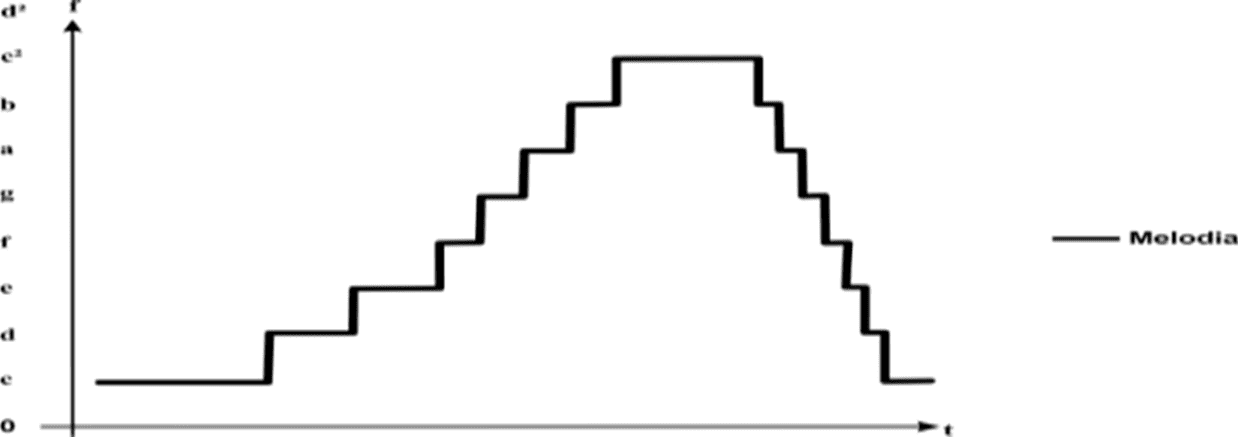
Graphic 2. Simple melody in quaternary rhythm.

c)

Graphic 3. Melody with a harmony.

5. HARMONY OF MUSICAL ACCOMPANIMENT

Given any melody , you can determine your musical accompaniment harmony by applying the Harmonic Module    developed in this study. In each measure of this melody, which transforms melodic musical notes into harmonics, through the operation   between them , whose resulting harmony is adjusted to an existing major or minor mode accompaniment chord harmony (ALMADA, 2012), as example of the melody below.

Harmony of:

Adjustment of   to the chord of Dó major:

Adjustment of   to the Dó minor chord as a function of

Adjustment of to the Fá major chord:

Adjustment of to the chord of Dó major:

Adjustment of   to the chord of Ré minor:

Simple harmony of:

Operation   in between and

The accompanying harmony   it’s a simple harmony. In the example above, the harmonies found in the harmonic modules were adjusted to the most suitable existing major and minor chords, taking into account the influence of the tonic note of the chord of melody Dó major  . As demonstrated, in some bars, musical notes of short duration were left without musical chords, without harming the harmony of the melody .

5.1 MUSICAL ACCOMPANIMENT MELODY

These musical accompaniment harmonies can be turned into an accompaniment melody. To do this, simply apply the Melodic Module to these harmonies , which transforms a harmony into several melodies through Operation   between your harmonic notes, that for a triad or three musical notes in harmony  , will result in six distinct melodies  .

Due to the permutation between these three musical notes to form the note arrangements in melodies   and for a tetrad or four musical notes , will result in twenty-four distinct melodies, due to the permutation of four being equal to 24 melodic arrangements . From there, just choose one of these melodies for the musical accompaniment of the melodic monomial of this harmony, subtitling it separately. In this case, the duration time of each note is determined by the inverse of the number of musical notes per second , than for a triad or three musical notes  (n=3), is a third of a second long , as example below.

Dó major chord:

  melodies

Subtitle:

Graphic 4. Melody &4 with an accompanying melody.

 

6. MEASURES OF MUSICAL MONOMIS

The musical monomials of a melody or a harmony in general will provide two types of musical measures important to Music, one called Musical Period, which measures the duration of a melodic monomial  , harmonic  and composed of melodic with harmonic , scaled in seconds ; and another called Musical Texture , which measures the appearance of musical notes in the structure of a melodic monomial , harmonic or compound, scaled in musical notes . The ratio between Melodic Texture and Melodic Period determines the Melodic Dynamics of musical notes in the structure of a melodic monomial.

6.1 PERIOD AND TEXTURE OF A MELODIC MONOMIUM

A melodic monomial presents its musical notes continuously distributed in space-time, forming a Melodic Period , determined by the sum of the duration times of its musical notes , scaled in seconds . The Melodic Texture , is determined by the number   of musical notes in your melodic period.

The Ratio between Melodic Texture and Melodic Period   determines the melodic dynamics of musical notes per second in the structure of this monomial, as shown below.

1) Melodic monomial  

Melodic period:

Melodic texture: four musical notes

Melodic dynamics: slow melody

2) Melodic monomial  

Melodic period:

Melodic texture: sixteen musical notes

Melodic dynamics: very fast melody

6.2 PERIOD AND TEXTURE OF A HARMONIC MONOMIUM

A harmonic monomial   presents its musical notes interconnected at the same time and they are usually rhythmic or of the same duration. Therefore, its Harmonic Period   is equal to the duration time of any musical note in its structure , scaled in seconds .

However, it can happen that a harmonic monomial is arrhythmic or presents its musical notes with different durations. In this case, several different harmonies will occur, with different harmonic periods and the melody between them results in the total harmonic period of this monomial  . In addition, the Harmonic Texture , is determined by the number of musical notes in harmony in the harmonic period, as shown below.

1) Rhythmic harmonic monomial

Harmonic period:

Harmonic texture:

2) Arrhythmic harmonic monomial

Harmonic period:

Arrhythmic harmonic texture:

6.3 PERIOD AND TEXTURE OF A MELODIC POLYNOMIUM

A rhythmic melodic polynomial is one where its monomials have equal periods. In this way, the product of the number   of bars for its period , determines the duration time of this polynomial, scaled in seconds or minutes.

Even if this polynomial is composed with melodies and harmonies, the calculation of its duration would be the same, while its total melodic texture remains the number of musical notes in that Duration Time.

The ratio of this Total Melodic Texture to the Total Duration Time forms the Melodic Dynamics of musical notes in this polynomial, being scaled in musical notes per second.

When the melodic polynomial is composed of a harmony, its total Harmonic Texture   is determined by the arithmetic mean of the harmonic textures of all its harmonic monomials of its bars , as shown below.

Polynomial duration time

Melodic period of

Beat numbers:

Total duration time:

Full melodic texture:

Melodic dynamics: (Melody with slow dynamics)

All harmonic textures are equal to:

Total harmonic texture: (Simple texture)

7. PLAGIARISM BETWEEN MELODIC POLYNOMIS

Normally, plagiarisms are equalities that occur between melodic monomials and melodic polynomials   and, how these monomials are formed by musical notes continuously distributed that plotted on a graph in the Cartesian coordinate system, show their melodic lines, which can be compared with each other, showing their similarities or differences, those who present their melodic lines are considered plagiarism, that is, that coincide on the graph, placing them one on top of the other, or even transporting the musical notes of the monomials considered plagiarism to the tonality of the notes of the original monomials. Below is an example of plagiarism monomials.

Equal melodic monomials: and .

Graphic 5. Melodic monomials .

 

7.1 PLAGIARISM PERCENTAGE

When a continuous part of a melodic polynomial is plagiarism of another, that is, it has a percentage of plagiarism or equality in relation to the original polynomial, the identified similarities can be calculated by the formula , where   is the number of melodic monomials or bars with plagiarism, and is the total number of monomials or measures of the original polynomial, without the melodic repetitions. For example, given a melody with fifty bars and, among them, ten consecutive bars were plagiarized in another tune, so:

8. STRUCTURE OF A RHYTHM

Rhythm is a phenomenon that occurs in the duration of any system, being divided into equal parts to keep itself in balance. This is how it happens in the rhythm of a melody, where its duration   is divided into parts of equal periods, called measures, which are continuously linked as a function of the Operation , as well, each measure is also divided into equal parts of smaller periods, called units of time , which are also continuously interconnected as a function of the Operation   .

It is known that the duration of any period , has an initial duration    and final , soon, . Furthermore, this initial duration   consists of a beat   audible or non-audible, caused by an impulse , given by a force for an instantaneous duration, remaining silent for the remainder of its duration , therefore, the period of any measure is formed by its initial beat  in tune with your time of silence .

In a single bar, in addition to the beat of your period with your time of silence , still exists, in its interior, due to the Operation  , the beats of the units of time, with their times of silence  , the result of which makes the first beat twice as strong as the others  , and the sound effect is called the Rhythmic Cadence of the Measure  , that has a beat speed called the Rhythmic Tempo of the Measure, being inversely proportional to the period of this unit of time , scaled in beats per second   or beats per minute .

In this context, the shorter the duration of this unit of time, the greater the rhythmic tempo of these beats, which provides two rhythmic movements in a physical body in its area of operation, one of which is called Rhythmic Regency  , where a body without leaving its resting position, follows the movement of the Rhythmic Tempo of these beats, and another called Rhythmic Dance  , where a body moves from its resting position to other distinct positions, depending on the rhythmic tempo of these beats.

8.1 LAW OF TONIC ACCENTUATION OF BARRES

The property of the first beat of the time unit of a measure being stronger than the other beats in the same measure originated the Law of Tonic Accentuation of the Bars that marks, in an incisive way, any musical note that occupies that first position in the bars of a rhythm. Also accentuating any syllable of any word that occupies that position, modifying or not its orthographic tonic accentuation, whatever the spoken language of the world. In the case of a rest placed in this position and a musical note in the next position, a musical effect called Contratempo occurs.

8.2 STRUCTURE OF A COMPOUND COMPASS

A measure is called a compound when more than one distinct rhythmic cadence occurs in its period  , formed by other distinct time units  . In this case, the Compound bar can be either Melodic or Harmonic.

In the Melodic Compound Measure, the rhythmic cadences of the time units depend on the Operation , resulting in a Melodic Rhythmic Cadence  . Between them originates a melodic rhythmic tempo  , a melodic rhythmic regency   and a melodic rhythmic dance  .

In the Harmonic Compound Measure, the rhythmic cadences of the different time units  and  are depending on the Operation , resulting in a Harmonic Rhythmic Cadence between them  .

On condition that , the resulting Rhythmic Cadence is determined by the unit of time with the shortest duration  , in this case, the resulting harmonic rhythmic Tempo is given by the period of the smallest unit of time  , with its rhythmic harmonic conducting normally a function of the rhythmic tempo of the largest unit of time   and its rhythmic harmonic dance   depending on the major and minor rhythmic tempo .

8.3 HARMONIC RHYTHM

The Rhythmic Cadence of a bar is usually melodic , due to its time units being a function of the Operation . However, this cadence can be harmonic with the periods of its time units as a function of the Transaction , resulting in a single unit of time, with its melodic rhythmic cadence . For example, when a group of people are silent for a certain period of time or when several clocks are in sync.

9. FINAL CONSIDERATIONS

This article aimed to develop an algebraic language to mathematically structure Music, using only letters, numbers and symbols to write the sounds of musical notes in an alphanumeric way, representing its main sound characteristics, such as: frequency , amplitude and duration time , in a single expression to identify a sound wave.

In the end, it appears that the Mathematics of Music was only possible with the development of Operation   and its inverse Operation , providing the groupings of sound waves of musical notes, respectively in the formations of harmonies of instrumental accompaniments and melodies that appear at all times in the inspiration of a composer, making the study of music simpler, with a sound language more understandable and adapted to current technology of the scientific studies of the Science of Music. Finally, with the demonstration of the Mathematical Structure of Music, it can be said that a musical composition is a mathematical structure of sound.

REFERENCE

ALMADA, Carlos. Harmonia Funcional. Editora Unicamp, 2ª Edição, 2012.

GUEST, Ian. Harmonia – Método Prático. Editora Luminar. Vol. 1, p. 33 a 41, 2020.

HELERBROCK, Rafael. Intensidade do som. Mundo da educação, s.d. Disponível em: https://mundoeducacao.uol.com.br/fisica/velocidade-intensidade-som.htm. Acesso em: 22  de julho de 2022.

SILVA, Luiz Paulo Moreira. Progressão geométrica. Brasil Escola, s.d. Disponível em: https://brasilescola.uol.com.br/matematica/progressao-geometrica.htm. Acesso em? 22 de julho de 2022.

VIANA, Arnóbio Araújo. A operação harmonização (H) e sua inversa operação melodiação (M). Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 07, Ed. 03, Vol. 03, pp. 144-171. Março de 2022. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/operacao-harmonizacao, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/operacao-melodiacao. Acesso em: 22 de julho de 2022.

^[1] Graduated in Electrical Engineering, op. Electronics from the Federal University of Pará-UFPA. ORCID: 0000-0001-7010-9114.

Sent: July, 2022.

Approved: August, 2022.