Patterns of repetitions in division by prime numbers

PEER REVIEW

D’AGOSTINO, José Rubens Buccolo ^[1]

D’AGOSTINO, José Rubens Buccolo. Patterns of repetitions in division by prime numbers.  Revista Científica Multidisciplinar Núcleo do Conhecimento. Year 08, Ed. 01, Vol. 01, pp. 96-109. January 2023. ISSN:2448-0959, Access link in: https://www.nucleodoconhecimento.com.br/mathematical-olympiads/prime-numbers, DOI: 10.32749/nucleodoconhecimento.com.br/mathematical-olympiads/prime-numbers

ABSTRACT

The topic of this peer review explores possibilities of repeating patterns involving prime numbers. For this, analyzes of division of natural numbers by prime numbers are demonstrated. Additionally, comparisons are made between intervals of dividends, as well as between quotients, using algorithms and spreadsheets. And finally, events that demonstrate proof of authenticity are graphically presented.

Keywords: Primes patterns, Prime numbers indexation, Factorization and primes, Prime numbers architecture, Quantum physics and prime numbers.

1. INTRODUCTION

This peer review results from the observation of long mathematical operations and sequential development of algorithms, necessary to show consistency in the connections between prime numbers. In the methodology used, answers are systematically distributed in spreadsheets according to the appearance of new results, allowing new facts computed to expand the possibilities of reaching intended evolutionary answers. Such direction of steps embodies an irreplaceable form of research when unexpected discoveries occur, that is, a path that needs to be based on solid data that until then were unknown. Therefore, with each new information that appears, specific algorithms need to be created, which safely validate the new data that are added to the research.

Next, spreadsheets and graphs will be sequentially presented, proving the existence of correlations in the sequence of prime numbers. I believe that from the cases demonstrated in this research, more questions arise that instigate scholars and can also be applied to other sciences.

2. DEMONSTRATION OF THE EXISTENCE OF REPETITION PATTERNS IN DIVISION BY PRIME NUMBERS

Discoveries about prime numbers and their applications are always surprising, and this is precisely the central theme of this peer review, presented below.

Considering that every natural number (n) is divisible at least once by a prime number (p), resulting in an integer quotient (q), we can create an equation defining integer intervals (I), that is:

(n2/p1=q2) – (n1/p1=q1) = I

Therefore, sequentially dividing natural numbers (n1,n2,n3…) by the same prime number (p) and subsequently subtracting the integer quotients resulting from these divisions (q2-q1), will define a sequence of intervals(I), as shown horizontally in the table below, Figure 1. Note that in the sequence of divisions by 7, which is marked in yellow, we can observe the occurrence of repetition patterns, which every eight cells are repeated until infinity.

Figure 1. Spreadsheet with patterns of interval repetitions (I) between quotients

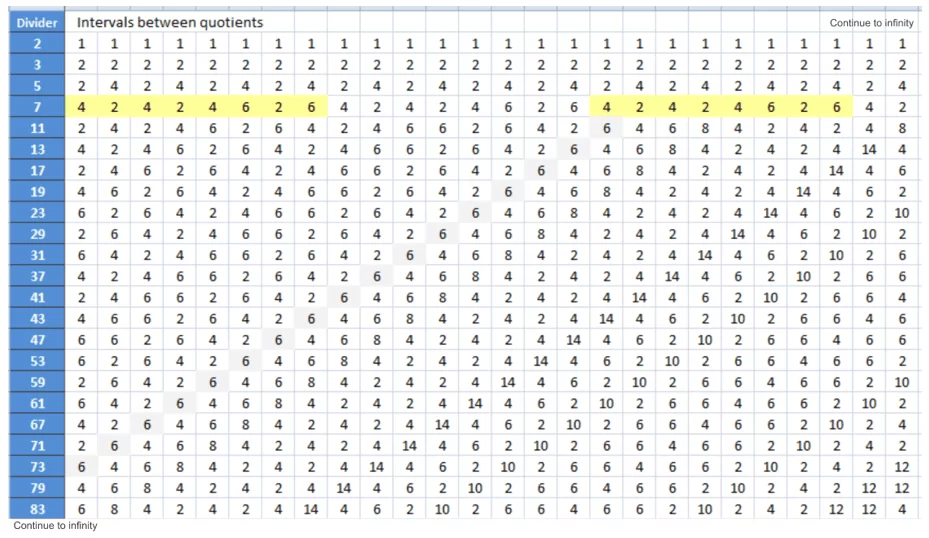
In divisions by 2 to 7, of this table, we can observe that there are interval patterns (I), which are repeated at a frequency of (p1, p2, p3, p4) as follows: One (I) for division by 2 and by 3; Two (I) for division by 5; and Eight (I) for division by 7 etc.

Transversal sequences with repetition of values are also marked in this table, which we will be able to understand why they happen at the end of this peer review.

3. ALL PRIME NUMBERS CREATE A REPEATING PATTERN WHEN THEY ARE SEQUENTIAL DIVISORS

In the following tables, in Figure 2, we can see that repetition patterns tend to repeat themselves to infinity. Thus, knowing that (I) is the interval of places between the sequence of quotients, these results show us that there are patterns of interval repetition, starting from: Eight (I) for division by 7; Forty-eight (I) for division by 11; Four hundred and eighty (I) for division by 13 and One million, six hundred and fifty-eight thousand, eight hundred and eighty (I) for division by 23.

Figure 2. Tables containing partial patterns of divisions by different prime numbers

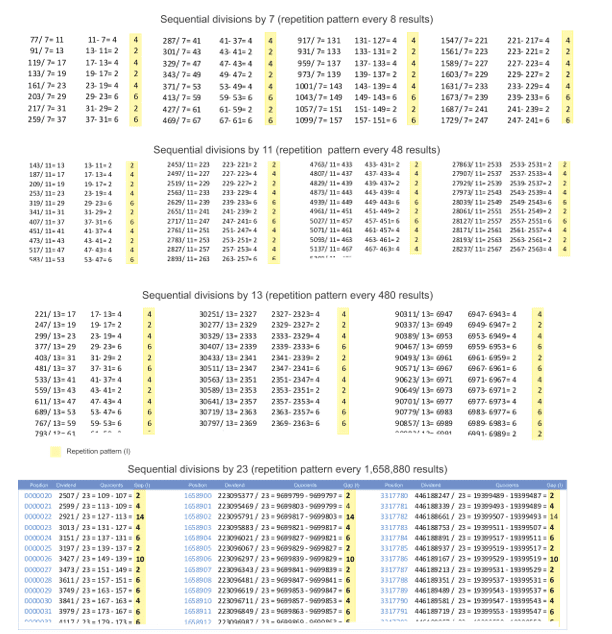
4. ANY PRIME NUMBER, WHEN IT IS A DIVISOR GENERATES AN INDEX OF NUMERICAL DISTANCE BETWEEN THE CORRESPONDING DIVIDENDS

For over two thousand years, tables containing prime numbers have attracted our attention. Recently, with the development of Algorithms that generate large tables, it has become possible to visualize new fundamentals in the behavior of these figures. One of the unusual concepts is that in the sequential division of any natural number (D) by the same prime number (P), after a random period, a repetition pattern occurs between the quotient intervals (I). When these repeating patterns are found, it is possible to recognize the existence of an index for each prime number, which is a constant interval between the corresponding dividends. Below is a diagram representing the behavior of such indices (Fig. 3).

Figure 3. Diagram demonstrating that there is an index (X) between corresponding dividends (D) for divisions by prime number

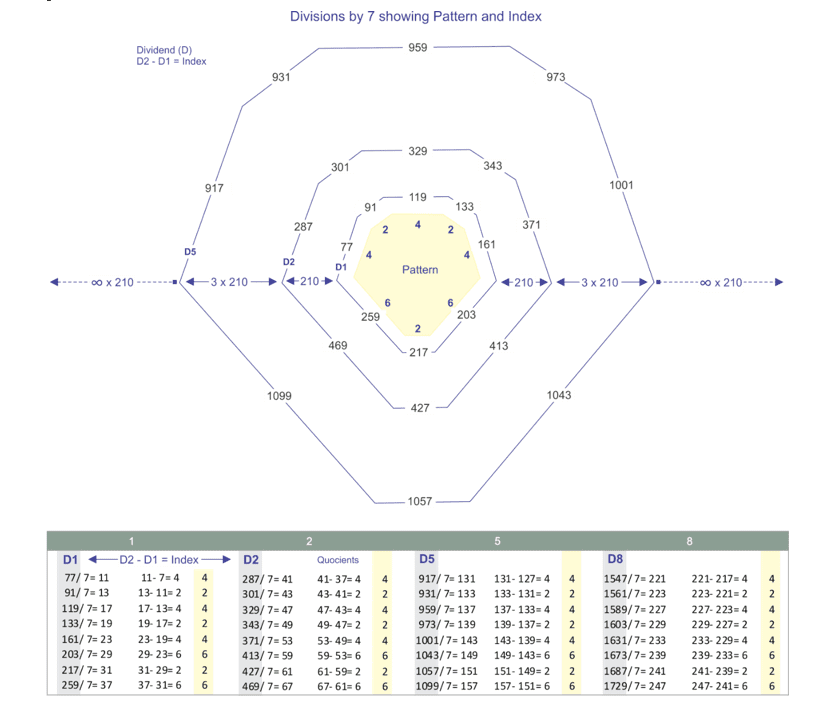
If we consider the repetition patterns (P) being a prime divisor that defines a bounded sequence, then we will realize that (P) represents a spiral expanding to infinity, starting from a common center.

When comparing the columns of the table above, we can see that the dividends (D1) if subtracted from the corresponding dividends (D2), define the same index value (X), which expands in a straight line with perfect homogeneity in all directions towards infinity.

5. THERE ARE ALWAYS CORRESPONDENCES IN THE SEQUENCE OF DIVISIONS BY THE SAME PRIME NUMBERS

We observed in the reading of this peer review that there are many correspondence in the divisions by prime numbers. In the table below, the intervals between dividends are marked, as well as between divisions by the same prime number, thus making sure that both are repetition patterns projecting synchronically to infinity

Figure 4. Complete repeating pattern for prime number 13, displayed horizontally

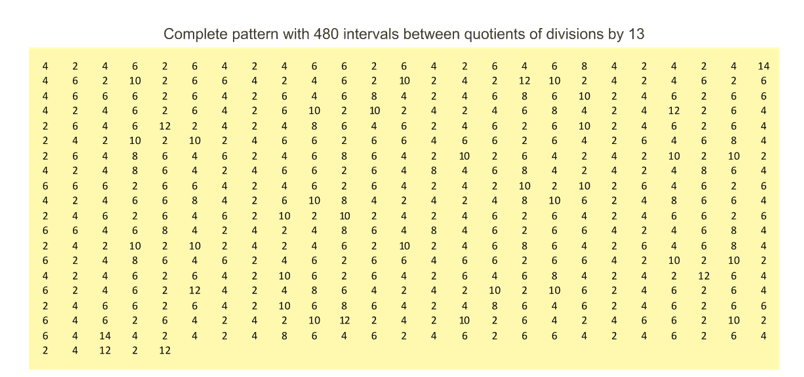
6. TABLES DEMONSTRATING THE EXISTENCE OF REPEATING PATTERNS, AS WELL AS THE EXISTENCE OF AN INDEX FOR ANY OF THE PRIME NUMBERS, WHICH APPARENTLY CAN ENCOMPASS AN INFINITE NUMBER OF DIGITS

The discovery that there is an index for each prime number, which links a specific dividend (D) with its larger pairs, going towards infinity, also allows us to know another striking pattern, as these indexers (X) are directly related to the sum of the intervals (I) that occur with its previous prime number (P), thus defining yet another pattern: Sum (P2(I)) = P1(X), as we can see at the end of the table below (Fig. 5)

Figure 5. Table with prime numbers, quantity of intervals, total sum of intervals and indices between dividends

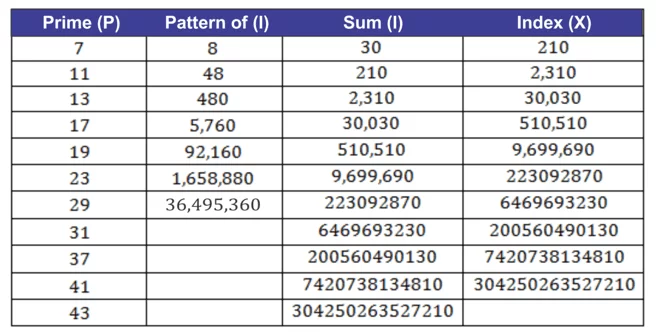
In the four tables below there are references to the Indexes (X) that were presented in Figure 5 from the division by the prime numbers 29 to 41

Despite the certainty that there are patterns of division by prime numbers, which is shown in the tables and graphs above, the question remains whether it is possible to have a single equation that allows defining the next patterns of repetition with divisions by prime numbers greater than 29. Even so, using algorithms we can find the last dividend of any repeating pattern, thus verifying that there really are infinite repeating patterns in subsequent divisions by prime numbers. However, for divisions above the number 41 it is necessary to use more powerful equipment to achieve the necessary results. Therefore, it is still a need to create long tables of intervals between quotients of divisions by prime numbers, until such repetition patterns naturally present themselves, in case we want to know quantities of existing intervals, their specific values and their geometric details.

Even if the divisions by primes are progressively calculated, which demonstrate the existence of correspondences between the dividends and, thus, allow us to identify the specific index for each prime number, it still seems that there is no way to calculate the patterns of intervals between quotients without producing complete tables.

7. INTEGERS SEQUENTIALLY DIVIDED BY THE SAME PRIME NUMBER WILL RESULT IN A PERIODIC SEQUENCE OF PRIME QUOTIENTS

As examples of this effect, note that the first four dividends, divided by the prime 7, are 49, 77, 91, 119 resulting in the quotients 7, 11, 13, 17. Then, for divided by 11, they are 121, 143, 187, 209 resulting in the quotients 11, 13, 17, 19. Just like, those divided by 13 are 169, 221, 247, 299, resulting in the quotients 13, 17, 19, 23. And further those divided by 29, which are 841 , 899, 1073, 1189 resulting in the sequence of prime quotients 29, 31, 37, 41. Continuing like this to infinity.

These periodic sequences of prime quotients are the cause of the existing gap positions found in Figure 1, when they create an oblique line repeating the same interval value as the previous line.

Another important detail of these repetition patterns is that they happen the same for both positive and negative dividends, perfectly mirroring the patterns of intervals between quotients, and also generate the same indices.

8. CONCLUSIONS

With the emergence of new processors, it is possible to create tables with huge amounts of cells and thus be able to prove that sequences with extraordinary divisions can generate repetitive patterns of intervals between quotients, thus allowing to define another mathematical fact. Of course, it’s not just machines that can have new mathematical results, behind them is the need for scholars to develop algorithms. Thus, intuition and human observation are, in these cases, indispensable for new discoveries to occur in the sciences. And some of these long-awaited discoveries even relate to the peculiarities of prime numbers.

In this peer review, I hope to have demonstrated that there are intriguing patterns of repetition between intervals of dividends when divided by the same prime number. At the same time, these patterns give evidence of the existence of a specific index for each prime number that projects towards infinity. Perhaps the possible revelation of these events can also find mathematical solutions that involve or help other sciences, thus fulfilling another important step in scientific discoveries.

^[1] Bachelor’s Degree in Industrial Design. ORCID: 0000-0002-7149-9780.

Sent: December, 2022.

Approved: December, 2022.