ОРИГИНАЛЬНАЯ СТАТЬЯ
PEREIRA, Olavo de Carvalho [1]
PEREIRA, Olavo de Carvalho. Предельный вычисление функции без использования ![]() и
и ![]() . Revista Científica Multidisciplinar Núcleo do Conhecimento. Год. 06, изд. 08, Том. 04, стр. 05-31. Август 2021 г. ISSN: 2448-0959, Ссылка для доступа: https://www.nucleodoconhecimento.com.br/математические-олимпиады/предельный-вычисление, DOI: 10.32749/nucleodoconhecimento.com.br/ru/129231
. Revista Científica Multidisciplinar Núcleo do Conhecimento. Год. 06, изд. 08, Том. 04, стр. 05-31. Август 2021 г. ISSN: 2448-0959, Ссылка для доступа: https://www.nucleodoconhecimento.com.br/математические-олимпиады/предельный-вычисление, DOI: 10.32749/nucleodoconhecimento.com.br/ru/129231
СВОДКА
Проконсультированная библиография ни в одном из проанализированных случаев не дает расчета предела функции, а только «показывает», что значения, представленные в качестве «предела», удовлетворяют определению предела функции, выраженному через неравенства с участием![]() и
и ![]() , поэтому в этой теме имеется пробел, который в настоящей статье предлагается заполнить путем принципиального использования понятия определенной функции, а также определения выражения «
, поэтому в этой теме имеется пробел, который в настоящей статье предлагается заполнить путем принципиального использования понятия определенной функции, а также определения выражения «![]() стремится к некоторому числу» с соответствующим равенством.
стремится к некоторому числу» с соответствующим равенством.
Ключевые слова: предел функции, предельное исчисление, латеральные пределы, бесконечные пределы, пределы на бесконечности.
1. ВВЕДЕНИЕ
В этой статье представлен «вычисление предела функции», чтобы заполнить существующий пробел в этой теме.
Представление расчета, упомянутого в решении нескольких пределов, является основной задачей статьи.
Дополнительным образом мы намерены прояснить, действительно ли необходимо вычислять или нет предел функции.
Мы также очень просто обсудим случай, когда простая функция, определенная на некотором числе, непрерывна на этом числе.
Хотя геометрическая интерпретация всегда важна, здесь мы приблизимся только к представленному алгебраическому «предельному исчислению».
1.1 ПРЕДЕЛЬНЫЙ ВЫЧИСЛЕНИЕ ФУНКЦИИ
Определение предела функции представлено в учебниках по математике как оценка.
Например: Leithold (1994 г.) дает следующее определение предела функции:
Seja ![]() uma função definida para todo número em algum intervalo aberto contendo
uma função definida para todo número em algum intervalo aberto contendo ![]() , exceto possivelmente no próprio número
, exceto possivelmente no próprio número ![]() O limite de
O limite de ![]() quando
quando ![]() tende a
tende a ![]() será
será ![]() , escrito como
, escrito como ![]() se a seguinte afirmativa for verdadeira:
se a seguinte afirmativa for verdadeira:
Dado ![]() qualquer, existe um
qualquer, existe um ![]() , tal que, se
, tal que, se ![]() então
então ![]() .‘‘
.‘‘
A definição acima afirma que os valores de ![]() tendem a um limite
tendem a um limite ![]() quando
quando ![]() tende a um número
tende a um número ![]() , se o valor absoluto da diferença entre
, se o valor absoluto da diferença entre ![]() e
e ![]() puder se tornar tão pequeno quanto desejarmos, tomando
puder se tornar tão pequeno quanto desejarmos, tomando![]() suficientemente próximo de
suficientemente próximo de ![]() , mas não igual a
, mas não igual a ![]() .
.
С другой стороны, Lezzi, Murakami и Machado (1991 г.) высказываются примерно в том же определении:
Seja ![]() um intervalo aberto ao qual pertence o número real
um intervalo aberto ao qual pertence o número real ![]() . Seja
. Seja ![]() uma função definida para
uma função definida para ![]() Dizemos que o limite de
Dizemos que o limite de ![]() , quando
, quando ![]() tende a
tende a ![]() , é
, é ![]() , e escrevemos
, e escrevemos ![]() se para todo
se para todo ![]() , existir
, existir ![]() tal que se
tal que se
![]() então
então ![]() .
.
Munem и Foulis (1982 г.) используют следующее определение:
Se ![]() é uma função e
é uma função e ![]() é um número, entende-se a notação
é um número, entende-se a notação ![]() como «o limite de
como «o limite de ![]() » quando
» quando![]() tende a
tende a ![]() é
é ![]() isto é,
isto é, ![]() se aproxima do número
se aproxima do número ![]() quando
quando ![]() se aproxima de
se aproxima de ![]() .
.
Как видно из вышеприведенных определений, предел представлен![]() просто чтобы удовлетворить само определение.
просто чтобы удовлетворить само определение.
Никакой расчет этого предела не представлен в любое время.
В данной статье представлен «предельный расчет» функции, которую можно использовать во всех случаях, когда необходимо выполнить такую операцию.
Теперь к аргументу.
Для некоторых функций, не определенных в определенном числе, для того, чтобы с максимально возможной точностью знать, каково будет их значение в этом числе, принято оценивать их в значениях, близких к тому числу, для которого они не определенный.
Пример: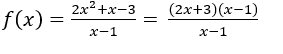 установить для всех
установить для всех ![]() кроме
кроме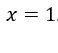 .
.
Если мы заменим![]() на 1 имеем неопределенность
на 1 имеем неопределенность ![]() .
.
Так как функция не определена, т. е. не существует при значении 1, то мы оцениваем ее значение, близкое к 1, так как наша цель — узнать значение функции, по крайней мере, близкое к 1, так как его не существует ![]() .
.
Для значений ![]() , отлично от 1, больше или меньше 1, porém очень близко к 1,
, отлично от 1, больше или меньше 1, porém очень близко к 1, ![]() , тогда
, тогда![]() будет равно 1, и будет иметь значения близкие к 5, как мы увидим ниже:
будет равно 1, и будет иметь значения близкие к 5, как мы увидим ниже:
Давайте назначим ![]() ценности
ценности![]() , то есть мы берем значения
, то есть мы берем значения ![]() все ближе и ближе к 1, но меньше 1. Значения
все ближе и ближе к 1, но меньше 1. Значения ![]() найдены:
найдены:
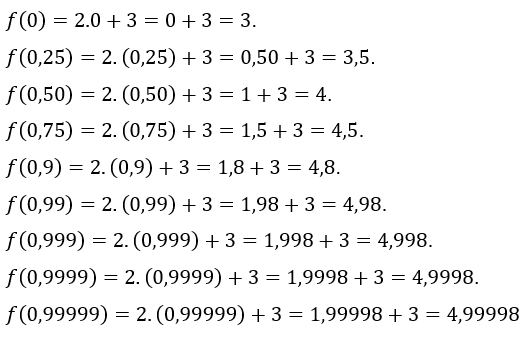
Теперь давайте назначим![]() ценности
ценности ![]() , то есть мы берем значения
, то есть мы берем значения ![]() ближе и ближе к 1, но больше 1. Значения
ближе и ближе к 1, но больше 1. Значения ![]() найдены:
найдены: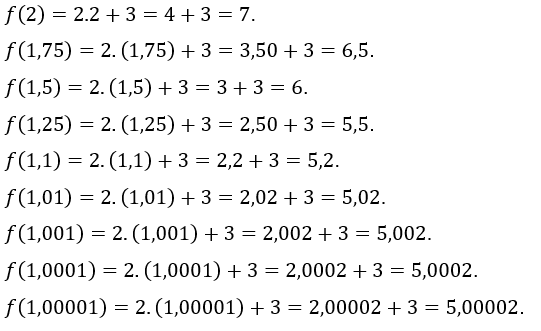
Как видно, в обоих случаях, как ![]() приближается к 1,
приближается к 1, ![]() приближается к 5, что приводит нас к мысли, что это предел
приближается к 5, что приводит нас к мысли, что это предел ![]() .
.
Однако здесь не производился предельный «расчет», а только оценка ![]() , когда
, когда ![]() принимает значения очень близкие к 1.
принимает значения очень близкие к 1.
Таким образом, значение 5 является «кандидатом» на то, чтобы быть пределом, который нам еще нужно вычислить.
Проконсультированные авторы структурируют определение предела с точки зрения неравенств из подобных примеров и принимают оценочное значение, в данном случае 5, как действительно предел функции.
В связи с этим они утверждают, что ![]() , потому что для любого
, потому что для любого ![]() , каким бы маленьким оно ни было, есть
, каким бы маленьким оно ни было, есть ![]() , такой, что если
, такой, что если ![]() тогда
тогда ![]() .
.
Предельное определение, данное в начале, не имеющее предельных вычислений, используется для «доказательства», что данные числа без указания того, где они были взяты, являются пределами функций.
Мы покажем, что определение предела не доказывает, не доказывает, что данное число является пределом функции, а только «показывает», что данное число является пределом.
Давайте на примере проясним разницу между «показом» и «демонстрацией».
- Покажите, что 2 является корнем уравнения
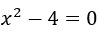 .
.
Это означает, что если мы заменим ![]() на 2, мы будем иметь ноль в результате уравнения.
на 2, мы будем иметь ноль в результате уравнения.
Посмотрим![]() .
.
Это был пример «демонстрации», то есть только что-то показывалось, ничего не демонстрировалось, ничего не вычислялось, только подменялось предоставленное значение.
Другое дело, когда вы говорите: докажите, что 2 — это корень, это решение уравнения![]() .
.
В этом случае мы должны вычислить, решить уравнение и посмотреть, получим ли мы ![]() .
.
Что ж, решая ее, мы имеем: ![]() , скоро
, скоро![]() , и извлекая квадратный корень с обеих сторон, получаем:
, и извлекая квадратный корень с обеих сторон, получаем: ![]() , Это,
, Это, ![]() или же
или же ![]() .
.
Тогда одно из значений ![]() это действительно 2.
это действительно 2.
При этом было «продемонстрировано», что 2 действительно является корнем уравнения ![]() .
.
Мы увидим на приведенных ниже примерах, что нет доказательства, а есть только «показ», что данное число является пределом данной функции.
Пример. Используйте определение предела, чтобы «доказать», что ![]() .
.
Здесь не сказано, как был сделан вывод, что предел равен 5, и не сказано, откуда взято это число.
Мы обсудим, в общих чертах, решение, представленное в консультируемых книгах:
Первое требование определения состоит в том, что![]() быть определено на каждом числе некоторого открытого интервала, содержащего 3, за исключением, возможно, 3. Так как
быть определено на каждом числе некоторого открытого интервала, содержащего 3, за исключением, возможно, 3. Так как ![]() определено для всех действительных чисел, любой открытый интервал, содержащий 3, будет удовлетворять этому требованию. Теперь нам нужно показать, что для всех
определено для всех действительных чисел, любой открытый интервал, содержащий 3, будет удовлетворять этому требованию. Теперь нам нужно показать, что для всех ![]() есть один
есть один ![]() , такой, что если
, такой, что если ![]() тогда
тогда![]() Мы должны
Мы должны![]() , скоро
, скоро![]() и
и ![]()
У нас есть тогда, ![]() и
и ![]()
Это утверждение указывает на то, что![]() является удовлетворительной дельтой.
является удовлетворительной дельтой.
При таком выборе![]() имеем следующий аргумент:
имеем следующий аргумент:![]() , então
, então ![]() , тогда
, тогда![]() , então
, então ![]() тогда
тогда ![]() , тогда
, тогда ![]()
Это просто «показывает» из определения предела, что![]()
Как мы видели, доказательства не было, а была только «показуха», так как, дав число 5, мы просто подставили его и данную функцию в определение предела функции.
Давайте перейдем к еще одному примеру: используйте определение, чтобы «доказать», что![]() .
.
Снова дается число, в данном случае 4, в качестве предела, но не говорится, откуда было взято это число.
Вот решение, в общих чертах:
В качестве ![]() определено для всех действительных чисел, любой открытый интервал, содержащий 2, будет удовлетворять первому требованию определения.
определено для всех действительных чисел, любой открытый интервал, содержащий 2, будет удовлетворять первому требованию определения.
Мы должны показать, что для всех![]() , есть один
, есть один ![]() , такой, что
, такой, что
Если![]() тогда
тогда![]()
Скоро![]() тогда
тогда![]()
Нам нужно поставить ограничение на ![]() что дает нам неравенство, включающее
что дает нам неравенство, включающее![]() . Такое ограничение делается для выбора необходимого по определению открытого интервала. Мы выбираем ассортимент
. Такое ограничение делается для выбора необходимого по определению открытого интервала. Мы выбираем ассортимент ![]() и это подразумевает, что
и это подразумевает, что ![]() . Затем
. Затем ![]() и
и ![]() , тогда
, тогда![]() тогда
тогда![]() тогда
тогда![]() тогда
тогда![]() .
.
Теперь у нас есть![]() и
и ![]() , тогда
, тогда![]() Так как наша цель получить
Так как наша цель получить ![]() , мы должны потребовать
, мы должны потребовать ![]() С этим
С этим 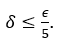
Используя это![]() мы завершили так называемое «доказательство».
мы завершили так называемое «доказательство».
Как мы видели выше, снова ничего не было доказано, кроме того, что число, данное в качестве предела, в данном случае 4, удовлетворяет определению предела.
Не было вычислений, чтобы показать, что число 4 действительно является пределом.
С этого момента мы будем приводить предельное исчисление функции.
Прежде чем представить сам «расчет», оценим![]() в тех же значениях
в тех же значениях![]() приведенных выше, но считая их соединениями числа 1.
приведенных выше, но считая их соединениями числа 1.
Это покажет, в общих чертах, рассуждения, используемые для вычисления предела функции.
Функция![]() , действует для всех
, действует для всех ![]() .
.
За![]() или же
или же ![]() , мы должны
, мы должны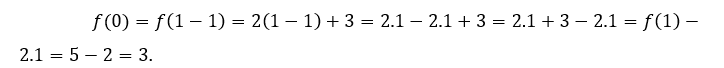
За ![]() или же
или же ![]() , мы должны
, мы должны 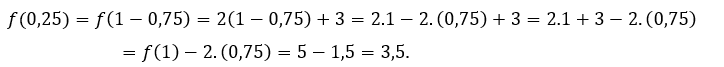 За
За ![]() или же
или же ![]() мы должны
мы должны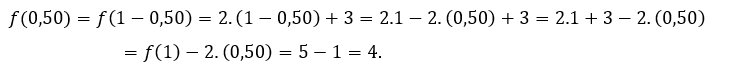
За![]() или же
или же ![]() мы должны
мы должны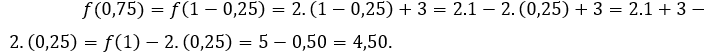 За
За ![]() или же
или же ![]() , мы должны
, мы должны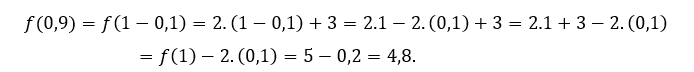
За![]() или же
или же ![]() , мы должны
, мы должны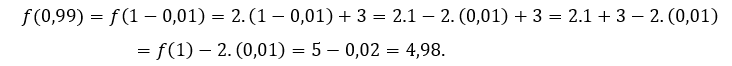
За ![]() или же
или же ![]() мы должны
мы должны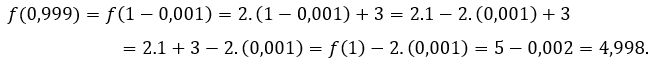
За ![]() или же
или же ![]() , мы должны
, мы должны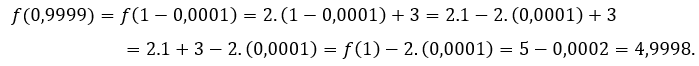
За![]() или же
или же ![]() , мы должны
, мы должны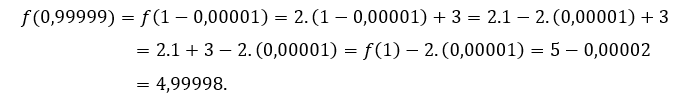
Мы проверили некоторые значения![]() меньше 1.
меньше 1.
Сейчас будем оценивать ![]() при значениях больше 1, но близких к 1.
при значениях больше 1, но близких к 1.
За![]() или же
или же ![]() , мы должны
, мы должны 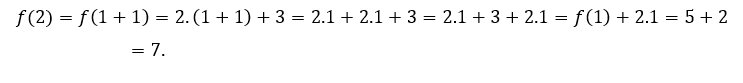
За![]() или же
или же ![]() мы должны
мы должны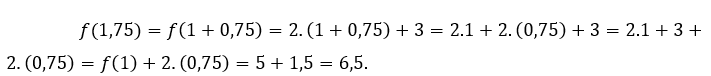
За![]() или же
или же ![]() мы должны
мы должны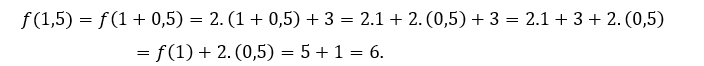
За![]() или же
или же ![]() , мы должны
, мы должны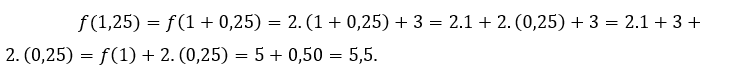
За![]() или же
или же ![]() , мы должны
, мы должны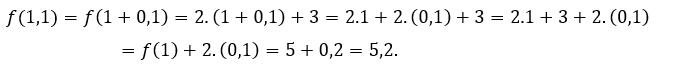
За![]() или же
или же ![]() мы должны
мы должны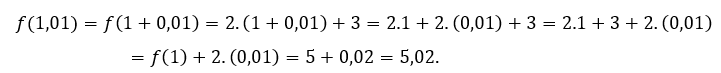
За![]() или же
или же ![]() , мы должны
, мы должны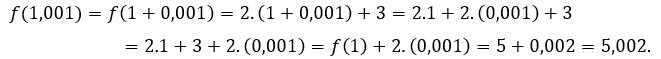
За![]() или же
или же ![]() , мы должны
, мы должны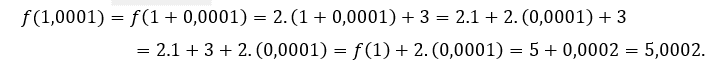
За![]() или же
или же ![]() , мы должны
, мы должны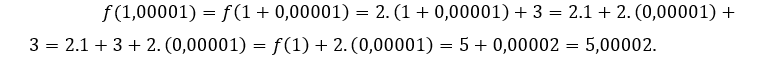
Из вышеизложенного мы понимаем, что чем больше ![]() приближается к 1, тем больше
приближается к 1, тем больше ![]() приближается к 5, то есть когда
приближается к 5, то есть когда ![]() стремится к 1,
стремится к 1, ![]() стремится к 5.
стремится к 5.
Мы наблюдали в расчетах выше, во всех значениях, присвоенных![]() , появление постоянной
, появление постоянной ![]() к которому прибавлялось или вычиталось значение, которое стремилось к нулю, а
к которому прибавлялось или вычиталось значение, которое стремилось к нулю, а ![]() приближался к 1.
приближался к 1.
Таким образом, эта константа является «кандидатом» на роль упомянутого выше «предела», т. е. указывает на то, что мы можем иметь ![]() .
.
Теперь мы сформулируем описанную выше ситуацию в полуобобщенном виде, чтобы представить сам «предельный расчет».
Выражение «![]() стремится к 1», представленному
стремится к 1», представленному ![]() , это эквивалентно
, это эквивалентно ![]() , или же
, или же ![]() , когда
, когда ![]() стремится к нулю,
стремится к нулю, ![]() , и
, и ![]() .
.
При этом выражение![]() , замена
, замена ![]() за
за ![]() или же
или же ![]() , это эквивалентно
, это эквивалентно![]() , или же
, или же ![]() , Это,
, Это, ![]() , или же
, или же ![]() .
.
Из вышеприведенного равенства можно «вычислить» значение предела![]() когда
когда ![]() стремится к 1, так как достаточно вычислить значение
стремится к 1, так как достаточно вычислить значение ![]() , или же
, или же ![]() .
.
Сделаем теперь, используя ту же функцию, что и раньше, вычисление для![]() , Когда
, Когда ![]() .
.
Таким образом, у нас остается:
![]() тогда
тогда![]() независимо от того
независимо от того ![]() , и
, и ![]() стремится к нулю, когда
стремится к нулю, когда ![]() , то есть он настолько мал, что приближается к нулю сколь угодно далеко.
, то есть он настолько мал, что приближается к нулю сколь угодно далеко.
Расчет для ![]() , это,
, это, ![]() , аналогично и дает тот же результат.
, аналогично и дает тот же результат.
Посмотрим: ![]()
Теперь мы вычислим ряд пределов функций, чтобы проиллюстрировать применение упомянутого «исчисления».
- Давайте посчитаем
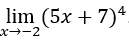 .
.
В качестве![]() , мы можем сделать, например,
, мы можем сделать, например, ![]() ,
, ![]() и
и ![]() .
.
Оставаться с![]()
![]() условия в
условия в ![]() которые все стремятся к нулю.
которые все стремятся к нулю.
Тогда результат будет ![]()
- Давайте посчитаем
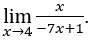
В качестве ![]() , мы можем сделать, например,
, мы можем сделать, например, ![]() ,
, ![]() и
и ![]() .
.
Оставаться с
![]() , потому что числитель стремится к 4, а знаменатель стремится к
, потому что числитель стремится к 4, а знаменатель стремится к ![]() .
.
- Давайте посчитаем
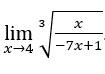 .
.
Как мы видели выше, в итоге у нас останется
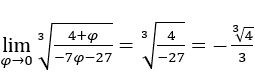
- Давайте посчитаем
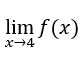 как показано ниже.
как показано ниже.
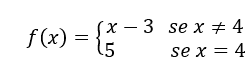 .
.
Мы должны вычислить ![]() , потому что что бы ни случилось с
, потому что что бы ни случилось с ![]() когда
когда ![]() .
.
В качестве ![]() , мы можем сделать, например,
, мы можем сделать, например, ![]()
![]() и
и ![]() .
.
Оставаться с![]() , тогда
, тогда![]() .
.
Быть![]() , установить для всех
, установить для всех ![]() , кроме
, кроме ![]() .
.
Давайте рассмотрим ![]() это,
это, ![]() , для которого
, для которого ![]() сводится к
сводится к ![]() .
.
- Давайте рассчитаем
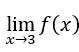 . Мы должны
. Мы должны 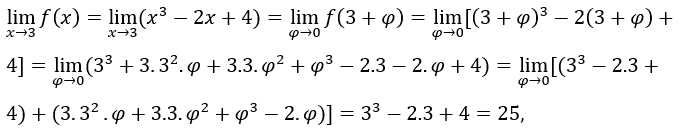 , однажды, когда
, однажды, когда 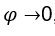 , выражение
, выражение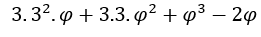 стремится к нулю.
стремится к нулю.
Затем
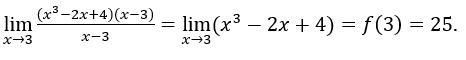
Теперь рассмотрим следующий пример: ![]() , установить для всех
, установить для всех ![]() , и вычислить его предел, когда
, и вычислить его предел, когда ![]() стремится к 2.
стремится к 2.
За![]() условие существования функции,
условие существования функции, ![]() , и когда
, и когда ![]() мы можем сделать, например,
мы можем сделать, например, ![]() , с
, с ![]()
![]() и нам нужно будет вычислить предел
и нам нужно будет вычислить предел![]() .
.
В качестве![]() , выражение
, выражение ![]() как правило
как правило ![]() , тогда и будет предел,
, тогда и будет предел, ![]() .
.
В итоге у нас осталось:![]() .
.
Наблюдение.
Мы могли бы применить «исчисление» непосредственно к функции, не разделяя сначала множитель, общий для числителя и знаменателя.
Посмотрим![]()
На самом деле мы можем применить «исчисление» непосредственно к функции, не делая над ней предварительной «подготовки».
Теперь мы приведем несколько примеров предельных вычислений с использованием тригонометрических и экспоненциальных функций, чтобы проиллюстрировать вышеизложенное.
Рассмотрим функцию ![]() , установить для всех
, установить для всех ![]() , кроме
, кроме 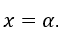
Вспоминая: ![]() означает, например, что
означает, например, что![]() , где
, где![]() ,
, ![]() .
.
Подставляя это значение x в исходное уравнение выше, мы получаем: 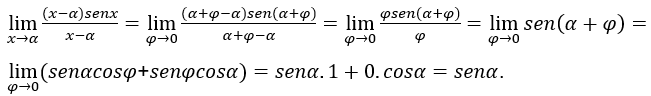
, в то время как ![]() .
.
Другой пример: рассмотрим функцию![]() установить для всех
установить для всех ![]() , кроме
, кроме ![]() .
.
- Давайте рассчитаем
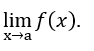
- Делая замену
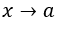 для, например,
для, например, 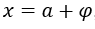 , с
, с 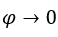 ,
, 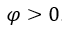 . У нас есть:
. У нас есть: 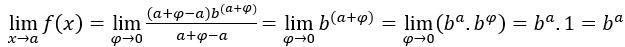 , поскольку
, поскольку 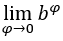 равно 1 и
равно 1 и 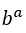 независимо от того
независимо от того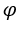 .
.
Теперь давайте вычислим предел функций, заданных в начале, чтобы подтвердить значения заданных пределов.
- Давайте посчитаем
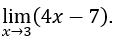
В качестве![]() , мы можем сделать, например,
, мы можем сделать, например, ![]() ,
, ![]() и
и ![]() и у нас осталось
и у нас осталось![]()
- Давайте посчитаем
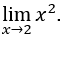
В качестве![]() , мы можем сделать, например,
, мы можем сделать, например, ![]() ,
, ![]() и
и ![]() и у нас осталось
и у нас осталось![]()
Как видно из «расчетов» выше, пределы, приведенные в предыдущих примерах, были правильными.
Мы продемонстрируем только одну теорему о пределах, чтобы проиллюстрировать исчисление, показанное здесь.
Теорема. Если ![]() и
и ![]() любые константы, то
любые константы, то ![]() .
.
Просто рассчитайте предел, выполнив, например, ![]()
![]() и
и ![]()
Оставаться с: ![]() , тогда
, тогда ![]() стремится к нулю, так как
стремится к нулю, так как ![]() стремится к нулю.
стремится к нулю.
В представленном «расчете» есть безмерная простота.
В этом случае не вызывает сомнений, что предел![]() .
.
Теперь мы будем использовать представленное «предельное исчисление» для вычисления пределов функций в различных обстоятельствах.
- Давайте посчитаем
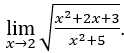
В качестве ![]() , так что мы можем сделать, например,
, так что мы можем сделать, например, ![]() ,
, ![]() и
и ![]()
Оставаться с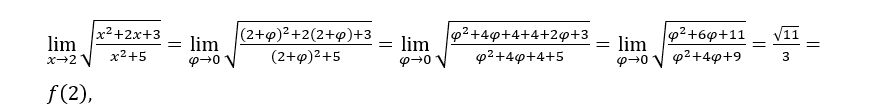 , однажды
, однажды ![]() стремится к 11 и
стремится к 11 и ![]() стремится к 9.
стремится к 9.
- Давайте посчитаем
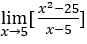 .
.
В качестве x → 5, так что мы можем сделать, например, ![]() ,
, ![]() и
и ![]()
Оставаться с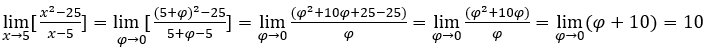
Замечено, что не нужно было «подготавливать» функцию для применения «исчисления», то есть не нужно было писать функцию как ![]() и, наконец, как
и, наконец, как ![]()
- Давайте посчитаем
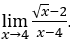 .
.
В случаях с радикалами, к которым прибавляется или вычитается действительное число, при прямой подстановке значения ![]() приводит к неопределенности
приводит к неопределенности ![]() мы должны подготовить уравнение, потому что прямое применение «исчисления» не устраняет неопределенность, как мы увидим ниже.
мы должны подготовить уравнение, потому что прямое применение «исчисления» не устраняет неопределенность, как мы увидим ниже.
Что происходит в этом случае, так это то, что есть множитель, общий как для числителя, так и для знаменателя, но он выражается только тогда, когда мы делим либо числитель на знаменатель, либо знаменатель на числитель.
В настоящее время это переводится в математику как рационализация.
Давайте посмотрим на примере выше: если мы разделим знаменатель на числитель, так как показатель степени
![]() в знаменателе 1, а в показателе
в знаменателе 1, а в показателе ![]() в числителе меньше, то есть стоит
в числителе меньше, то есть стоит ![]() мы будем иметь:
мы будем иметь: ![]() и подставив, будем иметь
и подставив, будем иметь 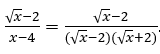 .
.
Таким образом, мы можем выразить множитель, общий для числителя и знаменателя.
Другой способ — разделить числитель на знаменатель, но в этом случае мы должны сделать то же самое — это рационализация, так как показатель степени ![]() в числителе меньше, чем показатель степени
в числителе меньше, чем показатель степени ![]() знаменатель, поэтому его нужно умножить на множитель
знаменатель, поэтому его нужно умножить на множитель ![]() сделать его показатель по крайней мере равным показателю знаменателя.
сделать его показатель по крайней мере равным показателю знаменателя.
Это известная рационализация, которую мы делаем.
Сделаем расчет сначала, без подготовки.
В качестве ![]() мы можем сделать, например,
мы можем сделать, например, ![]() ,
,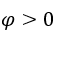 и
и ![]() .
.
Оставаться с![]() Мы наблюдаем необходимость рационализации, так как предел еще не определен, когда
Мы наблюдаем необходимость рационализации, так как предел еще не определен, когда ![]() в числителе и знаменателе, стремясь к
в числителе и знаменателе, стремясь к ![]()
Дальше будем умножать и делить на ![]() , и мы будем с
, и мы будем с ![]()
Теперь проведем расчет, подготовив функцию перед ее применением.
![]() .
.
Как прямая замена 4 приводит к неопределенности![]() означает, что числитель и знаменатель имеют общий множитель
означает, что числитель и знаменатель имеют общий множитель ![]() или же
или же ![]()
В этом случае, поскольку это радикал минус действительное число, способ, используемый для «высвобождения» общего множителя, — это рационализация.
Перед вычислением предела умножим и разделим числитель и знаменатель функции на![]()
Оставаться с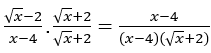 . В этой функции мы уже можем применить исчисление. посмотрим:
. В этой функции мы уже можем применить исчисление. посмотрим: 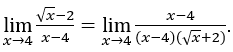
В качестве ![]() мы можем сделать, например,
мы можем сделать, например, ![]() ,
, ![]() и
и ![]()
Оставаться с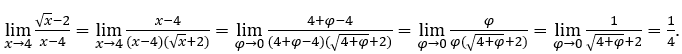
1.2 БОКОВЫЕ ОГРАНИЧЕНИЯ
В случаях, когда функция определена для каждого действительного числа, кроме действительного числа![]() , когда мы вычисляем его предел с независимой переменной, стремящейся к
, когда мы вычисляем его предел с независимой переменной, стремящейся к ![]() , как и в приведенных выше примерах, не имеет значения, используем ли мы
, как и в приведенных выше примерах, не имеет значения, используем ли мы ![]() сколько
сколько ![]() ,
, ![]() и
и ![]() , так как он установлен на все числа слева и справа от
, так как он установлен на все числа слева и справа от ![]() .
.
И, конечно же, это не функция предложения.
Когда функция не определена слева или справа от числа ![]() и мы должны вычислить его предел с помощью
и мы должны вычислить его предел с помощью ![]() стремясь к, мы должны использовать значение
стремясь к, мы должны использовать значение ![]() как может быть дело.
как может быть дело.
Когда ![]() и мы делаем
и мы делаем ![]() или же
или же ![]() ,
, ![]() и
и ![]() , тогда
, тогда ![]() указывает на то, что
указывает на то, что ![]() приближается
приближается ![]() для значений, превышающих
для значений, превышающих ![]() , и поэтому приближается
, и поэтому приближается ![]() справа.
справа.
Расчет, сделанный с ![]() следовательно, это предел, когда
следовательно, это предел, когда ![]() как правило
как правило ![]() справа.
справа.
Следовательно, это правый предел.
Мы используем ![]() для вычисления левого предела.
для вычисления левого предела.
Мы знаем, что предел существует только тогда, когда существуют и равны односторонние пределы.
- Давайте посчитаем
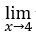 √x – 4.
√x – 4.
Мы знаем, что функция существует только для![]() , это,
, это, ![]()
Следовательно, левого предела нет, а значит, и рассматриваемого предела не существует.
Но есть правый предел, который можно вычислить, подставив ![]() за
за ![]() ,
, ![]() и
и ![]()
![]()
- Рассчитаем односторонние пределы.
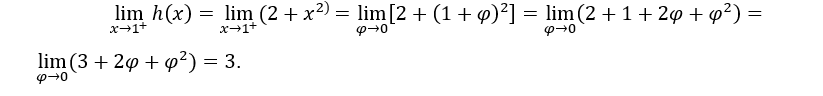
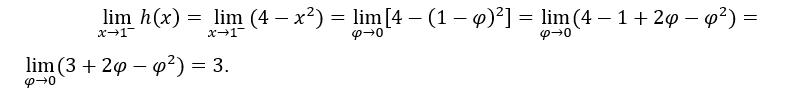
Как они одинаковы,![]()
В приведенном выше расчете мы сделали ![]() , вычислить правый предел и
, вычислить правый предел и ![]() для вычисления левого предела.
для вычисления левого предела.
Мы рассчитываем лимит ![]() определяется
определяется
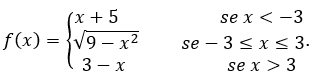
- Давайте посчитаем
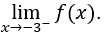
Затем мы должны вычислить,![]()
Мы сделаем это тогда, ![]() ,
, ![]() и
и ![]()
- Давайте посчитаем
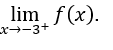
Затем мы должны вычислить, ![]()
Мы сделаем это тогда, ![]() ,
, ![]() и
и ![]()
Оставаться с
![]()
- Давайте посчитаем
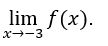
В качестве ![]() затем
затем ![]() не существует.
не существует.
- Давайте посчитаем
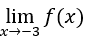 .
.
Затем мы должны вычислить,![]()
Мы сделаем это тогда, ![]() ,
, ![]() и
и ![]()
Оставаться с
![]()
- Давайте посчитаем
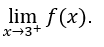
Затем мы должны вычислить, ![]()
мы сделаем это тогда, ![]() ,
, ![]() и
и ![]()
Оставаться с
![]() Давайте посчитаем
Давайте посчитаем 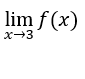
В качестве![]() , тогда
, тогда 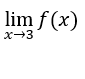 существует и равен нулю.
существует и равен нулю.
1.3 БЕСКОНЕЧНЫЕ ПРЕДЕЛЫ
Те, чьи функциональные значения увеличиваются или уменьшаются без ограничений, когда независимая переменная становится все ближе и ближе к фиксированному числу, могут быть решены в равной степени с помощью представленного здесь предельного «вычисления», с тем преимуществом, что не нужно беспокоиться о теоремах.
Перед применением «расчета» вспомним следующие ситуации:
![]()
- Рассчитаем следующий предел
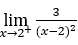 .
.
В качестве![]() , мы должны сделать
, мы должны сделать ![]() ,
, ![]() и
и![]()
Оставаться с ![]() .
.
- Давайте посчитаем сейчас
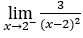 .
.
В качестве![]() , мы должны сделать
, мы должны сделать ![]() ,
, ![]() и
и ![]()
Оставаться с![]() .
.
- Давайте посчитаем
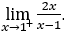 .
.
В качестве ![]() , мы должны сделать
, мы должны сделать ![]() ,
, ![]() и
и ![]()
Оставаться с ![]() ,потому что числитель стремится к 2, а знаменатель стремится к нулю через положительные значения.
,потому что числитель стремится к 2, а знаменатель стремится к нулю через положительные значения.
- Давайте посчитаем сейчас
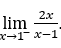 .
.
В качестве![]() , мы должны сделать
, мы должны сделать ![]() ,
, ![]() и
и ![]()
Оставаться с ![]() , потому что числитель стремится к 2, а знаменатель стремится к нулю через отрицательные значения.
, потому что числитель стремится к 2, а знаменатель стремится к нулю через отрицательные значения.
- Давайте посчитаем
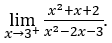
В качестве![]() , мы должны сделать
, мы должны сделать ![]() ,
, ![]() и
и ![]()
Оставаться с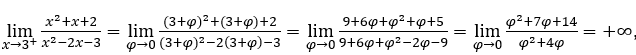 потому что числитель стремится к 14, а знаменатель стремится к нулю для положительных значений.
потому что числитель стремится к 14, а знаменатель стремится к нулю для положительных значений.
- Давайте посчитаем сейчас
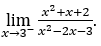
В качестве ![]() , мы должны сделать
, мы должны сделать ![]() ,
, ![]() и
и ![]()
Оставаться с![]() , так как числитель стремится к 14, а знаменатель стремится к нулю для отрицательных значений, так как
, так как числитель стремится к 14, а знаменатель стремится к нулю для отрицательных значений, так как ![]() стремится к нулю всегда для положительных значений.
стремится к нулю всегда для положительных значений.
В этом случае знаменатель равен ![]() когда бы ни
когда бы ни![]() , это похоже на
, это похоже на ![]() , знаменатель всегда отрицательный.
, знаменатель всегда отрицательный.
- Давайте посчитаем
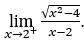
В качестве ![]() , мы должны сделать
, мы должны сделать ![]() ,
, ![]() и
и ![]()
Мы как
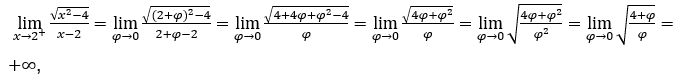 потому что числитель стремится к 2, а знаменатель стремится к нулю для положительных значений.
потому что числитель стремится к 2, а знаменатель стремится к нулю для положительных значений.
- Давайте посчитаем
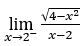
В качестве ![]() , мы должны сделать
, мы должны сделать ![]() ,
, ![]() и
и ![]()
Оставаться с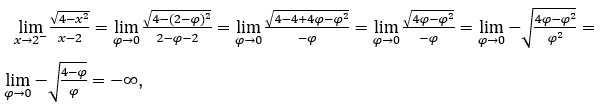 , потому что числитель стремится к -2, а знаменатель стремится к нулю для положительных значений.
, потому что числитель стремится к -2, а знаменатель стремится к нулю для положительных значений.
В этих двух случаях нам удалось ![]() в радикал, потому что он всегда положителен.
в радикал, потому что он всегда положителен.
- Давайте посчитаем
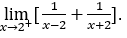
В качестве![]() , мы должны сделать
, мы должны сделать ![]() ,
, ![]() и
и ![]()
Оставаться с![]() потому что числитель стремится к 4, а знаменатель стремится к нулю для положительных значений.
потому что числитель стремится к 4, а знаменатель стремится к нулю для положительных значений.
Примечание Мы могли бы напрямую заменить значение![]() в исходном уравнении.
в исходном уравнении.
- Давайте посчитаем
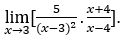
В качестве![]() , мы должны сделать
, мы должны сделать ![]() ,
, ![]() и
и ![]()
Оставаться с ![]() , потому что числитель стремится к 35, а знаменатель стремится к нулю для отрицательных значений, поскольку отрицательно для < 1.
, потому что числитель стремится к 35, а знаменатель стремится к нулю для отрицательных значений, поскольку отрицательно для < 1.
- Давайте посчитаем
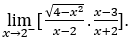
В качестве ![]() , мы сделаем
, мы сделаем ![]() ,
, ![]() и
и ![]()
Оставаться с 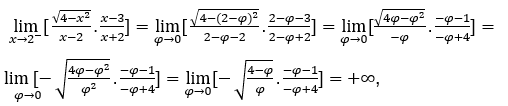 , потому что числитель стремится
, потому что числитель стремится ![]() а знаменатель стремится к
а знаменатель стремится к ![]() по положительным значениям.
по положительным значениям.
1.4 ПРЕДЕЛЫ В БЕСКОНЕЧНОСТИ
Точно так же, как и для пределов, упомянутых до сих пор, в использованной литературе также не представлен расчет пределов на бесконечности, а только оценивается функция, когда независимая переменная увеличивается или уменьшается на неопределенный срок.
Результат оценки используется в качестве порога.
Посмотрим.
Учитывая функцию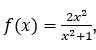 , мы относим к
, мы относим к ![]() ценности
ценности![]() и так далее, позволяя ему расти бесконечно. Соответствующие функциональные значения будут
и так далее, позволяя ему расти бесконечно. Соответствующие функциональные значения будут![]()
Мы наблюдаем, что когда ![]() растет, принимая положительные значения, функциональные значения приближаются к 2.
растет, принимая положительные значения, функциональные значения приближаются к 2.
Когда независимая переменная ![]() неограниченно растет, через положительные значения запишем
неограниченно растет, через положительные значения запишем![]() на приведенном примере был сделан вывод, что
на приведенном примере был сделан вывод, что 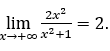
Как видно выше, из приведенного примера предельный расчет функции не приводился, а было лишь замечено, что при ![]() увеличилась на положительные значения, функция приблизилась к 2.
увеличилась на положительные значения, функция приблизилась к 2.
Это значение 2 затем использовалось как предел функции.
Ниже мы представим «вычисление» предела функций, когда независимая переменная стремится к ![]() или
или ![]()
В случаях, когда ![]() , мы сделаем
, мы сделаем ![]() и
и ![]() , потому что, как мы видели выше, когда
, потому что, как мы видели выше, когда ![]() стремится к нулю для положительных значений,
стремится к нулю для положительных значений, ![]() как правило
как правило ![]() , и с этим,
, и с этим, ![]() как правило
как правило ![]()
В случаях, когда ![]() , мы сделаем
, мы сделаем 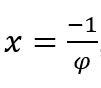
![]() и
и ![]() , поскольку, как мы видели выше, при стремлении φ к нулю положительными значениями
, поскольку, как мы видели выше, при стремлении φ к нулю положительными значениями![]() ,
,![]() стремится, и с этим,
стремится, и с этим, ![]() как правило
как правило ![]() .
.
- Давайте посчитаем
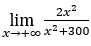 .
.
В качестве 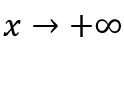 , мы сделаем
, мы сделаем 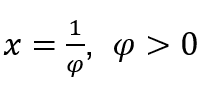 и
и ![]()
Оставаться с ![]() потому что числитель стремится к 2, а знаменатель стремится к 1.
потому что числитель стремится к 2, а знаменатель стремится к 1.
- Давайте посчитаем
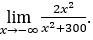
В качестве ![]() , мы сделаем
, мы сделаем ![]() и
и ![]()
Оставаться с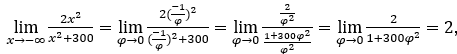 , потому что числитель стремится к 2, а знаменатель стремится к 1.
, потому что числитель стремится к 2, а знаменатель стремится к 1.
- Давайте посчитаем
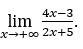
В качестве ![]() , мы сделаем
, мы сделаем![]() и
и ![]()
Оставаться с![]() , потому что числитель стремится к 4, а знаменатель стремится к 2.
, потому что числитель стремится к 4, а знаменатель стремится к 2.
- Давайте посчитаем
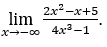
В качестве![]() , мы сделаем
, мы сделаем![]()
![]() и
и ![]()
Оставаться с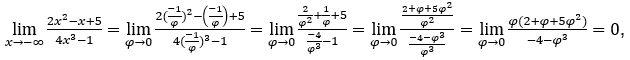 потому что числитель стремится к нулю, а знаменатель стремится к -4.
потому что числитель стремится к нулю, а знаменатель стремится к -4.
- Давайте посчитаем

В качестве ![]() , мы сделаем
, мы сделаем ![]() и
и ![]()
Оставаться с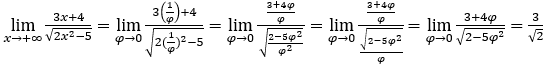 , потому что числитель стремится к 3, а знаменатель стремится к
, потому что числитель стремится к 3, а знаменатель стремится к ![]()
- Давайте посчитаем
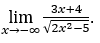
В качестве![]() , мы сделаем
, мы сделаем![]()
![]() и
и ![]()
Оставаться с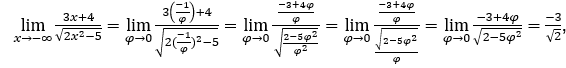 , потому что числитель стремится к -3, а знаменатель стремится к
, потому что числитель стремится к -3, а знаменатель стремится к ![]()
- Давайте посчитаем
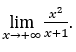
В качестве![]() , мы сделаем
, мы сделаем![]() и
и ![]()
Оставаться с 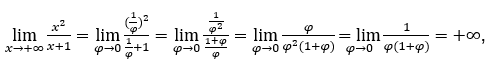 потому что числитель равен 1, а знаменатель стремится к нулю для положительных значений.
потому что числитель равен 1, а знаменатель стремится к нулю для положительных значений.
- Давайте посчитаем
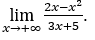
В качестве ![]() , мы сделаем
, мы сделаем ![]() =
= ![]() φ > 0 и φ → 0.
φ > 0 и φ → 0.
Оставаться с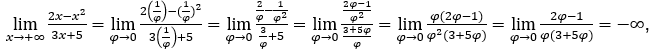 потому что числитель стремится к -1, а знаменатель стремится к нулю для положительных значений.
потому что числитель стремится к -1, а знаменатель стремится к нулю для положительных значений.
- Давайте посчитаем
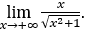
В качестве![]() , мы сделаем
, мы сделаем ![]() и
и ![]()
Оставаться с 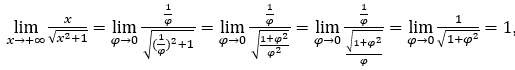 потому что числитель равен 1, а знаменатель стремится к 1.
потому что числитель равен 1, а знаменатель стремится к 1.
- Давайте посчитаем сейчас
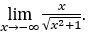
В качестве ![]() , мы сделаем
, мы сделаем ![]() и
и ![]()
Оставаться с 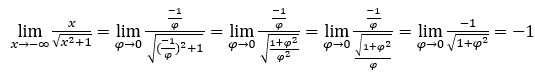 , потому что числитель равен -1, а знаменатель стремится к 1.
, потому что числитель равен -1, а знаменатель стремится к 1.
- Давайте посчитаем
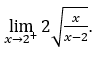
В качестве ![]() , мы должны сделать
, мы должны сделать ![]() ,
, ![]()
Оставаться с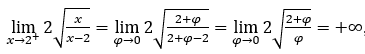 , потому что числитель стремится
, потому что числитель стремится ![]() и знаменатель стремится к нулю для положительных значений.
и знаменатель стремится к нулю для положительных значений.
- Давайте посчитаем сейчас
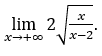
В качестве![]() , мы сделаем
, мы сделаем ![]() и
и ![]()
Оставаться с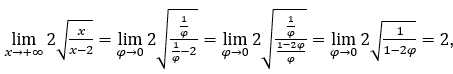 потому что числитель стремится к 2, а знаменатель стремится к 1.
потому что числитель стремится к 2, а знаменатель стремится к 1.
Наблюдение.
Вычисление пределов на бесконечности нельзя применять, например, к тригонометрическим функциям, так как одни из них меняются в определенном интервале, а другие неограниченно возрастают или убывают в зависимости от рассматриваемого значения.
Например, если мы попытаемся вычислить![]() , мы бы прошлись по всем значениям диапазона бесконечное количество раз
, мы бы прошлись по всем значениям диапазона бесконечное количество раз ![]() , потому что для всех
, потому что для всех ![]() ,
, ![]() , то есть мы не пришли бы ни к какому определенному значению.
, то есть мы не пришли бы ни к какому определенному значению.
Действительно, полиномиальные функции или функции, выраженные отношениями между полиномами, являются наиболее подходящими для применения пределов.
2. КОММЕНТАРИИ
1) Представленный предельный расчет возник в результате идентификации выражения ![]() стремится к определенному числу
стремится к определенному числу ![]() с равенством
с равенством ![]() , или же
, или же ![]() , с
, с![]() и
и ![]() , с тех пор, действительно, когда
, с тех пор, действительно, когда ![]() ,
, ![]() и
и ![]() как правило
как правило ![]() и с этим,
и с этим, ![]() как правило
как правило ![]()
В случае пределов на бесконечности замена выражения![]() как правило
как правило ![]() он был
он был ![]() , и замена выражения
, и замена выражения ![]() как правило
как правило ![]() он был
он был ![]() , с
, с ![]() и
и ![]()
Замена имеет наибольший смысл, потому что, действительно, когда ![]() , всегда для положительных значений,
, всегда для положительных значений,![]() иметь тенденцию
иметь тенденцию ![]() и
и ![]() как правило
как правило ![]() , вызывая
, вызывая ![]() действительно склонны
действительно склонны ![]() или
или ![]() , как может быть дело.
, как может быть дело.
Если заменить, то в случае, когда![]() как правило
как правило![]() или
или ![]() о
о ![]() за,
за, ![]() или же
или же ![]() и
и ![]() , результат был бы тот же.
, результат был бы тот же.
Пример.
- Давайте посчитаем
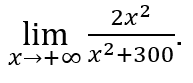
Мы сделаем ![]() и
и ![]()
Оставаться с
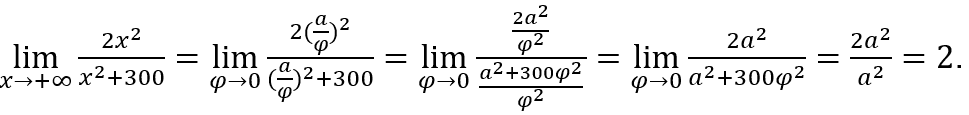
2. Как видно из различных примеров, представленное «предельное исчисление» довольно «беглое» и имеет прямое применение, без необходимости обращаться к теоремам или «организовывать» функцию перед выполнением вычислений, за исключением случаев, когда нам нужно рационализировать.
Этот факт приносит много спокойствия при вычислении предела функции, потому что представленный «вычисление» является истинным синтезом этого предмета.
Например, «вычисление» можно использовать непосредственно над функцией ![]() , без необходимости его организовывать, то есть выражать как
, без необходимости его организовывать, то есть выражать как 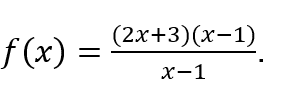
Посмотрим. ![]()
В качестве![]() , мы можем сделать, например,
, мы можем сделать, например, ![]() и
и ![]()
Оставаться с
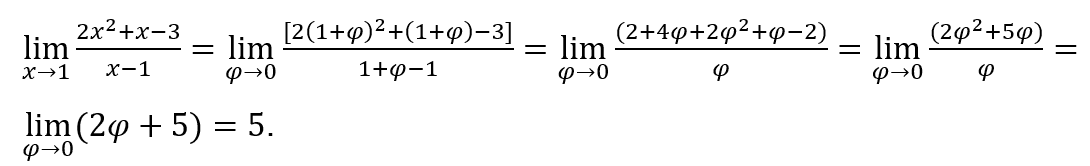
Это дает огромное преимущество по сравнению с нынешним изложением этого предмета, которое, помимо того, что не представляет каких-либо расчетов пределов, оказывается довольно «застрявшим» на огромном количестве теорем, которые необходимо учитывать при «оценках» пределов, поскольку а также «организаций», что необходимо сделать по функциям до «оценки» их предела.
3) К представленному «предельному исчислению» я хотел бы добавить некоторые оценки практического характера.
а) Имеет смысл вычислять предел функции только вблизи значения, для которого он не определен.
Если функция определена для определенного значения, то есть если функция существует для определенного значения, нет смысла вычислять предел вблизи этого значения, поскольку мы знаем, сколько стоит функция при этом значении.
Например, быть![]()
Эта функция определена для всех ![]() , он существует для всех
, он существует для всех ![]()
Поэтому было бы неразумно вычислять, например, ![]() , так как функция существует для
, так как функция существует для ![]() , то есть зачем вычислять этот предел, если можно просто подставить
, то есть зачем вычислять этот предел, если можно просто подставить ![]() на 3 дюйма
на 3 дюйма ![]() и мы получаем значение функции в 3, то есть,
и мы получаем значение функции в 3, то есть, ![]()
При этом сотни упражнений больше не имеют смысла для существования.
Очевидно, что функции, рассматриваемые в этой статье,![]()
b) Используя понятие предела, мы сделаем здесь замечание о непрерывности функции.
По расчетной книжке Lethold (1994 г.),определение непрерывной функции в точке переводится так:
Dizemos que a função ![]() é contínua no número a se e somente se as seguintes condições forem satisfeitas:
é contínua no número a se e somente se as seguintes condições forem satisfeitas:
(i) ![]() existe;
existe;
(ii) ![]() existe;
existe;
(iii) ![]()
Se uma ou mais de uma dessas condições não forem verificadas em ![]() , a função
, a função![]() será descontínua em
será descontínua em ![]()
Так Lima (1978 г.) определяет непрерывность функции:
Uma função ![]() diz-se contínua no ponto
diz-se contínua no ponto ![]() quando é possível tornar
quando é possível tornar ![]() arbitrariamente próximo de
arbitrariamente próximo de ![]() desde que se tome
desde que se tome ![]() suficientemente próximo de
suficientemente próximo de ![]()
Em termos precisos, diremos que ![]() é contínua no ponto
é contínua no ponto ![]() quando, para todo
quando, para todo ![]() dado arbitrariamente, pudermos achar
dado arbitrariamente, pudermos achar ![]() tal que
tal que ![]() e
e ![]() impliquem
impliquem ![]()
Мы знаем, что если функция определена на некотором интервале, т. е. если она существует для каждого числа, содержащегося в некотором интервале, то нет смысла вычислять предел этой функции для некоторого числа в этом интервале, так как мы можем просто оцените функцию для каждого числа в этом диапазоне.
Проще говоря: если функция, представленная только одним выражением, всего одним предложением, существует для определенного числа ![]() , то совершенно необязательно вычислять предел функции для
, то совершенно необязательно вычислять предел функции для ![]() , так как просто мы можем вычислить значение функции в
, так как просто мы можем вычислить значение функции в ![]()
Конечно, если бы мы вычислили этот предел, как мы это сделали выше, то он был бы равен ![]()
Как указано выше, имеет смысл вычислять предел функции только вокруг числа, для которого он не определен.
Поэтому, если мы анализируем функции, представленные только одним выражением, говоря, что функция существует для определенного числа ![]() , означает, что существует предел этой функции в
, означает, что существует предел этой функции в ![]() этот предел является значением функции в
этот предел является значением функции в ![]() , и при этом нам не нужно вычислять предел этой функции в этом числе
, и при этом нам не нужно вычислять предел этой функции в этом числе ![]()
Применяя это к приведенному выше определению непрерывной функции, пункты (ii) и (iii) определения станут излишними, так как в пункте (i) утверждается, что![]() существуют.
существуют.
Следовательно, для функций, представленных «только одним выражением», простое утверждение о том, что функция![]() , определяется числом
, определяется числом ![]() то есть простое утверждение, что
то есть простое утверждение, что ![]() существует достаточно, чтобы заключить, что функция непрерывна при этом числе
существует достаточно, чтобы заключить, что функция непрерывна при этом числе![]()
Точно так же с этим наблюдением о непрерывных функциях сотни упражнений теряют смысл.
Пример: пусть функция ![]() которое определено для каждого действительного числа, т. е. существует для каждого
которое определено для каждого действительного числа, т. е. существует для каждого ![]() настоящий.
настоящий.
Таким образом, нет необходимости рассчитывать лимит![]() ни за какое значение
ни за какое значение ![]() , потому что в этом случае, быть определено в
, потому что в этом случае, быть определено в ![]() является синонимом ограничения в
является синонимом ограничения в ![]() и что этот предел равен значению функции в
и что этот предел равен значению функции в ![]() считается.
считается.
Тогда функция![]() непрерывно для всех
непрерывно для всех ![]()
3. ВЫВОД
Выше мы показываем, что на самом деле теория пределов несовершенна по отношению к исчислению предела, и поэтому она окружает себя рядом аргументов, основанных на определении предела, чтобы восполнить этот пробел.
Затем мы представляем «вычисление предела функции» и показываем, что оно синтезирует все упомянутое, а потому имеет непосредственное применение.
Мы надеемся внести свой вклад в лучшее понимание такого фундаментального предмета математики.
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
IEZZI, Gelson; MURAKAMI, Carlos et all. Fundamentos de Matemática Elementar, vol. 8, 1991.
LEITHOLD, Louis. O Cálculo com Geometria Analítica, vol. 1, 1994.
LIMA, Elon Lages. Curso de Análise, vol. 1, 1978.
MUNEM, Mustafa A. e FOULIS, David J. Cálculo, vol. 1, 1982.
[1] Степень бакалавра математики Университета Бразилиа.
Отправлено: Июнь 2021 г.
Утверждено: Август 2021 г.