Demonstration of the conjecture of the imperfect odd number

ORIGINAL ARTICLE

SANTOS, Adecio da Silva ^[1]

SANTOS, Adecio da Silva. Demonstration of the conjecture of the imperfect odd number. Revista Científica Multidisciplinar Núcleo do Conhecimento. 04 year, Ed. 05, Vol. 07, pp. 176-185. May 2019. ISSN: 2448-0959.

SUMMARY

Among about 48 open problems (Conjectures) of mathematics in the area of Number Theory, the Perfect Odd Numbers Conjecture to be proven in this article. The method we used for the test was demonstration by reduction to absurdity. And we purposely modified the name of the problem for Imperfect Odd Number Conjecture, because we found it more consistent with the solution found. In addition we leave in annex a list of several open problems of mathematics.

Keywords: Conjecture, Demonstration, Odd Perfect.

1. INTRODUCTION

The 21st century generation is full of technological innovations, which allow us to know practically the entire globe, and communicate “instantly” from anywhere on the planet.

Mathematics played a very important role in the construction as a whole of our present society. Its accuracy and accuracy of its results leaves no margin for error. But if you leave it still, it’s purposeful.

A science like this so rich and sovereign has a particularity, it does not allow ego or arrogance to have much space in the minds of its scholars, because as much as it can be respected, even admired, in our present times there are still mathematical problems that no one in history has ever been able to prove them yet.

Approximately 417 problems are unsolved in the most varied fields of mathematics. The reader interested in know them can check the reference (1). But we emphasize that some of them can never be demonstrated, although they are true, this is guaranteed by Gödel’s Incompleteness Theorems.

Our article exposes the proof of one of these open problems of mathematics, namely the Conjecture of The Perfect Odd Numbers, but we renamed it the Conjecture of the Imperfect Odd Number because we find this sentence more coherent with our result.

We used for both the method of demonstration by reduction to absurdity, the property of trichotomy and a result in the text we call property: (P), in addition to some algebraic manipulations.

At the end we leave, in ANNEX A, a very eclectic list of various mathematical conjectures.

2. THEORETICAL FRAMEWORK

In this part we give credit to the references that contributed significantly to the preparation of our article.

Which were the reference (2), because it provided us with the basis of mathematical logical reasoning so that we could find the final result of the work supported by logically coherent arguments. This reference also made us walk from the beginning to the end of the demonstration through the principles of Non-Contradiction and the Third Excluded that were our two “legs” until we reached our result.

It was also important to reference (3) because it provided a maturity through its exercises so that we could have a path of how to attack the problem under analysis in this article by the demonstration method by reduction to absurdity.

Finally, we leave the references (4), (5) and the list of problems in ANNEX A to the reader interested in learning more about the Conjecture of Perfect Odd Numbers, in addition to other conjectures of Number Theory and more problems of the various fields of mathematics.

3. CONJECTURE OF IMPERFECT ODD NUMBER

The field of mathematics studies known as Number Theory has about 48 open problems. Among these is what we will call the Conjecture of the Imperfect Odd Number. However, this problem is better known as The Perfect Odd Numbers Conjecture. And it states that there is no perfect odd number. However, we modified the name of the conjecture purposely, because we found it more consistent with our result.

According to the portal www.matematica.br: “A number is said perfect if it is equal to the sum of its own dividers. A positive number N dividers themselves are all positive integer dividers of N except the N itself.” (6)

To this day, perfect even numbers are known. The mathematicians who studied this theme the most were Euclid, Euler and Descartes. In addition, it is also known a formula for all the perfect even numbers. It was first studied by Euclid and was later completed by Euler.

Summarized explanations of the above are found in several academic papers. But according to Jeane Barbosa Ferreira and Marcos Ferreira de Melo:

Euclid argues that if “q” is a prime number such as 2q-1 that is also prime, then the formula n = 2^q-1(2^q-1) generates perfect even numbers. Long after, Euler (1707-1783) proved that every perfect pair number is obtained by the above recipe, thus establishing the reciprocal of Euclid’s theorem. It is worth noting that the prime numbers of the ^form 2q-1 are known as Mersenne’s cousins. (7)

That’s why the perfect odd numbers conjecture exists. Since the analysis of the perfect even numbers is well advanced. The first mathematician who mentioned the conjecture of the Perfect Odd Numbers was Descartes. And until this article, no one had yet proven or refuted the claim.

Our article presents a proof of the Conjecture of Perfect Odd Numbers, and for this we use the definition of perfect number, a result shown in the text we call property (P), the property of trichotomy and some algebraic manipulations. All this in a logical construction based on the technique of demonstration by reduction to absurdity.

We leave below the utterance of the conjecture and its demonstration.

In addition, if there is any error in the evidence, we would like readers to go deeper into their studies in order to show and fix it. Every contribution is welcome.

Imperfect Odd Number Conjecture: There is no perfect odd number.

DEMONSTRATION: First we prove that every perfect natural number, N, has the property (P): 1+d₁+d₂+d₃+…+d_n-1, where: 1< d₁< d₂< d₃< …<d_n-1<d_n are all the proper divisors of N.

In fact, note that N= 1+d₁+d₂+d₃+…+d_n-1+d_n, because N is a perfect number. Suppose, now, absurdly, that 1+d₁+d₂+d₃+…+d_{n-1 <} d_n and adding, in both members of the previous inequality, the term d_n we find the following expression 1+d₁+d₂+d₃+…+d_n-1+(d_n)<d_n+(d_n)⇒1+d₁+d₂+d₃+…+d_n-1+(d_n)<2d_n. So we have to
d_n<1+d₁+d₂+d₃+…+d_n-1+(d_n)<2d_n⇒d_n<N<2d_n⇒1<<2. However, as d_n divides N we find the natural between 1 and 2. Which is ABSURD!

On the other hand, let’s assume it is absurd, but only this time that inequality is
d_n<1+d₁+d₂+d₃+…+d_n-1. Now, adding, in both members of the previous inequality, the term d_n we found d_n+(d_n)<1+d₁+d₂+d₃+…+d_n-1+d_n which implies in
2d_n<1+d₁+d₂+d_n+…+d_n-1+(d_n), that is, 2d_n<N (I) . Also note that ≤d_n⇒N≤d₁.d_n (II), because d_n is the greatest divisor of N. So of (I) and (II) is 2d_n<N≤d₁.d_n, dividing all members of the last inequality by d_n we have 2<≤d₁ (III), but how d₁ is the smallest divisor of N other than 1 and is a divisor of N inequality (III) provides us that =d₁⇒N=d₁.d_n is that  2<d₁, so this means that all the divisors of are odd, because if there was any divisor of being even then 2=d₁, which is absurd in our assumption. From here we have 4 (four) situations to analyze:

1st situation: d₁ divide d_i ∀i= 1,2,3,4,…,n, because d₁ is the smallest divisor of N. And this implies that d_i=d₁ⁱ ∀=1,2,3,4,…,n, because if there were any d_i other than power
d₁ then this would generate a new divisor of N other than d_i ∀=1,2,3,4,…,n, which is absurd. So this situation means that 1+d₁²+d₁³+d₁⁴+…+d₁ⁿ=N=d_{1 .} d_n=d₁.d₁ⁿ=d₁ⁿ⁺¹, but by the formula of the sum of a finite P.G we have 1+d₁²+d₁³+d₁⁴+…+d₁ⁿ=1+d₁²., that is ,1+d₁².=d₁ⁿ⁺¹⇒1+= d₁ⁿ⁺¹⇒= d₁ⁿ⁺¹⇒ d₁-1+d₁ⁿ⁺¹–d₁² = (d₁-1).d₁ⁿ⁺¹=d₁ⁿ⁺²–d₁ⁿ⁺¹ ⇒d₁-1+d₁ⁿ⁺¹–d₁²=d₁ⁿ⁺² – d₁ⁿ⁺¹, then we have to d₁+2d₁ⁿ⁺¹ – d₁² –d₁ⁿ⁺² =1⇒d₁(1+2d₁ⁿ–d₁–d₁ⁿ⁺¹)=1⇒d₁ divides 1, absurd!

2nd situation:d₁ divides some d_j and others don’t stop j=1, 2, 3, 4,…,n. So we have to N=1+(d₁+d_j1+d_j2+…+d_jk) + (d_i1 +…+d_im ), where d₁ ,d_j1 ,d_j2 ,…,djk are the numbers divisible by d₁ and d_i1 ,…,d_im they are not. And the numbers 1,d₁ ,d_j1 ,d_j2 ,…,d_jk ,d_i1 ,…,d_im are all the proper divisors of N.

Let’s say the highest power of d₁ that divides N is _d¹n. So we can rewrite all the dividers themselves of how:

1, (d₁, d₁², …, d₁ⁿ), (d₁d_i1, d₁d_i2, …, d₁d_im), (d₁²d_i1, d₁²d_i2, …, d₁²d_im), …, (d₁ⁿd_i1, d₁ⁿd_i2, …. d₁ⁿd_im), (d_i1,d_i2, …, d_im).

Therefore, with this new writing, we have to add the dividers of N’s own is:

N=1+(d₁+d₁²+…+d₁ⁿ) + (d₁d_i1+…+d₁d_im) +(d₁²d_i1+…+d₁²d_im)+ … …+(d₁ⁿd_i1+…+d₁ⁿd_im) + (d_i1+d_i2+…+d_im)

= 1+(d₁+d₁²+…+d₁ⁿ)+(d₁+d₁²+…+d₁ⁿ)d_i1+…+(d₁+d₁²+…+d₁ⁿ)d_im++(d_i1+d_i2+…+d_im)

=1+(d₁+d₁²+…+d₁ⁿ) + (d₁+d₁²+…+d₁ⁿ)(d_i1+…+d_im)+(d_i1+…+d_im)

=1+(d₁+d₁²+…+d₁ⁿ) +(d₁+d₁²+…+d₁ⁿ+1) . (d_i1+…+d_im)

=(1+d₁+d₁²+…+ d₁ⁿ) . (1+d_i1+…+d_im)

Mas N=d₁.d_n=(1+d₁+d₁2+…+d₁n) . (1+d_i1+…+d_im)^,and this implies that

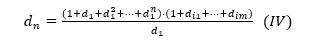
On the other hand, d_n=d₁^{n .} d_im^* (V) , where d_im^* is the largest number among d_i1, …, d_im.

Finally, by (IV) and (V) we have:but this gives us that N =(1+d₁+d₁²+…+d₁ⁿ) . (1+d_i1+…+d_im) = d₁ⁿ⁺¹ . _di^m* ,ie , d1n+1_, would be a divisor of n itself that would not be on our list of dividers own of N. What is a, ABSURD!

3rd situation_:d₁ does not share a_ny dj, but has prime factors in common with some d_j for j=2, 3, 4,…, n. This implies that these prime factors in common divide N and would be smaller than d₁ which is the smallest, absurd N divider!

Situation 4: d₁ does not divide any d_j, moreover, d₁ and dj do not have prime factors in common for all j=2, 3, 4, …, n.

So as N=d1 . d_n, We have to d₂, d₃, d₄, …, d_n-1 divide d_n, because they do not share
d₁by the fact of being d₁ the smallest divisor of N. Now, notice that ≠ d₁ ∀i= 1,3,4,5…,n because if = d_i for some d_i, this would imply that d_n=d₂ . d_i⇒ N=d₁ . d₂ . d_i, but as d₁ has no prime factors in common with no di _we are obliged to accept d₁ . d₂ e d₁ . _di as new dividers of N, nonsense! Because all n dividers have already been listed, and the same by our 4th situation is not divisible by d₁. That is, it is even different from all d_i, but this, too, would generate another number that is not on the list of all the dividers of N, another nonsense!

Therefore, by trichotomy, we only have the choice 1+d₁+d₂+d₃+…+d_n-1=d_n.

Finally, let us suppose, absurdly, that there is a perfect odd number, say 2k+1. Now, let’s 1<I₁<I₂<I₃<…<I_2n  being all the 2k+1 dividers themselves. Note that I₁,I₂,I₃,…,I_2n are odd numbers and in an even amount of numbers, because the sum of an even amount of odd numbers is even and plus 1 results in an odd.

But by the property (P), which we have proved is valid for every perfect number, we have to 1+I₁+I₂+I₃+…+I_2n-1=I_2n. Now, note this 1+I₁+I₂+I₃+…+I_2n-1 is even, as it is the sum of an even amount of odd numbers (we consider the 1 being odd) and I_2n is odd. That is, we find a natural number that is even and odd simultaneously, ABSURD!

Therefore, there is no perfect odd natural number.

4. FINAL CONSIDERATIONS

Our article presents a demonstration of the Conjecture of Perfect Odd Numbers, but the renaming of Imperfect Odd Conjecture due to is more consistent with our result. But mathematics has beyond this many other open problems. And the main goal of our work is to encourage readers to also try to solve more open problems in the area. Achieving with this the increase of researchers in the most varied fields of mathematics in our country.

In the most we expect suggestions for the improvement of our article, constructive criticisms, too. And that our article provides continuation for many other academic works.

5.  REFERENCES

1. Portal do openproblemgarden. Disponível em: http://www.openproblemgarden.org/op/odd

_perfect_number. Acesso em 22 de abril de 2019.

2. ALENCAR FILHO, Edgard de. Iniciação à Lógica Matemática. 18 Ed. São Paulo: Nobel, 1975.

3. LIMA, Elon Lages Análise Real. vol. 1 Coleção Matemática Universitária, SBM,. Rio de Janeiro, 2001.

4. Canal A Matemaníaca por Julia Jaccoud. Disponível em: https://www.youtube.com/watch?v=

CHZBYfAmkcE. Acesso em 21 de abril de 2019.

5. Portal do Impa. Disponível em https://impa.br/noticias/problemas-do-milenio-da-geometria-a-fisica-quantica/. Acesso em 21 de abril de 2019.

6. Portal da matematica. Disponível em:http: //www.matematica.br/historia/nperfeitos.html. Acesso em 21 de abril de 2019.

7. Portal da ufc. Disponível em: http://www.periodicos.ufc.br/eu/article/view/15284/15570 Acesso em 22 de abril de 2019.

ANNEX A

LIST OF MATHEMATICAL CONJECTURES

1. P versus NP

2. Hodge conjecture

3. Riemann Hypothesis

4. Existence of Yang-Mills and mass range

5. Existence and smoothness of Navier-Stokes

6. Birch and Swinnerton-Dyer conjecture

7. Beal conjecture

8. Fermat-Catalan conjecture

9. Goldbach (strong) conjecture

10. Collatz conjecture

11. Erdös conjecture

12. Magic Square Number Conjecture

13. Andrica’s conjecture

14. Conjecture of twin cousins

15. Legendre conjecture

16. Happy ending problem

17. Gauss circle problem

18. Inverse Galois problem

19. Littlewood conjecture

20. Long arithmetic progressions of the rainbow

21. Monotonic Arithmetic Progressions of 4 Terminations

22. The double cap conjecture

23. Beneš conjecture

24. Surreal product length

25. Combinatorial coverage projects

26. A zero point in a linear mapping

27. Broad partition conjecture

28. Ramsey numbers diagonally

29. The additive basis conjecture

30. Are all Fermat numbers free of squares?

^[1]Graduated and master in mathematics.

Submitted: April, 2019.

Approved: May, 2019.