ARTIGO ORIGINAL
PEREIRA, Olavo de Carvalho [1]
PEREIRA, Olavo de Carvalho. Cálculo de limite de uma função sem a utilização de![]() e
e ![]() . Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 06, Ed. 08, Vol. 04, pp. 05-31. Agosto 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/calculo-de-limite, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/calculo-de-limite
. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 06, Ed. 08, Vol. 04, pp. 05-31. Agosto 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/calculo-de-limite, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/calculo-de-limite
RESUMO
A bibliografia consultada não apresenta, em nenhum dos casos analisados, cálculo de limite de uma função, mas apenas “mostra” que os valores apresentados como sendo o “limite” satisfazem a definição de limite de uma função expressa através de desigualdades envolvendo ![]() e
e ![]() , havendo, portanto, uma lacuna nesse tema, que o presente artigo vem preencher utilizando-se fundamentalmente do conceito de função definida, bem como pela identificação da expressão “
, havendo, portanto, uma lacuna nesse tema, que o presente artigo vem preencher utilizando-se fundamentalmente do conceito de função definida, bem como pela identificação da expressão “ ![]() tende a certo número” com uma igualdade correspondente.
tende a certo número” com uma igualdade correspondente.
Palavras-Chave: limite de uma função, cálculo de limite, limites laterais, limites infinitos, limites no infinito.
1. INTRODUÇÃO
Esse artigo apresenta o “cálculo de limite de uma função” no intuito de preencher uma lacuna existente nesse assunto.
A apresentação do cálculo mencionado na solução de diversos limites é o objetivo principal do artigo.
De forma suplementar, intencionamos esclarecer sobre a real necessidade de se calcular, ou não, o limite de uma função.
Também discorreremos, de uma maneira bem singela, sobre o caso em que uma função simples, definida em certo número, é contínua nesse número.
Embora a interpretação geométrica seja sempre importante, faremos aqui uma abordagem apenas algébrica do “cálculo de limite” apresentado.
1.1 CÁLCULO DE LIMITE DE UMA FUNÇÃO
A definição de limite de uma função é apresentada nos livros de matemática através de uma estimativa.
Por exemplo: Leithold (1994) apresenta a definição de limite de uma função da seguinte forma:
Seja ![]() uma função definida para todo número em algum intervalo aberto contendo
uma função definida para todo número em algum intervalo aberto contendo ![]() , exceto possivelmente no próprio número
, exceto possivelmente no próprio número ![]() O limite de
O limite de ![]() quando
quando ![]() tende a
tende a ![]() será
será ![]() , escrito como
, escrito como ![]() se a seguinte afirmativa for verdadeira:
se a seguinte afirmativa for verdadeira:
Dado ![]() qualquer, existe um
qualquer, existe um ![]() , tal que, se
, tal que, se ![]() então
então ![]() .‘‘
.‘‘
A definição acima afirma que os valores de ![]() tendem a um limite
tendem a um limite ![]() quando
quando ![]() tende a um número
tende a um número ![]() , se o valor absoluto da diferença entre
, se o valor absoluto da diferença entre ![]() e
e ![]() puder se tornar tão pequeno quanto desejarmos, tomando
puder se tornar tão pequeno quanto desejarmos, tomando![]() suficientemente próximo de
suficientemente próximo de ![]() , mas não igual a
, mas não igual a ![]() .
.
Já Lezzi, Murakami e Machado (1991) assim se expressam sobre a mesma definição:
Seja ![]() um intervalo aberto ao qual pertence o número real
um intervalo aberto ao qual pertence o número real ![]() . Seja
. Seja ![]() uma função definida para
uma função definida para ![]() Dizemos que o limite de
Dizemos que o limite de ![]() , quando
, quando ![]() tende a
tende a ![]() , é
, é ![]() , e escrevemos
, e escrevemos ![]() se para todo
se para todo ![]() , existir
, existir ![]() tal que se
tal que se
![]() então
então ![]() .
.
Munem e Foulis (1982) usam a seguinte definição:
Se ![]() é uma função e
é uma função e ![]() é um número, entende-se a notação
é um número, entende-se a notação ![]() como “o limite de
como “o limite de ![]() ” quando
” quando![]() tende a
tende a ![]() é
é ![]() isto é,
isto é, ![]() se aproxima do número
se aproxima do número ![]() quando
quando ![]() se aproxima de
se aproxima de ![]() .
.
Como se depreende das definições acima, é apresentado um limite ![]() apenas para satisfazer a própria definição.
apenas para satisfazer a própria definição.
Não se apresenta em nenhum momento o cálculo de tal limite.
O presente artigo apresenta o “cálculo de limite” de uma função que pode ser utilizado em todos os casos em que seja necessário efetuar-se tal operação.
Vamos, então, ao argumento.
Para algumas funções, não definidas em certo número, no intuito de saber, com a máxima precisão possível, qual seria seu valor naquele número, costuma-se fazer a avaliação das mesmas em valores próximos daquele número para o qual não estão definidas.
Exemplo: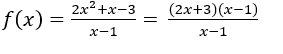 definida para todo
definida para todo ![]() exceto
exceto 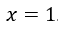 .
.
Se substituirmos o ![]() por 1, teremos a indeterminação
por 1, teremos a indeterminação ![]() .
.
Como a função não está definida, isto é, não existe para o valor 1, avaliamos, então, seu valor próximo de 1, pois nosso objetivo é conhecer o valor da função, pelo menos, próximo de 1, uma vez que ela não existe para ![]() .
.
Para valores de ![]() , diferentes de 1, maiores ou menores que 1, porém bem próximos de 1,
, diferentes de 1, maiores ou menores que 1, porém bem próximos de 1, ![]() , pois
, pois ![]() será igual a 1, e terá valores próximos de 5, como veremos abaixo:
será igual a 1, e terá valores próximos de 5, como veremos abaixo:
Vamos atribuir a ![]() os valores
os valores![]() , isto é, estamos tomando valores de
, isto é, estamos tomando valores de ![]() cada vez mais próximos de 1, porém menores do que 1. Os valores de
cada vez mais próximos de 1, porém menores do que 1. Os valores de ![]() encontrados são:
encontrados são:
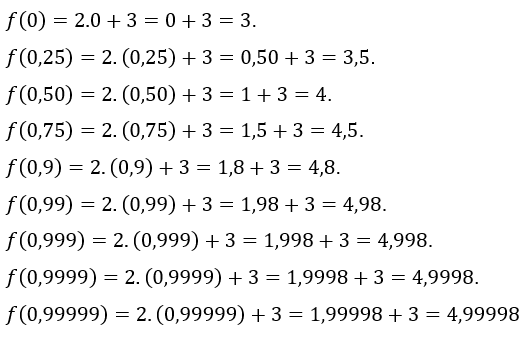
Agora vamos atribuir a ![]() os valores
os valores ![]() , isto é, estamos tomando valores de
, isto é, estamos tomando valores de ![]() cada vez mais próximos de 1, porém maiores que 1. Os valores de
cada vez mais próximos de 1, porém maiores que 1. Os valores de ![]() encontrados são:
encontrados são: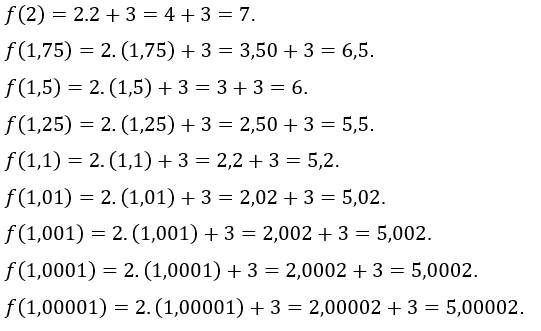
Como se observa, em ambos os casos, à medida que ![]() se aproxima de 1,
se aproxima de 1, ![]() se aproxima de 5, levando-nos a crer que seja esse o limite de
se aproxima de 5, levando-nos a crer que seja esse o limite de ![]() .
.
Entretanto, não foi feito aqui nenhum “cálculo” de limite, mas apenas uma avaliação de ![]() , quando
, quando ![]() assume valores bem próximos de 1.
assume valores bem próximos de 1.
De forma que o valor 5 é “candidato” a ser o limite que, ainda, precisamos calcular.
Os autores consultados estruturam a definição de limite em termos de desigualdades a partir de exemplos como esse e assumem o valor estimado, no caso o 5, como realmente o limite da função.
A esse propósito, afirmam que ![]() , pois para qualquer
, pois para qualquer ![]() , não importa o quão pequeno ele seja, existe um
, não importa o quão pequeno ele seja, existe um ![]() , tal que se
, tal que se ![]() então
então ![]() .
.
A definição de limite dada no início, que não possui nenhum cálculo de limite, é utilizada para “provar” que números fornecidos, sem nenhuma indicação de onde foram tirados, são limites de funções.
Evidenciaremos que a definição de limite não prova, não demonstra, que dado número é o limite de uma função, mas apenas “mostra” que o número fornecido é o limite.
Vamos usar um exemplo para tornar clara a diferença entre uma “mostração” e uma “demonstração”.
- Mostre que 2 é raiz da equação
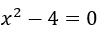 .
.
Isto significa que, se substituirmos o ![]() pelo 2, teremos zero como resultado da equação.
pelo 2, teremos zero como resultado da equação.
Vejamos ![]() .
.
Esse foi exemplo de “mostração”, isto é, apenas se mostrou alguma coisa, não se demonstrou nada, não se calculou nada, apenas se substituiu o valor fornecido.
Diferente é quando se diz: demonstre que 2 é raiz, é solução da equação ![]() .
.
Nesse caso, temos que calcular, resolver a equação, e ver se obtemos ![]() .
.
Bem, resolvendo, temos: ![]() , logo
, logo ![]() , e extraindo a raiz quadrada em ambos os lados temos:
, e extraindo a raiz quadrada em ambos os lados temos: ![]() , isto é,
, isto é, ![]() ou
ou ![]() .
.
Logo um dos valores de ![]() realmente é 2.
realmente é 2.
Com isto, ficou “demonstrado” que realmente 2 é raiz da equação ![]() .
.
Veremos, nos exemplos dados a seguir, que não existe uma demonstração, mas apenas uma “mostração” de que o número fornecido é limite da função dada.
Exemplo. Use a definição de limite para “provar” que ![]() .
.
Aqui não se fala como se chegou à conclusão de que o limite é 5, nem se diz de onde esse número foi tirado.
Abordaremos, em linhas gerais, a solução apresentada nos livros consultados:
A primeira exigência da definição é que ![]() seja definida em todo número de algum intervalo aberto contendo 3, exceto possivelmente em 3. Como
seja definida em todo número de algum intervalo aberto contendo 3, exceto possivelmente em 3. Como ![]() está definida para todos os números reais, qualquer intervalo aberto contendo 3 irá satisfazer esse requisito. Precisamos mostrar agora que para todo
está definida para todos os números reais, qualquer intervalo aberto contendo 3 irá satisfazer esse requisito. Precisamos mostrar agora que para todo ![]() existe um
existe um ![]() , tal que se
, tal que se ![]() então
então ![]() temos que
temos que![]()
, logo ![]() e
e ![]()
Temos, então, ![]() e
e ![]()
Essa afirmativa indica que ![]() é um delta satisfatório.
é um delta satisfatório.
Com essa escolha de ![]() temos o seguinte argumento:
temos o seguinte argumento:![]() , então
, então ![]() , então
, então ![]() , então
, então ![]() então
então ![]() , pois
, pois ![]()
Isso apenas “mostra”, a partir da definição de limite, que ![]()
Como vimos, não houve uma demonstração, mas apenas uma “mostração”, uma vez que, fornecido o número 5, fizemos simplesmente a substituição dele e da função dada, na definição de limite de uma função.
Vamos a mais um exemplo: use a definição para “provar” que ![]() .
.
Novamente é fornecido um número, no caso o 4, como sendo o limite, mas não se diz de onde esse número foi tirado.
Vamos à solução apresentada, em linhas gerais:
Como ![]() está definido para todos os números reais, qualquer intervalo aberto contendo 2 satisfará o primeiro requisito da definição.
está definido para todos os números reais, qualquer intervalo aberto contendo 2 satisfará o primeiro requisito da definição.
Precisamos mostrar que para todo ![]() , existe um
, existe um ![]() , tal que
, tal que
Se ![]() então
então ![]()
Logo ![]() então
então ![]()
Precisamos colocar uma restrição sobre ![]() que nos dê uma desigualdade envolvendo
que nos dê uma desigualdade envolvendo ![]() . Tal restrição é feita para selecionarmos o intervalo aberto requerido pela definição. Escolhemos o intervalo
. Tal restrição é feita para selecionarmos o intervalo aberto requerido pela definição. Escolhemos o intervalo ![]() e isto implica que
e isto implica que ![]() . Então
. Então ![]() e
e ![]() , então
, então ![]() então
então ![]() então
então ![]() então
então ![]() .
.
Agora temos ![]() e
e ![]() , então
, então ![]() Como nossa meta é obter
Como nossa meta é obter ![]() , devemos requerer
, devemos requerer ![]() Com isto
Com isto 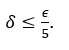
Usando esse ![]() concluímos a chamada “prova”.
concluímos a chamada “prova”.
Como vimos acima, novamente não se provou nada, mas apenas se mostrou que o número fornecido como sendo o limite, no caso o 4, satisfaz à definição de limite.
Não houve nenhum cálculo para evidenciar que o número 4 é realmente o limite.
Faremos, a partir deste ponto, a apresentação do cálculo de limite de uma função.
Antes de apresentar o “cálculo” propriamente dito, vamos avaliar ![]() nos mesmos valores de
nos mesmos valores de ![]() fornecidos acima, porém considerando-os como compostos do número 1.
fornecidos acima, porém considerando-os como compostos do número 1.
Isto mostrará, em linhas gerais, o raciocínio utilizado para fazer o cálculo de limite da função.
A função é ![]() , válida para todo
, válida para todo ![]() .
.
Para ![]() ou
ou ![]() , temos que
, temos que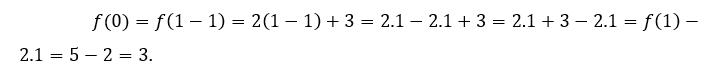
Para ![]() ou
ou ![]() , temos que
, temos que 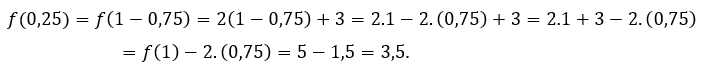 Para
Para ![]() ou
ou ![]() temos que
temos que 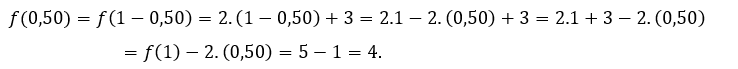
Para ![]() ou
ou ![]() temos que
temos que 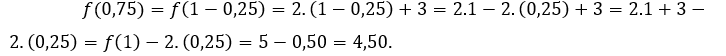 Para
Para ![]() ou
ou ![]() , temos que
, temos que 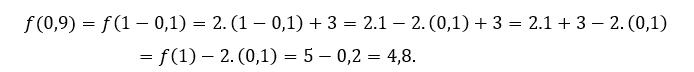
Para ![]() ou
ou ![]() , temos que
, temos que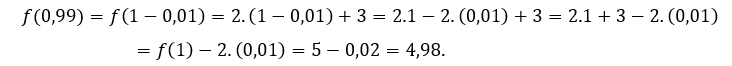
Para ![]() ou
ou ![]() temos que
temos que 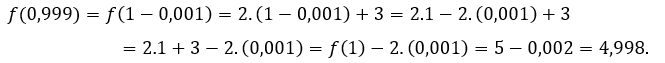
Para ![]() ou
ou ![]() , temos que
, temos que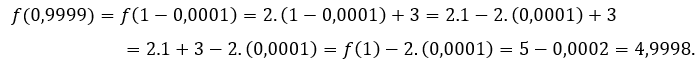
Para ![]() ou
ou ![]() , temos que
, temos que 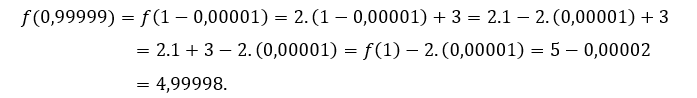
Testamos alguns valores de ![]() menores que 1.
menores que 1.
Agora faremos a avaliação de ![]() em valores maiores que 1, porém próximos de 1.
em valores maiores que 1, porém próximos de 1.
Para ![]() ou
ou ![]() , temos que
, temos que 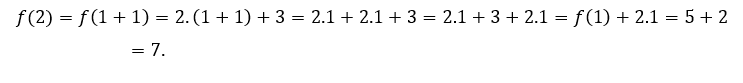
Para ![]() ou
ou ![]() temos que
temos que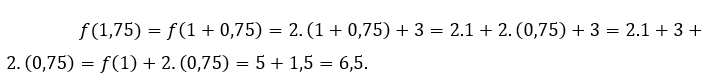
Para ![]() ou
ou ![]() temos que
temos que 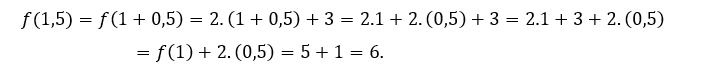
Para ![]() ou
ou ![]() , temos que
, temos que 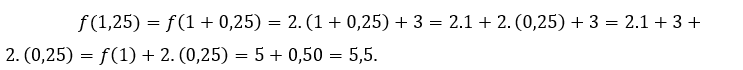
Para ![]() ou
ou ![]() , temos que
, temos que 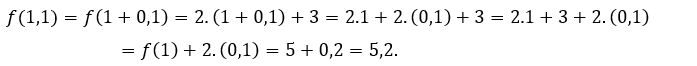
Para ![]() ou
ou ![]() temos que
temos que 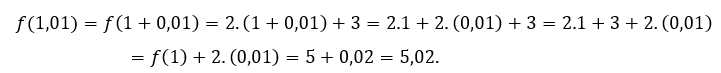
Para ![]() ou
ou ![]() , temos que
, temos que 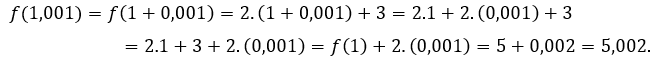
Para ![]() ou
ou ![]() , temos que
, temos que 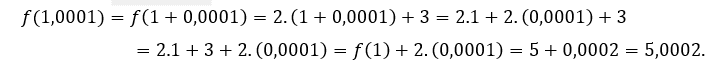
Para ![]() ou
ou ![]() , temos que
, temos que 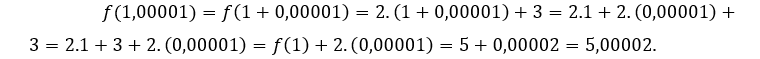
Pelo exposto acima, percebemos que, quanto mais ![]() se aproxima de 1, tanto mais
se aproxima de 1, tanto mais ![]() se aproxima de 5, isto é, quando
se aproxima de 5, isto é, quando ![]() tende a 1,
tende a 1, ![]() tende a 5.
tende a 5.
Observamos nos cálculos acima, em todos os valores atribuídos a ![]() , o aparecimento de uma constante
, o aparecimento de uma constante ![]() à qual se somou ou se subtraiu um valor que ia tendendo a zero, à medida que
à qual se somou ou se subtraiu um valor que ia tendendo a zero, à medida que ![]() ia se aproximando de 1.
ia se aproximando de 1.
Essa constante é, portanto, “candidata” a ser o “limite” mencionado acima, isto é, há um indicativo de que poderemos ter ![]() .
.
Expressaremos agora, a situação acima, de uma forma semi genérica para apresentar o “cálculo do limite” propriamente dito.
A expressão “![]() tende a 1″, representada por
tende a 1″, representada por ![]() , é equivalente a
, é equivalente a ![]() , ou
, ou ![]() , quando
, quando ![]() tende a zero,
tende a zero, ![]() , e
, e ![]() .
.
Com isto, a expressão ![]() , substituindo
, substituindo ![]() por
por ![]() ou
ou ![]() , é equivalente a
, é equivalente a ![]() , ou
, ou ![]() , isto é,
, isto é, ![]() , ou
, ou ![]() .
.
A partir da igualdade acima, é possível “calcular” o valor do limite de ![]() quando
quando ![]() tende a 1, pois basta calcular o valor de
tende a 1, pois basta calcular o valor de ![]() , ou
, ou ![]() .
.
Faremos, agora, utilizando a mesma função anterior, o cálculo para ![]() , quando
, quando ![]() .
.
Dessa forma, ficamos com:
![]() pois
pois ![]() independe de
independe de ![]() , e
, e ![]() tende a zero quando
tende a zero quando ![]() , isto é, é tão pequeno que se aproxima de zero, tanto quanto desejarmos.
, isto é, é tão pequeno que se aproxima de zero, tanto quanto desejarmos.
O cálculo para ![]() , isto é,
, isto é, ![]() , é análogo e produz o mesmo resultado.
, é análogo e produz o mesmo resultado.
Vejamos: ![]()
Calcularemos, agora, uma série de limites de funções, para exemplificar a aplicação do “cálculo” mencionado.
- Calculemos
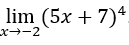 .
.
Como ![]() , podemos fazer, por exemplo,
, podemos fazer, por exemplo, ![]() ,
, ![]() e
e ![]() .
.
Ficamos com ![]()
![]() termos em
termos em ![]() que tendem todos a zero.
que tendem todos a zero.
Logo o resultado será ![]()
- Calculemos
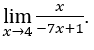
Como ![]() , podemos fazer, por exemplo,
, podemos fazer, por exemplo, ![]() ,
, ![]() e
e ![]() .
.
Ficamos com![]() , pois o numerador tende para 4 e o denominador tende para
, pois o numerador tende para 4 e o denominador tende para ![]() .
.
- Calculemos
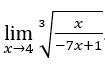 .
.
Como vimos acima, no final ficaremos com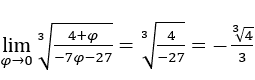
- Calculemos
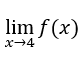 conforme abaixo.
conforme abaixo.
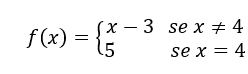 .
.
Devemos calcular ![]() , pois não importa o que acontece com
, pois não importa o que acontece com ![]() quando
quando ![]() .
.
Como ![]() , podemos fazer, por exemplo,
, podemos fazer, por exemplo, ![]()
![]() e
e ![]() .
.
Ficamos com ![]() , pois
, pois![]() .
.
Seja ![]() , definida para todo
, definida para todo ![]() , exceto
, exceto ![]() .
.
Consideremos ![]() isto é,
isto é, ![]() , para o qual
, para o qual ![]() se reduz a
se reduz a ![]() .
.
- Calculemos o
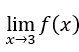 . Temos que
. Temos que 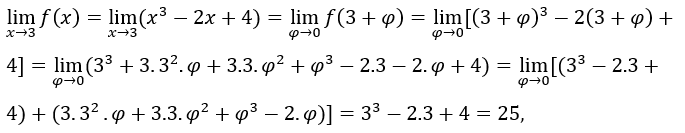 , uma vez que, quando
, uma vez que, quando 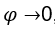 , a expressão
, a expressão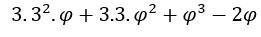 tende a zero.
tende a zero.
Então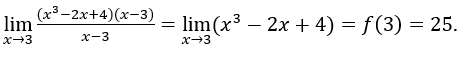
Agora consideremos o seguinte exemplo: ![]() , definida para todo
, definida para todo ![]() , e calculemos o seu limite quando
, e calculemos o seu limite quando ![]() tende a 2.
tende a 2.
Para ![]() condição de existência da função,
condição de existência da função, ![]() , e quando
, e quando ![]() podemos fazer, por exemplo,
podemos fazer, por exemplo, ![]() , com
, com ![]()
![]() e teremos que calcular o limite
e teremos que calcular o limite![]() .
.
Como ![]() , a expressão
, a expressão ![]() tende a
tende a ![]() , e o limite será, então,
, e o limite será, então, ![]() .
.
Concluindo, ficamos com: ![]() .
.
Observação.
Poderíamos ter aplicado o “cálculo” diretamente sobre a função, sem antes dividir o fator comum ao numerador e ao denominador.
Vejamos ![]()
Aliás, podemos aplicar o “cálculo” diretamente sobre a função, sem antes fazer uma “preparação” sobre ela.
Daremos agora alguns exemplos de cálculo de limite envolvendo função trigonométrica e exponencial no intuito de exemplificar o consolidado acima.
Consideremos a função ![]() , definida para todo
, definida para todo ![]() , exceto
, exceto 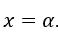
Recordando: ![]() significa, por exemplo, que
significa, por exemplo, que![]() , onde
, onde ![]() ,
, ![]() .
.
Substituindo esse valor de x na equação original acima, temos: 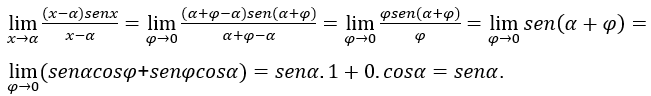
Pois, ![]() e
e ![]() são independentes de
são independentes de ![]() e o
e o![]()
, enquanto o ![]() .
.
Outro exemplo: consideremos a função![]() definida para todo
definida para todo ![]() , exceto
, exceto ![]() .
.
- Calculemos o
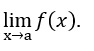
- Fazendo a substituição
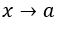 por, por exemplo,
por, por exemplo, 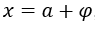 , com
, com 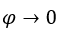 ,
, 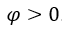 . Temos:
. Temos: 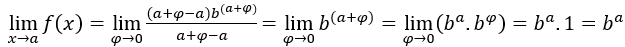 , pois o
, pois o 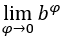 é 1 e
é 1 e 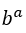 independe de
independe de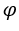 .
.
Agora vamos calcular o limite das funções dadas no início para confirmar os valores dos limites fornecidos.
- Calculemos
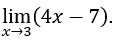
Como ![]() , podemos fazer, por exemplo,
, podemos fazer, por exemplo, ![]() ,
, ![]() e
e ![]() e ficamos com
e ficamos com ![]()
- Calculemos
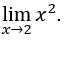
Como ![]() , podemos fazer, por exemplo,
, podemos fazer, por exemplo, ![]() ,
, ![]() e
e ![]() e ficamos com
e ficamos com ![]()
Como se depreende dos “cálculos” acima, os limites fornecidos nos exemplos anteriores estavam corretos.
Vamos demonstrar apenas um teorema sobre limites para exemplificar o cálculo aqui exposto.
Teorema. Se ![]() e
e ![]() forem constantes quaisquer, então
forem constantes quaisquer, então ![]() .
.
Basta calcular o limite fazendo, por exemplo, ![]()
![]() e
e ![]()
Ficamos com: ![]() , pois
, pois ![]() tende para zero, uma vez que
tende para zero, uma vez que ![]() tende para zero.
tende para zero.
Nota-se uma simplicidade imensa no “cálculo” apresentado.
Nesse caso não resta dúvida de que o limite é ![]() .
.
Agora utilizaremos o “cálculo de limite” apresentado para calcular limites de funções em diversas circunstâncias.
- Calculemos
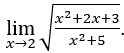
Como ![]() , então podemos fazer, por exemplo,
, então podemos fazer, por exemplo, ![]() ,
, ![]() e
e ![]()
Ficamos com 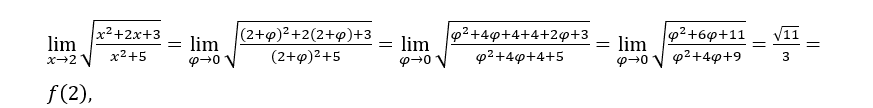 , uma vez que
, uma vez que ![]() tende para 11 e
tende para 11 e ![]() tende para 9.
tende para 9.
- Calculemos
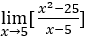 .
.
Como x → 5, então podemos fazer, por exemplo, ![]() ,
, ![]() e
e ![]()
Ficamos com 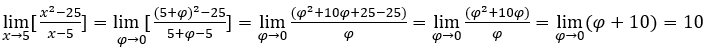
Observa-se que não foi necessário “preparar” a função para aplicar o “cálculo”, isto é, não foi necessário escrever a função como ![]() e, finalmente, como
e, finalmente, como ![]()
- Calculemos
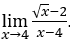 .
.
Nos casos envolvendo radicais, ao qual estão somados ou subtraídos um número real, quando a substituição direta do valor de ![]() conduz à indeterminação
conduz à indeterminação ![]() temos que preparar a equação, pois a aplicação direta do “cálculo” não desfaz a indeterminação, como veremos abaixo.
temos que preparar a equação, pois a aplicação direta do “cálculo” não desfaz a indeterminação, como veremos abaixo.
O que ocorre nesse caso é que existe um fator comum ao numerador e ao denominador, mas que só é expresso quando efetuamos a divisão, seja do numerador pelo denominador, seja do denominador pelo numerador.
Isso se traduz atualmente em matemática como racionalização.
Vejamos no exemplo acima: se dividirmos o denominador pelo numerador, uma vez que o expoente de ![]() no denominador é 1 e o expoente de
no denominador é 1 e o expoente de ![]() no numerador é menor, isto é, vale
no numerador é menor, isto é, vale ![]() teremos:
teremos: ![]() e substituindo, ficaremos com
e substituindo, ficaremos com 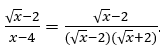 .
.
Conseguimos, com isso, expressar o fator comum ao numerador e ao denominador.
A outra maneira é dividirmos o numerador pelo denominador, mas, nesse caso, devemos fazer mesmo é a racionalização, uma vez que o expoente de ![]() no numerador é menor que o expoente de
no numerador é menor que o expoente de ![]() no denominador, necessitando, por isso, de ser multiplicado por um fator em
no denominador, necessitando, por isso, de ser multiplicado por um fator em ![]() para tornar o seu expoente, pelo menos, igual ao expoente do denominador.
para tornar o seu expoente, pelo menos, igual ao expoente do denominador.
Essa é a famosa racionalização que fazemos.
Faremos primeiro o cálculo, sem preparação.
Como ![]() , podemos fazer, por exemplo,
, podemos fazer, por exemplo, ![]() ,
,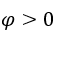 e
e ![]() .
.
Ficamos com ![]() Observamos a necessidade de racionalizar, pois o limite ainda fica indeterminado quando
Observamos a necessidade de racionalizar, pois o limite ainda fica indeterminado quando ![]() no numerador e no denominador, tendendo para
no numerador e no denominador, tendendo para ![]()
Multiplicaremos e dividiremos, então, por ![]() , e ficaremos com
, e ficaremos com ![]()
Agora faremos o cálculo, preparando a função antes de aplicá-lo.
![]() .
.
Como a substituição direta de 4 conduz à indeterminação ![]() , significa que o numerador e o denominador têm como fator comum
, significa que o numerador e o denominador têm como fator comum ![]() ou
ou ![]()
Nesse caso, como se trata de um radical menos um número real, a maneira utilizada para “liberar” o fator comum é através de racionalização.
Antes de calcular o limite, multiplicaremos e dividiremos o numerador o denominador da função por ![]()
Ficamos com 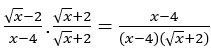 . Nessa função, já podemos aplicar o cálculo. Vejamos:
. Nessa função, já podemos aplicar o cálculo. Vejamos: 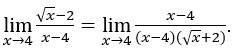
Como ![]() podemos fazer, por exemplo,
podemos fazer, por exemplo, ![]() ,
, ![]() e
e ![]()
Ficamos com 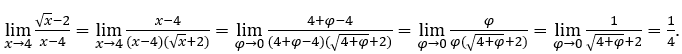
1.2 LIMITES LATERAIS
Nos casos em que uma função está definida para todo número real, exceto um número real ![]() , quando calculamos seu limite com a variável independente tendendo a
, quando calculamos seu limite com a variável independente tendendo a ![]() , como nos exemplos dados acima, tanto faz utilizarmos
, como nos exemplos dados acima, tanto faz utilizarmos ![]() quanto
quanto ![]() ,
, ![]() e
e ![]() , uma vez que ela está definida para todos os números à esquerda e à direita de
, uma vez que ela está definida para todos os números à esquerda e à direita de ![]() .
.
E é claro, não se tratando de uma função sentença.
Quando uma função não está definida à esquerda ou à direta de um número ![]() e tenhamos que calcular seu limite com
e tenhamos que calcular seu limite com ![]() tendendo a, devemos utilizar o valor de
tendendo a, devemos utilizar o valor de ![]() conforme o caso.
conforme o caso.
Quando ![]() e fazemos
e fazemos ![]() , ou
, ou ![]() ,
, ![]() e
e ![]() , então
, então ![]() indica que
indica que ![]() está se aproximando de
está se aproximando de ![]() por valores maiores que
por valores maiores que ![]() , e, portanto, está se aproximando de
, e, portanto, está se aproximando de ![]() pela direita.
pela direita.
O cálculo feito com ![]() é, portanto, o limite quando
é, portanto, o limite quando ![]() tende a
tende a ![]() pela direita.
pela direita.
É, por isso, o limite lateral direito.
Utilizamos ![]() para calcular o limite lateral esquerdo.
para calcular o limite lateral esquerdo.
Sabemos que o limite existe somente quando os limites laterais existem e são iguais.
- Calculemos
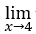 √x – 4.
√x – 4.
Sabemos que a função existe somente para ![]() , isto é,
, isto é, ![]()
Logo, não existe o limite lateral esquerdo e, com isto, não existe o limite em questão.
Mas existe o limite lateral direito que pode ser calculado substituindo ![]() por
por ![]() ,
, ![]() e
e ![]()
![]()
![]()
- Calculemos os limites laterais.
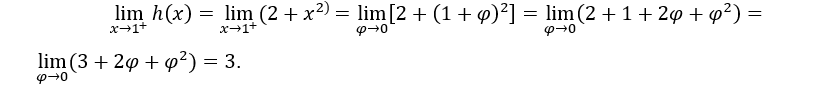
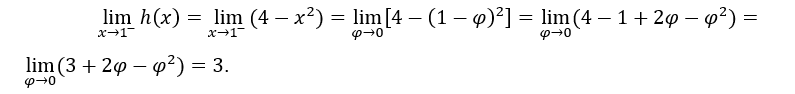
Como são iguais,![]()
No cálculo acima, fizemos ![]() , para calcular o limite lateral direito e
, para calcular o limite lateral direito e ![]() para calcular o limite lateral esquerdo.
para calcular o limite lateral esquerdo.
Calculemos o limite de ![]() definida por
definida por
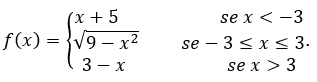
- Calculemos
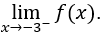
Devemos calcular, então,![]()
Faremos, então, ![]() ,
, ![]() e
e ![]()
- Calculemos
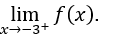
Devemos calcular, então,![]()
Faremos, então, ![]() ,
, ![]() e
e ![]()
Ficamos com ![]()
- Calculemos
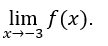
Como ![]() então o
então o ![]() não existe.
não existe.
- Calculemos
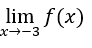 .
.
Devemos calcular, então,![]()
Faremos, então, ![]() ,
, ![]() e
e ![]()
Ficamos com ![]()
- Calculemos
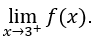
Devemos calcular, então, ![]()
Faremos, então, ![]() ,
, ![]() e
e ![]()
Ficamos com
![]() Calculemos
Calculemos 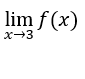
Como ![]() , então
, então 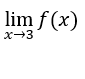 existe e é igual a zero.
existe e é igual a zero.
1.3 LIMITES INFINITOS
Aqueles cujos valores funcionais aumentam ou diminuem sem limitação, quando a variável independente se aproxima cada vez mais de um número fixo, podem ser resolvidos igualmente pelo “cálculo” de limite aqui apresentado, com a vantagem de não precisar se preocupar com teoremas.
Antes de aplicar o “cálculo”, relembremos as seguintes situações:
![]()
- Calculemos o seguinte limite
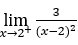 .
.
Como ![]() , devemos fazer
, devemos fazer ![]() ,
, ![]() e
e ![]()
Ficamos com ![]() .
.
- Calculemos agora
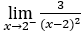 .
.
Como ![]() , devemos fazer
, devemos fazer ![]() ,
, ![]() e
e ![]()
Ficamos com ![]() .
.
- Calculemos
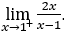 .
.
Como ![]() , devemos fazer
, devemos fazer ![]() ,
, ![]() e
e ![]()
Ficamos com ![]() , pois o numerador tende a 2, enquanto o denominador tende a zero através de valores positivos.
, pois o numerador tende a 2, enquanto o denominador tende a zero através de valores positivos.
- Calculemos agora
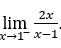 .
.
Como ![]() , devemos fazer
, devemos fazer ![]() ,
, ![]() e
e ![]()
Ficamos com ![]() , pois o numerador tende a 2 e o denominador tende a zero através de valores negativos.
, pois o numerador tende a 2 e o denominador tende a zero através de valores negativos.
- Calculemos
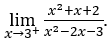
Como ![]() , devemos fazer
, devemos fazer ![]() ,
, ![]() e
e ![]()
Ficamos com 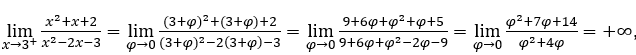 pois o numerador tende para 14, enquanto o denominador tende a zero por valores positivos.
pois o numerador tende para 14, enquanto o denominador tende a zero por valores positivos.
- Calculemos agora
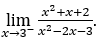
Como ![]() , devemos fazer
, devemos fazer ![]() ,
, ![]() e
e ![]()
Ficamos com ![]() , pois o numerador tende para 14, enquanto o denominador tende a zero por valores negativos, uma vez que
, pois o numerador tende para 14, enquanto o denominador tende a zero por valores negativos, uma vez que ![]() tende a zero sempre por valores positivos.
tende a zero sempre por valores positivos.
Neste caso o denominador é ![]() sempre que
sempre que![]() , e como
, e como ![]() , o denominador é sempre negativo.
, o denominador é sempre negativo.
- Calculemos
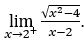
Como ![]() , devemos fazer
, devemos fazer ![]() ,
, ![]() e
e ![]()
Ficamos como 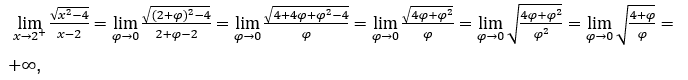 pois o numerador tende para 2 e o denominador tende para zero por valores positivos.
pois o numerador tende para 2 e o denominador tende para zero por valores positivos.
- Calculemos
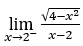
Como ![]() , devemos fazer
, devemos fazer ![]() ,
, ![]() e
e ![]()
Ficamos com 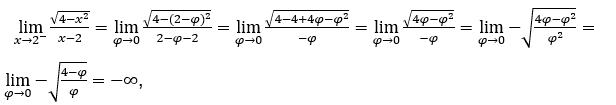 , pois o numerador tende para -2 e o denominador tende para zero por valores positivos.
, pois o numerador tende para -2 e o denominador tende para zero por valores positivos.
Nesses dois casos pudemos passar o ![]() para dentro do radical porque ele é sempre positivo.
para dentro do radical porque ele é sempre positivo.
- Calculemos
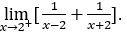
Como ![]() , devemos fazer
, devemos fazer ![]() ,
, ![]() e
e ![]()
Ficamos com ![]() pois o numerador tende para 4, enquanto o denominador tende para zero por valores positivos.
pois o numerador tende para 4, enquanto o denominador tende para zero por valores positivos.
Obs. Poderíamos ter substituído diretamente o valor de ![]() na equação original.
na equação original.
- Calculemos
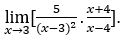
Como ![]() , devemos fazer
, devemos fazer ![]() ,
, ![]() e
e ![]()
Ficamos com ![]() , pois o numerador tende para 35, enquanto o denominador tende para zero por valores negativos, uma vez que é negativo para < 1.
, pois o numerador tende para 35, enquanto o denominador tende para zero por valores negativos, uma vez que é negativo para < 1.
- Calculemos
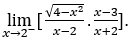
Como ![]() , faremos
, faremos ![]() ,
, ![]() e
e ![]()
Ficamos com 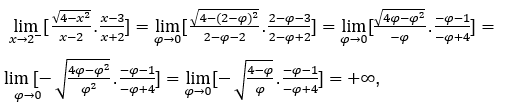 , pois o numerador tende para
, pois o numerador tende para ![]() e o denominador tende para
e o denominador tende para ![]() por valores positivos.
por valores positivos.
1.4 LIMITES NO INFINITO
Da mesma forma que para os limites mencionados até aqui, a literatura consultada também não apresenta cálculo de limites no infinito, mas apenas faz uma avaliação da função quando a variável independente cresce ou decresce indefinidamente.
O resultado da avaliação é utilizado como sendo o limite.
Vejamos.
Dada a função 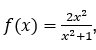 , atribuímos a
, atribuímos a ![]() os valores
os valores ![]() e assim por diante, permitindo que aumente indefinidamente. Os valores funcionais correspondentes serão
e assim por diante, permitindo que aumente indefinidamente. Os valores funcionais correspondentes serão ![]()
Observamos que, quando ![]() cresce, tomando valores positivos, os valores funcionais aproximam-se de 2.
cresce, tomando valores positivos, os valores funcionais aproximam-se de 2.
Quando uma variável independente ![]() cresce indefinidamente, através de valores positivos, escrevemos
cresce indefinidamente, através de valores positivos, escrevemos ![]() o exemplo dado, foi tirada a conclusão de que
o exemplo dado, foi tirada a conclusão de que 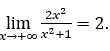
Conforme visto acima, do exemplo dado, não foi apresentado nenhum cálculo de limite da função, mas apenas se observou que, à medida que ![]() aumentava, por valores positivos, a função se aproximava de 2.
aumentava, por valores positivos, a função se aproximava de 2.
Esse valor 2 foi, então, utilizado como sendo o limite da função.
Apresentaremos, abaixo, o “cálculo” de limite de funções quando a variável independente tende a ![]() ou a
ou a ![]()
Nos casos em que ![]() , faremos
, faremos ![]() e
e ![]() , pois, como vimos acima, quando
, pois, como vimos acima, quando ![]() tende a zero por valores positivos,
tende a zero por valores positivos, ![]() tende a
tende a ![]() , e, com isso,
, e, com isso, ![]() tende a
tende a ![]()
Nos casos em que ![]() , faremos
, faremos 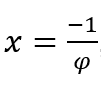
![]() e
e ![]() , pois, como vimos acima, quando φ tende a zero por valores positivos
, pois, como vimos acima, quando φ tende a zero por valores positivos![]() ,
,![]() tende a, e, com isso,
tende a, e, com isso, ![]() tende a
tende a ![]() .
.
- Calculemos
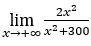 .
.
Como 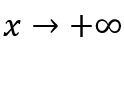 , faremos
, faremos 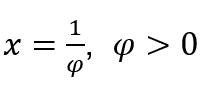 e
e ![]()
Ficamos com ![]() pois o numerador tende para 2 e denominador tende para 1.
pois o numerador tende para 2 e denominador tende para 1.
- Calculemos
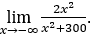
Como ![]() , faremos
, faremos ![]() e
e ![]()
Ficamos com 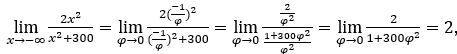 , pois o numerador tende para 2 e o denominador tende para 1.
, pois o numerador tende para 2 e o denominador tende para 1.
- Calculemos
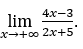
Como ![]() , faremos
, faremos![]() e
e ![]()
Ficamos com ![]() , pois o numerador tende para 4 e o denominador tende para 2.
, pois o numerador tende para 4 e o denominador tende para 2.
- Calculemos
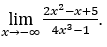
Como ![]() , faremos
, faremos![]()
![]() e
e ![]()
Ficamos com 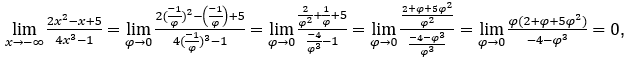 pois o numerador tende a zero e o denominador tende a -4.
pois o numerador tende a zero e o denominador tende a -4.
- Calculemos
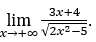
Como ![]() , faremos
, faremos ![]() e
e ![]()
Ficamos com 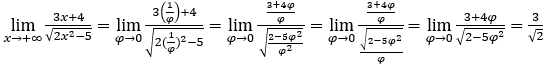 , pois o numerador tende para 3 e o denominador tende para
, pois o numerador tende para 3 e o denominador tende para ![]()
- Calculemos
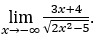
Como ![]() , faremos
, faremos ![]()
![]() e
e ![]()
Ficamos com 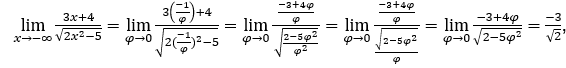 , pois o numerador tende para -3 e o denominador tende para √2.
, pois o numerador tende para -3 e o denominador tende para √2.
- Calculemos
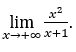
Como![]() , faremos
, faremos ![]() e
e ![]()
Ficamos com 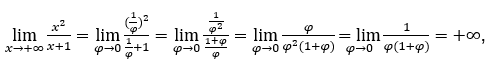 pois o numerador é 1 e o denominador tende a zero por valores positivos.
pois o numerador é 1 e o denominador tende a zero por valores positivos.
- Calculemos
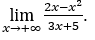
Como ![]() , faremos
, faremos ![]() =
= ![]() φ > 0 e φ → 0.
φ > 0 e φ → 0.
Ficamos com 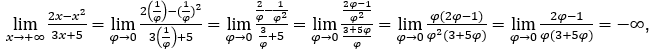 pois o numerador tende para -1 e o denominador tende para zero por valores positivos.
pois o numerador tende para -1 e o denominador tende para zero por valores positivos.
- Calculemos
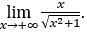
Como ![]() , faremos
, faremos ![]() e
e ![]()
Ficamos com 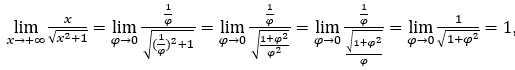 pois o numerador é 1 e o denominador tende para 1.
pois o numerador é 1 e o denominador tende para 1.
- Calculemos agora
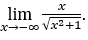
Como ![]() , faremos
, faremos ![]() e
e ![]()
Ficamos com 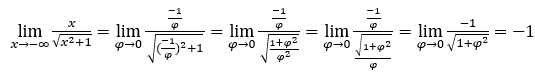 , pois o numerador é -1 e o denominador tende para 1.
, pois o numerador é -1 e o denominador tende para 1.
- Calculemos
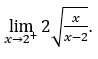
Como ![]() , devemos fazer
, devemos fazer ![]() ,
, ![]()
Ficamos com 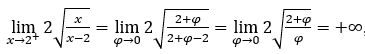 , pois o numerador tende para
, pois o numerador tende para ![]() e o denominador tende para zero por valores positivos.
e o denominador tende para zero por valores positivos.
- Calculemos agora
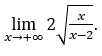
Como ![]() , faremos
, faremos ![]() e
e ![]()
Ficamos com 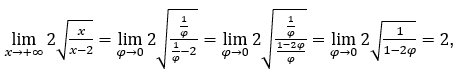 pois o numerador tende para 2 e o denominador tende para 1.
pois o numerador tende para 2 e o denominador tende para 1.
Observação.
Cálculo de limites no infinito não pode ser aplicado, por exemplo, às funções trigonométricas, uma vez que algumas delas variam em certo intervalo, e outras crescem ou decrescem indefinidamente, dependendo do valor considerado.
Por exemplo, se tentássemos calcular o ![]() , passaríamos infinitas vezes por todos os valores do intervalo
, passaríamos infinitas vezes por todos os valores do intervalo ![]() , pois, para todo
, pois, para todo ![]() ,
, ![]() , isto é, não chegaríamos a valor algum definido.
, isto é, não chegaríamos a valor algum definido.
Realmente as funções polinomiais, ou funções expressas por razões entre polinômios, são as mais adequadas à aplicação de limites.
2. OBSERVAÇÕES
1) O cálculo de limite apresentado surgiu da identificação da expressão ![]() tende a um certo número
tende a um certo número ![]() com a igualdade
com a igualdade ![]() , ou
, ou ![]() , com
, com![]() e
e ![]() , uma vez que, realmente, quando
, uma vez que, realmente, quando ![]() ,
, ![]() e
e ![]() tendem para
tendem para ![]() e, com isso,
e, com isso, ![]() tende para
tende para ![]()
No caso de limites no infinito, a substituição para a expressão ![]() tende para
tende para ![]() foi
foi![]() , e a substituição para a expressão
, e a substituição para a expressão ![]() tende para
tende para ![]() foi
foi ![]() , com
, com ![]() e
e ![]()
A substituição faz o maior sentido, pois, realmente, quando ![]() , sempre por valores positivos,
, sempre por valores positivos,![]() tende
tende ![]() e
e ![]() tende a
tende a ![]() , fazendo com que
, fazendo com que ![]() tenda realmente a
tenda realmente a ![]() ou a
ou a ![]() , conforme o caso.
, conforme o caso.
Se substituíssemos, no caso em que ![]() tende a
tende a![]() ou a
ou a ![]() o
o ![]() por,
por, ![]() ou
ou ![]() e
e ![]() , o resultado seria o mesmo.
, o resultado seria o mesmo.
Um exemplo.
- Calculemos
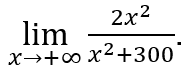
Faremos ![]() e
e ![]()
Ficamos com 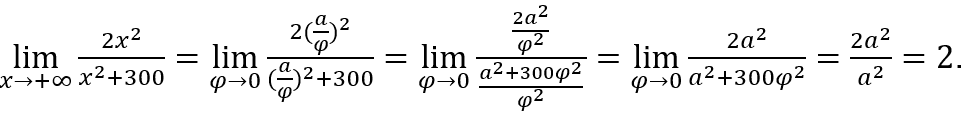
2. Como visto nos diversos exemplos, o “cálculo de limite” apresentado é bastante “fluente” e de aplicação direta, sem a necessidade de consultar teoremas ou de “organizar” a função antes de efetuar o cálculo, exceto quando temos que racionalizar.
Esse fato traz bastante tranquilidade na hora de calcularmos o limite de uma função, pois o “cálculo” apresentado constitui uma verdadeira síntese desse assunto.
Por exemplo, o “cálculo” pode ser utilizado diretamente sobre a função ![]() , sem a necessidade de organizá-la, isto é, de expressá-la como
, sem a necessidade de organizá-la, isto é, de expressá-la como 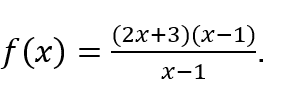
Vejamos. ![]()
Como![]() , podemos fazer, por exemplo,
, podemos fazer, por exemplo, ![]() e
e ![]()
Ficamos com 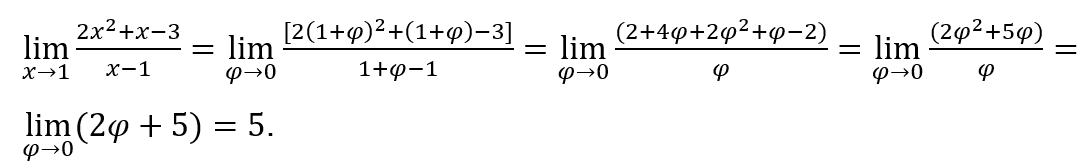
Isso traz uma enorme vantagem em relação à atual apresentação desse assunto que, além de não apresentar nenhum cálculo de limite, se mostra bastante “engessada” pela quantidade imensa de teoremas que devem ser considerados nas “avaliações” dos limites, bem como das “organizações” que devem ser feitas sobre as funções antes de “estimar” o seu limite.
3) Gostaria de acrescentar, ao “cálculo de limite” apresentado, umas avaliações de natureza prática.
a) Só tem sentido calcular o limite de uma função próximo de um valor para o qual ela não esteja definida.
Se a função está definida para certo valor, isto é, se a função existe para certo valor, não tem nenhum sentido calcular o limite próximo desse valor, uma vez que conhecemos quanto vale a função naquele valor.
Por exemplo, seja ![]()
Esta função é definida para todo ![]() , ela existe para todo
, ela existe para todo ![]()
Logo, seria fora de propósito calcularmos, por exemplo, ![]() , uma vez que a função existe para
, uma vez que a função existe para ![]() , isto é, para que calcularmos esse limite se podemos simplesmente substituir
, isto é, para que calcularmos esse limite se podemos simplesmente substituir ![]() por 3 em
por 3 em ![]() e obtermos o valor da função em 3, isto é,
e obtermos o valor da função em 3, isto é, ![]()
Com isto, centenas de exercícios deixam de ter razão de existir.
Obviamente as funções consideradas nesse artigo são de ![]()
b) Por se utilizar do conceito de limite, faremos aqui uma observação sobre continuidade de uma função.
Conforme livro de cálculo de Lethold (1994), a definição de função contínua num ponto assim se traduz:
Dizemos que a função ![]() é contínua no número a se e somente se as seguintes condições forem satisfeitas:
é contínua no número a se e somente se as seguintes condições forem satisfeitas:
(i) ![]() existe;
existe;
(ii) ![]() existe;
existe;
(iii) ![]()
Se uma ou mais de uma dessas condições não forem verificadas em ![]() , a função
, a função![]() será descontínua em
será descontínua em ![]()
Assim Lima (1978) define continuidade de uma função:
Uma função ![]() diz-se contínua no ponto
diz-se contínua no ponto ![]() quando é possível tornar
quando é possível tornar ![]() arbitrariamente próximo de
arbitrariamente próximo de ![]() desde que se tome
desde que se tome ![]() suficientemente próximo de
suficientemente próximo de ![]()
Em termos precisos, diremos que ![]() é contínua no ponto
é contínua no ponto ![]() quando, para todo
quando, para todo ![]() dado arbitrariamente, pudermos achar
dado arbitrariamente, pudermos achar ![]() tal que
tal que ![]() e
e ![]() impliquem
impliquem ![]()
Sabemos que, se uma função está definida num certo intervalo, isto é, se ela existe para todo número contido num certo intervalo, então não há sentido algum em calcularmos o limite dessa função para algum número desse intervalo, uma vez que podemos simplesmente avaliar a função em todo número desse intervalo.
Em termos mais simples: se uma função, representada por apenas uma expressão, por apenas uma sentença, existe para certo número ![]() , então é totalmente desnecessário calcularmos o limite da função para
, então é totalmente desnecessário calcularmos o limite da função para ![]() , uma vez que, simplesmente, podemos calcular o valor da função em
, uma vez que, simplesmente, podemos calcular o valor da função em ![]()
É claro que, se calculássemos esse limite, como fizemos acima, ele seria ![]()
Como foi dito acima, só tem sentido calcular o limite de uma função em torno de um número para o qual ela não esteja definida.
Sendo assim, se estamos analisando funções representadas por apenas uma expressão, dizer que uma função existe para um certo número ![]() , significa dizer que existe o limite dessa função em
, significa dizer que existe o limite dessa função em ![]() sendo esse limite o valor da função em
sendo esse limite o valor da função em ![]() , e com isso não precisamos calcular o limite dessa função nesse número
, e com isso não precisamos calcular o limite dessa função nesse número ![]()
Aplicando isso à definição acima, de função contínua, os itens (ii) e (iii) da definição se tornarão desnecessários, uma vez que no item (i) se afirmar que ![]() existe.
existe.
Logo, para funções representadas por “apenas uma expressão”, a simples afirmação de que ela, a função ![]() , está definida num número
, está definida num número ![]() , isto é, a simples afirmação de que
, isto é, a simples afirmação de que ![]() existe é o suficiente para concluir que a função é contínua naquele número
existe é o suficiente para concluir que a função é contínua naquele número ![]()
Da mesma forma, com essa observação sobre funções contínuas, centenas de exercícios perdem a razão de existir.
Exemplo: seja a função![]() que é definida para todo número real, isto é, existe para todo
que é definida para todo número real, isto é, existe para todo ![]() real.
real.
Com isto, não há necessidade de se calcular o limite de ![]() para nenhum valor de
para nenhum valor de ![]() , pois neste caso, estar definida em
, pois neste caso, estar definida em ![]() é sinônimo de possuir limite em
é sinônimo de possuir limite em ![]() e que esse limite é igual ao valor da função no
e que esse limite é igual ao valor da função no ![]() considerado.
considerado.
Logo a função![]() é contínua para todo
é contínua para todo ![]()
3. CONCLUSÃO
No exposto, mostramos que, realmente, a teoria de limites é deficitária em relação a um cálculo de limite e, por isso, se cerca de uma série de argumentos baseados na definição de limite no intuito de preencher tal lacuna.
Apresentamos, então, o “cálculo de limite de uma função” e mostramos que ele sintetiza todo o assunto mencionado, tendo, por isso, aplicação direta.
Esperamos estar contribuindo para uma melhor compreensão de um assunto tão fundamental em matemática.
REFERÊNCIAS
IEZZI, Gelson; MURAKAMI, Carlos et all. Fundamentos de Matemática Elementar, vol. 8, 1991.
LEITHOLD, Louis. O Cálculo com Geometria Analítica, vol. 1, 1994.
LIMA, Elon Lages. Curso de Análise, vol. 1, 1978.
MUNEM, Mustafa A. e FOULIS, David J. Cálculo, vol. 1, 1982.
[1] Graduação, bacharelado em matemática, pela Universidade de Brasília.
Enviado: Junho, 2021.
Aprovado: Agosto, 2021.