ARTÍCULO ORIGINAL
PEREIRA, Olavo de Carvalho [1]
PEREIRA, Olavo de Carvalho. Limite el cálculo de una función sin usar ![]() y
y ![]() . Revista Científica Multidisciplinar Núcleo do Conhecimento. Año. 06, ed. 08, vol. 04, pág. 05-31. Agosto 2021. ISSN: 2448-0959, Enlace de acceso: https://www.nucleodoconhecimento.com.br/olimpiada-de-matematica/limite-el-calculo, DOI: 10.32749/nucleodoconhecimento.com.br/olimpiada-de-matematica/limite-el-calculo
. Revista Científica Multidisciplinar Núcleo do Conhecimento. Año. 06, ed. 08, vol. 04, pág. 05-31. Agosto 2021. ISSN: 2448-0959, Enlace de acceso: https://www.nucleodoconhecimento.com.br/olimpiada-de-matematica/limite-el-calculo, DOI: 10.32749/nucleodoconhecimento.com.br/olimpiada-de-matematica/limite-el-calculo
RESUMEN
La bibliografía consultada no presenta, en ninguno de los casos analizados, un cálculo del límite de una función, sino que sólo “muestra” que los valores presentados como “límite” satisfacen la definición de límite de una función expresada a través de desigualdades implicando ![]() y
y ![]() , existe, por tanto, un vacío en este tema, que el presente artículo viene a llenar utilizando fundamentalmente el concepto de función definida, así como identificando la expresión “
, existe, por tanto, un vacío en este tema, que el presente artículo viene a llenar utilizando fundamentalmente el concepto de función definida, así como identificando la expresión “ ![]() tiende a un cierto número” con una igualdad correspondiente.
tiende a un cierto número” con una igualdad correspondiente.
Palabras clave: Límite De Una Función, Cálculo De Límites, Límites Laterales, Límites Infinitos, Límites En El Infinito.
1. INTRODUCCIÓN
Este artículo presenta el “cálculo del límite de una función” con el fin de llenar un vacío existente en este tema.
La presentación del cálculo mencionado en la solución de varios límites es el objetivo principal del artículo.
De forma complementaria, pretendemos aclarar la necesidad real de calcular, o no, el límite de una función.
También discutiremos, de manera muy simple, el caso en que una función simple, definida en un cierto número, es continua en ese número.
Aunque la interpretación geométrica siempre es importante, aquí solo tomaremos un enfoque algebraico del “cálculo límite” presentado.
1.1 CÁLCULO DEL LÍMITE DE UNA FUNCIÓN
La definición del límite de una función se presenta en los libros de texto de matemáticas como una estimación.
Por ejemplo: Leithold (1994) presenta la definición de límite de una función de la siguiente manera:
Ser![]() una función definida para cada número en algún intervalo abierto que contiene
una función definida para cada número en algún intervalo abierto que contiene ![]() , excepto posiblemente en el propio número
, excepto posiblemente en el propio número ![]() El límite de
El límite de ![]() cuando
cuando![]() tiende a
tiende a ![]() será
será ![]() , escrito como
, escrito como ![]() si la siguiente afirmación es verdadera:
si la siguiente afirmación es verdadera:
Ya![]() cualquiera, hay un
cualquiera, hay un ![]() , tal que, si
, tal que, si ![]() entonces
entonces![]() .‘‘
.‘‘
La definición anterior establece que los valores de ![]() tienden a un límite
tienden a un límite![]() cuando
cuando![]() tiende a un número
tiende a un número ![]() , si el valor absoluto de la diferencia entre
, si el valor absoluto de la diferencia entre ![]() y
y ![]() puede volverse tan pequeño como queramos, tomando
puede volverse tan pequeño como queramos, tomando![]() lo suficientemente cerca de
lo suficientemente cerca de ![]() , pero no igual a
, pero no igual a ![]() .
.
Lezzi, Murakami y Machado (1991) se expresan de la siguiente manera en la misma definición:
Sea ![]() un intervalo abierto al que pertenece el número real
un intervalo abierto al que pertenece el número real ![]() . Sea
. Sea![]() una función definida para
una función definida para![]() Decimos que el límite de
Decimos que el límite de ![]() , cuando
, cuando![]() tiende a
tiende a ![]() , é
, é ![]() , y escribimos
, y escribimos ![]() si por todo
si por todo![]() , existir
, existir ![]() tal que si
tal que si ![]() então
então ![]() .
.
Munem y Foulis (1982) utilizan la siguiente definición:
Si ![]() es una función y
es una función y ![]() es un número, entiende la notación
es un número, entiende la notación ![]() como “el límite de
como “el límite de ![]() ” cuando
” cuando![]() tende a
tende a ![]() es
es ![]() esto es,
esto es,![]() se acerca al numero
se acerca al numero![]() cuando
cuando ![]() enfoques
enfoques ![]() .
.
Como puede verse en las definiciones anteriores, se presenta un límite ![]() sólo para satisfacer la propia definición.
sólo para satisfacer la propia definición.
En ningún momento se presenta el cálculo de este límite.
Este artículo presenta el “cálculo del límite” de una función que se puede utilizar en todos los casos en los que es necesario realizar tal operación.
Ahora, vamos al argumento.
Para algunas funciones, no definidas en un número determinado, para saber, con la máxima precisión posible, cuál sería su valor en ese número, se acostumbra evaluarlas en valores cercanos a ese número para el que no están definido.
Ejemplo: 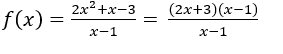 establecer a todos
establecer a todos ![]() excepto
excepto![]() .
.
Si reemplazamos el ![]() por 1, tenemos la indeterminación
por 1, tenemos la indeterminación ![]() .
.
Como la función no está definida, es decir, no existe para el valor 1, evaluamos entonces su valor cercano a 1, ya que nuestro objetivo es conocer el valor de la función, al menos, cercano a 1, ya que no existe para ![]() .
.
Para valores de ![]() , diferente de 1, mayor o menor que 1, pero muy cercano a 1,
, diferente de 1, mayor o menor que 1, pero muy cercano a 1, ![]() , entonces
, entonces![]() será igual a 1, y tendrá valores cercanos a 5, como veremos a continuación:
será igual a 1, y tendrá valores cercanos a 5, como veremos a continuación:
Vamos a asignar a![]() los valores
los valores![]() , es decir, estamos tomando valores de
, es decir, estamos tomando valores de ![]() más y más cerca de 1, pero más pequeños que 1. Los valores de
más y más cerca de 1, pero más pequeños que 1. Los valores de ![]() encontrados son:
encontrados son:
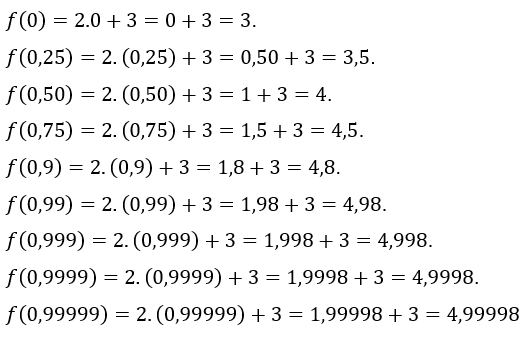
Ahora vamos a asignar el ![]() los valores
los valores![]() ,es decir, estamos tomando valores de
,es decir, estamos tomando valores de ![]() más y más cerca de 1, pero mayor que 1. Los valores de
más y más cerca de 1, pero mayor que 1. Los valores de![]() encontrados son:
encontrados son: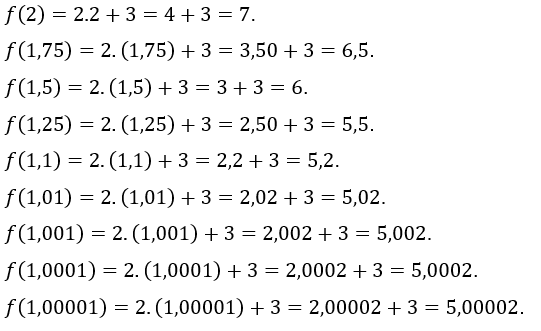
Como puede verse, en ambos casos, como ![]() enfoques 1,
enfoques 1, ![]() se acerca a 5, lo que nos lleva a creer que este es el límite de
se acerca a 5, lo que nos lleva a creer que este es el límite de ![]() .
.
Sin embargo, aquí no se hizo ningún “cálculo” límite, sino sólo una evaluación de![]() , cuando
, cuando ![]() toma valores muy cercanos a 1.
toma valores muy cercanos a 1.
Entonces, el valor 5 es “candidato” a ser el límite que aún necesitamos calcular.
Los autores consultados estructuran la definición de límite en términos de desigualdades a partir de ejemplos como este y asumen el valor estimado, en este caso 5, como realmente el límite de la función.
En este sentido, afirman que ![]() , porque para cualquier
, porque para cualquier![]() ,por pequeño que sea, hay un
,por pequeño que sea, hay un ![]() , tal que si
, tal que si ![]() entonces
entonces![]() .
.
La definición de límite dada al principio, que no tiene cálculo de límite, se usa para “probar” que números dados, sin indicación de dónde fueron tomados, son límites de funciones.
Mostraremos que la definición de límite no prueba, no demuestra, que un número dado sea el límite de una función, sino que sólo “muestra” que el número proporcionado es el límite.
Usemos un ejemplo para aclarar la diferencia entre un “espectáculo” y una “demostración”.
- Demostrar que 2 es la raíz de la ecuación
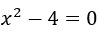 .
.
Esto significa que si reemplazamos el ![]() por 2, tendremos cero como resultado de la ecuación.
por 2, tendremos cero como resultado de la ecuación.
Veamos![]() .
.
Este fue un ejemplo de “demostración”, es decir, solo se mostró algo, no se demostró nada, no se calculó nada, solo se reemplazó el valor proporcionado.
Es diferente cuando dices: prueba que 2 es una raíz, es una solución de la ecuación ![]() .
.
En ese caso, tenemos que calcular, resolver la ecuación y ver si obtenemos ![]() .
.
Bueno, resolviendo tenemos: ![]() , luego
, luego ![]() ,y sacando la raíz cuadrada en ambos lados tenemos:
,y sacando la raíz cuadrada en ambos lados tenemos:![]() , esto es,
, esto es, ![]() o
o![]() .
.
Entonces uno de los valores de![]() realmente es 2.
realmente es 2.
Con esto se “demostró” que 2 es realmente la raíz de la ecuación![]() .
.
Veremos, en los ejemplos dados a continuación, que no hay prueba, sino solo una “muestra” de que el número dado es el límite de la función dada.
Ejemplo. Use la definición de límite para “probar” que ![]() .
.
Aquí no se dice cómo se llegó a la conclusión de que el límite es 5, ni se dice de dónde se tomó ese número.
Discutiremos, en términos generales, la solución presentada en los libros consultados:
El primer requisito de la definición es que![]() definirse en cada número de algún intervalo abierto que contenga 3, excepto posiblemente en 3. Como
definirse en cada número de algún intervalo abierto que contenga 3, excepto posiblemente en 3. Como ![]() está definido para todos los números reales, cualquier intervalo abierto que contenga 3 satisfará este requisito. Tenemos que mostrar ahora que para todos
está definido para todos los números reales, cualquier intervalo abierto que contenga 3 satisfará este requisito. Tenemos que mostrar ahora que para todos ![]() existe uno
existe uno ![]() , tal que si
, tal que si ![]() então
então ![]() tenemos que
tenemos que ![]() , luego
, luego ![]() y
y ![]()
Tenemos entonces, ![]() e
e ![]()
Esta declaración indica que![]() es un delta satisfactorio.
es un delta satisfactorio.
Con esta elección de ![]() tenemos el siguiente argumento:
tenemos el siguiente argumento:![]() , entonces
, entonces![]() , entonces
, entonces![]() entonces
entonces![]() entonces
entonces![]() , entonces
, entonces ![]()
Esto simplemente “muestra”, a partir de la definición de límite, que ![]()
Como hemos visto, no había demostración, sino sólo un “show”, ya que, dado el número 5, simplemente lo sustituíamos y la función dada, en la definición del límite de una función.
Vayamos a un ejemplo más: usa la definición para “probar” que ![]() .
.
De nuevo, se da un número, en este caso el 4, como límite, pero no se dice de dónde se tomó este número.
Aquí está la solución, en términos generales:
Como ![]() está definido para todos los números reales, cualquier intervalo abierto que contenga 2 satisfará el primer requisito de la definición.
está definido para todos los números reales, cualquier intervalo abierto que contenga 2 satisfará el primer requisito de la definición.
Tenemos que demostrar que para todos ![]() , existe uno
, existe uno ![]() , tal que
, tal que
Si ![]() então
então ![]()
Luego ![]() então
então ![]()
Tenemos que poner una restricción a ![]() que nos da una desigualdad que implica
que nos da una desigualdad que implica ![]() . Tal restricción se hace para seleccionar el intervalo abierto requerido por la definición. Elegimos la gama
. Tal restricción se hace para seleccionar el intervalo abierto requerido por la definición. Elegimos la gama ![]() y esto implica que
y esto implica que ![]() . Entonces
. Entonces![]() y
y ![]() , entonces
, entonces![]() entonces
entonces![]() entonces
entonces![]() . Entonces
. Entonces![]() .
.
Ahora tenemos ![]() y
y ![]() , entonces
, entonces![]() como nuestro objetivo es conseguir
como nuestro objetivo es conseguir![]() , debemos exigir
, debemos exigir ![]() Con este
Con este 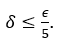
Usando esto![]() hemos completado la llamada “prueba”.
hemos completado la llamada “prueba”.
Como vimos anteriormente, de nuevo no se probó nada, sino solo que el número dado como límite, en este caso 4, satisface la definición de límite.
No hubo ningún cálculo que mostrara que el número 4 es realmente el límite.
A partir de aquí, presentaremos el cálculo límite de una función.
Antes de presentar el “cálculo” en sí, evaluemos ![]() en los mismos valores de
en los mismos valores de![]() dado anteriormente, pero considerándolos como compuestos del número 1.
dado anteriormente, pero considerándolos como compuestos del número 1.
Esto mostrará, en términos generales, el razonamiento utilizado para calcular el límite de la función.
la funcion es ![]() , válido para todos
, válido para todos![]() .
.
Para ![]() o
o ![]() , tenemos que
, tenemos que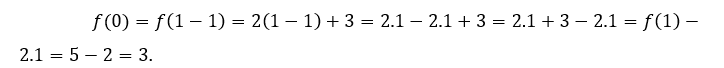
Para ![]() o
o ![]() , tenemos que
, tenemos que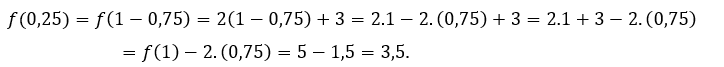
Para ![]() o
o ![]() tenemos que
tenemos que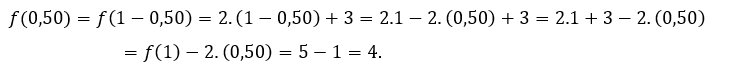
Para ![]() o
o ![]() tenemos que
tenemos que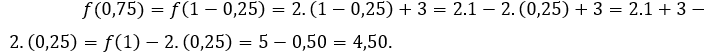 Para
Para ![]() o
o ![]() , tenemos que
, tenemos que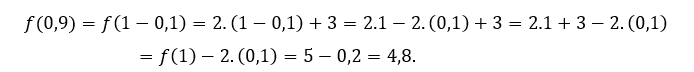
Para ![]() o
o ![]() , tenemos que
, tenemos que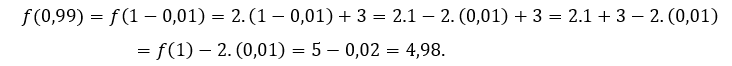
Para ![]() o
o ![]() tenemos que
tenemos que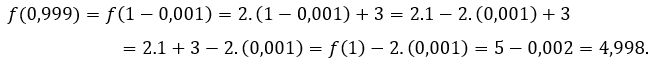
Para ![]() o
o ![]() , tenemos que
, tenemos que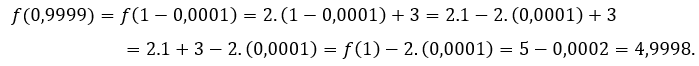
Para ![]() o
o ![]() , tenemos que
, tenemos que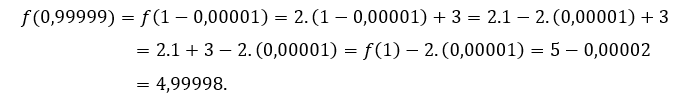
Probamos algunos valores de![]() menos que 1.
menos que 1.
Ahora evaluaremos ![]() en valores mayores a 1 pero cercanos a 1.
en valores mayores a 1 pero cercanos a 1.
Para ![]() o
o ![]() , tenemos que
, tenemos que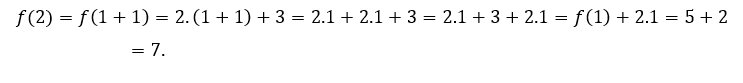
Para ![]() o
o ![]() tenemos que
tenemos que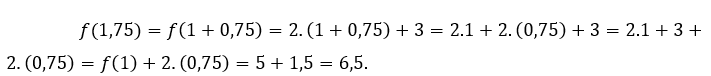
Para ![]() o
o ![]() tenemos que
tenemos que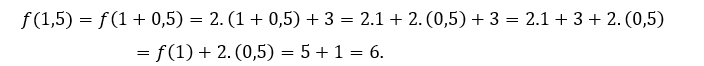
Para ![]() o
o ![]() tenemos que
tenemos que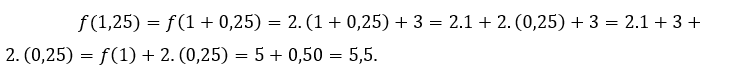
Para ![]() o
o ![]() tenemos que
tenemos que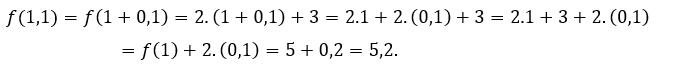
Para ![]() o
o ![]() tenemos que
tenemos que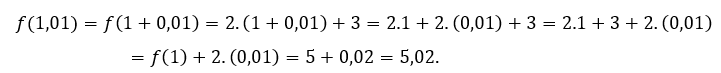
Para ![]() o
o ![]() , tenemos que
, tenemos que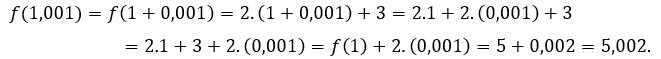
Para ![]() o
o ![]() , tenemos que
, tenemos que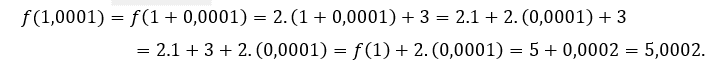
Para ![]() o
o ![]() , tenemos que
, tenemos que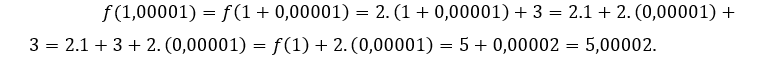
De lo anterior, nos damos cuenta de que cuanto más![]() se aproxima a 1, más
se aproxima a 1, más![]() tiende a 5, es decir, cuando
tiende a 5, es decir, cuando ![]() tiende a 1,
tiende a 1, ![]() tienden a 1,
tienden a 1,
Observamos en los cálculos anteriores, en todos los valores asignados a ![]() , la aparición de una constante
, la aparición de una constante ![]() al que se le sumaba o restaba un valor, que tendía a cero, como
al que se le sumaba o restaba un valor, que tendía a cero, como ![]() se acercaba a la 1.
se acercaba a la 1.
Esta constante es, por tanto, una “candidata” a ser el “límite” mencionado anteriormente, es decir, hay un indicio de que podemos tener ![]() .
.
Ahora expresaremos la situación anterior de una manera semigenérica para presentar el “cálculo del límite” en sí.
La expresion “![]() tiende a 1″, representado por
tiende a 1″, representado por ![]() ,es equivalente a
,es equivalente a ![]() , o
, o ![]() , cuando
, cuando ![]() tiende a cero,
tiende a cero, ![]() , e
, e ![]() .
.
Con esto, la expresión ![]() , reemplazando
, reemplazando ![]() por
por ![]() o
o ![]() , es equivalente a
, es equivalente a![]() , o
, o![]() , esto es,
, esto es,![]() , o
, o ![]() .
.
A partir de la igualdad anterior, es posible “calcular” el valor del límite de![]() cuando
cuando ![]() tiende a 1, ya que basta con calcular el valor de
tiende a 1, ya que basta con calcular el valor de ![]() , o
, o ![]() .
.
Ahora haremos, usando la misma función que antes, el cálculo para![]() , cuando
, cuando ![]() .
.
De esta forma, nos quedamos con:
![]() entonces
entonces![]() a pesar de
a pesar de![]() , y
, y ![]() tiende a cero cuando
tiende a cero cuando ![]() , es decir, es tan pequeño que se aproxima a cero tanto como queramos.
, es decir, es tan pequeño que se aproxima a cero tanto como queramos.
El calculo de ![]() , esto es,
, esto es, ![]() , es análoga y produce el mismo resultado.
, es análoga y produce el mismo resultado.
Veamos:![]()
Calcularemos ahora una serie de límites de funciones, para ejemplificar la aplicación del mencionado “cálculo”.
- Calculemos
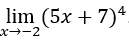 .
.
Cómo![]() , podemos hacer, por ejemplo,
, podemos hacer, por ejemplo, ![]() ,
, ![]() y
y ![]() .
.
Quédamonos con ![]()
![]() términos en
términos en ![]() que todo tiende a cero. Entonces el resultado será
que todo tiende a cero. Entonces el resultado será![]() .
.
- Calculemos
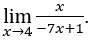
Cómo ![]() , podemos hacer, por ejemplo,
, podemos hacer, por ejemplo,![]() ,
, ![]() y
y ![]() .
.
Quédamonos con
![]() , porque el numerador tiende a 4 y el denominador tiende a
, porque el numerador tiende a 4 y el denominador tiende a ![]() .
.
- Calculemos
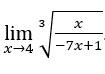 .
.
Como vimos arriba, al final nos quedaremos con
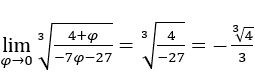
- Calculemos
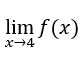 conforme abajo.
conforme abajo.
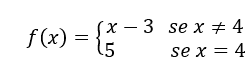 .
.
Debemos calcular![]() ,porque pase lo que pase
,porque pase lo que pase![]() cuando
cuando ![]() .
.
Cómo ![]() , podemos hacer, por ejemplo,
, podemos hacer, por ejemplo, ![]() ,
, ![]() y
y ![]() .
.
Quédamonos con ![]() , entonces
, entonces![]() .
.
Sea ![]() , establecer a todos
, establecer a todos ![]() , excepto
, excepto ![]() .
.
Consideremos ![]() esto es,
esto es, ![]() , para el cual
, para el cual ![]() reduce a
reduce a![]() .
.
- Calculemos el
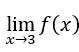 . Tenemos que
. Tenemos que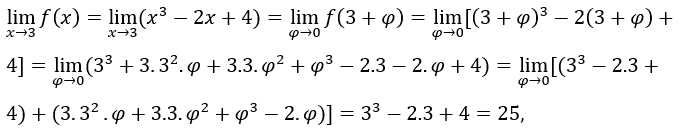 una vez cuando
una vez cuando 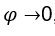 la expresion
la expresion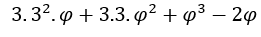 tiende a cero.
tiende a cero.
Entonces
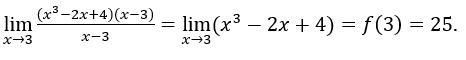
Ahora consideremos el siguiente ejemplo: ![]() , establecer a todos
, establecer a todos ![]() , y calcule su límite cuando
, y calcule su límite cuando![]() tiende a 2.
tiende a 2.
Para ![]() condición de existencia de la función,
condición de existencia de la función, ![]() , y cuando
, y cuando ![]() podemos hacer, por ejemplo,
podemos hacer, por ejemplo, ![]() , con
, con![]()
![]() y tendremos que calcular el limite
y tendremos que calcular el limite![]() .
.
Cómo ![]() , la expresion
, la expresion ![]() tiende a
tiende a ![]() , y el límite será entonces,
, y el límite será entonces, ![]() .
.
En conclusión, nos quedamos con: ![]() .
.
Observación.
Podríamos haber aplicado “cálculo” directamente a la función, sin dividir primero el factor común al numerador y al denominador.
Veamos ![]()
De hecho, podemos aplicar el “cálculo” directamente sobre la función, sin antes hacer una “preparación” sobre ella.
Ahora daremos algunos ejemplos de cálculo de límites que involucran funciones trigonométricas y exponenciales para ejemplificar el consolidado anterior.
Consideremos la función ![]() , establecer a todos
, establecer a todos ![]() , excepto
, excepto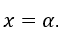
Recordando: ![]() significa, por ejemplo, que
significa, por ejemplo, que![]() , donde
, donde ![]() ,
, ![]() .
.
Sustituyendo este valor de x en la ecuación original anterior, tenemos: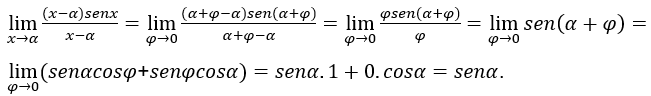
Entonces, ![]() y
y ![]() son independientes de
son independientes de![]() e o
e o![]() , mientras que la
, mientras que la ![]() .
.
Outro exemplo: consideremos a função ![]() establecer a todos
establecer a todos ![]() , expceto
, expceto ![]() .
.
- Calculemos el
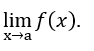
- Haciendo la sustitución
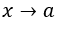 para, por ejemplo,
para, por ejemplo, 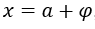 , con
, con 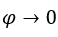 ,
, 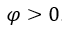 . Tenemos:
. Tenemos: 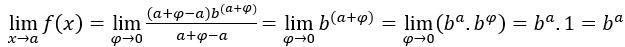 , porque el
, porque el 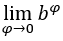 é 1 e
é 1 e 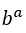 a pesar de
a pesar de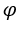 .
.
Ahora calculemos el límite de las funciones dadas al principio para confirmar los valores de los límites dados.
- Calculemos
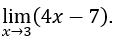
Cómo ![]() , podemos hacer, por ejemplo,
, podemos hacer, por ejemplo, ![]() ,
, ![]() y
y ![]() y nos quedamos
y nos quedamos![]()
- Calculemos
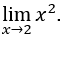
Cómo ![]() , podemos hacer, por ejemplo,
, podemos hacer, por ejemplo, ![]() ,
, ![]() y
y ![]() y nos quedamos
y nos quedamos![]()
Como se puede ver en los “cálculos” anteriores, los límites dados en los ejemplos anteriores eran correctos.
Demostraremos solo un teorema sobre los límites para ejemplificar el cálculo que se muestra aquí.
Teorema. Si ![]() e
e ![]() son constantes cualesquiera, entonces
son constantes cualesquiera, entonces ![]() .
.
Simplemente calcule el límite haciendo, por ejemplo,![]()
![]() y
y ![]()
Quédamonos con:![]() , entonces
, entonces![]() tiende a cero, ya que
tiende a cero, ya que ![]() tiende a cero.
tiende a cero.
Hay una inmensa sencillez en el “cálculo” presentado.
En este caso, no hay duda de que el límite es![]() .
.
Ahora usaremos el “cálculo de límites” presentado para calcular los límites de las funciones en varias circunstancias.
- Calculemos
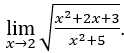
Cómo ![]() , para que podamos hacer, por ejemplo,
, para que podamos hacer, por ejemplo, ![]() ,
, ![]() y
y ![]()
Quédamonos con 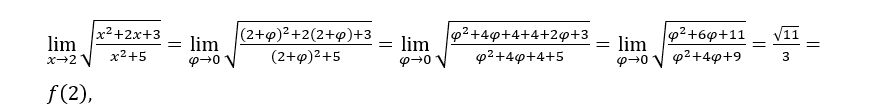 una vez que
una vez que ![]() tiende a 11 y
tiende a 11 y ![]() tiende a 9.
tiende a 9.
- Calculemos
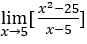 .
.
Cómo x → 5, por lo que podemos hacer, por ejemplo, ![]() ,
, ![]() y
y ![]()
Quédamonos con![]()
Se observa que no fue necesario “preparar” la función para aplicar el “cálculo”, es decir, no fue necesario escribir la función como ![]() y, finalmente, cómo
y, finalmente, cómo ![]()
- Calculemos
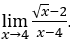 .
.
En los casos de radicales, a los que se suma o resta un número real, cuando la sustitución directa del valor de ![]() conduce a la indeterminación
conduce a la indeterminación ![]() tenemos que preparar la ecuación, porque la aplicación directa del “cálculo” no deshace la indeterminación, como veremos a continuación.
tenemos que preparar la ecuación, porque la aplicación directa del “cálculo” no deshace la indeterminación, como veremos a continuación.
Lo que pasa en este caso es que hay un factor común tanto al numerador como al denominador, pero eso solo se expresa cuando dividimos, o el numerador por el denominador, o el denominador por el numerador.
Esto actualmente se traduce en matemáticas como racionalización.
Veamos en el ejemplo anterior: si dividimos el denominador por el numerador, ya que el exponente de ![]() en el denominador es 1 y el exponente de
en el denominador es 1 y el exponente de ![]() en el numerador es menor, es decir, vale
en el numerador es menor, es decir, vale![]() tenemos:
tenemos: ![]() y sustituyendo tendremos
y sustituyendo tendremos 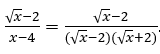 .
.
Por lo tanto, podemos expresar el factor común al numerador y al denominador.
La otra forma es dividir el numerador por el denominador, pero en este caso debemos hacer lo mismo es la racionalización, ya que el exponente de ![]() en el numerador es menor que el exponente de
en el numerador es menor que el exponente de ![]() denominador, y por lo tanto necesita ser multiplicado por un factor en
denominador, y por lo tanto necesita ser multiplicado por un factor en ![]() hacer su exponente al menos igual al exponente del denominador.
hacer su exponente al menos igual al exponente del denominador.
Esta es la famosa racionalización que hacemos.
Primero haremos el cálculo, sin preparación.
Cómo ![]() , podemos hacer, por ejemplo,
, podemos hacer, por ejemplo, ![]() ,
,![]() y
y![]() .
.
Quédamonos con![]() Observamos la necesidad de racionalizar, ya que el límite aún no está determinado cuando
Observamos la necesidad de racionalizar, ya que el límite aún no está determinado cuando ![]() en el numerador y denominador, tendiendo a
en el numerador y denominador, tendiendo a ![]()
Luego multiplicaremos y dividiremos por![]() , y estaremos con
, y estaremos con![]()
Ahora haremos el cálculo, preparando la función antes de aplicarla.
![]() .
.
Cómo la sustitución directa de 4 conduce a la indeterminación![]() significa que el numerador y el denominador tienen como factor común
significa que el numerador y el denominador tienen como factor común ![]() ou
ou ![]()
En este caso, al tratarse de un radical menos un número real, la forma que se utiliza para “liberar” el factor común es a través de la racionalización.
Antes de calcular el límite, multiplicaremos y dividiremos el numerador y el denominador de la función por ![]()
Quédamonos con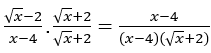 . En esta función, ya podemos aplicar el cálculo. Veamos:
. En esta función, ya podemos aplicar el cálculo. Veamos: ![]()
Cómo ![]() podemos hacer, por ejemplo,
podemos hacer, por ejemplo, ![]() ,
, ![]() y
y ![]()
Quédamonos con ![]()
1.2 LIMITES LATERAIS
En los casos en que se define una función para cada número real excepto un número real![]() , cuando calculamos su límite con la variable independiente que tiende a
, cuando calculamos su límite con la variable independiente que tiende a ![]() , como en los ejemplos dados arriba, no importa si usamos
, como en los ejemplos dados arriba, no importa si usamos![]() cuánto
cuánto ![]() ,
, ![]() y
y ![]() , ya que está configurado para todos los números a la izquierda y a la derecha de
, ya que está configurado para todos los números a la izquierda y a la derecha de ![]() .
.
Y, por supuesto, esta no es una función de oración.
Cuando una función no está definida a la izquierda o a la derecha de un número ![]() y tenemos que calcular su límite con
y tenemos que calcular su límite con ![]() tendiendo a, debemos usar el valor de
tendiendo a, debemos usar el valor de![]() según el caso puede ser.
según el caso puede ser.
Cuando ![]() y lo hacemos
y lo hacemos ![]() o
o ![]() ,
, ![]() y
y ![]() , entonces
, entonces![]() indica que
indica que ![]() se acerca
se acerca![]() para valores mayores que
para valores mayores que ![]() , y por lo tanto se acerca
, y por lo tanto se acerca![]() a la derecha.
a la derecha.
El cálculo realizado con ![]() es, por tanto, el límite cuando
es, por tanto, el límite cuando ![]() tiende a
tiende a ![]() a la derecha.
a la derecha.
Es, por tanto, el límite de la derecha.
Usamos ![]() para calcular el límite izquierdo.
para calcular el límite izquierdo.
Sabemos que el límite existe solo cuando los límites unilaterales existen y son iguales.
- Calculemos
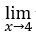 √x – 4.
√x – 4.
Sabemos que la función existe sólo para ![]() , esto es,
, esto es, ![]()
Por tanto, no hay límite por la izquierda y, por tanto, el límite en cuestión no existe.
Pero existe el límite de la mano derecha que se puede calcular sustituyendo![]() por
por![]() ,
, ![]() y
y ![]()
![]()
- Calculemos los límites unilaterales.
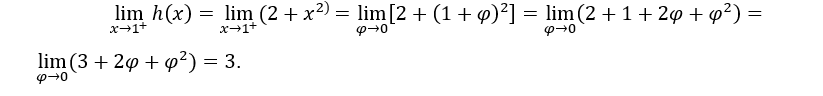
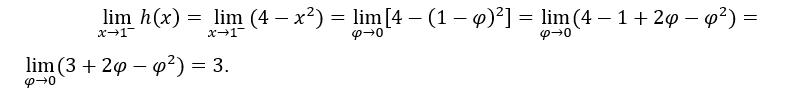
como son iguales,![]()
En el cálculo anterior, hicimos ![]() ,para calcular el límite derecho y
,para calcular el límite derecho y ![]() para calcular el límite izquierdo.
para calcular el límite izquierdo.
Calculamos el límite de ![]() definido por
definido por
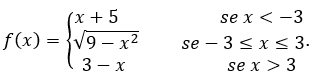
- Calculemos
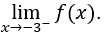
Entonces debemos calcular![]()
entonces haremos ![]() ,
, ![]() y
y ![]()
- Calculemos
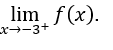
Entonces debemos calcular![]()
Lo haremos entonces, ![]() ,
, ![]() y
y ![]()
Quédamonos con
![]()
- Calculemos
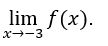
Cómo ![]() entonces
entonces ![]() no existe.
no existe.
- Calculemos
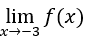 .
.
Entonces debemos calcular,![]()
Lo haremos entonces, ![]() ,
, ![]() y
y ![]()
Quédamonos con
![]()
- Calculemos
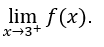
Entonces debemos calcular, ![]()
lo haremos entonces, ![]() ,
, ![]() y
y ![]()
Quédamonos con
![]()
- Calculemos
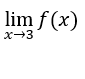
Cómo ![]() , entonces
, entonces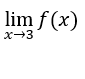 existe y es igual a cero.
existe y es igual a cero.
1.3 LIMITES INFINITOS
Aquellos cuyos valores funcionales aumentan o disminuyen sin limitación, cuando la variable independiente se acerca cada vez más a un número fijo, pueden ser resueltos igualmente por el “cálculo” de límite aquí presentado, con la ventaja de no tener que preocuparse por teoremas.
Antes de aplicar el “cálculo”, recordemos las siguientes situaciones:
![]()
- Calculemos el siguiente límite
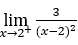 .
.
Cómo ![]() ,debemos hacer
,debemos hacer ![]() ,
, ![]() y
y ![]()
Quédamonos con ![]() .
.
- Calculemos ahora
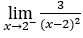 .
.
Cómo ![]() , debemos hacer
, debemos hacer ![]() ,
, ![]() y
y ![]()
Quédamonos con ![]() .
.
- Calculemos
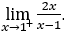 .
.
Cómo ![]() , debemos hacer
, debemos hacer ![]() ,
, ![]() y
y ![]()
Quédamonos con ![]() , porque el numerador tiende a 2, mientras que el denominador tiende a cero a través de valores positivos.
, porque el numerador tiende a 2, mientras que el denominador tiende a cero a través de valores positivos.
- Calculemos ahora
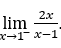 .
.
Cómo ![]() , debemos hacer
, debemos hacer ![]() ,
, ![]() y
y ![]()
Quédamonos con ![]() , porque el numerador tiende a 2 y el denominador tiende a cero a través de valores negativos.
, porque el numerador tiende a 2 y el denominador tiende a cero a través de valores negativos.
- Calculemos
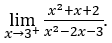
Cómo ![]() , debemos hacer
, debemos hacer ![]() ,
, ![]() y
y ![]()
Quédamonos con 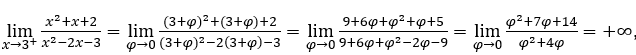 porque el numerador tiende a 14, mientras que el denominador tiende a cero para valores positivos.
porque el numerador tiende a 14, mientras que el denominador tiende a cero para valores positivos.
- Calculemos ahora
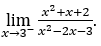
Cómo ![]() , debemos hacer
, debemos hacer ![]() ,
, ![]() y
y ![]()
Quédamonos con![]() , ya que el numerador tiende a 14, mientras que el denominador tiende a cero para valores negativos, ya que
, ya que el numerador tiende a 14, mientras que el denominador tiende a cero para valores negativos, ya que ![]() tiende a cero siempre para valores positivos.
tiende a cero siempre para valores positivos.
En este caso el denominador es ![]() siempre que
siempre que![]() , y cómo
, y cómo ![]() , el denominador es siempre negativo.
, el denominador es siempre negativo.
- Calculemos
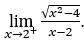 .
.
Cómo ![]() , debemos hacer
, debemos hacer ![]() ,
, ![]() y
y ![]()
Quédamonos con 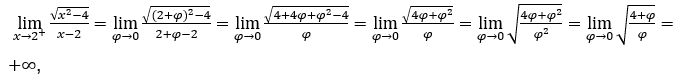 porque el numerador tiende a 2 y el denominador tiende a cero para valores positivos.
porque el numerador tiende a 2 y el denominador tiende a cero para valores positivos.
- Calculemos
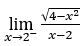
Cómo ![]() , debemos hacer
, debemos hacer ![]() ,
, ![]()
y ![]()
Quédamonos con 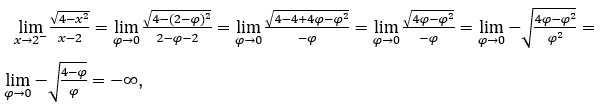 , porque el numerador tiende a 2 y el denominador tiende a cero para valores positivos.
, porque el numerador tiende a 2 y el denominador tiende a cero para valores positivos.
En estos dos casos, pudimos ![]() en el radical porque siempre es positivo.
en el radical porque siempre es positivo.
- Calculemos
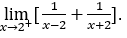 .
.
Cómo ![]() , debemos hacer
, debemos hacer ![]() ,
, ![]() y
y ![]()
Quédamonos con ![]() porque el numerador tiende a 4, mientras que el denominador tiende a cero para valores positivos.
porque el numerador tiende a 4, mientras que el denominador tiende a cero para valores positivos.
Nota Podríamos haber sustituido directamente el valor de ![]() en la ecuación original.
en la ecuación original.
- Calculemos
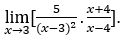
Cómo ![]() , debemos hacer
, debemos hacer ![]() ,
, ![]() y
y ![]()
Quédamonos con ![]() , porque el numerador tiende a 35, mientras que el denominador tiende a cero para valores negativos, ya que es negativo para < 1.
, porque el numerador tiende a 35, mientras que el denominador tiende a cero para valores negativos, ya que es negativo para < 1.
- Calculemos
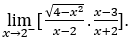
Cómo ![]() , nosotros lo haremos
, nosotros lo haremos ![]() ,
, ![]() y
y ![]()
Quédamonos con 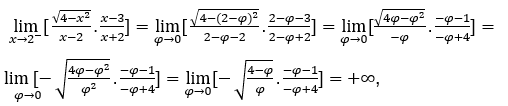 , porque el numerador tiende a
, porque el numerador tiende a![]() y el denominador tiende a
y el denominador tiende a ![]() por valores positivos.
por valores positivos.
1.4 LÍMITES AL INFINITO
Al igual que para los límites mencionados hasta ahora, la literatura consultada tampoco presenta un cálculo de límites en el infinito, sino que solo evalúa la función cuando la variable independiente crece o decrece indefinidamente.
El resultado de la evaluación se utiliza como umbral.
Veamos.
Dada la función 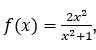 , atribuimos a
, atribuimos a![]() los valores
los valores![]() y así sucesivamente, permitiéndole crecer indefinidamente. Los valores funcionales correspondientes serán
y así sucesivamente, permitiéndole crecer indefinidamente. Los valores funcionales correspondientes serán
![]()
Observamos que cuando![]() crece, tomando valores positivos, los valores funcionales se acercan a 2.
crece, tomando valores positivos, los valores funcionales se acercan a 2.
Cuando una variable independiente ![]() crece indefinidamente, a través de valores positivos, escribimos
crece indefinidamente, a través de valores positivos, escribimos![]() el ejemplo dado, se llegó a la conclusión de que
el ejemplo dado, se llegó a la conclusión de que 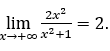
Como se vio anteriormente, del ejemplo dado, no se presentó ningún cálculo de límite de la función, pero solo se observó que, como ![]() aumentada, en valores positivos, la función se acercaba a 2.
aumentada, en valores positivos, la función se acercaba a 2.
Este valor 2 se usó luego como el límite de la función.
Presentaremos, a continuación, el “cálculo” de límite de funciones cuando el variable independiente tiende a![]() o el
o el ![]()
En los casos en que ![]() ,nosotros lo haremos
,nosotros lo haremos ![]() y
y ![]() ,porque, como vimos anteriormente, cuando
,porque, como vimos anteriormente, cuando ![]() tiende a cero para valores positivos,
tiende a cero para valores positivos, ![]() tiende a
tiende a ![]() , y, con eso,
, y, con eso, ![]() tiende a
tiende a ![]()
En los casos en que ![]() , nosotros lo haremos
, nosotros lo haremos 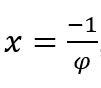
![]() y
y ![]() , porque, como vimos arriba, cuando
, porque, como vimos arriba, cuando ![]() tiende a cero para valores positivos
tiende a cero para valores positivos![]() ,
,![]() tiende a, y con eso,
tiende a, y con eso, ![]() tiende a
tiende a![]() .
.
- Calculemos
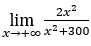 .
.
Cómo ![]() , haremos
, haremos 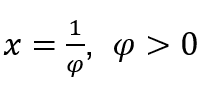 y
y ![]()
Quédamonos con ![]() porque el numerador tiende a 2 y el denominador tiende a 1.
porque el numerador tiende a 2 y el denominador tiende a 1.
- Calculemos
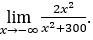 .
.
Cómo ![]() , haremos
, haremos ![]() y
y ![]()
Quédamonos con 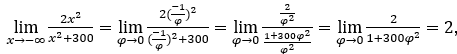 ,porque el numerador tiende a 2 y el denominador tiende a 1.
,porque el numerador tiende a 2 y el denominador tiende a 1.
- Calculemos
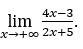
Cómo ![]() , haremos
, haremos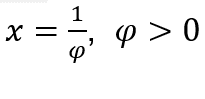 y
y ![]()
Quédamonos con 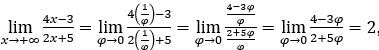 , porque el numerador tiende a 4 y el denominador tiende a 2.
, porque el numerador tiende a 4 y el denominador tiende a 2.
- Calculemos
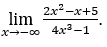
Cómo ![]() , haremos
, haremos![]()
![]() y
y ![]()
Quédamonos con 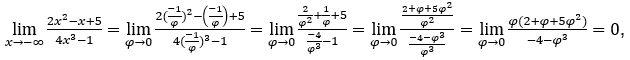 porque el numerador tiende a cero y el denominador tiende a -4.
porque el numerador tiende a cero y el denominador tiende a -4.
- Calculemos

Cómo ![]() , haremos
, haremos ![]() y
y ![]()
Quédamonos con 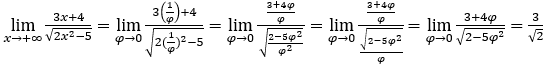 , porque el numerador tiende a 3 y el denominador tiende a
, porque el numerador tiende a 3 y el denominador tiende a ![]()
- Calculemos
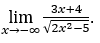
Cómo ![]() , haremos
, haremos ![]()
![]() y
y ![]()
Quédamonos con 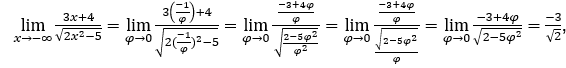 , porque el numerador tiende a -3 y el denominador tiende a √2.
, porque el numerador tiende a -3 y el denominador tiende a √2.
- Calculemos
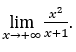
Cómo![]() , haremos
, haremos ![]() y
y ![]()
Quédamonos con 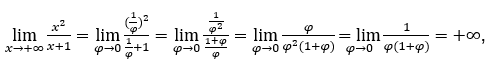 porque el numerador es 1 y el denominador tiende a cero para valores positivos.
porque el numerador es 1 y el denominador tiende a cero para valores positivos.
- Calculemos
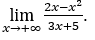
Cómo ![]() , haremos
, haremos ![]() =
= ![]() φ > 0 y φ → 0.
φ > 0 y φ → 0.
Quédamonos con 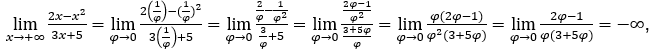 porque el numerador tiende a -1 y el denominador tiende a cero para valores positivos.
porque el numerador tiende a -1 y el denominador tiende a cero para valores positivos.
- Calculemos
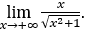
Cómo ![]() , haremos
, haremos ![]() y
y ![]()
Quédamonos con 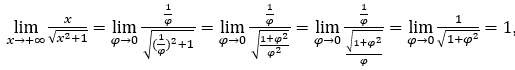 porque el numerador es 1 y el denominador tiende a 1.
porque el numerador es 1 y el denominador tiende a 1.
- Calculemos ahora
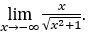
Cómo ![]() , haremos
, haremos ![]() y
y ![]()
Quédamonos con 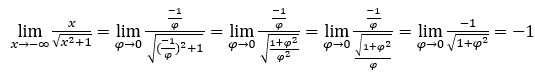 , porque el numerador es -1 y el denominador tiende a 1.
, porque el numerador es -1 y el denominador tiende a 1.
- Calculemos
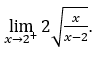
Cómo ![]() , debemos hacer
, debemos hacer ![]() ,
, ![]()
Quédamonos con 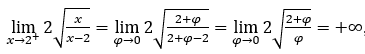 , porque el numerador tiende a
, porque el numerador tiende a ![]() y el denominador tiende a cero para valores positivos.
y el denominador tiende a cero para valores positivos.
- Calculemos ahora
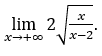
Cómo ![]() , haremos
, haremos ![]() e
e ![]()
Quédamonos con 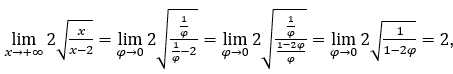 porque el numerador tiende a 2 y el denominador tiende a 1.
porque el numerador tiende a 2 y el denominador tiende a 1.
Observación.
El cálculo de límites en el infinito no se puede aplicar, por ejemplo, a funciones trigonométricas, ya que algunas varían en un intervalo determinado, y otras aumentan o disminuyen indefinidamente, según el valor considerado.
Por ejemplo, si tratamos de calcular el![]() , recorreríamos todos los valores del rango infinitas veces
, recorreríamos todos los valores del rango infinitas veces![]() , porque, por todo
, porque, por todo![]() ,
, ![]() , es decir, no llegaríamos a ningún valor definido.
, es decir, no llegaríamos a ningún valor definido.
De hecho, las funciones polinómicas, o funciones expresadas por cocientes entre polinomios, son las más adecuadas para aplicar límites.
2. OBSERVACIÓN
1) El cálculo del límite presentado surgió de la identificación de la expresión![]() tiende a un cierto número
tiende a un cierto número ![]() con igualdad
con igualdad ![]() , o
, o ![]() , con
, con![]() e
e ![]() , desde, realmente, cuando
, desde, realmente, cuando![]() ,
, ![]() y
y ![]() tiende a
tiende a ![]() y con eso,
y con eso, ![]() tiende a
tiende a ![]()
En el caso de límites en el infinito, la sustitución de la expresión ![]() tiende a
tiende a ![]() él era
él era ![]() , y la sustitución de la expresión
, y la sustitución de la expresión![]() tiende a
tiende a ![]() foi
foi ![]() , con
, con ![]() y
y ![]()
La sustitución tiene más sentido, porque, en realidad, cuando![]() , siempre por valores positivos,
, siempre por valores positivos,![]() tiende
tiende ![]() y
y ![]() tiende a
tiende a ![]() , haciendo que
, haciendo que ![]() tienda realmente a
tienda realmente a ![]() o
o ![]() , según el caso puede ser.
, según el caso puede ser.
Si sustituimos, en el caso de que![]() tiende a
tiende a![]() o
o ![]() o
o ![]() por,
por, ![]() o
o ![]() y
y ![]() , el resultado seria el mismo.
, el resultado seria el mismo.
Un ejemplo.
- Calculemos
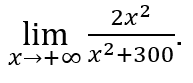
Haremos ![]() e
e ![]()
Quédamonos con
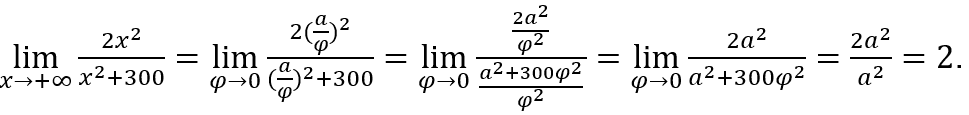
2. Como se ve en los distintos ejemplos, el “cálculo límite” presentado es bastante “fluido” y de aplicación directa, sin necesidad de consultar teoremas ni de “organizar” la función antes de realizar el cálculo, salvo cuando tengamos que racionalizar.
Este hecho trae mucha tranquilidad a la hora de calcular el límite de una función, ya que el “cálculo” presentado es una verdadera síntesis de este tema.
Por ejemplo, “cálculo” se puede utilizar directamente sobre la función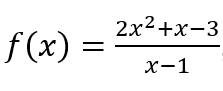 , sin necesidad de organizarlo, es decir, de expresarlo como
, sin necesidad de organizarlo, es decir, de expresarlo como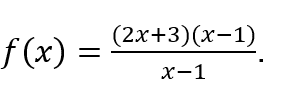
Veamos. ![]()
Cómo![]() , podemos hacer, por ejemplo,
, podemos hacer, por ejemplo, ![]() y
y ![]()
Quédamonos con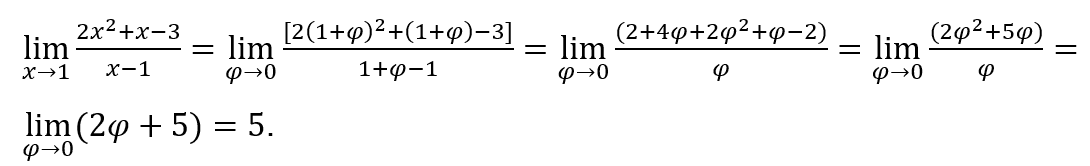
Esto trae una enorme ventaja sobre la presentación actual de este tema que, además de no presentar ningún cálculo de límites, se muestra bastante “atascado” por la inmensa cantidad de teoremas que deben ser considerados en las “evaluaciones” de límites, así como de las “organizaciones” que debe hacerse sobre las funciones antes de “estimar” su límite.
3) Me gustaría añadir, al “cálculo de límites” presentado, algunas valoraciones de carácter práctico.
a) Sólo tiene sentido calcular el límite de una función cerca de un valor para el que no está definido.
Si la función está definida para cierto valor, es decir, si la función existe para cierto valor, no tiene sentido calcular el límite cerca de ese valor, ya que sabemos cuánto vale la función en ese valor.
Por ejemplo, ser ![]()
Esta función está definida para todos ![]() , existe para todos
, existe para todos![]()
Por lo tanto, no sería razonable calcular, por ejemplo, ![]() ,ya que la función existe para
,ya que la función existe para ![]() , es decir, ¿por qué calcular este límite si simplemente podemos sustituir
, es decir, ¿por qué calcular este límite si simplemente podemos sustituir ![]() por 3 en
por 3 en ![]() y obtenemos el valor de la función en 3, es decir,
y obtenemos el valor de la función en 3, es decir, ![]()
Con esto, cientos de ejercicios ya no tienen razón de existir.
Evidentemente las funciones consideradas en este artículo son de ![]()
b) Usando el concepto de límite, haremos aquí una observación sobre la continuidad de una función.
Según el libro de cálculo de Lethold (1994), la definición de una función continua en un punto se traduce de la siguiente manera:
Decimos que la función ![]() es continua en el número a si y solo si se cumplen las siguientes condiciones:
es continua en el número a si y solo si se cumplen las siguientes condiciones:
(i) ![]() existe;
existe;
(ii) ![]() existe;
existe;
(iii) ![]()
Si una o más de estas condiciones no se verifican, la función![]() será discontinuo en
será discontinuo en ![]() .
.
Entonces lima (1978) define la continuidad de una función:
una función![]() se dice que es continua en el punto
se dice que es continua en el punto ![]() cuando es posible hacer
cuando es posible hacer ![]() arbitrariamente cerca de
arbitrariamente cerca de ![]() siempre y cuando se tome
siempre y cuando se tome ![]() lo suficientemente cerca de
lo suficientemente cerca de ![]()
En términos precisos, diremos que![]() es continua en el punto
es continua en el punto![]() cuando, por todos
cuando, por todos ![]() dado arbitrariamente, podemos encontrar
dado arbitrariamente, podemos encontrar ![]() tal que
tal que ![]() y
y ![]() implicar
implicar![]()
Sabemos que si una función está definida en cierto intervalo, es decir, si existe para cada número contenido en cierto intervalo, entonces no tiene sentido calcular el límite de esa función para algún número en ese intervalo, ya que podemos simplemente evalúe la función en cada número en ese rango.
En términos más simples: si una función, representada por una sola expresión, por una sola oración, existe para un cierto número ![]() entonces es totalmente innecesario calcular el límite de la función para
entonces es totalmente innecesario calcular el límite de la función para ![]() , ya que, simplemente, podemos calcular el valor de la función en
, ya que, simplemente, podemos calcular el valor de la función en![]()
Por supuesto, si tuviéramos que calcular este límite, como lo hicimos anteriormente, sería ![]()
Como se indicó anteriormente, solo tiene sentido calcular el límite de una función alrededor de un número para el que no está definido.
Por lo tanto, si estamos analizando funciones representadas por una sola expresión, diciendo que existe una función para cierto número ![]() , significa que hay un límite de esta función en
, significa que hay un límite de esta función en![]() siendo este límite el valor de la función en
siendo este límite el valor de la función en ![]() , y con eso no necesitamos calcular el límite de esta función en ese número
, y con eso no necesitamos calcular el límite de esta función en ese número ![]()
Aplicando esto a la definición anterior de una función continua, los puntos (ii) y (iii) de la definición se volverán innecesarios, ya que en el punto (i) se establece que![]() existe.
existe.
Por lo tanto, para funciones representadas por “una sola expresión”, la simple declaración de que la función![]() , se define en un numero
, se define en un numero ![]() es decir, la simple afirmación de que
es decir, la simple afirmación de que![]() existe es suficiente para concluir que la función es continua en ese número
existe es suficiente para concluir que la función es continua en ese número![]()
Asimismo, con esta observación sobre las funciones continuas, cientos de ejercicios pierden su razón de ser.
Ejemplo: dejar que la función ![]() que está definido para todo número real, es decir, existe para todo
que está definido para todo número real, es decir, existe para todo ![]() real.
real.
Por lo tanto, no hay necesidad de calcular el límite de ![]() sin valor de
sin valor de ![]() ,porque en este caso, se define en
,porque en este caso, se define en ![]() es sinónimo de tener un límite en
es sinónimo de tener un límite en ![]() y que este límite es igual al valor de la función en
y que este límite es igual al valor de la función en ![]() consideró.
consideró.
Entonces la función![]() es continuo para todos
es continuo para todos![]()
3. CONCLUSIÓN
En lo anterior mostramos que, de hecho, la teoría de los límites es deficiente en relación con un cálculo de límite y, por lo tanto, se rodea de una serie de argumentos basados en la definición de límite para llenar este vacío.
A continuación presentamos el “cálculo del límite de una función” y demostramos que sintetiza todo el tema mencionado, teniendo, por tanto, aplicación directa.
Esperamos estar contribuyendo a una mejor comprensión de un tema tan fundamental en las matemáticas.
REFERENCIAS
IEZZI, Gelson; MURAKAMI, Carlos et all. Fundamentos de Matemática Elementar, vol. 8, 1991.
LEITHOLD, Louis. O Cálculo com Geometria Analítica, vol. 1, 1994.
LIMA, Elon Lages. Curso de Análise, vol. 1, 1978.
MUNEM, Mustafa A. e FOULIS, David J. Cálculo, vol. 1, 1982.
[1]Licenciado en Matemáticas por la Universidad de Brasilia.
Enviado: Junio de 2021.
Aprobado: Agosto de 2021.