ARTICOLO ORIGINALE
PEREIRA, Olavo de Carvalho [1]
PEREIRA, Olavo de Carvalho. Limitare il calcolo di una funzione senza l’uso di ![]() e
e ![]() . Revista Científica Multidisciplinar Núcleo do Conhecimento. Anno. 06, ed. 08, vol. 04, pag. 05-31. Agosto 2021. ISSN: 2448-0959, Link di accesso: https://www.nucleodoconhecimento.com.br/olimpiadi-di-matematica/limitare-il-calcolo, DOI: 10.32749/nucleodoconhecimento.com.br/olimpiadi-di-matematica/limitare-il-calcolo
. Revista Científica Multidisciplinar Núcleo do Conhecimento. Anno. 06, ed. 08, vol. 04, pag. 05-31. Agosto 2021. ISSN: 2448-0959, Link di accesso: https://www.nucleodoconhecimento.com.br/olimpiadi-di-matematica/limitare-il-calcolo, DOI: 10.32749/nucleodoconhecimento.com.br/olimpiadi-di-matematica/limitare-il-calcolo
RIEPILOGO
La bibliografia consultata non presenta, in nessuno dei casi analizzati, un calcolo del limite di una funzione, ma si limita a “mostrare” che i valori presentati come “limite” soddisfano la definizione di limite di una funzione espressa attraverso disuguaglianze coinvolgente ![]() e
e ![]() , c’è quindi una lacuna in questo tema, che il presente articolo viene a colmare utilizzando fondamentalmente il concetto di funzione definita, oltre che individuando l’espressione “
, c’è quindi una lacuna in questo tema, che il presente articolo viene a colmare utilizzando fondamentalmente il concetto di funzione definita, oltre che individuando l’espressione “ ![]() tende ad un certo numero” con una corrispondente uguaglianza.
tende ad un certo numero” con una corrispondente uguaglianza.
Parole chiave: limite di una funzione, calcolo limite, limiti laterali, limiti infiniti, limiti all’infinito.
1. INTRODUZIONE
Questo articolo presenta il “calcolo del limite di una funzione” al fine di colmare una lacuna esistente in questo argomento.
La presentazione del calcolo citato nella soluzione di più limiti è l’obiettivo principale dell’articolo.
In modo integrativo si intende chiarire la reale necessità di calcolare o meno il limite di una funzione.
Discuteremo anche, in modo molto semplice, il caso in cui una funzione semplice, definita in un certo numero, è continua in quel numero.
Sebbene l’interpretazione geometrica sia sempre importante, qui ci avvicineremo solo al “calcolo limite” algebrico presentato.
1.1 CALCOLO LIMITE DI UNA FUNZIONE
La definizione del limite di una funzione è presentata nei libri di testo di matematica come una stima.
Ad esempio: Leithold (1994) presenta la definizione del limite di una funzione come segue:
Seja ![]() uma função definida para todo número em algum intervalo aberto contendo
uma função definida para todo número em algum intervalo aberto contendo ![]() , exceto possivelmente no próprio número
, exceto possivelmente no próprio número ![]() O limite de
O limite de ![]() quando
quando ![]() tende a
tende a ![]() será
será ![]() , escrito como
, escrito como ![]() se a seguinte afirmativa for verdadeira:
se a seguinte afirmativa for verdadeira:
Dado ![]() qualquer, existe um
qualquer, existe um ![]() , tal que, se
, tal que, se ![]() então
então ![]() .‘‘
.‘‘
A definição acima afirma que os valores de ![]() tendem a um limite
tendem a um limite ![]() quando
quando ![]() tende a um número
tende a um número ![]() , se o valor absoluto da diferença entre
, se o valor absoluto da diferença entre ![]() e
e ![]() puder se tornar tão pequeno quanto desejarmos, tomando
puder se tornar tão pequeno quanto desejarmos, tomando![]() suficientemente próximo de
suficientemente próximo de ![]() , mas não igual a
, mas não igual a ![]() .
.
D’altra parte, Lezzi, Murakami e Machado (1991) si esprimono sulla stessa definizione:
Seja ![]() um intervalo aberto ao qual pertence o número real
um intervalo aberto ao qual pertence o número real ![]() . Seja
. Seja ![]() uma função definida para
uma função definida para ![]() Dizemos que o limite de
Dizemos que o limite de ![]() , quando
, quando ![]() tende a
tende a ![]() , é
, é ![]() , e escrevemos
, e escrevemos ![]() se para todo
se para todo ![]() , existir
, existir ![]() tal que se
tal que se
![]() então
então ![]() .
.
Munem e Foulis (1982) utilizzano la seguente definizione:
Se ![]() é uma função e
é uma função e ![]() é um número, entende-se a notação
é um número, entende-se a notação ![]() como “o limite de
como “o limite de ![]() ” quando
” quando![]() tende a
tende a ![]() é
é ![]() isto é,
isto é, ![]() se aproxima do número
se aproxima do número ![]() quando
quando ![]() se aproxima de
se aproxima de ![]() .
.
Come si può vedere dalle definizioni di cui sopra, viene presentato un limite![]() solo per soddisfare la definizione stessa.
solo per soddisfare la definizione stessa.
Nessun calcolo di questo limite viene presentato in nessun momento.
Questo articolo presenta il “calcolo limite” di una funzione che può essere utilizzata in tutti i casi in cui sia necessario eseguire tale operazione.
Ora, passiamo all’argomento.
Per alcune funzioni, non definite in un certo numero, per conoscere, con la massima precisione possibile, quale sarebbe il loro valore in quel numero, è consuetudine valutarle in valori prossimi a quel numero per cui non sono definito.
Esempio: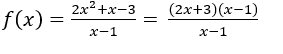 impostato su tutti
impostato su tutti ![]() tranne
tranne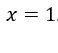 .
.
Se sostituiamo il ![]() per 1 abbiamo l’indeterminazione
per 1 abbiamo l’indeterminazione ![]() .
.
Poiché la funzione non è definita, cioè non esiste per il valore 1, ne valutiamo quindi il valore prossimo a 1, poiché il nostro obiettivo è conoscere il valore della funzione, almeno, vicino a 1, poiché non esiste per ![]() .
.
Per valori di ![]() , diverso da 1, maggiore o minore di 1, ma molto vicino a 1,
, diverso da 1, maggiore o minore di 1, ma molto vicino a 1, ![]() , poi
, poi ![]() sarà uguale a 1, e avrà valori prossimi a 5, come vedremo di seguito:
sarà uguale a 1, e avrà valori prossimi a 5, come vedremo di seguito:
Assegniamo a![]() i valori
i valori![]() , cioè, stiamo assumendo valori di
, cioè, stiamo assumendo valori di ![]() sempre più vicino a 1, ma inferiore a 1. I valori di
sempre più vicino a 1, ma inferiore a 1. I valori di ![]() trovati sono:
trovati sono:
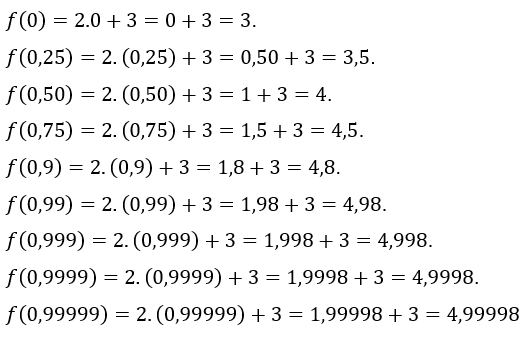
Ora assegniamo il![]() i valori
i valori ![]() , cioè, stiamo assumendo valori di
, cioè, stiamo assumendo valori di ![]() sempre più vicino a 1, ma maggiore di 1. I valori di
sempre più vicino a 1, ma maggiore di 1. I valori di![]() trovati sono:
trovati sono: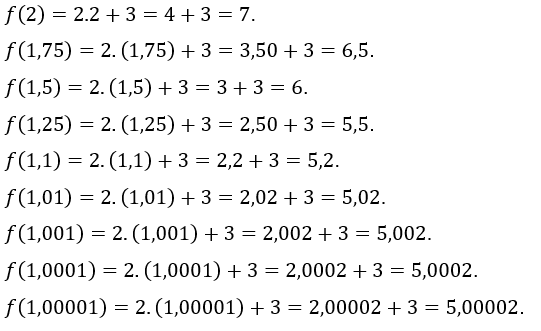
Come si può notare, in entrambi i casi, come![]() approcci 1,
approcci 1, ![]() se aproxima de 5, levando-nos a crer que seja esse o limite de
se aproxima de 5, levando-nos a crer que seja esse o limite de ![]() .
.
Tuttavia, qui non è stato fatto alcun “calcolo” di limite, ma solo una valutazione di ![]() , quando
, quando![]() assume valori molto vicini a 1.
assume valori molto vicini a 1.
Quindi il valore 5 è “candidato” per essere il limite che dobbiamo ancora calcolare.
Gli autori consultati strutturano la definizione di limite in termini di disuguaglianze da esempi come questo e assumono il valore stimato, in questo caso 5, come proprio limite della funzione.
A questo proposito, lo affermano![]() , perché per qualsiasi
, perché per qualsiasi ![]() , non importa quanto sia piccolo, c’è a
, non importa quanto sia piccolo, c’è a ![]() , tale che se
, tale che se ![]() poi
poi![]() .
.
La definizione di limite data all’inizio, che non ha alcun calcolo del limite, serve per “dimostrare” che dati dati, senza indicazione di dove sono stati presi, sono limiti di funzioni.
Mostreremo che la definizione di limite non prova, non dimostra, che un dato numero è il limite di una funzione, ma solo “mostra” che il dato numero è il limite.
Usiamo un esempio per chiarire la differenza tra uno “spettacolo” e una “dimostrazione”.
- Mostra che 2 è la radice dell’equazione
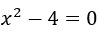 .
.
Ciò significa che se sostituiamo il![]() per 2, avremo zero come risultato dell’equazione.
per 2, avremo zero come risultato dell’equazione.
vediamo![]() .
.
Questo è stato un esempio di “dimostrazione”, cioè solo qualcosa è stato mostrato, nulla è stato dimostrato, nulla è stato calcolato, solo il valore fornito è stato sostituito.
È diverso quando dici: dimostra che 2 è una radice, è una soluzione dell’equazione![]() .
.
In tal caso, dobbiamo calcolare, risolvere l’equazione e vedere se otteniamo ![]() .
.
Bene, risolvendolo, abbiamo: ![]() , presto
, presto![]() ,e prendendo la radice quadrata da entrambi i lati otteniamo:
,e prendendo la radice quadrata da entrambi i lati otteniamo: ![]() , questo è,
, questo è, ![]() o
o ![]() .
.
Poi uno dei valori di ![]() davvero è 2.
davvero è 2.
Con questo, è stato “dimostrato” che 2 è davvero la radice dell’equazione![]() .
.
Vedremo, negli esempi riportati di seguito, che non c’è una prova, ma solo uno “spettacolo” che il numero dato è il limite della funzione data.
Esempio. Usa la definizione del limite per “dimostrarlo”.![]() .
.
Qui non si dice come si sia giunti alla conclusione che il limite sia 5, né si dice da dove sia stato preso quel numero.
Discuteremo, in termini generali, la soluzione presentata nei libri consultati:
Il primo requisito della definizione è quello![]() essere definito su ogni numero di qualche intervallo aperto contenente 3, tranne eventualmente su 3. As
essere definito su ogni numero di qualche intervallo aperto contenente 3, tranne eventualmente su 3. As ![]() è definito per tutti i numeri reali, qualsiasi intervallo aperto contenente 3 soddisferà questo requisito. Dobbiamo dimostrarlo ora a tutti
è definito per tutti i numeri reali, qualsiasi intervallo aperto contenente 3 soddisferà questo requisito. Dobbiamo dimostrarlo ora a tutti ![]() c’è uno
c’è uno ![]() , tale che se
, tale che se ![]() poi
poi ![]() dobbiamo
dobbiamo![]() , presto
, presto ![]() e
e ![]()
Abbiamo, quindi,![]() e
e ![]()
Questa affermazione lo indica![]() è un delta soddisfacente.
è un delta soddisfacente.
Con questa scelta di ![]() abbiamo il seguente argomento:
abbiamo il seguente argomento:![]() , poi
, poi![]() , poi
, poi![]() , poi
, poi![]() poi
poi ![]() , poi
, poi ![]()
Questo proprio “mostra”, dalla definizione di limite, quello ![]()
Come abbiamo visto, non c’era una dimostrazione, ma solo uno “spettacolo”, poiché, dato il numero 5, nella definizione del limite di una funzione abbiamo semplicemente sostituito esso e la funzione data.
Andiamo a un altro esempio: usa la definizione per “dimostrarlo”![]() .
.
Anche in questo caso viene fornito un numero, in questo caso 4, come limite, ma non è detto da dove sia stato preso questo numero.
Ecco la soluzione, in termini generali:
Come ![]() è definito per tutti i numeri reali, qualsiasi intervallo aperto contenente 2 soddisferà il primo requisito della definizione.
è definito per tutti i numeri reali, qualsiasi intervallo aperto contenente 2 soddisferà il primo requisito della definizione.
Dobbiamo dimostrarlo a tutti ![]() , c’è uno
, c’è uno ![]() , tale che
, tale che
Se ![]() poi
poi ![]()
Presto ![]() poi
poi![]()
Dobbiamo porre un vincolo ![]() che ci dà una disuguaglianza coinvolgente
che ci dà una disuguaglianza coinvolgente ![]() . Tale restrizione viene fatta per selezionare l’intervallo di apertura richiesto dalla definizione. Scegliamo la gamma
. Tale restrizione viene fatta per selezionare l’intervallo di apertura richiesto dalla definizione. Scegliamo la gamma ![]() e questo implica quello
e questo implica quello ![]() . Quindi
. Quindi![]() e
e ![]() , poi
, poi![]() poi
poi![]() poi
poi![]() poi
poi![]() .
.
Ora abbiamo![]() e
e ![]() , poi
, poi![]() Come il nostro obiettivo è quello di ottenere
Come il nostro obiettivo è quello di ottenere ![]() , dobbiamo richiedere
, dobbiamo richiedere ![]() Con questo
Con questo 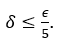
Usando questo![]() abbiamo completato la cosiddetta “prova”.
abbiamo completato la cosiddetta “prova”.
Come abbiamo visto sopra, ancora una volta non è stato dimostrato nulla, ma solo che il numero dato come limite, in questo caso 4, soddisfa la definizione di limite.
Non c’era alcun calcolo per dimostrare che il numero 4 è davvero il limite.
Da questo punto in poi presenteremo il calcolo limite di una funzione.
Prima di presentare il “calcolo” stesso, valutiamo ![]() negli stessi valori di
negli stessi valori di ![]() dati sopra, ma considerandoli composti di numero 1.
dati sopra, ma considerandoli composti di numero 1.
Questo mostrerà, in termini generali, il ragionamento utilizzato per calcolare il limite della funzione.
La funzione è![]() , valido per tutti
, valido per tutti ![]() .
.
Per ![]() ou
ou ![]() , dobbiamo
, dobbiamo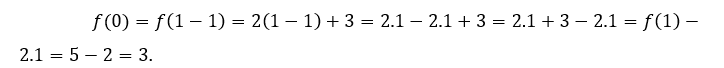
Per ![]() ou
ou ![]() , dobbiamo
, dobbiamo 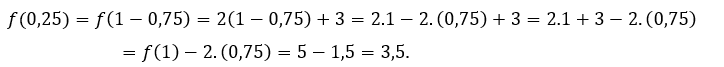 Per
Per ![]() ou
ou ![]() , dobbiamo
, dobbiamo 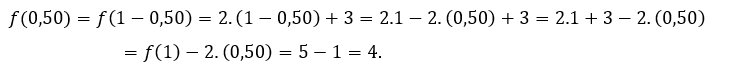
Per ![]() ou
ou ![]() dobbiamo
dobbiamo 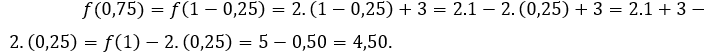 Per
Per ![]() ou
ou ![]() , dobbiamo
, dobbiamo 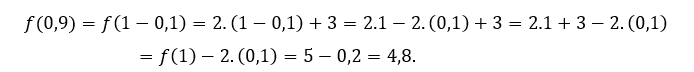
Per ![]() ou
ou ![]() , dobbiamo
, dobbiamo 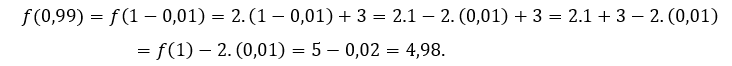
Per ![]() ou
ou ![]() , dobbiamo
, dobbiamo 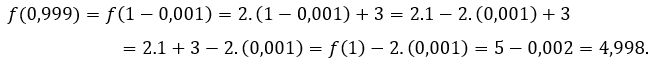
Per ![]() ou
ou ![]() , dobbiamo
, dobbiamo 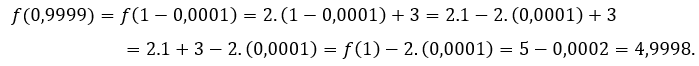
Per ![]() ou
ou ![]() , dobbiamo
, dobbiamo 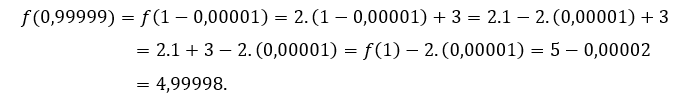
Abbiamo testato alcuni valori di![]() più piccolo di 1.
più piccolo di 1.
Ora valuteremo ![]() a valori maggiori di 1 ma vicini a 1.
a valori maggiori di 1 ma vicini a 1.
Per ![]() ou
ou ![]() , dobbiamo
, dobbiamo 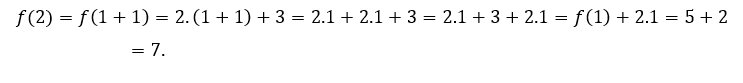
Per ![]() ou
ou ![]() dobbiamo
dobbiamo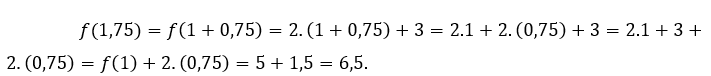
Per ![]() ou
ou ![]() dobbiamo
dobbiamo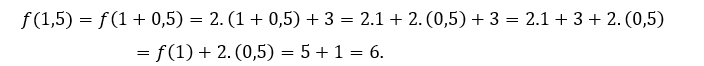
Per ![]() ou
ou ![]() , dobbiamo
, dobbiamo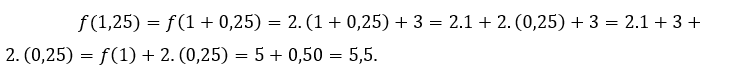
Per ![]() ou
ou ![]() , dobbiamo
, dobbiamo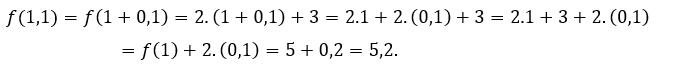
Per ![]() ou
ou ![]() dobbiamo
dobbiamo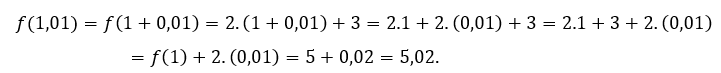
Per ![]() ou
ou ![]() , dobbiamo
, dobbiamo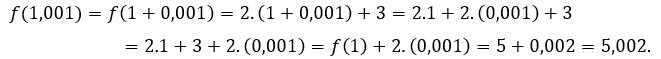
Per ![]() ou
ou ![]() , dobbiamo
, dobbiamo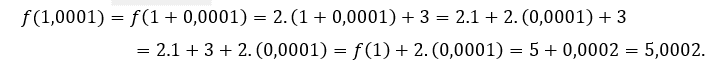
Per ![]() ou
ou ![]() , dobbiamo
, dobbiamo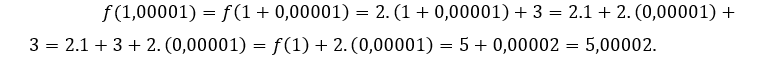
Da quanto sopra, ci rendiamo conto che più![]() si avvicina a 1, di più
si avvicina a 1, di più ![]() si avvicina a 5, cioè quando
si avvicina a 5, cioè quando ![]() tende a 1,
tende a 1, ![]() tende a 5.
tende a 5.
Abbiamo osservato nei calcoli sopra, in tutti i valori assegnati![]() , l’apparenza di una costante
, l’apparenza di una costante ![]() a cui è stato aggiunto o sottratto un valore, che tendeva a zero, come
a cui è stato aggiunto o sottratto un valore, che tendeva a zero, come ![]() si stava avvicinando 1.
si stava avvicinando 1.
Questa costante è, quindi, un “candidato” ad essere il “limite” di cui sopra, cioè c’è un’indicazione che potremmo avere ![]() .
.
Esprimeremo ora la situazione sopra in modo semigenerico per presentare il “calcolo del limite” stesso.
L’espressione “![]() tende a 1″, rappresentato da
tende a 1″, rappresentato da ![]() , è equivalente a
, è equivalente a ![]() , o
, o ![]() , quando
, quando ![]() tende a zero,
tende a zero, ![]() , e
, e ![]() .
.
Con questo, l’espressione![]() , sostituzione
, sostituzione ![]() per
per ![]() o
o ![]() , è equivalente a
, è equivalente a ![]() , o
, o ![]() , questo è,
, questo è, ![]() , ou
, ou ![]() .
.
Dalla suddetta uguaglianza è possibile “calcolare” il valore del limite di ![]() quando
quando ![]() tende a 1, poiché è sufficiente per calcolare il valore di
tende a 1, poiché è sufficiente per calcolare il valore di ![]() , o
, o ![]() .
.
Ora faremo, usando la stessa funzione di prima, il calcolo per![]() , quando
, quando ![]() .
.
In questo modo ci resta:
![]() poi
poi![]() indipendentemente da
indipendentemente da ![]() , e
, e ![]() tende a zero quando
tende a zero quando ![]() , cioè, è così piccolo che si avvicina allo zero per quanto vogliamo.
, cioè, è così piccolo che si avvicina allo zero per quanto vogliamo.
Il calcolo per![]() , questo è,
, questo è, ![]() , è analogo e produce lo stesso risultato.
, è analogo e produce lo stesso risultato.
Vediamo: ![]()
Calcoleremo ora una serie di limiti di funzioni, per esemplificare l’applicazione del suddetto “calcolo”.
- Calculemos
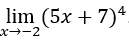 .
.
Come![]() , possiamo fare, per esempio,
, possiamo fare, per esempio, ![]() ,
, ![]() e
e ![]() .
.
Rimanere con ![]()
![]() termini in
termini in ![]() che tendono tutti a zero.
che tendono tutti a zero.
Allora il risultato sarà ![]()
- Calcoliamo
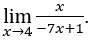
Come ![]() , possiamo fare, ad esempio,
, possiamo fare, ad esempio, ![]() ,
, ![]() e
e ![]() .
.
Rimanere con
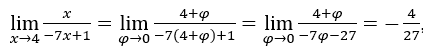 , perché il numeratore tende a 4 e il denominatore tende a
, perché il numeratore tende a 4 e il denominatore tende a ![]() .
.
- Calcoliamo
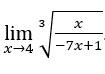 .
.
Come abbiamo visto sopra, alla fine ci resterà
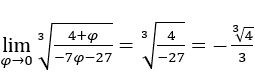
- Calcoliamo
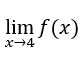 come sotto.
come sotto.
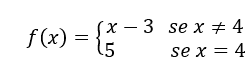 .
.
Dobbiamo calcolare ![]() , perché qualunque cosa accada succede a
, perché qualunque cosa accada succede a ![]() quando
quando ![]() .
.
Come ![]() , possiamo fare, per esempio,
, possiamo fare, per esempio, ![]()
![]() e
e ![]() .
.
Rimanere con![]() , poi
, poi![]() .
.
Essere![]() , impostato su tutti
, impostato su tutti ![]() , tranne
, tranne ![]() .
.
Consideriamo ![]() questo è,
questo è, ![]() , per cui
, per cui ![]() si riduce a
si riduce a ![]() .
.
- Calcoliamo il
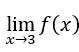 . Dobbiamo
. Dobbiamo 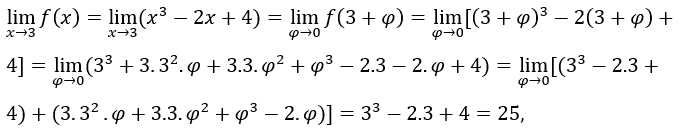 , una volta, quando
, una volta, quando 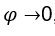 l’espressione
l’espressione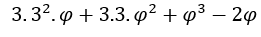 tende a zero.
tende a zero.
Quindi
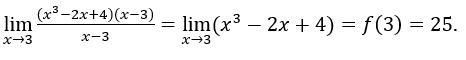
Consideriamo ora il seguente esempio: ![]() , impostato su tutti
, impostato su tutti ![]() , e calcolarne il limite quando
, e calcolarne il limite quando ![]() tende a 2.
tende a 2.
Per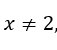 condizione di esistenza della funzione,
condizione di esistenza della funzione, ![]() , e quando
, e quando ![]() possiamo fare, per esempio,
possiamo fare, per esempio, ![]() , com
, com ![]()
![]() e dovremo calcolare il limite
e dovremo calcolare il limite![]() .
.
Come![]() , l’espressione
, l’espressione ![]() tende a
tende a ![]() , e il limite sarà allora,
, e il limite sarà allora, ![]() .
.
In conclusione, ci resta: ![]() .
.
Osservazione.
Avremmo potuto applicare il “calcolo” direttamente alla funzione, senza prima dividere il fattore comune al numeratore e denominatore.
Vediamo![]()
Possiamo infatti applicare il “calcolo” direttamente sulla funzione, senza prima fare una “preparazione” su di essa.
Daremo ora alcuni esempi di calcolo dei limiti che coinvolgono funzioni trigonometriche ed esponenziali per esemplificare quanto sopra consolidato.
Consideriamo la funzione![]() , impostato su tutti
, impostato su tutti ![]() , tranne
, tranne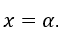
Ricordando: ![]() significa, per esempio, quello
significa, per esempio, quello![]() , dove
, dove![]() ,
, ![]() .
.
Sostituendo questo valore di x nell’equazione originale sopra, otteniamo: 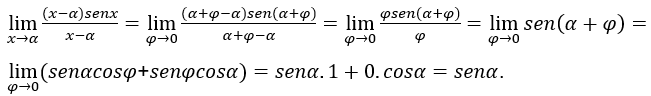
Quindi, ![]() sono indipendenti da
sono indipendenti da ![]() è il
è il 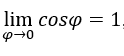 , mentre il
, mentre il ![]() .
.
Un altro esempio: considera la funzione ![]() impostato su tutti
impostato su tutti ![]() , tranne
, tranne![]() .
.
- Calcoliamo il
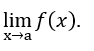
- Effettuando la sostituzione
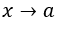 per, per esempio,
per, per esempio, 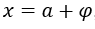 , com
, com 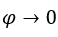 ,
, 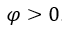 . Abbiamo:
. Abbiamo: 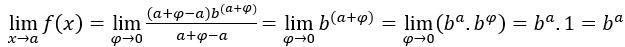 , perché il
, perché il 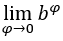 è 1 e
è 1 e 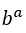 indipendentemente da
indipendentemente da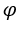 .
.
Ora calcoliamo il limite delle funzioni date all’inizio per confermare i valori dei limiti dati.
- Calcoliamo
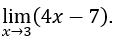
Come![]() , possiamo fare, per esempio,
, possiamo fare, per esempio, ![]() ,
, ![]() e
e ![]() e ci resta
e ci resta![]()
- Calcoliamo
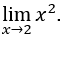
Come![]() , possiamo fare, per esempio,
, possiamo fare, per esempio, ![]() ,
, ![]() e
e 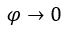 e ci resta
e ci resta![]()
Come si può vedere dai “calcoli” di cui sopra, i limiti dati negli esempi precedenti erano corretti.
Dimostreremo solo un teorema sui limiti per esemplificare il calcolo qui mostrato.
Teorema. Se ![]() e
e ![]() sono delle costanti, quindi
sono delle costanti, quindi ![]() .
.
Basta calcolare il limite facendo, per esempio, ![]()
![]() e
e ![]()
Rimanere con: ![]() , poi
, poi ![]() tende a zero, poiché
tende a zero, poiché ![]() tende a zero.
tende a zero.
C’è un’immensa semplicità nel “calcolo” presentato.
In questo caso, non c’è dubbio che il limite sia![]() .
.
Utilizzeremo ora il “calcolo dei limiti” presentato per calcolare i limiti delle funzioni in varie circostanze.
- Calcoliamo
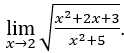
Come ![]() , così possiamo fare, per esempio,
, così possiamo fare, per esempio, ![]() ,
, ![]() e
e ![]()
Rimanere con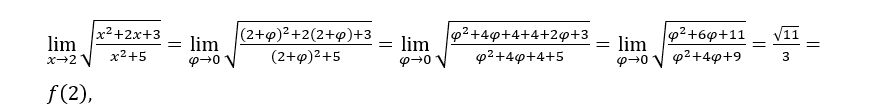 , una volta
, una volta ![]() tende a 11 e
tende a 11 e ![]() tende a 9.
tende a 9.
- Calcoliamo
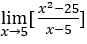 .
.
Come x → 5, così possiamo fare, per esempio, ![]() ,
, ![]() e
e ![]()
Rimanere con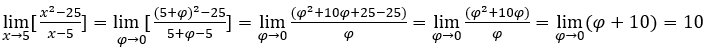
Si osserva che non era necessario “preparare” la funzione per applicare il “calcolo”, cioè non era necessario scrivere la funzione come ![]() e, infine, come
e, infine, come ![]()
- Calcoliamo
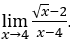 .
.
Nei casi che coinvolgono radicali, a cui viene aggiunto o sottratto un numero reale, quando la sostituzione diretta del valore di![]() porta all’indeterminazione
porta all’indeterminazione ![]() dobbiamo preparare l’equazione, perché l’applicazione diretta del “calcolo” non annulla l’indeterminazione, come vedremo più avanti.
dobbiamo preparare l’equazione, perché l’applicazione diretta del “calcolo” non annulla l’indeterminazione, come vedremo più avanti.
Quello che succede in questo caso è che esiste un fattore comune sia al numeratore che al denominatore, ma che si esprime solo quando dividiamo, o il numeratore per il denominatore, o il denominatore per il numeratore.
Questo si traduce attualmente in matematica come razionalizzazione.
Vediamo nell’esempio sopra: se dividiamo il denominatore per il numeratore, poiché l’esponente di ![]() al denominatore è 1 e l’esponente di
al denominatore è 1 e l’esponente di ![]() nel numeratore è più piccolo, cioè vale
nel numeratore è più piccolo, cioè vale ![]() avremo:
avremo: ![]() e sostituendo, avremo
e sostituendo, avremo 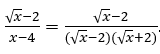 .
.
Siamo quindi in grado di esprimere il fattore comune al numeratore e denominatore.
L’altro modo è dividere il numeratore per il denominatore, ma in questo caso dobbiamo fare la stessa cosa è la razionalizzazione, poiché l’esponente di ![]() al numeratore è minore dell’esponente di
al numeratore è minore dell’esponente di ![]() denominatore, e quindi deve essere moltiplicato per un fattore in
denominatore, e quindi deve essere moltiplicato per un fattore in ![]() per rendere il suo esponente almeno uguale all’esponente del denominatore.
per rendere il suo esponente almeno uguale all’esponente del denominatore.
Questa è la famosa razionalizzazione che facciamo.
Faremo prima il calcolo, senza preparazione.
Come ![]() , possiamo fare, per esempio,
, possiamo fare, per esempio, ![]() ,
,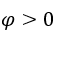 e
e ![]() .
.
Rimanere con![]() Osserviamo la necessità di razionalizzare, poiché il limite è ancora indeterminato quando
Osserviamo la necessità di razionalizzare, poiché il limite è ancora indeterminato quando ![]() al numeratore e denominatore, tendente a
al numeratore e denominatore, tendente a ![]()
Quindi moltiplichiamo e divideremo per![]() , e saremo con
, e saremo con ![]()
Ora faremo il calcolo, preparando la funzione prima di applicarla.
![]() .
.
Come la sostituzione diretta di 4 porta all’indeterminazione ![]() , significa che numeratore e denominatore hanno come fattore comune
, significa che numeratore e denominatore hanno come fattore comune ![]() o
o ![]()
In questo caso, trattandosi di un radicale meno un numero reale, il modo utilizzato per “rilasciare” il fattore comune è attraverso la razionalizzazione.
Prima di calcolare il limite, moltiplichiamo e divideremo il numeratore e il denominatore della funzione per![]()
Rimanere con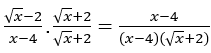 . In questa funzione possiamo già applicare il calcolo. Vediamo:
. In questa funzione possiamo già applicare il calcolo. Vediamo: 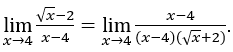
Come![]() possiamo fare, per esempio,
possiamo fare, per esempio, ![]() ,
, ![]() e
e ![]()
Rimanere con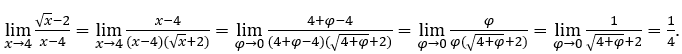
1.2 LIMITI LATERALI
Nei casi in cui una funzione è definita per ogni numero reale tranne un numero reale![]() , quando ne calcoliamo il limite con la variabile indipendente tendente a
, quando ne calcoliamo il limite con la variabile indipendente tendente a ![]() , come negli esempi forniti sopra, non importa se usiamo
, come negli esempi forniti sopra, non importa se usiamo ![]() quanto
quanto ![]() ,
, ![]() e
e ![]() , poiché è impostato su tutti i numeri a sinistra ea destra di
, poiché è impostato su tutti i numeri a sinistra ea destra di ![]() .
.
E, naturalmente, questa non è una funzione di frase.
Quando una funzione non è definita a sinistra oa destra di un numero![]() e dobbiamo calcolarne il limite con
e dobbiamo calcolarne il limite con ![]() tendendo a, dobbiamo usare il valore di
tendendo a, dobbiamo usare il valore di ![]() nel caso che fosse.
nel caso che fosse.
Quando![]() e lo facciamo
e lo facciamo ![]() , o
, o ![]() ,
, ![]() e
e ![]() , poi
, poi ![]() indica che
indica che ![]() si avvicina
si avvicina ![]() per valori maggiori di
per valori maggiori di ![]() , e, quindi, si avvicina da destra.
, e, quindi, si avvicina da destra.
Il calcolo effettuato con![]() è, quindi, il limite quando
è, quindi, il limite quando ![]() tende a
tende a ![]() sulla destra.
sulla destra.
È, quindi, il limite di destra.
Noi usiamo ![]() per calcolare il limite di sinistra.
per calcolare il limite di sinistra.
Sappiamo che il limite esiste solo quando i limiti unilaterali esistono e sono uguali.
- Calcoliamo
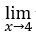 √x – 4.
√x – 4.
Sappiamo che la funzione esiste solo per![]() , questo è,
, questo è, ![]()
Pertanto, non esiste il limite di sinistra e, quindi, il limite in questione non esiste.
Ma c’è il limite di destra che può essere calcolato sostituendo![]() per
per![]() ,
, ![]() e
e ![]()
![]()
Essere![]()
- Calcoliamo i limiti unilaterali.
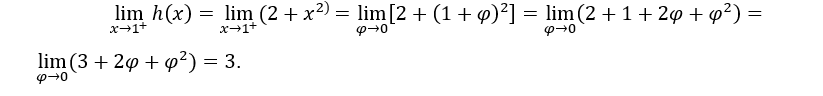
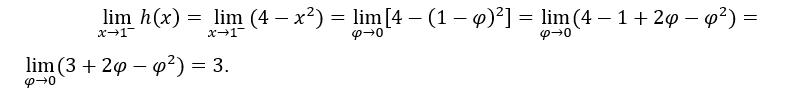
Come sono la stessa cosa,![]()
Nel calcolo sopra, abbiamo fatto![]() , per calcolare il limite di destra e
, per calcolare il limite di destra e ![]() per calcolare il limite di sinistra.
per calcolare il limite di sinistra.
Calcoliamo il limite di ![]() definito da
definito da
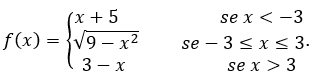
- Calcoliamo
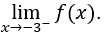
Bisogna poi calcolare,![]()
Lo faremo allora, ![]() ,
, ![]() e
e ![]()
- Calcoliamo
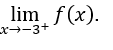
Bisogna poi calcolare,![]()
Lo faremo allora, ![]() ,
, ![]() e
e ![]()
Rimanere con
![]()
- Calcoliamo
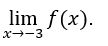
Come ![]() poi il
poi il ![]() non esiste.
non esiste.
- Calcoliamo
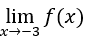 .
.
Bisogna poi calcolare,![]()
Lo faremo allora, ![]() ,
, ![]() e
e ![]()
Rimanere con
![]()
- Calcoliamo
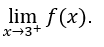
Bisogna poi calcolare, ![]()
Lo faremo allora, ![]() ,
, ![]() e
e ![]()
Rimanere con
![]()
- Calcoliamo
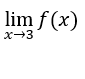
Come ![]() , poi
, poi 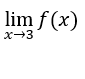 esiste ed è uguale a zero.
esiste ed è uguale a zero.
1.3 LIMITI INFINITI
Quelli i cui valori funzionali aumentano o diminuiscono senza limitazione, quando la variabile indipendente si avvicina sempre di più a un numero fisso, possono essere risolti ugualmente dal “calcolo” limite qui presentato, con il vantaggio di non doversi preoccupare di teoremi.
Prima di applicare il “calcolo”, ricordiamo le seguenti situazioni:
![]()
- Calcoliamo il seguente limite
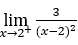 .
.
Come ![]() , dobbiamo fare
, dobbiamo fare ![]() ,
, ![]() e
e ![]()
Rimanere con ![]() .
.
- Calcoliamo ora
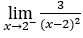 .
.
Come ![]() , dobbiamo fare
, dobbiamo fare ![]() ,
, ![]() e
e ![]()
Rimanere con![]() .
.
- Calcoliamo
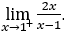 .
.
Come ![]() , dobbiamo fare
, dobbiamo fare ![]() ,
, ![]() e
e ![]()
Rimanere con![]() , perché il numeratore tende a 2, mentre il denominatore tende a zero per valori positivi.
, perché il numeratore tende a 2, mentre il denominatore tende a zero per valori positivi.
- Calcoliamo ora
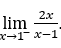 .
.
Come ![]() , dobbiamo fare
, dobbiamo fare ![]() ,
, ![]() e
e ![]()
Rimanere con 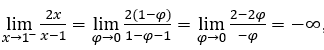 , perché il numeratore tende a 2 e il denominatore tende a zero per valori negativi.
, perché il numeratore tende a 2 e il denominatore tende a zero per valori negativi.
- Calcoliamo
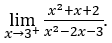
Come![]() , dobbiamo fare
, dobbiamo fare ![]() ,
, ![]() e
e ![]()
Rimanere con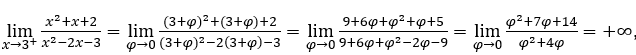 perché il numeratore tende a 14, mentre il denominatore tende a zero per valori positivi.
perché il numeratore tende a 14, mentre il denominatore tende a zero per valori positivi.
- Calcoliamo ora
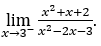
Come ![]() , dobbiamo fare
, dobbiamo fare ![]() ,
, ![]() e
e ![]()
Rimanere con ![]() , poiché il numeratore tende a 14, mentre il denominatore tende a zero per valori negativi, poiché
, poiché il numeratore tende a 14, mentre il denominatore tende a zero per valori negativi, poiché ![]() tende a zero sempre per valori positivi.
tende a zero sempre per valori positivi.
In questo caso il denominatore è![]() Ogni volta che
Ogni volta che![]() , è come
, è come ![]() , il denominatore è sempre negativo.
, il denominatore è sempre negativo.
- Calcoliamo
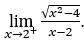
Come ![]() , dobbiamo fare
, dobbiamo fare ![]() ,
, ![]() e
e ![]()
Siamo come 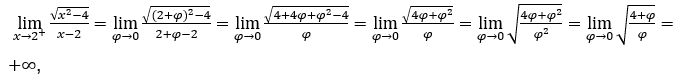 perché il numeratore tende a 2 e il denominatore tende a zero per valori positivi.
perché il numeratore tende a 2 e il denominatore tende a zero per valori positivi.
- Calcoliamo
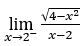
Come ![]() , dobbiamo fare
, dobbiamo fare ![]() ,
, ![]() e
e ![]()
Rimanere con 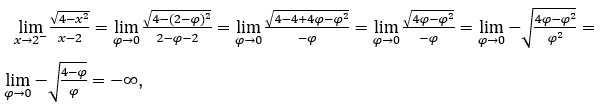 , perché il numeratore tende a -2 e il denominatore tende a zero per valori positivi.
, perché il numeratore tende a -2 e il denominatore tende a zero per valori positivi.
In questi due casi ci siamo riusciti![]() nel radicale perché è sempre positivo.
nel radicale perché è sempre positivo.
- Calcoliamo
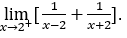
Come ![]() , dobbiamo fare
, dobbiamo fare ![]() ,
, ![]() e
e ![]()
Rimanere con![]() perché il numeratore tende a 4, mentre il denominatore tende a zero per valori positivi.
perché il numeratore tende a 4, mentre il denominatore tende a zero per valori positivi.
Nota Avremmo potuto sostituire direttamente il valore di![]() nell’equazione originale.
nell’equazione originale.
- Calcoliamo
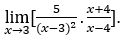
Come![]() , dobbiamo fare
, dobbiamo fare ![]() ,
, ![]() e
e ![]()
Rimanere con ![]() , perché il numeratore tende a 35, mentre il denominatore tende a zero per valori negativi, poiché è negativo per < 1.
, perché il numeratore tende a 35, mentre il denominatore tende a zero per valori negativi, poiché è negativo per < 1.
- Calcoliamo
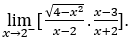
Come ![]() , lo faremo
, lo faremo![]() ,
, ![]() e
e ![]()
Rimanere con 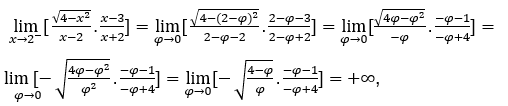 , perché il numeratore tende a farlo
, perché il numeratore tende a farlo ![]() e tende il denominatore
e tende il denominatore ![]() da valori positivi.
da valori positivi.
1.4 LIMITI NELL’INFINITO
Allo stesso modo dei limiti fin qui citati, anche la letteratura consultata non presenta un calcolo dei limiti all’infinito, ma valuta la funzione solo quando la variabile indipendente aumenta o diminuisce indefinitamente.
Il risultato della valutazione viene utilizzato come soglia.
Vediamo.
Data la funzione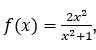 , attribuiamo a
, attribuiamo a![]() i valori
i valori![]() e così via, permettendogli di crescere indefinitamente. I valori funzionali corrispondenti saranno
e così via, permettendogli di crescere indefinitamente. I valori funzionali corrispondenti saranno
![]()
Osserviamo che quando![]() cresce, assumendo valori positivi, si avvicinano i valori funzionali 2.
cresce, assumendo valori positivi, si avvicinano i valori funzionali 2.
Quando una variabile indipendente![]() cresce all’infinito, attraverso valori positivi, scriviamo
cresce all’infinito, attraverso valori positivi, scriviamo ![]() l’esempio dato, la conclusione è stata tratta che
l’esempio dato, la conclusione è stata tratta che 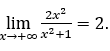
Come visto sopra, dall’esempio dato, non è stato presentato alcun calcolo limite della funzione, ma si è solo osservato che, come ![]() aumentata, di valori positivi, la funzione si avvicinava 2.
aumentata, di valori positivi, la funzione si avvicinava 2.
Questo valore 2 è stato quindi utilizzato come limite della funzione.
Presenteremo, di seguito, il “calcolo” del limite delle funzioni quando tende la variabile indipendente ![]() o il
o il ![]()
Nei casi in cui ![]() , lo faremo
, lo faremo 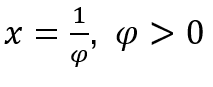 e
e ![]() , perché, come abbiamo visto sopra, quando
, perché, come abbiamo visto sopra, quando ![]() tende a zero per valori positivi,
tende a zero per valori positivi, ![]() tende a
tende a ![]() , e con quello,
, e con quello, ![]() tende a
tende a ![]()
Nei casi in cui ![]() , lo faremo
, lo faremo 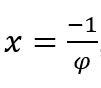
![]() e
e ![]() , perché, come abbiamo visto sopra, quando φ tende a zero per valori positivi
, perché, come abbiamo visto sopra, quando φ tende a zero per valori positivi![]() ,
,![]() tende a, e con quello,
tende a, e con quello, ![]() tende a
tende a ![]() .
.
- Calcoliamo
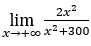 .
.
Come ![]() , lo faremo
, lo faremo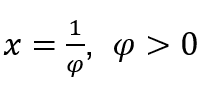 e
e ![]()
Rimanere con![]() perché il numeratore tende a 2 e il denominatore tende a 1.
perché il numeratore tende a 2 e il denominatore tende a 1.
- Calcoliamo
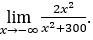
Come ![]() , lo faremo
, lo faremo ![]() e
e ![]()
Rimanere con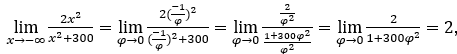 , perché il numeratore tende a 2 e il denominatore tende a 1.
, perché il numeratore tende a 2 e il denominatore tende a 1.
- Calcoliamo
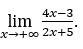
Come ![]() , lo faremo
, lo faremo 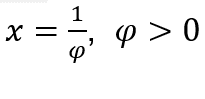 e
e ![]()
Rimanere con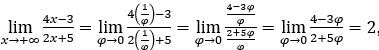 , perché il numeratore tende a 4 e il denominatore tende a 2.
, perché il numeratore tende a 4 e il denominatore tende a 2.
- Calcoliamo
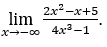
Come ![]() , lo faremo
, lo faremo![]()
![]() e
e ![]()
Rimanere con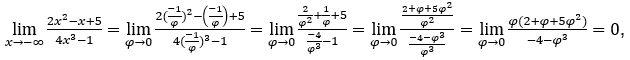 perché il numeratore tende a zero e il denominatore tende a -4.
perché il numeratore tende a zero e il denominatore tende a -4.
- Calcoliamo

Come ![]() , lo faremo
, lo faremo ![]() e
e ![]()
Rimanere con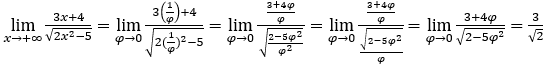 , perché il numeratore tende a 3 e il denominatore tende a
, perché il numeratore tende a 3 e il denominatore tende a ![]()
- Calcoliamo
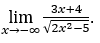
Come ![]() , lo faremo
, lo faremo![]()
![]() e
e ![]()
Rimanere con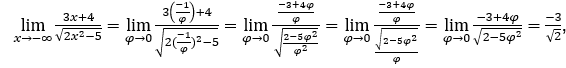 , perché il numeratore tende a -3 e il denominatore tende a √2.
, perché il numeratore tende a -3 e il denominatore tende a √2.
- Calcoliamo
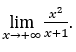
Come ![]() , lo faremo
, lo faremo![]() e
e ![]()
Rimanere con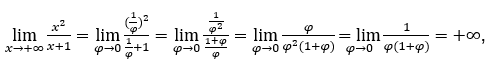 perché il numeratore è 1 e il denominatore tende a zero per valori positivi.
perché il numeratore è 1 e il denominatore tende a zero per valori positivi.
- Calcoliamo
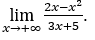
Come ![]() , lo faremo
, lo faremo ![]() =
= ![]() φ > 0 e φ → 0.
φ > 0 e φ → 0.
Rimanere con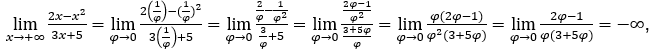 perché il numeratore tende a -1 e il denominatore tende a zero per valori positivi.
perché il numeratore tende a -1 e il denominatore tende a zero per valori positivi.
- Calcoliamo
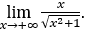
Come ![]() , lo faremo
, lo faremo ![]() e
e ![]()
Rimanere con 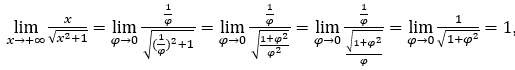 perché il numeratore è 1 e il denominatore tende a 1.
perché il numeratore è 1 e il denominatore tende a 1.
- Calcoliamo ora
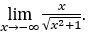
Come ![]() , lo faremo
, lo faremo![]() e
e ![]()
Rimanere con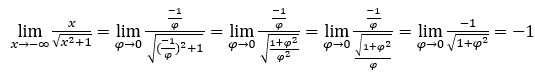 , perché il numeratore è -1 e il denominatore tende a 1.
, perché il numeratore è -1 e il denominatore tende a 1.
- Calcoliamo
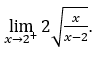
Come ![]() , dobbiamo fare
, dobbiamo fare ![]() ,
, ![]()
Rimanere con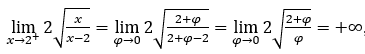 , perché il numeratore tende a farlo
, perché il numeratore tende a farlo ![]() e il denominatore tende a zero per valori positivi.
e il denominatore tende a zero per valori positivi.
- Calcoliamo ora
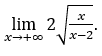
Come ![]() , lo faremo
, lo faremo ![]() e
e ![]()
Rimanere con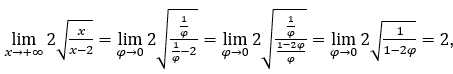 perché il numeratore tende a 2 e il denominatore tende a 1.
perché il numeratore tende a 2 e il denominatore tende a 1.
Osservazione.
Il calcolo dei limiti all’infinito non può essere applicato, ad esempio, alle funzioni trigonometriche, poiché alcune di esse variano in un determinato intervallo, altre aumentano o diminuiscono indefinitamente, a seconda del valore considerato.
Ad esempio, se proviamo a calcolare il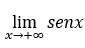 , passeremmo attraverso tutti i valori dell’intervallo infinite volte
, passeremmo attraverso tutti i valori dell’intervallo infinite volte ![]() , perché, per tutti
, perché, per tutti ![]() ,
, ![]() , cioè, non arriveremmo a nessun valore definito.
, cioè, non arriveremmo a nessun valore definito.
Infatti, le funzioni polinomiali, o funzioni espresse da rapporti tra polinomi, sono le più adatte per l’applicazione di limiti.
2. COMMENTI
1) Il calcolo del limite presentato è nato dall’identificazione dell’espressione ![]() tende ad un certo numero
tende ad un certo numero ![]() con uguaglianza
con uguaglianza ![]() , o
, o ![]() , insieme a
, insieme a![]() e
e ![]() , da quando, davvero, da quando
, da quando, davvero, da quando ![]() ,
, 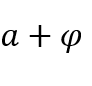 e
e ![]() tendere a
tendere a ![]() e con quello,
e con quello, ![]() tende a
tende a ![]()
Nel caso di limiti all’infinito, la sostituzione dell’espressione![]() tende a
tende a ![]() è stato
è stato ![]() , e la sostituzione dell’espressione
, e la sostituzione dell’espressione ![]() tende a
tende a ![]() è stato
è stato ![]() , insieme a
, insieme a ![]() e
e ![]()
La sostituzione ha più senso, perché, davvero, quando![]() , sempre per valori positivi,
, sempre per valori positivi,![]() tendere
tendere![]() e
e ![]() tende a
tende a ![]() , causando
, causando ![]() tendere davvero a
tendere davvero a ![]() o il
o il ![]() , nel caso che fosse.
, nel caso che fosse.
Se sostituiamo, nel caso in cui![]() tende a
tende a![]() o il
o il ![]() o
o ![]() per,
per, ![]() o
o 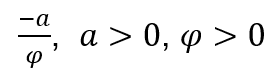 e
e ![]() , il risultato sarebbe lo stesso.
, il risultato sarebbe lo stesso.
Un esempio.
- Calcoliamo
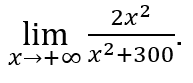
Lo faremo ![]() e
e ![]()
Rimanere con
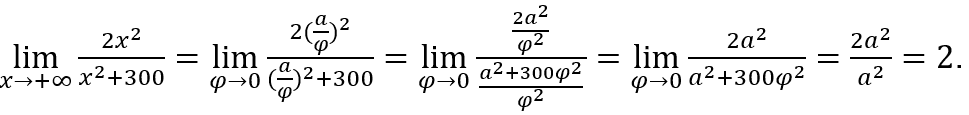
2. Come si vede nei vari esempi, il “calcolo limite” presentato è abbastanza “fluente” e di diretta applicazione, senza la necessità di consultare teoremi o di “organizzare” la funzione prima di eseguire il calcolo, salvo quando si deve razionalizzare.
Questo fatto porta molta tranquillità nel calcolare il limite di una funzione, in quanto il “calcolo” presentato è una vera sintesi di questo argomento.
Ad esempio, “calcolo” può essere utilizzato direttamente sopra la funzione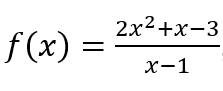 , senza bisogno di organizzarlo, cioè di esprimerlo come
, senza bisogno di organizzarlo, cioè di esprimerlo come 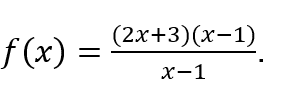
Vediamo. ![]()
Come![]() , possiamo fare, per esempio,
, possiamo fare, per esempio, ![]() e
e ![]()
Rimanere con
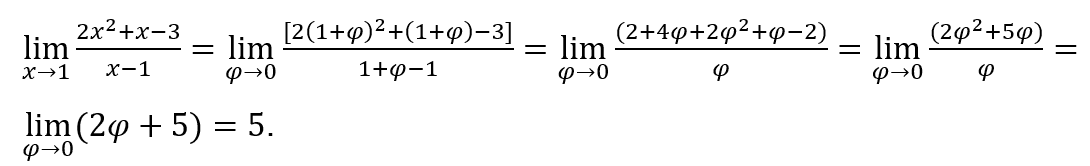
Ciò comporta un enorme vantaggio rispetto all’attuale presentazione di questo argomento che, oltre a non presentare alcun calcolo limite, si mostra abbastanza “bloccato” dall’immensa quantità di teoremi che devono essere considerati nelle “valutazioni” dei limiti, in quanto nonché delle “organizzazioni”, che si deve fare sulle funzioni prima di “stimarne” il limite.
3) Vorrei aggiungere, al “calcolo limite” presentato, alcune valutazioni di carattere pratico.
a) Ha senso solo calcolare il limite di una funzione vicino a un valore per il quale non è definita.
Se la funzione è definita per un certo valore, cioè se la funzione esiste per un certo valore, non ha senso calcolare il limite vicino a quel valore, poiché sappiamo quanto vale la funzione a quel valore.
Per esempio, essere![]()
Questa funzione è definita per tutti![]() , esiste per tutti
, esiste per tutti ![]()
Pertanto, sarebbe irragionevole calcolare, ad esempio,, ![]() , poiché la funzione esiste per
, poiché la funzione esiste per ![]() , cioè, perché calcolare questo limite se possiamo semplicemente sostituire
, cioè, perché calcolare questo limite se possiamo semplicemente sostituire ![]() di 3 pollici
di 3 pollici ![]() e otteniamo il valore della funzione a 3, cioè
e otteniamo il valore della funzione a 3, cioè ![]()
Con questo, centinaia di esercizi non hanno più motivo di esistere.
Ovviamente le funzioni considerate in questo articolo sono di ![]()
b) Utilizzando il concetto di limite, faremo qui un’osservazione sulla continuità di una funzione.
Secondo il libro di calcolo di Lethold (1994), la definizione di una funzione continua in un punto si traduce come segue:
Dizemos que a função ![]() é contínua no número a se e somente se as seguintes condições forem satisfeitas:
é contínua no número a se e somente se as seguintes condições forem satisfeitas:
(i) ![]() existe;
existe;
(ii) ![]() existe;
existe;
(iii) ![]()
Se uma ou mais de uma dessas condições não forem verificadas em ![]() , a função
, a função![]() será descontínua em
será descontínua em ![]()
Quindi Lima (1978) definisce la continuità di una funzione:
Uma função ![]() diz-se contínua no ponto
diz-se contínua no ponto ![]() quando é possível tornar
quando é possível tornar ![]() arbitrariamente próximo de
arbitrariamente próximo de ![]() desde que se tome
desde que se tome ![]() suficientemente próximo de
suficientemente próximo de ![]()
Em termos precisos, diremos que ![]() é contínua no ponto
é contínua no ponto ![]() quando, para todo
quando, para todo ![]() dado arbitrariamente, pudermos achar
dado arbitrariamente, pudermos achar ![]() tal que
tal que ![]() e
e ![]() impliquem
impliquem ![]()
Sappiamo che se una funzione è definita su un certo intervallo, cioè se esiste per ogni numero contenuto in un certo intervallo, allora non ha senso calcolare il limite di quella funzione per un certo numero in quell’intervallo, poiché possiamo valuta semplicemente la funzione su ogni numero in quell’intervallo.
In parole povere: se una funzione, rappresentata da una sola espressione, da una sola frase, esiste per un certo numero ![]() allora non è assolutamente necessario calcolare il limite della funzione per
allora non è assolutamente necessario calcolare il limite della funzione per ![]() , poiché, semplicemente, possiamo calcolare il valore della funzione in
, poiché, semplicemente, possiamo calcolare il valore della funzione in ![]()
Naturalmente, se dovessimo calcolare questo limite, come abbiamo fatto sopra, lo sarebbe ![]()
Come affermato sopra, ha senso calcolare il limite di una funzione solo attorno a un numero per il quale non è definito.
Pertanto, se stiamo analizzando funzioni rappresentate da una sola espressione, diciamo che esiste una funzione per un certo numero ![]() , significa che c’è un limite di questa funzione in
, significa che c’è un limite di questa funzione in ![]() questo limite è il valore della funzione in
questo limite è il valore della funzione in ![]() , e con ciò non abbiamo bisogno di calcolare il limite di questa funzione in quel numero
, e con ciò non abbiamo bisogno di calcolare il limite di questa funzione in quel numero![]()
Applicando questo alla definizione sopra di una funzione continua, gli elementi (ii) e (iii) della definizione diventerà superfluo, poiché nella voce (i) per affermarlo ![]() esiste.
esiste.
Pertanto, per le funzioni rappresentate da “una sola espressione”, la semplice affermazione che essa, la funzione![]() , è definito in un numero
, è definito in un numero ![]() cioè la semplice affermazione che
cioè la semplice affermazione che ![]() esiste è sufficiente per concludere che la funzione è continua in quel numero
esiste è sufficiente per concludere che la funzione è continua in quel numero![]()
Allo stesso modo, con questa osservazione sulle funzioni continue, centinaia di esercizi perdono la loro ragion d’essere.
Esempio: lascia la funzione ![]() che è definito per ogni numero reale, cioè esiste per ogni
che è definito per ogni numero reale, cioè esiste per ogni ![]() vero.
vero.
Pertanto, non è necessario calcolare il limite di![]() per nessun valore di
per nessun valore di ![]() , perché in questo caso, essere definito in
, perché in questo caso, essere definito in ![]() è sinonimo di avere un limite
è sinonimo di avere un limite ![]() e che questo limite è uguale al valore della funzione in
e che questo limite è uguale al valore della funzione in ![]() considerato.
considerato.
Poi la funzione ![]() è continua per tutti
è continua per tutti![]()
3. CONCLUSIONE
In quanto sopra, dimostriamo che, in effetti, la teoria dei limiti è carente in relazione a un calcolo del limite e, quindi, si circonda di una serie di argomentazioni basate sulla definizione di limite per colmare questa lacuna.
Presentiamo, quindi, il “calcolo del limite di una funzione” e mostriamo che esso riassume tutto l’argomento citato, avendo, quindi, diretta applicazione.
Ci auguriamo di poter contribuire a una migliore comprensione di una materia così fondamentale in matematica.
RIFERIMENTI
IEZZI, Gelson; MURAKAMI, Carlos et all. Fundamentos de Matemática Elementar, vol. 8, 1991.
LEITHOLD, Louis. O Cálculo com Geometria Analítica, vol. 1, 1994.
LIMA, Elon Lages. Curso de Análise, vol. 1, 1978.
MUNEM, Mustafa A. e FOULIS, David J. Cálculo, vol. 1, 1982.
[1] Laurea in Matematica presso l’Università di Brasilia.
Inviato: Giugno 2021.
Approvato: Agosto 2021.