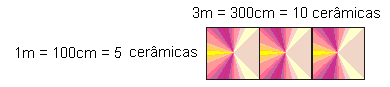ARTÍCULO ORIGINAL
SCHWANTES, Vilson [1], XAVIER, Márcio Pizzete [2], SCHWANTES, Eloísa Bernardete Finkler [3], SCHWANTES, Daniel [4], JUNIOR, Affonso Celso Gonçalves [5], KRACKE, Elisa [6], JUNIOR, Élio Conradi [7]
SCHWANTES, Vilson. Et al. Etnomatemática: Una reflexión sobre las matemáticas utilizadas por los albañiles. Revista Científica Multidisciplinar Núcleo do Conhecimento. año 04, Ed. 07, Vol. 13, págs. 46-66. Julio de 2019. ISSN: 2448-0959
1. RESUMEN
Este artículo es el resultado de reflexiones sobre etnomatemática y análisis de sesiones de estudio realizadas con Bricklayers en el municipio de Mercedes – PR. Encuentra motivación en los escritos del profesor Ubiratan D’ Ambrosio que reconoce la presencia del conocimiento matemático en diversos espacios culturales. El enfoque de la investigación investiga de forma dialogante con cada profesional, a través de situaciones problemáticas, que las matemáticas utilizan para hacer el presupuesto de la cantidad de cerámica necesaria para recubrir paredes y suelos. En la investigación realizada con los albañiles, fue interesante saber si estos eran formales o informales. Las declaraciones evidenciaron un entendimiento de que el conocimiento matemático es dinámico, un producto cultural, que emerge en diversos sectores de la actividad humana y circula en y a través del mundo de la vida, consolidándose en la escuela.
Palabras clave: educación matemática, etnomatemática, situaciones problemáticas, sesiones de estudio, presupuesto cerámico.
2. INTRODUCCIÓN
En todas las culturas, a lo largo de la historia, encontramos registros de actividades desarrolladas que denotan la existencia y necesidad de algún tipo de conocimiento matemático. Se trata de un conocimiento empírico, utilizado en el ejercicio de varias profesiones, pasado por generaciones y utilizado, a menudo, sin que la gente se dé cuenta de esta presencia.
Cuando se utiliza el razonamiento matemático para resolver una situación problemática, a veces es posible solución, sin necesariamente haber asistido a una escuela. El conocimiento matemático puede ser desarrollado naturalmente por la práctica diaria, por ejemplo, en el trabajo de los albañiles, profesionales que utilizan rutinariamente tales conocimientos.
Durante muchas décadas en la historia de la educación, el conocimiento derivado de las prácticas sociales fue ignorado y no discutido en la escuela. Hoy en día, la propuesta de investigar los conocimientos matemáticos presentes en los estudiantes ‘ vive fuera del contexto escolar está ganando cada vez más espacio. Este conocimiento construido por el hombre en el espacio y la temporalidad constituye un legado precioso que debe ser considerado en los planes de estudios escolares, o en la metodología adoptada. Hay muchos educadores que creen que el conocimiento del silo se puede construir a partir de conceptos presentes en la vida cotidiana de las profesiones, de las personas.
Para el profesor Ubiratan D’ambrósio, incluso antes de entrar en la escuela, todos los niños ya tienen conocimientos matemáticos. Este conocimiento es, para el investigador, una etnomatemática[8]. El autor quiere decirnos que el conocimiento no es sólo el resultado de años de estudio, sino también el fruto de las experiencias vividas entre los ciudadanos de los mismos o diferentes grupos sociales.
Según el investigador, la principal propuesta de Etnomathematics es buscar entender el conocimiento matemático / hacer de cada grupo de interés, comunidad, personas o nación. En este sentido, sus escritos consideran la etnomatemática:
“… Las matemáticas practicadas por grupos culturales, como comunidades urbanas y rurales, grupos de trabajadores, clases profesionales, niños de cierto grupo de edad, sociedades indígenas y tantos otros grupos que se identifican por objetivos y tradiciones Común a los grupos “. (2001, p.9).
El autor ve a Ethnomathematics como:
“… Una estrategia desarrollada por la especie humana a lo largo de su historia para explicar, entender, gestionar y convivir con la realidad sensible, perceptible y con su imaginaria, naturalmente dentro de un contexto natural y cultural” (D’ AMBROSIUS, 1996, p. 7)
Los albañiles, a veces analfabetos y la mayor parte del tiempo con poca educación, utilizan conocimientos matemáticos para construir casas, hacer anidamiento de cerámica, construir paredes, edificios, considerados todavía hoy en día, construcciones sólidas y robustas. Ciertamente existe en este trabajo, especialmente en los cálculos y en la organización del razonamiento matemático utilizado, un conocimiento que se puede aprovechar en el contexto escolar, o en la integración de los estudiantes con una tendencia a este tipo de profesión, ya sea en un enfoque Disciplina matemática más práctica. Para Carneiro,
[…] Enseñar matemáticas en esta concepción permitirá al alumno vincular los conceptos que trabajan en clase con su experiencia diaria, de acuerdo con su entorno natural, social y cultural. No se trata de rechazar las matemáticas académicas, sino de incorporar valores que se experimentan en experiencias grupales, teniendo en cuenta los lazos histórico-culturales (CARNEIRO, 2012, p. 3).
En las últimas décadas, el número de educadores que estudian etnomatemáticamente ha crecido como un programa de investigación y / o como una propuesta de trabajo pedagógico. Entre otros, los objetivos de estos profesores es conocer los procesos de generación, organización y difusión del conocimiento y las ideas matemáticas presentes dentro de los grupos culturales, y cómo desarrollar acciones en el campo de la enseñanza de las matemáticas que permitan Contextualización de los contenidos formales cubiertos en el aula.
La perspectiva de la Etnomatemática nos permite trabajar en el aula una propuesta educativa que fomenta a estudiantes y profesores en el desarrollo de la creatividad, dando lugar tanto a nuevas y ricas formas de aprendizaje. Esta riqueza sociocultural que se incorpora al proceso de aprendizaje docente, en palabras del profesor Ubiratan D’Ambrosio, forma parte “de un programa que tiene como objetivo explicar los procesos de generación, organización y transmisión de conocimiento en diversos Sistemas culturales y las fuerzas interactivas que actúan sobre y entre los tres procesos. ” (D’AMBRÓSIO, 1993, p.7).
Otra perspectiva de la etnomatemática ha sido desarrollada por la investigadora brasileña Gelsa Knijnik. Para este autor, la Etnomatemática
Estudiar los Discursos Eurocéntricos que instituyen Matemáticas académicas y escolares; Analizar los efectos de la verdad producida por los discursos de las matemáticas académicas y académicas; Discutir cuestiones de diferencia en la educación matemática, considerando la centralidad de la cultura y las relaciones de poder que la establecen; y examinar los juegos de idiomas que constituyen cada una de las diferentes matemáticas, analizando sus similitudes familiares. (KNIJNIK, 2006, p.120).
En los estudios de Knijnik, el autor caracteriza a la Etnomatemática como una matemática producida por grupos sociales que utilizan sus conocimientos para llevar a cabo sus actividades. Knijnik (2002, p. 33), haciendo un contrapunto entre las matemáticas formales e informa[9]les, reflexiona que[…] si -adquirir los conocimientos producidos por las matemáticas académicas, utilizando, cuando se enfrentan a situaciones reales, la que parece más apropiada.
Según Giardinetto (1999), “El maestro puede y debe utilizar el conocimiento diario como punto de apoyo al proceso de enseñanza-aprendizaje” (pág. 68), llevando al estudiante al campo de la argumentación, desarrollando el hábito de la lectura crítica, la investigación, Cuestionamiento, de creatividad, indispensable para la formación ciudadana. Así, se valoran y se evidencia el conocimiento previo de los alumnos, formando a partir de estos, otros conocimientos, siempre de los conocidos.
Lo importante es el establecimiento de lazos de conocimiento de la comunidad con el conocimiento de la escuela y el conocimiento de la escuela con el conocimiento de la comunidad. A través de este establecimiento y estas relaciones es posible atribuir significado a ambos conocimientos.
La tesis defendida por el autor es que la escuela, más que para reproducir el conocimiento diario, debe estar mediando entre esto y el conocimiento de la escuela, es decir, debe poner a disposición de las nuevas generaciones la sabiduría elaborada por la humanidad, que se revela como un producto Histórico y social. Estos conocimientos deben socializarse, ya que “no es el individuo singular construir todos los conocimientos, sino tener el derecho de acceso a este conocimiento constituido” (GIARDINETTO, 1999, p. 47).
Para D’ambrósio (2001), en este contexto, el conocimiento presenta un carácter dinámico, siempre abierto a nuevos enfoques. Para ello, el profesor debe mantenerse al día, realizar constantemente evaluaciones de su práctica, practicar nuevas metodologías de enseñanza, así como mejorar las acciones pedagógicas previamente experimentadas, en la perspectiva de que puedan contribuir a la Pedagógica.
Breda, Lima y Guimarés (2011, p. 15), en sus estudios afirman que:
Empecé a ver la propuesta de Etnomathematics como una posibilidad de diferenciar el trabajo que el profesor desarrolla en las escuelas, es decir, la práctica conteudista y sin sentido puede ser sustituta por un maestro orientado por una nueva mirada, que fomente La apreciación del contexto sociocultural de la educación, sus procesos de pensamiento y sus formas de entender, explicar y ejercer su práctica en la sociedad contemporánea u[…]na invitación a revisitar sus prácticas pedagógicas y sus efectos o incluso mirar su papel, Como profesor que se ocupa de diferentes perspectivas de la asignatura en el contexto escolar.
Así, en el contexto escolar, como un programa de estudio que busca conocer y entender los conocimientos producidos y utilizados dentro de diferentes culturas, la etnomatemáticación se puede explorar para ayudar en el trabajo de enseñanza, haciendo que los estudiantes puedan Comprender las diversas “matemáticas” utilizadas en otros contextos, valorando la diversidad cultural y el desarrollo intelectual y creativo de cada pueblo, de cada cultura o comunidad.
Los profesores de matemáticas, según D’ambrosius (2001), tenemos que ser claros y estar en perfecta armonía con nuestro papel de educador frente a la misión de preparar a nuestros jóvenes para un futuro feliz. Necesitamos enseñar Sí matemáticas, pero también sobre la humanidad. A este respecto, el autor hace hincapié en que,
La propuesta pedagógica de la Etnomatemática es hacer de las matemáticas algo vivo, lidiando con situaciones reales en el tiem[agora]po y el espaci[aqui]o. Y, a través de la crítica, cuestionando el aquí y el ahora. Al hacerlo, nos sumergimos en raíces culturales y practicamos dinámicas culturales. Estamos reconociendo efectivamente en la educación la importancia de diversas culturas y tradiciones en la formación de una nueva civilización, intercultural y transdisciplinaria. (D’AMBRÓSIO, 2001, p. 46).
Para que esto sea una realidad, el profesor necesita revisar diariamente su práctica docente, elaborar un proyecto pedagógico que valore siempre el conocimiento y la historia de cada alumno, buscando en esta individualidad un nuevo y práctico contexto para el arte de Enseñar. Es importante que el maestro en el aula, además de disfrutar y partir del conocimiento que el alumno aporta del entorno en el que vive, lo anime a creer que también desempeña un papel importante en la (re) construcción de conocimientos sociales y culturales, así como conocimientos Matemático.
En palabras de Rosa Neto, las matemáticas deben interpretarse como un producto sociocultural natural de un pueblo, porque,
Las matemáticas fueron creadas y ha sido desarrollada por el hombre de acuerdo a sus necesidades. (…) La cultura es una forma de adaptación porque es una forma de actuar sobre el medio ambiente que se construyó junto con ella. (ROSA NETO, 2002, p.7 e 19).
En este contexto, existe una relación significativa entre las matemáticas y la cultura, tanto como resultado de nuestra adaptación según las necesidades de supervivencia a través de los tiempos, representando la cultura que nos han dejado las generaciones pasadas, un legado empírico , sistemático y científico.
3. JUSTIFICACIÓN
Las matemáticas siempre han sido consideradas como una ciencia base de varias áreas del conocimiento. El dominio de sus conocimientos es fundamental para resolver situaciones problemáticas en varias áreas. Dada esta importancia y relevancia es necesario buscar nuevas formas (métodos) para enseñarlo, buscando siempre una mayor eficiencia para el proceso de enseñanza-aprendizaje en el contexto escolar.
Muchas investigaciones en el área también destacan los bajos ingresos de los estudiantes con respecto al aprendizaje de la disciplina, diciendo que hay una necesidad de una mayor contextualización de los contenidos para producir un mejor aprendizaje. Su enseñanza considerada, a menudo por estudiantes, padres e incluso maestros, como abstracto, distante de la realidad, es decir, lo que se enseña en el aula, se les presenta distantes de las necesidades diarias fuera de la escuela.
Esta falta de vínculo con la vida cotidiana y, también, el exceso de simbología que se enseña en matemáticas en las escuelas, a veces promueve la difusión de ideas equivocadas en relación con esta disciplina en el contexto escolar. La tesis que defendemos encuentra fundamentos teóricos en los escritos del profesor Ubiratan D’ambrósio, en la perspectiva de que la producción de conocimiento matemático no puede separarse de los movimientos sociales y la cultura de quienes producen este conocimiento.
En este sentido, podemos afirmar que hay un entretejido entre las matemáticas producidas, la sociedad que la produce y la cultura que subvenciona esta producción. Este entretejido está construido a varias manos a través de un proceso cognitivo, mediado por la acción creativa de varios actores, todos motivados por la necesidad de leer, entender y explicar la realidad en la que viven.
Si nos fijamos en la historia de la humanidad y las ciencias, percibimos que no sólo las matemáticas, sino también otras áreas del conocimiento se construirán y reconstruirán, siendo resignados en cada momento histórico y de acuerdo con las demandas de la sociedad. Pompeyo y Monteiro (2001), en el libro Las Matemáticas y los temas transversales enfatizan que el maestro necesita entender el alcance actual de su papel en la sociedad, porque, según los autores,
Los profesores actuales se enfrentan a un gran reto: educados en un proceso fragmentado, tendrán que superar los límites que esta formación les impone y extrapolar los límites de los contenidos vistos de forma parcial e histórica (POMPEU y MONTEIRO, 2001, p. 15).
Dadas las exigencias de tal magnitud, es necesario que busquemos entender el proceso epistemológico de las matemáticas, es decir, el proceso generativo de este conocimiento, la razón de su organización y sistematización. Minimizar este marco ha sido en las últimas décadas una preocupación de varios educadores e investigadores.
Para Rolim,
Pensar en el contexto histórico-cultural en el proceso de enseñanza del aprendizaje de las matemáticas es considerar que “hacer” implica más que reglas y técnicas; reconocer que como ciencia, las matemáticas son en sí mismas un edificio de la humanidad (ROLIM, 2010, p. 43).
Es un hecho que la propuesta educativa caracterizada por prácticas educativas que promueven la educación sociocultural, permitiendo en el aula el establecimiento de relaciones de aprendizaje para satisfacer las necesidades diarias de los estudiantes, ha ido creciendo Cada vez más como alternativa pedagógica. Según D’ambrósio, esto significa construir condiciones para que el alumno también pueda hacer frente en el aula a diferentes situaciones de su vida diaria.
Es una perspectiva que hace más contextualizada la enseñanza de las matemáticas, con valoraciones e inquietudes de carácter sociocultural. Según D’ambrósio (2001), la Etnomatemática es el área de la educación que busca reflexionar sobre el conocimiento matemático que se genera a partir de la interacción en un grupo cultural en particular. Para el autor, las clases de matemáticas, en esta perspectiva, se basan en los conocimientos matemáticos desde el exterior hasta el aula, y estos conocimientos deben desarrollarse a partir de la experiencia del estudiante.
D’ambrósio (2001, p. 22) A este respecto, también hace la siguiente declaración:
La vida cotidiana está impregnada del conocimiento y la creación de la cultura. En cada momento, los individuos están comparando, clasificando, midiendo, explicando, generalizando, infiriendo y, de alguna manera, evaluando, utilizando los instrumentos materiales e intelectuales propios de su cultura (D’ambrósio, 2001, p. 22).
En nuestro estudio, la pregunta guía fue: ¿Qué tipo de matemáticas (formales o informales) utilizan albañiles para hacer el presupuesto de la cantidad de cerámica necesaria para recubrir paredes y pisos. Era evidente que el masón profesional ejerce sus funciones de trabajo utilizando habilidades matemáticas aprendidas de la práctica diaria. Para Monteiro (2002, p. 102), “El know-how cultural tiene otras rutas de validación, otra lógica para su configuración. La pregunta es por qué uno se ha vuelto universal y legitimado y el otro no lo es. ” En esta perspectiva, el autor nos remite a situaciones similares a las experimentadas en esta investigación.
Según Gerdes:
Durante siglos, los albañiles, a veces analfabetos y, la mayoría de las veces, con muy poca educación, construyen casas, paredes y otros edificios, todavía considerados construcciones sólidas y robustas hoy en día. Así, existe en su trabajo, en la forma en que hacen sus cálculos y organizan su razonamiento matemático, una sabiduría que puede ser rejada en el contexto escolar, o en la integración de ciertos estudiantes con tendencia a este tipo de profesiones o en un Enfoque más “práctico” y más cercano a la vida cotidiana para los estudiantes en general. Esta situación se menciona en el trabajo de esta línea de investigación, a saber, en la terminología de Gerdes, como “matemáticas oprimidas”, o “matemáticas ocultas o congeladas” (GERDES, 1991, p. 29).
En la investigación partemos de la suposición de que los albañiles, grupo elegido para hacer esta investigación, constituyen un grupo de trabajadores que hacen uso diario de una amplia variedad de conocimientos matemáticos en su vida diaria y sin este conocimiento no sería desarrollar o realizar cualquier actividad en la construcción civil. Sin embargo, teniendo en cuenta que generalmente tienen poca educación, fue interesante saber cómo adquirieron estos conocimientos matemáticos o si se proporcionaron a través de la práctica diaria.
En este contexto, este trabajo de investigación también puede contribuir a desmitificar la idea de que las matemáticas son una ciencia para pocos, entendiendo que no hay un solo lenguaje matemático, sino múltiples formas de pensamiento Matemática, cada una organizada y estructurada dentro de su contexto social.
Para ambos la escuela necesita desarrollar proyectos educativos que permitan el intercambio de experiencias con actividades donde las matemáticas se utilizan diariamente. En esta interacción, además de permitir el intercambio de experiencias, se crean lazos y se establecen otras relaciones pedagógicas con el mundo vivido fuera de la escuela y esto puede ser un camino facilitador en el aprendizaje de la disciplina.
Según D’ambrósio, las clases de matemáticas deben basarse en los conocimientos matemáticos desde el exterior hasta el aula, y este conocimiento debe desarrollarse a partir de la experiencia del estudiante. Por lo tanto, el autor afirma que el conocimiento etnomatemático del grupo/comunidad tiene mucho valor, porque sirve, es eficiente y adecuado para muchas cosas, propio de esa cultura, a ese etno, y no hay necesidad de reemplazarlo. Del mismo modo, las matemáticas del grupo dominante le sirven, es útil y no hay manera de ignorarlo (D’ambrósio, 2001, p. 80).
Para Carneiro,
[…] Enseñar matemáticas en esta concepción permitirá al alumno vincular los conceptos que trabajan en clase con su experiencia diaria, de acuerdo con su entorno natural, social y cultural. No se trata de rechazar las matemáticas académicas, sino de incorporar valores que se experimentan en experiencias grupales, teniendo en cuenta los lazos histórico-culturales (CARNEIRO, 2012, p. 3).
4. PROBLEMATIZING PARA CONOCER LAS MANERAS DE MATEMATIZAR DE LOS BRICKLAYERS
En el trabajo de investigación realizado con el grupo de albañiles, elaboramos algunas situaciones problemáticas, para comprobar que las matemáticas son utilizadas por estos profesionales para hacer el presupuesto de la cantidad de cerámica necesaria para recubrir paredes y suelos. Este estudio se llevó a cabo desde la perspectiva de D’ambrósio y ROSA, que consideran la Etnomatemática como un programa de investigación en historia y filosofía de las matemáticas, con implicaciones pedagógicas, cuando los autores consideran:
Así, este programa de investigación representa una metodología de investigación que busca analizar las prácticas matemáticas locales, ya que busca valorar, difundir y respetar el conocimiento matemático (ideas, nociones, procedimientos, procesos y prácticas) que Origen en diversos contextos culturales a lo largo de la historia (D’AMBRÓSIO y ROSA 2016, p. 17).
Situación-Problema: Para calcular el número de baldosas rectangulares de tamaño cm, [20 por 30]necesario para recubrir el suelo del baño de una galería de arte, dimensiones 6, 00m por 4, 50m (Lezzi, 1996, p. 223), Oscar considerado como “punto de partida las dimensiones del suelo del suelo del piso de la Baño. Tomando el tamaño de la cerámica, vamos a optar por 6m que es divisible tanto por el lado cerámico de los 20cm como en los 30 cm. Ya los 4, 50m no.
Esta medida sólo es divisible por el 3[medida do outro lado da cerâmica]0. Por lo tanto, opté por lo que sería más simple, tomando los 6m [600cm]divididos por 30cm, alcanzando el número exacto de 20 cerámicas en la dirección de la longitud. Ahora, tomando la cerámica en la dirección del lado de 20cm llegué al número de 30 lajotas.
Ya en los 4, 50m, divisible por 30, tomé el 4, 50m [450cm]y dividido por 30cm, alcanzando el número de 15 azulejos que caben en la anchura. Así que hay 15 azulejos en el sentido de los 30 cm. Para llegar al cálculo tomé los 30 azulejos que van en la longitud m[600cm]ás los 15 que van en ancho, se multiplicaron y alcanzaron el número de azulejos necesarios, que sería 450 azulejos “.
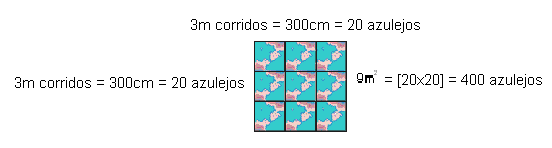
El razonamiento empleado por el Mason Sérgio para hacer este mismo presupuesto, demuestra, según D’ambrosius (2001) que “en diferentes ambientes, la etnomatemática es diferente” (pág. 35). Así, el Masón comienza su discurso enfatizando que “primero hay que descubrir los metros cuadrados de la zona, serían tiempos[operação de multiplicação]. Encontré 27m2, así que tengo que averiguar cuántas baldosas caben en un metro cuadrado. Como los 30c[medida do comprimento da placa cerâmica]m no dieron precisión en un metro, yo estaba aumentando y usé 3m, luego cerrado con 10 lajotas. Este resultado de 10 azulejos, multiplicado por 5 azulejos que caben en ancho. Encontré el número de 50 azulejos en 3m2 “. Visualice en secuencia el pensamiento deductivo utilizado por el albañil para poder hacer el presupuesto.
Continuando con la explicación, Sérgio informa que después de que se encontró con que en 3m2 caben 50 piezas, fue sólo “… Tome estos 27m2, dividir por 3 que me resultó 9 partes iguales. Por lo tanto, 9 veces 50, da el resultado de la cantidad de cerámica que va a través de la zona. Son 450 cerámicas y todavía tienen que ver la rotura. ”
El cálculo del presupuesto realizado por el Mason Alberto, también señaló “450 cerámicas. Hice side times de lado de cerámica, 0, 20m por 0, 30m alcanzando el número 0, 06m2. Este resultado representa el área de cada cerámica. Ahora hice tiempos laterales lado del suelo del baño, 6m por 4, 50m y alcanzó el resultado de 27m2. Entonces, la superficie del baño, 27m2 dividido por los metros cuadrados de una parte 0, 06m2, dio 450 cerámicas “.
En la resolución del enunciado: cuántas baldosas cuadradas de 15cm a parte de los mismos se necesitan para recubrir internamente una piscina con 15m de longitud, 6m de ancho y 1, 20m de profundidad (LEZZI,1991, p. 195), Oscar informó: “Elegí convertir estos 15m en 1.500 cm divididos por 15cm de la Lajota, dio lugar a 100 azulejos en la longitud de un lado de la piscina. Así que en el otro lado dará el mismo número, es decir, esta fila multiplicada por 2, da 200 azulejos, que caben en ambos lados de la longitud.
El mismo procedimiento que utilicé en la anchura, a saber, el 6m es 600cm y estos 600cm divididos por 15 me dio 40 azulejos que irían en un ancho. Como tenemos dos anchos aquí, multiplicando por 2, encontré 80 azulejos. Añadiendo 200 azulejos de longitud con 80 de ancho, llegué al número de 280 azulejos, que necesitan ser multiplicados por la profundidad que es 1, 20m, es decir 120cm. Antes, sin embargo, dividí estos 12[medida da profundidade]0cm, por 15c[medida do azulejo]m y encontré 8 azulejos que irían en la profundidad de la piscina. Ahora, tomando la longitud y sumando con el ancho, me refiero a los 200 azulejos más los 80 azulejos, veces las 8 baldosas de la profundidad, llegué al número de 2.240 azulejos.
Todavía tenemos que encontrar el número de azulejos de la parte inferior de la piscina. Esto es fácil de calcular porque las dimensiones de longitud y anchura de la parte inferior son las mismas que los lados, media 6m por 15m. Por lo tanto, van 100 cerámicas de longitud y 40 en el ancho de la parte inferior, totalizando 4.000 cerámicas en la parte inferior de la piscina. Añadiendo el número de azulejos de los lados y la parte inferior llegué al número de 6.240 cerámicas “. El Mason también destacó que “siempre necesitará una reserva” para evitar posibles averías, entre otras.
El reconocimiento de la existencia de “otras formas de pensamiento”, como postula D’ambrósio (2001, p. 17), es evidente en el razonamiento matemático empleado por Sérgio para hacer este mismo presupuesto. Al comunicar su pensamiento el albañil destaca que “primero necesito conocer los metros cuadrados de par[laterais]ed y suelo. 15m más 6m, más de 15m y más 6m, daría el lateral[42m corridos]. Esto por 1, 20m,[profundidade da piscina] da 50, 4m2 de área.
Entonces encontraré las imágenes de abaj[15m vezes 6m = 90m2]o. Todos lo somos. Lo hice y di 140, 4m2. Ahora necesito averiguar cuántas baldosas caben en cada metro cuadrado. Sólo que como las baldosas son 15cm por 15cm, en un metro n[corrido]o se cierra. Entonces estaba agregando hasta que llegué a 3m. En 3m[corridos], hay 20 lajotas. Luego tomé 3 por 3, [multiplicado por]se[cada face da piscina representa uma figura plana – duas dimensões]ría un total de 9m2 que dio 400 Lajotas “. Visualizar en la representación que sigue, el razonamiento empleado por el albañil para el esclarecimiento de la situación problemática.
Continuando con la explicación de sus procedimientos, Sérgio sigue: “Tomé el total de M2 de la piscina, dividido por 9[9 partes]. Dio 15,6 partes iguales de 9m2 cada un[140,4m2 : 9m2 = 15,6]a. Estas 15,6 piezas equivalen a la cantidad de cerámica que estaba en 9m2, es decir, 400 cerámicas. Entonces, en cada parte sería 15,6 veces 400, igual a 6.240 cerámicas”.
Cuestionado incluso si el presupuesto de 6.240 cerámicas daría suficiente para recubrir la piscina, Sérgio destaca fácilmente: necesitaría alrededor de un 5% más de este total debido a la rotura.
Para el profesor D’Ambrosio, los grupos humanos producen conocimientos que, aunque no están muy extendidos en los espacios formales de enseñanza, es un conocimiento válido y que la escuela, así como la investigación en educación matemática necesitan reconocer y profundizar para enriquecer el acto Educativo.
D’ambrósio (2001, p. 22-23), señala además que,
Hay numerosos estudios sobre la etnomatemática de la vida cotidiana. Es una etnomatemática no aprehendida en las escuelas, sino en el entorno familiar, en el entorno de los juguetes y el trabajo, recibidos de amigos y colegas.
La resolución de este problema de situación para Alberto mostró un conocimiento que se identifica con el procedimiento que sería utilizado por un profesor de matemáticas. Nota su explicación: “La longitud de los lados de la piscina 15m + 15m, también añadiendo la anchura 6m + 6m da el perímetro de la piscina, 42m. Ahora 42m por 1, 20m de la profundidad de 50, 40m2 de área en los lados de la piscina. La parte inferior de la piscina tiene superficie de 15m por 6m y da 90m2. Añadiendo el área lateral y la parte inferior, me refiero a los 50, 40m2 más los 90m2 da 140, 40m2. Esto dividido por el tamaño de la baldosa que es 15cm por 15cm y que en M2 da 0, 0225m2, totaliza 6.240 azulejos. Ahora sólo tiene que añadir un poco al búfer de interrupción. ”
Para Demo (1996), la construcción del conocimiento parte del conocimiento incorporado por cada individuo en su experiencia sociocultural. Esto ha sido evidente en las formas de matematizar utilizadas por cada uno de los albañiles. Para el autor “No hay tablero superficial, analfabetismo absoluto; Todos hablan, se comunican, utilizan un vocabulario básico, manejan conceptos dentro del sentido común, tienen referencias a la realidad en la que se insertan”(p. 32).
Al entrar en la escuela, todo el mundo ya ha acumulado algún conocimiento, incluso si está dentro del sentido común. Compartimos con D’ambrosius (1993), cuando postulamos que tenemos que entender que cuando comienza la educación formal, el niño ya tiene una etnomatemática que le permite enfrentar las interpretaciones de las matemáticas sistemáticas de la escuela.
Las formas Matematizar de los albañiles denotan según Marqués (2000) que “los procesos de aprendizaje se insertan inevitablemente en comunidades comunicativas y públicas en las que los hombres aprenden unos de otros y unos con otros” (pág. 29). Según la comprensión de Pompeyo y Monteiro (2001), “un proceso educativo significativo comienza con la interacción de la escuela y la comunidad” (pág. 55), cuyas relaciones pueden resignar el papel de la escuela como un lugar privilegiado para el intercambio de experiencias a Comprender mejor el conocimiento que circula en la vida cotidiana.
En las manifestaciones (verbalizaciones) expresadas por los albañiles en las sesiones de estudio, especialmente a partir de la realización matemática de estos profesionales, en base a su experiencia laboral, en el intercambio de conocimientos que ya han participado a lo largo de sus vidas, muestran Que es posible que la educación formal valore y valide este conocimiento previo, su cultura y su entorno social. Creemos que un trabajo educativo que deja, en la vía diálogo de este conocimiento, Enrique y contextualiza el conocimiento matemático de la escuela.
En palabras de Rolim
Pensar en el contexto histórico-cultural en el proceso de enseñanza del aprendizaje de las matemáticas es considerar que “hacer” implica más que reglas y técnicas; reconocer que como ciencia, las matemáticas son en sí mismas un edificio de la humanidad (ROLIM, 2010, P. 43).
En nuestra comprensión, desde esta perspectiva, se establece en el acto educativo una relación ampliamente utilizada en el mundo de los negocios, donde se habla y se practica la expresión “ganar-ganar”. En una negociación, esta expresión tiene una característica: nadie pierde, todos ganan. Se establece entre la empresa y el proveedor una relación ideal.
Para la Ley Educativa, esta relación es pedagógicamente ideal, es decir, estudiantes, profesores, todo el contexto que forma parte del proceso educativo, siendo felices, triunfando. Entonces se entiende que, al igual que en los negocios, es posible lograr pedagógicamente en el aula la relación “ganar-ganar”, simplemente hacer una buena y nueva planificación, en la que se inserta esta posibilidad.
Una perspectiva pedagógica en la que, así como en el mundo empresarial, donde el empresario y el proveedor deben exponer sus percepciones, sus puntos de vista y sus ideas de manera adecuada y en el momento oportuno, sin juzgar entre sí el comportamiento del otro, en la escuela, de alguna manera Profesor respetando y valorando los conocimientos previos de sus alumnos.
Y cuando en la escuela, el conocimiento de la vida cotidiana entra en “confrontación” con el conocimiento formal, que podemos recordar dialógicamente que en el mundo de los negocios, a menudo el proveedor piensa diferente del empresario, sin embargo, esta relación no es o nunca debe ser Conflicto o causar algún desgaste. Necesita en la escuela, así como en los negocios, representar una gran oportunidad de aprendizaje para todos los involucrados en este proceso.
Los discursos de los albañiles, participantes de la investigación, mostraron que los conocimientos de matemáticas que poseen, fueron adquiridos la mayor parte del tiempo en el desarrollo y mejora de su profesión, en el práctica del día a día, o incluso, viendo a otros realizar la La misma actividad.
Las conversaciones que tuvimos con los albañiles a lo largo de las sesiones de estudio mostraron que los conocimientos producidos fuera del ámbito escolar son importantes y le concierne al maestro rescatarlos y acercarlos al aula, haciendo que la educación formal sea significativa y Articulado con la realidad en la que se inserta el estudiante.
5. OBJETIVOS
5.1 Demostrar que la Etnomatemática es parte de nuestra vida diaria y reflexionar sobre la posibilidad de que los grupos sociales [pedreiros]organizados produzcan matemáticas en sus diferentes formas de expresión dentro de su ámbito de acción, discutiendo en la escuela las formas de producir Significados de la vida cotidiana; 5.2 Presentar la Etnomatemática como uno de los caminos hacia una educación renovada, dentro del mayor movimiento llamado educación matemática, hecho posible desde esta perspectiva, por la reflexión entre profesor, estudiante y comunidad, tratando de superar la Conocimiento que ambos poseen, modificándolos y transformando el aula en un espacio democrático de intercambio de conocimiento; 5.3 Percibir la etnomatemática como una interesante alternativa pedagógica al trabajo en el aula, desmitificar las matemáticas y abordar las necesidades reales del día a día de los estudiantes.
6. METODOLOGÍA
El trabajo de investigación se llevó a cabo a través de diferentes momentos, a saber: estudio bibliográfico sobre etnomatemática, sesiones de estudio con albañiles en las que se propuso-problema situaciones con el propósito de investigar Profesional sobre los conocimientos matemáticos que uti[formais ou informais]lizan para hacer el presupuesto de la cantidad de cerámica necesaria para recubrir paredes y suelos. Reflexión sobre posibles conexiones entre las matemáticas y la realidad en la posibilidad de establecer vínculos entre el conocimiento matemático del albañil, construido a partir de sus necesidades de día a día profesional, utilizando prácticas La vida cotidiana y las matemáticas escolares.
7. CONTRIBUCION EXPECTADA
Teniendo en cuenta que a lo largo del trabajo de investigación, basado en el discurso de los albañiles, percibimos que estos profesionales para resolver las situaciones problemáticas propuestas, no siempre fueron apoyados en el conocimiento de las matemáticas escolares.
Mientras que estaba claro que los albañiles aplicaban los conocimientos matemáticos de una manera práctica e intuitiva, utilizando estrategias específicas, no utilizando las fórmulas matemáticas que se enseñan en la escuela.
Esperamos que la enseñanza de las matemáticas en el aula a través del enfoque etnomatemá[10]tico permita a profesores y estudiantes aprender sobre la diversidad cultural misma de las matemáticas. Que los resultados de esta investigación ayuden en el desarrollo de una metodología que contribuya a la enseñanza de las matemáticas, aportando posibilidades de cambios en la práctica docente, abordando la práctica pedagógica escolar con los conocimientos producidos en situaciones De la vida de los estudiantes.
Que a partir de esta reflexión la práctica pedagógica en el aula puede reorientarse al desarrollo de la plena ciudadanía de los alumnos. Que, según Pinheiro y Rosa (2016), el:
[…] Los profesores de matemáticas se sumergen en la dinámica cultural de los estudiantes y utilizan estrategias de enseñanza y aprendizaje que valoran la dimensión cultural en el aula, para que se pueda desarrollar una educación matemática inclusiva que pueda desarrollarse eficazmente Contribuir a la transformación social (pág. 79).
Así, a partir de las sesiones de estudio y del texto elaborado, pretendemos provocar a los lectores la posibilidad de intervención pedagógica, basada en la realidad del alumno, uniendo la teoría y la práctica en la construcción del conocimiento sinfín. También se espera que las reflexiones resultantes de la lectura del texto permitan una nueva mirada a la realidad y a la educación matemática, desde la perspectiva de la producción de conocimiento desde la práctica diaria.
El objetivo es contribuir a la Constitución del profesor investigador de su práctica, despertándole a aprender de manera continua a ser profesor, de acuerdo con las necesidades educativas actuales, transformando el aula en un ambiente de intercambio de conocimientos, Rescatar el conocimiento histórico socialmente construido por la humanidad.
8. REFERENCIAS BIBLIOGRÁFICAS
BREDA, Adriana LIMA, Valderez Marina do Rosário e GUIMARÃES, Gleny Terezinha Duro. A utilização da Etnomatemática nos cursos de formação continuada de professores: implicações das relações de poder saber na produção de subjetividades. Curitiba. Novembro de 2011. Disponível em: http://educere.bruc.com.br/CD2011/pdf/4668 _ 2898.pdf. Acessado em: 20/08/2017.
CARNEIRO, K. T. A. Cultura Surda na aprendizagem matemática da sala de recurso do Instituto Felipe Smaldone: uma abordagem etnomatemática. Anais do 4º Congresso Brasileiro de Etnomatemática. Belém, PA: ICEm4, 2012.
D’Ambrósio Ubiratan. Etnomatemática: Arte ou técnica de explicar e conhecer. Editora Ática, Série Fundamentos, 2. edição, São Paulo, 1993.
——-. Educação matemática: da teoria à prática. 13ª ed. Campinas: Papirus, 1996. (Coleção Perspectivas em Educação Matemática).
————-. Etnomatemática – elo entre as tradições e a modernidade. Coleção Tendências em Educação Matemática, 1. Belo Horizonte: Autêntica, 2001, 112p.
D’AMBROSIO, U.; ROSA, M. Um diálogo com Ubiratan D’Ambrosio: uma conversa brasileira sobre etnomatemática. In BANDEIRA, F. A.; GONÇALVES, P. G. F. (Orgs.). Etnomatemáticas pelo Brasil: aspectos teóricos, ticas de matema e práticas escolares. Curitiba, PR: Editora CRV. 2016. pp. 13-37.
DEMO, Pedro. Pesquisa e construção de conhecimento: Metodologia científica no caminho de Habermas. 3.ed. Rio de Janeiro: Tempo Brasileiro, 1996. 125p.
GERDES, Paulus. Etnomatemática: Cultura, Matemática, Educação. Maputo. Instituto Superior Pedagógico, 1991.
GIARDINETTO, José Roberto Boettger. Matemática escolar e matemática da vida cotidiana. Coleção polêmicas do nosso tempo, autores associados, Campinas – São Paulo, 1999, 128p.
LEZZI, Gelson; Dolce, Osvaldo; Machado, Antonio. Matemática e Realidade. 5ª série, 3. edição reformulada, Atual, São Paulo, 1996, 250p.
————–. Matemática e Realidade. 5ª série, 2. edição, Atual, São Paulo, 1991, 213p.
KNIJNIK, Gelsa. O saber popular e o saber acadêmico na luta pela terra. Revista da Sociedade Brasileira de Educação Matemática. Educação Matemática em Revista. Ano 9, n. 1, p. 27-39, 2002.
————–. Educação matemática, culturas e o conhecimento na luta pela terra. Santa Cruz do Sul, EDUNISC, 2006, 239 p.
MARQUES, Mário Osorio. A aprendizagem na mediação social do aprendido e da docência. Ijuí, Editora UNIJUÍ, 2. edição, 2000, 144 p.
MONTEIRO, A.; Pombeu, G. Jr. A matemática e os temas transversais. Editora Moderna, São Paulo, 2001, 160p.
MONTEIRO, Alexandrina. Reflexão e Ação: Revista do Departamento de Educação/UNISC. Vol. 10, n. 1 (jan./jun.2002) — Santa Cruz do Sul: EDUNISC, 2002.
A Etnomatemática em Cenários de Escolarização: alguns elementos de reflexão. Alexandrina Monteiro, p. 93 – 108.
PINHEIRO, R. C.; ROSA, M. Uma perspectiva etnomatemática para o processo de ensino e aprendizagem de alunos Surdos. RPEM, v. 5, n. 9, p. 56-83, 2016.
ROLIM, Carmem Lucia Artioli. Fórmulas de Silêncio: metodologias no processo de ensino da Matemática. In: SANTOS, Jocyléia Santana. ZAMBONI, Ernesta. Potencialidades Investigativas da Educação. Goiânia: Ed. da PUC Goiás, 2010.
ROSA NETO, R. Didática da matemática, São Paulo: Ática, 2002.
8. Entendido con una práctica pedagógica que valora las matemáticas de diferentes grupos culturales, teniendo en cuenta los conceptos informales construidos por las asignaturas a través de sus experiencias fuera del contexto de la escuela.
9. En esta reflexión, tratamos las matemáticas formales e informales en la idea de que la primera se considera de una escuela, científica, sistemática, legitimada y asociada con contextos de aula y la segunda como conocimiento diario, espontáneo, del día a día, Asociado con las calles, la experiencia y la vida en comunidades, contextos sociales.
10. En este trabajo se utilizó para designar la investigación de las concepciones, tradiciones y prácticas matemáticas de un grupo[pedreiros] social y el trabajo pedagógico que se puede desarrollar en la perspectiva que el grupo interpreta y codifica sus conocimientos; Adquirir los conocimientos producidos por las matemáticas académicas, utilizando, cuando se enfrenta a situaciones contextualizadas, la que parece más apropiada.
[1] Master en Ciencias de la Educación – Matemáticas, UNIJUI – RS. Licenciatura y Especialización en Ciencias y Matemáticas. Prof. Asistente del CCA – Centro de Ciencias Agrícolas, Campus del Mariscal Cândido Rondon, UNIOESTE, PR – Brasil.
[2] Máster en Desarrollo Rural Sostenible-UNIOESTE, Especialista en Matemáticas, Física-UNIPAR, Gestión de Personas y Educación Especial con énfasis en Discapacidad Múltiple-UNIASSELVI, Graduado en Matemáticas con énfasis en Física-UNIPAR.
[3] Especialización en Enseñanza de Ciencias Exactas – Matemáticas, Física y Química. UNIOESTE – Universidad Estatal de Paraná Occidental. Graduación: Ciencias y Matemáticas. UNIJUI, RS. Profesor de la Escuela Estatal de Paraná.
[4] Profesor de Protección Fitosanitaria y Salud Humana en la Pontificia Universidad Católica de Chile, Departamento de Ciencias Vegetales, ocupa un puesto interdisciplinario compartido entre la Facultad de Agronomía e Ingeniería Forestal (FAIF), la Facultad de Medicina y la Facultad de Química. Profesor investigador asociado al Grupo de Estudio sobre Suelos y Medio Ambiente (GESOMA – UNIOESTE). Máster en Agronomía por UNIOESTE, Doctorado en Agronomía por UNIOESTE (2013-2016) – Periodo Sandwich (Beca CAPES) de la Universidad de Lisboa, en el Instituto Superior de Agronomía (ULisboa).
[5] Productividad de investigación Nivel 1C por CNPq en el área de Ciencias Ambientales con tres Postdocs, UEM-PR (Brasil), Universidad de Santiago de Compostela (España), UFG-GO (Brasil). Actualmente es profesor asociado en UNIOESTE-PR y actúa como profesor e investigador en el Centro de Ciencias Agrarias, enseñando química. Profesor del Programa de Maestría en Ciencias Agrícolas de la UEM. Actualmente es consultor ad hoc para CNPq, CAPES y Fundação Araucária. Actúa como consultor ambiental voluntario con MP-SP y CONAMA-DF.
[6] Licenciado en Agronomía – UNIOESTE – Universidad Estatal de Paraná Occidental – Licenciado en Administración – Unip – Universidade Paulista.
[7] Estudiante de maestría en Agronomía (Producción de Plantas) de la Universidad Estatal de Paraná Occidental (UNIOESTE). Ingeniero Agrónomo egresado de UNIOESTE (2014-2018), actúa como investigador asociado al Grupo de Estudio de Suelos y Medio Ambiente (GESOMA – UNIOESTE).
Enviado: Junio de 2019.
Aprobado: Julio de 2019.