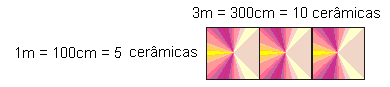ORIGINAL-ARTIKEL
SCHWANTES, Vilson [1], XAVIER, Márcio Pizzete [2], SCHWANTES, Eloísa Bernardete Finkler [3], SCHWANTES, Daniel [4], JUNIOR, Affonso Celso Gonçalves [5], KRACKE, Elisa [6], JUNIOR, Élio Conradi [7]
SCHWANTES, Vilson. Et al. Ethnomathematik: Eine Reflexion über die Mathematik, die von Maurern verwendet wird. Revista Científica Multidisciplinar Núcleo do Conhecimento. 04-Jahr, Ed. 07, Band 13, S. 46-66. Juli 2019. ISSN: 2448-0959
1. ZUSAMMENFASSUNG
Dieser Artikel ist das Ergebnis von Überlegungen zur Ethnomathematik und Analyse von Studiensitzungen, die mit Bricklayers in der Gemeinde Mercedes – PR durchgeführt wurden. Motivation findet er in den Schriften von Professor Ubiratan D’ Ambrosio, der das Vorhandensein von mathematischem Wissen in verschiedenen Kulturräumen erkennt. Der Schwerpunkt der Forschung untersucht dialogisch mit jedem Profi, durch Problemsituationen, die Mathematik verwenden, um das Budget der Menge der Keramik notwendig, um Wände und Böden zu beschichten. In der Forschung mit den Maurern war es interessant zu wissen, ob diese formal oder informell waren. Die Aussagen zeigten ein Verständnis dafür, dass mathematisches Wissen dynamisch ist, ein kulturelles Produkt, das in verschiedenen Bereichen menschlichen Handelns auftaucht und in und durch die Welt des Lebens zirkuliert und sich in der Schule festiert.
Schlagworte: mathematische Bildung, Ethnomathematik, Problemsituationen, Studiensitzungen, Keramikbudget.
2. EINFÜHRUNG
In allen Kulturen, im Laufe der Geschichte, finden wir Aufzeichnungen von entwickelten Aktivitäten, die die Existenz und Notwendigkeit einer Art von mathematischem Wissen bezeichnen. Dies ist ein empirisches Wissen, das in der Ausübung mehrerer Berufe verwendet wird, über Generationen weitergegeben und oft verwendet wird, ohne dass die Menschen diese Präsenz bemerken.
Wenn mathematische Sandern, um eine Problemsituation zu lösen, ist es manchmal möglich, zu lösen, ohne notwendigerweise eine Schule besucht. Mathematisches Wissen kann natürlich durch die tägliche Praxis entwickelt werden, zum Beispiel in der Arbeit von Maurern, Profis, die dieses Wissen routinemäßig verwenden.
Viele Jahrzehnte lang wurde in der Geschichte der Erziehung das Wissen aus sozialen Praktiken ignoriert und in der Schule nicht diskutiert. Heute gewinnt der Vorschlag, das mathematische Wissen zu untersuchen, das im Leben der Schüler außerhalb des schulischen Kontextes vorhanden ist, immer mehr Raum. Dieses Wissen, das der Mensch im Raum und in der Zeitlichkeit aufgebaut hat, stellt ein wertvolles Vermächtnis dar, das in den Lehrplänen der Schulen oder in der angewandten Methodik berücksichtigt werden muss. Es gibt viele Pädagogen, die glauben, dass Systate-Wissen aus Konzepten konstruiert werden kann, die im täglichen Leben der Berufe, der Menschen vorhanden sind.
Für Professor Ubiratan D’ambrrésio verfügen alle Kinder bereits über mathematische Kenntnisse, noch bevor sie die Schule betreten. Dieses Wissen ist für den Forscher eine Ethnomathematik[8]. Der Autor möchte uns sagen, dass Wissen nicht nur das Ergebnis jahrelanger Studien ist, sondern auch das Ergebnis der Erfahrungen, die unter den Bürgern derselben oder verschiedener sozialer Gruppen gelebt werden.
Laut dem Forscher ist der Hauptvorschlag der Ethnomathematik zu versuchen, das mathematische Wissen/Machen jeder Gruppe von Interesse, Gemeinschaft, Menschen oder Nation zu verstehen. In diesem Sinne betrachten seine Schriften Ethnomathematik:
“… Die Mathematik, die von kulturellen Gruppen praktiziert wird, wie städtische und ländliche Gemeinschaften, Gruppen von Arbeitnehmern, Berufsklassen, Kinder einer bestimmten Altersgruppe, indigene Gesellschaften und so viele andere Gruppen, die sich durch Ziele und Traditionen identifizieren Gemeinsam für Gruppen “. (2001, p.9).
Der Autor sieht Ethnomathematik wie:
“… Eine Strategie, die von der menschlichen Spezies im Laufe ihrer Geschichte entwickelt wurde, um zu erklären, zu verstehen, zu verwalten und mit der sensiblen Realität zu leben, wahrnehmbar und mit ihrem imaginären, natürlich in einem natürlichen und kulturellen Kontext. ” (D’AMBROSIUS, 1996, S. 7)
Maurer, manchmal Analphabeten und die meiste Zeit mit wenig Schulbildung, verwenden mathematisches Wissen, um Häuser zu bauen, keramische Nistplätze zu machen, Mauern zu bauen, Gebäude, die noch heute betrachtet werden, solide und robuste Konstruktionen. Es existiert sicherlich in dieser Arbeit, vor allem in den Berechnungen und in der Organisation der mathematischen Argumentation verwendet, ein Wissen, das im schulischen Kontext genutzt werden kann, oder in der Integration von Schülern mit einer Tendenz zu dieser Art von Beruf, entweder in einem Ansatz Mehr praktische Mathematik-Disziplin. Für Carneiro,
[…] Mathematik unterricht in dieser Konzeption wird es dem Schüler ermöglichen, die Inder-Konzepte mit ihrer täglichen Erfahrung zu verknüpfen, entsprechend ihrem natürlichen, sozialen und kulturellen Umfeld. Es geht nicht darum, die akademische Mathematik abzulehnen, sondern Werte zu berücksichtigen, die in Gruppenerfahrungen erfahren sind, wenn man die historisch-kulturellen Bindungen betrachtet (CARNEIRO, 2012, S. 3).
In den letzten Jahrzehnten ist die Zahl der Pädagogen, die Ethnomathematik studieren, als Forschungsprogramm und/oder als Vorschlag für pädagogische Arbeit gewachsen. Die Ziele dieser Lehrer sind unter anderem, die Prozesse der Generierung, Organisation und Verbreitung von Wissen und mathematischen Ideen in kulturellen Gruppen zu kennen, und wie man Maßnahmen im Bereich der Mathematiklehre entwickelt, die die Kontextualisierung der im Klassenzimmer behandelten formalen Inhalte.
Die Perspektive von Ethnomathematik ermöglicht es uns, im Klassenzimmer einen pädagogischen Vorschlag zu arbeiten, der Schüler und Lehrer in der Entwicklung von Kreativität ermutigt, die sowohl zu neuen als auch zu reichen Formen des Lernens führt. Dieser soziokulturelle Reichtum, der in den Lernprozess des Lehrens einfließt, ist nach den Worten von Professor Ubiratan D’Ambrosio Teil eines “Programms, das darauf abzielt, die Prozesse der Generierung, Organisation und Weitergabe von Wissen in verschiedenen Kulturelle Systeme und die interaktiven Kräfte, die auf und zwischen den drei Prozessen wirken. ” (D’AMBRÓSIO, 1993, p.7).
Eine weitere Perspektive der Ethnomathematik wurde von der brasilianischen Forscherin Gelsa Knijnik entwickelt. Für diesen Autor erlaubt Ethnomathematics
Um die eurozentrischen Diskurse zu studieren, die akademische und schulische Mathematik einführen; Analysieren Sie die Auswirkungen der Wahrheit, die durch die Diskurse der akademischen und wissenschaftlichen Mathematik erzeugt wird; Diskutieren Sie Fragen der Unterschiede in der mathematischen Bildung, unter Berücksichtigung der Zentralität der Kultur und der Machtverhältnisse, die sie etablieren; und untersuchen Sie die Sprachspiele, die jede der verschiedenen Mathematik ausmachen, und analysieren ihre familiären Ähnlichkeiten. (KNIJNIK, 2006, p.120).
In Knijniks Studien charakterisiert der Autor Ethnomathematik als mathematikal, die von sozialen Gruppen produziert wird, die ihr Wissen nutzen, um ihre Aktivitäten zu erfüllen. Knijnik (2002, S. 33), der einen Kontrapunkt zwischen formaler und informeller Mathematik mach[9]t, denkt darüber nac[…]h, dass, wenn man das von der akademischen Mathematik produzierte Wissen erwirbt, wenn man mit realen Situationen konfrontiert wird, diejenige, die angemessener erscheint.
Giardinetto (1999): “Der Lehrer kann und sollte das tägliche Wissen als Unterstützung für den Lehr-Lern-Prozess nutzen” (S. 68), indem er den Schüler in den Bereich der Argumentation bringt und die Gewohnheit des kritischen Lesens, der Forschung, der Fragen, Kreativität, unverzichtbar für die Bürgerausbildung. So werden sie geschätzt und das Vorwissen der Schüler belegt, die sich aus diesen, anderen Kenntnissen, immer aus dem Bekannten, erschließen.
Wichtig ist die Etablierung von Wissensbindungen der Gemeinschaft mit dem Wissen der Schule und dem Wissen der Schule mit dem Wissen der Gemeinschaft. Durch diese Etablierung und diese Beziehungen ist es möglich, beiden Wissen Bedeutung enden zu können.
Die thesesis, die der Autor verteidigt, ist, dass die Schule, mehr als das tägliche Wissen zu reproduzieren, zwischen diesem und dem schulischen Wissen vermitteln muss, das heißt, sie muss den neuen Generationen die Weisheit der Menschheit zugänglich machen, die sich als Produkt entpuppt. Historisch und sozial. Diese Kenntnisse müssen sozialisiert werden, denn “es ist nicht das einzelne Individuum, um alles Wissen zu konstruieren, sondern das Recht auf Zugang zu diesem Wissen konstituiert zu haben” (GIARDINETTO, 1999, S. 47).
Für D’ambrsio (2001) stellt Wissen in diesem Zusammenhang einen dynamischen Charakter dar, der immer offen für neue Ansätze ist. Dazu muss der Lehrer auf dem Laufenden bleiben, ständig seine Praxis bewerten, neue Lehrmethoden praktizieren und die zuvor erlebten pädagogischen Maßnahmen verbessern, so dass sie zur pädagogisch.
Breda, Lima und Guimarées (2011, S. 15), in ihren Studien sagen, dass:
Ich begann, den Vorschlag der Ethnomathematik als eine Möglichkeit zu betrachten, die Arbeit zu unterscheiden, die der Lehrer in den Schulen entwickelt, das heißt, die conteudistische und bedeutungslose Praxis kann durch einen Lehrer ersetzt werden, der durch ein neues Aussehen orientiert ist, das fördert Die Wertschätzung des soziokulturellen Kontextes des Erziehens, seiner Denkprozesse und seiner Wege des Verstehens, Erklärens und Ausübens seiner Praxis in der heutigen Gesellschaft, eine E[…]inladung, seine pädagogischen Praktiken und seine Auswirkungen zu überdenken oder sogar seine Rolle zu betrachten, Als Dozent, der sich mit unterschiedlichen Sichtweisen im schulischen Kontext auseinandersetzt.
So kann im schulischen Kontext, als Einstudiengang, das versucht, das in verschiedenen Kulturen produzierte und verwendete Wissen zu kennen und zu verstehen, Ethnomathematik erforscht werden, um die Lehrtätigkeit zu unterstützen, so dass die Schüler Die verschiedenen “Mathematik” zu verstehen, die in anderen Kontexten verwendet werden, schätzen die kulturelle Vielfalt und die intellektuelle und kreative Entwicklung jedes Volkes, jeder Kultur oder Gemeinschaft.
Wir Mathematiklehrer, so D’ambrosius (2001), müssen klar sein und in perfekter Harmonie mit unserer Rolle als Erzieher vor der Mission sein, unsere jungen Menschen auf eine glückliche Zukunft vorzubereiten. Wir müssen Ja Mathematik lehren, aber auch über die Menschheit. In diesem Zusammenhang betont der Autor,
Der pädagogische Vorschlag der Ethnomathematik ist es, Mathematik lebendig zu machen, mit realen Situationen in Zeit und [agora]Raum umzugehe[aqui]n. Und durch Kritik das Hier und Jetzt in Frage zu stellen. Dabei tauchen wir in kulturelle Wurzeln ein und praktizieren kulturelle Dynamik. Wir erkennen in der Bildung effektiv die Bedeutung verschiedener Kulturen und Traditionen für die Bildung einer neuen Zivilisation, die überkulturell und transdisziplinär ist. (D’AMBRÓSIO, 2001, p. 46).
Um dies Wirklichkeit werden zu lassen, muss der Lehrer täglich seine Unterrichtspraxis überprüfen, ein pädagogisches Projekt erarbeiten, das immer das Wissen und die Geschichte jedes Schülers schätzt und in dieser Individualität einen neuen und praktischen Kontext für die Kunst der unterrichten. Es ist wichtig, dass der Lehrer im Klassenzimmer, zusätzlich zu genießen und ausgehend von dem Wissen, das der Schüler aus der Umgebung, in der er lebt, bringt, ihn zu glauben, dass er auch eine wichtige Rolle bei der (Wieder-)Konstruktion von sozialem und kulturellem Wissen sowie Wissen spielt mathematiker.
Nach den Worten von Rosa Neto muss Mathematik als natürliches soziokulturelles Produkt eines Volkes interpretiert werden, weil,
Mathematik wurde geschaffen und wurde vom Menschen nach seinen Bedürfnissen entwickelt. (…) Kultur ist eine Form der Anpassung, weil sie eine Art des Handelns auf die Umwelt ist, die mit ihr gebaut wurde. (ROSA NETO, 2002, p.7 e 19).
In diesem Zusammenhang besteht eine signifikante Beziehung zwischen Mathematik und Kultur, sowohl als Ergebnis unserer Anpassung an die Bedürfnisse des Überlebens im Laufe der Zeit, die die Kultur darstellt, die uns vergangene Generationen hinterlassen haben, ein empirisches Vermächtnis , systematisch und wissenschaftlich.
3. RECHTFERTIGUNG
Mathematik wurde seit jeher als Grundlagenwissenschaft mehrerer Wissensgebiete angesehen. Die Beherrschung seines Wissens ist von grundlegender Bedeutung, um Problemsituationen in mehreren Bereichen zu lösen. Angesichts dieser Bedeutung und Relevanz ist es notwendig, nach neuen Formen (Methoden) zu suchen, um sie zu unterrichten, immer auf der Suche nach mehr Effizienz für den Lehr-Lern-Prozess im schulischen Kontext.
Viele Forschungen in diesem Bereich weisen auch auf das geringe Einkommen der Studierenden in Bezug auf das Erlernen der Disziplin hin und sagen, dass es notwendig ist, die Inhalte stärker zu kontextualisieren, um ein besseres Lernen zu ermöglichen. Sein Unterricht, der oft von Schülern, Eltern und sogar Lehrern als abstrakt, realitätsfern, d.h. von dem, was im Klassenzimmer gelehrt wird, betrachtet wird, stellt sich ihnen fern von den täglichen Bedürfnissen außerhalb der Schule vor.
Dieser Mangel an Verbundenheit mit dem Alltag und auch der Überschuss an Symbologie, die in Mathematik in Schulen gelehrt wird, fördert manchmal die Verbreitung falscher Ideen in Bezug auf diese Disziplin im schulischen Kontext. Die These, die wir verteidigen, findet theoretische Grundlagen in den Schriften von Professor Ubiratan D’ambr’sio, in der Perspektive, dass die Produktion von mathematischem Wissen nicht von den sozialen Bewegungen und der Kultur derer, die dieses Wissen produzieren, losgelöst werden kann.
In diesem Sinne können wir bestätigen, dass es eine Verflechtung zwischen der produzierten Mathematik, der Gesellschaft, die sie produziert, und der Kultur, die diese Produktion subventioniert. Diese Verflechtung wird durch einen kognitiven Prozess auf mehrere Hände aufgebaut, vermittelt durch das kreative Handeln verschiedener Akteure, die alle durch die Notwendigkeit motiviert sind, die Realität, in der sie leben, zu lesen, zu verstehen und zu erklären.
Wenn wir uns die Geschichte der Menschheit und der Wissenschaften ansehen, erkennen wir, dass nicht nur die Mathematik, sondern auch andere Bereiche des Wissens aufbauen und wieder aufbauen werden, die in jedem historischen Moment und nach den Anforderungen der Gesellschaft zurücktreten werden. Pompey und Monteiro (2001), in dem Buch Die Mathematik und die transversalen Themen betonen, dass der Lehrer den aktuellen Umfang seiner Rolle in der Gesellschaft zu verstehen, weil, nach den Autoren,
Die derzeitigen Lehrer stehen vor einer großen Herausforderung: Sie werden in einem fragmentierten Prozess ausgebildet die Grenzen überwinden müssen, die ihnen diese Formation auferlegt, und die Grenzen der Inhalte, die teilweise und a-historisch gesehen werden, extrapolieren müssen (POMPEU und MONTEIRO, 2001, S. 15).
Angesichts der Anforderungen dieser Größenordnung ist es notwendig, dass wir versuchen, den erkenntnistheoretischen Prozess der Mathematik zu verstehen, das heißt, den generativen Prozess dieses Wissens, den Grund für seine Organisation und Systematisierung. Die Minimierung dieses Rahmens war in den letzten Jahrzehnten ein Anliegen mehrerer Pädagogen und Forscher.
Für Rolim,
Über den historisch-kulturellen Kontext im Prozess des Mathematikunterrichts nachzudenken, ist zu bedenken, dass “Tun” mehr beinhaltet als Regeln und Techniken; ist anzuerkennen, dass die Mathematik als Wissenschaft selbst ein Gebäude der Menschheit ist (ROLIM, 2010, S. 43).
Es ist eine Tatsache, dass der Bildungsvorschlag, der durch pädagogische Praktiken gekennzeichnet ist, die soziokulturelle Bildung fördern und im Klassenzimmer die Schaffung von Lernbeziehungen ermöglichen, um den täglichen Bedürfnissen der Schüler gerecht zu werden, zugenommen hat. Mehr und mehr als pädagogische Alternative. Dies bedeutet laut D’ambrsio, Bedingungen zu schaffen, damit der Schüler auch im Klassenzimmer mit unterschiedlichen Situationen seines täglichen Lebens zurechtkommt.
Es ist eine Perspektive, die den Mathematikunterricht kontextualisierter macht, mit Bewertungen und Anliegen soziokultureller Art. Nach D’ambrsio (2001) ist Ethnomathematik der Bildungsbereich, der versucht, über das mathematische Wissen nachzudenken, das aus der Interaktion in einer bestimmten kulturellen Gruppe entsteht. Für den Autor basieren die Mathematikklassen in dieser Perspektive auf dem mathematischen Wissen von außen in den Unterricht, und dieses Wissen sollte aus der Erfahrung des Schülers entwickelt werden.
D’ambrsio (2001, S. 22) In diesem Zusammenhang gibt er auch folgende Erklärung ab:
Der Alltag ist mit dem Wissen und der Herstellung von Kultur imprägniert. In jedem Moment vergleichen, klassieren, messen, erklären, verallgemeinern, folgeren und bewerten sie in gewisser Weise die materiellen und intellektuellen Instrumente, die ihrer Kultur entsprechen (D’ambr’sio, 2001, S. 22).
In unserer Studie war die Leitfrage: Welche Art von Mathematik (formal oder informell) verwenden Maurer, um das Budget der Menge an Keramik benötigt, um Wände und Böden zu beschichten. Es war offensichtlich, dass der professionelle Mason seine Arbeitsfunktionen mit mathematischen Fähigkeiten aus der täglichen Praxis gelernt übt. Für Monteiro (2002, S. 102) “hat das kulturelle Know-how andere Validierungspfade, eine andere Logik für seine Konfiguration. Die Frage ist, warum das eine universell und legitimiert geworden ist und der andere nicht. ” In dieser Perspektive verweist uns der Autor auf Situationen, die denen dieser Untersuchung ähneln.
Laut Gerdes:
Jahrhundertelang bauten die Maurer, manchmal Analphabeten und meist mit sehr wenig Schulbildung, Häuser, Mauern und andere Gebäude, die heute noch als solide und robuste Bauten betrachtet werden. So existiert es in ihrer Arbeit, in der Art und Weise, wie sie ihre Berechnungen durchführen und ihre mathematische Argumentation organisieren, eine Weisheit, die im schulischen Kontext oder in der Integration bestimmter Schüler mit einer Tendenz zu dieser Art von Berufen oder in einem Mehr “praktische” Herangehensweise und näher an den Alltag für Studenten im Allgemeinen. Diese Situation wird in der Arbeit dieser Forschungslinie erwähnt, nämlich in Gerdes ‘ Terminologie, als “unterdrückte Mathematik” oder “versteckte oder eingefrorene Mathematik” (GERDES, 1991, S. 29).
In der Forschung gehen wir von der Annahme aus, dass die Maurer, gruppe gewählt, um diese Untersuchung zu machen, bilden eine Gruppe von Arbeitern, die täglich Gebrauch einer Vielzahl von mathematischen Kenntnissen in ihrem täglichen Leben und ohne dieses Wissen wäre nicht jede Tätigkeit im Tiefbau zu entwickeln oder durchzuführen. Angesichts der Tatsache, dass sie in der Regel wenig Schulbildung haben, war es interessant zu wissen, wie sie diese mathematischen Kenntnisse erworben haben oder ob sie durch die tägliche Praxis zur Verfügung gestellt wurden.
In diesem Zusammenhang kann diese investigative Arbeit auch dazu beitragen, die Idee zu entmystifizieren, dass Mathematik eine Wissenschaft für wenige ist, zu verstehen, dass es nicht eine einzige mathematische Sprache, sondern mehrere Formen des Denkens gibt. Mathematisch, jede organisiert und strukturiert in ihrem sozialen Kontext.
Für beide muss die Schule Bildungsprojekte entwickeln, die den Austausch von Erfahrungen mit Aktivitäten ermöglichen, bei denen Mathematik täglich verwendet wird. In dieser Interaktion werden neben dem Erfahrungsaustausch auch Bindungen geschaffen und andere pädagogische Beziehungen zur Welt geknüpft, die außerhalb der Schule gelebt wird, und dies kann ein erleichternder Weg beim Erlernen der Disziplin sein.
Der Mathematikunterricht sollte auf dem mathematischen Wissen von außen in den Unterricht basieren, und dieses Wissen sollte aus der Erfahrung des Schülers entwickelt werden. So bestätigt der Autor, dass das ethnomathematische Wissen der Gruppe/Gemeinschaft viel Wert hat, weil es dient, effizient und geeignet für viele Dinge ist, die dieser Kultur eigen sind, zu diesem Ethno, und es gibt keine Notwendigkeit, es zu ersetzen. In ähnlicher Weise dient ihm die Mathematik der dominanten Gruppe, sie ist nützlich und es gibt keine Möglichkeit, sie zu ignorieren (D’ambr’sio, 2001, S. 80).
Für Carneiro,
[…] Mathematik unterricht in dieser Konzeption wird es dem Schüler ermöglichen, die Inder-Konzepte mit ihrer täglichen Erfahrung zu verknüpfen, entsprechend ihrem natürlichen, sozialen und kulturellen Umfeld. Es geht nicht darum, die akademische Mathematik abzulehnen, sondern Werte zu berücksichtigen, die in Gruppenerfahrungen erfahren sind, wenn man die historisch-kulturellen Bindungen betrachtet (CARNEIRO, 2012, S. 3).
4. PROBLEMATISIEREND, DIE WEGE DES MATEMATIZAREN DER MAURER ZU KENNEN
In der Untersuchungsarbeit mit der Gruppe der Maurer durchgeführt, haben wir einige Problemsituationen ausgearbeitet, um festzustellen, dass Mathematik von diesen Fachleuten verwendet wird, um das Budget der Menge der Keramik notwendig, um Wände und Böden zu beschichten. Diese Studie wurde aus der Perspektive von D’ambrsio und ROSA durchgeführt, die Ethnomathematik als ein Forschungsprogramm in Geschichte und Philosophie der Mathematik betrachten, mit pädagogischen Implikationen, wenn die Autoren betrachten:
Dieses Forschungsprogramm stellt also eine Forschungsmethodik dar, die darauf abzielt, lokale mathematische Praktiken zu analysieren, da es versucht, mathematisches Wissen (Ideen, Begriffe, Verfahren, Verfahren und Praktiken), die Ursprung in verschiedenen kulturellen Kontexten im Laufe der Geschichte (D’AMBR-SIO und ROSA 2016, S. 17).
Situationsproblem: Um die Anzahl der rechteckigen Fliesen der Größe cm zu b[20 por 30]erechnen, notwendig, um den Badezimmerboden einer Kunstgalerie zu beschichten, Abmessungen 6, 00m x 4, 50m (Lezzi, 1996, S. 223), Oscar als “Anfangspunkt die Abmessungen des Bodens der badezimmer. Bei der Größe der Keramik entscheiden wir uns für 6m, die sowohl durch die Keramikseite der 20cm als auch in der 30 cm teilbar ist. Schon die 4, 50m nicht.
Diese Maßnahme ist nur durch die 30 teilba[medida do outro lado da cerâmica]r. Also entschied ich mich für das, was einfacher wäre, indem ic[600cm]h die 6m geteilt durch 30cm, erreichen die genaue Anzahl von 20 Keramik in Richtung der Länge. Nun, mit der Töpferei in Richtung der 20cm Seite erreichte ich die Zahl von 30 Lajotas.
Bereits in der 4, 50m, teilbar durch 30, nahm ich die 4, [450cm]50m und geteilt durch 30cm, erreichen die Anzahl der 15 Fliesen, die in die Breite passen. So gibt es 15 Fliesen im Sinne der 30cm. Um die Berechnung zu erreichen, nahm ich die 30 Fliesen, die in der Länge plus[600cm] die 15 gehen, die in der Breite gehen, multipliziert und erreichte die Anzahl der notwendigen Fliesen, die 450 Fliesen sein würde “.
Die Argumentation des Mason Sérgio, das gleiche Budget zu machen, zeigt laut D’ambrosius (2001), dass “in verschiedenen Umgebungen Ethnomathematik anders ist” (S. 35). So beginnt der Mason seine Rede und betont: “Zuerst muss man die Quadratmeter des Areals entdecken, es wären Zeiten[operação de multiplicação]. Ich fand 27m2, also muss ich herausfinden, wie viele Fliesen in einen Quadratmeter passen. Da die 30cm n[medida do comprimento da placa cerâmica]icht genau in einem Meter geben, wurde ich erhöht und verwendet 3m, dann geschlossen mit 10 Lajotas. Dieses Ergebnis von 10 Fliesen, multipliziert mit 5 Fliesen, die in der Breite passen. Ich fand die Anzahl von 50 Fliesen in 3m2 “. Visualisieren Sie nacheinander den deduktiven Gedanken, den der Maurer verwendet, um das Budget zu machen.
Sérgio berichtet, dass, nachdem er festgestellt hat, dass in 3m2 50 Stück passen, es nur “… Nehmen Sie diese 27m2, dividieren durch 3, was mich 9 gleiche Teile. Daher, 9 mal 50, gibt das Ergebnis der Menge an Keramik, die über die Fläche geht. Sie sind 450 Keramik und müssen noch die Pause zu sehen. ”
Die Budgetberechnung von der Mason Alberto durchgeführt, auch auf “450 Keramik. Ich habe Nebenzeiten Keramik Seite, 0, 20m mal 0, 30m erreichen die Zahl 0, 06m2. Dieses Ergebnis stellt den Bereich jeder Keramik dar. Jetzt habe ich Seitliche Seite des Badezimmerbodens, 6m mal 4, 50m und erreichte das Ergebnis von 27m2. Dann, das Bad Footage, 27m2 geteilt durch die Quadratmeter eines Teils 0, 06m2, gab 450 Keramik “.
In der Auflösung der Aushakte: Wie viele quadratische Fliesen von 15cm beiseite werden benötigt, um intern einen Pool mit 15m Länge, 6m Breit und 1, 20m tief zu beschichten (LEZZI,1991, S. 195), Oscar berichtete: “Ich habe mich entschieden, diese 15m in 1.500 cm geteilt durch 15cm des Lajota, führte zu 100 Fliesen in der Länge einer Seite des Pools. So auf der anderen Seite wird die gleiche Zahl geben, d.h. diese Zeile multipliziert mit 2, gibt 200 Fliesen, die auf beiden Seiten der Länge passen.
Das gleiche Verfahren, das ich in der Breite verwendet, nämlich die 6m ist 600cm und diese 600cm geteilt durch 15 gab mir 40 Fliesen, die in einer Breite gehen würde. Da wir hier zwei Breiten haben, multiplizierend mit 2, fand ich 80 Fliesen. Hinzufügen von 200 Fliesen in der Länge mit 80 der Breite, erreichte ich die Anzahl der 280 Fliesen, die mit der Tiefe multipliziert werden müssen, die 1, 20m, dh 120cm ist. Vorher jedoch teilte ich diese 12[medida da profundidade]0cm, um 15c[medida do azulejo]m und fand 8 Fliesen, die in die Tiefe des Pools gehen würde. Nun, unter der Länge und Addierung mit der Breite, meine ich die 200 Fliesen plus die 80 Fliesen, mal die 8 Fliesen der Tiefe, erreichte ich die Anzahl der 2.240 Fliesen.
Wir müssen noch die Anzahl der Fliesen von der Unterseite des Pools zu finden. Dies ist leicht zu berechnen, da die Länge und Breite Abmessungen des Bodens sind die gleichen wie die Seiten, bedeuten 6m durch 15m. So gehen sie 100 Keramik in der Länge und 40 in der Breite des Bodens, insgesamt 4.000 Keramik enthoben am Boden des Pools. Addiert die Anzahl der Fliesen der Seiten und der Unterseite erreichte ich die Anzahl von 6.240 Keramik “. Der Mason betonte auch, dass “sie immer eine Reservierung brauchen werden”, um mögliche Ausfälle zu verhindern, unter anderem.
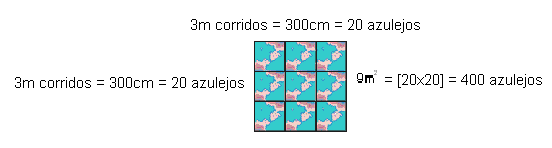
Die Anerkennung der Existenz “anderer Denkformen”, wie sie D’ambrsio (2001, S. 17) postuliert, zeigt sich in der mathematischen Argumentation, die Sérgio anstellt, um denselben Haushalt zu machen. Der Maurer betont, dass “zunächst die Quadratmeter Wand und Boden kennen[laterais] müssen. 15m plus 6m, über 15m und mehr 6m, würde die Seitliche gebe[42m corridos]n. Dieses Mal 1, 20m[profundidade da piscina], gibt 50, 4m2 Fläche.
Dann finde ich das Filmmaterial von unte[15m vezes 6m = 90m2]n. Wir sind alle. Ich tat und gab 140, 4m2. Jetzt muss ich herausfinden, wie viele Fliesen in jeden Quadratmeter passen. Nur das, da die Fliesen 15cm x 15cm sind, in einem Meter sch[corrido]ließt nicht. Dann fügte ich hinzu, bis ich auf 3m kam. In 3m [corridos]gibt es 20 Lajotas. Dann nahm ich 3 mal [multiplicado por]3, [cada face da piscina representa uma figura plana – duas dimensões]wäre insgesamt 9m2, die 400 Lajotas gab “. Visualisieren Sie in der folgenden Darstellung die Argumentation des Maurers zur Aufklärung der Problemsituation.
Sérgio setzt die Erläuterung seiner Verfahren fort: “Ich nahm die Summe von M2 aus dem Pool, geteilt durch 9[9 partes]. Gave 15.6 gleiche Teile von 9m2 jede[140,4m2 : 9m2 = 15,6]r. Diese 15,6 Teile entsprechen dem Vergleich der Keramikmenge von 9m2, d.h. 400 Keramiken. Dann, in jedem Teil wäre 15,6 mal 400, gleich 6.240 Keramik “.
Selbst wenn das Budget von 6.240 Keramiken genug geben würde, um den Pool zu beschichten, betont Sérgio gerne: Würde etwa 5% mehr von diesem Gesamtwert wegen des Bruchs benötigen.
Für Professor D’Ambrosio produzieren menschliche Gruppen Wissen, das zwar nicht in formalen Unterrichtsräumen weit verbreitet ist, aber ein gültiges Wissen ist und dass die Schule sowie die Forschung in der Mathematikerziehung erkennen und vertiefen müssen, um den Akt zu bereichern. erzieherisch.
D’ambrsio (2001, S. 22-23) stellt ferner fest, dass
Es gibt zahlreiche Studien über die Ethnomathematik des Alltags. Es ist eine Ethnomathematik, die nicht in Schulen, sondern im familiären Umfeld, im Umfeld von Spielzeug und Arbeit, von Freunden und Kollegen aufgenommen wird.
Die Lösung dieses Situationsproblems für Alberto zeigte ein Wissen, das mit dem Verfahren identifiziert wird, das von einem Mathematiklehrer verwendet werden würde. Beachten Sie seine Erklärung: “Die Länge des Schwimmbades Seiten 15m + 15m, auch hinzufügen der Breite 6m + 6m gibt den Umfang des Schwimmbades, 42m. Jetzt 42m mal 1, 20m aus der Tiefe von 50, 40m2 Fläche an den Seiten des Pools. Der Boden des Pools hat eine Fläche von 15m mal 6m und gibt 90m2. Wenn ich die seitenweite und den Boden hinzufüge, meine ich die 50, 40m2 plus die 90m2 ergibt 140, 40m2. Diese dividiert durch die Größe der Fliese, die 15cm x 15cm ist und die in M2 ergibt 0, 0225m2, summiert sich auf 6.240 Fliesen. Fügen Sie jetzt einfach ein wenig zum Pausenpuffer hinzu. ”
Für Demo (1996) beginnt der Aufbau von Wissen aus dem Wissen, das jeder Einzelne in seine soziokulturellen Erfahrungen einfließen lässt. Dies hat sich in den Formen des Matematizars gezeigt, die von jedem maurern verwendet werden. Für den Autor “Es gibt kein flaches Brett, absoluten Analphabetismus; Alle sprechen, kommunizieren, verwenden ein Grundvokabular, verwalten Konzepte im gesunden Menschenverstand, haben Verweise auf die Realität, in die sie eingefügt werden”(S. 32).
Beim Betreten der Schule hat jeder bereits etwas Wissen angesammelt, auch wenn es im gesunden Menschenverstand liegt. Wir teilten mit D’ambrosius (1993), als wir postulierten, dass wir verstehen müssen, dass, wenn die formale Schule beginnt, das Kind bereits eine Ethnomathematik hat, die es ihm erlaubt, sich den Interpretationen der systematischen Mathematik der Schule zu stellen.
Die Matematizar-Formen der Maurer bezeichnen laut Marques (2000) darauf, dass “die Lernprozesse unweigerlich in kommunikative und öffentliche Gemeinschaften eingefügt werden, in denen die Menschen voneinander und miteinander lernen” (S. 29). Nach dem Verständnis von Pompeius und Monteiro (2001) beginnt “ein sinnvoller Bildungsprozess mit dem Zusammenspiel von Schule und Gemeinschaft” (S. 55), dessen Beziehungen die Rolle der Schule als privilegierter Ort für den Erfahrungsaustausch mit Das wissen, was im Alltag zirkuliert, besser verstehen.
In den Manifestationen (Verbalisierungen), die von den Maurern in den Studiensitzungen ausgedrückt werden, vor allem aus der mathematischen Herstellung dieser Fachleute, basierend auf ihrer Arbeitserfahrung, im Austausch von Wissen, das sie bereits ihr ganzes Leben lang teilgenommen haben, zeigen Dass es der formalen Bildung möglich ist, dieses Vorwissen, seine Kultur und sein soziales Umfeld zu schätzen und zu validieren. Wir glauben, dass eine pädagogische Arbeit, die, dialogisch von diesem Wissen, Enrique verlässt und kontextualisiert das mathematische Wissen der Schule.
In den Worten von Rolim
Über den historisch-kulturellen Kontext im Prozess des Mathematikunterrichts nachzudenken, ist zu bedenken, dass “Tun” mehr beinhaltet als Regeln und Techniken; ist anzuerkennen, dass mathematik als Naturwissenschaften selbst ein Gebäude der Menschheit ist (ROLIM, 2010, S. 43).
Aus dieser Perspektive wird aus dieser Perspektive eine Beziehung etabliert, die in der Geschäftswelt weit verbreitet ist, wo der Ausdruck “Win-Win” gesprochen und praktiziert wird. In einer Verhandlung hat dieser Ausdruck ein Merkmal: Niemand verliert, jeder gewinnt. Es ist zwischen Unternehmen und Lieferant eine ideale Beziehung etabliert.
Für das Bildungsgesetz ist diese Beziehung pädagogisch ideal, d.h. Schüler, Lehrer, der gesamte Kontext, der Teil des Bildungsprozesses ist, glücklich zu sein, erfolgreich zu sein. Es versteht sich dann, dass es, wie in der Wirtschaft, im Klassenzimmer pädagogisch die “Win-Win”-Beziehung zu erreichen, einfach eine gute und neue Planung zu machen, in die diese Möglichkeit eingefügt wird.
Eine pädagogische Perspektive, in der Unternehmer und Lieferant, wie auch in der Geschäftswelt, ihre Wahrnehmungen, ihre Ansichten und ihre Ideen angemessen und zum richtigen Zeitpunkt offenlegen sollten, ohne das Verhalten des anderen in der Schule in einer Weise zu beurteilen, Lehrer respektiert und bewertet das Vorwissen seiner Schüler.
Und wenn in der Schule das Wissen des Alltags in “Konfrontation” mit formalem Wissen eintritt, dass wir uns dialogisch daran erinnern können, dass in der Geschäftswelt oft der Lieferant anders denkt als der Unternehmer, aber diese Beziehung ist oder sollte nie sein Konflikt oder verursachen etwas Verschleiß. Es muss in der Schule und in der Wirtschaft eine große Lernmöglichkeit für alle, die an diesem Prozess beteiligt sind, darstellen.
Die Reden der Maurer, Teilnehmer der Forschung, zeigten, dass die Kenntnisse der Mathematik, die sie besitzen, wurden die meiste Zeit in der Entwicklung und Verbesserung ihres Berufs erworben, in der Praxis von Tag zu Tag, oder sogar zu sehen, andere führen die Gleiche Aktivität.
Die Gespräche, die wir während der Studiensitzungen mit den Maurern geführt haben, zeigten, dass das außerhalb des Schulumfangs produzierte Wissen wichtig ist und es Sache des Lehrers ist, sie zu retten und sie näher an den Unterricht heranzuführen, was die formale Bildung sinnvoll macht und Artikuliert mit der Realität, in die der Student eingefügt wird.
5. ZIELE
5.1 Zeigen Sie, dass Ethnomathematik Teil unseres täglichen Lebens ist, und reflektieren Sie die Möglichkeit organisierter gesellschaft[pedreiros]licher Gruppen, Die Mathematik in ihren verschiedenen Ausdrucksformen in ihrem Aktionsbereich produzieren, und diskutieren Sie in der Schule die Art und Weise der Produktion Bedeutungen des Alltags; 5.2 Ethnomathematik als einen der Wege zu einer erneuerten Bildung zu präsentieren, innerhalb der größeren Bewegung genannt Mathematik-Bildung, ermöglicht in dieser Perspektive, durch die Reflexion zwischen Lehrer, Schüler und Gemeinschaft, versuchen, die Wissen, das sie beide besitzen, sie modifizieren und das Klassenzimmer in einen demokratischen Raum des Wissensaustauschs verwandeln; 5.3 Ethnomathematik als interessante pädagogische Alternative zur Arbeit im Klassenzimmer wahrzunehmen, Mathematik zu entmystifizieren und sich den wirklichen Notwendigkeiten des Tagestages der Schüler zu nähern.
6. METHODIK
Die Untersuchungsarbeit wurde durch verschiedene Momente durchgeführt, nämlich: bibliographische Studie über Ethnomathematik, Studiensitzungen mit Maurern, in denen Situationen vorgeschlagen wurden-Problem mit dem Zweck, dialogisch mit jedem Professionell über die mathematischen Kenntnisse,[formais ou informais] die sie verwenden, um das Budget der Menge der Keramik benötigt, um Wände und Böden zu beschichten. Reflexion über mögliche Zusammenhänge zwischen Mathematik und Realität in der Möglichkeit, Bindungen zwischen den mathematischen Kenntnissen des Maurers herzustellen, konstruiert aus ihren Bedürfnissen des berufstäglichen Alltags, mit Hilfe von Praktiken Alltag und Schulmathematik.
7. ERWARTETER BEITRAG
Wenn man bedenkt, dass wir während der gesamten Untersuchungsarbeit, basierend auf dem Diskurs der Maurer, feststellen, dass diese Fachleute, um die vorgeschlagenen Problemsituationen zu lösen, nicht immer in den Kenntnissen der Schulmathematik unterstützt wurden.
Während es klar war, dass die Maurer mathematisches Wissen auf praktische und intuitive Weise anwendeten, mit spezifischen Strategien, nicht mit den mathematischen Formeln in der Schule gelehrt.
Wir hoffen, dass der Unterricht Mathematik im Klassenzimmer durch den ethnomathematic[10]s Ansatz ermöglicht Es Lehrern und Schülern, über die kulturelle Vielfalt der Mathematik zu lernen. Dass die Ergebnisse dieser Forschung bei der Entwicklung einer Methodik helfen, die zum Unterrichten der Mathematik beiträgt, Möglichkeiten für Veränderungen in der Unterrichtspraxis bringt, sich der schulpädagogischen Praxis mit dem in Situationen produzierten Wissen nähert Von den Studenten Leben.
Dass aus dieser Reflexion die pädagogische Praxis im Klassenzimmer auf die Entwicklung der vollen Bürgerschaft der Schüler umgestaltet werden kann. Das, nach Pinheiro und Rosa (2016), die:
[…] Mathematiklehrer tauchen in die kulturelle Dynamik der Schüler ein und nutzen Lehr- und Lernstrategien, die die kulturelle Dimension im Klassenzimmer schätzen, so dass eine inklusive mathematische Bildung entwickelt werden kann, die effektiv Beitrag zur gesellschaftlichen Transformation (S. 79).
So wollen wir aus den Studiensitzungen und dem produzierten Text die Leser zu der Möglichkeit einer pädagogischen Intervention provozieren, die auf der Realität des Studenten basiert und Theorie und Praxis beim Aufbau von systefined-Wissen vereint. Es ist auch zu hoffen, dass die Reflexionen, die sich aus der Lektüre des Textes ergeben, einen neuen Blick auf die Realität und die mathematische Ausbildung ermöglichen, aus der Perspektive der Produktion von Wissen aus der täglichen Praxis.
Ziel ist es, zur Konstitution des Forschers Professor seiner Praxis beizutragen, indem er ihn dazu verleitet, kontinuierlich zu lernen, lehrer zu sein, entsprechend den aktuellen pädagogischen Bedürfnissen, und das Klassenzimmer in ein Umfeld des Wissensaustauschs verwandelt. Rettung des historischen Wissens, das von der Menschheit sozial aufgebaut wurde.
8. BIBLIOGRAPHISCHE HINWEISE
BREDA, Adriana LIMA, Valderez Marina do Rosário e GUIMARÃES, Gleny Terezinha Duro. A utilização da Etnomatemática nos cursos de formação continuada de professores: implicações das relações de poder saber na produção de subjetividades. Curitiba. Novembro de 2011. Disponível em: http://educere.bruc.com.br/CD2011/pdf/4668 _ 2898.pdf. Acessado em: 20/08/2017.
CARNEIRO, K. T. A. Cultura Surda na aprendizagem matemática da sala de recurso do Instituto Felipe Smaldone: uma abordagem etnomatemática. Anais do 4º Congresso Brasileiro de Etnomatemática. Belém, PA: ICEm4, 2012.
D’Ambrósio Ubiratan. Etnomatemática: Arte ou técnica de explicar e conhecer. Editora Ática, Série Fundamentos, 2. edição, São Paulo, 1993.
——-. Educação matemática: da teoria à prática. 13ª ed. Campinas: Papirus, 1996. (Coleção Perspectivas em Educação Matemática).
————-. Etnomatemática – elo entre as tradições e a modernidade. Coleção Tendências em Educação Matemática, 1. Belo Horizonte: Autêntica, 2001, 112p.
D’AMBROSIO, U.; ROSA, M. Um diálogo com Ubiratan D’Ambrosio: uma conversa brasileira sobre etnomatemática. In BANDEIRA, F. A.; GONÇALVES, P. G. F. (Orgs.). Etnomatemáticas pelo Brasil: aspectos teóricos, ticas de matema e práticas escolares. Curitiba, PR: Editora CRV. 2016. pp. 13-37.
DEMO, Pedro. Pesquisa e construção de conhecimento: Metodologia científica no caminho de Habermas. 3.ed. Rio de Janeiro: Tempo Brasileiro, 1996. 125p.
GERDES, Paulus. Etnomatemática: Cultura, Matemática, Educação. Maputo. Instituto Superior Pedagógico, 1991.
GIARDINETTO, José Roberto Boettger. Matemática escolar e matemática da vida cotidiana. Coleção polêmicas do nosso tempo, autores associados, Campinas – São Paulo, 1999, 128p.
LEZZI, Gelson; Dolce, Osvaldo; Machado, Antonio. Matemática e Realidade. 5ª série, 3. edição reformulada, Atual, São Paulo, 1996, 250p.
————–. Matemática e Realidade. 5ª série, 2. edição, Atual, São Paulo, 1991, 213p.
KNIJNIK, Gelsa. O saber popular e o saber acadêmico na luta pela terra. Revista da Sociedade Brasileira de Educação Matemática. Educação Matemática em Revista. Ano 9, n. 1, p. 27-39, 2002.
————–. Educação matemática, culturas e o conhecimento na luta pela terra. Santa Cruz do Sul, EDUNISC, 2006, 239 p.
MARQUES, Mário Osorio. A aprendizagem na mediação social do aprendido e da docência. Ijuí, Editora UNIJUÍ, 2. edição, 2000, 144 p.
MONTEIRO, A.; Pombeu, G. Jr. A matemática e os temas transversais. Editora Moderna, São Paulo, 2001, 160p.
MONTEIRO, Alexandrina. Reflexão e Ação: Revista do Departamento de Educação/UNISC. Vol. 10, n. 1 (jan./jun.2002) — Santa Cruz do Sul: EDUNISC, 2002.
A Etnomatemática em Cenários de Escolarização: alguns elementos de reflexão. Alexandrina Monteiro, p. 93 – 108.
PINHEIRO, R. C.; ROSA, M. Uma perspectiva etnomatemática para o processo de ensino e aprendizagem de alunos Surdos. RPEM, v. 5, n. 9, p. 56-83, 2016.
ROLIM, Carmem Lucia Artioli. Fórmulas de Silêncio: metodologias no processo de ensino da Matemática. In: SANTOS, Jocyléia Santana. ZAMBONI, Ernesta. Potencialidades Investigativas da Educação. Goiânia: Ed. da PUC Goiás, 2010.
ROSA NETO, R. Didática da matemática, São Paulo: Ática, 2002.
8. Verstanden mit einer pädagogischen Praxis, die die Mathematik verschiedener kultureller Gruppen schätzt, unter Berücksichtigung der informellen Konzepte, die von den Probanden durch ihre Erfahrungen außerhalb des Kontextes der Schule konstruiert wurden.
9. In dieser Reflexion behandeln wir formale und informelle Mathematik in der Idee, dass die erste als eine Schule betrachtet wird, wissenschaftlich, systematisch, legitimiert und mit Klassenzimmerkontexten verbunden und die zweite als tägliche, spontane, Kenntnis des Täglichen, Verbunden mit Straßen, Erfahrung und Leben in Gemeinschaften, sozialen Kontexten.
10. In dieser Arbeit verwendet, um die Untersuchung der Konzeptionen, Traditionen und mathematischen Praktiken einer sozialen Gruppe und die p[pedreiros]ädagogische Arbeit, die in der Perspektive entwickelt werden kann, dass die Gruppe interpretiert und kodifiziert ihr Wissen; Erwerben Sie das Wissen, das von der akademischen Mathematik produziert wird, indem Sie, wenn sie mit kontextualisierten Situationen konfrontiert werden, diejenige, die besser geeignet scheint.
[1] Master in Didaktik der Naturwissenschaften – Mathematik, UNIJUI – RS. Abschluss und Spezialisierung in Naturwissenschaften und Mathematik. Prof. Assistent des CCA – Zentrums für Agrarwissenschaften, Campus von Marschall Cândido Rondon, UNIOESTE, PR – Brasilien.
[2] Master in Nachhaltiger Entwicklung des ländlichen Raums-UNIOESTE, Mathematikspezialist, Physik-UNIPAR, Personalmanagement und Sonderpädagogik mit Schwerpunkt Mehrfachbehinderung-UNIASSELVI, Abschluss in Mathematik mit Schwerpunkt Physik-UNIPAR.
[3] Spezialisierung im naturwissenschaftlichen Unterricht – Mathematik, Physik und Chemie. UNIOESTE – Staatliche Universität von Western Paraná. Abschluss: Naturwissenschaften und Mathematik. UNIJUI, RS. Professor der staatlichen Schule von Paraná.
[4] Er ist Professor für Pflanzenschutz und menschliche Gesundheit an der Päpstlichen Katholischen Universität von Chile, Abteilung für Pflanzenwissenschaften. Seine interdisziplinäre Position teilen sich die Fakultät für Agronomie und Ingeniería Forestal (FAIF), die Fakultät für Medizin und die Fakultät für Chemie. Forschungsprofessor in der Arbeitsgruppe Boden und Umwelt (GESOMA – UNIOESTE). Master in Agronomie von UNIOESTE, PhD in Agronomie von UNIOESTE (2013-2016) – Sandwich-Periode (CAPES-Stipendium) von der Universität Lissabon, am Instituto Superior de Agronomia (ULisboa).
[5] Research Productivity Level 1C von CNPq im Bereich Umweltwissenschaften mit drei Postdocs, UEM-PR (Brasilien), Universität Santiago de Compostela (Spanien), UFG-GO (Brasilien). Derzeit ist er außerordentlicher Professor an der UNIOESTE-PR und Professor und Forscher am Zentrum für Agrarwissenschaften, wo er Chemie lehrt. Dozent im Masterstudiengang Agrarwissenschaften an der UEM. Derzeit ist er Ad-hoc-Berater bei CNPq, CAPES und Fundação Araucária. Arbeitet als freiwilliger Umweltberater bei MP-SP und CONAMA-DF.
[6] Bachelor in Agronomie – UNIOESTE – Staatliche Universität von Western Paraná – Absolvent der Verwaltung – Unip – Universidade Paulista.
[7] Masterstudent in Agronomie (Pflanzenproduktion) an der Staatlichen Universität von West-Paraná (UNIOESTE). Agraringenieur, Absolvent der UNIOESTE (2014-2018), arbeitet als Forscher in der Arbeitsgruppe für Boden und Umwelt (GESOMA – UNIOESTE).
Eingereicht: Juni 2019.
Genehmigt: Juli 2019.