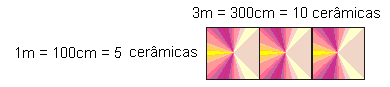ARTICLE ORIGINAL
SCHWANTES, Vilson [1], XAVIER, Márcio Pizzete [2], SCHWANTES, Eloísa Bernardete Finkler [3], SCHWANTES, Daniel [4], JUNIOR, Affonso Celso Gonçalves [5], KRACKE, Elisa [6], JUNIOR, Élio Conradi [7]
SCHWANTES, Vilson. Et al. Ethnomathématiques: Une réflexion sur les mathématiques utilisées par les maçons. Revista Científica Multidisciplinar Núcleo do Conhecimento. 04 année, Ed. 07, vol. 13, p. 46-66. juillet 2019. ISSN: 2448-0959
1. RÉSUMÉ
Cet article est le résultat de réflexions sur les ethnomathématiques et l’analyse des sessions d’étude menées avec Bricklayers dans la municipalité de Mercedes – PR. Il trouve la motivation dans les écrits du professeur Ubiratan D’Ambrosio qui reconnaît la présence de connaissances mathématiques dans divers espaces culturels. L’objectif de la recherche étudie dialogiquement avec chaque professionnel, à travers des situations problématiques, que les mathématiques utilisent pour rendre le budget de la quantité de céramique nécessaire pour enrober les murs et les planchers. Dans la recherche menée avec les maçons, il était intéressant de savoir si elles étaient formelles ou informelles. Les déclarations ont démontré une compréhension que la connaissance mathématique est dynamique, un produit culturel, qui émerge dans divers secteurs de l’activité humaine et circule dans et à travers le monde de la vie, se consolidant dans l’école.
Mots-clés: éducation mathématique, ethnomathématiques, situations problématiques, sessions d’étude, budget céramique.
2. INTRODUCTION
Dans toutes les cultures, tout au long de l’histoire, nous trouvons des enregistrements d’activités développées qui dénotent l’existence et la nécessité d’une sorte de connaissance mathématique. Il s’agit d’une connaissance empirique, utilisée dans l’exercice de plusieurs professions, transmise à travers les générations et utilisée, souvent, sans que l’on s’en aperçoive.
Lorsque vous utilisez un raisonnement mathématique pour résoudre une situation problématique, il est parfois possible de résoudre, sans nécessairement avoir fréquenté une école. Les connaissances mathématiques peuvent être développées naturellement par la pratique quotidienne, par exemple, dans le travail des maçons, des professionnels qui utilisent régulièrement ces connaissances.
Pendant de nombreuses décennies dans l’histoire de l’éducation, les connaissances découlant des pratiques sociales ont été ignorées et n’ont pas été discutées à l’école. Aujourd’hui, la proposition d’étudier les connaissances mathématiques présentes dans la vie des élèves en dehors du contexte scolaire gagne de plus en plus d’espace. Cette connaissance construite par l’homme dans l’espace et la temporalité constitue un héritage précieux qui doit être pris en compte dans les programmes scolaires, ou dans la méthodologie adoptée. Il y a beaucoup d’éducateurs qui croient que la connaissance de systate peut être construite à partir des concepts présents dans la vie quotidienne des professions, des personnes.
Pour le professeur Ubiratan D’ambràsio, avant même d’entrer à l’école, tous les enfants ont déjà des connaissances mathématiques. Cette connaissance est, pour le chercheur, une ethnomathématiqu[8]e. L’auteur veut nous dire que la connaissance n’est pas seulement le résultat d’années d’études, mais aussi le fruit des expériences vécues parmi les citoyens des mêmes groupes sociaux ou différents.
Selon le chercheur, la principale proposition de l’ethnomathématiques est de chercher à comprendre les connaissances mathématiques / fabrication de chaque groupe d’intérêt, communauté, personnes ou nation. En ce sens, ses écrits considèrent l’ethnomathématique :
“… Les mathématiques pratiquées par les groupes culturels, tels que les communautés urbaines et rurales, les groupes de travailleurs, les classes professionnelles, les enfants d’un certain groupe d’âge, les sociétés autochtones, et tant d’autres groupes qui s’identifient par des objectifs et des traditions Commun aux groupes “. (2001, p.9).
L’auteur voit ethnomathématiques comme :
“… Une stratégie développée par l’espèce humaine tout au long de son histoire pour expliquer, comprendre, gérer et vivre avec la réalité sensible, perceptible et avec son imaginaire, naturellement dans un contexte naturel et culturel. (D’AMBROSIUS, 1996, p. 7)
Les maçons, parfois analphabètes et la plupart du temps peu scolarisés, utilisent les connaissances mathématiques pour construire des maisons, faire des nids en céramique, construire des murs, des bâtiments, considérés encore aujourd’hui, des constructions solides et robustes. Il existe certainement dans ce travail, en particulier dans les calculs et dans l’organisation du raisonnement mathématique utilisé, une connaissance qui peut être exploitée dans le contexte scolaire, ou dans l’intégration des élèves ayant une tendance à ce type de profession, soit dans une approche Discipline mathématique plus pratique. Pour Carneiro,
[…] Enseigner les mathématiques dans cette conception permettra à l’élève de lier les concepts travaillant en classe à leur expérience quotidienne, en fonction de leur environnement naturel, social et culturel. Il ne s’agit pas de rejeter les mathématiques académiques, mais plutôt d’intégrer des valeurs vécues dans les expériences de groupe, compte tenu des liens historico-culturels (CARNEIRO, 2012, p. 3).
Au cours des dernières décennies, le nombre d’éducateurs qui étudient l’ethnomathématique a augmenté en tant que programme de recherche et/ou en tant que proposition de travail pédagogique. Entre autres, les objectifs de ces enseignants sont de connaître les processus de génération, d’organisation et de diffusion des connaissances et des idées mathématiques présentes au sein des groupes culturels, et comment développer des actions dans le domaine de l’enseignement des mathématiques qui permettent Contextualisation du contenu formel couvert dans la salle de classe.
La perspective de l’ethnomathématique nous permet de travailler en classe une proposition éducative qui encourage les élèves et les enseignants dans le développement de la créativité, conduisant à la fois à des formes nouvelles et riches de l’apprentissage. Cette richesse socioculturelle qui est intégrée dans le processus d’enseignement, selon les mots du professeur Ubiratan D’Ambrosio, fait partie d’un « programme qui vise à expliquer les processus de génération, d’organisation et de transmission des connaissances dans divers Les systèmes culturels et les forces interactives qui agissent sur et entre les trois processus. (D’AMBRÓSIO, 1993, p.7).
Une autre perspective de l’ethnomathématique a été développée par la chercheuse brésilienne Gelsa Knijnik. Pour cet auteur, ethnomathématiques permet
Étudier les discours eurocentriques qui instituent les mathématiques académiques et scolaires; Analyser les effets de la vérité produits par les discours des mathématiques académiques et savantes; Discutez des questions de différence dans l’enseignement mathématique, compte tenu de la centralité de la culture et des relations de pouvoir qui l’établissent; et examiner les jeux de langue qui constituent chacune des différentes mathématiques, en analysant leurs similitudes familiales. (KNIJNIK, 2006, p.120).
Dans les études de Knijnik, l’auteur caractérise l’ethnomathématiques comme une mathématique produite par des groupes sociaux qui utilisent leurs connaissances pour accomplir leurs activités. Knijnik (2002, p. 33), faisant un contrepoint entre les mathématiques formelles et informelle[9]s, réfléchit que si -[…] acquérir les connaissances produites par les mathématiques académiques, en utilisant, lorsqu’il est confronté à des situations réelles, celui qui semble plus approprié.
Selon Giardinetto (1999), « l’enseignant peut et doit utiliser les connaissances quotidiennes comme un point de soutien pour le processus d’enseignement-apprentissage » (p. 68), amenant l’élève dans le domaine de l’argumentation, développant l’habitude de la lecture critique, de la recherche, Questionnement, de créativité, indispensable à la formation des citoyens. Ainsi, ils sont appréciés et mis en évidence la connaissance antérieure des étudiants, formant à partir de ces, d’autres connaissances, toujours à partir du connu.
L’important est l’établissement de liens de connaissance de la communauté avec la connaissance de l’école et la connaissance de l’école avec la connaissance de la communauté. Grâce à cet établissement et à ces relations, il est possible d’attribuer un sens aux deux connaissances.
La thèse défendue par l’auteur est que l’école, plus que de reproduire les connaissances quotidiennes, doit être la médiation entre cela et la connaissance de l’école, c’est-à-dire, il doit mettre à la disposition des nouvelles générations la sagesse élaborée par l’humanité, qui se révèle comme un produit Historique et social. Ces connaissances doivent être socialisées, car « ce n’est pas l’individu singulier de construire toutes les connaissances, mais d’avoir le droit d’accéder à ces connaissances constituées » (GIARDINETTO, 1999, p. 47).
Dans ce contexte, dans ce contexte, la connaissance présente un caractère dynamique, toujours ouvert à de nouvelles approches. Pour cela, l’enseignant doit se tenir au courant, constamment évaluer sa pratique, pratiquer de nouvelles méthodologies d’enseignement, ainsi qu’améliorer les actions pédagogiques déjà vécues, dans la perspective qu’elles peuvent contribuer à la pédagogique.
Breda, Lima et Guimaraes (2011, p. 15), dans leurs études, affirment que :
J’ai commencé à considérer la proposition d’ethnomathématiques comme une possibilité de différencier le travail que l’enseignant développe dans les écoles, c’est-à-dire que la pratique conteudiste et dénuée de sens peut être remplacée par un enseignant orienté par un nouveau look, qui favorise L’appréciation du contexte socioculturel de l’éducation, de ses processus de pensée et de ses façons de comprendre, d’expliquer et d’exercer sa pratique dans la société cont[…]emporaine est une invitation à revoir ses pratiques pédagogiques et ses effets, voire à son rôle, En tant que conférencier qui traite de différentes perspectives de matière dans le contexte scolaire.
Ainsi, dans le contexte scolaire, en tant que programme d’étude qui cherche à connaître et à comprendre les connaissances produites et utilisées dans différentes cultures, l’ethnomathématique peut être explorée pour aider à l’enseignement du travail, ce qui rend les élèves peuvent Comprendre les différentes « mathématiques » utilisées dans d’autres contextes, valoriser la diversité culturelle et le développement intellectuel et créatif de chaque peuple, de chaque culture ou communauté.
Nous, professeurs de mathématiques, selon D’ambrosius (2001), nous devons être clairs et être en parfaite harmonie avec notre rôle d’éducateur face à la mission de préparer nos jeunes à un avenir heureux. Nous devons enseigner oui mathématiques, mais aussi sur l’humanité. À cet égard, l’auteur souligne :
La proposition pédagogique de l’ethnomathématique est de faire des mathématiques quelque chose de vivant, face à des situations réelles dans le [agora]temps et l’espac[aqui]e. Et, par la critique, remettre en question l’ici et maintenant. Ce faisant, nous nous immergeons dans les racines culturelles et pratiquons la dynamique culturelle. Nous reconnaissons effectivement dans l’éducation l’importance de diverses cultures et traditions dans la formation d’une nouvelle civilisation, interculturelle et transdisciplinaire. (D’AMBRÓSIO, 2001, p. 46).
Pour en faire une réalité, l’enseignant doit revoir quotidiennement sa pratique d’enseignement, élaborer un projet pédagogique qui valorise toujours les connaissances et l’histoire de chaque élève, cherchant dans cette individualité un contexte nouveau et pratique pour l’art de enseigner. Il est important que l’enseignant en classe, en plus de jouir et de partir de la connaissance que l’élève apporte de l’environnement dans lequel il vit, l’encourager à croire qu’il joue également un rôle important dans la (re) construction des connaissances sociales et culturelles, ainsi que des connaissances mathématicien.
Selon Rosa Neto, les mathématiques doivent être interprétées comme un produit socioculturel naturel d’un peuple, parce que,
Les mathématiques ont été créées et ont été développées par l’homme en fonction de ses besoins. (…) La culture est une forme d’adaptation parce que c’est une façon d’agir sur l’environnement qui a été construit avec elle. (ROSA NETO, 2002, p.7 e 19).
Dans ce contexte, il existe une relation significative entre les mathématiques et la culture, à la fois en raison de notre adaptation en fonction des besoins de survie à travers le temps, représentant la culture que les générations passées nous ont laissé, un héritage empirique , systématique et scientifique.
3. JUSTIFICATION
Les mathématiques ont toujours été considérées comme une science de base de plusieurs domaines de la connaissance. La maîtrise de ses connaissances est fondamentale pour résoudre les situations problématiques dans plusieurs domaines. Compte tenu de cette importance et de cette pertinence, il est nécessaire de chercher de nouvelles formes (méthodes) pour l’enseigner, toujours à la recherche d’une plus grande efficacité pour le processus d’enseignement-apprentissage dans le contexte scolaire.
De nombreuses recherches dans le domaine mettent également en évidence le faible revenu des étudiants en ce qui concerne l’apprentissage de la discipline, en disant qu’il est nécessaire d’une plus grande contextualisation du contenu pour mieux apprendre. Son enseignement considéré, souvent par les élèves, les parents et même les enseignants, comme abstrait, éloigné de la réalité, c’est-à-dire ce qui est enseigné en classe, se présente à eux loin des besoins quotidiens en dehors de l’école.
Ce manque de lien avec la vie quotidienne et, aussi, l’excès de symbologie enseignée en mathématiques à l’école, favorise parfois la diffusion d’idées erronées par rapport à cette discipline dans le contexte scolaire. La thèse que nous défendons trouve des fondements théoriques dans les écrits du professeur Ubiratan D’ambrsio, dans la perspective que la production de connaissances mathématiques ne peut pas être détachée des mouvements sociaux et de la culture de ceux qui produisent cette connaissance.
En ce sens, nous pouvons affirmer qu’il y a un entrelacement entre les mathématiques produites, la société qui les produit et la culture qui subventionne cette production. Cet entrelacement est construit à plusieurs mains à travers un processus cognitif, médiatisé par l’action créative de divers acteurs, tous motivés par la nécessité de lire, comprendre et expliquer la réalité dans laquelle ils vivent.
Si nous regardons l’histoire de l’humanité et des sciences, nous percevons que non seulement les mathématiques, mais aussi d’autres domaines de la connaissance se développeront et se rebâtiront, étant resignifiés à chaque moment historique et selon les exigences de la société. Pompée et Monteiro (2001), dans le livre Les Mathématiques et les thèmes transversaux soulignent que l’enseignant a besoin de comprendre la portée actuelle de son rôle dans la société, parce que, selon les auteurs,
Les enseignants actuels sont confrontés à un grand défi : éduqués dans un processus fragmenté, ils devront dépasser les limites que cette formation leur impose et extrapoler les limites du contenu vu de manière partielle et historique (POMPEU et MONTEIRO, 2001, p. 15).
Compte tenu des exigences d’une telle ampleur, il est nécessaire que nous cherchions à comprendre le processus épistémologique des mathématiques, c’est-à-dire le processus génératif de cette connaissance, la raison de son organisation et de sa systématisation. La réduction de ce cadre a été, au cours des dernières décennies, une préoccupation de plusieurs éducateurs et chercheurs.
Pour Rolim,
Penser au contexte historico-culturel dans le processus d’enseignement de l’apprentissage des mathématiques, c’est considérer que « faire » implique plus que des règles et des techniques; est de reconnaître qu’en tant que science, les mathématiques sont elles-mêmes un bâtiment de l’humanité (ROLIM, 2010, p. 43).
Il est un fait que la proposition éducative caractérisée par des pratiques éducatives qui favorisent l’éducation socioculturelle, permettant en classe l’établissement de relations d’apprentissage pour répondre aux besoins quotidiens des élèves, a augmenté De plus en plus comme une alternative pédagogique. Selon D’ambrôsio, cela signifie construire des conditions afin que l’élève puisse également faire face dans la salle de classe avec différentes situations de sa vie quotidienne.
C’est une perspective qui rend l’enseignement des mathématiques plus contextualisé, avec des évaluations et des préoccupations de nature socioculturelle. Selon D’ambrôsio (2001), l’ethnomathématique est le domaine de l’éducation qui cherche à réfléchir sur les connaissances mathématiques qui sont générées par l’interaction dans un groupe culturel particulier. Pour l’auteur, les cours de mathématiques, dans cette perspective, sont basés sur les connaissances mathématiques de l’extérieur dans la salle de classe, et ces connaissances devraient être développées à partir de l’expérience de l’élève.
À cet égard, D’ambrôsio (2001, p. 22) À cet égard, il fait également la déclaration suivante :
La vie quotidienne est imprégnée de la connaissance et de la création de la culture. À chaque instant, les individus comparent, classibilisent, mesurent, expliquent, généralisent, inférez et, d’une certaine manière, évaluent, en utilisant les instruments matériels et intellectuels qui sont propres à leur culture (D’ambrôsio, 2001, p. 22).
Dans notre étude, la question directrice était la suivante: Quel genre de mathématiques (formelles ou informelles) utilisent des maçons pour faire le budget de la quantité de céramique nécessaire pour enrober les murs et les planchers. Il était évident que le maçon professionnel exerce ses fonctions de travail en utilisant des compétences mathématiques acquises à partir de la pratique quotidienne. Pour Monteiro (2002, p. 102), « le savoir-faire culturel a d’autres voies de validation, une autre logique pour sa configuration. La question est de savoir pourquoi l’un est devenu universel et légitimé et l’autre ne l’est pas. Dans cette perspective, l’auteur nous renvoie à des situations semblables à celles vécues dans cette enquête.
Selon Gerdes:
Pendant des siècles, les maçons, parfois analphabètes et, la plupart du temps, avec très peu de scolarité, construire des maisons, des murs et d’autres bâtiments, encore considéré comme des constructions solides et robustes aujourd’hui. Ainsi, il existe dans leur travail, dans la façon dont ils font leurs calculs et d’organiser leur raisonnement mathématique, une sagesse qui peut être harnée dans le contexte scolaire, ou dans l’intégration de certains étudiants ayant une tendance à ce type de professions ou dans un Approche plus « pratique » et plus proche de la vie quotidienne pour les étudiants en général. Cette situation est mentionnée dans les travaux de ce domaine de recherche, à savoir, dans la terminologie de Gerdes, comme « mathématiques opprimées », ou « mathématiques cachées ou gelées » (GERDES, 1991, p. 29).
Dans la recherche, nous partons de l’hypothèse que les maçons, groupe choisi pour faire cette enquête, constituent un groupe de travailleurs qui font un usage quotidien d’une grande variété de connaissances mathématiques dans leur vie quotidienne et sans cette connaissance ne serait pas possible de développer ou d’effectuer toute activité dans la construction civile. Cependant, étant donné qu’ils ont généralement peu de scolarité, il était intéressant de savoir comment ils ont acquis ces connaissances mathématiques ou si elles ont été fournies par la pratique quotidienne.
Dans ce contexte, ce travail d’investigation peut aussi contribuer à démystifier l’idée que les mathématiques sont une science pour quelques-uns, en comprenant qu’il n’y a pas un seul langage mathématique, mais de multiples formes de pensée Mathématique, chacun organisé et structuré dans son contexte social.
Pour les deux l’école a besoin de développer des projets éducatifs qui permettent l’échange d’expériences avec des activités où les mathématiques sont utilisées quotidiennement. Dans cette interaction, en plus de permettre l’échange d’expériences, des liens sont créés et d’autres relations pédagogiques sont établies avec le monde vécu en dehors de l’école et cela peut être un chemin de facilitation dans l’apprentissage de la discipline.
Selon D’ambrôsio, les cours de mathématiques devraient être basés sur les connaissances mathématiques de l’extérieur dans la salle de classe, et ces connaissances devraient être développées à partir de l’expérience de l’élève. Ainsi, l’auteur affirme que la connaissance ethnomathématique du groupe / communauté a beaucoup de valeur, parce qu’il sert, est efficace et adapté à beaucoup de choses, propre à cette culture, à cet ethno, et il n’est pas nécessaire de le remplacer. De même, les mathématiques du groupe dominant le servent, il est utile et il n’y a aucun moyen de l’ignorer (D’ambrâsio, 2001, p. 80).
Pour Carneiro,
[…] Enseigner les mathématiques dans cette conception permettra à l’élève de lier les concepts travaillant en classe à leur expérience quotidienne, en fonction de leur environnement naturel, social et culturel. Il ne s’agit pas de rejeter les mathématiques académiques, mais plutôt d’intégrer des valeurs vécues dans les expériences de groupe, compte tenu des liens historico-culturels (CARNEIRO, 2012, p. 3).
4. PROBLEMATISER POUR CONNAÎTRE LES VOIES DE MATEMATIZAR DES MAÇONS
Dans le travail d’enquête effectué avec le groupe de maçons, nous avons élaboré quelques situations problématiques, pour s’assurer que les mathématiques sont utilisées par ces professionnels pour faire le budget de la quantité de céramique nécessaire pour enrober les murs et les planchers. Cette étude a été réalisée du point de vue de D’ambrôsio et ROSA, qui considèrent l’ethnomathématiques comme un programme de recherche en histoire et philosophie des mathématiques, avec des implications pédagogiques, lorsque les auteurs considèrent:
Ainsi, ce programme de recherche représente une méthodologie de recherche qui cherche à analyser les pratiques mathématiques locales, car il cherche à valoriser, diffuser et respecter les connaissances mathématiques (idées, notions, procédures, processus et pratiques) qui Originaire de divers contextes culturels tout au long de l’histoire (D’AMBR-SIO et ROSA 2016, p. 17).
Situation-problème: Pour calculer le nombre de tuiles rectangulaires de taille c[20 por 30]m, nécessaire pour enrober le sol de la salle de bain d’une galerie d’art, dimensions 6, 00m par 4, 50m (Lezzi, 1996, p. 223), Oscar considéré comme “point de départ les dimensions du sol de la salle de Bains. Prenant la taille de la céramique, nous opterons pour 6m qui est divisible à la fois par le côté céramique du 20cm comme dans les 30 cm. Déjà le 4, 50m pas.
Cette mesure n’est divisible que par les 3[medida do outro lado da cerâmica]0. J’ai donc opté pour ce qui serait plus simple, en prenant le [600cm]6m divisé par 30cm, atteignant le nombre exact de 20 céramiques dans le sens de la longueur. Maintenant, en prenant la poterie dans la direction du côté 20cm j’ai atteint le nombre de 30 lajotas.
Déjà dans le 4, 50m, divisible par 30, j’ai pris le 4, 5[450cm]0m et divisé par 30cm, atteignant le nombre de 15 tuiles qui s’adaptent dans la largeur. Il y a donc 15 tuiles dans le sens des 30cm. Pour atteindre le calcul, j’ai pris les 30 tuiles qui vont dans la lo[600cm]ngueur plus les 15 qui vont en largeur, multiplié et atteint le nombre de tuiles nécessaires, qui serait 450 tuiles “.
Le raisonnement utilisé par le Mason Sérgio pour faire ce même budget, démontre, selon D’ambrosius (2001) que « dans des environnements différents, les ethnomathématiques sont différentes » (p. 35). Ainsi, le maçon commence son discours en soulignant que «d’abord vous avez besoin de découvrir les mètres carrés de la région, il serait temp[operação de multiplicação]s. J’ai trouvé 27m2, donc je dois comprendre combien de tuiles s’adaptent dans un mètre carré. Comme le 30cm[medida do comprimento da placa cerâmica] ne donne pas précis dans un mètre, j’ai été l’augmentation et utilisé 3m, puis fermé avec 10 lajotas. Ce résultat de 10 tuiles, multipliéparparparparpare par 5 tuiles qui s’adaptent en largeur. J’ai trouvé le nombre de 50 tuiles en 3m2 “. Visualisez dans l’ordre la pensée déductive utilisée par le maçon pour être en mesure de faire le budget.
Poursuivant l’explication, Sérgio rapporte qu’après avoir constaté que dans 3m2 s’adapter à 50 pièces, il était seulement “… Prenez ces 27m2, diviser par 3 qui m’a abouti à 9 parties égales. Ainsi, 9 fois 50, donne le résultat de la quantité de céramique qui va à travers la région. Ils sont 450 céramiques et doivent encore voir la rupture.
Le calcul du budget effectué par le Maçon Alberto, a également souligné “450 céramiques. J’ai fait côté fois côté céramique, 0, 20m fois 0, 30m atteignant le nombre 0, 06m2. Ce résultat représente la superficie de chaque céramique. Maintenant, j’ai fait côté temps côté du sol de la salle de bains, 6m fois 4, 50m et a atteint le résultat de 27m2. Puis, les pieds de salle de bains, 27m2 divisés par les mètres carrés d’une partie 0, 06m2, a donné 450 céramiques “.
Dans la résolution de l’énonce: combien de tuiles carrées de 15cm de côté sont nécessaires pour enrober en interne une piscine de 15m de longueur, 6m de large et 1, 20m de profondeur (LEZZI,1991, p. 195), Oscar a rapporté: “J’ai choisi de transformer ces 15m en 1500 cm divisés par 15cm de la Lajota, a entraîné 100 tuiles dans la longueur d’un côté de la piscine. Donc, de l’autre côté donnera le même nombre, c’est-à-dire cette ligne multipliée par 2, donne 200 tuiles, qui s’adaptent des deux côtés de la longueur.
La même procédure que j’ai utilisé dans la largeur, à savoir le 6m est 600cm et ces 600cm divisés par 15 m’a donné 40 tuiles qui iraient dans une largeur. Comme nous avons deux largeurs ici, multipliant par 2, j’ai trouvé 80 tuiles. Ajoutant 200 tuiles de longueur avec 80 de largeur, j’ai atteint le nombre de 280 tuiles, qui doivent être multipliées par la profondeur qui est 1, 20m, soit 120cm. Avant, cependant, j’ai divisé ces 12[medida da profundidade]0cm, par 15c[medida do azulejo]m et a trouvé 8 tuiles qui iraient dans la profondeur de la piscine. Maintenant, en prenant la longueur et en ajoutant avec la largeur, je veux dire les 200 tuiles plus les 80 tuiles, fois les 8 tuiles de la profondeur, j’ai atteint le nombre de 2.240 tuiles.
Nous devons encore trouver le nombre de tuiles du fond de la piscine. Ceci est facile à calculer parce que les dimensions de longueur et de largeur du fond sont les mêmes que les côtés, moyenne 6m par 15m. Ainsi, ils vont 100 céramiques de longueur et 40 dans la largeur du fond, totalisant 4.000 céramiques au fond de la piscine. Ajout du nombre de tuiles des côtés et le fond j’ai atteint le nombre de 6.240 céramiques “. Le maçon a également souligné que «vous aurez toujours besoin d’une réservation» pour éviter d’éventuelles pannes, entre autres.
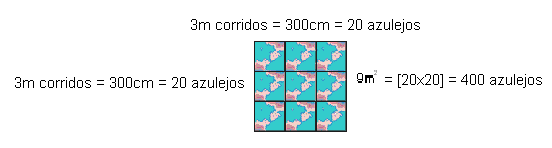
La reconnaissance de l’existence d'”autres formes de pensée”, comme postule D’ambrâsio (2001, p. 17), est évidente dans le raisonnement mathématique utilisé par Sérgio pour faire ce même budget. En communiquant sa pensée, le maçon souligne que « d’abord j’ai besoin de connaître les mètres carrés de mu[laterais]r et de sol. 15m plus 6m, plus de 15m et plus 6m, donnerait le latéra[42m corridos]l. Cette fois 1, 20m, d[profundidade da piscina]onne 50, 4m2 de surface.
Ensuite, je vais trouver les images du fon[15m vezes 6m = 90m2]d. Nous le sommes tous. Je l’ai fait et donné 140, 4m2. Maintenant, j’ai besoin de savoir combien de tuiles s’adaptent dans chaque mètre carré. Seulement que les tuiles sont 15cm par 15cm, dans un mètre n[corrido]e ferme pas. Puis j’ajoutais jusqu’à ce que je suis arrivé à 3m. En 3m,[corridos] il y a 20 lajotas. Ensuite, j’ai pris 3 foi[multiplicado por]s 3[cada face da piscina representa uma figura plana – duas dimensões], serait un total de 9m2 qui a donné 400 Lajotas “. Visualisez dans la représentation qui suit, le raisonnement employé par le maçon pour l’élucidation de la situation problématique.
Poursuivant l’explication de ses procédures, Sérgio suit: “J’ai pris le total de M2 de la piscine, divisé par 9[9 partes]. Donné 15,6 parties égales de 9m2 chacun[140,4m2 : 9m2 = 15,6]e. Ces 15,6 parties égalent la quantité de céramique qui était en 9m2, soit 400 céramiques. Ensuite, dans chaque partie serait 15,6 fois 400, soit 6 240 céramiques ”
Interrogé même si le budget de 6 240 céramiques suffirait à enrober la piscine, Sérgio souligne volontiers : il faudrait environ 5 % de plus de ce total en raison de la rupture.
Pour le professeur D’Ambrosio, les groupes humains produisent des connaissances qui, bien qu’elles ne soient pas répandues dans les espaces d’enseignement formels, sont une connaissance valable et que l’école, ainsi que la recherche en mathématiques, doivent reconnaître et approfondir l’acte. d’enseignement.
D’ambrôsio (2001, p. 22-23), note en outre que,
Il existe de nombreuses études sur les ethnomathématiques de la vie quotidienne. Il s’agit d’un ethnomathématique non appréhendé dans les écoles, mais dans l’environnement familial, dans l’environnement des jouets et du travail, reçu d’amis et de collègues.
La résolution de ce problème de situation pour Alberto a montré une connaissance qui est identifiée avec la procédure qui serait utilisée par un professeur de mathématiques. Remarquez son explication: “La longueur des côtés de la piscine 15m – 15m, ajoutant également la largeur de 6m – 6m donne le périmètre de la piscine, 42m. Maintenant 42m fois 1, 20m de la profondeur de 50, 40m2 de surface sur les côtés de la piscine. Le fond de la piscine a une superficie de 15m fois 6m et donne 90m2. Ajout de la surface latérale et le fond, je veux dire les 50, 40m2 plus le 90m2 donne 140, 40m2. Celui-ci divisé par la taille de la tuile qui est 15cm par 15cm et que dans M2 donne 0, 0225m2, totalise 6.240 tuiles. Maintenant, il suffit d’ajouter un peu à la pause tampon.
Pour Demo (1996), la construction du savoir commence à partir des connaissances incorporées par chaque individu dans son expérience socioculturelle. Cela a été évident dans les formes de matematizar utilisés par chacun des maçons. Pour l’auteur ” Il n’y a pas de tableau superficiel, d’analphabétisme absolu ; Tous parlent, communiquent, utilisent un vocabulaire de base, gèrent des concepts dans le bon sens, ont des références à la réalité dans laquelle ils sont insérés “(p. 32).
En entrant à l’école, tout le monde a déjà accumulé quelques connaissances, même si c’est dans le bon sens. Nous avons partagé avec D’ambrosius (1993), lorsque nous avons postulé que nous devons comprendre que lorsque la scolarité formelle commence, l’enfant a déjà une ethnomathématique qui lui permet de faire face aux interprétations des mathématiques systématiques de l’école.
Les formes Matematizar des maçons indiquent selon Marques (2000) que « les processus d’apprentissage sont inévitablement insérés dans les communautés communicatives et publiques dans lesquelles les hommes apprennent les uns des autres et les uns avec les autres » (p. 29). Selon la compréhension de Pompée et Monteiro (2001), « un processus éducatif significatif commence par l’interaction de l’école et de la communauté » (p. 55), dont les relations peuvent démissionner du rôle de l’école en tant que lieu privilégié d’échange d’expériences Mieux comprendre les connaissances qui circulent dans la vie quotidienne.
Dans les manifestations (verbalisations) exprimées par les maçons dans les sessions d’étude, en particulier de la fabrication mathématique de ces professionnels, sur la base de leur expérience de travail, dans l’échange de connaissances qu’ils ont déjà participé tout au long de leur vie, montrent Qu’il est possible pour l’éducation formelle de valoriser et de valider cette connaissance antérieure, sa culture et son environnement social. Nous croyons qu’un travail éducatif qui laisse, dialogiquement de cette connaissance, Enrique et contextualise la connaissance mathématique de l’école.
Selon Rolim
Penser au contexte historico-culturel dans le processus d’enseignement de l’apprentissage des mathématiques, c’est considérer que « faire » implique plus que des règles et des techniques; est de reconnaître qu’en tant que science, les mathématiques sont elles-mêmes un bâtiment de l’humanité (ROLIM, 2010, P. 43).
À notre avis, de ce point de vue, il est établi dans la Loi sur l’éducation une relation largement utilisée dans le monde des affaires, où l’expression « gagnant-gagnant » est parlée et pratiquée. Dans une négociation, cette expression a une caractéristique : personne ne perd, tout le monde gagne. Il est établi entre l’entreprise et le fournisseur une relation idéale.
Pour la Loi sur l’éducation, cette relation est pédagogiquement idéale, c’est-à-dire les élèves, les enseignants, tout le contexte qui fait partie du processus éducatif, être heureux, réussir. Il est alors entendu que, tout comme dans les affaires, il est possible d’atteindre pédagogiquement dans la salle de classe la relation «gagnant-gagnant», il suffit de faire une bonne et nouvelle planification, dans laquelle cette possibilité est insérée.
Une perspective pédagogique dans laquelle, ainsi que dans le monde des affaires, où les entrepreneurs et les fournisseurs doivent exposer leurs perceptions, leurs points de vue et leurs idées de manière appropriée et au moment opportun, sans juger l’un du comportement de l’autre, à l’école, d’une manière Enseignant respectant et valorisant les connaissances antérieures de ses élèves.
Et quand à l’école, la connaissance de la vie quotidienne entre en “confrontation” avec des connaissances formelles, que nous pouvons dialogiquement se rappeler que dans le monde des affaires, souvent le fournisseur pense différent de l’entrepreneur, cependant, cette relation n’est pas ou ne devrait jamais être Conflit ou causer une certaine usure. Il a besoin à l’école, ainsi qu’en affaires, pour représenter une excellente occasion d’apprentissage pour toutes les personnes impliquées dans ce processus.
Les discours des maçons, participants à la recherche, ont montré que les connaissances des mathématiques qu’ils possèdent, ont été acquises la plupart du temps dans le développement et l’amélioration de leur profession, dans la pratique de la journée au jour le jour, ou même, voir d’autres effectuer le Même activité.
Les conversations que nous avons eues avec les maçons tout au long des sessions d’étude ont montré que les connaissances produites en dehors du champ d’application de l’école sont importantes et qu’il appartient à l’enseignant de les sauver et de les rapprocher de la salle de classe, ce qui rend l’éducation formelle significative et Articulé avec la réalité dans laquelle l’élève est inséré.
5. OBJECTIFS
5.1 Montrer que l’ethnomathématique fait partie de notre vie quotidienne et réfléchir à la possibilité que des groupes sociaux organisés p[pedreiros]roduisent des mathématiques dans leurs différentes formes d’expression dans leur champ d’action, en discutant à l’école des façons de produire Significations de la vie quotidienne; 5.2 Présenter l’ethnomathématique comme l’un des chemins vers une éducation renouvelée, au sein du plus grand mouvement appelé l’enseignement des mathématiques, rendu possible dans cette perspective, par la réflexion entre l’enseignant, l’élève et la communauté, cherchant à surmonter le Les connaissances qu’ils possèdent tous les deux, les modifiant et transformant la salle de classe en un espace démocratique d’échange de connaissances; 5.3 Percevoir l’ethnomathématique comme une alternative pédagogique intéressante au travail en classe, démystifier les mathématiques et approcher les véritables nécessités du quotidien des élèves.
6. MÉTHODOLOGIE
Le travail d’enquête a été accompli à travers différents moments, à savoir: étude bibliographique sur l’ethnomathématique, séances d’étude avec des maçons dans lesquels des situations ont été proposées-problème dans le but d’enquêter dialogiquement avec chaque Professionnel sur les connaissances mathématiques qu’ils [formais ou informais]utilisent pour faire le budget de la quantité de céramique nécessaire pour enrober les murs et les planchers. Réflexion sur les liens possibles entre les mathématiques et la réalité dans la possibilité d’établir des liens entre les connaissances mathématiques du maçon, construites à partir de leurs besoins de professionnels au jour le jour, en utilisant des pratiques La vie quotidienne et les mathématiques scolaires.
7. CONTRIBUTION ATTENDUE
Considérant que tout au long du travail d’enquête, basé sur le discours des maçons, nous percevons que ces professionnels pour résoudre les situations problématiques proposées, n’ont pas toujours été soutenus dans la connaissance des mathématiques scolaires.
Alors qu’il était clair que les maçons appliquaient les connaissances mathématiques d’une manière pratique et intuitive, en utilisant des stratégies spécifiques, et non en utilisant les formules mathématiques enseignées à l’école.
Nous espérons que l’enseignement des mathématiques en classe à travers l’approche ethnomathématique [10]permettra aux enseignants et aux élèves d’en apprendre davantage sur la diversité culturelle même des mathématiques. Que les résultats de cette recherche aident à l’élaboration d’une méthodologie qui contribue à l’enseignement des mathématiques, apportant des possibilités de changements dans la pratique de l’enseignement, l’approche de la pratique pédagogique scolaire avec les connaissances produites dans les situations De la vie des étudiants.
Que, à partir de cette réflexion, la pratique pédagogique en classe puisse être réorientée vers le développement de la pleine citoyenneté des élèves. Que, selon Pinheiro et Rosa (2016), le:
[…] Les professeurs de mathématiques s’immergent dans la dynamique culturelle des élèves et utilisent des stratégies d’enseignement et d’apprentissage qui valorisent la dimension culturelle en classe, de sorte qu’une éducation mathématique inclusive puisse être développée qui pourrait effectivement Contribuer à la transformation sociale (p. 79).
Ainsi, à partir des sessions d’étude et du texte produit, nous visons à provoquer les lecteurs à la possibilité d’une intervention pédagogique, basée sur la réalité de l’étudiant, unissant la théorie et la pratique dans la construction de connaissances systefined. Il est également à espérer que les réflexions résultant de la lecture du texte permettront un nouveau regard sur la réalité et sur l’éducation mathématique, du point de vue de la production de connaissances à partir de la pratique quotidienne.
L’objectif est de contribuer à la Constitution du chercheur Professeur de sa pratique, l’éveillant d’apprendre de manière continue à être un enseignant, en fonction des besoins éducatifs actuels, transformant la salle de classe en un environnement d’échange de connaissances, Sauver la connaissance historique-socialement construite par l’humanité.
8. RÉFÉRENCES BIBLIOGRAPHIQUES
BREDA, Adriana LIMA, Valderez Marina do Rosário e GUIMARÃES, Gleny Terezinha Duro. A utilização da Etnomatemática nos cursos de formação continuada de professores: implicações das relações de poder saber na produção de subjetividades. Curitiba. Novembro de 2011. Disponível em: http://educere.bruc.com.br/CD2011/pdf/4668 _ 2898.pdf. Acessado em: 20/08/2017.
CARNEIRO, K. T. A. Cultura Surda na aprendizagem matemática da sala de recurso do Instituto Felipe Smaldone: uma abordagem etnomatemática. Anais do 4º Congresso Brasileiro de Etnomatemática. Belém, PA: ICEm4, 2012.
D’Ambrósio Ubiratan. Etnomatemática: Arte ou técnica de explicar e conhecer. Editora Ática, Série Fundamentos, 2. edição, São Paulo, 1993.
——-. Educação matemática: da teoria à prática. 13ª ed. Campinas: Papirus, 1996. (Coleção Perspectivas em Educação Matemática).
————-. Etnomatemática – elo entre as tradições e a modernidade. Coleção Tendências em Educação Matemática, 1. Belo Horizonte: Autêntica, 2001, 112p.
D’AMBROSIO, U.; ROSA, M. Um diálogo com Ubiratan D’Ambrosio: uma conversa brasileira sobre etnomatemática. In BANDEIRA, F. A.; GONÇALVES, P. G. F. (Orgs.). Etnomatemáticas pelo Brasil: aspectos teóricos, ticas de matema e práticas escolares. Curitiba, PR: Editora CRV. 2016. pp. 13-37.
DEMO, Pedro. Pesquisa e construção de conhecimento: Metodologia científica no caminho de Habermas. 3.ed. Rio de Janeiro: Tempo Brasileiro, 1996. 125p.
GERDES, Paulus. Etnomatemática: Cultura, Matemática, Educação. Maputo. Instituto Superior Pedagógico, 1991.
GIARDINETTO, José Roberto Boettger. Matemática escolar e matemática da vida cotidiana. Coleção polêmicas do nosso tempo, autores associados, Campinas – São Paulo, 1999, 128p.
LEZZI, Gelson; Dolce, Osvaldo; Machado, Antonio. Matemática e Realidade. 5ª série, 3. edição reformulada, Atual, São Paulo, 1996, 250p.
————–. Matemática e Realidade. 5ª série, 2. edição, Atual, São Paulo, 1991, 213p.
KNIJNIK, Gelsa. O saber popular e o saber acadêmico na luta pela terra. Revista da Sociedade Brasileira de Educação Matemática. Educação Matemática em Revista. Ano 9, n. 1, p. 27-39, 2002.
————–. Educação matemática, culturas e o conhecimento na luta pela terra. Santa Cruz do Sul, EDUNISC, 2006, 239 p.
MARQUES, Mário Osorio. A aprendizagem na mediação social do aprendido e da docência. Ijuí, Editora UNIJUÍ, 2. edição, 2000, 144 p.
MONTEIRO, A.; Pombeu, G. Jr. A matemática e os temas transversais. Editora Moderna, São Paulo, 2001, 160p.
MONTEIRO, Alexandrina. Reflexão e Ação: Revista do Departamento de Educação/UNISC. Vol. 10, n. 1 (jan./jun.2002) — Santa Cruz do Sul: EDUNISC, 2002.
A Etnomatemática em Cenários de Escolarização: alguns elementos de reflexão. Alexandrina Monteiro, p. 93 – 108.
PINHEIRO, R. C.; ROSA, M. Uma perspectiva etnomatemática para o processo de ensino e aprendizagem de alunos Surdos. RPEM, v. 5, n. 9, p. 56-83, 2016.
ROLIM, Carmem Lucia Artioli. Fórmulas de Silêncio: metodologias no processo de ensino da Matemática. In: SANTOS, Jocyléia Santana. ZAMBONI, Ernesta. Potencialidades Investigativas da Educação. Goiânia: Ed. da PUC Goiás, 2010.
ROSA NETO, R. Didática da matemática, São Paulo: Ática, 2002.
8. Compris avec une pratique pédagogique qui valorise les mathématiques des différents groupes culturels, en tenant compte des concepts informels construits par les sujets à travers leurs expériences en dehors du contexte de l’école.
9. Dans cette réflexion, nous traitons les mathématiques formelles et informelles dans l’idée que la première est considérée comme une école, scientifique, systématique, légitime et associée aux contextes de classe et la seconde comme quotidienne, spontanée, la connaissance du jour au jour le jour, Associé à la rue, l’expérience et la vie dans les communautés, les contextes sociaux.
10. Dans ce travail utilisé pour désigner l’étude des conceptions, des traditions et des pratiques mathématiques d’un groupe social et [pedreiros]le travail pédagogique qui peut être développé dans la perspective que le groupe interprète et codifier leurs connaissances; Acquérir les connaissances produites par les mathématiques académiques, en utilisant, lorsqu’ils sont confrontés à des situations contextualisées, celui qui semble plus approprié.
[1] Master en sciences, mathématiques, UNIJUI – RS. Diplôme et spécialisation en sciences et en mathématiques. Prof. Assistant du CCA – Centre des sciences agronomiques, Campus du maréchal Cândido Rondon, UNIOESTE, PR – Brésil.
[2] Master en développement rural durable-UNIOESTE, Spécialiste en mathématiques, Physique-UNIPAR, Gestion du personnel et éducation spéciale avec une spécialisation en handicap multiple-UNIASSELVI, Diplômé en mathématiques avec une spécialisation en physique-UNIPAR.
[3] Spécialisation en enseignement scientifique exact – Mathématiques, physique et chimie. UNIOESTE – Université d’État de Western Paraná. Graduation: Science et Mathématiques. UNIJUI, RS. Professeur à l’école publique de Paraná.
[4] Professeur de protection des végétaux et de santé humaine au département des sciences végétales de l’Université pontificale catholique du Chili, il occupe un poste interdisciplinaire partagé entre la Faculté d’agronomie et l’Ingeniería Forestal (FAIF), les facultés de médecine et de chimie. Professeur de recherche associé au groupe d’étude sols et environnement (GESOMA – UNIOESTE). Master en agronomie de UNIOESTE, doctorat en agronomie de UNIOESTE (2013-2016) – Période Sandwich (Bourse CAPES) de l’Université de Lisbonne, à l’Instituto Superior de Agronomia (ULisboa).
[5] Niveau de productivité 1C du CNPq dans le domaine des sciences de l’environnement avec trois post-doctorants, UEM-PR (Brésil), Université de Santiago de Compostela (Espagne), UFG-GO (Brésil). Il est actuellement professeur associé à UNIOESTE-PR et professeur et chercheur au Centre des sciences agraires, où il enseigne la chimie. Chargée de cours au programme de master en sciences agricoles de l’UEM. Il est actuellement consultant ad hoc auprès du CNPq, de CAPES et de la Fundação Araucária. Agit à titre de consultant bénévole en environnement auprès de MP-SP et de CONAMA-DF.
[6] Premier cycle en agronomie – UNIOESTE – Université d’État de Western Paraná – Diplômé en administration – Unip – Universidade Paulista.
[7] Étudiante à la maîtrise en agronomie (production végétale) de l’Université d’État de Western Paraná (UNIOESTE). Ingénieur agronome diplômé d’UNIOESTE (2014-2018), agit en tant que chercheur associé au groupe d’étude des sols et de l’environnement (GESOMA – UNIOESTE).
Soumis : juin 2019.
Approuvé : juillet 2019.