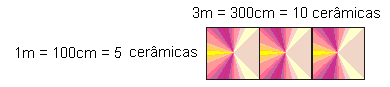ARTIGO ORIGINAL
SCHWANTES, Vilson [1], XAVIER, Márcio Pizzete [2], SCHWANTES, Eloísa Bernardete Finkler [3], SCHWANTES, Daniel [4], JUNIOR, Affonso Celso Gonçalves [5], KRACKE, Elisa [6], JUNIOR, Élio Conradi [7]
SCHWANTES, Vilson. Et al. Etnomatemática: Uma reflexão sobre a matemática utilizada por pedreiros. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 07, Vol. 13, pp. 46-66. Julho de 2019. ISSN: 2448-0959
1. RESUMO
Este artigo é resultado de reflexões sobre etnomatemática e análise de sessões de estudo realizadas com pedreiros do Município de Mercedes – PR. Encontra motivação nos escritos do professor Ubiratan D´Ambrósio que reconhece a presença do conhecimento matemático em espaços culturais diversos. O foco da pesquisa investiga dialogicamente com cada profissional, por meio de situações-problema, que matemática utilizam para fazer o orçamento da quantidade de cerâmica necessária para revestir paredes e pisos. Na pesquisa realizada com os pedreiros interessava saber se esses conhecimentos eram formais ou informais. As falas evidenciaram uma compreensão de que o saber matemático é dinâmico, produto cultural, aflora em diversos setores da atividade humana e circula no e pelo mundo da vida consolidando-se na escola.
Palavras-chave: Educação matemática, etnomatemática, situações-problema, sessões de estudo, orçamento cerâmico.
2. INTRODUÇÃO
Em todas as culturas, ao longo da história, encontramos registros de atividades desenvolvidas que denotam a existência e necessidade de algum tipo de saber matemático. Trata-se de um conhecimento empírico, utilizado no exercício de diversas profissões, repassado por gerações e utilizado, muitas vezes, sem que as pessoas percebam essa presença.
Ao usar um raciocínio matemático para resolver uma situação- problema, às vezes é possível a solução, sem necessariamente ter frequentado uma escola. O saber matemático pode ser desenvolvido naturalmente pela prática diária, como por exemplo, no trabalho dos pedreiros, profissionais que utilizam cotidianamente tais conhecimentos.
Durante muitas décadas na história da educação, o conhecimento advindo de práticas sociais era desprestigiado e não discutido na escola. Atualmente vem ganhando cada vez mais espaço a proposta de investigar o saber matemático presente na vida dos alunos fora do contexto escolar. Esse conhecimento construído pelo homem no espaço e na temporalidade, constitui-se como um precioso legado que deve ser considerado nos currículos escolares, ou então, na metodologia adotada. São muitos os educadores que acreditam que o conhecimento sistematizado pode ser construído a partir de conceitos presentes na vida cotidiana das profissões, das pessoas.
Para o professor Ubiratan D’Ambrósio, mesmo antes de entrar para a escola, todas as crianças já apresentam conhecimentos matemáticos. Estes conhecimentos são, para o pesquisador, uma Etnomatemática[8]. O autor quer nos dizer que o conhecimento não é resultado apenas de anos de estudo, mas também fruto das experiências vividas entre os cidadãos de um mesmo ou de diferentes grupos sociais.
Segundo o pesquisador a principal proposta da etnomatemática é procurar entender o saber/fazer matemático de cada grupo de interesse, comunidade, povo ou nação. Neste sentido seus escritos consideram a etnomatemática:
“…a matemática praticada por grupos culturais, tais como comunidades urbanas e rurais, grupos de trabalhadores, classes profissionais, crianças de uma certa faixa etária, sociedades indígenas, e tantos outros grupos que se identificam por objetivos e tradições comuns aos grupos”. (2001, p.9).
O autor vê a etnomatemática como:
“…uma estratégia desenvolvida pela espécie humana ao longo da sua história para explicar, para entender, para manejar e conviver com a realidade sensível, perceptível e com o seu imaginário, naturalmente dentro de um contexto natural e cultural.” (D´AMBRÓSIO, 1996, p.7)
Pedreiros, por vezes analfabetos e na maioria das vezes com pouca escolaridade, utilizam conhecimentos matemáticos para construir casas, fazer assentamento cerâmico, construir muros, edifícios, considerados ainda hoje, construções sólidas e resistentes. Certamente existe neste trabalho, especialmente nos cálculos e na organização do raciocínio matemático utilizado, um conhecimento que pode ser aproveitado no âmbito escolar, quer na integração de alunos com tendência a este tipo de profissão, quer numa abordagem mais prática da disciplina de matemática. Para Carneiro,
[…] ensino da matemática nesta concepção permitirá ao aluno vincular os conceitos trabalhando em classe a sua experiência cotidiana, de acordo com o seu ambiente natural, social e cultural. Não se trata de rejeitar a matemática acadêmica, mas sim incorporar a ela valores que são vivenciados nas experiências em grupo, considerando os vínculos histórico-culturais (CARNEIRO, 2012, p.3).
Nas últimas décadas tem crescido o número de educadores que estudam a etnomatemática como um programa de pesquisa e/ou como proposta para o trabalho pedagógico. Dentre outros, os objetivos desses professores é conhecer os processos de geração, organização e difusão de conhecimentos e ideias matemáticas presentes no interior de grupos culturais, e como desenvolver ações na área do ensino da matemática que permitam a contextualização dos conteúdos formais abordados em sala de aula.
A perspectiva da etnomatemática nos permite trabalhar em sala de aula uma proposta educacional que estimule alunos e professores no desenvolvimento da criatividade, conduzindo ambos a novas e ricas formas de aprendizagem. Esta riqueza sociocultural que passa a ser incorporada no processo ensino aprendizagem, nas palavras do Professor Ubiratan D’Ambrosio, faz parte de “um programa que visa explicar os processos de geração, organização e transmissão de conhecimentos em diversos sistemas culturais e as forças interativas que agem nos e entre os três processos”. (D’AMBRÓSIO, 1993, p.7).
Outra perspectiva de etnomatemática vem sendo desenvolvida pela pesquisadora brasileira Gelsa Knijnik. Para essa autora, a etnomatemática permite
estudar os discursos eurocêntricos que instituem as matemáticas acadêmica e escolar; analisar os efeitos de verdade produzidos pelos discursos das matemáticas acadêmica e escolar; discutir questões da diferença na educação matemática, considerando a centralidade da cultura e as relações de poder que a instituem; e examinar os jogos de linguagem que constituem cada uma das diferentes matemáticas, analisando suas semelhanças de família. (KNIJNIK, 2006, p.120).
Nos estudos de Knijnik, a autora caracteriza a etnomatemática como uma matemática produzida por grupos sociais que usam seus saberes para realizar suas atividades. Knijnik (2002, p. 33), fazendo um contraponto entre a Matemática formal e a informal[9], pondera que se ―[…] adquira o conhecimento produzido pela matemática acadêmica, utilizando, quando se defrontar com situações reais, aquele que lhe parecer mais adequado.
Segundo Giardinetto (1999), “o professor pode e deve utilizar o conhecimento cotidiano como ponto de apoio para o processo de ensino-aprendizagem” (p.68), trazendo o aluno para o campo da argumentação, desenvolvendo o hábito da leitura crítica, da pesquisa, do questionamento, da criatividade, imprescindíveis para uma formação cidadã. Dessa forma ficam valorizados e evidenciados os saberes prévios dos alunos, formando-se a partir destes, outros conhecimentos, sempre a partir do conhecido.
O importante é o estabelecimento de vínculos do conhecimento da comunidade com o conhecimento da escola e do conhecimento da escola com o conhecimento da comunidade. Através deste estabelecimento e destas relações é possível atribuir significado para ambos os saberes.
A tese defendida pelo autor é que a escola, mais do que reproduzir o saber cotidiano, deve ser mediadora entre este e os conhecimentos escolares, ou seja, deve colocar à disposição das novas gerações o conhecimento elaborado pela humanidade, que se revela como produto histórico e social. Estes saberes precisam ser socializados, uma vez que “não se trata do indivíduo singular construir todo saber, mas ter direito ao acesso a esse saber constituído” (GIARDINETTO, 1999, p. 47).
Para D’Ambrósio (2001), neste contexto o conhecimento apresenta um caráter dinâmico, sempre aberto a novos enfoques. Para isso, o professor deve manter-se atualizado, fazer constantemente avaliações de sua prática, praticar novas metodologias de ensino, bem como aprimorar ações pedagógicas já vivenciadas anteriormente, na perspectiva de que estas possam vir a contribuir com o fazer pedagógico.
Breda, Lima e Guimarães (2011, p. 15), em seus estudos afirmam que:
Passei a olhar a proposta da etnomatemática como uma possibilidade de diferenciar o trabalho que o professor desenvolve nas escolas, ou seja, a prática conteudista e sem significado poderá ser substituída por um fazer docente orientado por um novo olhar, que fomente a valorização do contexto sociocultural do educando, seus processos de pensamento e seus modos de entender, explicar e exercer sua prática na sociedade contemporânea […] um convite para revisitar suas práticas pedagógicas e seus efeitos ou até mesmo olhar seu papel, enquanto docente que lida com diferentes perspectivas de sujeito no contexto escolar.
Assim, no contexto escolar, como programa de estudo que procura conhecer e entender o conhecimento produzido e utilizado dentro das diferentes culturas, a etnomatemática pode ser explorada para auxiliar no trabalho docente, fazendo com que os alunos possam compreender as diversas “matemáticas” utilizadas em contextos outros, valorizando-se a diversidade cultural e o desenvolvimento intelectual e criativo de cada povo, de cada cultura ou comunidade.
Nós professores de matemática, segundo D’Ambrósio (2001), temos que ter claro e estar em perfeita sintonia com nosso papel de educador frente a missão de preparar nossos jovens para um futuro feliz. Precisamos ensinar sim matemática, mas também sobre humanidade. Neste aspecto, o autor enfatiza,
A proposta pedagógica da Etnomatemática é fazer da matemática algo vivo, lidando com as situações reais no tempo [agora] e no espaço [aqui]. E, através da crítica, questionar o aqui e o agora. Ao fazer isso, mergulhamos nas raízes culturais e praticamos a dinâmica cultural. Estamos efetivamente reconhecendo na educação a importância de várias culturas e tradições na formação de uma nova civilização, transcultural e transdisciplinar. (D’AMBRÓSIO, 2001, p. 46).
Para tornar isso uma realidade, o professor precisa rever cotidianamente sua prática docente, elaborar um projeto pedagógico que valorize sempre o conhecimento e a história de cada aluno, buscando nesta individualidade um contexto novo e prático para a arte de ensinar. É importante que o professor em sala de aula, além de aproveitar e partir do conhecimento que o aluno traz do meio em que vive, incentivá-lo a acreditar que ele também tem um papel importante na (re)construção do conhecimento social e cultural, como do conhecimento matemático.
Nas palavras de Rosa Neto, a matemática precisa ser interpretada como produto sociocultural natural de um povo, pois,
A matemática foi criada e vem sendo desenvolvida pelo homem em função de suas necessidades. (…) A cultura é uma forma de adaptação porque é uma forma de atuação sobre o ambiente que foi construído juntamente com ela. (ROSA NETO, 2002, p.7 e 19).
Neste contexto, existe uma significativa relação entre a matemática e a cultura, ambas como resultado de nossa adaptação em função de necessidades de sobrevivência através dos tempos, representando a cultura que gerações passadas nos deixaram, um legado empírico, sistemático e científico.
3. JUSTIFICATIVA
A matemática sempre foi considerada como ciência base de várias áreas do conhecimento. O domínio de seu conhecimento é fundamental para a resolução de situações-problema das mais diversas áreas. Dada essa importância e relevância faz-se necessário procurar novas formas (métodos) para ensiná-la, buscando sempre maior eficiência para o processo ensino-aprendizagem no âmbito escolar.
Muitas pesquisas na área também destacam o baixo rendimento dos alunos no que diz respeito a aprendizagem da disciplina, dizendo que há necessidade de uma maior contextualização dos conteúdos para ocorrer um melhor aprendizado. Seu ensino considerado, muitas vezes por alunos, pais e até professores, como abstrato, distante da realidade, ou seja, o que se ensina em sala de aula, apresenta-se para eles distante das necessidades diárias fora da escola.
Essa falta de vínculo com o cotidiano e, também, o excesso de simbologia ensinado na matemática nas escolas, promove por vezes a difusão de ideias equivocadas com relação a essa disciplina no contexto escolar. A tese que defendemos encontra fundamentação teórica nos escritos do Professor Ubiratan D’Ambrósio, na perspectiva de que a produção do conhecimento matemático não pode estar desvinculada dos movimentos sociais e da cultura de quem produz esse conhecimento.
Nesse sentido, podemos afirmar que há um entrelaçamento entre a matemática produzida, a sociedade que a produz e a cultura que subsidia essa produção. Esse entrelaçamento é construído a várias mãos através de um processo cognitivo, mediado pela ação criativa de diversos atores, todos motivados pela necessidade de ler, compreender e explicar a realidade em que vivem.
Se olharmos para a história da humanidade e das ciências, percebemos que não só a matemática, mas também outras áreas do conhecimento vão se construindo e reconstruindo, sendo ressignificados a cada momento histórico e de acordo com as exigências da sociedade. Pompeu e Monteiro (2001), no livro A Matemática e os temas transversais enfatizam de que o professor precisa compreender a abrangência atual do seu papel na sociedade, pois, segundo os autores,
Os professores atuais têm pela frente um grande desafio: educados num processo fragmentado, terão de superar os limites que essa formação lhes impõe e extrapolar as fronteiras de conteúdos vistos de forma parcial e a-histórica (POMPEU e MONTEIRO, 2001, p.15).
Diante de exigências de tamanha amplitude é necessário que procuremos entender o processo epistemológico da matemática, ou seja, o processo gerativo desse conhecimento, o porquê de sua organização e sistematização. Minimizar este quadro tem sido nas últimas décadas uma preocupação de vários educadores e pesquisadores.
Para Rolim,
Pensar o contexto histórico-cultural no processo ensino aprendizagem da Matemática é considerar que o “fazer” envolve mais que regras e técnicas; é reconhecer que enquanto ciência, a Matemática é ela própria, uma construção da humanidade (ROLIM, 2010, p.43).
É fato que a proposta educacional caracterizada por práticas educativas que propiciem educar socioculturalmente, permitindo em sala de aula o estabelecimento de relações de aprendizagem para atender as necessidades cotidianas dos estudantes, vem crescendo cada vez mais como alternativa pedagógica. De acordo com D’Ambrósio isso significa construir condições para que o aluno possa lidar também em sala de aula com situações diversas do seu cotidiano.
Trata-se de uma perspectiva que torna o ensino de matemática mais contextualizado, com valorizações e preocupações de natureza sociocultural. Conforme D’Ambrósio (2001), a etnomatemática é a área da educação que busca refletir sobre o conhecimento matemático que é gerado a partir da interação num determinado grupo cultural. Para o autor, as aulas de matemática, nesta perspectiva, têm por base o conhecimento matemático de fora para dentro da sala de aula, e estes conhecimentos devem ser desenvolvidos a partir da experiência do aluno.
D’Ambrósio (2001, p. 22) a esse respeito, faz ainda a seguinte afirmação:
O cotidiano está impregnado dos saberes e fazeres próprios da cultura. A todo instante, os indivíduos estão comparando, classificando, medindo, explicando, generalizando, inferindo e, de algum modo, avaliando, usando os instrumentos materiais e intelectuais que são próprios à sua cultura (D’AMBRÓSIO, 2001, p.22).
No nosso estudo, a questão norteadora foi: De que tipo de matemática (formal ou informal) utilizam-se pedreiros para fazer o orçamento da quantidade de cerâmica necessária para revestir paredes e pisos. Ficou evidente que o profissional pedreiro exerce suas funções laborais utilizando-se de habilidades matemáticas aprendidas com a prática cotidiana. Para Monteiro (2002, p.102), “O saber-fazer cultural tem outros caminhos de validação, outra lógica para sua configuração. A questão é por que um se tornou universal e legitimado e o outro não”. Nesta perspectiva a autora nos remete para situações semelhantes às vivenciadas nesta investigação.
Segundo Gerdes:
Há séculos que os pedreiros, por vezes analfabetos e, na maioria das vezes, com muita pouca escolaridade, constroem casas, muros e outros edifícios, considerados ainda hoje, construções sólidas e resistentes. Assim, existe no seu trabalho, no modo como fazem os seus cálculos e organizam os seus raciocínios matemáticos, uma sabedoria que poderá ser aproveitada no âmbito escolar, quer na integração de determinados alunos com tendência a este tipo de profissões quer numa abordagem mais “prática” e mais próxima do quotidiano para os alunos em geral. Esta situação encontra-se referida em trabalhos desta linha de pesquisa, nomeadamente, na terminologia de Gerdes, como “matemática oprimida”, ou “matemática escondida ou congelada” (GERDES, 1991, p.29).
Na pesquisa partimos do pressuposto que os pedreiros, grupo escolhido para fazer esta investigação, constituem um grupo de trabalhadores que fazem uso diariamente de uma grande variedade de saberes matemáticos no seu cotidiano e sem esse conhecimento não seria possível desenvolver ou executar qualquer atividade na construção civil. Porém, considerando que geralmente possuem pouca escolaridade, interessava saber como adquiriram esses conhecimentos matemáticos ou se lhes foram proporcionados através prática diária.
Dentro deste contexto este trabalho investigativo pode contribuir para, inclusive, desmistificar a ideia de que a matemática é uma ciência para poucos, entendendo-se que não existe uma única linguagem matemática, mas sim múltiplas formas de pensamento matemático, cada qual organizado e estruturado dentro do seu contexto social.
Para tanto a escola precisa desenvolver projetos educacionais que possibilitem a troca de experiências com atividades onde a matemática é utilizada cotidianamente. Nesta interação, além de permitir-se a troca de experiências, criam-se vínculos e se estabelecem relações pedagógicas outras com o mundo vivido fora da escola e isso pode ser um caminho facilitador na aprendizagem da disciplina.
Segundo D’Ambrósio as aulas de matemática devem ter por base o conhecimento matemático de fora para dentro da sala de aula, e estes conhecimentos devem ser desenvolvidos a partir da experiência do aluno. Deste modo, o autor afirma que o conhecimento etnomatemático do grupo/comunidade tem muito valor, pois lhe serve, é eficiente e adequado para muitas coisas, próprias àquela cultura, àquele etno, e não há por que substituí-lo. Da mesma forma, a matemática do grupo dominante lhe serve, é útil e não há como ignorá-la (D’AMBRÓSIO, 2001, p. 80).
Para Carneiro,
[…] ensino da matemática nesta concepção permitirá ao aluno vincular os conceitos trabalhando em classe a sua experiência cotidiana, de acordo com o seu ambiente natural, social e cultural. Não se trata de rejeitar a matemática acadêmica, mas sim incorporar a ela valores que são vivenciados nas experiências em grupo, considerando os vínculos histórico-culturais (CARNEIRO, 2012, p.3).
4. PROBLEMATIZANDO PARA CONHECER AS FORMAS DE MATEMATIZAR DOS PEDREIROS
No trabalho investigativo realizado com o grupo de pedreiros, elaboramos algumas situações-problema, para averiguar que matemática é utilizada por estes profissionais para fazer o orçamento da quantidade de cerâmica necessária para revestir paredes e pisos. Este estudo foi realizado na perspectiva de D’AMBRÓSIO e ROSA, que consideram a etnomatemática como um programa de pesquisa em história e filosofia da matemática, com implicações pedagógicas, quando os autores consideram:
Então, esse programa de pesquisa representa uma metodologia de investigação que busca analisar as práticas matemáticas locais, pois visa valorizar, difundir e respeitar o conhecimento matemático (ideias, noções, procedimento, processos e práticas) que se originam em diversos contextos culturais no decorrer da história (D’AMBRÓSIO e ROSA 2016, p. 17).
Situação-problema: Para calcular o número de lajotas retangulares de tamanho [20 por 30]cm, necessárias para revestir o piso do banheiro de uma Galeria de Artes, de dimensões 6,00m por 4,50m (LEZZI, 1996, p.223), Oscar considerou como “ponto de partida as dimensões do piso do banheiro. Pegando o tamanho da cerâmica, a gente vai optar por 6m que é divisível tanto pelo lado da cerâmica dos 20cm como nos 30 cm. Já os 4,50m não.
Esta medida só é divisível pelo 30 [medida do outro lado da cerâmica]. Então, eu optei pelo que seria mais simples, pegando o 6m [600cm] dividido por 30cm, chegando ao número exato de 20 cerâmicas no sentido do comprimento. Agora, pegando a cerâmica no sentido dos 20cm de lado cheguei ao número de 30 lajotas.
Já nos 4,50m, divisível por 30, peguei os 4,50m [450cm] e dividi por 30cm, chegando ao número de 15 lajotas que cabem na largura. Então, são 15 lajotas no sentido dos 30cm. Para chegar no cálculo peguei as 30 lajotas que vão no comprimento [600cm] mais as 15 que vão na largura, multipliquei e cheguei ao número de lajotas necessárias, que seriam 450 lajotas”.
O raciocínio empregado pelo pedreiro Sérgio para fazer este mesmo orçamento, demonstra, segundo D’Ambrósio (2001) que “em ambientes diferentes, as etnomatemáticas são diferentes” (p.35). Assim, o pedreiro inicia a sua alocução enfatizando que “Primeiro é preciso descobrir os metros quadrados da área, seria vezes [operação de multiplicação]. Encontrei 27m2, daí eu tenho que descobrir quantos azulejos cabem em um metro quadrado. Como o 30cm [medida do comprimento da placa cerâmica] não dava exato em um metro, fui aumentando e usei 3m corridos, aí fechou com 10 lajotas. Este resultado de 10 lajotas, multipliquei por 5 lajotas que cabem na largura. Encontrei o número de 50 lajotas em 3m2”. Visualize na seqüência o pensamento dedutivo utilizado pelo pedreiro para conseguir fazer o orçamento.
Continuando a explicação, Sérgio relata que depois que descobriu que em 3m2 cabem 50 peças, foi só “… pegar esses 27m2, dividir por 3 que me resultou 9 partes iguais. Daí, 9 vezes 50, dá o resultado da quantidade de cerâmica que vai em toda a área. São 450 cerâmicas e ainda teria que ver a quebra”.
O cálculo orçamentário realizado pelo pedreiro Alberto, também apontou “450 cerâmicas. Fiz lado vezes lado da cerâmica, 0,20m vezes 0,30m chegando ao número 0,06m2. Este resultado representa a área de cada cerâmica. Agora fiz lado vezes lado do chão do banheiro, 6m vezes 4,50m e cheguei ao resultado de 27m2. Então, a metragem do banheiro, 27m2 dividido pelos metros quadrados de uma peça 0,06m2, deu 450 cerâmicas”.
Na resolução do de enunciado: Quantos azulejos quadrados de 15cm de lado são necessários para revestir internamente uma piscina com 15m de comprimento, 6m de largura e 1,20m de profundidade (LEZZI,1991, p.195), Oscar relatou: “Optei em transformar estes 15m em 1.500cm que divididos pelos 15cm da lajota, resultou em 100 azulejos no comprimento de um lado da piscina. Então, no outro lado vai dar o mesmo número, ou seja, essa fileira multiplicada por 2, dá 200 azulejos, que cabem nas duas laterais do comprimento.
O mesmo procedimento usei na largura, ou seja, o 6m são 600cm e esses 600cm dividido por 15 me deu 40 azulejos que iriam numa largura. Como temos aqui duas larguras, multiplicando por 2, encontrei 80 azulejos. Somando 200 azulejos do comprimento com os 80 da largura, cheguei ao número de 280 azulejos, que precisam ser multiplicados pela profundidade que é de 1,20m, ou seja, 120cm. Antes, porém, dividi esses 120cm [medida da profundidade], por 15cm [medida do azulejo] e encontrei 8 azulejos que iriam na profundidade da piscina. Agora, pegando o comprimento e somando com a largura, quer dizer os 200 azulejos mais os 80 azulejos, vezes os 8 azulejos da profundidade, cheguei ao número de 2.240 azulejos.
Falta ainda achar o número de azulejos do fundo da piscina. Isso é fácil para calcular, pois as dimensões comprimento e largura do fundo são as mesmas das laterais, quer dizer 6m por 15m. Então, vão 100 cerâmicas no comprimento e 40 na largura do fundo, totalizando 4.000 cerâmicas no fundo da piscina. Somando o número de azulejos das laterais e do fundo cheguei ao número de 6.240 cerâmicas”. O pedreiro ressaltou ainda que “sempre vai-se precisar de uma reserva” para prevenir possíveis quebras, entre outros.
O reconhecimento da existência “de outras formas de pensar”, como postula D’Ambrósio (2001, p.17), evidencia-se no raciocínio matemático empregado por Sérgio para fazer este mesmo orçamento. Ao comunicar seu pensamento o pedreiro ressalta que “primeiro preciso saber os metros quadrados de parede [laterais] e de chão. 15m mais 6m, mais 15m e mais 6m, daria a lateral [42m corridos]. Isto vezes 1,20m [profundidade da piscina], dá 50,4m2 de área.
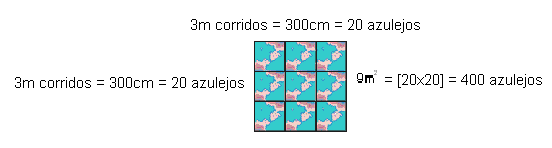
Depois descubro a metragem do fundo [15m vezes 6m = 90m2]. Somo tudo. Eu fiz e deu 140,4m2. Agora preciso descobrir quantos azulejos cabem em cada metro quadrado. Só que como os azulejos são de 15cm por 15cm, em um metro [corrido] não fecha. Aí eu fui acrescentando até chegar em 3m. Em 3m [corridos], são 20 lajotas. Daí eu peguei 3 vezes [multiplicado por] 3 [cada face da piscina representa uma figura plana – duas dimensões], seria um total de 9m2 que deu 400 lajotas”. Visualize na representação que segue, o raciocínio empregado pelo pedreiro para a elucidação da situação-problema.
Dando continuidade a explicação de seus procedimentos, Sérgio assim prossegue: “Eu peguei o total de m2 da piscina, dividi por 9 [9 partes]. Deu 15,6 partes iguais de 9m2 cada [140,4m2 : 9m2 = 15,6]. Essas 15,6 partes iguais vezes a quantia de cerâmica que foi em 9m2, ou seja, 400 cerâmicas. Então, em cada parte seria 15,6 vezes 400, igual a 6.240 cerâmicas”.
Questionado ainda se o orçamento de 6.240 cerâmicas daria o suficiente para revestir a piscina, Sérgio prontamente enfatiza: precisaria de uns 5% a mais deste total por causa da quebra.
Para o Professor D’Ambrósio, grupos humanos produzem um conhecimento que, embora não difundido nos espaços formais de ensino é um conhecimento válido e que a escola, assim como a pesquisa em educação matemática precisam reconhecer e aprofundar para enriquecer o ato educativo.
D’Ambrósio (2001, p. 22-23), observa ainda que,
Há inúmeros estudos sobre a Etnomatemática do cotidiano. É uma Etnomatemática não apreendida nas escolas, mas no ambiente familiar, no ambiente dos brinquedos e do trabalho, recebida de amigos e colegas.
A resolução desta situação-problema para Alberto mostrou um conhecimento que se identifica com o procedimento que seria usado por um professor de matemática. Observe sua explanação: “O comprimento dos lados da piscina 15m+15m, somando também a largura 6m+6m dá o perímetro da piscina, 42m. Agora 42m vezes 1,20m da profundidade da 50,40m2 de área nas laterais da piscina. O fundo da piscina tem área de 15m vezes 6m e dá 90m2. Somando a área lateral e do fundo, quer dizer, os 50,40m2 mais os 90m2 dá 140,40m2. Isto dividido pelo tamanho do azulejo que é de 15cm por 15cm e que em m2 dá 0,0225m2, totaliza 6.240 azulejos. Agora é só acrescentar um pouco para a reserva de quebra”.
Para Demo (1996), a construção do conhecimento começa a partir dos saberes incorporados por cada indivíduo na sua vivência sócio-cultural. Isto transpareceu nas formas de matematizar utilizadas por cada um dos pedreiros. Para o autor “não existe tábua rasa, analfabetismo absoluto; todos falam, se comunicam, usam um vocabulário básico, manejam conceitos dentro do senso comum, possuem referências da realidade em que estão inseridos” (p.32).
Ao ingressarem na escola todos já tem acumulado algum conhecimento, mesmo que seja no âmbito do senso comum. Compartilhamos com D’Ambrósio (1993), ao postular que precisamos entender que quando a escolarização formal começa, a criança já possui uma etnomatemática que lhe permite fazer frente às interpretações da matemática sistematizada da escola.
As formas de matematizar dos pedreiros denotam de acordo com Marques (2000) que “os processos de aprendizagem se inserem inevitavelmente em comunidades comunicativas e públicas em que os homens aprendem uns dos outros e uns com os outros” (p.29). Segundo o entendimento de Pompeu e Monteiro (2001), “um processo educacional significativo inicia-se com a interação de escola e comunidade” (p.55), cujas relações podem ressignificar o papel da escola como local privilegiado de troca de experiências para se entender melhor o saber que circula no cotidiano.
Nas manifestações (verbalizações) expressas pelos pedreiros nas sessões de estudo, sobretudo a partir do fazer matemático destes profissionais, fundamentada na sua experiência laboral, na troca de saberes de que já participaram ao longo de suas vidas, mostram que é possível o ensino formal valorizar e validar esses conhecimentos prévios, sua cultura e seu meio social. Acreditamos que um trabalho educativo que parte, dialogicamente destes conhecimentos, enrique e contextualiza o saber matemático escolar.
Nas palavras de Rolim
Pensar o contexto histórico-cultural no processo ensino aprendizagem da Matemática é considerar que o “fazer” envolve mais que regras e técnicas; é reconhecer que enquanto ciência, a Matemática é ela própria, uma construção da humanidade (ROLIM, 2010, P.43).
No nosso entendimento, a partir desta perspectiva, fica estabelecido no ato educativo uma relação muito usada no mundo dos negócios, onde se fala e prática muito a expressão “ganha-ganha”. Numa negociação, essa expressão tem uma característica: ninguém perde, todos ganham. Fica a partir disso estabelecido entre empresa e fornecedor uma relação ideal.
Para o ato educativo, essa relação é pedagogicamente a ideal, ou seja, alunos, professores, todo o contexto que faz parte do processo educativo, sendo feliz, tendo sucesso. Fica então compreendido que, assim como nos negócios, é possível pedagogicamente conseguirmos em sala de aula a relação “ganha-ganha”, basta fazer um bom e novo planejamento, no qual essa possibilidade esteja inserida.
Uma perspectiva pedagógica em que, assim como no mundo dos negócios, onde empresário e fornecedor devem expor suas percepções, seus pontos de vista e suas ideias de forma adequada e no momento oportuno, sem julgar um o comportamento do outro, na escola, de forma análoga, professor respeitando e valorizando os saberes prévios de seus alunos.
E, quando na escola, os saberes do cotidiano entrarem em “confronto” com os saberes formais, que possamos dialogicamente lembrar que no mundo dos negócios, muitas vezes o fornecedor pensa diferente do empresário, porém, esta relação não é ou nunca deveria ser conflituosa ou causar algum desgaste. Precisa na escola, assim como nos negócios, representar uma grande oportunidade de aprendizagem para todos os envolvidos nesse processo.
As falas dos pedreiros, participantes da pesquisa, mostraram que os conhecimentos de matemática que possuem, foram adquiridos na maioria das vezes no desenvolvimento e aperfeiçoamento de sua profissão, na prática do dia a dia, ou ainda, vendo outros realizarem a mesma atividade.
As conversas que tivemos com os pedreiros ao longo das sessões de estudo mostraram que os saberes produzidos fora do âmbito escolar são importantes e cabe ao professor resgatá-los e aproximá-los da sala de aula, fazendo com que o ensino formal seja significativo e articulado com a realidade em que o aluno está inserido.
5. OBJETIVOS
5.1 Mostrar que a Etnomatemática faz parte do nosso cotidiano e refletir sobre a possibilidade dos grupos sociais organizados [pedreiros] produzirem matemática nas suas diferentes formas de expressão dentro de seu âmbito de ação, discutindo na escola os modos de produção de significados do cotidiano; 5.2 Apresentar a Etnomatemática como um dos caminhos para uma educação renovada, dentro do movimento maior denominado de educação matemática, possibilitada nesta perspectiva, pela reflexão entre professor, aluno e comunidade, buscando-se a superação dos conhecimentos que ambos possuem, modificando-os e transformando a sala de aula num espaço democrático de troca de saberes; 5.3 Perceber a Etnomatemática como uma alternativa pedagógica interessante para o trabalho em sala de aula, desmistificando a Matemática e aproximando-a das reais necessidades do dia-a-dia dos educandos.
6. METODOLOGIA
O trabalho investigativo foi realizado através de momentos distintos, quais sejam: Estudo bibliográfico sobre Etnomatemática, sessões de estudo com pedreiros nas quais foram propostas situações-problema com o propósito de investigar dialogicamente com cada profissional sobre os conhecimentos matemáticos [formais ou informais] que utilizam para fazer o orçamento da quantidade de cerâmica necessária para revestir paredes e pisos. Reflexão sobre possíveis conexões entre matemática e realidade na possibilidade do estabelecimento de vínculos entre o conhecimento matemático do pedreiro, construído a partir de suas necessidades do dia-a-dia profissional, utilizando-se de práticas cotidianas e a matemática escolar.
7. CONTRIBUIÇÃO ESPERADA
Considerando que durante todo o trabalho investigativo, baseado nas falas dos pedreiros, percebemos que estes profissionais para resolverem as situações-problema propostas, nem sempre se apoiavam nos conhecimentos da matemática escolar.
Considerando que ficou claro que os pedreiros aplicam o conhecimento matemático de forma prática e intuitiva, utilizando-se de estratégias específicas, não utilizando as fórmulas matemática ensinadas na escola.
Esperamos que ensinar matemática em sala de aula através da abordagem Etnomatemática[10], permita aos professores e alunos aprenderem sobre a própria diversidade cultural da matemática. Que os resultados desta pesquisa auxiliem no desenvolvimento de uma metodologia que contribua com o ensino da matemática, trazendo possibilidades de mudanças na prática docente, aproximando a prática pedagógica escolar com o conhecimento produzido em situações concretas da vida dos alunos.
Que a partir desta reflexão a prática pedagógica em sala de aula possa ser reorientada para o desenvolvimento da plena cidadania dos alunos. Que, segundo Pinheiro e Rosa (2016), os:
[…] professores de matemática mergulhem na dinâmica cultural dos alunos e utilizem estratégias de ensino e aprendizagem que valorizem a dimensão cultural existente na sala de aula, para que se desenvolva uma educação matemática inclusiva que possa efetivamente contribuir para a transformação social (p. 79).
Assim sendo, a partir das sessões de estudo e do texto produzido, almeja-se provocar os leitores para a possibilidade da intervenção pedagógica, a partir da realidade do aluno, unindo-se teoria e prática na construção do saber sistematizado. Espera-se também que as reflexões decorrentes da leitura do texto permitam um novo olhar sobre a realidade e sobre a educação matemática, na perspectiva da produção do conhecimento a partir da prática cotidiana.
Pretende-se por fim contribuir na constituição do professor pesquisador de sua prática, despertando-o a aprender de maneira continuada a ser professor, segundo as atuais necessidades educacionais, transformando a sala de aula num ambiente de troca de saberes, resgatando conhecimentos histórico-socialmente construídos pela humanidade.
8. REFERÊNCIAS BIBLIOGRÁFICAS
BREDA, Adriana LIMA, Valderez Marina do Rosário e GUIMARÃES, Gleny Terezinha Duro. A utilização da Etnomatemática nos cursos de formação continuada de professores: implicações das relações de poder saber na produção de subjetividades. Curitiba. Novembro de 2011. Disponível em: http://educere.bruc.com.br/CD2011/pdf/4668 _ 2898.pdf. Acessado em: 20/08/2017.
CARNEIRO, K. T. A. Cultura Surda na aprendizagem matemática da sala de recurso do Instituto Felipe Smaldone: uma abordagem etnomatemática. Anais do 4º Congresso Brasileiro de Etnomatemática. Belém, PA: ICEm4, 2012.
D’Ambrósio Ubiratan. Etnomatemática: Arte ou técnica de explicar e conhecer. Editora Ática, Série Fundamentos, 2. edição, São Paulo, 1993.
——-. Educação matemática: da teoria à prática. 13ª ed. Campinas: Papirus, 1996. (Coleção Perspectivas em Educação Matemática).
————-. Etnomatemática – elo entre as tradições e a modernidade. Coleção Tendências em Educação Matemática, 1. Belo Horizonte: Autêntica, 2001, 112p.
D’AMBROSIO, U.; ROSA, M. Um diálogo com Ubiratan D’Ambrosio: uma conversa brasileira sobre etnomatemática. In BANDEIRA, F. A.; GONÇALVES, P. G. F. (Orgs.). Etnomatemáticas pelo Brasil: aspectos teóricos, ticas de matema e práticas escolares. Curitiba, PR: Editora CRV. 2016. pp. 13-37.
DEMO, Pedro. Pesquisa e construção de conhecimento: Metodologia científica no caminho de Habermas. 3.ed. Rio de Janeiro: Tempo Brasileiro, 1996. 125p.
GERDES, Paulus. Etnomatemática: Cultura, Matemática, Educação. Maputo. Instituto Superior Pedagógico, 1991.
GIARDINETTO, José Roberto Boettger. Matemática escolar e matemática da vida cotidiana. Coleção polêmicas do nosso tempo, autores associados, Campinas – São Paulo, 1999, 128p.
LEZZI, Gelson; Dolce, Osvaldo; Machado, Antonio. Matemática e Realidade. 5ª série, 3. edição reformulada, Atual, São Paulo, 1996, 250p.
————–. Matemática e Realidade. 5ª série, 2. edição, Atual, São Paulo, 1991, 213p.
KNIJNIK, Gelsa. O saber popular e o saber acadêmico na luta pela terra. Revista da Sociedade Brasileira de Educação Matemática. Educação Matemática em Revista. Ano 9, n. 1, p. 27-39, 2002.
————–. Educação matemática, culturas e o conhecimento na luta pela terra. Santa Cruz do Sul, EDUNISC, 2006, 239 p.
MARQUES, Mário Osorio. A aprendizagem na mediação social do aprendido e da docência. Ijuí, Editora UNIJUÍ, 2. edição, 2000, 144 p.
MONTEIRO, A.; Pombeu, G. Jr. A matemática e os temas transversais. Editora Moderna, São Paulo, 2001, 160p.
MONTEIRO, Alexandrina. Reflexão e Ação: Revista do Departamento de Educação/UNISC. Vol. 10, n. 1 (jan./jun.2002) — Santa Cruz do Sul: EDUNISC, 2002.
A Etnomatemática em Cenários de Escolarização: alguns elementos de reflexão. Alexandrina Monteiro, p. 93 – 108.
PINHEIRO, R. C.; ROSA, M. Uma perspectiva etnomatemática para o processo de ensino e aprendizagem de alunos Surdos. RPEM, v. 5, n. 9, p. 56-83, 2016.
ROLIM, Carmem Lucia Artioli. Fórmulas de Silêncio: metodologias no processo de ensino da Matemática. In: SANTOS, Jocyléia Santana. ZAMBONI, Ernesta. Potencialidades Investigativas da Educação. Goiânia: Ed. da PUC Goiás, 2010.
ROSA NETO, R. Didática da matemática, São Paulo: Ática, 2002.
8. Entendida com uma prática pedagógica que valoriza a matemática dos diferentes grupos culturais, levando em consideração os conceitos informais construídos pelos sujeitos através de suas experiências fora do contexto da escola.
9. Tratamos, nesta reflexão, a matemática formal e a informal na ideia que a primeira é considerada de natureza escolar, científica, sistematizada, legitimada e associada a contextos de sala de aula e a segunda como do cotidiano, espontânea, conhecimento do dia a dia, associada às ruas, à experiência e a vivência nas comunidades, a contextos sociais.
10. Neste trabalho utilizado para designar a investigação das concepções, tradições, e práticas matemáticas de um grupo social [pedreiros] e o trabalho pedagógico que pode ser desenvolvido na perspectiva de que o grupo interprete e codifique seu conhecimento; adquira o conhecimento produzido pela matemática acadêmica, utilizando, quando se defrontar com situações contextualizadas, aquele que lhe parecer mais adequado.
[1] Mestrado em Educação nas Ciências – Matemática. UNIJUI: Universidade Regional do Noroeste do Estado do Rio Grande do Sul, RS. Especialização: Ensino de Ciências. FAFIG: Faculdade Estadual de Filosofia, Ciências e Letras de Guarapuava. Graduação em Matemática. UPF: Universidade de Passo Fundo, RS. Graduação em Ciências. FACIP: Faculdade de Ciências e Pedagogia de Lages, SC.
[2] Mestrando Em Desenvolvimento Rural Sustentável, Especialista Em Matemática, Física, Gestão De Pessoas E Educação Especial com Ênfase Na Deficiência Múltipla, Graduado Em Matemática Com Ênfase Em Física.
[3] Especialização em Ensino de Ciências Exatas – Matemática, Física e Química. UNIOESTE – Universidade Estadual do Oeste do Paraná. Graduação: Ciências – Licenciatura Plena – Habilitação Matemática. UNIJUI: Universidade Regional do Noroeste do Estado do Rio Grande do Sul, RS. Graduação: Ciências – Licenciatura de 1º. Grau. UNIJUI: Universidade Regional do Noroeste do Estado do Rio Grande do Sul, RS.
[4] Professor da área de Proteção de Plantas e Saúde Humana da Pontifícia Universidad Católica de Chile, Departamento de Ciências Vegetales, ocupa um cargo interdisciplinar compartilhado entre a Facultad de Agronomía e Ingeniería Forestal (FAIF), Facultad de Medicina y Facultad de Química. Professor pesquisador associado ao Grupo de Estudos em Solos e Meio Ambiente (GESOMA – UNIOESTE). Mestre em Agronomia pela UNIOESTE, Doutor em Agronomia pela UNIOESTE (2013-2016) – Período Sanduíche (Bolsista CAPES) pela Universidade de Lisboa, no Instituto Superior de Agronomia (ULisboa).
[5] Pós-Doutor Em Ciências Ambientais.
[6] Graduanda em Agronomia – UNIOESTE – Universidade Estadual do Oeste do Paraná- Graduanda de Administração – Unip – Universidade Paulista.
[7] Mestrando Em Agronomia.
Enviado: Junho, 2019.
Aprovado: Julho, 2019.