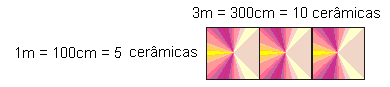ARTICOLO ORIGINALE
SCHWANTES, Vilson [1], XAVIER, Márcio Pizzete [2], SCHWANTES, Eloísa Bernardete Finkler [3], SCHWANTES, Daniel [4], JUNIOR, Affonso Celso Gonçalves [5], KRACKE, Elisa [6], JUNIOR, Élio Conradi [7]
SCHWANTES, Vilson. Et al. Ethnomathematics: Una riflessione sulla matematica usata dai muratori. Revista Científica Multidisciplinar Núcleo do Conhecimento. anno 04, Ed. 07, Vol. 13, pp. 46-66. luglio 2019. ISSN: 2448-0959
1. RIEPILOGO
Questo articolo è il risultato di riflessioni sull’etnomatematica e l’analisi delle sessioni di studio condotte con Bricklayers nel comune di Mercedes – PR. Egli trova motivazione negli scritti del professor Ubiratan D – Ambrosio che riconosce la presenza della conoscenza matematica in diversi spazi culturali. Il focus della ricerca indaga dialogicamente con ogni professionista, attraverso situazioni problematiche, che la matematica utilizza per rendere il budget della quantità di ceramiche necessarie per rivestire pareti e pavimenti. Nella ricerca condotta con i muratori, era interessante sapere se questi erano formali o informali. Le dichiarazioni hanno dimostrato una comprensione che la conoscenza matematica è dinamica, un prodotto culturale, che emerge in vari settori dell’attività umana e circola dentro e attraverso il mondo della vita, consolidandosi nella scuola.
Parole chiave: educazione matematica, etnomatematica, situazioni problematiche, sessioni di studio, budget ceramico.
2. INTRODUZIONE
In tutte le culture, nel corso della storia, troviamo registrazioni di attività sviluppate che denotano l’esistenza e la necessità di qualche tipo di conoscenza matematica. Questa è una conoscenza empirica, utilizzata nell’esercizio di diverse professioni, passata attraverso generazioni e usata, spesso, senza che le persone se ne accorgessi di questa presenza.
Quando si utilizza il ragionamento matematico per risolvere una situazione problematica, a volte è possibile risolvere, senza aver necessariamente frequentato una scuola. La conoscenza matematica può essere sviluppata naturalmente dalla pratica quotidiana, ad esempio, nel lavoro dei muratori, professionisti che utilizzano abitualmente tali conoscenze.
Per molti decenni nella storia dell’istruzione, le conoscenze derivanti dalle pratiche sociali sono state ignorate e non discusse a scuola. Al giorno d’oggi, la proposta di indagare le conoscenze matematiche presenti nella vita degli studenti al di fuori del contesto scolastico sta guadagnando sempre più spazio. Questa conoscenza costruita dall’uomo nello spazio e nella temporalità costituisce una preziosa eredità che deve essere considerata nei programmi scolastici, o nella metodologia adottata. Ci sono molti educatori che credono che la conoscenza della sileria possa essere costruita con concetti presenti nella vita quotidiana delle professioni, delle persone.
Per il professor Ubiratan D’ambrsio, ancor prima di entrare a scuola, tutti i bambini hanno già conoscenze matematiche. Questa conoscenza è, per il ricercatore, un’etnomatematica[8]. L’autore vuole dirci che la conoscenza non è solo il risultato di anni di studio, ma anche il frutto delle esperienze vissute tra i cittadini dello stesso gruppo sociale o di diversi gruppi sociali.
Secondo il ricercatore, la proposta principale di Etnomathematics è quello di cercare di capire la conoscenza matematica / fare di ogni gruppo di interesse, comunità, persone o nazione. In questo senso, i suoi scritti considerano l’etnomatematica:
“… La matematica praticata da gruppi culturali, come le comunità urbane e rurali, gruppi di lavoratori, classi professionali, bambini di una certa fascia di età, società indigene, e tanti altri gruppi che si identificano da obiettivi e tradizioni Comune ai gruppi “. (2001, p.9).
L’autore vede Ethnomathematics come:
“… Una strategia sviluppata dalla specie umana nel corso della sua storia per spiegare, comprendere, gestire e vivere con la realtà sensibile, percepibile e con il suo immaginario, naturalmente all’interno di un contesto naturale e culturale. ” (D: AMBROSIUS, 1996, 7)
Gli studenti di mattoni, a volte analfabeti e la maggior parte del tempo con poca scolarnatura, usano conoscenze matematiche per costruire case, fare nidificazione ceramica, costruire muri, edifici, considerati ancora oggi, costruzioni solide e robuste. Esiste certamente in questo lavoro, soprattutto nei calcoli e nell’organizzazione del ragionamento matematico utilizzato, una conoscenza che può essere sfruttata nel contesto scolastico, o nell’integrazione di studenti con tendenza a questo tipo di professione, sia in un approccio Disciplina matematica più pratica. Per Carneiro,
[…] Insegnare la matematica in questa concezione permetterà allo studente di collegare i concetti che lavorano in classe alla loro esperienza quotidiana, secondo il loro ambiente naturale, sociale e culturale. Non si tratta di rifiutare la matematica accademica, ma piuttosto di incorporare valori che sono sperimentati in esperienze di gruppo, considerando i legami storico-culturali (CARNEIRO, 2012, p. 3).
Negli ultimi decenni, il numero di educatori che studiano l’etnomatematica è cresciuto come un programma di ricerca e/o come proposta per il lavoro pedagogico. Tra gli altri, gli obiettivi di questi insegnanti è quello di conoscere i processi di generazione, organizzazione e diffusione della conoscenza e delle idee matematiche presenti all’interno dei gruppi culturali, e come sviluppare azioni nel campo dell’insegnamento della matematica che consentono il Contestualizzazione dei contenuti formali trattati in classe.
La prospettiva di Ethnomathematics ci permette di lavorare in classe una proposta educativa che incoraggia studenti e insegnanti nello sviluppo della creatività, portando sia a nuove e ricche forme di apprendimento. Questa ricchezza socioculturale che si inserisce nel processo di apprendimento didattico, nelle parole del professor Ubiratan D’Ambrosio, fa parte di “un programma che mira a spiegare i processi di generazione, organizzazione e trasmissione della conoscenza in vari I sistemi culturali e le forze interattive che agiscono su e tra i tre processi. ” (D’AMBRÓSIO, 1993, p.7).
Un’altra prospettiva di etnomatematica è stata sviluppata dalla ricercatrice brasiliana Gelsa Knijnik. Per questo autore, Ethnomathematics permette
Studiare i Discorsi Eurocentrici che imistitutiscono matematica accademica e scolastica; Analizzare gli effetti della verità prodotti dai discorsi della matematica accademica e accademica; Discutere questioni di differenza nell’educazione matematica, considerando la centralità della cultura e le relazioni di potere che la stabiliscono; ed esaminare i giochi linguistici che costituiscono ciascuno dei diversi dati matematici, analizzando le loro somiglianze familiari. (KNIJNIK, 2006, p.120).
Negli studi di Knijnik, l’autore caratterizza Ethnomathematics come una matematica prodotta da gruppi sociali che usano le loro conoscenze per svolgere le loro attività. Knijnik (2002, p. 33), facendo un contrappunto tra matematica formale e informale,[9] riflette sul fat[…]to che se, acquisissero le conoscenze prodotte dalla matematica accademica, usando, di fronte a situazioni reali, quella che sembra più appropriata.
Secondo Giardinetto (1999), “L’insegnante può e deve utilizzare la conoscenza quotidiana come punto di sostegno al processo di insegnamento-apprendimento” (p. 68), portando lo studente nel campo dell’argomentazione, sviluppando l’abitudine alla lettura critica, alla ricerca, Interrogatori, creatività, indispensabili per la formazione dei cittadini. Così, sono apprezzati e hanno dimostrato la conoscenza precedente degli studenti, che si formano da queste, altre conoscenze, sempre dal noto.
L’importante è l’istituzione di legami di conoscenza della comunità con la conoscenza della scuola e la conoscenza della scuola con la conoscenza della comunità. Attraverso questa creazione e queste relazioni è possibile attribuire il significato a entrambe le conoscenze.
La tesi difesa dall’autore è che la scuola, più che riprodurre la conoscenza quotidiana, deve mediare tra questa e la conoscenza della scuola, cioè deve mettere a disposizione delle nuove generazioni la saggezza elaborata dall’umanità, che si rivela come un prodotto Storico e sociale. Queste conoscenze devono essere socializzate, poiché “non è l’individuo singolare a costruire tutta la conoscenza, ma ad avere il diritto di accedere a questa conoscenza costituita” (GIARDINETTO, 1999, p. 47).
Per D’ambrèsio (2001), in questo contesto, la conoscenza presenta un carattere dinamico, sempre aperto a nuovi approcci. Per questo, l’insegnante deve tenersi aggiornato, fare costantemente valutazioni della sua pratica, mettere in pratica nuove metodologie didattiche, nonché migliorare le azioni pedagogiche precedentemente sperimentate, nella prospettiva che possano contribuire alla Pedagogico.
Breda, Lima e Guimaràes (2011, p. 15), nei loro studi affermano che:
Ho iniziato a considerare la proposta di Etnomatematica come una possibilità di differenziare il lavoro che l’insegnante sviluppa nelle scuole, cioè la pratica conteudista e senza senso può essere sostituita da un insegnante orientato da un nuovo look, che favorisce L’apprezzamento del contesto socio-culturale dell’educazione, i suoi processi di pensiero e i suoi modi di intendere, spiegando ed esercitando la sua pratica nella società contemporanea […]un invito a rivisitare le sue pratiche pedagogiche e i suoi effetti o addirittura a guardare al suo ruolo, Come docente che si occupa di diverse prospettive di materia nel contesto scolastico.
Così, nel contesto scolastico, come programma di studio che cerca di conoscere e comprendere le conoscenze prodotte e utilizzate all’interno di culture diverse, l’etnomatematica può essere esplorata per assistere nell’insegnamento del lavoro, rendendo gli studenti possono Comprendere le varie “matematica” utilizzate in altri contesti, valorizzando la diversità culturale e lo sviluppo intellettuale e creativo di ogni popolo, di ogni cultura o comunità.
Noi insegnanti di matematica, secondo D’ambrosius (2001), dobbiamo essere chiari ed essere in perfetta armonia con il nostro ruolo di educatori di fronte alla missione di preparare i nostri giovani per un futuro felice. Dobbiamo insegnare a Sì la matematica, ma anche l’umanità. A questo proposito, l’autore sottolinea,
La proposta pedagogica di Ethnomathematics è quella di rendere la matematica qualcosa di vivo, affrontando situazioni reali nel temp[agora]o e nello spazi[aqui]o. E, attraverso le critiche, mettendo in discussione il qui e ora. Così facendo, ci immergiamo nelle radici culturali e pratichiamo le dinamiche culturali. Riconosciamo effettivamente nell’educazione l’importanza di varie culture e tradizioni nella formazione di una nuova civiltà, interculturale e transdisciplinare. (D’AMBRÓSIO, 2001, p. 46).
Per realizzarlo, l’insegnante ha bisogno di rivedere ogni giorno la sua pratica didattica, elaborare un progetto pedagogico che valorizza sempre la conoscenza e la storia di ogni studente, cercando in questa individualità un contesto nuovo e pratico per l’arte del insegnare. È importante che l’insegnante in classe, oltre a godere e a partire dalla conoscenza che lo studente porta dall’ambiente in cui vive, lo incoraggi a credere che svolga anche un ruolo importante nella (ri) costruzione della conoscenza sociale e culturale, così come la conoscenza matematico.
Nelle parole di Rosa Neto, la matematica deve essere interpretata come un prodotto socioculturale naturale di un popolo, perché,
La matematica è stata creata ed è stata sviluppata dall’uomo in base alle sue esigenze. (…) La cultura è una forma di adattamento perché è un modo di agire sull’ambiente che è stato costruito insieme ad esso. (ROSA NETO, 2002, p.7 e 19).
In questo contesto, c’è una relazione significativa tra matematica e cultura, sia come risultato del nostro adattamento secondo le esigenze di sopravvivenza attraverso i tempi, rappresentando la cultura che le generazioni passate ci hanno lasciato, un’eredità empirica , sistematico e scientifico.
3. GIUSTIFICAZIONE
La matematica è sempre stata considerata una scienza di base di diverse aree di conoscenza. La padronanza delle sue conoscenze è fondamentale per risolvere situazioni problematiche in diversi settori. Data questa importanza e rilevanza, è necessario cercare nuove forme (metodi) per insegnarlo, cercando sempre una maggiore efficienza per il processo di insegnamento-apprendimento nel contesto scolastico.
Molte ricerche nell’area evidenziano anche il basso reddito degli studenti rispetto all’apprendimento della disciplina, dicendo che c’è bisogno di una maggiore contestualizzazione dei contenuti per ottenere un migliore apprendimento. Il suo insegnamento considerato, spesso da studenti, genitori e persino insegnanti, come astratto, lontano dalla realtà, cioè ciò che viene insegnato in classe, si presenta a loro lontani dai bisogni quotidiani al di fuori della scuola.
Questa mancanza di legame con la vita quotidiana e, inoltre, l’eccesso di simbologia insegnato in matematica nelle scuole, a volte promuove la diffusione di idee sbagliate in relazione a questa disciplina nel contesto scolastico. La tesi che difendiamo trova fondamenti teorici negli scritti del professor Ubiratan D’ambrìsio, nella prospettiva che la produzione della conoscenza matematica non può essere distaccata dai movimenti sociali e dalla cultura di coloro che producono questa conoscenza.
In questo senso, possiamo affermare che c’è un intreccio tra la matematica prodotta, la società che la produce e la cultura che sovvenziona questa produzione. Questo intreccio è costruito su più mani attraverso un processo cognitivo, mediato dall’azione creativa di vari attori, tutti motivati dalla necessità di leggere, capire e spiegare la realtà in cui vivono.
Se guardiamo alla storia dell’umanità e alle scienze, percepiamo che non solo la matematica, ma anche altre aree della conoscenza costruiranno e ricostruiranno, essendo rassegnazione in ogni momento storico e secondo le esigenze della società. Pompeo e Monteiro (2001), nel libro La Matematica e i temi trasversali sottolineano che l’insegnante ha bisogno di capire l’attuale portata del suo ruolo nella società, perché, secondo gli autori,
Gli insegnanti attuali devono affrontare una grande sfida: istruiti in un processo frammentato, dovranno superare i limiti che questa formazione impone loro ed estrapolare i confini dei contenuti visti in modo parziale e storico (POMPEU e MONTEIRO, 2001, pag. 15).
Date le esigenze di tale grandezza, è necessario cercare di comprendere il processo epistemologico della matematica, cioè il processo generativo di questa conoscenza, la ragione per la sua organizzazione e sistematizzazione. La riduzione di questo quadro è stata negli ultimi decenni una preoccupazione di diversi educatori e ricercatori.
Per Rolim,
Pensare al contesto storico-culturale nel processo di insegnamento dell’apprendimento della matematica è considerare che il “fare” coinvolge più di regole e tecniche; è riconoscere che come scienza, la matematica è essa stessa un edificio dell’umanità (ROLIM, 2010, p. 43).
È un dato di fatto che la proposta educativa caratterizzata da pratiche educative che promuovono l’educazione socioculturalmente, consentendo in classe l’instaurazione di relazioni di apprendimento per soddisfare le esigenze quotidiane degli studenti, è cresciuta Sempre più come alternativa pedagogica. Secondo D’ambrasio, questo significa costruire le condizioni in modo che lo studente possa anche far fronte in classe con diverse situazioni della sua vita quotidiana.
È una prospettiva che rende l’insegnamento della matematica più contestualizzato, con valutazioni e preoccupazioni di natura socioculturale. Secondo D’ambrèsio (2001), Ethnomathematics è l’area dell’educazione che cerca di riflettere sulla conoscenza matematica generata dall’interazione in un particolare gruppo culturale. Per l’autore, le lezioni di matematica, in questa prospettiva, si basano sulle conoscenze matematiche dall’esterno in classe, e queste conoscenze dovrebbero essere sviluppate dall’esperienza dello studente.
D’ambrìsio (2001, p. 22) A questo proposito, fa anche la seguente dichiarazione:
La vita di tutti i giorni è impregnata della conoscenza e della cultura. In ogni momento, gli individui confrontano, classificano, misurano, spiegano, generalizzano, deducono e, in qualche modo, valutano, utilizzano gli strumenti materiali e intellettuali che sono appropriati per la loro cultura (D’ambrèsio, 2001, p. 22).
Nel nostro studio, la domanda guida era: Che tipo di matematica (formale o informale) utilizzare muratori per rendere il budget della quantità di ceramica necessaria per coprire pareti e pavimenti. Era evidente che il Mason professionista esercita le sue funzioni di lavoro utilizzando abilità matematiche apprese dalla pratica quotidiana. Per Monteiro (2002, p. 102), “Il know-how culturale ha altri percorsi di validazione, un’altra logica per la sua configurazione. La domanda è perché uno è diventato universale e legittimato e l’altro non lo è.” In questa prospettiva, l’autore ci fa riferimento a situazioni simili a quelle sperimentate in questa indagine.
Secondo Gerdes:
Per secoli, i muratori, a volte analfabeti e, la maggior parte del tempo, con pochissime scolarture, costruiscono case, muri e altri edifici, ancora oggi considerati costruzioni solide e robuste. Così, esiste nel loro lavoro, nel modo in cui fanno i loro calcoli e organizzano il loro ragionamento matematico, una saggezza che può essere armorata nel contesto scolastico, o nell’integrazione di alcuni studenti con una tendenza a questo tipo di professioni o in un Approccio più “pratico” e più vicino alla vita quotidiana per gli studenti in generale. Questa situazione è menzionata nel lavoro di questa linea di ricerca, vale a dire nella terminologia di Gerdes, come “matematica oppressa”, o “matematica nascosta o congelata” (GERDES, 1991, p. 29).
Nella ricerca partiamo dall’assunto che i muratori, gruppo scelto per fare questa indagine, costituiscono un gruppo di lavoratori che fanno uso quotidiano di una vasta gamma di conoscenze matematiche nella loro vita quotidiana e senza questa conoscenza non sarebbe sviluppare o svolgere qualsiasi attività nell’edilizia civile. Tuttavia, considerando che generalmente hanno poca scolarità, era interessante sapere come hanno acquisito queste conoscenze matematiche o se sono stati forniti attraverso la pratica quotidiana.
In questo contesto, questo lavoro investigativo può anche contribuire a demistificare l’idea che la matematica è una scienza per pochi, comprendendo che non c’è un singolo linguaggio matematico, ma molteplici forme di pensiero Matematica, ognuna organizzata e strutturata all’interno del suo contesto sociale.
Per entrambi la scuola ha bisogno di sviluppare progetti educativi che consentano lo scambio di esperienze con attività in cui la matematica viene utilizzata quotidianamente. In questa interazione, oltre a permettere lo scambio di esperienze, si creano legami e si instaurano altre relazioni pedagogiche con il mondo vissuto al di fuori della scuola e questo può essere un percorso facilitante nell’apprendimento della disciplina.
Secondo D’ambrsio, le lezioni di matematica dovrebbero essere basate sulle conoscenze matematiche dall’esterno all’esterno della classe, e questa conoscenza dovrebbe essere sviluppata dall’esperienza dello studente. Così, l’autore afferma che la conoscenza etnomatematica del gruppo / comunità ha molto valore, perché serve, è efficiente e adatto a molte cose, proprio a quella cultura, a quella etno, e non c’è bisogno di sostituirla. Allo stesso modo, la matematica del gruppo dominante lo serve, è utile e non c’è modo di ignorarlo (D’ambr-sio, 2001, p. 80).
Per Carneiro,
[…] Insegnare la matematica in questa concezione permetterà allo studente di collegare i concetti che lavorano in classe alla loro esperienza quotidiana, secondo il loro ambiente naturale, sociale e culturale. Non si tratta di rifiutare la matematica accademica, ma piuttosto di incorporare valori che sono sperimentati in esperienze di gruppo, considerando i legami storico-culturali (CARNEIRO, 2012, p. 3).
4. PROBLEMATAlIA I PIÙ DI MATEMATIzar DEI BRICKLAYERS
Nel lavoro investigativo svolto con il gruppo di muratori, abbiamo elaborato alcune situazioni problematiche, per accertare che la matematica è utilizzata da questi professionisti per rendere il budget della quantità di ceramiche necessarie per coprire pareti e pavimenti. Questo studio è stato condotto dal punto di vista di D’ambrsio e ROSA, che considerano Ethnomathematics come un programma di ricerca nella storia e nella filosofia della matematica, con implicazioni pedagogiche, quando gli autori considerano:
Quindi, questo programma di ricerca rappresenta una metodologia di ricerca che cerca di analizzare le pratiche matematiche locali, in quanto cerca di valorizzare, diffondere e rispettare le conoscenze matematiche (idee, nozioni, procedure, processi e pratiche) che Ha origine in vari contesti culturali nel corso della storia (D’AMBR-SIO e ROSA 2016, p. 17).
Situazione-problema: Per calcolare il numero di piastrelle rettangolari di dimensi[20 por 30]oni cm, necessarie per rivestire il pavimento del bagno di una galleria d’arte, dimensioni 6, 00m per 4, 50m (Lezzi, 1996, p. 223), Oscar considerato come “punto di partenza le dimensioni del pavimento del bagno. Prendendo le dimensioni della ceramica, opteremo per 6m che è divisibile sia dal lato ceramico dei 20cm come nei 30 cm. Già i 4, 50m no.
Questa misura è divisibile solo dal 3[medida do outro lado da cerâmica]0. Così, ho optato per ciò che sarebbe stato più semplice, prendend[600cm]o il 6m diviso 30cm, raggiungendo il numero esatto di 20 ceramiche in direzione della lunghezza. Ora, prendendo la ceramica in direzione del lato 20cm ho raggiunto il numero di 30 lajotas.
Già nei 4, 50m, divisibili per 30, ho preso il 4, 50m e [450cm]diviso per 30cm, raggiungendo il numero di 15 piastrelle che rientrano nella larghezza. Quindi ci sono 15 tessere nel senso di 30cm. Per raggiungere il calcolo ho preso le 30 tessere che vanno in lunghezza [600cm]più le 15 che vanno in larghezza, moltiplicato e raggiunto il numero di piastrelle necessarie, che sarebbe 450 piastrelle “.
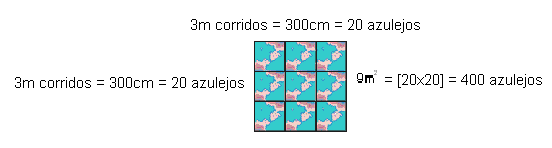
Il ragionamento impiegato dal massone Sérgio per realizzare questo stesso bilancio dimostra, secondo D’ambrosius (2001) che “in ambienti diversi, gli Etnomathematics sono diversi” (p. 35). Così, il massone inizia il suo discorso sottolineando che “prima è necessario scoprire i metri quadrati della zona, sarebbe temp[operação de multiplicação]i. Ho trovato 27m2, quindi devo capire quante tessere si adattano in un metro quadrato. Come il 30cm[medida do comprimento da placa cerâmica] non ha dato preciso in un metro, stavo aumentando e usato 3m, poi chiuso con 10 lajotas. Questo risultato di 10 tessere, moltiplicato per 5 tessere che si adattano in larghezza. Ho trovato il numero di 50 piastrelle in 3m2 “. Visualizza in sequenza il pensiero deduttivo utilizzato dal muratore per essere in grado di fare il budget.
Continuando la spiegazione, Sérgio riferisce che dopo aver scoperto che in 3m2 si adattavano a 50 pezzi, era solo “… Prendi questi 27m2, dividi per 3 che mi hanno portato 9 parti uguali. Quindi, 9 per 50, dà il risultato della quantità di ceramiche che attraversa l’area. Sono 450 ceramiche e devono ancora vedere la pausa. ”
Il calcolo del budget eseguito dal massone Alberto, ha anche sottolineato “450 ceramiche. Ho fatto side times lato ceramica, 0, 20m per 0, 30m raggiungendo il numero 0, 06m2. Questo risultato rappresenta l’area di ogni ceramica. Ora ho fatto tempi laterali del pavimento del bagno, 6m per 4, 50m e ha raggiunto il risultato di 27m2. Poi, il filmato del bagno, 27m2 diviso per i metri quadrati di una parte 0, 06m2, ha dato 450 ceramiche “.
Nella risoluzione dell’enunciate: quante piastrelle quadrate di 15 cm di distanza sono necessarie per rivestire internamente una piscina di 15 m di lunghezza, larga 6 m e profonda 20 m (LE-I,1991, p. 195), Oscar ha riferito: “Ho scelto di trasformare questi 15m in 1.500 cm diviso per 15 cm del Lajota, ha portato a 100 piastrelle nella lunghezza di un lato della piscina. Quindi dall’altra parte darà lo stesso numero, cioè questa riga moltiplicata per 2, dà 200 piastrelle, che si adattano su entrambi i lati della lunghezza.
La stessa procedura che ho usato nella larghezza, vale a dire il 6m è 600cm e questi 600cm diviso per 15 mi ha dato 40 piastrelle che sarebbero andate in una larghezza. Come abbiamo due larghezze qui, moltiplicando per 2, ho trovato 80 piastrelle. Aggiungendo 200 tessere di lunghezza con 80 di larghezza, ho raggiunto il numero di 280 tessere, che devono essere moltiplicate per la profondità che è 1, 20m, cioè 120cm. Prima, però, ho diviso questi 120cm, [medida da profundidade]per 15cm e h[medida do azulejo]o trovato 8 piastrelle che andrebbero nella profondità della piscina. Ora, prendendo la lunghezza e sommando con la larghezza, voglio dire le 200 piastrelle più le 80 piastrelle, per le 8 piastrelle della profondità, ho raggiunto il numero di 2.240 piastrelle.
Dobbiamo ancora trovare il numero di piastrelle dal fondo della piscina. Questo è facile da calcolare perché le dimensioni di lunghezza e larghezza della parte inferiore sono le stesse dei lati, significa 6m per 15m. Così, vanno 100 ceramiche in lunghezza e 40 nella larghezza del fondo, per un totale di 4.000 ceramiche nella parte inferiore della piscina. Aggiungendo il numero di piastrelle dei lati e il fondo ho raggiunto il numero di 6.240 ceramiche “. Il massone ha anche sottolineato che “avrete sempre bisogno di una prenotazione” per evitare possibili guasti, tra gli altri.
Il riconoscimento dell’esistenza di “altre forme di pensiero”, come postula D’ambrèsio (2001, p. 17), è evidente nel ragionamento matematico impiegato da Sérgio per fare questo stesso bilancio. Comunicando il suo pensiero il muratore sottolinea che “prima ho bisogno di conoscere i metri quadrati di parete [laterais]e pavimento. 15m più 6m, oltre 15m e più 6m, darebbe il lateral[42m corridos]e. Questo per 1, 20[profundidade da piscina]m, dà 50, 4m2 area.
Poi troverò il filmato dal basso[15m vezes 6m = 90m2]. Lo siamo tutti. Ho fatto e dato 140, 4m2. Ora ho bisogno di scoprire quante tessere si adattano in ogni metro quadrato. Solo che come le piastrelle sono 15cm per 15cm, in un metro no[corrido]n si chiude. Poi stavo aggiungendo fino a quando sono arrivato a 3m. In 3m,[corridos] ci sono 20 lajota. Poi ho preso 3 per 3, [multiplicado por]sare[cada face da piscina representa uma figura plana – duas dimensões]bbe un totale di 9m2 che ha dato 400 Lajotas “. Visualizza nella rappresentazione che segue, il ragionamento impiegato dal muratore per chiarire la situazione problematica.
Continuando la spiegazione delle sue procedure, Sérgio segue: “Ho preso il totale di M2 dalla piscina, diviso per 9[9 partes]. Ha dato 15,6 parti uguali di 9m2 ciascun[140,4m2 : 9m2 = 15,6]o. Queste 15,6 parti equivalgono a volte la quantità di ceramica che era in 9m2, cioè 400 ceramiche. Poi, in ogni parte sarebbe 15,6 per 400, pari a 6.240 ceramiche “.
Interrogato anche se il budget di 6.240 ceramiche darebbe abbastanza per rivestire la piscina, Sérgio sottolinea prontamente: avrebbe bisogno di circa il 5% in più di questo totale a causa della rottura.
Per il professor D’Ambrosio, i gruppi umani producono conoscenze che, anche se non diffuse negli spazi didattici formali, è una conoscenza valida e che la scuola, così come la ricerca in matematica educazione hanno bisogno di riconoscere e approfondire per arricchire l’atto Educativo.
D’ambrìsio (2001, p. 22-23), rileva inoltre che,
Ci sono numerosi studi sull’etnomatematica della vita quotidiana. Si tratta di un’etnomatematica non apprellata nelle scuole, ma nell’ambiente familiare, nell’ambiente dei giocattoli e del lavoro, ricevuti da amici e colleghi.
La risoluzione di questo problema di situazione per Alberto ha mostrato una conoscenza che è identificato con la procedura che sarebbe stata utilizzata da un insegnante di matematica. Si noti la sua spiegazione: “La lunghezza dei lati della piscina 15m s 15m, aggiungendo anche la larghezza 6m s 6m dà il perimetro della piscina, 42m. Ora 42m per 1, 20m dalla profondità di 50, 40m2 di area ai lati della piscina. Il fondo della piscina ha una superficie di 15m per 6m e dà 90m2. Aggiungendo l’area laterale e il fondo, voglio dire il 50, 40m2 più il 90m2 dà 140, 40m2. Questo diviso per la dimensione della piastrella che è 15cm per 15cm e che in M2 dà 0, 0225m2, ammonta a 6.240 piastrelle. Ora basta aggiungere un po ‘al buffer di break. ”
For Demo (1996), la costruzione della conoscenza inizia dalla conoscenza incorporata da ogni individuo nella loro esperienza socio-culturale. Questo è stato evidente nelle forme di matematizar utilizzate da ciascuno dei muratori. Per l’autore “Non c’è tavola poco profonda, analfabetismo assoluto; Tutti parlano, comunicano, usano un vocabolario di base, gestiscono concetti nel senso comune, hanno riferimenti alla realtà in cui sono inseriti “(p. 32).
Entrando nella scuola, tutti hanno già accumulato una certa conoscenza, anche se è all’interno del buon senso. Abbiamo condiviso con D’ambrosius (1993), quando abbiamo postulato che abbiamo bisogno di capire che quando inizia la scuola formale, il bambino ha già un’etnomatematica che gli permette di affrontare le interpretazioni della matematica sistematica della scuola.
Le forme Matematizar dei muratori denotano secondo Marques (2000) che “i processi di apprendimento sono inevitabilmente inseriti in comunità comunicative e pubbliche in cui gli uomini imparano gli uni dagli altri e con l’altro” (p. 29). Secondo la comprensione di Pompeo e Monteiro (2001), “un processo educativo significativo inizia con l’interazione della scuola e della Comunità” (p. 55), le cui relazioni possono rassegnare il ruolo della scuola come luogo privilegiato per lo scambio di esperienze Comprendere meglio le conoscenze che circolano nella vita di tutti i giorni.
Nelle manifestazioni (verbalizzazione) espresse dai muratori nelle sessioni di studio, in particolare dalla creazione matematica di questi professionisti, sulla base della loro esperienza lavorativa, nello scambio di conoscenze che hanno già partecipato nel corso della loro vita, mostrano Che l’istruzione formale sia possibile valorizzare e convalidare questa conoscenza precedente, la sua cultura e il suo ambiente sociale. Crediamo che un lavoro educativo che lascia, dialogicamente di questa conoscenza, Enrique e contestualizza la conoscenza matematica della scuola.
Nelle parole di Rolim
Pensare al contesto storico-culturale nel processo di insegnamento dell’apprendimento della matematica è considerare che il “fare” coinvolge più di regole e tecniche; è riconoscere che come scienza, la matematica è essa stessa un edificio dell’umanità (ROLIM, 2010, P. 43).
Nella nostra comprensione, da questa prospettiva, si stabilisce nell’Atto educativo una relazione ampiamente utilizzata nel mondo degli affari, dove l’espressione “win-win” è parlata e praticata. In una trattativa, questa espressione ha una caratteristica: nessuno perde, tutti vincono. Si stabilisce tra azienda e fornitore un rapporto ideale.
Per l’Atto educativo, questo rapporto è pedagogicamente ideale, cioè studenti, insegnanti, l’intero contesto che fa parte del processo educativo, essere felici, avere successo. Si comprende quindi che, come nel mondo degli affari, è possibile raggiungere pedagogicamente in classe il rapporto “win-win”, basta fare una buona e nuova pianificazione, in cui questa possibilità è inserita.
Una prospettiva pedagogica in cui, così come nel mondo degli affari, dove imprenditore e fornitore dovrebbero esporre le loro percezioni, le loro opinioni e le loro idee in modo appropriato e al momento opportuno, senza giudicare il comportamento dell’altro, a scuola, in un modo Insegnante nel rispetto e nella valorizzare la conoscenza precedente dei suoi studenti.
E quando a scuola, la conoscenza della vita quotidiana entra in “confronto” con la conoscenza formale, che possiamo ricordare dialogicamente che nel mondo degli affari, spesso il fornitore pensa diverso dall’imprenditore, tuttavia, questo rapporto non è o non dovrebbe mai essere Conflitto o causare qualche usura. Ha bisogno a scuola, così come negli affari, per rappresentare una grande opportunità di apprendimento per tutti coloro che sono coinvolti in questo processo.
I discorsi dei muratori, partecipanti alla ricerca, hanno mostrato che la conoscenza della matematica che possiedono, sono stati acquisiti la maggior parte del tempo nello sviluppo e nel miglioramento della loro professione, nella pratica di tutti i giorni, o addirittura, vedendo gli altri eseguire il Stessa attività.
Le conversazioni che abbiamo avuto con i muratori durante le sessioni di studio hanno dimostrato che le conoscenze prodotte al di fuori dell’ambito scolastico sono importanti e spetta all’insegnante salvarli e avvicinarli alla classe, rendendo significativa l’istruzione formale e Articolato con la realtà in cui lo studente è inserito.
5. OBIETTIVI
5.1 Mostra che l’Etnomatematica fa parte della nostra vita quotidiana e riflette sulla possibilità di gruppi sociali organizzati c[pedreiros]he producono matematica nelle loro diverse forme di espressione nel loro ambito d’azione, discutendo a scuola i modi per produrre Significati della vita quotidiana; 5.2 Presentare l’Etnomatematica come una delle vie per una rinnovata educazione, all’interno del più grande movimento chiamato educazione matematica, reso possibile in questa prospettiva, dalla riflessione tra insegnante, studente e comunità, cercando di superare la Conoscenza che entrambi possiedono, modificandoli e trasformando l’aula in uno spazio democratico di scambio di conoscenza; 5.3 Per percepire l’etnomatematica come un’interessante alternativa pedagogica al lavoro in classe, Demistificare la matematica e avvicinarsi alle reali necessità delle vere necessità degli studenti giorno per giorno.
6. METODOLOGIA
Il lavoro investigativo è stato realizzato attraverso diversi momenti, vale a dire: studio bibliografico sull’etnomatematica, sessioni di studio con muratori in cui le situazioni sono state proposte-problema con lo scopo di indagare dialogicamente con ogni Professionista circa le conoscenze matematich[formais ou informais]e che usano per rendere il budget della quantità di ceramica necessaria per coprire pareti e pavimenti. Riflessione sulle possibili connessioni tra matematica e realtà nella possibilità di stabilire legami tra le conoscenze matematiche del muratore, costruite dalle loro esigenze quotidiane, utilizzando le pratiche La vita di tutti i giorni e la matematica scolastica.
7. CONTRIBUTO PREVISTO
Considerando che in tutto il lavoro investigativo, basato sul discorso dei muratori, percepiamo che questi professionisti per risolvere le situazioni problematiche proposte, non sono sempre stati sostenuti nella conoscenza della matematica scolastica.
Mentre era chiaro che i muratori applicavano conoscenze matematiche in modo pratico e intuitivo, usando strategie specifiche, non utilizzando le formule matematiche insegnate a scuola.
Speriamo che l’insegnamento della matematica in classe attraverso l’approccio etnomatemati[10]ca permette agli insegnanti e agli studenti di conoscere la diversità culturale stessa della matematica. Che i risultati di questa ricerca aiutano nello sviluppo di una metodologia che contribuisce all’insegnamento della matematica, portando possibilità di cambiamenti nella pratica dell’insegnamento, avvicinandosi alla pratica pedagogica scolastica con le conoscenze prodotte in situazioni Delle vite degli studenti.
Che da questa riflessione la pratica pedagogica in classe può essere riorientata allo sviluppo della piena cittadinanza degli studenti. Che, secondo Pinheiro e Rosa (2016), il:
[…] Gli insegnanti di matematica si immergono nelle dinamiche culturali degli studenti e utilizzano strategie di insegnamento e apprendimento che valorizzano la dimensione culturale in classe, in modo da poter sviluppare un’educazione matematica inclusiva che potrebbe essere efficacemente Contribuire alla trasformazione sociale (p. 79).
Così, dalle sessioni di studio e dal testo prodotto, puntiamo a provocare i lettori alla possibilità di un intervento pedagogico, basato sulla realtà dello studente, unendo teoria e pratica nella costruzione di conoscenze sismiche. Si spera inoltre che le riflessioni derivanti dalla lettura del testo consentano un nuovo sguardo alla realtà e all’educazione matematica, dal punto di vista della produzione della conoscenza dalla pratica quotidiana.
L’obiettivo è quello di contribuire alla Costituzione del ricercatore Professore della sua pratica, suscitandolo per imparare in modo continuo ad essere un insegnante, secondo le attuali esigenze educative, trasformando l’aula in un ambiente di scambio di conoscenze, Soccorrere la conoscenza storica-socialmente costruita dall’umanità.
8. RIFERIMENTI BIBLIOGRAFICI
BREDA, Adriana LIMA, Valderez Marina do Rosário e GUIMARÃES, Gleny Terezinha Duro. A utilização da Etnomatemática nos cursos de formação continuada de professores: implicações das relações de poder saber na produção de subjetividades. Curitiba. Novembro de 2011. Disponível em: http://educere.bruc.com.br/CD2011/pdf/4668 _ 2898.pdf. Acessado em: 20/08/2017.
CARNEIRO, K. T. A. Cultura Surda na aprendizagem matemática da sala de recurso do Instituto Felipe Smaldone: uma abordagem etnomatemática. Anais do 4º Congresso Brasileiro de Etnomatemática. Belém, PA: ICEm4, 2012.
D’Ambrósio Ubiratan. Etnomatemática: Arte ou técnica de explicar e conhecer. Editora Ática, Série Fundamentos, 2. edição, São Paulo, 1993.
——-. Educação matemática: da teoria à prática. 13ª ed. Campinas: Papirus, 1996. (Coleção Perspectivas em Educação Matemática).
————-. Etnomatemática – elo entre as tradições e a modernidade. Coleção Tendências em Educação Matemática, 1. Belo Horizonte: Autêntica, 2001, 112p.
D’AMBROSIO, U.; ROSA, M. Um diálogo com Ubiratan D’Ambrosio: uma conversa brasileira sobre etnomatemática. In BANDEIRA, F. A.; GONÇALVES, P. G. F. (Orgs.). Etnomatemáticas pelo Brasil: aspectos teóricos, ticas de matema e práticas escolares. Curitiba, PR: Editora CRV. 2016. pp. 13-37.
DEMO, Pedro. Pesquisa e construção de conhecimento: Metodologia científica no caminho de Habermas. 3.ed. Rio de Janeiro: Tempo Brasileiro, 1996. 125p.
GERDES, Paulus. Etnomatemática: Cultura, Matemática, Educação. Maputo. Instituto Superior Pedagógico, 1991.
GIARDINETTO, José Roberto Boettger. Matemática escolar e matemática da vida cotidiana. Coleção polêmicas do nosso tempo, autores associados, Campinas – São Paulo, 1999, 128p.
LEZZI, Gelson; Dolce, Osvaldo; Machado, Antonio. Matemática e Realidade. 5ª série, 3. edição reformulada, Atual, São Paulo, 1996, 250p.
————–. Matemática e Realidade. 5ª série, 2. edição, Atual, São Paulo, 1991, 213p.
KNIJNIK, Gelsa. O saber popular e o saber acadêmico na luta pela terra. Revista da Sociedade Brasileira de Educação Matemática. Educação Matemática em Revista. Ano 9, n. 1, p. 27-39, 2002.
————–. Educação matemática, culturas e o conhecimento na luta pela terra. Santa Cruz do Sul, EDUNISC, 2006, 239 p.
MARQUES, Mário Osorio. A aprendizagem na mediação social do aprendido e da docência. Ijuí, Editora UNIJUÍ, 2. edição, 2000, 144 p.
MONTEIRO, A.; Pombeu, G. Jr. A matemática e os temas transversais. Editora Moderna, São Paulo, 2001, 160p.
MONTEIRO, Alexandrina. Reflexão e Ação: Revista do Departamento de Educação/UNISC. Vol. 10, n. 1 (jan./jun.2002) — Santa Cruz do Sul: EDUNISC, 2002.
A Etnomatemática em Cenários de Escolarização: alguns elementos de reflexão. Alexandrina Monteiro, p. 93 – 108.
PINHEIRO, R. C.; ROSA, M. Uma perspectiva etnomatemática para o processo de ensino e aprendizagem de alunos Surdos. RPEM, v. 5, n. 9, p. 56-83, 2016.
ROLIM, Carmem Lucia Artioli. Fórmulas de Silêncio: metodologias no processo de ensino da Matemática. In: SANTOS, Jocyléia Santana. ZAMBONI, Ernesta. Potencialidades Investigativas da Educação. Goiânia: Ed. da PUC Goiás, 2010.
ROSA NETO, R. Didática da matemática, São Paulo: Ática, 2002.
8. Inteso con una pratica pedagogica che valorizza la matematica di diversi gruppi culturali, tenendo conto dei concetti informali costruiti dalle materie attraverso le loro esperienze al di fuori del contesto della scuola.
9. In questa riflessione, trattiamo la matematica formale e informale nell’idea che la prima sia considerata come scuola, scientifica, sistematica, legittimata e associata ai contesti scolastici e la seconda come quotidiana, spontanea, a conoscenza del giorno per giorno, Associato con le strade, l’esperienza e la vita in comunità, contesti sociali.
10. In questo lavoro utilizzato per designare l’indagine delle concezioni, tradizioni e pratiche matematiche di un gruppo so[pedreiros]ciale e il lavoro pedagogico che può essere sviluppato nella prospettiva che il gruppo interpreta e codifica le loro conoscenze; Acquisire le conoscenze prodotte dalla matematica accademica, utilizzando, di fronte a situazioni contestualizzate, quella che sembra più appropriata.
[1] Master in Scienze dell’educazione – Matematica, UNIJUI – RS. Laurea e specializzazione in scienze e matematica. Prof. Assistente del CCA – Center for Agricultural Sciences, Campus del maresciallo Cândido Rondon, UNIOESTE, PR – Brasile.
[2] Master in Sviluppo rurale sostenibile-UNIOESTE, Specialista in matematica, Fisica-UNIPAR, Gestione delle persone e istruzione speciale con enfasi sulla disabilità multipla-UNIASSELVI, Laureato in Matematica con specializzazione in Fisica-UNIPAR.
[3] Specializzazione in Insegnamento delle scienze esatte – Matematica, fisica e chimica. UNIOESTE – Università statale del Paraná occidentale. Laurea: Scienza e Matematica. UNIJUI, RS. Professore della Scuola statale di Paraná.
[4] Professore di protezione delle piante e salute umana presso la Pontificia Università Cattolica del Cile, Dipartimento di Scienze Vegetali, ricopre una posizione interdisciplinare condivisa tra la Facoltà di Agronomia e Ingeniería Forestal (FAIF), Facoltà di Medicina e Facoltà di Chimica. Professore di ricerca associato al gruppo di studio sui suoli e l’ambiente (GESOMA – UNIOESTE). Master in Agronomia presso UNIOESTE, PhD in Agronomia presso UNIOESTE (2013-2016) – Periodo Sandwich (borsa di studio CAPES) presso l’Università di Lisbona, presso l’Instituto Superior de Agronomia (ULisboa).
[5] Research Productivity Level 1C di CNPq nell’area delle scienze ambientali con tre Postdocs, UEM-PR (Brasile), Università di Santiago de Compostela (Spagna), UFG-GO (Brasile). Attualmente è professore associato presso l’UNIOESTE-PR ed è professore e ricercatore presso il Centro di scienze agrarie, insegnando chimica. Docente al Master in Scienze agrarie presso UEM. Attualmente è consulente ad hoc di CNPq, CAPES e Fundação Araucária. Funge da consulente ambientale volontario con MP-SP e CONAMA-DF.
[6] Laurea in Agronomia – UNIOESTE – Università di Stato del Paraná occidentale – Laurea in Amministrazione – Unip – Universidade Paulista.
[7] Studente master in Agronomia (produzione vegetale) presso l’Università statale del Paraná occidentale (UNIOESTE). Ingegnere agrario laureato presso UNIOESTE (2014-2018), lavora come ricercatore associato al gruppo di studio su suolo e ambiente (GESOMA – UNIOESTE).
Inviato: giugno 2019.
Approvato: luglio 2019.