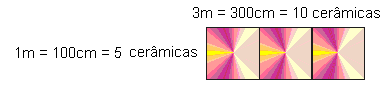ORIGINAL ARTICLE
SCHWANTES, Vilson [1], XAVIER, Márcio Pizzete [2], SCHWANTES, Eloísa Bernardete Finkler [3], SCHWANTES, Daniel [4], JUNIOR, Affonso Celso Gonçalves [5], KRACKE, Elisa [6], JUNIOR, Élio Conradi [7]
SCHWANTES, Vilson. Et al. Ethnomathematics: A reflection on the mathematics used by bricklayers. Revista Científica Multidisciplinar Núcleo do Conhecimento. 04 year, Ed. 07, Vol. 13, pp. 46-66. July 2019. ISSN: 2448-0959
1. SUMMARY
This article is a result of reflections on ethnomathematics and Analysis of study sessions conducted with Bricklayers in the municipality of Mercedes – PR. He finds motivation in the writings of Professor Ubiratan D ´ Ambrosio who recognizes the presence of mathematical knowledge in diverse cultural spaces. The focus of the research investigates dialogically with each professional, through problem situations, which mathematics use to make the budget of the quantity of ceramics necessary to coat walls and floors. In the research conducted with the bricklayers, it was interesting to know whether these were formal or informal. The statements evidenced an understanding that mathematical knowledge is dynamic, a cultural product, which emerges in various sectors of human activity and circulates in and through the world of life, consolidating itself in the school.
Keywords: mathematical education, ethnomathematics, problem situations, study sessions, ceramic budget.
2. INTRODUCTION
In all cultures, throughout history, we find records of developed activities that denote the existence and necessity of some kind of mathematical knowledge. This is an empirical knowledge, used in the exercise of several professions, passed through generations and used, often, without people noticing this presence.
When using mathematical reasoning to solve a problem situation, it is sometimes possible to solution, without necessarily having attended a school. Mathematical knowledge can be developed naturally by daily practice, for example, in the work of bricklayers, professionals who routinely use such knowledge.
For many decades in the history of education, the knowledge arising from social practices was disregarded and not discussed at school. Nowadays, the proposal to investigate the mathematical knowledge present in the students ‘ lives outside the school context is gaining more and more space. This knowledge built by man in space and temporality constitutes a precious legacy that must be considered in school curricula, or in the methodology adopted. There are many educators who believe that systate knowledge can be constructed from concepts present in the daily life of the professions, of people.
For Professor Ubiratan D’ambrósio, even before entering the school, all children already have mathematical knowledge. This knowledge is, for the researcher, an ethnomathematics[8]. The author wants to tell us that knowledge is not only the result of years of study, but also the fruit of the experiences lived among the citizens of the same or different social groups.
According to the researcher, the main proposal of Ethnomathematics is to seek to understand the mathematical knowledge/making of each group of interest, community, people or nation. In this sense, his writings consider ethnomathematics:
“… The mathematics practiced by cultural groups, such as urban and rural communities, groups of workers, professional classes, children of a certain age group, indigenous societies, and so many other groups that identify themselves by objectives and traditions Common to groups “. (2001, p.9).
The author sees Ethnomathematics as:
“… A strategy developed by the human species throughout its history to explain, to understand, to manage and live with the sensitive reality, perceptible and with its imaginary, naturally within a natural and cultural context. ” (D ´ AMBROSIUS, 1996, p. 7)
Bricklayers, sometimes illiterate and most of the time with little schooling, use mathematical knowledge to build houses, make ceramic nesting, build walls, buildings, considered still today, solid and sturdy constructions. It certainly exists in this work, especially in the calculations and in the organization of mathematical reasoning used, a knowledge that can be harnessed in the school context, or in the integration of students with a tendency to this type of profession, either in an approach More practical mathematics discipline. For Carneiro,
[…] Teaching mathematics in this conception will allow the student to link the concepts working in class to their daily experience, according to their natural, social and cultural environment. It is not about rejecting academic mathematics, but rather incorporating values that are experienced in group experiences, considering the historical-cultural bonds (CARNEIRO, 2012, p. 3).
In recent decades, the number of educators studying ethnomathematics has grown as a research program and/or as a proposal for pedagogical work. Among others, the objectives of these teachers is to know the processes of generation, organization and dissemination of knowledge and mathematical ideas present within cultural groups, and how to develop actions in the field of mathematics teaching that allow the Contextualization of the formal contents covered in the classroom.
The perspective of Ethnomathematics allows us to work in the classroom an educational proposal that encourages students and teachers in the development of creativity, leading both to new and rich forms of learning. This sociocultural richness that is incorporated into the teaching learning process, in the words of Professor Ubiratan D’Ambrosio, is part of “a program that aims to explain the processes of generation, organization and transmission of knowledge in various Cultural systems and the interactive forces that act on and between the three processes. ” (D’AMBRÓSIO, 1993, p.7).
Another perspective of ethnomathematics has been developed by the Brazilian researcher Gelsa Knijnik. For this author, Ethnomathematics allows
To study the Eurocentric Discourses that institute academic and school Mathematics; Analyze the effects of truth produced by the discourses of academic and scholarly mathematics; Discuss issues of difference in mathematical education, considering the centrality of culture and the power relations that establish it; and examine the language games that constitute each of the different mathematics, analyzing their family similarities. (KNIJNIK, 2006, p.120).
In Knijnik’s studies, the author characterizes Ethnomathematics as a mathematics produced by social groups that use their knowledge to accomplish their activities. Knijnik (2002, p. 33), making a counterpoint between formal and informal mathema[9]tics, ponders tha[…]t if ― acquire the knowledge produced by academic mathematics, using, when confronted with real situations, the one that seems more appropriate.
According to Giardinetto (1999), “The teacher can and should use daily knowledge as a point of support for the teaching-learning process” (p. 68), bringing the student into the field of argumentation, developing the habit of critical reading, research, Questioning, of creativity, indispensable for citizen training. Thus, they are valued and evidenced the previous knowledge of the students, forming from these, other knowledge, always from the known.
The important thing is the establishment of bonds of knowledge of the community with the knowledge of the school and the knowledge of the school with the knowledge of the community. Through this establishment and these relationships it is possible to attribute meaning to both knowledges.
The thesis defended by the author is that the school, more than to reproduce the daily knowledge, must be mediating between this and the school knowledge, that is, it must make available to the new generations the wisdom elaborated by mankind, which reveals itself as a product Historical and social. These knowledges need to be socialized, since “it is not the singular individual to construct all knowledge, but to have the right to access to this knowledge constituted” (GIARDINETTO, 1999, p. 47).
For D’ambrósio (2001), in this context, knowledge presents a dynamic character, always open to new approaches. For this, the teacher must keep up to date, constantly make assessments of his practice, practice new teaching methodologies, as well as improve pedagogical actions previously experienced, in the perspective that they may contribute to the Pedagogical.
Breda, Lima and Guimarães (2011, p. 15), in their studies state that:
I started to look at the proposal of Ethnomathematics as a possibility of differentiating the work that the teacher develops in schools, that is, the conteudist and meaningless practice can be replaced by a teacher oriented by a new look, that fosters The appreciation of the socio-cultural context of the educating, its processes of thought and its ways of understanding, explaining and exercising its practice in contemporary soc[…]iety an invitation to revisit its pedagogical practices and its effects or even look at its role, As a lecturer who deals with different perspectives of subject in the school context.
Thus, in the school context, as a study program that seeks to know and understand the knowledge produced and used within different cultures, ethnomathematics can be explored to assist in teaching work, making students can To understand the various “mathematics” used in other contexts, valuing the cultural diversity and the intellectual and creative development of each people, of each culture or community.
We teachers of mathematics, according to D’ambrosius (2001), we have to be clear and be in perfect harmony with our role as educator in front of the mission of preparing our young people for a happy future. We need to teach Yes mathematics, but also about humanity. In this respect, the author emphasizes,
The pedagogical proposal of Ethnomathematics is to make mathematics something alive, dealing with real situations in [agora]time and spac[aqui]e. And, through criticism, questioning the here and now. In doing so, we immerse ourselves in cultural roots and practice cultural dynamics. We are effectively recognizing in education the importance of various cultures and traditions in the formation of a new civilization, cross-cultural and transdisciplinary. (D’AMBRÓSIO, 2001, p. 46).
To make this a reality, the teacher needs to review daily his teaching practice, elaborate a pedagogical project that always values the knowledge and history of each student, seeking in this individuality a new and practical context for the art of Teach. It is important that the teacher in the classroom, in addition to enjoying and starting from the knowledge that the student brings from the environment in which he lives, encourage him to believe that he also plays an important role in the (re) construction of social and cultural knowledge, as well as knowledge Mathematician.
In the words of Rosa Neto, mathematics needs to be interpreted as a natural sociocultural product of a people, because,
Mathematics was created and has been developed by man according to his needs. (…) Culture is a form of adaptation because it is a way of acting on the environment that was built along with it. (ROSA NETO, 2002, p.7 e 19).
In this context, there is a significant relationship between mathematics and culture, both as a result of our adaptation according to the needs of survival through the times, representing the culture that past generations have left us, an empirical legacy , systematic and scientific.
3. JUSTIFICATION
Mathematics has always been regarded as a base science of several areas of knowledge. The mastery of its knowledge is fundamental to solve problem situations in several areas. Given this importance and relevance it is necessary to look for new forms (methods) to teach it, always seeking greater efficiency for the teaching-learning process in the school context.
Many researches in the area also highlight the low income of students with respect to the learning of the discipline, saying that there is a need for greater contextualization of the contents to occur better learning. His teaching considered, often by students, parents and even teachers, as abstract, distant from reality, that is, what is taught in the classroom, presents themselves to them distant from the daily needs outside the school.
This lack of bond with everyday life and, also, the excess of symbology taught in mathematics in schools, sometimes promotes the diffusion of mistaken ideas in relation to this discipline in the school context. The thesis that we defend finds theoretical foundations in the writings of Professor Ubiratan D’ambrósio, in the perspective that the production of mathematical knowledge cannot be detached from the social movements and culture of those who produce this knowledge.
In this sense, we can affirm that there is an interweaving between the produced mathematics, the society that produces it and the culture that subsidizes this production. This interweaving is built to several hands through a cognitive process, mediated by the creative action of various actors, all motivated by the need to read, understand and explain the reality in which they live.
If we look at the history of mankind and the sciences, we perceive that not only mathematics, but also other areas of knowledge will build and rebuild, being resignified at every historical moment and according to the demands of society. Pompey and Monteiro (2001), in the book The Mathematics and the transversal themes emphasize that the teacher needs to understand the current scope of his role in society, because, according to the authors,
Current teachers face a great challenge: educated in a fragmented process, they will have to overcome the limits that this formation imposes on them and extrapolate the boundaries of content seen in a partial and a-historical way (POMPEU and MONTEIRO, 2001, p. 15).
Given the demands of such magnitude, it is necessary that we seek to understand the epistemological process of mathematics, that is, the generative process of this knowledge, the reason for its organization and systematization. Minimizing this framework has been in recent decades a concern of several educators and researchers.
For Rolim,
Thinking about the historical-cultural context in the process of teaching mathematics learning is to consider that “doing” involves more than rules and techniques; is to acknowledge that as a science, mathematics is itself a building of humanity (ROLIM, 2010, p. 43).
It is a fact that the educational proposal characterized by educational practices that promote socioculturally educating, allowing in the classroom the establishment of learning relationships to meet the daily needs of students, has been growing More and more as a pedagogical alternative. According to D’ambrósio, this means constructing conditions so that the student can also cope in the classroom with different situations of his/her daily life.
It is a perspective that makes the teaching of mathematics more contextualized, with valuations and concerns of a sociocultural nature. According to D’ambrósio (2001), Ethnomathematics is the area of education that seeks to reflect on the mathematical knowledge that is generated from the interaction in a particular cultural group. For the author, the mathematics classes, in this perspective, are based on the mathematical knowledge from the outside into the classroom, and these knowledge should be developed from the student’s experience.
D’ambrósio (2001, p. 22) In this respect, also makes the following statement:
Everyday life is impregnated with the knowledge and making of culture. At every moment, individuals are comparing, classitizing, measuring, explaining, generalizing, inferring and, in some way, evaluating, using the material and intellectual instruments that are proper to their culture (D’ambrósio, 2001, p. 22).
In our study, the guiding question was: What kind of mathematics (formal or informal) use bricklayers to make the budget of the amount of ceramics needed to coat walls and floors. It was evident that the professional Mason exerts his work functions using mathematical skills learned from daily practice. For Monteiro (2002, p. 102), “The cultural know-how has other validation paths, another logic for its configuration. The question is why one has become universal and legitimized and the other is not. ” In this perspective, the author refers us to situations similar to those experienced in this investigation.
According to Gerdes:
For centuries, the bricklayers, sometimes illiterate and, most of the time, with very little schooling, build houses, walls and other buildings, still considered solid and sturdy constructions today. Thus, it exists in their work, in the way they do their calculations and organize their mathematical reasoning, a wisdom that can be harnated in the school context, or in the integration of certain students with a tendency to this type of professions or in a More “practical” approach and closer to everyday life for students in general. This situation is mentioned in the work of this line of research, namely, in Gerdes ‘ terminology, as “oppressed mathematics”, or “hidden or frozen Mathematics” (GERDES, 1991, p. 29).
In the research we start from the assumption that the bricklayers, group chosen to make this investigation, constitute a group of workers who make daily use of a wide variety of mathematical knowledge in their daily life and without this knowledge would not be possible to develop or perform any activity in civil construction. However, considering that they generally have little schooling, it was interesting to know how they acquired these mathematical knowledge or whether they were provided through daily practice.
Within this context, this investigative work can also contribute to demystifying the idea that mathematics is a science for few, understanding that there is not a single mathematical language, but multiple forms of thought Mathematical, each organized and structured within its social context.
For both the school needs to develop educational projects that allow the exchange of experiences with activities where mathematics is used daily. In this interaction, besides allowing the exchange of experiences, bonds are created and other pedagogical relationships are established with the world lived outside the school and this can be a facilitating path in the learning of the discipline.
According to D’ambrósio, mathematics classes should be based on the mathematical knowledge from outside into the classroom, and this knowledge should be developed from the student’s experience. Thus, the author affirms that the ethnomathematical knowledge of the group/community has much value, because it serves, is efficient and suitable for many things, proper to that culture, to that ethno, and there is no need to replace it. Similarly, the mathematics of the dominant group serves him, it is useful and there is no way to ignore it (D’ambrósio, 2001, p. 80).
For Carneiro,
[…] Teaching mathematics in this conception will allow the student to link the concepts working in class to their daily experience, according to their natural, social and cultural environment. It is not about rejecting academic mathematics, but rather incorporating values that are experienced in group experiences, considering the historical-cultural bonds (CARNEIRO, 2012, p. 3).
4. PROBLEMATIZING TO KNOW THE WAYS OF MATEMATIZAR OF THE BRICKLAYERS
In the investigative work carried out with the group of bricklayers, we elaborated some problem situations, to ascertain that mathematics is used by these professionals to make the budget of the quantity of ceramics necessary to coat walls and floors. This study was carried out from the perspective of D’ambrósio and ROSA, who consider Ethnomathematics as a research program in history and philosophy of mathematics, with pedagogical implications, when the authors consider:
So, this research program represents a research methodology that seeks to analyze local mathematical practices, as it seeks to value, disseminate and respect mathematical knowledge (ideas, notions, procedures, processes and practices) that Originate in various cultural contexts throughout history (D’AMBRÓSIO and ROSA 2016, p. 17).
Situation-Problem: To calculate the number of rectangular tiles of size c[20 por 30]m, necessary to coat the bathroom floor of an art gallery, dimensions 6, 00m by 4, 50m (Lezzi, 1996, p. 223), Oscar considered as “starting point the dimensions of the floor of the Bathroom. Taking the size of the ceramics, we will opt for 6m which is divisible both by the ceramic side of the 20cm as in the 30 cm. Already the 4, 50m not.
This measure is only divisible by the 3[medida do outro lado da cerâmica]0. So, I opted for what would be simpler, taking the 6m di[600cm]vided by 30cm, reaching the exact number of 20 ceramics in the direction of length. Now, taking the pottery in the direction of the 20cm side I reached the number of 30 lajotas.
Already in the 4, 50m, divisible by 30, I took the 4[450cm], 50m and divided by 30cm, reaching the number of 15 tiles that fit in the width. So there are 15 tiles in the sense of the 30cm. To reach the calculation I took the 30 tiles that go in the length[600cm] plus the 15 that go in width, multiplied and reached the number of necessary tiles, which would be 450 tiles “.
The reasoning employed by the Mason Sérgio to make this same budget, demonstrates, according to D’ambrosius (2001) that “in different environments, Ethnomathematics are different” (p. 35). Thus, the Mason begins his speech emphasizing that “first you need to discover the square meters of the area, it would be times[operação de multiplicação]. I found 27m2, so I have to figure out how many tiles fit in a square metre. As the 30cm [medida do comprimento da placa cerâmica]did not give accurate in one meter, I was increasing and used 3m, then closed with 10 lajotas. This result of 10 tiles, multiplied by 5 tiles that fit in width. I found the number of 50 tiles in 3m2 “. Visualize in sequence the deductive thought used by the bricklayer to be able to make the budget.
Continuing the explanation, Sérgio reports that after he found that in 3m2 fit 50 pieces, it was only “… Take these 27m2, divide by 3 which resulted me 9 equal parts. Hence, 9 times 50, gives the result of the amount of ceramics that goes across the area. They are 450 ceramics and still have to see the break. ”
The budget calculation performed by the Mason Alberto, also pointed out “450 ceramics. I did side times ceramic side, 0, 20m times 0, 30m reaching the number 0, 06m2. This result represents the area of each ceramics. Now I did side times side of the bathroom floor, 6m times 4, 50m and reached the result of 27m2. Then, the bathroom footage, 27m2 divided by the square meters of a part 0, 06m2, gave 450 ceramics “.
In the resolution of the enunciate: how many square tiles of 15cm aside are needed to internally coat a pool with 15m in length, 6m wide and 1, 20m deep (LEZZI,1991, p. 195), Oscar reported: “I chose to turn these 15m into 1,500 cm divided by 15cm of the Lajota, resulted in 100 tiles in the length of one side of the pool. So on the other side will give the same number, i.e. this row multiplied by 2, gives 200 tiles, which fit on both sides of the length.
The same procedure I used in the width, namely the 6m is 600cm and these 600cm divided by 15 gave me 40 tiles that would go in a width. As we have two widths here, multiplying by 2, I found 80 tiles. Adding 200 tiles in length with 80 of width, I reached the number of 280 tiles, which need to be multiplied by the depth that is 1, 20m, ie 120cm. Before, however, I divided these [medida da profundidade]120cm, by 1[medida do azulejo]5cm and found 8 tiles that would go in the depth of the pool. Now, taking the length and adding up with the width, I mean the 200 tiles plus the 80 tiles, times the 8 tiles of the depth, I reached the number of 2,240 tiles.
We still have to find the number of tiles from the bottom of the pool. This is easy to calculate because the length and width dimensions of the bottom are the same as the sides, mean 6m by 15m. So, they go 100 ceramics in length and 40 in the width of the bottom, totaling 4,000 ceramics at the bottom of the pool. Adding the number of tiles of the sides and the bottom I reached the number of 6,240 ceramics “. The Mason also stressed that “you will always need a reservation” to prevent possible breakdowns, among others.
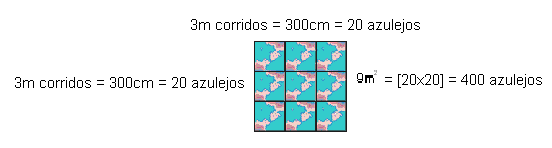
The recognition of the existence of “other forms of thinking”, as postulates D’ambrósio (2001, p. 17), is evident in the mathematical reasoning employed by Sérgio to make this same budget. By communicating his thinking the bricklayer emphasizes that “first I need to know the square meters of wal[laterais]l and floor. 15m plus 6m, over 15m and more 6m, would give the latera[42m corridos]l. This times 1, 20m[profundidade da piscina], gives 50, 4m2 area.
Then I’ll find the footage from the botto[15m vezes 6m = 90m2]m. We are all. I did and gave 140, 4m2. Now I need to find out how many tiles fit in every square metre. Only that as the tiles are 15cm by 15cm, in a meter does[corrido] not close. Then I was adding until I got to 3m. In 3m, [corridos]there are 20 lajotas. Then I took 3 times 3,[multiplicado por] wo[cada face da piscina representa uma figura plana – duas dimensões]uld be a total of 9m2 that gave 400 Lajotas “. Visualize in the representation that follows, the reasoning employed by the bricklayer for the elucidation of the problem situation.
Continuing the explanation of his procedures, Sérgio follows: “I took the total of M2 from the pool, divided by 9[9 partes]. Gave 15.6 equal parts of 9m2 each[140,4m2 : 9m2 = 15,6]. These 15.6 parts equal times the amount of ceramics that was in 9m2, i.e. 400 ceramics. Then, in each part would be 15.6 times 400, equal to 6,240 ceramics “.
Questioned even if the budget of 6,240 ceramics would give enough to coat the pool, Sérgio readily emphasizes: would need about 5% more of this total because of the breakage.
For Professor D’Ambrosio, human groups produce knowledge that, although not widespread in formal teaching spaces, is a valid knowledge and that the school, as well as research in mathematics education need to recognize and deepen to enrich the act Educational.
D’ambrósio (2001, p. 22-23), notes further that,
There are numerous studies on the ethnomathematics of everyday life. It is an ethnomathematics not apprehended in schools, but in the family environment, in the environment of toys and work, received from friends and colleagues.
The resolution of this situation-problem for Alberto showed a knowledge that is identified with the procedure that would be used by a mathematics teacher. Notice its explanation: “The length of the swimming pool sides 15m + 15m, also adding the width 6m + 6m gives the perimeter of the swimming pool, 42m. Now 42m times 1, 20m from the depth of 50, 40m2 of area on the sides of the pool. The bottom of the pool has area of 15m times 6m and gives 90m2. Adding the lateral area and the bottom, I mean the 50, 40m2 plus the 90m2 gives 140, 40m2. This divided by the size of the tile that is 15cm by 15cm and that in M2 gives 0, 0225m2, totalizes 6,240 tiles. Now just add a little to the break buffer. ”
For Demo (1996), the construction of knowledge begins from the knowledge incorporated by each individual in their socio-cultural experience. This has been apparent in the forms of matematizar used by each of the bricklayers. For the author “There is no shallow board, absolute illiteracy; All speak, communicate, use a basic vocabulary, manage concepts within common sense, have references to the reality in which they are inserted “(p. 32).
When entering the school, everyone has already accumulated some knowledge, even if it is within the common sense. We shared with D’ambrosius (1993), when we postulated that we need to understand that when formal schooling begins, the child already has an ethnomathematics that allows him to face the interpretations of the systematic mathematics of the school.
The Matematizar forms of the bricklayers denote according to Marques (2000) that “the learning processes are inevitably inserted into communicative and public communities in which men learn from each other and with one another” (p. 29). According to the understanding of Pompey and Monteiro (2001), “a meaningful educational process begins with the interaction of school and Community” (p. 55), whose relations can resignify the role of the school as a privileged place for exchanging experiences to Better understand the knowledge circulating in everyday life.
In the manifestations (verbalizations) expressed by the bricklayers in the study sessions, especially from the mathematical making of these professionals, based on their work experience, in the exchange of knowledge that they have already participated throughout their lives, show That it is possible for formal education to value and validate this previous knowledge, its culture and its social environment. We believe that an educative work that leaves, dialogically of this knowledge, Enrique and contextualizes the mathematical knowledge of school.
In the words of Rolim
Thinking about the historical-cultural context in the process of teaching mathematics learning is to consider that “doing” involves more than rules and techniques; is to acknowledge that as a science, mathematics is itself a building of humanity (ROLIM, 2010, P. 43).
In our understanding, from this perspective, it is established in the Educational act a relationship widely used in the business world, where the expression “win-win” is spoken and practiced. In a negotiation, this expression has a characteristic: no one loses, everyone wins. It is established between company and supplier an ideal relationship.
For the educational Act, this relationship is pedagogically ideal, that is, students, teachers, the whole context that is part of the educational process, being happy, succeeding. It is then understood that, just as in business, it is possible to pedagogically achieve in the classroom the “win-win” relationship, just make a good and new planning, in which this possibility is inserted.
A pedagogical perspective in which, as well as in the business world, where entrepreneur and supplier should expose their perceptions, their views and their ideas appropriately and at the opportune time, without judging one the behaviour of the other, at school, in a way Teacher respecting and valuing the previous knowledge of his students.
And when in school, the knowledge of everyday life enters into “confrontation” with formal knowledge, that we can dialogically remember that in the business world, often the supplier thinks different from the entrepreneur, however, this relationship is not or should never be Conflict or cause some wear and tear. It needs at school, as well as in business, to represent a great learning opportunity for everyone involved in this process.
The speeches of the bricklayers, participants of the research, showed that the knowledge of mathematics they possess, were acquired most of the time in the development and improvement of their profession, in the practice of day to day, or even, seeing others perform the Same activity.
The conversations we had with the bricklayers throughout the study sessions showed that the knowledge produced outside the school scope is important and it is up to the teacher to rescue them and bring them closer to the classroom, making formal education meaningful and Articulated with the reality in which the student is inserted.
5. GOALS
5.1 Show that Ethnomathematics is part of our daily life and reflect on the possibility of organized social groups produci[pedreiros]ng mathematics in their different forms of expression within their scope of action, discussing in school the ways of producing Meanings of everyday life; 5.2 To present Ethnomathematics as one of the paths to a renewed education, within the greater movement called mathematics education, made possible in this perspective, by the reflection between teacher, student and community, seeking to overcome the Knowledge they both possess, modifying them and transforming the classroom into a democratic space of exchange of knowledge; 5.3 To perceive ethnomathematics as an interesting pedagogical alternative to work in the classroom, Demystifying mathematics and approaching the real necessities of the day-to-day of the students.
6. METHODOLOGY
The investigative work was accomplished through different moments, namely: bibliographical study on ethnomathematics, study sessions with bricklayers in which situations were proposed-problem with the purpose of investigating dialogically with each Professional about the mathematical [formais ou informais]knowledge they use to make the budget of the quantity of ceramics needed to coat walls and floors. Reflection on possible connections between mathematics and reality in the possibility of establishing bonds between the mathematical knowledge of the bricklayer, constructed from their needs of professional day-to-day, using practices Everyday life and school mathematics.
7. EXPECTED CONTRIBUTION
Considering that throughout the investigative work, based on the discourse of the bricklayers, we perceive that these professionals to solve the problem situations proposed, were not always supported in the knowledge of school mathematics.
Whereas it was clear that the bricklayers applied mathematical knowledge in a practical and intuitive way, using specific strategies, not using the mathematical formulas taught at school.
We hope that teaching mathematics in the classroom through the ethnomathematics a[10]pproach allows teachers and students to learn about the very cultural diversity of mathematics. That the results of this research help in the development of a methodology that contributes to the teaching of mathematics, bringing possibilities for changes in teaching practice, approaching school pedagogical practice with the knowledge produced in situations Of the students ‘ lives.
That from this reflection the pedagogical practice in the classroom can be reoriented to the development of the full citizenship of the students. That, according to Pinheiro and Rosa (2016), the:
[…] Mathematics teachers immerse themselves in the cultural dynamics of students and use teaching and learning strategies that value the cultural dimension in the classroom, so that an inclusive mathematical education can be developed that could effectively Contribute to social transformation (p. 79).
Thus, from the study sessions and the text produced, we aim to provoke the readers to the possibility of pedagogical intervention, based on the reality of the student, uniting theory and practice in the construction of systefined knowledge. It is also hoped that the reflections resulting from the reading of the text allow a new look at the reality and on the mathematical education, from the perspective of the production of knowledge from the daily practice.
The aim is to contribute to the Constitution of the researcher Professor of his practice, arousing him/her to learn in a continuous way to be a teacher, according to current educational needs, transforming the classroom into an environment of exchange of knowledge, Rescuing historical knowledge-socially built by mankind.
8. BIBLIOGRAPHICAL REFERENCES
BREDA, Adriana LIMA, Valderez Marina do Rosário e GUIMARÃES, Gleny Terezinha Duro. A utilização da Etnomatemática nos cursos de formação continuada de professores: implicações das relações de poder saber na produção de subjetividades. Curitiba. Novembro de 2011. Disponível em: http://educere.bruc.com.br/CD2011/pdf/4668 _ 2898.pdf. Acessado em: 20/08/2017.
CARNEIRO, K. T. A. Cultura Surda na aprendizagem matemática da sala de recurso do Instituto Felipe Smaldone: uma abordagem etnomatemática. Anais do 4º Congresso Brasileiro de Etnomatemática. Belém, PA: ICEm4, 2012.
D’Ambrósio Ubiratan. Etnomatemática: Arte ou técnica de explicar e conhecer. Editora Ática, Série Fundamentos, 2. edição, São Paulo, 1993.
——-. Educação matemática: da teoria à prática. 13ª ed. Campinas: Papirus, 1996. (Coleção Perspectivas em Educação Matemática).
————-. Etnomatemática – elo entre as tradições e a modernidade. Coleção Tendências em Educação Matemática, 1. Belo Horizonte: Autêntica, 2001, 112p.
D’AMBROSIO, U.; ROSA, M. Um diálogo com Ubiratan D’Ambrosio: uma conversa brasileira sobre etnomatemática. In BANDEIRA, F. A.; GONÇALVES, P. G. F. (Orgs.). Etnomatemáticas pelo Brasil: aspectos teóricos, ticas de matema e práticas escolares. Curitiba, PR: Editora CRV. 2016. pp. 13-37.
DEMO, Pedro. Pesquisa e construção de conhecimento: Metodologia científica no caminho de Habermas. 3.ed. Rio de Janeiro: Tempo Brasileiro, 1996. 125p.
GERDES, Paulus. Etnomatemática: Cultura, Matemática, Educação. Maputo. Instituto Superior Pedagógico, 1991.
GIARDINETTO, José Roberto Boettger. Matemática escolar e matemática da vida cotidiana. Coleção polêmicas do nosso tempo, autores associados, Campinas – São Paulo, 1999, 128p.
LEZZI, Gelson; Dolce, Osvaldo; Machado, Antonio. Matemática e Realidade. 5ª série, 3. edição reformulada, Atual, São Paulo, 1996, 250p.
————–. Matemática e Realidade. 5ª série, 2. edição, Atual, São Paulo, 1991, 213p.
KNIJNIK, Gelsa. O saber popular e o saber acadêmico na luta pela terra. Revista da Sociedade Brasileira de Educação Matemática. Educação Matemática em Revista. Ano 9, n. 1, p. 27-39, 2002.
————–. Educação matemática, culturas e o conhecimento na luta pela terra. Santa Cruz do Sul, EDUNISC, 2006, 239 p.
MARQUES, Mário Osorio. A aprendizagem na mediação social do aprendido e da docência. Ijuí, Editora UNIJUÍ, 2. edição, 2000, 144 p.
MONTEIRO, A.; Pombeu, G. Jr. A matemática e os temas transversais. Editora Moderna, São Paulo, 2001, 160p.
MONTEIRO, Alexandrina. Reflexão e Ação: Revista do Departamento de Educação/UNISC. Vol. 10, n. 1 (jan./jun.2002) — Santa Cruz do Sul: EDUNISC, 2002.
A Etnomatemática em Cenários de Escolarização: alguns elementos de reflexão. Alexandrina Monteiro, p. 93 – 108.
PINHEIRO, R. C.; ROSA, M. Uma perspectiva etnomatemática para o processo de ensino e aprendizagem de alunos Surdos. RPEM, v. 5, n. 9, p. 56-83, 2016.
ROLIM, Carmem Lucia Artioli. Fórmulas de Silêncio: metodologias no processo de ensino da Matemática. In: SANTOS, Jocyléia Santana. ZAMBONI, Ernesta. Potencialidades Investigativas da Educação. Goiânia: Ed. da PUC Goiás, 2010.
ROSA NETO, R. Didática da matemática, São Paulo: Ática, 2002.
8. Understood with a pedagogical practice that values the mathematics of different cultural groups, taking into account the informal concepts constructed by the subjects through their experiences outside the context of the school.
9. In this reflection, we treat formal and informal mathematics in the idea that the first is considered of a school, scientific, systematic, legitimated and associated with classroom contexts and the second as daily, spontaneous, knowledge of day to day, Associated with streets, experience and living in communities, social contexts.
10. In this work used to designate the investigation of the conceptions, traditions, and mathematical practices of a social[pedreiros] group and the pedagogical work that can be developed in the perspective that the group interprets and codify their knowledge; Acquire the knowledge produced by academic mathematics, using, when confronted with contextualized situations, the one that seems more appropriate.
[1] Master in Science Education – Mathematics, UNIJUI – RS. Degree and Specialization in Science and Mathematics. Prof. Assistant of the CCA – Center for Agricultural Sciences, Campus of Marshal Cândido Rondon, UNIOESTE, PR – Brazil.
[2] Master in Sustainable Rural Development-UNIOESTE, Mathematics Specialist, Physics-UNIPAR, People Management and Special Education with emphasis on Multiple Disability-UNIASSELVI, Graduated in Mathematics with emphasis in Physics-UNIPAR.
[3] Specialization in Exact Science Teaching – Mathematics, Physics and Chemistry. UNIOESTE – State University of Western Paraná. Graduation: Science and Mathematics. UNIJUI, RS. Professor of the State Education Network of the State of Paraná.
[4] Professor of Plant Protection and Human Health at the Pontifical Catholic University of Chile, Department of Plant Sciences, he holds an interdisciplinary position shared between the Faculty of Agronomy and Ingeniería Forestal (FAIF), Faculty of Medicine and Faculty of Chemistry. Research Professor associated with the Study Group on Soils and Environment (GESOMA – UNIOESTE). Master in Agronomy from UNIOESTE, PhD in Agronomy from UNIOESTE (2013-2016) – Sandwich Period (CAPES Scholarship) from the University of Lisbon, at the Instituto Superior de Agronomia (ULisboa).
[5] Research Productivity Level 1C by CNPq in the area of Environmental Sciences with three Postdocs, UEM-PR (Brazil), University of Santiago de Compostela (Spain), UFG-GO (Brazil). He is currently an Associate Professor at UNIOESTE-PR and acts as a professor and researcher at the Center for Agrarian Sciences, teaching chemistry. Lecturer in the Master Program in Agricultural Sciences at UEM. He is currently ad hoc consultant to CNPq, CAPES and Fundação Araucária. Acts as volunteer environmental consultant with MP-SP and CONAMA-DF.
[6] Undergraduate student in agronomy-UNIOESTE-State University of the west of Paraná-undergraduate administration-Unip-Universidade Paulista.
[7] Master student in Agronomy (Plant Production) from the State University of Western Paraná (UNIOESTE). Agricultural Engineer graduated from UNIOESTE (2014-2018), acts as a researcher associated with the Study Group on Soils and Environment (GESOMA – UNIOESTE).
Submitted: June, 2019.
Approved: July, 2019.