ARTÍCULO ORIGINAL
OLIVEIRA, José Luiz de Jesus Egues de [1], SILVA, Edevaldo Maximo da [2], SANTOS, Cleidison Da Silva [3], PONTES, Dalila Fonseca [4], SILVA, Jandaira Fernandes da [5], QUEIROZ, Jose Pereira de [6], SANTANA, Zenóbia Conceição Castro [7]
OLIVEIRA, José Luiz de Jesus Egues de. Et al. Construcción educativa de la geometría y el uso de materiales concretos como proceso de aprendizaje. Revista Científica Multidisciplinar Núcleo do Conhecimento. Año 05, Ed. 10, Vol. 10, págs. 46-61. Octubre de 2020. ISSN: 2448-0959, Enlace de acceso: https://www.nucleodoconhecimento.com.br/educacion-es/construccion-educativa, DOI: 10.32749nucleodoconhecimento.com.br/educacion-es/construccion-educativa
RESUMEN
La investigación destacó por una reflexión didáctica que satisface la necesidad de construcciones experimentales en el aula, con materiales concretos para ayudar en el proceso de enseñanza y aprendizaje de la geometría en la escuela primaria. En este sentido de atribuir un análisis a este problema, tenemos como eje, la educación matemática, como una forma de estimular a los estudiantes para el desarrollo de talleres en los que apuntaban a la construcción de materiales didácticos como un proceso de aprendizaje de las matemáticas. El proceso de construcción del concepto de geometría que atribuyen las habilidades y competencias a desarrollar en los alumnos en esta etapa, permitió a los mismos desarrollar un tipo particular de pensamiento para entender, describir y representar, de forma organizada, los espacios geométricos, informando la importancia que este contenido tiene en su vida social como ciudadano. A través de la construcción de figuras geométricas con materiales manipulados, estudiamos todos los conceptos de la figura, a través de esta herramienta, estimulando así el interés y la motivación de los alumnos, proporcionándoles un razonamiento geométrico y matemático. Las definiciones de geometría se pueden construir sucesivamente, tomando como base el conocimiento previo de los alumnos o no, en el que destacamos que los educadores deben crear actividades en las que los alumnos realicen consultas de situaciones relacionadas con dimensiones geométricas, teniendo así experiencias de significado y dirección de sí mismos y de alguna figura insertada en el espacio. Sin embargo, para la absorción de este proceso de enseñanza y aprendizaje, además de presentar teorías a los alumnos, era necesario mostrar las figuras geométricas por sus características físicas, es decir, de tal manera que la naturaleza nos proporciona y no sólo por sus propiedades y conceptos definidos. Finalmente, la investigación nos permitió analizar la capacidad intelectual de cada alumno seleccionado para este fin.
Palabras clave: Educación Matemática, construcción educativa, geometría.
1. INTRODUCCIÓN
Como profesionales de la Educación y de diversas áreas, pensamos en esta investigación impulsada por el deseo de dialogar sobre la enseñanza del aprendizaje de las matemáticas, más específicamente observar la importancia de la Geometría en el menú educativo del alumno y, en particular, en la escuela primaria. También como investigadores y conocedores de los espacios geométricos, destacamos el argumento de Malba Tahan (1967, p.31) en su texto que dice: “Lo que hace difícil enseñar matemáticas es el inalterable hábito latino de empezar siempre con lo abstracto, sin pasar por el concreto”. Otros autores también tienen una importancia muy relevante en esta parte de las matemáticas. También abordaremos el casi abandono de la geometría en la educación básica, reportado en algunos estudios que abordamos como base para este trabajo. También destacamos las especificidades relativas a la enseñanza de los contenidos de geometría en el contexto del mundo físico para la enseñanza, así como las habilidades que esta área de las matemáticas debe proporcionar para que los estudiantes sean incluidos en una sociedad educativa de facto.
Sin embargo, el proceso de enseñanza-aprendizaje de Matemáticas es objeto de mucho estudio y discusión, porque siempre surgen nuevas metodologías para satisfacer una demanda que cambia constantemente en diversas modalidades de enseñanza.
Dadas las especificidades del proceso de aprendizaje de las matemáticas en la escuela primaria, y la perspectiva del desarrollo de herramientas para estimular la capacidad intelectual de los estudiantes y al mismo tiempo valorar el uso de las matemáticas en la vida cotidiana en la que se pueden resolver innumerables problemas, la discusión de la importancia de los contenidos didácticos que implican geometría sale a primer lugar, porque es un camino muy interesante , es extremadamente importante poder proporcionar al estudiante una visión más organizada del mundo en el que vive. De hecho, es muy importante estudiar esta área de las matemáticas y es defendido por varios educadores, en los que se discuten aquí y se discuten a continuación, de acuerdo con la importancia y especificidades de esta área.
Con esta investigación intentamos contribuir a la enseñanza de la educación matemática, basada en el desarrollo de habilidades y competencias en los estudiantes.
El desarrollo de talleres dirigidos a la construcción de materiales manipulables didácticos para el proceso de enseñanza y aprendizaje, explorando los conceptos geométricos que contemplan las habilidades y competencias que desarrollarán los estudiantes durante la etapa llamada “construcción educativa”, permitirá al estudiante desarrollar un tipo particular de pensamiento para entender, describir y representar, de manera organizada, el mundo en el que vive , informándolo de la importancia de este contenido. Por lo tanto, un día pueden utilizar este producto educativo en su vida social, o en la vida cotidiana, además de permitir un aumento en la visión del uso de los conocimientos básicos geométricos.
2. TENDENCIAS DIDÁCTICAS PEDAGÓGICAS EN LA ENSEÑANZA DE LA GEOMETRÍA
Creemos que la construcción educativa fijó el proceso de aprendizaje almacenando así el contenido transmitido, que se llevaron a cabo con materiales de hormigón manipulados.
Según Duval (1995), la geometría implica tres formas de proceso cognitivo: que llenan funciones epistemológicas específicas;
Visualización de la exploración heurística de una situación compleja; Construcción de configuraciones, que se pueden trabajar como un modelo, en el que las acciones realizadas representadas y los resultados observados están vinculados a los objetos matemáticos representados; Razonamiento, que es el proceso que conduce a la prueba y la explicación. (DUVAL, 1995).
Según el autor, estas tres especies de procesos cognitivos están entrelazadas en su sinergia y cognitivamente necesarias para el dominio de la geometría. Por otro lado, la heurística de los problemas de geometría se refiere a un registro espacial que da paso a formas de interpretaciones autónomas.
Para Duval (1988), los problemas de geometría presentan una gran originalidad en relación con muchas tareas matemáticas que se pueden proponer a los estudiantes. Además, el autor dice que favorecer el desarrollo de funciones cognitivas organizando problemas matemáticos de geometría cercana que requieren el mismo conocimiento, determina una categorización cognitiva indispensable para el aprendizaje.
Según Machado (2005), la mayoría de los problemas de la enseñanza y el aprendizaje de la geometría son de origen didáctico y linguístico. Para Duval (1995), la coordinación de los diferentes registros de representación (escritura algebraica, figuras geométricas, discurso en el lenguaje natural) vinculada al tratamiento del conocimiento no funciona espontáneamente, incluso en el curso de una enseñanza que moviliza esta diversidad de registros.
Sin embargo, el estudio propuesto debe permitir al alumno hacer una interpretación diferente de la geometría a su alrededor, ya que ejercitar en su memoria a través del contacto, es decir, “el concreto”, puede adquirir conocimientos en este contexto educativo, y que servirá como herramienta para ser incorporado a su vida diaria.
Según Fiorentini:
Varios cambios metodológicos se señalan como tendencias de enseñanza que buscan privilegiar la participación de los estudiantes, considerando la construcción del conocimiento como una forma de aprendizaje. El conocimiento matemático emerge del mundo físico y es extraído por el hombre a través de los sentidos. (FIORENTINI, 1995, p.9).
Los Parámetros Curriculares Nacionales (PCN, 1998) también reconocen la falta de protagonismo que se ha dado a esta área de Matemáticas y también destaca que desarrolla un papel fundamental en la formación del estudiante como ciudadano.
Para (MACHADO, 2005), la mayoría de los problemas de la enseñanza y el aprendizaje de la geometría son de origen didáctico y linguístico.
Los autores anteriores citan estos aspectos en los procesos de aprendizaje que están entrelazados en su sinergia y cognitivamente necesarios para el dominio de la geometría. Por otro lado, la heurística de los problemas de geometría se refiere a un registro espacial que da paso a formas de interpretaciones autónomas.
Esperamos que la metodología aplicada sea una tendencia pedagógica en nuestra vida diaria en esta área trabajada, y que podamos utilizarla en nuestras clases, como herramienta de aprendizaje en clases de geometría.
3. EL USO DE MATERIALES DE HORMIGÓN EN LA ENSEÑANZA DE LA GEOMETRÍA
Los obstáculos y dificultades encontrados por los estudiantes en el momento del aprendizaje de las matemáticas en sí son innumerables. Hay quienes no pueden entenderlo e incluso el maestro de enseñanza es desaprobado en una declaración y aquellos que, cuando están aprobados, todavía no aplican los conocimientos adquiridos. Es decir, no entienden su verdadera importancia.
Por lo tanto, varios estudios muestran que el uso de materiales manipulados produce un mayor rendimiento en los estudiantes que su uso, en todas las edades y en todos los años de la escuela. Este uso es una indicación metodológica que se valora desde el momento de la adquisición hasta el momento de la construcción de conceptos que pueden ocurrir en todos los niveles de la educación. Así surge la pregunta: ¿puede el material concreto como uso pedagógico facilitar la enseñanza y el aprendizaje de las matemáticas? Según Carraher y Schilemann (1988), afirman en su investigación que “no necesitamos objetos en el aula, sino objetivos. Necesitamos situaciones en las que la solución de un problema implique el uso de principios lógicos matemáticos que se deben enseñar” (p.179). Esto se debe a que el material “a pesar de estar formado por objetivos, puede ser considerado como un conjunto de objetos ‘abstractos’ que sólo se encuentran en la escuela con el propósito de enseñar, y no tiene ninguna conexión con el mundo del niño” (pág. 180). Para él, el hormigón para los niños no es necesario, porque los objetos manipuladores pueden ser abstractos en las manos en diversas situaciones que el niño tendrá que enfrentar socialmente. Por otro lado, Fiorentini y Miorim (1990), confirman sus palabras pronunciadas anteriormente y explican que detrás de cada material utilizado, se oculta una visión de la educación matemática del hombre y del mundo. Esto significa que hay una propuesta pedagógica que justifica este uso.
A partir de esta investigación, también encontramos preguntas para el público de niños con necesidades especiales. ¿Cómo se produciría este uso? ¿Cómo sería el proceso de enseñanza y aprendizaje para esos niños? Así, la educadora italiana y también la médica Maria Montessori, nos responde aportando resultados tras la investigación con niños excepcionales, desarrollados a principios de este siglo con diversos materiales manipuladores centrados en las propias matemáticas. Se creía que no había aprendizaje sin acción: “nada se debe dar al niño, en el campo de las matemáticas, sin presentarle primero una situación concreta que le lleve a actuar para actuar, a experimentar, a descubrir, y por lo tanto, a sumergirse en la abstracción”. (AZEVEDO, 1979, p. 27)
Siguiendo estas reflexiones percibimos que este material concreto mencionado aquí y colocado como objeto de aplicabilidad para un aprendizaje efectivo nos hace darnos cuenta de que hay una necesidad de un ejercicio de las facultades sintéticas y analíticas del niño como el autor a continuación afirma que:
Se deben ejercer las facultades sintéticas y analíticas del niño. Sintético para permitir al estudiante construir un concepto a partir del hormigón. Analítico porque en este proceso el niño discerne en el objeto esos elementos que constituyen la globalización. Para ello el objeto tiene que ser móvil, que puede sufrir una transformación para que el niño pueda identificar la operación subyacente (CASTELUNUOVO, 1970, p.82-91)
Los materiales manipulados pueden ser fundamentales para que se produzca el aprendizaje y no siempre el más apropiado es el ya construido o más hermoso. Al fomentar la construcción educativa por parte de los niños estamos pensando en facilitar el proceso de aprendizaje y es en este momento que nos damos cuenta de que la participación concreta de la misma hace que dicho proceso tenga realmente una validación. Así nos comparamos con el currículo nacional de educación básica que establece: Competencias esenciales (IDEB, 2001), con respecto al uso de los recursos, establece que:
Materiales manipulados de diversa dosis es, a lo largo de toda la escolaridad, un recurso privilegiado como punto de partida o apoyo de muchas tareas escolares, en particular las destinadas a promover actividades de investigación y comunicación matemática entre los estudiantes… […] Todos los estudiantes deben aprender a usar no sólo la calculadora primaria, sino también, a medida que progresan en la educación básica, los estudiantes deben tener la oportunidad de trabajar con la hoja de cálculo y con varios programas educativos, incluyendo gráficos de funciones y geometría dinámica (2001, p.17).
4. METODOLOGÍA
La metodología utilizada es cualitativa, bibliográfica y experimental. La investigación fue desarrollada durante talleres pedagógicos, organizados por módulos que permitieron al mismo tiempo desarrollar las actividades relacionadas con “Construcción de Materiales Didácticos como Proceso de Enseñanza y Aprendizaje”, que aquí caracterizamos como “construcción educativa”.
Hicimos los talleres con reuniones que se dividieron con el fin de poner al estudiante en contacto con el tema. Aplicamos los conceptos de las figuras relacionadas con los textos seleccionados del libro de matemáticas de la disciplina de la geometría. Otras lecturas fueron seleccionadas de acuerdo con el desarrollo de la obra. Utilizamos como conceptos de planificación geométrica de figuras en el espacio bidimensional y ensamblamos figuras geométricas de espacio tridimensional. En esta fase, el aprendizaje de la geometría se realiza mediante actividades relacionadas con la acción, debe haber un predominio de hormigón sobre lo simbólico, por lo tanto el estudiante manipula y construye objetos de diversas formas para luego analizar sus características físicas y geométricas. Desde esta perspectiva, deben llevarse a cabo actividades geométricas que permitan la exploración de conceptos relacionados con el espacio y la forma, contribuyendo al curso que se centra en la formación de un estudiante insertado, ya que deben entender el mundo geométrico en el que vive.
4.1 DE LOS TALLERES APLICADOS
Se realizaron dos talleres en una clase de noveno grado de primaria, compuesta por 27 estudiantes de la mañana del concejal estatal Bento Muniz del municipio de Tangará da Serra-MT. Así, se aplicó una evaluación diagnóstica, también concebida como una prueba previa, y con el objetivo de tener información sobre los conocimientos previos de los estudiantes en el contexto de la geometría euclidiana, porque según la Ley LDB de Directrices y Bases Nacionales (1961)
Las directrices y propuestas emitidas por el MEC (Ministério de Educación) destacan y refuerzan la necesidad de reconocer los conocimientos previos de los alumnos, utilizándolos como una herramienta que facilita el aprendizaje y como factor motivador, ya que de esta manera, el alumno se convierte en sujeto activo en el proceso de escolarización, ya no siendo meros receptores de conocimiento.
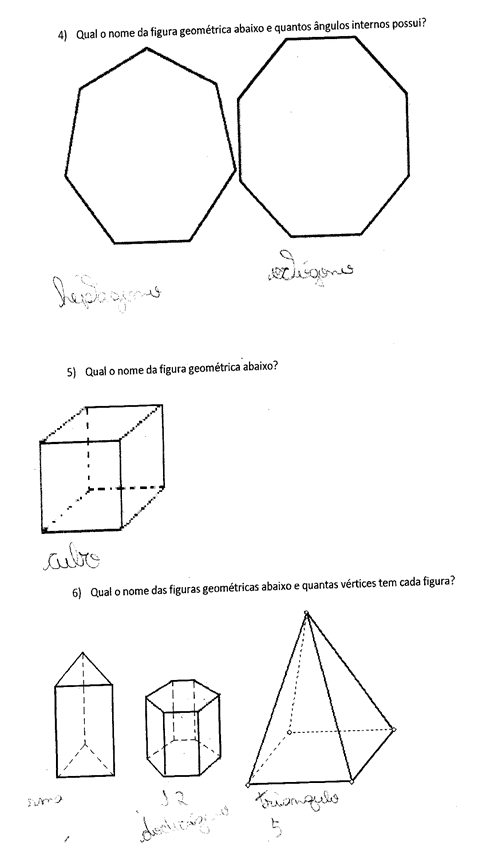
Las cifras presentan el cuestionario presentado, así como las respuestas de algunos estudiantes. Las tres primeras preguntas tenían como objetivo verificar la comprensión de los alumnos en la concepción de las definiciones de polígonos y poliedros, así como la denominación de algunas figuras geométricas elementales. Observamos que la mayoría de los estudiantes no habían concebido las definiciones cuestionadas, lo que va en contra de las declaraciones de Almouloud (2005) en las que el autor afirma que varios estudios apuntan a esta disciplina como uno de los problemas de aprendizaje. Y esto se hace más evidente cuando nos fijamos en los otros temas contenidos en la prueba.
Figura 01 – PROPUESTA APLICADA.
Figura 2 – CONTINUIDAD DE LA PRUEBA
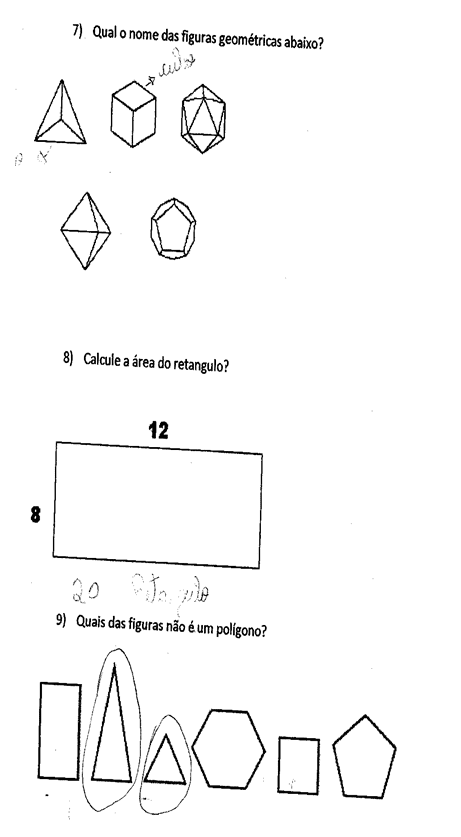
Fuente: Propio (2011)
Figura – 3. Construcciones

Fuente: Propio (2011)
Figura – 4. Construcciones

Fuente: Propio (2011)+
Figura – 5. Construcciones

Fuente: Propio (2011)
En esta investigación, se encontró que la gran mayoría de los estudiantes no reconocen las formas poligonales y no poligonales y no saben cómo relacionarlas con el número de sus lados y vértices, y todavía muestran segmentar la geometría de su vida diaria, aunque la vida cotidiana es el promotor del estudio de la geometría como se indica por el autor a continuación:
El conocimiento matemático emerge del mundo físico y es extraído por el hombre a través de los sentidos” y Miguel y Miorim, (1986, p.66), que afirman: “La geometría es tan importante para la humanidad que hace inconcebible cuestionar la necesidad de estudiarlo en la escuela, porque el mundo en el que vivimos es casi espontáneamente geométrico y su uso en la vida cotidiana es casi una necesidad humana. (FIORENTINI, 1995 p. 9.)
Tal vez esta situación se agrave por la forma en que los maestros presentan este contenido, que según los PCN es tan importante como en el pasado.
Las cuestiones relacionadas con las formas y relaciones entre ellas, con las posibilidades de ocupación espacial, con la localización y desplazamiento de objetos en el espacio, vistos desde diferentes ángulos son tan necesarias hoy como lo eran en el pasado. Las situaciones cotidianas y el ejercicio de diversas profesiones, como la ingeniería, la bioquímica, la coreografía, la arquitectura, la mecánica, etc., requieren la capacidad del individuo para pensar geométricamente (PCNs p. 122 – 1998).
En un segundo momento, se propusieron construcciones de las cifras planas. Durante las construcciones se encontró que los estudiantes realmente entienden las formas geométricas presentadas a través de las construcciones con cartón, es decir, el hormigón. Cuadrado, rectangular, triangular, circular, pentagonal, hexagonal, heptagonal, antitogonal, eneagonal, decagonal, dodecagonal, tridecagonal, tetradecagonal, pentadecagonal, todos diseñados en cartolines para ser cortados y finalmente construidos fueron ensamblados. Observamos que la construcción por parte de los alumnos contribuyó a la creación de significados de los propios alumnos, con interés en participar más que si estas figuras fueran presentadas en la pizarra por el maestro. Lo que refuerza los dichos de Azevedo (2006, p.27), que creía que no había aprendizaje sin acción: “nada debe ser dado al niño, en el campo de las matemáticas, sin presentarle primero una situación concreta que le lleva a actuar para pensar, experimentar, descubrir, y por lo tanto, sumergirse en la abstracción”.
También se abrió un espacio donde los alumnos tuvieron la oportunidad de cuestionar y discutir sobre las actividades realizadas y la relación de las formas en nuestra convivencia. Pero después de que se abrió el debate para comentarios, algunos estudiantes sólo contribuyeron si fueron instigados y se les pidió que hicieran un comentario. El comentario más frecuente de los alumnos fue que nunca habían participado en un proceso de enseñanza de esta manera y que les resultaba interesante y placentero construir las cifras en lugar de simplemente ver al maestro presentarlas. Así Machado (2005) afirma que la mayoría de los problemas de la enseñanza y el aprendizaje de la geometría son de origen didáctico y linguístico; y Pavanello (1993), explica que algunos factores relacionados con tales dificultades pueden estar relacionados con la falta de interés de los estudiantes generada por la falta de recursos didácticos, la falta de profesores interesados para utilizar estos diferentes recursos didácticos con el fin de desarrollar una enseñanza atractiva y de calidad, que puede utilizar nuevas concepciones didácticas como el uso de materiales concretos o juegos pedagógicos en el desarrollo de sus prácticas didácticas.
A través de esta actividad, fue posible verificar que el potencial educativo proporcionado por las construcciones de figuras planas es muy relevante para fines didácticos pedagógicos y atractivo para establecer la correlación entre el contenido del tema a tratar.
En esta etapa, también se pidió a los estudiantes que construyeran las figuras planas en grupos, donde debían ser pintadas con los crayones. Este tipo de actividad lleva al estudiante a hacer una planificación previa de la construcción, ya que requiere conocimiento de formas geométricas o polígonos y requiere habilidades motoras para manejar los materiales.
El taller para la construcción de figuras planas, además de dinámicas fue recreativo, motivador y pedagógicamente atractivo, porque en varias ocasiones los grupos discutieron qué polígono construiría, porque segundo. Fiorentini y Miorim (1990) “dice que detrás de cada material utilizado, se oculta una visión de la educación, las matemáticas, el hombre y el mundo; es decir, hay, detrás, una propuesta pedagógica que la justifica”.
Cabe destacar que fue posible observar que el taller como un proceso didáctico para las actividades, a través de los recursos visuales y la experimentación, provoca un cambio en la postura del alumno, con una mayor motivación y participación de la mayoría, lo que representa una mayor implicación de los alumnos en relación con el contenido de la geometría, ya que según Castelunuovo:
El hormigón debe tener un doble propósito: “ejercer las facultades sintéticas y analíticas del niño”; para permitir al estudiante construir un concepto a partir del hormigón; analítica porque, en este proceso el niño logra discernir en el objeto aquellos elementos que constituyen la globalización. Para ello, el objeto tiene que ser móvil, que puede sufrir una transformación para que el elemento secundario pueda identificar la operación subyacente. (CASTELUNUOVO, 1970, p.82-91).
También se hicieron sólidos geométricos, pero antes presentamos algunos conceptos de figuras geométricas de tres dimensiones acrílicas como pirámides, prismas, cubos, dodecaedro, icosahedro, tetraedro, octaedro, esfera, cilindro para ellos, para hacer una planificación previa y sólo entonces ensamblar los sólidos, pero algunos estudiantes ya habían adquirido los conceptos de las formas planas en el taller anterior, porque para el montaje de sólidos requiere conocimientos de los espacios geométricos planos y requiere capacidad de motor para manejar los materiales , según algunos estudiantes nunca había trabajado con estos sólidos concretamente. Cartón, palo de barbacoa, palo de contacto, pegamento de contacto, tijeras, etc. se utilizaron para ensamblar los sólidos geométricos.
En cada figura construida, se utilizó la planificación del taller y se aplicó la relación de sólidos geométricos con las figuras planas, los ensamblajes se hicieron consecutivamente, y también se analizaron las formas acrílicas del modelo para la planificación. Este potencial pedagógico interactúa condicionalmente con los estudiantes en las construcciones de las figuras, abriendo la discusión sobre cómo ser montado, fue un ejercicio de paciencia para la conclusión de estos concretos.
También podemos utilizar la interdisciplinariedad en este proceso pedagógico, ya que, según los Parámetros Nacionales del Currículo (1998-MEC):
El profesor debe ser el mediador que fomente el desarrollo de procedimientos que contribuyan a desarrollar en el estudiante el interés de buscar nuevos horizontes y compartir los conocimientos adquiridos en diferentes situaciones. Teniendo en cuenta esta orientación, existe una gran necesidad de promover la interdisciplinariedad y contextualización de las disciplinas y especialmente de las matemáticas
Es decir, para facilitar aún más la visión amplia de los objetos y sus relaciones. Sin embargo, enfatizamos que, se puede ver que no todos los estudiantes realmente tienen una visión general de las figuras tridimensionales y observamos que algunos de ellos tenían dudas todavía para ensamblar una de las formas de un sólido. También encontramos que este tipo de acción prepara al estudiante para buscar soluciones y al mismo tiempo obtiene este proceso dinámico de aprendizaje pedagógico para explorar el razonamiento ante las construcciones de formas geométricas. Verificamos que esta actividad se realizaba con gran compromiso y participación de los estudiantes, sin embargo, en algún momento había una necesidad de acompañar a algunos estudiantes en el proceso de montaje de los sólidos geométricos. Hemos grabado algunos comentarios hechos por ellos, tales como:
- “Creemos que tomar una clase de geometría a través de construcciones geométricas aprende mucho más y además de ser divertido”.
- “Además de aprender en teoría podemos aprender mejor en la práctica, el maestro no sólo está pasando en la pizarra y es más interesante tomar clases prácticas”.
Es evidente la importancia de esta actividad desarrollada en el ámbito educativo, ya que esta transposición didáctica muestra la realidad en el aula y trabajando con esta actividad colaborativa verificamos la importancia de compartir juntos esta actividad esencial en la vida de los estudiantes y educadores de matemáticas.
Este potencial pedagógico presenta acciones que se pueden implementar en el entorno escolar. El experimento y la aproximación de la teoría geométrica en sus vidas contribuyen a las actividades educativas, llevando a los estudiantes a estar más interesados en el aprendizaje de la geometría.
5. CONSIDERACIONES FINALES
La investigación muestra que la incorporación de actividades que favorecen la interacción social, la cooperación y la experimentación en el aula puede marcar la diferencia en el entorno escolar, ya que el contexto social en el que se insertan estos alumnos no está aislado de la escuela, y una de las tareas de la misma es promover una educación que permita la vida social de los alumnos. La participación colaborativa efectiva es otro punto que destacamos con los talleres, teniendo en cuenta que se demostró que era un punto positivo, que se ve reforzado por Lorenzato (2006) cuando afirma que: La enseñanza es diferente de la enseñanza. Enseñar es dar condiciones para que el estudiante construya sus propios conocimientos.
También destacamos que el uso de materiales concretos en la enseñanza de la geometría además de promover la interacción de los estudiantes con el objeto de estudio y a partir de esta interacción pueden construir sus conocimientos, también promover discusiones en el sentido de identificar de esta manera en la vida cotidiana de los estudiantes, lo que acorta la distancia de los conceptos matemáticos y su aplicabilidad además de ser más interesantes y significativas , sirviendo como alternativa para enseñar geometría que se escapa de lo tradicional.
Es cabe destacar que los talleres desarrollados lograron sus objetivos que partiendo del desarrollo de habilidades que permiten la abstracción de contenidos geométricos, que pueden ser utilizados para entender, describir y representar de manera organizada el mundo en el que vivimos.
Se cree que la investigación en sí es factible como metodología de trabajo cuando se prepara previamente y ofrece potencial para la simplicidad presentada en su desarrollo, contribuyendo así al proceso de enseñanza aprendiendo geometría y matemáticas.
Por lo tanto, llegamos a la conclusión de que la elaborada “construcción educativa” tuvo un resultado gratificante, con mucha interacción logramos nuestros objetivos en el proceso de enseñanza y aprendizaje de matemáticas, esperamos que con este trabajo se incluya como tendencia en el proceso educativo de estudiantes y educadores.
REFERENCIAS
ABNT-ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6022: informação e documentação: artigo em publicação periódica científica impressa: apresentação. Rio de Janeiro, 2014. Acesso em 19/03/2012.
ARAÚJO, J.L.; BORBA, M.C. Construindo Pesquisas Coletivamente em Educação Matemática. In: BORBA, M. C.; ARAUJO, J. L. (Org.). Pesquisa Qualitativa em Educação Matemática. Belo Horizonte: Autêntica, 2004.
AZEVEDO, Edith D. M. Apresentação do trabalho matemático pelo sistema montessoriano. In: Revista de Educação e Matemática, n. 3, 1979 (p. 26-27).
BRASIL, Ministério de Educação. PARÂMETROS CURRICULARES NACIONAIS – Matemática – 5ª a 8ª séries, 1998, MEC.
CARRAHER, T. N. Na vida dez, na escola zero. São Paulo: Cortez, 1998.
CASTELNUOVO, E. Didática de La Matemática Moderna. México: Ed Trillas, 1970.
FIORENTINI, Darío. MIORIM, Maria Ângela. Uma reflexão sobre o uso de materiais concretos e jogos no ensino da Matemática. Publicado no Boletim SBEM – SP, ano 4 – n° 7.
FIORENTINI, Dario; LORENZATO, Sérgio. Investigação em Educação Matemática: pressupostos teóricos e metodológicos. Campinas, SP: Autores Associados, 2006 (Coleção Formação de Professores). Artigos da Secretaria de educação do estado de São Paulo
GIMENO SACRISTÁN, J. (2000). O currículo: Uma reflexão sobre a prática (3ª Ed.). Porto Alegre: Artmed.
MACHADO, Silvia Dias Alcântara. Aprendizagem em Matemática – Registro de Representação Semiótica, Campinas-SP; Papirus Educação, 2005, p.11-30, p.125-133.
MATEMÁTICA DIVERTIDA/POLIEDRIS. Disponível em: http://pt.wikipedia.org/wiki/S%C3%B3lidos_geom%C3%A9tricos Acesso em 29/05/2012. jan/julho de 1995.
MINISTÉRIO DA EDUCAÇÃO. Lei nº 4.024 de 20 de dezembro de 1961. Lei de Diretrizes e Bases da Educação Nacional. Diário Oficial [da] República Federativa do Brasil, Brasília, DF, 27 dez. 1961
NCTM (1991). Normas profissionais para o ensino da Matemática. Lisboa: Associação de professores de Matemática e Instituo de Inovação Educacional.
PAVANELLO, Regina Maria, O Abandono do Ensino da Geometria no Brasil: Causa e Consequências. Revista ZETETIKÉ – Editorial – ano1 – n.1 – mar. 1993, p. 7-18.
PAVANELLO, Regina Maria, Por Que Ensinar /Aprender Geometria? Universidade Estadual de Maringá.
PORQUE ENSINAR/APRENDER GEOMETRIA? Disponível em: www.sbempaulista.org.br/epem/anais/mesas_redondas/mr21-regina.doc. Revista – Sociedade Brasileira de Educação Matemática. Rio de Janeiro, n. 4, p.3-13,
TAHAN, Malba. Didática da Matemática 1967, p.31.
[1] Estudiante de doctorado en Educación en UNR-Argentina, Profesor de Matemáticas y Policía Criminal de MT.
[2] Doctorado en Educación; especialista en Gestión Escolar y Gestión de Personas; Graduación en Inglés Portugués/Inglés y su literatura, licenciatura y licenciatura en Educación Física.
[3] Estudiante de doctorado en Educación en la Universidad Nacional de Rosario – Unr, Argentina, tiene un título en Letras – Inglés de Castelo Branco College (2006). Derecho y Filosofía. Especialización en Lengua Inglesa.
[4] Estudiante de doctorado en Educación en la Universidad Nacional de Rosario – UNR Argentina. Graduado en Letras Vernáculas por la UFBA – Universidad Federal de Bahía. Posee un posgrado y currículo, didáctica y evaluación de la Universidad Estatal de Bahía – UNEB, Postgrado en Metodología de Enseñanza de Lengua Portuguesa y literatura de la Facultad Regional de Filosofía, Ciencias y Letras de Candeias- Bahía. Formación en español certificada por DUCLE – ARGENTINA. Profesor de español y portugués. Gerente del Colegio Estatal Profesor Maria Leal Lopes, Nova Ibia – Bahía.
[5] Estudiante de doctorado en Educación en la Universidad Nacional de Rosario – UNR Argentina, Licenciatura en Letras. Universidad del Estado de Bahía, UNEB y pedagogía por la Facultad Regional de Filosofía, Ciencias y Letras de Candeias- Bahía. Máster Profesional en Teología. Escuela Superior de Educación, EST, Brasil. Especialización en Estudios Linguísticos y Literarios. Universidad Federal de Bahía – UFBA. Especialización en Planificación y Gestión de Sist. Educ. Distancia. Universidad Estatal de Bahía, UNEB. Especialización en Metodología de Educación Superior. Facultades Integradas de Patos – FIP, Especialización en Metodología Docente para la Educación Profesional, UNEB-BAHIA. Brasil. Formación en español certificada por DUCLE – ARGENTINA.
[6] Graduado en Letras Portuguesas e Inglesas por UEG, post graduado en enseñanza de educación superior, de Ucan Rj; posgrado en tecnología en educación de Puc Río de Janeiro y postgrado en metodología de escuela primaria de la UFG. Asistiendo al Doctorado en Educación en UNR argentina.
[7] Licenciado en Geografía por la Universidad Católica de Salvador. Año 1987. Se graduó en Metodología de la Enseñanza de Geografía. Doctor en Educación por la Universidad Nacional de Rosario -UNR Argentina.
Enviado: Julio, 2020.
Aprobado: Octubre de 2020.