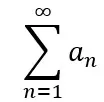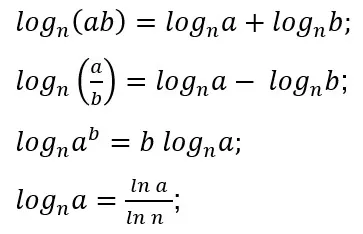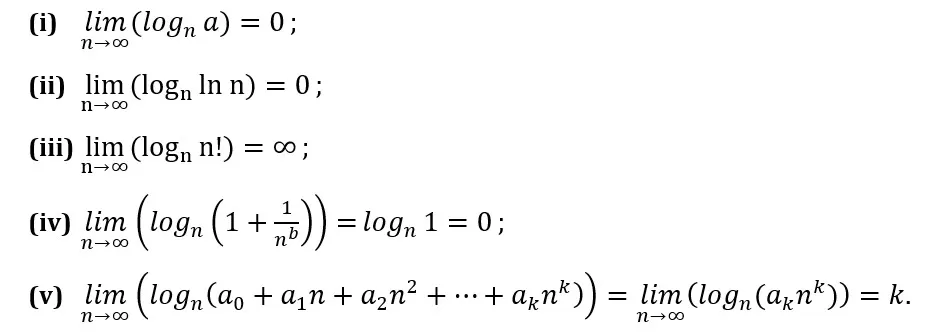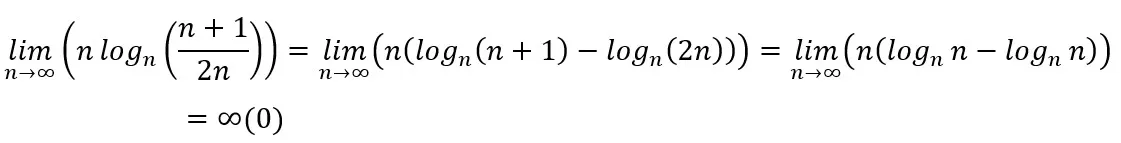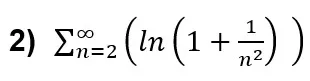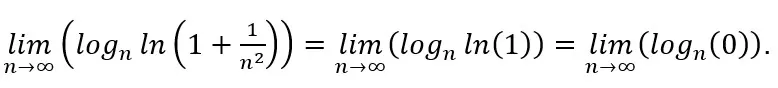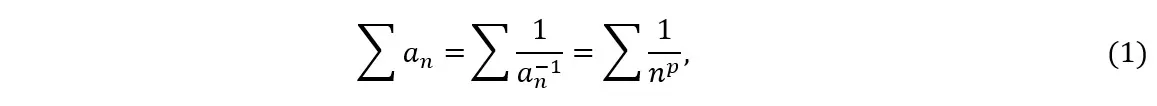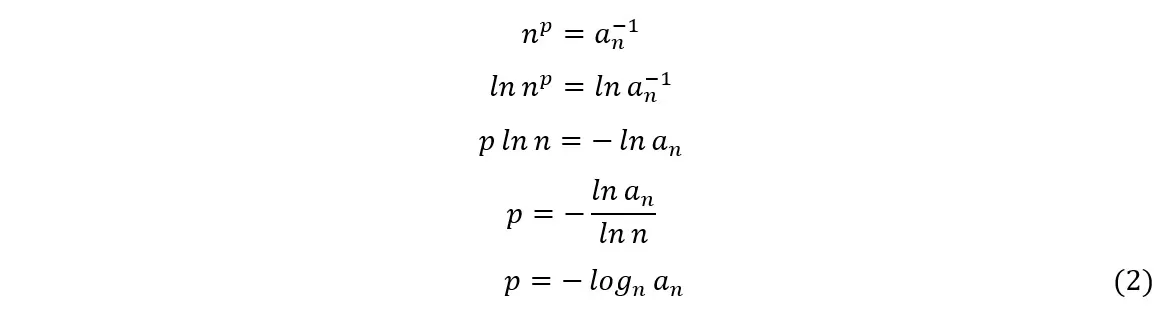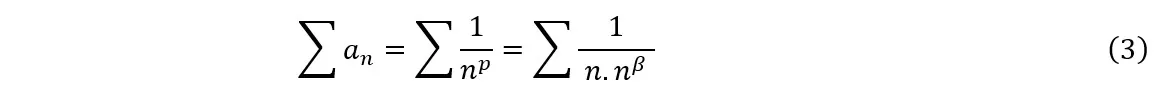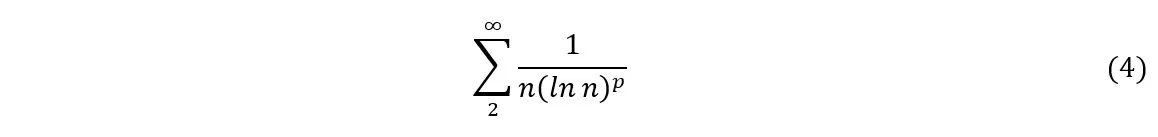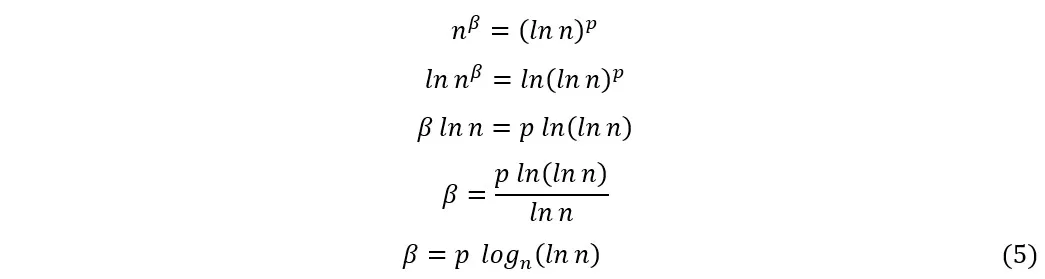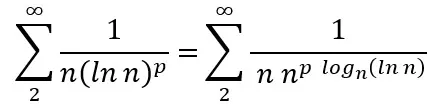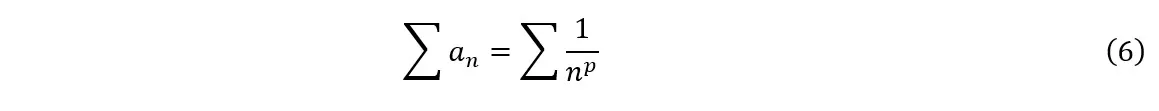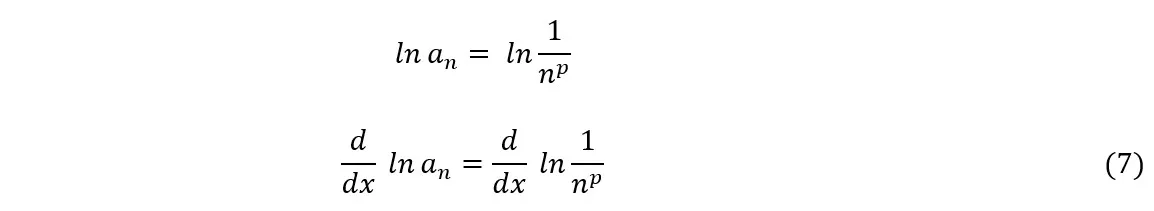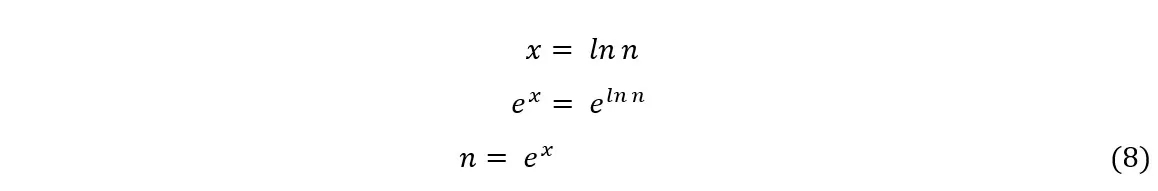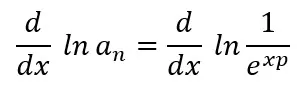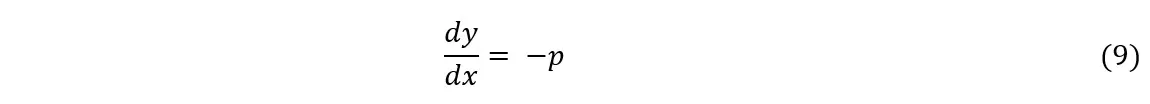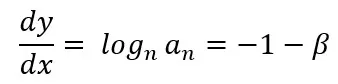Prueba del logaritmo enésimo para verificar la convergencia absoluta de series

ARTÍCULO ORIGINAL

MORAIS, Cláudio Marcelo ^[1]

MORAIS, Cláudio Marcelo. Prueba del logaritmo enésimo para verificar la convergencia absoluta de series. Revista Científica Multidisciplinar Núcleo do Conhecimento. Año 08, Ed. 09, Vol. 01, pp. 78-97. Septiembre de 2023. ISSN: 2448-0959, Enlace de acceso: https://www.nucleodoconhecimento.com.br/olimpiada-de-matematica/prueba-del-logaritmo, DOI: 10.32749/nucleodoconhecimento.com.br/olimpiada-de-matematica/prueba-del-logaritmo

RESUMEN

En este artículo presento una prueba de convergencia absoluta para series numéricas infinitas utilizando el concepto de logaritmo de base n indeterminada. Aunque existen casos en los que esta prueba resulta de difícil aplicación y otros en los que se pueden obtener resultados inconclusos, debe ser considerada como un recurso adicional que los estudiantes de matemáticas pueden utilizar junto con las pruebas ya disponibles para verificar la convergencia absoluta de una serie.

Palabras clave: Convergencia, Series, Prueba.

1. INTRODUCCIÓN

En los cursos de cálculo, al enfrentarse con el estudio de series infinitas, al estudiante se le presentan una variedad de pruebas para verificar si una serie numérica converge hacia un valor determinado o si diverge, es decir, si la suma de sus términos tiende hacia un valor finito (L) o tiende hacia más infinito o menos infinito, cuando el número de términos (n) de la serie también tiende hacia infinito (∞).

Una serie infinita consta de una secuencia de términos ordenados, generalmente en orden decreciente, sumados entre sí. Una serie infinita, o simplemente una serie, se puede expresar en la forma:

Donde los puntos suspensivos al final indican que los términos de la serie continúan a medida que n tiende al infinito. La serie también se puede expresar de manera más compacta utilizando la notación sigma:

A través del análisis del término general podemos saber si la serie converge o no. Para ello, se han desarrollado numerosas pruebas de convergencia, como el test de comparación, el test de la razón, el test de la integral, el test de la raíz, entre otros (Simmons, 1996). Mi propuesta en este artículo es presentar una prueba que sirva como una opción adicional al alcance del estudiante de matemáticas para determinar la convergencia absoluta de una serie numérica infinita.

2. LOGARITMO DE BASE N

2.1 DEFINICIÓN DE LOGARITMO ENÉSIMO

El concepto de logaritmo fue introducido por el matemático escocés John Napier en 1614 y puede considerarse uno de los mayores avances científicos del siglo XVII, facilitando la vida de aquellos que necesitaban realizar cálculos numéricos en una época en la que no existían calculadoras disponibles. En este sentido, su importancia ha sido comparada con el avance proporcionado por el sistema numérico decimal desarrollado por los indios (Hobson, 1914). A pesar de que la llegada de computadoras y calculadoras electrónicas ha cambiado la forma en que las personas realizan cálculos, el logaritmo, estudiado como una función, todavía conserva su importancia teórica esencial para las matemáticas y sus aplicaciones (Simmons, 1996). La función logarítmica puede describirse en la forma

donde x es un número real positivo, llamado logaritmando, yes un número real positivo y distinto de 1, llamado base del logaritmo. El valor deacaba por nombrar el tipo de logaritmo: para, tenemos el logaritmo de base dos; para , tenemos el logaritmo de base 3, y así sucesivamente. Los logaritmos de base 10 y base e, debido a su importancia, reciben nombres especiales: el logaritmo de base 10 se llama logaritmo decimal o logaritmo común, mientras que llamamos logaritmo natural o neperiano al de base , donde e es un número irracional que tiene un valor aproximado de 2,718281828.

Definiremos el logaritmo de base, o logaritmo enésimo, de un número, como el logaritmo de base indeterminada. Así, si es un número real, podemos escribir

A diferencia de lo que sucede con los logaritmos de base determinada, no es posible obtener el valor del logaritmo enésimo de un número, ya que es desconocido. A primera vista, esto puede no parecer muy útil, pero el propósito aquí es utilizar el logaritmo enésimo para realizar operaciones sobre los términos generales de las series, donde se convierte en la variable indexada por el operador sigma. De esta manera, intentaremos implementar un método para probar si una serie converge o no, aprovechando las propiedades operativas de los logaritmos cuando sea posible.

2.2 OPERACIONES CON LOGARITMOS ENÉSIMOS

El logaritmo de base enésima posee las mismas propiedades operativas que los demás logaritmos, ya que siguen las reglas del producto, del cociente, de la potencia y del cambio de base, como se indica a continuación:

3. PRUEBA DE CONVERGENCIA

3.1 DESCRIPCIÓN DE LA PRUEBA

A partir de ahora, propondremos una prueba para verificar la convergencia absoluta de series basada en el uso del logaritmo enésimo. De esta manera, dada una serie infinita de términos no negativos, comenzaremos por encontrar el logaritmo enésimo de su término general a_n y, si la variable n todavía está presente, calcularemos el límite de ese logaritmo, con n ttendiendo al infinito, si dicho límite existe. Dicho esto, la prueba se llevará a cabo de la siguiente manera:

La aplicación de la prueba sin la necesidad de utilizar límites solo ocurrirá en aquellos raros casos en los que el término general de la serie esté compuesto únicamente por potencias de n con exponentes numéricos. En otros casos, inevitablemente tendremos que recurrir al uso de límites. Es interesante notar que al usar la forma log_n(a_n) en lugar de la forma equivalente ln (a_n)/ln n, a menudo podremos calcular el límite del término general aplicando las propiedades de los logaritmos, evitando caer en una indeterminación del tipo ∞/∞. Sin embargo, en otras ocasiones, al calcular el logaritmo enésimo del término general, aún llegaremos a algún tipo de indeterminación, de modo que no será posible conocer el valor del límite. En estos casos, será necesario aplicar la regla de L’Hôpital al logaritmo enésimo en la forma equivalente ln (a_n)/ln n para eliminar la indeterminación, pero este procedimiento generalmente es laborioso a tal punto que no se recomienda seguir adelante, ya que es probable que uno o más de los tests conocidos sean más apropiados para probar la convergencia de la serie.

3.2 ALGUNOS EJEMPLOS DE USO DE LA PRUEBA

3.2.1 CÁLCULO DIRECTO DE log_n a_n

En los casos más simples, el término general (a_n) está compuesto únicamente por la variable n elevada a alguna potencia numérica entera o fraccionaria. De esta manera, no será necesario calcular ningún límite para aplicar la prueba de convergencia.

3.2.2 CASOS EN LOS QUE EL LÍMITE DE log_n a_n ES FÁCIL DE CALCULAR

Destacaremos ahora algunos casos en los que los límites del logaritmo enésimo del término general son relativamente fáciles de calcular, es decir, consideraremos casos en los que no haya indeterminación en el cálculo de los límites y donde aparezca uno de los siguientes resultados triviales:

Estos resultados pueden ser fácilmente obtenidos por el estudiante, ya que en (i) el valor del logaritmo de una constante (a) tiende a cero a medida que n tiende al infinito. En el caso (ii), donde la constante es reemplazada por el logaritmo natural de n, el valor de ln n crece mucho más lentamente que n, de modo que el logaritmo enésimo también tiende a cero. En el caso (iii) ocurre lo contrario, ya que n! crece demasiado rápido en comparación con n, lo que hace que el logaritmo tienda finalmente al infinito. En (iv), la fracción tiende a cero a medida que n tiende al infinito. Por último, en (v), el término de mayor grado del polinomio determina el comportamiento final del límite a medida que n tiende al infinito. Veamos algunos ejemplos.

3.2.3 ALGUNOS LÍMITES NOTABLES

En el cálculo del límite de log_n a_n es muy común encontrarse con una indeterminación del tipo (∞)(0). Para abordar esta indeterminación, a continuación se presentan algunos resultados que se pueden recordar fácilmente y que nos permitirán aplicar el test del logaritmo enésimo a una gran cantidad de series de manera bastante directa. Veamos:

En el caso (i), el límite también es fácil de obtener, ya que n crece asintóticamente más rápido que , a medida que n tiende al infinito. Por lo tanto, si a no es igual a 1, lo que haría que el logaritmo sea igual a cero para todo n, el logaritmo proporcionará un signo positivo o negativo para el límite, dependiendo de si a es mayor o menor que 1. En (ii), aunque el comportamiento del límite puede no ser tan evidente como en (i), se puede decir que el exponente p está asociado con la rapidez con la que el límite tiende a cero, mientras que b está asociado con la rapidez con la que el límite tiende al infinito. El mismo razonamiento se aplica al caso (iii). Veamos algunos ejemplos:

3.3 ALGUNAS OBSERVACIONES

(i) Existen casos en los que un simple cambio en el orden de las operaciones puede eliminar una indeterminación. Veamos un ejemplo:

En un primer intento, aplicamos la propiedad del logaritmo del cociente antes de calcular el límite, llegando así a una indeterminación:

Por otro camino, calculamos primero el límite dentro de paréntesis y luego utilizamos el resultado visto en el ítem 3.2.3 (i) y comprobamos que la serie converge:

(ii) En algunas situaciones, al calcular el límite de, aplicando las propiedades de los logaritmos, llegaremos a log_n0 o a alguna indeterminación, como la diferencia entre infinitos, el producto de infinito por cero, el cociente entre infinitos, el cociente entre ceros o la razón entre cero e infinito. Sin embargo, esto no significa necesariamente que el límite no exista. Esto simplemente significa que la prueba del logaritmo enésimo no es una forma práctica de determinar la convergencia o no de la serie, ya que para ello sería necesario aplicar la regla de L’Hôpital al logaritmo enésimo en su forma ln(a_n)/ln(n), incluyendo las manipulaciones algebraicas necesarias. En estos casos, a menudo encontraremos una prueba existente que es menos laboriosa de aplicar. Por ejemplo, sabemos que la siguiente serie converge a aproximadamente 1,29686:

Aplicando el test del logaritmo enésimo y trabajando solo con las propiedades de los logaritmos, se obtiene el siguiente resultado:

Sin embargo, después de aplicar la regla de L’Hôpital a ln(a_n)/ln(n) y realizar algunas operaciones que involucran límites, encontramos que:

Por lo tanto, la serie converge como se esperaba. La convergencia de esta serie puede verificarse más fácilmente aplicando la prueba de comparación con límite.

4. DISCUSIÓN DE LA PRUEBA

4.1 DEDUCCIÓN

La presente prueba consiste básicamente en realizar la prueba de comparación con la serie mediante el uso del logaritmo de base enésima, con la esperanza de obtener una facilidad de cálculo donde se puedan utilizar las propiedades operativas de los logaritmos (ver sección 2.2), ya sea a través de la aplicación directa de esas propiedades o en conjunto con la noción de límite de una función. Para iniciar nuestra deducción, consideremos los casos en los que es posible calcular directamente el logaritmo del término general (ver 3.2.1). En primer lugar, escribamos el término general como el inverso de una potencia de n:

Donde n es un número entero y p es un número real. A partir de las igualdades anteriores, obtendremos:

Sustituyendo (2) en (1), obtendremos:

Como sabemos (Simmons, 1996), si p>1, la serie converge. Si p≤ 1, la serie diverge. Finalmente, sustituyendo p por — en estas desigualdades y multiplicando ambos lados por , obtendremos que la serie:

4.2 CUANDO LA PRUEBA ES INCONCLUYENTE

En la sección 3.2.1, vimos los casos en los que se calcula directamente log_n a_n é Sin embargo, como vimos inmediatamente después, a menudo quedaremos con la variable n después de calcular el logaritmo enésimo del término general de una serie dada. El uso de la noción de límite nos permite extender la aplicabilidad de la prueba, ya que cuando calculamos el límite del logaritmo a medida que n tiende al infinito, podemos utilizar el valor de este límite como el resultado de la prueba para determinar si la serie converge o no (ver sección 3.1). Sin embargo, esta ventaja tiene un cierto precio, ya que hay casos en los que este límite nos proporciona un resultado que hace que la prueba sea inconclusa.

El hecho de que una serie converja o no depende de la rapidez con la que el término general tiende a cero (Simmons, 1996). Si ordenamos las series desde aquellas que convergen más rápidamente, pasando por aquellas que convergen cada vez más lentamente, luego hacia las series que divergen más lentamente y avanzando hacia las que divergen cada vez más rápido, podemos definir el intervalo entre las series como el intervalo donde ocurre la transición de series convergentes a series divergentes. Escribamos las series de este intervalo usando un exponente auxiliar β, de manera que β sea una función de n, como sigue:

Así que si, entonces tenemos p>1 y la serie converge. Si , entonces tenemos p<1 y la serie diverge. Sin embargo, si, la convergencia o no de la serie dependerá de la velocidad con la que β tienda a cero, es decir, la serie convergerá siempre que β tienda a cero lo suficientemente rápido. Por ejemplo, mediante el test de la integral (Simmons, 1996), se puede verificar que la siguiente serie diverge para p=1 y converge para p>1:

Calculando el exponente β para esta serie, obtendremos:      

Sustituyendo (5) en (3) e igualando a (4), obtenemos:

Como se calculó en (5) es igual a cero para todo p, concluimos que para todo p. Pero, como sabemos, para ciertos valores de p la serie converge y, para otros, diverge. Por lo tanto, podemos ver que la prueba del logaritmo enésimo es inconclusa en estos casos[3], ya que tanto puede haber series convergentes como divergentes para las cuales la prueba resulta en —1. Veamos algunos ejemplos:

5. EL LOGARITMO ENÉSIMO COMO DERIVADA

Una forma muy interesante para que el estudiante pueda visualizar el comportamiento de una serie es mediante el uso de gráficos con escalas logarítmicas. En estos gráficos, las series cuyos términos generales están formados por potencias de n con exponentes exclusivamente numéricos se presentan como rectas, y cuanto más rápidamente una serie diverge, menor será la pendiente de esa recta. Así, las series que divergen rápidamente dan lugar a rectas que se acercan más a la horizontal en comparación con las rectas trazadas a partir de las series que divergen lentamente. Por otro lado, cuanto más rápido converge la serie, más inclinada será su recta en el gráfico, es decir, estará más cerca de la vertical que otras que convergen más lentamente. En cambio, los gráficos de las series cuyos términos generales presentan exponentes que son funciones de la variable indexada n, generalmente se presentan inicialmente como curvas exponenciales, pero a medida que n tiende al infinito, los gráficos se acercan a líneas rectas. El gráfico de la figura 1 a continuación fue trazado con ejes en escala logarítmica natural e ilustra algunos ejemplos de lo que se ha dicho. En él, las series convergentes están indicadas con cv y las divergentes con dv. A simple vista, se puede observar cómo las dos series más a la izquierda, con exponente n, convergen rápidamente, acercándose a la vertical, mientras que en la parte superior tenemos algunas series que divergen.

Figura 1: Gráfico de la Figura 2: Gráfico de ln a_n vs. ln n para algunas series

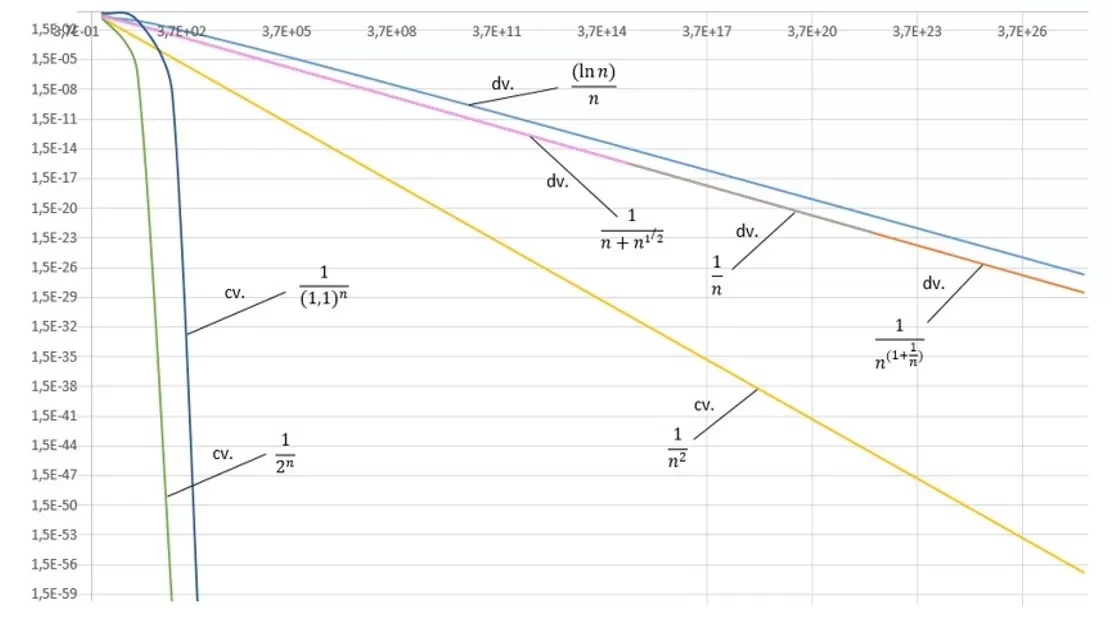
Cuanto más rápidamente la serie diverja, más cerca estará su recta en el gráfico de la horizontal. También se nota cómo dos de las series presentadas, que contienen exponentes fraccionarios, divergen de manera prácticamente idéntica a la serie de término general 1/n, lo que muestra cómo el exponente fraccionario tiene muy poco impacto en el comportamiento de esas series. Personalmente, creo que este tipo de visualización puede ser una herramienta útil desde el punto de vista educativo al introducir el concepto de convergencia de una serie. Ahora veamos cómo el logaritmo enésimo está relacionado con este tipo de gráfico.

En la figura 2 tenemos el gráfico de ln a_n versus ln n, donde la curva representa la progresión de los términos de una serie a medida que n tiende al infinito, y cuya forma general ya se ha visto anteriormente, que se da por:

Figura 2: Gráfico ln a_n vs. ln n

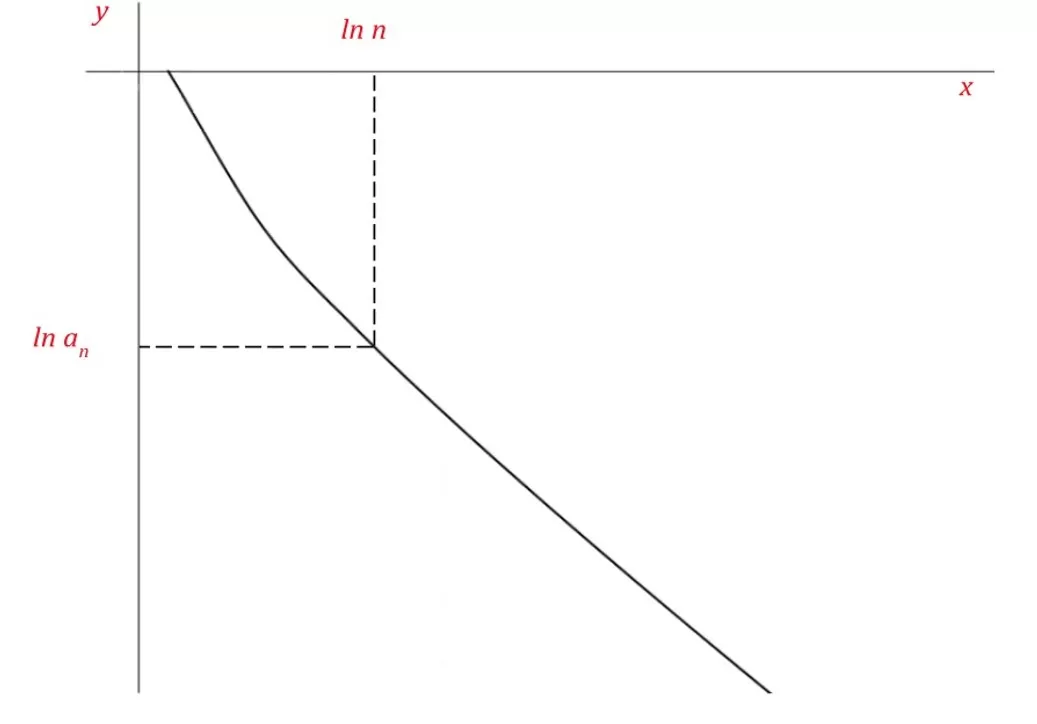
Tomando el término general y calculando la derivada del logaritmo natural en ambos lados, obtendremos

A partir del gráfico, tomando x = ln n, obtendremos

Sustituyendo (8) en (7), obtenemos:

Finalmente, sustituyendo ln a_n por y y calculando la derivada del término a la derecha, obtendremos:

Sin embargo, ya sabemos que el logaritmo enésimo del término general en (6) es, por lo tanto, podemos escribir:

Es decir, el logaritmo enésimo del término general es igual a la derivada de la curva de la serie en el gráfico de ln a_n x ln n. Si sustituimos p por 1+β, donde β es una función de n, podemos escribir:

Al calcular y encontrar un valor real δ, significa que el gráfico tiende a una recta con un coeficiente angular . Por lo tanto no tienda a , el logaritmo enésimo nos proporcionará el coeficiente angular de la recta que se forma en el gráfico ln a_n vs. ln n a medida que ln n tienda al infinito.

6. CONCLUSIÓN

El uso del logaritmo en base n para determinar si una serie infinita converge absolutamente o no puede ser una alternativa interesante a los métodos existentes, siempre y cuando el límite del logaritmo enésimo del término general de la serie, en caso de que sea necesario calcularlo, se pueda obtener de manera relativamente sencilla. Para aplicar la prueba, podemos utilizar no solo las propiedades operativas de los logaritmos, sino también algunos resultados básicos ya conocidos. En los casos en los que la indeterminación persista, se puede eliminar aplicando la regla de L’Hôpital al logaritmo enésimo del término general en la forma ln(a_n)/ln(n), pero en estos casos, generalmente el esfuerzo no valdrá la pena, ya que probablemente haya una o más pruebas ya conocidas que se pueden utilizar para determinar la convergencia de manera más rápida. Al trazar el gráfico de una serie con ejes en escala logarítmica natural, podemos ver que el logaritmo enésimo del término general en un punto cualquiera del gráfico no es más que la derivada de la curva en ese punto.

REFERENCIAS

HOBSON, Ernest William. John Napier and the invention of logarithms. Cambridge: The University Press, 1914.

SIMMONS, George Finlay. Calculus with analytic geometry. 2. ed. New York: McGraw-Hill, 1996.

APÉNDICE – NOTA AL PIE

2. En la sección 4.2 discutiremos mejor esta condición.

3. Este caso, aunque presenta solo una familia específica de series formadas a medida que se varía el exponente p, es una condición suficiente para demostrar la naturaleza inconclusa de la prueba cuando su resultado, obtenido a través del límite, es . Sin embargo, sería interesante mostrar que el caso n(ln n)^p, con p>1, no es una excepción, es decir, mostrar que existen otras series convergentes cuyo logaritmo enésimo del término general es , ya que encontrar series que divergen es relativamente fácil.

^[1] Graduado en Física por la Universidad Federal de Minas Gerais (2000); Especialización en Instrumentación y Control de Procesos por el Servicio Nacional de Aprendizaje Industrial-SENAI; Licencia profesional de Técnico en Electrónica por el Instituto Monitor S/C Ltda. ORCID: 0009-0001-4633-3914. Currículo Lattes: http://lattes.cnpq.br/9333737637565760.

Enviado: 10 de julio de 2023.

Aprobado: 23 de agosto de 2023.