Demostración de la conjetura del número impar imperfecto

ARTÍCULO ORIGINAL

SANTOS, Adecio da Silva ^[1]

SANTOS, Adecio da Silva. Demostración de la conjetura del número impar imperfecto. Revista Científica Multidisciplinar Núcleo do Conhecimento. año 04, Ed. 05, Vol. 07, páginas 176-185. Mayo de 2019. ISSN: 2448-0959.

RESUMEN

Entre los 48 problemas abiertos (Conjeturas) de las matemáticas en el área de la Teoría de Números, la Conjetura de Números Impares Perfectos que se probarán en este artículo. El método que usamos para la prueba fue la demostración de la reducción al absurdo. Y modificamos deliberadamente el nombre del problema para La conjetura de número impar imperfecto, porque nos pareció más consistente con la solución encontrada. Además dejamos en anexo una lista de varios problemas abiertos de las matemáticas.

Palabras clave: Conjetura, Demostración, Extraño Perfecto.

1. INTRODUCCIÓN

La generación del siglo XXI está llena de innovaciones tecnológicas, que nos permiten conocer prácticamente todo el mundo, y comunicarnos “instantáneamente” desde cualquier parte del planeta.

Las matemáticas jugaron un papel muy importante en la construcción como una sociedad actual. Su precisión y precisión de sus resultados no deja margen de error. Pero si lo dejas quieto, es intencional.

Una ciencia como esta tan rica y soberana tiene una particularidad, no permite que el ego o la arrogancia tengan mucho espacio en la mente de sus eruditos, porque por mucho que pueda ser respetada, incluso admirada, en nuestros tiempos todavía hay problemas matemáticos que nadie en la historia ha sido capaz de probarlos todavía.

Aproximadamente 417 problemas están sin resolver en los más variados campos de las matemáticas. El lector interesado en conocerlos puede consultar la referencia (1). Pero enfatizamos que algunos de ellos nunca se pueden demostrar, aunque son ciertos, esto está garantizado por los Teoremas de Incompleto de Gédel.

Nuestro artículo expone la prueba de uno de estos problemas abiertos de las matemáticas, a saber, la Conjetura de Los Números Impares Perfectos, pero lo renombramos como la Conjetura del Número Impar Imperfecto porque encontramos esta frase más coherente con nuestro resultado.

Usamos tanto para el método de demostración por reducción al absurdo, la propiedad de la tricotomía y un resultado en el texto que llamamos propiedad: (P), además de algunas manipulaciones algebraicas.

Al final dejamos, en el ANEXO A, una lista muy ecléctica de varias conjeturas matemáticas.

2. MARCO TEÓRICO

En esta parte damos crédito a las referencias que contribuyeron significativamente a la preparación de nuestro artículo.

Que eran la referencia (2), porque nos proporcionó la base del razonamiento lógico matemático para que pudiéramos encontrar el resultado final de la obra apoyada por argumentos lógicamente coherentes. Esta referencia también nos hizo caminar desde el principio hasta el final de la demostración a través de los principios de la no contradicción y la tercera excluida que fueron nuestras dos “piernas” hasta que llegamos a nuestro resultado.

También era importante hacer referencia (3) porque proporcionaba una madurez a través de sus ejercicios para que pudiéramos tener un camino de cómo atacar el problema bajo análisis en este artículo mediante el método de demostración mediante la reducción al absurdo.

Finalmente, dejamos las referencias (4), (5) y la lista de problemas en el ANEXO A al lector interesado en aprender más sobre la Conjetura de Perfect Odd Numbers, además de otras conjeturas de La Teoría de Números y más problemas de los diversos campos de las matemáticas.

3. CONJETURA DE NÚMERO IMPAR IMPERFECTO

El campo de los estudios matemáticos conocido como Teoría de Números tiene alrededor de 48 problemas abiertos. Entre ellos está lo que llamaremos la Conjetura del Número Impar Imperfecto. Sin embargo, este problema es más conocido como The Perfect Odd Numbers Conjecture. Y dice que no hay un número impar perfecto. Sin embargo, modificamos el nombre de la conjetura a propósito, porque nos pareció más consistente con nuestro resultado.

Según el portal www.matematica.br: “Un número se dice perfecto si es igual a la suma de sus propios divisores. Un número positivo N divisores son todos los divisores enteros positivos de N excepto el N sí mismo.” (6)

Hasta el día de hoy, se conocen números pares perfectos. Los matemáticos que más estudiaron este tema fueron Euclides, Euler y Descartes. Además, también se conoce una fórmula para todos los números pares perfectos. Fue estudiado por primera vez por Euclid y más tarde completado por Euler.

Las explicaciones resumidas de lo anterior se encuentran en varios documentos académicos. Pero según Jeane Barbosa Ferreira y Marcos Ferreira de Melo:

Euclides argumenta que si “q” es un número primo como 2_q-1que también es primo, entonces la fórmula n á n = 2^q-1(2^q-1)  genera números pares perfectos. Mucho después, Euler (1707-1783) demostró que cada número de par perfecto se obtiene mediante la receta anterior, estableciendo así la reciprocidad del teorema de Euclides. Vale la pena señalar que los números primos de la forma 2^q-1 se conocen como primos de Mersenne. (7)

Es por eso que la conjetura perfecta de números impares existe. Dado que el análisis de los números pares perfectos está muy avanzado. El primer matemático que mencionó la conjetura de los Números Impares Perfectos fue Descartes. Y hasta este artículo, nadie había probado o refutado aún la afirmación.

Nuestro artículo presenta una prueba de la Conjetura de Perfect Odd Numbers, y para ello utilizamos la definición de número perfecto, un resultado que se muestra en el texto que llamamos propiedad (P), propiedad de la tricotomía y algunas manipulaciones algebraicas. Todo ello en una construcción lógica basada en la técnica de demostración mediante la reducción al absurdo.

Dejamos debajo de la expresión de la conjetura y su demostración.

Además, si hay algún error en la evidencia, nos gustaría que los lectores profundizaran en sus estudios para mostrarlo y solucionarlo. Cada contribución es bienvenida.

Conjetura de número impar imperfecto: No hay un número impar perfecto.

DEMOSTRACIÓN: Primero probamos que todo número natural perfecto, N, tiene la propiedad (P): 1+d₁+d₂+d₃+…+d_n-1, dónde 1< d₁< d₂< d₃< …<d_n-1<d_n son todos los divisores propios de N.

De hecho, tenga en cuenta que N = 1+d₁+d₂+d₃+…+d_n-1+d_n, porque N es un número perfecto. Supongamos ahora, absurdamente, que 1+d₁+d₂+d₃+…+d_{n-1 <} d_n y sumando, en ambos miembros de la desigualdad anterior, el término d_n encontramos la siguiente expresión 1+d₁+d₂+d₃+…+d_n-1+(d_n)<d_n+(d_n)⇒1+d₁+d₂+d₃+…+d_n-1+(d_n)<2d_n. Entonces tenemos que d_n<1+d₁+d₂+d₃+…+d_n-1+(d_n)<2d_n⇒d_n<N<2d_n⇒1<<2. Sin embargo, como dn divide N encontramos lo natural entre 1 y 2. ¡Lo cual es ABSURDO!

Por otro lado, supongamos que es absurdo, pero solo que esta vez la desigualdad es
d_n<1+d₁+d₂+d₃+…+d_n-1. Ahora, agregando, en ambos miembros de la desigualdad anterior, el término d_n encontramos d_n+(d_n)<1+d₁+d₂+d₃+…+d_n-1+d_n lo que implica en  2d_n<1+d₁+d₂+d_n+…+d_n-1+(d_n), o sea ,2d_n<N (I) . También tenga en cuenta que ≤d_n⇒N≤d₁.d_n (II), porque d_n es el mayor divisor de N. Entonces de (I) y (II) es
2d_n<N≤d₁.d_n, dividiendo todos los miembros de la última desigualdad por d_n tenemos
2<≤d₁ (III), pero como d₁ es el divisor más pequeño de N distinto de 1 e es un divisor de N desigualdad (III) nos proporciona que =d₁⇒N=d₁.d_n es que  2<d₁, así que esto significa que todos los divisores de son impares, porque si hubiera algún divisor de ser par entonces 2=d₁, lo cual es absurdo en nuestra suposición. A partir de aquí tenemos 4 (cuatro) situaciones para analizar:

1ra situación: d₁ dividir d_i ∀i= 1,2,3,4,…,n, porque d₁ es el divisor más pequeño de N. Y esto implica que d_i=d₁ⁱ ∀=1,2,3,4,…,n, porque si hubiera alguno d_i que no sea el poder d₁ entonces esto generaría un nuevo divisor de N distinto de d_i ∀=1,2,3,4,…,n, lo cual es absurdo. Entonces esta situación significa que 1+d₁²+d₁³+d₁⁴+…+d₁ⁿ=N=d_{1 .} d_n=d₁.d₁ⁿ=d₁ⁿ⁺¹, pero por la fórmula de la suma de un P.G finito tenemos 1+d₁²+d₁³+d₁⁴+…+d₁ⁿ=1+d₁²., o sea,1+d₁².=d₁ⁿ⁺¹⇒1+= d₁ⁿ⁺¹⇒= d₁ⁿ⁺¹⇒ d₁-1+d₁ⁿ⁺¹–d₁² = (d₁-1).d₁ⁿ⁺¹=d₁ⁿ⁺²–d₁ⁿ⁺¹ ⇒d₁-1+d₁ⁿ⁺¹–d₁²=d₁ⁿ⁺² – d₁ⁿ⁺¹, entonces tenemos que  d₁+2d₁ⁿ⁺¹ – d₁² –d₁ⁿ⁺² =1⇒d₁(1+2d₁ⁿ–d₁–d₁ⁿ⁺¹)=1⇒d₁ divide 1, absurdo!

2da situación: d₁ divide algunos d_j y otros no paran j=1, 2, 3, 4,…,n. Entonces tenemos que N=1+(d₁+d_j1+d_j2+…+d_jk) + (d_i1 +…+d_im ), Dónde d₁ ,d_j1 ,d_j2 ,…,djk son los números divisibles por d₁ e d_i1 ,…,d_im no son. Y los numeros 1,d₁ ,d_j1 ,d_j2 ,…,d_jk ,d_i1 ,…,d_im son todos los divisores propios de N.

Digamos que la potencia más alta _de d1 que divide N es ^d1n. Así que podemos reescribir todos los divisores de cómo:

1, (d₁, d₁², …, d₁ⁿ), (d₁d_i1, d₁d_i2, …, d₁d_im), (d₁²d_i1, d₁²d_i2, …, d₁²d_im), …, (d₁ⁿd_i1, d₁ⁿd_i2, …. d₁ⁿd_im), (d_i1,d_i2, …, d_im).

Por lo tanto, con esta nueva escritura, tenemos que añadir los divisores de N es:

N=1+(d₁+d₁²+…+d₁ⁿ) + (d₁d_i1+…+d₁d_im) +(d₁²d_i1+…+d₁²d_im)+ … …+(d₁ⁿd_i1+…+d₁ⁿd_im) + (d_i1+d_i2+…+d_im)

= 1+(d₁+d₁²+…+d₁ⁿ)+(d₁+d₁²+…+d₁ⁿ)d_i1+…+(d₁+d₁²+…+d₁ⁿ)d_im++(d_i1+d_i2+…+d_im)

=1+(d₁+d₁²+…+d₁ⁿ) + (d₁+d₁²+…+d₁ⁿ)(d_i1+…+d_im)+(d_i1+…+d_im)

=1+(d₁+d₁²+…+d₁ⁿ) +(d₁+d₁²+…+d₁ⁿ+1) . (d_i1+…+d_im)

=(1+d₁+d₁²+…+ d₁ⁿ) . (1+d_i1+…+d_im)

Mas N=d₁.d_n=(1+d₁+d₁2+…+d₁n) . (1+d_i1+…+d_im)^, y esto implica que

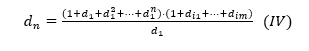
Por otro lado, d_n=d₁^{n .} d_im^* (V) , dónde d_im^* es el número más grande entre d_i1, …, d_im.

Finalmente, por (IV) y (V) tenemos:pero esto nos da que N = (1+d₁+d₁²+…+d₁ⁿ) . (1+d_i1+…+d_im) = d₁ⁿ⁺¹ . d_im* ,ie , d₁ⁿ⁺¹,sería un divisor de n sí mismo que no estaría en nuestra lista de divisores propios de N. ¿Qué es un, ABSURD!

3a situación: d₁ no comparte ningún d_j, pero tiene factores primos en común con algunos d_j para j.2, 3, 4,…, n. Esto implica que estos factores primos en la división común N y sería más pequeño que d₁ que es el divisor N más pequeño y absurdo!

Situación 4: d₁ no divide ningún d_j, por otra parte, d₁ y d_j no tienen factores primos en común para todos los j.2, 3, 4, …, n.

Así como N-d₁ . d_n, tenemos que d₂, d₃, d₄, …, d_n-1 dividir d_n, porque no comparten
d₁ por el hecho de ser  d₁ el divisor más pequeño de N. Ahora, observe que
 ≠ d₁ ∀i= 1,3,4,5…,n , porque si = d_i para algunos d_i, esto implicaría que
d_n=d₂ . d_i⇒ N=d₁ . d₂ . d_i, pero cómo d₁ no tiene factores primos en común con no di _estamos obligados a aceptar d₁ . d₂ e d₁ . d_i como nuevos divisores de N, sin sentido! Porque todos los divisores n ya han sido listados, y lo mismo por nuestra 4a situación no es divisible por d₁. Es decir, es incluso diferente de todos los di, pero esto, también, generaría otro número que no está en la lista de todos los divisores de N, otra tontería!

Por tanto, mediante tricotomía, solo tenemos la opción 1+d₁+d₂+d₃+…+d_n-1=d_n.

Por último, supongamos, absurdamente, que hay un número impar perfecto, digamos 2k+1. Ahora, vamos a1<I₁<I₂<I₃<…<I_2n siendo todos los divisores 2k+1 ellos mismos. Tenga en cuenta que I₁,I₂,I₃,…,I_2n son números impares y en una cantidad par de números, porque la suma de una cantidad par de números impares es par y más 1 resulta en una extraña.

Pero por la propiedad (P), que hemos demostrado que es válido para cada número perfecto, tenemos a 1+I₁+I₂+I₃+…+I_2n-1=I_2n. Ahora, tenga en cuenta que este 1+I₁+I₂+I₃+…+I_2n-1 es par, ya que es la suma de una cantidad par de números impares (consideramos que el 1 es impar) y I_2n es impar. Es decir, encontramos un número natural que es par y extraño simultáneamente, ABSURD!

Por lo tanto, no hay un número natural impar perfecto.

4. CONSIDERACIONES FINALES

Nuestro artículo presenta una demostración de la Conjetura de Perfect Odd Numbers, pero el cambio de nombre de Imperfect Odd Conjecture debido a es más consistente con nuestro resultado. Pero las matemáticas han superado a estos muchos otros problemas abiertos. Y el objetivo principal de nuestro trabajo es animar a los lectores a tratar también de resolver problemas más abiertos en la zona. Conseguir con esto el aumento de investigadores en los más variados campos de las matemáticas en nuestro país.

En lo más esperamos sugerencias para la mejora de nuestro artículo, críticas constructivas, también. Y que nuestro artículo proporciona continuación para muchas otras obras académicas.

5.  REFERENCIAS

1. Portal do openproblemgarden. Disponível em: http://www.openproblemgarden.org/op/odd

_perfect_number. Acesso em 22 de abril de 2019.

2. ALENCAR FILHO, Edgard de. Iniciação à Lógica Matemática. 18 Ed. São Paulo: Nobel, 1975.

3. LIMA, Elon Lages Análise Real. vol. 1 Coleção Matemática Universitária, SBM,. Rio de Janeiro, 2001.

4. Canal A Matemaníaca por Julia Jaccoud. Disponível em: https://www.youtube.com/watch?v=

CHZBYfAmkcE. Acesso em 21 de abril de 2019.

5. Portal do Impa. Disponível em https://impa.br/noticias/problemas-do-milenio-da-geometria-a-fisica-quantica/. Acesso em 21 de abril de 2019.

6. Portal da matematica. Disponível em:http: //www.matematica.br/historia/nperfeitos.html. Acesso em 21 de abril de 2019.

7. Portal da ufc. Disponível em: http://www.periodicos.ufc.br/eu/article/view/15284/15570 Acesso em 22 de abril de 2019.

ANEXO A

LISTA DE CONJECTURAS MATEMÁTICAS

1. P versus NP

2. Conjetura de Hodge

3. Hipótesis de Riemann

4. Existencia de Yang-Mills y rango de masa

5. Existencia y suavidad de Navier-Stokes

6. Conjetura de Birch y Swinnerton-Dyer

7. Conjetura de Beal

8. Conjetura fermat-catalana

9. Conjetura de Goldbach (fuerte)

10. Conjetura de Collatz

11. Conjetura de Erdös

12. Conjetura del número del cuadrado mágico

13. Conjetura de Andrica

14. Conjetura de primos gemelos

15. Conjetura de Legendre

16. Problema de final feliz

17. Problema del círculo de Gauss

18. Problema de Galois inverso

19. Conjetura de Littlewood

20. Largas progresiones aritméticas del arco iris

21. Progresiones aritméticas monotónicas de 4 terminaciones

22. La conjetura de la doble capitalización

23. Conjetura de Beneš

24. Longitud del producto surrealista

25. Proyectos de cobertura combinatoria

26. Un punto cero en un mapeo lineal

27. Conjetura de partición amplia

28. Números de Ramsey en diagonal

29. La conjetura de la base aditiva

30. ¿Todos los números de Fermat están libres de cuadrados?

^[1]Graduado y máster en Matemáticas.

 

Enviado: Abril, 2019.

Aprobado: Mayo de 2019.