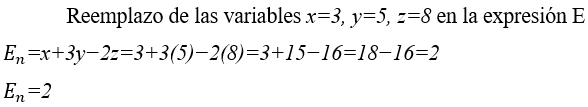La operación de armonización (H) y su operación de melodía inversa (M)

ARTÍCULO ORIGINAL

VIANA, Arnóbio Araújo ^[1]

VIANA, Arnóbio Araújo. La operación de armonización (H) y su operación de melodía inversa (M). Revista Científica Multidisciplinar Núcleo do Conhecimento. Año. 07, ed. 03, vol. 03, pág. 144-171. Marzo 2022. ISSN: 2448-0959, Enlace de acceso: https://www.nucleodoconhecimento.com.br/olimpiada-de-matematica/operacion-de-melodia

RESUMEN

La falta de una operación matemática para explicar las interacciones de las ondas, especialmente entre las ondas sonoras de las notas musicales, fue el problema que guió la construcción de este artículo. En este contexto, el objetivo de esta investigación, buscando una mejor visualización de una onda sonora simple, fue demostrar las operaciones desarrolladas por el autor de este material, compuesto por tres características más importantes para la Música: la amplitud, con frecuencia y el tiempo de duración. Así llegó la forma y, de esta forma, se analizan las estructuras musicales de una armonía y una melodía formadas por sus agrupaciones armónicas y melódicas, hasta obtener las propiedades operativas de estas organizaciones en sus fenómenos físicos. En la agrupación donde estas notas musicales se emiten simultáneamente, en el espacio o al mismo tiempo, las ondas sonoras se encuentran físicamente en Superposición, provocando interferencias entre ellas, originando así un efecto sonoro llamado por los músicos de Armonía. Evaluando esta estructura en el espacio y el tiempo, se desarrolló la operación matemática que provoca este fenómeno armónico, adoptando las operaciones fundamentales que surgieron, en esta interferencia integrada, una única operación especial, denominada Operación Armonización u Operación H. Como resultado de esta operación, también se desarrolló su funcionamiento inverso, donde las ondas de notas musicales se emiten de forma continua en el espacio o una tras otra en el tiempo, originando así un efecto sonoro denominado por los músicos como melodía. Analizando esta estructura en el espacio y el tiempo, también se desarrolló la operación matemática que origina este fenómeno, denominada Operación Melodiación u Operación M, sirviendo al propósito de esta investigación, que pretende dotar a la Ciencia de una visión matemática de las estructuras musicales de armonías y melodías musicales, proporcionando, en general, nuevas operaciones matemáticas, que pueden explicar fenómenos de la Naturaleza, simplificando su comprensión a la Ciencia.

Palabra clave: Armonización, Melodía, Armonía, Melodía.

1. INTRODUCCIÓN

A principios de 2006, el autor de este material desarrolló Operation Harmonization para los agrupamientos armónicos de ondas sonoras de las armonías de notas musicales y, Operación Melodiación, para los agrupamientos melódicos de ondas sonoras de sus melodías.

El problema que motivó la construcción de este material y el desarrollo de estas operaciones fue la falta de una operación matemática que explicara las interacciones de las ondas, especialmente entre las ondas sonoras de las notas musicales. En este contexto, el objetivo es demostrar las operaciones desarrolladas por el autor de este material, compuesto por tres características más importantes de la Música: la amplitud, con frecuencia y tiempo de duración .

Para el desarrollo de este, inicialmente, se consideró que sólo para las ondas sonoras y, posteriormente, en general, para cualquier otro elemento con o sin vibración, se presenta el fenómeno físico de “Superposición de Ondas”, donde, en el encuentro entre dos ondas, hay un aumento en la amplitud resultante entre ellas (SILVA, n.d.).

Usando la expresión, formulado en este estudio para representar una onda sonora, con las características: amplitud , frecuencia y tiempo de duración , es posible analizar de forma sencilla la interferencia entre dos ondas sonoras idénticas.

Cuando se encuentran en un punto común , cuando se encuentran en un lugar común , siendo la misma frecuencia, con la misma duración .

Evaluando el resultado de este fenómeno de interferencia, se observó que en el punto de encuentro p de la superposición entre estas dos ondas, además de la suma algebraica existente entre sus amplitudes , también existe la unión entre sus frecuencias en ese tiempo de duración, formando una sola onda sonora, con amplitud, frecuencia y tiempo de duración.

También se concluyó, en este análisis inicial, que estas dos operaciones, suma entre amplitudes y unión entre frecuencias, además de formar el resultado de este fenómeno, también integran una sola operación matemática, caracterizada por esta Dualidad Operacional. Esto explica la emisión simultánea de ondas de notas musicales, cuyo efecto sonoro se denomina Armonía. Por lo tanto, se admitió el nombre de Operación de Armonización u operación H, adoptando como símbolo matemático una barra inclinada izquierda (\), denominada operador H. Originándose, con este fenómeno, el Principio de Armonía, donde los elementos son armónicos, si existe una superposición entre ellos en su espacio-tiempo.

En consecuencia, se desarrolló su operación inversa, en la que las ondas sonoras salen de la condición de superposición y pasan a la condición ininterrumpida, donde el tiempo final de una onda es igual al tiempo inicial de la siguiente, etcétera, cuyo efecto de sonido es llamado Melodía por los músicos. Por lo tanto, se adoptó el nombre de Melodiación u operación M, con una barra diagonal derecha (/) como su símbolo matemático, llamado operador M, dando lugar al Principio de la Melodía, donde los elementos son melódicos, si hay continuidad entre ellos en sus espacios-tiempos.

2. HARMONIZATION OPERATION (H)

En términos generales, cuando dos o más ondas periódicas rítmicas, con diferentes frecuencias y amplitudes, están en funcionamiento Armonización o H , forman una agrupación armónica, llamada Armonía, donde la frecuencia resultante está determinada por la operación de unión entre sus frecuencias y la amplitud resultante por la operación de suma entre sus amplitudes, que pueden estar en la misma fase con signos iguales, en interferencia constructiva, o en fases opuestas con signos opuestos, en interferencia destructiva.

Cuantas más ondas de este tipo haya en esta operación, más frecuencias se unirán y más amplitudes añadidas en el resultado de esta Armonía , como se muestra en el siguiente ejemplo.

Operación Armonización y su Armonía entre tres ondas periódicas distintas y rítmicas:

 

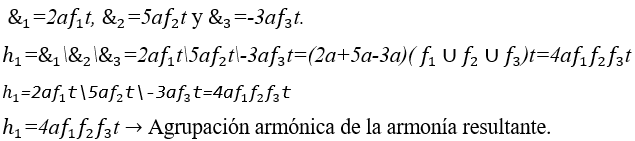
2.1 PROPIEDADES DE OPERACIÓN H (ARMONIZACIÓN)

2.2 ARMONÍA MUSICAL

En la operación de Armonización entre ondas sonoras, específicamente de notas musicales rítmicas, donde normalmente la armonía de un acorde musical principal está formada por una tríada o tres notas, con distintas frecuencias, el aumento de amplitud resultante es lineal (MORAIS, 2020).

Suponiendo que estas ondas son iguales y el hallazgo de que la intensidad del sonido humano es logarítmica con un valor de (SANTOS, s.d.), en este caso su adición es insignificante para ser notada . Si esta fracción se redondeará a uno, matemáticamente, es como si ella no existiera en esta armonía .

Debido a este fenómeno y considerando este redondeo, la armonía de esta operación se formó únicamente calculando la operación de unión entre sus frecuencias. Por lo tanto, para este resultado simplificado, no es necesario saber cuál es la intensidad del sonido a aplicarse en armonía con notas musicales en una operación H, ya que ésta puede ser cualquiera, sin perjuicio de la armonía de esta operación.

A continuación se describen algunas operaciones de H con notas musicales identificadas por sus números, donde las notas de A, B, C, D, E, F y G son respectivamente A, B, C, D, E, F, G, tomando como base la obra de Guest (2020, p. 33 a 41):

1) Cálculo de la armonía entre las notas musicales:, ambos con dos segundos de duración e intensidades sonoras normales.

2) Cálculo de la armonía entre las notas musicales: , los tres segundos de duración e intensidades de sonido normales.

3) Cálculo de la armonía entre las notas musicales: , todas intensidades de sonido normales y de un segundo de duración.

Nota: en este estudio se define que una armonía se nombra con sus frecuencias en orden ascendente y acento tónico en la última frecuencia. Por ejemplo,  es la armonía Ladomisol de un segundo de duración o un acorde de séptima menor menor  .

2.3 ARMONÍA UNITARIA

La Armonía Unitaria es el resultado de la operación H entre dos o más ondas periódicas iguales  , formando una agrupación armónica de una sola frecuencia , con su amplitud resultante y un tiempo de duración

Este tipo de armonía puede parecer, en este espacio-tiempo, que en su estructura sólo existe una onda periódica, sin embargo, en ella coexisten dos o más ondas periódicas iguales, ocupando el mismo espacio-tiempo, constituyendo un Conjunto Unitario Armónico capaz de generando, en su estructura unitaria, dos o más ondas periódicas continuas e iguales en un nuevo espacio-tiempo. A diferencia de un conjunto unitario simple formado por una sola onda, donde solo se genera una sola onda de su estructura.

De esta forma, dos o más armonías unitarias sólo serán iguales, se todas as suas características e quantidades forem iguais e, quando essa harmonia for formada somente por ondas sonoras de notas musicais, ela passa a ser considerada como uma Harmonia Uníssona , formando un solo sonido, con su frecuencia, amplitud y tiempo de duración , como se muestra en los ejemplos a continuación:

1) Armonía al unísono entre cuatro ondas rítmicas, con frecuencias iguales y amplitudes diferentes.

Gráfico 1: Armonía al unísono

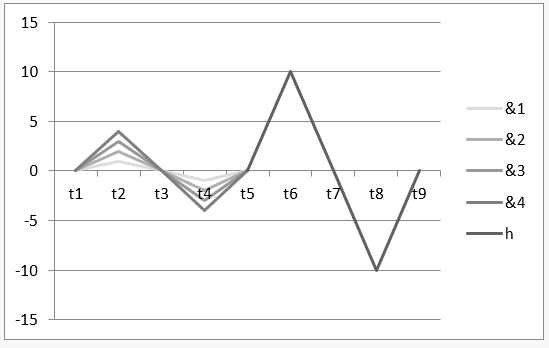
El gráfico 1 muestra el intervalo de tiempo hasta, que caracteriza la operación H  y, en el descanso de hasta, se demuestra el resultado de la operación o su armonía .

2) Armonía con interferencia destructiva entre dos ondas periódicas rítmicas:

Gráfico 2: Armonía con interferencia destructiva

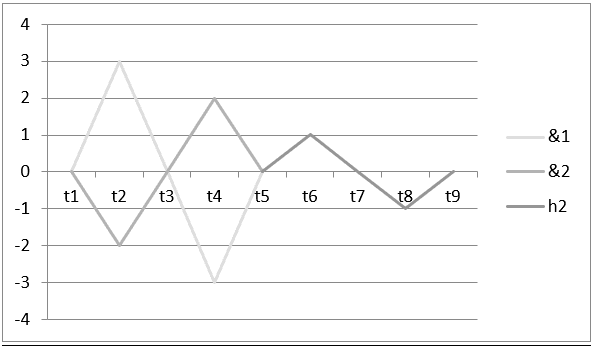
El intervalo de tiempohasta, que se muestra en el gráfico anterior, representa el resultado de la operación H  y, en el descanso de hasta, el resultado de esta operación o de su armonía se caracteriza .

3) Armonía constructiva y destructiva entre tres ondas:

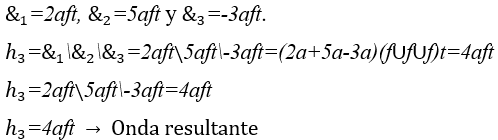
Gráfico 3: Armonía con interferencia constructiva y destructiva

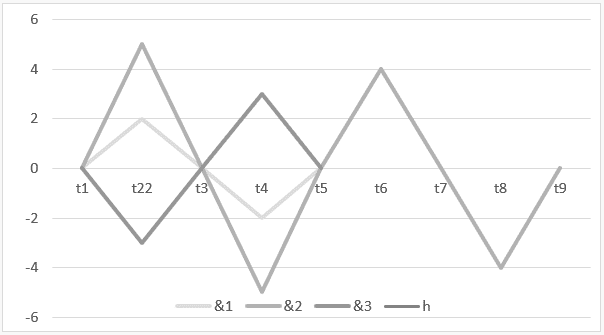
El descanso de tiempo hasta demostrar la operación H   y, en el descanso de hasta, el resultado de esta operación o de su armonía se representa .

4) Armonía entre cinco ondas de notas musicales iguales a la nota G, de dos segundos de duración.

2.4 ARMONÍA VACÍA

La armonía vacía es el resultado de la operación H entre una onda y su onda opuesta o la operación entre varias ondas y sus ondas opuestas , formando una agrupación armónica de una sola frecuencia , con su amplitud cero y un tiempo de duración

Este tipo de armonía, puede parecer, en este espacio-tiempo, que no hay onda periódica en su estructura. Sin embargo, coexiste con una frecuencia resultante, con amplitud cero , en un estado de vibración infinitamente diminuta, en la dimensión del tiempo, llamada Vibración Armónica Primordial (VPH), representada por un cero negado , constituyendo, por tanto, un Conjunto Vacío Armónico, denominado por la Ciencia de “Vacío Cuántico”, capaz de generar en su estructura, más de una vibración en un espacio-tiempo , diferente de un simple conjunto vacío, donde nada existe y nada se puede generar.

De esta forma, dos armonías vacías sólo serán iguales si sus características y cantidades son iguales. Cualquiera que sea la armonía vacía, ela é considerada o Elemento Neutro da operação Harmonização , por tratarse únicamente de un tiempo de duración activo, que oculta una o varias vibraciones inactivas o incapaces de interactuar con algún elemento activo.

Por tanto, el resultado de la armonía entre cualquier elemento neutro y un elemento activo es el propio elemento activo  , no importa cuál sea el origen de ese elemento neutro, si es con frecuencias iguales o con frecuencias iguales, independientemente de su duración

, ya que estas vibraciones coexisten solo en la Dimensión del Tiempo.

Cuando esta armonía está formada por ondas sonoras de notas musicales opuestas, la amplitud del sonido se elimina por completo de su frecuencia.
, originando en su lugar un silencio en el tiempo, formando una Armonía de Silencio. En este caso, su tiempo de silencio es percibido por el ser humano, debido a que su duración es igual o superior a una décima de segundo , siendo esta armonía conocida como Pausa Musical , que se demostrará en los ejemplos siguientes.

Cuando esta armonía está formada por vibraciones luminosas, se elimina totalmente la luminosidad de la amplitud de su frecuencia
, dando lugar, en su lugar, a una oscuridad en el tiempo, denominándose la Armonía de la Energía Oscura y, probablemente, la oscuridad que habita el Universo, es originada por esta armonía implícita en su inmenso Vacío Armónico.

1) Armonía entre dos ondas: , con su gráfica en el sistema cartesiano.

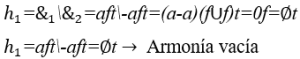
Gráfico 4: Armonía vacía de

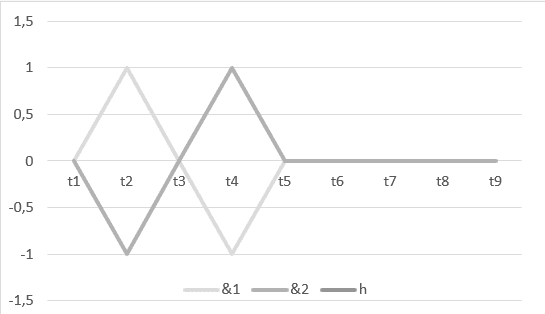
El intervalo de tiempo hasta, que se muestra en el gráfico anterior, representa la operación H y, el descanso de hasta , es el resultado de esta operación o de su armonía .

2) Armonía entre notas musicales: Do, de un segundo de duración, con amplitudes iguales e inversas .

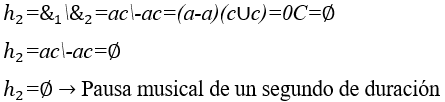
Nota: Armonía Vacía es un lugar en el espacio-tiempo donde existe la idea de que nada existe en él, sin embargo, puede estar lleno de vibraciones imperceptibles.

2.5 ARMONÍA INESTABLE

La Armonía Inestable es el resultado de la operación H entre dos o más ondas periódicas arrítmicas o de distinta duración, donde la de menor duración forma la armonía de esta operación , debido a la propiedad del ritmo de igualar las duraciones de esta onda a la más pequeña, dejando una parte de la duración de la más grande , donde permanece la armonía formada (/) .

Cuanto mayor sea el número de estas ondas arrítmicas en esta operación, mayor será la inestabilidad de la armonía formada , con degradaciones en armonías secundarias , si hay o no un resto continuo de la onda de mayor duración , de acuerdo con los ejemplos que se enumeran a continuación.

1) Armonía inestable entre dos ondas arrítmicas: , con su gráfico lineal en coordenadas cartesianas.

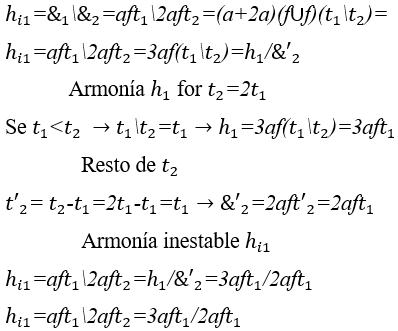
Gráfico 5: Armonía inestable de

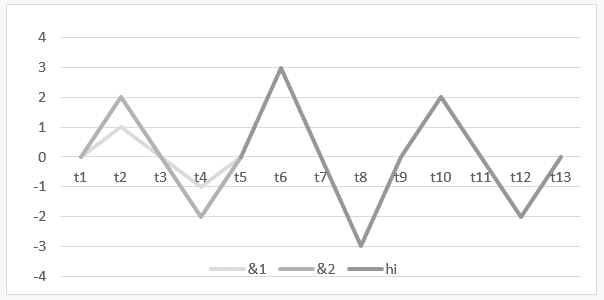
El intervalo de tiempo hasta, muestra la gráfica de la operación H  y, en el descanso de hasta , el resultado de esta operación o de su armonía se representa .

2) Armonía entre dos notas musicales arrítmicas: , respectivamente con sus duraciones de tres segundos.

3) Armonía inestable entre tres notas musicales arrítmicas: , respectivamente con duraciones de cuatro, tres y dos segundos, con su gráfica en el sistema de ejes cartesianos.

Gráfico 6: Armonía inestable de

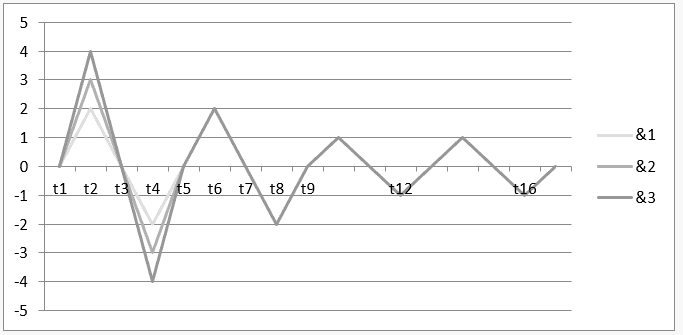
El intervalo de tiempo hasta, representa o gráfico da operação H y, en el descanso de t5 hasta t13, el resultado de esta operación o de su armonía se demuestra .

4) Armonía inestable entre tres notas musicales arrítmicas con frecuencias iguales:

5) Armonía inestable con armonía vacía entre dos ondas: , uno siendo el triple de la duración del otro.

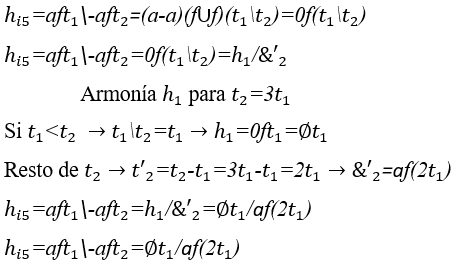
Gráfico 7: Armonía inestable con armonía vacía de

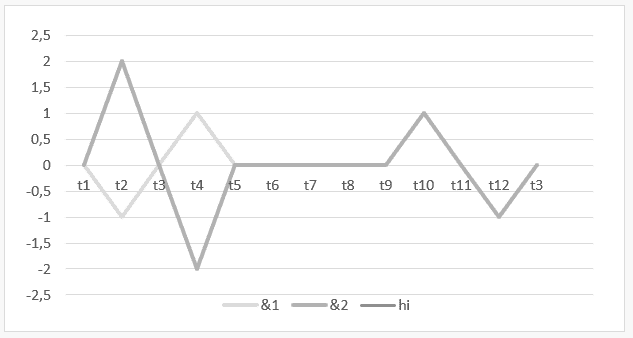
El intervalo de tiempo hasta, representa la operación H y, en el descanso de hasta, el resultado de esta operación o de su armonía se demuestra .

6) Armonía entre dos notas musicales G con amplitudes iguales en fases opuestas, una de tres segundos y la otra de dos segundos .

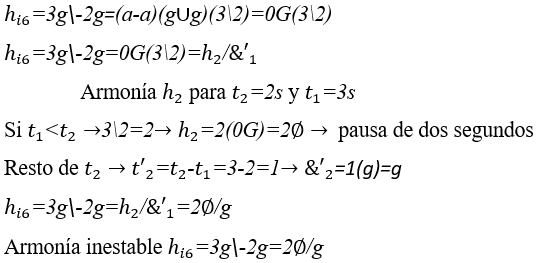
2.6 ARMONÍA NUMÉRICA

Cuando dos o más constantes numéricas, están en operación de Armonización o H, se consideran vibraciones rítmicas y, como tienen un solo parámetro, que puede ser frecuencia o amplitud, se unen a su vez como frecuencias    y se suman como amplitudes , formando la armonía de esta operación.

Cualquier clúster formado por una combinación de Análisis Combinatorio se considera el resultado de una operación H entre estos elementos, con el resultado de su amplitud implicado en la unión entre ellos, como se demuestra en los ejemplos siguientes.

1) Armonía entre las constantes numéricas 1 y 1

2) Armonía entre las constantes numéricas 1 y -1

3) Armonías entre constantes numéricas

4) Armonías entre constantes numéricas

5) Armonías entre constantes numéricas

6) Armonías entre una constante numérica y cualquier elemento neutro

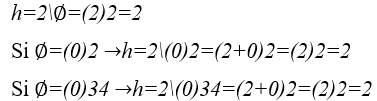
Observación: la armonía de la operación H entre cualquier constante numérica “n” y cualquier elemento neutro, es la propia constante numérica con amplitud igual a su valor . En esta operación sabemos que la amplitud del elemento neutro es cero , pero su frecuencia es indeterminada y aunque se supiera , estaría en la dimensión del tiempo, incapaz de interactuar con ningún elemento activo de ninguna dimensión.

3. OPERACIÓN MELODIACIÓN U OPERACIÓN M

La operación de Melodía o M, es la operación inversa de la Armonización, porque luego de finalizada la duración de una armonía, las vibraciones periódicas que estaban en superposición, pasan a la condición de Ininterrumpida, es decir, forman una continuidad entre sus espacios- veces, donde la hora de finalización de una duración es igual a la hora de inicio de la siguiente duración , sendo este fenômeno denominado de Princípio da Melodia.

Por lo tanto, cuando dos o más vibraciones periódicas  permanecer en funcionamiento M , el resultado es una agrupación melódica, que si son ondas de notas musicales, el efecto sonoro da como resultado una Melodía y si estos elementos son constantes numéricas en la operación M, también formarán una agrupación continua entre ellos, formando la melodía numérica de esa operación . De esta forma, cualquier grupo formado por un Array de las matemáticas del Análisis Combinatorio es el resultado de una operación M, que no es una propiedad conmutativa.

3.1 MELODÍA CON FRECUENCIAS IGUAL Y AMPLITUDES OPUESTAS

Normalmente, las notas musicales en una operación M tienen amplitudes en fase positiva, sin embargo, si hay una nota con amplitud en fase negativa, se puede modular a fase positiva, ya que la frecuencia se mantiene igual, produciendo el mismo efecto de sonido en el formado melodía
.

Sin embargo, este signo negativo puede permanecer en el cifrado de la nota musical y en el resultado de la melodía con un punto sobre él . Si este elemento es una constante numérica negativa en esta operación , También se puede modular a positivo o identificó un punto en la constante en la melodía resultante.

3.2 LA PAUSA DE LA MÚSICA (p)

La Pausa Musical es una nota musical con amplitud de frecuencia de sonido cero, representada por un cero negado. En otras palabras, es el elemento neutro de la operación H, y su función principal en una melodía es proporcionar una discontinuidad sonora entre las notas musicales melódicas o dejar un espacio sin sonido entre ellas . También puede estar implícito solo al comienzo del primer compás de un ritmo y al final del último compás de ese ritmo, completando sus períodos.

3.3 EJEMPLOS DE FUNCIONAMIENTO ENTRE ONDAS DE NOTAS MUSICALES

3.4 APLICACIÓN DE LA PROPIEDAD DISTRIBUTIVA DE LA OPERACIÓN H

Cuando una nota musical comienza en un compás y termina en otro sin perder su continuidad sonora, su cifra continuada recibe un apóstrofe en el siguiente compás, por ejemplo, .

3.5 EJEMPLOS DE OPERACIÓN M CON CONSTANTES NUMÉRICAS

4. ÁLGEBRA DE VIBRACIONES

El Álgebra de Vibraciones, no es más que Álgebra con al menos una de las operaciones de Armonización o Melodía en su expresión.

Aunque no presente ninguna de estas operaciones, puede ser modulado para el Álgebra de Vibraciones, a través de los módulos de ondas disponibles, tales como: el Módulo Melódico, que convierte una expresión algebraica en melodía; el módulo armónico , que transforma uma expressão algébrica em uma harmonia; o Módulo Composto , que transforma una expresión algebraica en una melodía con armonía, cuyos resultados normalmente arrítmicos son modulados a cualquier ritmo.

A través de los módulos de ritmo estándar, que organizan las células musicales en grupos sonoros rítmicos, sumando sus duraciones en períodos iguales, en compases: Binario , Ternario o Cuaternario . En este caso, el primer y el último compás de cualquier ritmo pueden estar incompletos con notas musicales, como se muestra en el siguiente ejemplo.

Dado a la expresión: y las constantes numéricas y sonoro . Los valores son calculados, numéricos, melódico , armónico es compuesto .

4.1 CÁLCULO DEL VALOR NUMÉRICO DE E=x+3y−2z

4.2 CÁLCULO DEL VALOR DEL SONIDO MELÓDICO DE E=x+3y−2z

El módulo melódico transforma una expresión algebraica numérica en una expresión algebraica melódica, reemplazando todas las operaciones existentes con operaciones M (/).

El resultado normalmente arrítmico se modula a cualquier ritmo, para organizar las notas musicales en una interpretación sencilla.

Nota: La operación M entre una constante numérica y un sonido constante, é igual à melodia da constante sonora veces .

Comentario: la elección de un ritmo es opcional y, si se optara por el módulo de ritmo ternario, la última nota se dividiría con una parte en el penúltimo compás y otra continua en el último compás, identificadas con un apóstrofo en su cifra.

4.3 VALOR MELÓDICO INTERACTIVO DE E=x+3y−2z

Cuando ocurre la sustitución en el módulo melódico, tanto de constantes sonoras como numéricas, la expresión melódica resultante se denomina interactiva, ya que incluye una dinámica física en función de la constante numérica, como se muestra en el siguiente ejemplo.

Dado a la expresión   y las constantes . Su valor melódico se calcula.

Note: el valor numérico tres (3) en el primer compás representa cualquier acción física, por ejemplo: contar de uno a tres en tiempo triple y luego tocar la melodía indicada en los siguientes compases . Este conteo en ritmo binario o cuaternario hace que la ejecución de esta dinámica compleja sea difícil de cumplir, por lo que es importante elegir un ritmo adecuado para una expresión melódica interactiva.

4.4 VALOR NUMÉRICO MELÓDICO DE E=x+3y−2z

Cuando en el módulo melódico las constantes son todas numéricas, el resultado es una agrupación melódica numérica, como se muestra en el siguiente ejemplo.

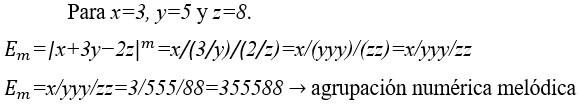
4.5 VALOR DEL SONIDO ARMÓNICO DE E=x+3y−2z

El módulo de sonido armónico  transforma una expresión algebraica numérica en una expresión algebraica de sonido armónico, reemplazando todas las operaciones existentes con operaciones H (\). El resultado suele ser arrítmico modulado a cualquier ritmo por su fácil ejecución.

Nota: la operación H entre una constante numérica y una constante sonora es igual a la armonía al unísono de la constante sonora.

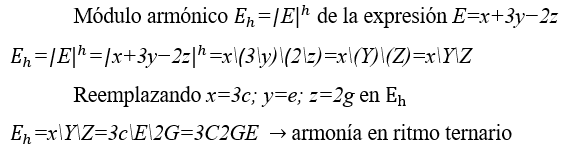
4.6 VALOR ARMÓNICO INTERACTIVO DE E=x+3y−2z

Cuando en el módulo armónico se produce el reemplazo tanto del sonido como de las constantes numéricas, la expresión armónica resultante se denomina interactiva, ya que incluye una dinámica física en función de la constante numérica, como se muestra en el siguiente ejemplo.

El valor del sonido armónico de la expresión se calcula , dadas las constantes .

Nota: el valor numérico tres (3) en la barra única representa cualquier acción física, por ejemplo: contar de uno a tres en tiempo triple mientras se ejecuta la armonía indicada. Este contar con otros ritmos hace que la ejecución de esta dinámica sea compleja y difícil de cumplir, por lo tanto, es muy importante elegir un ritmo para una expresión armónica interactiva.

4.7 VALOR NUMÉRICO ARMÓNICO DE E=x+3y−2z

Cuando en el módulo armónico las constantes son todas numéricas, el resultado es una agrupación armónica numérica, como se muestra a continuación.

4.8 COMPOUND SOUND VALUE OF E=x+3y−2z

El módulo compuesto   transforma una expresión algebraica numérica en expresiones sonoras con melodías y armonías, reemplazando todas las operaciones existentes por operaciones M y H. El resultado suele ser modulado arrítmicamente a cualquier ritmo por su sencilla ejecución. En este caso, existirá la opción de qué operaciones serán reemplazadas por las sonoras, y con cada elección se formará una expresión de sonido compuesto diferente, como se muestra en el ejemplo a continuación.

El valor del sonido compuesto de la expresión se calcula, reemplazando las dos primeras operaciones   por operaciones H y las dos últimas   por operaciones M, para las constantes de sonido

4.9 VALOR COMPUESTO INTERACTIVO DE E=x+3y−2z

Cuando la sustitución del sonido y las constantes numéricas ocurre en el módulo compuesto, la expresión de sonido compuesto resultante es interactiva, ya que incluye una dinámica física a través de la constante numérica, como se muestra en el ejemplo a continuación.

El valor del sonido compuesto de la expresión se calcula , reemplazando las dos primeras operaciones   por operaciones H y las dos últimas   por operações M, para as constantes numérica  y sonoro

4.10 VALOR NUMÉRICO COMPUESTO POR E=x+3y−2z

Cuando en el módulo compuesto solo se reemplazan constantes numéricas, el resultado es una agrupación compuesta numérica, como se muestra en el ejemplo a continuación.

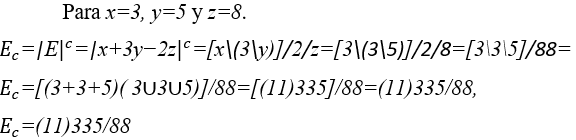
5. HIPÓTESIS CIENTÍFICA DEL AUTOR

Con el desarrollo de la operación de Armonización surgieron algunas hipótesis científicas planteadas por el autor de este material, en este estudio, para algunos fenómenos naturales.

5.1 DUALIDAD DE LUZ ONDA-PARTICULA

El fenómeno de la dualidad de onda-partícula de la luz, donde la luz tiene la característica de una onda o una partícula, puede explicarse por la propiedad de la Dualidad Operacional de la operación de Armonización.

Se sabe que la luz es una armonía formada por varios tonos de vibraciones de luz en funcionamiento Armonización o H , donde la amplitud resultante tiene como función la operación de suma entre las amplitudes de estas vibraciones.

Cuanto mayor sea el número de vibraciones en esta operación, mayor será la amplitud luminosa resultante  , influyendo, con esta cantidad de energía lumínica, en su lado particulado, mientras que su forma de onda se mantiene en función del funcionamiento de unión entre las frecuencias de estas vibraciones lumínicas, que forman la agrupación armónica de la armonía de esta operación , influenciando tu lado de onda.

Debido a la longitud de estas ondas, se mantiene este equilibrio entre estas dos características onda y partícula, lo que no ocurre con una onda sonora, debido a su gran longitud de onda en relación a la onda luminosa, prevaleciendo esta, preponderantemente, su lado ondulatorio, relativo a la insignificancia de su lado partícula.

5.2 ORIGEN DE LA ENERGÍA OSCURA

El fenómeno de la Energía Oscura existente en el Universo puede ser consecuencia de la Armonía Vacía, resultado de la operación de Armonización entre vibraciones de partículas luminosas opuestas, que eliminan las luminosidades de estas vibraciones , originándose en su lugar la Oscuridad que constituye la Energía Oscura, donde la frecuencia resultante de esta armonía coexiste en estado de Vibración Armónica Primordial (VPH) en un Vacío Armónico, también llamado Vacío Cuántico.

5.3 LA ESTRUCTURA DEL TIEMPO Y SU FUERZA DE EXPANSIÓN

Un intervalo de tiempo consta de un periodo , formado por un tiempo inicial   y un tiempo final , cuya diferencia entre ellos mide su duración . Estos periodos están interconectados de forma ininterrumpida, donde la hora de finalización de un periodo es igual a la hora de inicio del periodo siguiente y así sucesivamente, constituyendo un intervalo de tiempo cerrado de un período pasado, hasta un período presente, y abierto al comienzo de un período futuro, formando su Espacio-Tiempo , que por el Principio de Melodía es igual a la operación M entre estos períodos pasado , presente y futuro .

También se sabe que el tiempo inicial   de cada periodo está caracterizado por un Beat , provocado por un impulso intrínseco, dado por una fuerza de duración instantánea , dejando un tiempo de silencio   hasta el final de este periodo , dado por la diferencia entre el tiempo final de este periodo   y el tiempo de pulsación de este impulso .

Por tanto, se puede definir un periodo por la operación M, entre su tiempo de pulsación y su tiempo de silencio . Reemplazando los períodos por sus latidos en el Espacio-Tiempo , formamos la Cadencia Rítmica del Espacio-Tiempo , cuyo latido la velocidad, denominada tempo rítmico , es inversamente proporcional a su período , medida en pulsaciones por unidad de tiempo.

Cuanto más corto sea este período, mayor será su Tempo rítmico . Este fenómeno también promueve, con su influencia en el Espacio-Tiempo, dos movimientos en los cuerpos físicos ubicados en su campo de acción, uno de los cuales se denomina Regencia Rítmica , donde un cuerpo sin salir de su posición de reposo acompaña los latidos de la Rítmica. Tempo Rítmico , y otra denominada Danza Rítmica , donde un cuerpo se desplaza desde su posición de reposo a otras posiciones distintas, también debido al Tempo Rítmico  de esta cadencia rítmica.

Considerando un periodo, donde el tiempo de silencio es nulo , el tiempo de pulso instantáneo constituirá su menor duración , comprobándose que si por tanto , una fuerza de repulsión implícita en su estructura, considerada débil en su cadencia rítmica en el Espacio-Tiempo, pero capaz de alejar cualquier cuerpo celeste del Universo y promover con su Progreso Rítmico, Rítmico Dirección de movimientos y Danza Rítmica.

Se sabe que el Universo se está expandiendo y que sus galaxias se están alejando unas de otras, lo cual se explica por la Fuerza de Expansión del Tiempo de su Cadencia Rítmica y, considerando que las órbitas de las galaxias alrededor el centro del Universo son aproximadamente elípticos, por lo que su expansión acelerada aún no se explica por este acercamiento a su centro de gravedad, donde probablemente haya una armonía de los agujeros negros, con su fuerza de atracción.

Sin embargo, esta aceleración debería dejar de existir luego de que las galaxias se alejen de este centro, con una desaceleración y, aquellas que alcancen las órbitas más grandes, formarán el borde inestable del Universo, como una burbuja líquida inestable, ya que irían cambiando de forma en función de los infinitos de los afcentros máximos de estas galaxias en todas las direcciones, en relación con el centro del Universo.

5.4 LA SINGULARIDAD DEL BIG BANG Y LA OSCURIDAD DE LA TEORÍA RELIGIOSA

Se sabe que toda la materia está formada por átomos, que se encuentran en constante vibración, que a su vez están formados por partículas cada vez más pequeñas hasta llegar a la más pequeña de todas las partículas de materia, denominada Partícula Elemental o Primordial (ANJOS, s.f.), representado, en este estudio, por una vibración simple, con su frecuencia , amplitud y tiempo continuo . Asimismo, está su antipartícula primordial   de antimateria, con la misma frecuencia , opuesta amplitud y opuesto tiempo o armónico, es decir, en lugar de el tiempo va del presente al futuro en una cadencia melódica, viene del futuro al presente, en una cadencia armónica.

Estas vibraciones luminosas en la Operación H, formarán la Armonía Unitaria Primordial de la Energía Oscura, capaz de originar toda la energía de materia y antimateria contenida en su estructura en un estado de Vibración Armónica Primordial o en un Vacío Armónico, también llamado por la Ciencia del Vacío Cuántico .

Por tanto, para cualquier Teoría del Origen del Universo, siempre se admite la existencia de un punto de origen de todo, como la Singularidad del Big Bang, la Oscuridad de la Teoría Religiosa (Biblia) o cualquier otra, que siempre conduce a Armonía Unitaria Primordial de Energía Oscura, capaz de generar toda la energía para la formación tanto del Universo de Materia   en la Cadencia Rítmica del Tiempo Continuo, con su Fuerza de Expansión , así como toda la energía en la formación de la Antimateria o Universo Inmaterial en la Cadencia Rítmica  del Tiempo Armónico, llamado “Tiempo de Dios”, con su Fuerza de atracción infinita.

5.5 EL TIEMPO CERO DE LA CREACIÓN DEL UNIVERSO

Un período de tiempo, por breve que sea su duración, estará siempre formado por un tiempo inicial con pulsación, formado por una fuerza F, y un tiempo de duración de pulsación mayor que cero .

Considerando este tiempo inicial, se puede decir que el Universo tuvo su comienzo en un latido instantáneo , pero antes de que ocurriera este latido hubo un tiempo nulo o cero y, para que este Para ser cierto, debería haber más bien una Armonía del Vacío Primordial , formada por infinitas ondas-partículas de materia en armonía con infinitas ondas-partículas de antimateria.

En este caso, el continuo de tiempo del Universo material también estaba en armonía con su tiempo opuesto o anti continuo    del Universo de antimateria, resultando en tiempo nulo o Tiempo Cero en esta armonía, llena de energía acumulada en una sola frecuencia en Vibración Armónica Primordial.

Considerando el menor tiempo posible de existir en una armonía, con su latido, formado por una fuerza F con cierta intensidad, parece que el tiempo es una onda-partícula, donde F es su amplitud   y el inverso de su tiempo de pulsación es su frecuencia , que en Armonía con su onda-partícula opuesta, también con su amplitud opuesta   y su frecuencia, da como resultado una armonía vacía del Tiempo Cero del Principio del Universo.

5.6 ARMONÍA UNITARIA OMNIPOTENTE

En la formación del Universo Material, el tiempo continuo con su fuerza de expansión, fue formando las innumerables partículas distintas de materia, a través de sus combinaciones, con una sola partícula primordial  .

En el caso de la formación del Universo de Antimateria, el tiempo anti continuo o armónico, con su fuerza de atracción, formó la Armonía Unitaria Primordial , atrayendo todas las anti-vibraciones primordiales en una sola armonía, capaz de originar toda su estructura, formando el Universo Inmaterial o Antimateria , por lo tanto llamado Armonía Unitaria Omnipotente (Dios).

6. CONSIDERACIONES FINALES

Con el desarrollo de la operación Armonización y su operación Melodiación inversa, se logró crear una estructura matemática para la evaluación de las características musicales de una melodía, así como de una armonía, haciendo de la Música no solo un arte, sino también parte de la Ciencia.
También se hizo posible utilizar el Álgebra con expresiones no sólo numéricas, sino también sonoras, formando el Álgebra de las Vibraciones, con interacción entre valores numéricos y sonoros en el resultado de una expresión algebraica, permitiendo que un acto físico sea acompañado por un melodía o de una armonía, o incluso de una melodía acompañada de una armonía
También se proponía una nueva forma de mirar el Universo, a través de una perspectiva macro y micro, a través de la concepción de las estructuras de vibraciones armónicas y melódicas, ya que todo es vibración. Por lo tanto, algunas de las hipótesis planteadas por el autor de este material quedaron demostradas para algunas preguntas aún sin respuesta para la Ciencia, como la existencia de Dios.

REFERENCIAS

ANJOS, Talita Alves dos. Partículas elementares. Brasil Escola. Disponível em: https://brasilescola.uol.com.br/fisica/particulas-elementares.htm. Acesso em 21/03/2022.

GUEST, Ian. Harmonia – Método Prático. Editora Luminar. Vol. 1, p. 33 a 41, 2020.

MORAIS, Gustavo. Teoria musical para iniciantes: você sabe o que são os acordes? Terra, julho de 2020. Disponível em: https://www.terra.com.br/diversao/musica/teoria-musical-pra-iniciantes-voce-sabe-o-que-sao-os-acordes,7c62b1fa5e0fe37c8e0180310bc04200tnys05tj.html Acesso em: 20/03/2022.

SILVA, Domiciano Correa Marques da. Interferência de ondas. Brasil Escola. s.d. Disponível em: https://brasilescola.uol.com.br/fisica/interferencia-ondas.htm. Acesso em 17/03/2022.

SANTOS. Marco Aurélio da Silva. A Sensibilidade Auditiva. Mundo da educação. Disponível em: https://mundoeducacao.uol.com.br/fisica/a-sensibilidade-auditiva.htm. Acesso em: 20/03/2022.

^[1] Graduado en Ingeniería Eléctrica, op. Electrónica de la Universidad Federal de Pará-UFPA. ORCID: 0000-0001-7010-9114.

Enviado: Febrero de 2022.

Aprobado: Marzo de 2022.