ARTÍCULO ORIGINAL
BELLAS, Leonardo Dias [1]
BELLAS, Leonardo Dias. Cálculo de proporciones numéricas. Revista Científica Multidisciplinar Núcleo do Conhecimento. Año 05, Ed. 12, Vol. 02, págs. 144-162. Diciembre de 2020. ISSN: 2448-0959, Enlace de acceso: https://www.nucleodoconhecimento.com.br/olimpiada-de-matematica/proporciones-numericas
RESUMEN
En 2011, este autor hizo una observación lógica matemática y ha sido estudiada desde entonces, esta lógica se refiere a que todos y cada uno de los números pueden ser representados por un número secuencial del 1 al 9. Sin embargo, se hizo el descubrimiento de lo que se trataba de esta lógica y otro cálculo existente de la secuencia de Fibonacci estaba relacionado. Dicho esto, este estudio fue desarrollado para registrar información de esta lógica con respecto a este descubrimiento científico del Cálculo de La Proporción Numeral, y sobre la Lógica de Proporción Numeral y su relación con otros descubrimientos y conceptos científicos que han sido desarrollados por otros matemáticos previamente. Con el fin de discutir y demostrar estas observaciones matemáticas que no habían sido observadas previamente y proporcionar una nueva opción de cálculo más eficiente, ya que cualquier número puede ser representado por números secuenciales de 1 a 9. Así, a través del cálculo y la lógica de Numeral Proportion podemos identificarlo, además de demostrar su aplicabilidad en matemáticas y ciencias actuales.
Palabra clave: Relación numérica, secuencia de Fibonacci
1. INTRODUCCIÓN
La intención de este estudio es demostrar este descubrimiento matemático sobre las proporciones numéricas y mostrar su aplicabilidad en matemáticas actuales. A través de cálculos matemáticos y demostraciones, el cálculo de la proporción numérica se explicará y aplicará mediante el tratamiento de que cualquier número puede ser representado por un número secuencial de 1 a 9. Esta secuencia del 1 al 9 es una secuencia secuencial, ya que se repite de forma infinita y secuencial. Y así mostrar su relación con otro cálculo ya realizado, el de la secuencia de Fibonacci que es un coeficiente infinito de dos medidas sucesivas. Se obtiene el número irracional llamado (PHI), con un valor aproximado de 1.618 que también se conoce como proporción de oro o proporción dorada, según el matemático Leonardo de Pisa.
2. LÓGICA DE RELACIÓN DE ASPECTO NUMERAL
Al demostrar el cálculo de la relación de números, tenemos que hacer algunas observaciones matemáticas, como el ejemplo de la lógica de la relación de números. Como se ejemplifica en la siguiente tabla:
Tabla uno. Cálculo de la relación de aspecto lógico y numérico

Fuente: autor.
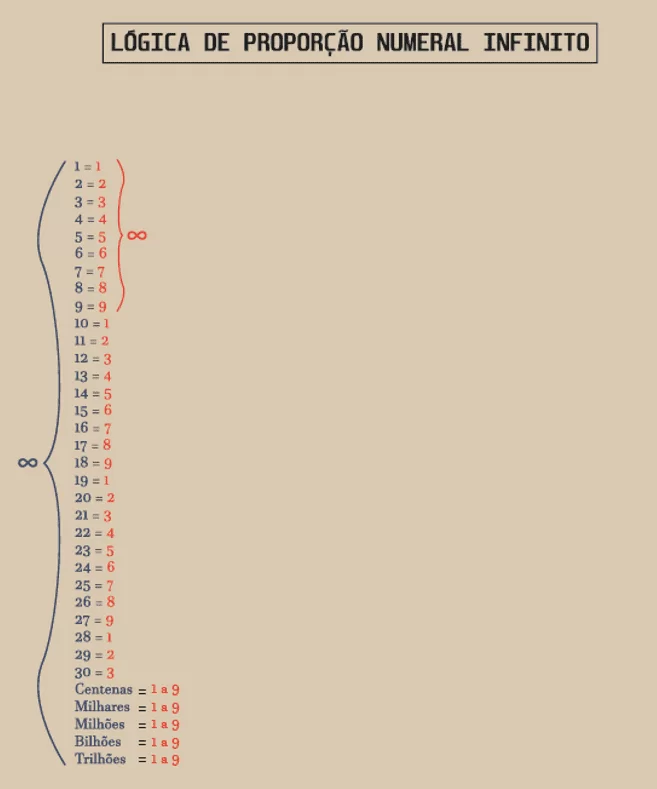
Así podemos observar que todos los enteros, decimales o dígitos de 0.000000…0001 a Infinito, cuando se añaden a su última variable es secuencial de 1 a 9, es decir, la suma de los dígitos de cualquier número, siendo cero neutro, es secuencial de 1 a 9 Infinitamente. Así que con esta lógica podemos observar que todos y cada uno de los números pueden ser representados por un número secuencial de 1 a 9, sigue una manera más simple de expresar esa Lógica.
Figura 1: Lógica de relación de aspecto numérico

Fuente: autor.
3. CÁLCULO DE LA RELACIÓN DE ASPECTO NUMERAL
Ahora vamos al cálculo de la relación de aspecto numérico. En este caso utilicé el alfabeto romano, pero se puede utilizar otro alfabeto u otro símbolo/código.
Figura 2: Cálculo de la relación de aspecto numérico

Fuente: autor.
Podemos observar que independientemente de si usamos números enteros o números de proporción de números, identificamos que en ambos cálculos los resultados son los mismos. Sin embargo, es observable que el uso de la lógica de relación de aspecto numérico para alcanzar el resultado es más simple. Debido a que no tiene que usar todo el alfabeto Infinito de enteros, solo la secuencia del 1 al 9. Este cálculo es como si hubiera roto la infinidad de enteros en una secuencia de 1 a 9 (Numeral). Porque cualquier número es secuencial de 1 a 9.
Echemos un vistazo al nombre João, por el entero se encuentra el número 1015115 y en la lógica numérica está el número 1616. Así, observamos que tanto el número 1015115 y 1616, como la suma de los dígitos hasta su última variable es igual a 5, por lo que podemos hacer una escala de los números, facilitando operaciones con gran volumen, secuenciando e identificando cada elemento de 1 a 9.
También podemos aplicar el cálculo de la proporción numérica a estas observaciones, en los millones siguientes:
Observando también en miles de millones:
También podemos observar en los diezmos:
Aquí en las dizymas podemos observar mejor el infinito que va de 9 a 1.
La base, o el principio que sustenta este razonamiento, es registrar el descubrimiento de este Cálculo de Proporción Numérica que demuestre que todos y cada uno de los números pueden ser representados por un número secuencial del 1 al 9 infinitamente. Ser claramente observado en la lógica y el cálculo de la proporción numeral, presentado aquí. Así que aplicaremos sus significados con ejemplos de matemáticas y lógica.
Por lo tanto, también podemos observar el infinito del 1 al 9.
4. INFINITO Y LA LÓGICA DE LA RELACIÓN NUMERAL
El ejemplo siguiente es el ejemplo identificando Infinity en la lógica de relación de aspecto numérico:
Figura 3: Lógica de relación de aspecto numérico
Fuente: autor
Al mirar el gráfico de arriba es posible ir al infinito, tanto en números enteros como en números numéricos. Y como se dijo anteriormente, divides los números enteros en números, y mirándolo así, ¿dónde es más fácil encontrar o contar hasta el infinito? ¿Contando los números enteros, pasando por miles, millones, billones, billones, etc. o contando sólo del 1 al 9? Mediante la observación lógica mediante el cálculo de la relación de aspecto numérico secuencial de 1 a 9, es más fácil y sencillo encontrar y contar hasta el infinito.
5. APLICACIONES DE CÁLCULO DE LA RELACIÓN DE ASPECTO NUMERAL
El cálculo de la proporción numeral puede ser muy útil, hace algún tiempo se llevó a cabo un descubrimiento científico de un nuevo sistema binario, que es un descubrimiento muy importante de un sistema para el funcionamiento de la electrónica como ordenadores, teléfonos inteligentes, videojuegos, etc. Es mucho más eficiente y seguro que el sistema actual. Este estudio fue publicado en esta misma revista científica, y el enlace estará en las referencias de este trabajo. Pero conocer este cálculo de la relación de números ayudó a descubrir el sistema Binario 2, y dio la base para identificar las diferencias lógicas entre los sistemas binarios, como en este caso a continuación donde se puede aplicar el cálculo de la relación de números. (BELLAS, 2019)
Figura 4: Secuencia del sistema binario

Fuente: Autor
Así que mirando las dos lógicas de los sistemas binarios y usando el cálculo de la relación numérica identificamos una lógica en cada sistema, tenemos en el sistema binario 1, una secuencia de 6 repeticiones 1, 2, 4, 8, 7, 5. Y la lógica del sistema binario 2, es una secuencia de 2 repeticiones 3 y 6. En las dos lógicas binarias los números se duplican hasta el infinito, pero en el sistema binario 1, se pliega hasta el infinito en una secuencia de 6 valores y en el sistema binario 2, se pliega hasta el infinito en una secuencia de 2 valores. Por lo tanto, el sistema binario 2 tiene más lógica matemática y es más eficiente que el sistema binario 1, matemática y lógicamente.
Una de las definiciones lógicas es, cuando una información se repite o tiene secuencia. En el caso del Sistema binario 1 se repite o tiene secuencia en una lógica de 6 factores, ya en el sistema binario 2 se repite o tiene secuencia en una lógica de 2 factores, por lo que el sistema binario 2 es más simple, es más lógico. Dos factores lógicos son más simples que 6 factores lógicos.
Hay un video en Youtube, con el título ”O Segredo dos números 3, 6 e 9” – Hechos Desconocidos. En este video se refiere a las observaciones de Nikola Tesla con respecto a los números 3 y 6, pero este video no sirvió como referencia para la realización de los descubrimientos científicos de este trabajo y también el del Sistema Binario 2, cuando este estudio comenzó a ser desarrollado y el Sistema Binario, por lo que también las observaciones de los números 3 y 6, así como el cálculo y la lógica de la proporción numérica , se realizaron de una manera diferente y antes del acceso a la información de dicha propuesta por Nikola Tesla en este vídeo.
Tesla encontró la relación de los dígitos 3 y 6, pero no lo relacionó con un código binario, no se relacionó con un sistema binario y programación, y no desarrolló un cálculo de relación numérica, pero Tesla observó la relación del Sistema Binario con Fibonacci y encontró el secuencial lógico 1, 2, 4, 8, 7, 5 del sistema binario 1 y también encontró secuencial 3 y 6 , pero no lo relacionó con un sistema binario, pero fue el científico que estuvo más cerca de encontrar un nuevo sistema binario. (TESLA, Youtube)
Y en el descubrimiento del Sistema Binario 2, los escaneos secuenciales 3 y 6 no fueron la primera observación hecha sobre el sistema binario 2, esta información es parte de así como muchos otros hechos durante el descubrimiento científico del sistema binario 2, tales como código binario, píxel redondo, descubrimiento de neutrones en la programación binaria y también identificar el 1 (uno) igual Pi , y otras diferencias entre el tipo de circuitos abiertos y cerrados en sistemas binarios y las diferencias en la programación binaria.
Sin embargo, este video ayuda en fundamentos en aspectos lógicos para hacer las observaciones científicas, matemáticas, lógicas y físicas de este estudio. En resumen para hacer los resultados de estos estudios, la información sobre la secuencia lógica de los números 3 y 6 de Tesla era desconocida, y viendo el video de Tesla, observó los números 3 y 6 de una manera diferente de cómo se observó en este estudio, en estos hallazgos científicos presentes aquí, se observaron exploraciones secuenciales 3 y 6 calculando la relación numérica.
Este video fue observado más tarde el descubrimiento y publicación del sistema binario 2 y también más tarde la publicación del proceso de patente en la PTO (Instituto Nacional de la Propiedad Industrial), pero por la calidad del material, porque el tema tiene las mismas referencias, y ha sido bien citado por uno de los mejores físicos en la ciencia moderna, y también para buscar una mayor observación sobre el tema , este video es muy útil.
Sigue esta cita de Tesla para representar la magnitud de lo que es entender en matemáticas y física la amplitud de conocimiento que es entender el significado de los números 3 y 6. ” Si conocieras la magnificencia de los números 3, 6 y 9, entonces tendrías la clave del Universo” (TESLA, Youtube)
Figura 5: Citar a Nikola Tesla 3 y 6.

Podemos decir que observar el infinito del 1 al 9 y así entender que todos y cada uno de los números pueden ser representados por esta secuencia de infinito, también tiene una gran magnificencia.
Sistema binario 2 es el descubrimiento científico tecnológico más importante hoy en día, ya que es una tecnología avanzada, un ordenador con tecnología Sistema binario 2 es muy superior a un ordenador con la tecnología actual de Sistema binario, y este cálculo es una de las ecuaciones más complejas que tenemos.
Hay varias diferencias técnicas que demuestran la superioridad del Sistema binario 2 al sistema binario 1, a continuación se citarán algunos como ejemplos:
1 – Diferencia en el tipo de Circuito Físico, en el Sistema Binario 1 se abre el circuito, es decir, es un circuito interrumpido y en el Sistema Binario 2 el circuito está cerrado, es decir, es un circuito continuo, esto genera una gran diferencia de superioridad en el rendimiento y la respuesta del Sistema. El circuito continuo es más eficiente que un circuito interrumpido.
2 – Otra diferencia técnica es que en el circuito Sistema binario 1 sólo funciona con dos elementos físicos y lógicos de la programación lo negativo y positivo, mientras que el Sistema Binario 2 funciona con tres elementos de programación físicos y lógicos negativos, neutros y positivos, con estos tres elementos en la programación el circuito se cierra debido al neutral, aportando así un rendimiento y resultado superiores , incluida la afectación a la seguridad del sistema. Una manera de expresarse técnicamente en el sentido de seguridad de la programación binaria, es que un sistema binario sin el circuito neutro está abierto, por lo que su puerta está abierta es insegura, y en el sistema binario con el circuito neutro está cerrado, por lo que en consecuencia su puerta está cerrada, por lo que el sistema binario 2 tiene más seguridad.
3 – Otros aspectos está en la programación de la lógica física de los Sistemas, en el sistema binario 1 sólo funciona con 1 π (un PI) sin neutral, mientras que en el sistema binario 2 la lógica física del sistema funciona con 2 π (dos PI) con neutral, esto trae una gran diferencia en el tipo de realidad virtual de los sistemas, en el Sistema binario 1 el píxel es cuadrado y en el sistema binario 2 el píxel es redondo, esto trae una gran diferencia en el tipo de realidad virtual de los sistemas, en el Sistema binario 1 el píxel es cuadrado y en el sistema binario 2 el píxel es redondo , afectando directamente al tipo de realidad, dimensión y gráficos del sistema, aportando más calidad, definición, velocidad, agilidad y lógica, aumentando también el procesamiento y la capacidad en el volumen de datos, aumentando así una mayor eficiencia en los aspectos lógicos en la programación del Sistema Binario 2. 2 π (dos PI) con neutro es mayor que 1 π (un PI) sin neutro.
4 – Y otra razón técnica importante es la diferencia entre los códigos binarios y las secuencias lógicas de los sistemas, como se explicó anteriormente en Sistema binario 1 es una secuencia lógica de seis factores y el sistema binario 2 es una secuencia lógica de dos factores, y esta diferencia en secuencias y códigos binarios afecta directamente tanto al volumen de procesamiento de datos como a la velocidad de respuesta del sistema binario 2, que es más ágil y lógicamente y Físicamente. Secuencial 3 y 6 es más lógico y eficiente que 1, 2, 4,8, 7, 5.
Hay otras diferencias técnicas y otra información, pero estos ejemplos anteriores son aquellos que demuestran las principales diferencias entre los sistemas, y el conjunto de estas diferencias técnicas entre los sistemas binarios demuestran la calidad superior de un sistema sobre el otro sistema.
El descubrimiento de la programación del sistema binario 2 es una de las programaciones lógicas que tenemos en uno de los grados más complejos y altos que existe hasta la fecha, y hacer observaciones matemáticas, lógicas y físicas usando sólo 0 (cero) y 1 (uno), es decir, ver sistemas en cero y uno, es un gran desafío.
En relación con los circuitos y la programación de sistemas binarios, una forma correcta que podemos expresar, es que un ordenador que piensa en ceros y unos, por lo que el descubrimiento científico del sistema binario 2, es un descubrimiento de una nueva forma o más eficiente para que un ordenador piense en ceros y unos.
Sistema binario 2 es la tecnología más avanzada que existe hoy en día. Los sistemas binarios son sistemas, porque realizan varias funciones, son circuitos lógicos y también programación, el sistema binario 2 es un nuevo sistema más eficiente y seguro para el funcionamiento de la electrónica, y diferencia una programación binaria del otro a través de la disposición lógica de ceros y unos.
Sin embargo, este estudio es para demostrar el descubrimiento del cálculo de la proporción de números, si desea más información sobre el sistema binario 2, el artículo está en referencias a este trabajo.
El sistema binario 2 funciona con las leyes de la relación numeral, procesa sus datos de 1 a 9, siendo así mucho más eficiente. El sistema binario 2 también funciona respetando las leyes de Fibonacci, y este estudio tiene referencia y relación también en el cálculo de la proporción numeral, porque son prácticamente lo mismo, los dos son un coeficiente de infinito, sólo una nueva forma matemática de calcular, expresar y observar parte de las leyes de Fibonacci fue descubierta. Estas observaciones se realizan aquí llamado cálculo de la proporción de números.
Después de un largo tiempo de estudio e investigación, y logros de observaciones por encima del cálculo de la proporción numérica, se encontró una relación entre este descubrimiento y otro estudio, el de la secuencia de Fibonacci (PHI). La lógica de la proporción numeral de 1 a 9 al Infinito está directamente relacionada con las leyes de Fibonacci, que también sigue las leyes matemáticas,
que a través de las medidas de la Serie Fibonacci, al analizar el coeficiente de dos medidas sucesivas, se obtiene el número irracional llamado (PHI), con un valor aproximado de 1.618. Y esta coyuntura de medidas basadas en este número se llama la Relación Dorada, o Relación Dorada, que se encuentra, por lo tanto, en flores, árboles, ondas, en galaxias, conchas, huracanes, en la cara simétrica del ser humano, en sus articulaciones óseas y en las características de los seres humanos, sus latidos del corazón y en su ADN. También en la refracción de la luz proporcionada por los electrones de los átomos, en vibraciones, en otras manifestaciones más (TANURE, en línea, s/p).
Y explica por qué la secuencia es del 1 al 9. A continuación podemos ver que el siguiente cuadrante es el doble de todos los anteriores, por ejemplo, el 2 es el doble del [1], el 3 es el doble del [1 y 2 ], 4 es el doble de [1, 2 y 3], 5 es el doble de [1, 2, 3 y 4] y así sucesivamente. Y siempre es secuencial de 1 a 9, siendo 9 el doble de todos sus predecesores, repitiendo así la lógica de Infinito: 1 2 3 4 5 6 7 8 9, 1 2 3 4 5 6 7 8 9, 1 2 3 4 5 6 7 8 9. Siempre el siguiente dígito duplica el número de sus predecesores. A continuación se muestra una forma de expresar la secuencia de Fibonacci
Figura 6: Secuencia de Fibonacci-PHI
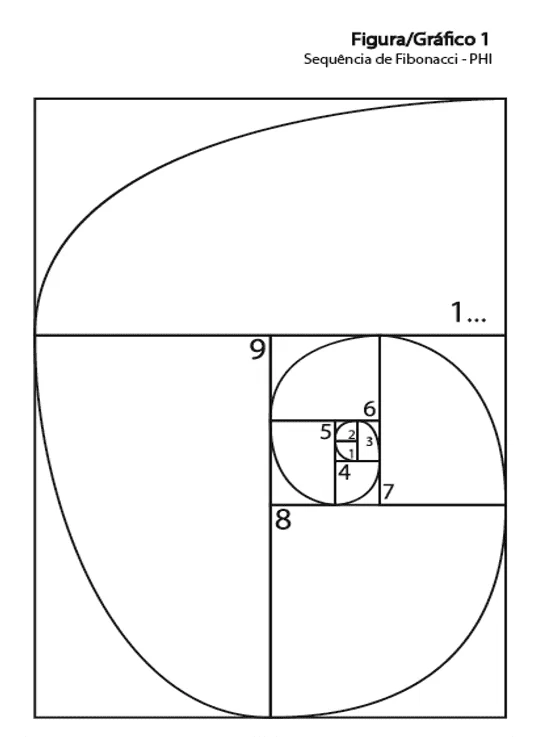
Fuente: Autor
Mirando el gráfico anterior llegamos a la conclusión de que:
9 x PHI 1 Infinito (Nueve veces la medida de fibonacci es igual a un Infinito) o
9 x 1.618 a 1 unidad Infinity o 1 unidad.
O 1 infinito a 1 unidad (una unidad infinita equivale a una unidad)
Por ejemplo, si encuentra matemáticamente la medida de Fibonacci que representa el infinito en una concha marina, esta concha marina se representa por ser 1 unidad, porque este coeficiente de infinito está presente o está firmado matemáticamente en esta unidad.
La medida de la proporción numérica o secuencia de Fibonacci que está representada por un coeficiente y lógica de proporción para calcular y encontrar el infinito, porque si se encuentra este coeficiente o cálculo presente en cualquier elemento, galaxia, planta o animal, ese ser o elemento se representa por ser 1 (una) unidad en las leyes de Fibonacci.
Todos los elementos y seres están firmados matemática, física y naturalmente con este coeficiente del Infinito.
Hay un Infinito firmado matemáticamente en cada unidad.
Otra cita encontrada sobre la secuencia de Fibonacci habla sobre la lógica de la relación como se ejemplifica a continuación:
es una sucesión de números que siguen un patrón.
La secuencia de Fibonacci no es más que el orden de los enteros, que normalmente se aparta de cero y uno en el que cada número siguiente corresponde a la suma de los dos dígitos anteriores. Esta continuidad se puede ver en varios fenómenos de la naturaleza.
La secuencia de Fibonacci fue nombrada por el matemático italiano Leonardo de Pisa, también conocido como Fibonacci. En 1202, a partir de esta secuencia numérica, el matemático informó del avance de una población de conejos.
Fórmula de Fibonacci
La sucesión de Fibonacci es una secuencia de enteros iniciada por cero y una, en la que cada término posterior corresponde a la suma de los dos números anteriores:
0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584… (Secuencia de Fibonacci – Educa + Brasil).
Y aquí podemos notar la diferencia de métodos de observación entre el cálculo de Fibonacci, y este cálculo matemático y lógico de la proporción numeral. Tanto la lógica de proporción numérica como la secuencia de Fibonacci son lo mismo, pero este coeficiente infinito se puede observar de estas dos maneras distintas. Como Fibonacci era una referencia para desarrollar este descubrimiento de la Lógica de La Proporción Numérica, porque en las dos observaciones tienen el mismo coeficiente de infinito, sólo la forma de ser observado cambia, por lo que también bautizaremos el cálculo de esta secuencia de 1 a 9 de este estudio por Fiboleo, por la razón de la relación entre los nombres de los autores de estas observaciones.
Secuencial de 1 a 9 como se ha demostrado en los cálculos presentes en este estudio, lógica de proporción numeral y cálculo de proporción numeral.
Aquí hay más información de las citas de secuencia de Fibonacci en las búsquedas en Internet:
Este método se aplica en el análisis de los mercados financieros, la teoría de juegos y la informática, así como las configuraciones biológicas y naturales. Modelos naturales. La secuencia de Fibonacci también se puede observar en fenómenos naturales). (Secuencia de Fibonacci – Educa + Brasil).
Aquí en esta cita podemos ver que habla de informática, es también donde se aplicó el cálculo de la proporción numeral para identificar un nuevo sistema binario, como se ejemplifica anteriormente en este estudio.
Echa un vistazo a más presupuestos sobre el cálculo, a continuación algunos de ellos:
Girasol: Los granos de girasol tienen semillas que están dispuestas en un conjunto de doble espiral. La mayoría de las veces es 21 en el sentido de las agujas del reloj y otros 34 en sentido contrario a las agujas del reloj.
Cono de pino: después del crecimiento de la fruta, las semillas forman una espiral doble con ocho en el sentido de las agujas del reloj y otras 13 en sentido contrario a las agujas del reloj.
Shell de vaciado: cada parte del shell tiene el tamaño de la suma de los dos predecesores. Se sabe que un coha tiene tres lados principales, por lo que suponiendo que un lado mide 2 (1 + 1), y el otro 5 (3 + 2) el tercero será 8 (5 + 3). (Secuencia de Fibonacci: Educa + Brasil).
Así que la lógica de la relación numérica, que es un secuencial de 1 a 9, es un coeficiente del infinito y por lo tanto podemos realizar la misma observación en fibonacci secuencial, que también es un coeficiente infinito. Pero aprender este cálculo es muy eficiente para las operaciones donde tiene un alto volumen de números de dígitos, porque podemos identificarlos en una secuencia lógica más simple, todos y cada uno de los números están representados por números secuenciales del 1 al 9 infinitamente.
CONCLUSIÓN
La conclusión de este estudio tiene como objetivo registrar el descubrimiento del cálculo de la proporción numérica y la lógica de la proporción numérica, y relacionar este descubrimiento del cálculo de la proporción numérica con el cálculo de Fibonacci, además de demostrar su aplicabilidad en matemáticas y especialmente en sistemas binarios y con respecto a su aplicación en relación con el infinito.
Este estudio puede proporcionar bases para nuevos descubrimientos científicos, como ya ha sucedido, y para la investigación. Puede ayudar a las personas a pensar nuevas formas de lidiar con los números, y es una forma más simple de calcular mediante la secuenciación de todos los valores al infinito de 1 a 9. En la lógica de la proporción numeral, el infinito se rompe de 1 a 9. También para presentar nueva información, una nueva forma sobre cómo observar, expresar, encontrar, calcular y descifrar el Infinito.
REFERENCIA
BELLAS, L.D. Sistema Binário 2 – Código Fechado. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 02, Vol. 05, pp. 110-151. Fevereiro de 2019. ISSN: 2448-0959. Disponível em: https://www.nucleodoconhecimento.com.br/tecnologia/sistema-binario-2-codigo-fechado
TANURE, A.C. Proporção Áurea e Sequência Fibonacci. Pagasus Portal. Disponível em: http://pegasus.portal.nom.br/proporcao-aurea-e-sequencia-de-fibonacci/
TESLA, N. Os segredos dos números 3, 6 e 9. Youtube – Fatos Desconhecidos https://www.youtube.com/watch?v=c2M9ZfZ5h5A&t=682s
Sequência de Fibonacci. Educa+Brasil. Disponível em: https://www.educamaisbrasil.com.br/enem/matematica/sequencia-de-fibonacci
[1] Licenciada en Administración de Empresas con especialización en Comercio Exterior.
Enviado: Mayo, 2020.
Aprobado: Diciembre de 2020.