ARTÍCULO ORIGINAL
SILVA, Sarley De Araújo [1], MAGNO, Rui Nelson Otoni [2]
SILVA, Sarley De Araújo. Probabilidad, gráfico de control aplicado al software de ciencia educativa. Revista Científica Multidisciplinar Núcleo do Conhecimento. Año 06, Ed. 06, Vol. 11, págs. 43 a 73. Junio de 2021. ISSN: 2448-0959, Enlace de acceso: https://www.nucleodoconhecimento.com.br/olimpiada-de-matematica/ciencia-educativa
RESUMEN
El presente estudio menciona la reducción de la variabilidad y las pérdidas debidas a causas especiales en las aplicaciones de las ciencias de la educación, con el objetivo de detectar y corregir las desviaciones de variabilidad a través de gráficos de control de software en problemas estadísticos aplicados. Así, se buscó estudiar conceptos sobre gráficos de control por variables y atributos en el control de anomalías. En la realización de este tema, se utilizó la metodología cuantitativa y el gráfico de control del Software Minitab. Los resultados obtenidos permitieron reducir las pérdidas y mejorar el proceso de calidad a través de ajustes de muestra entre los límites de control de minitab, proporcionando comprender y analizar las causas de las anomalías. Por lo tanto, se concluye que la herramienta de acciones correctivas es capaz de estabilizar las desviaciones estándar y mejorar la calidad de la probabilidad y las aplicaciones estadísticas.
Palabras clave: Probabilidad, Minitab Software, Gráfico de control.
1. INTRODUCCIÓN
La estadística es una rama de las matemáticas que utiliza la herramienta de probabilidad para explicar agrupaciones de datos, tanto en estudios observacionales como en experimentos para modelar, estimar y predecir fenómenos futuros. Su propósito es obtener, organizar, analizar datos, calcular gráficos de control, correlaciones y regresiones, posibilitando el control en variabilidad, aplicaciones estadísticas e instituciones educativas. Los métodos estadísticos se refieren a los datos obtenidos de las observaciones en forma de mediciones o conteo. A partir de la información es posible estudiar problemas estadísticos relacionados con el control de la variabilidad aplicado en las ciencias de la ingeniería, química, física, matemáticas, geografía, etc. El uso de software estadístico es una herramienta importante para los estudios y la aplicabilidad en el control de las variaciones en la probabilidad y los problemas estadísticos.
Las instituciones se preocupan por mantener altos índices de desempeño en cuanto a calidad y productividad debido a los requerimientos en la prestación de servicios. La información y las nuevas tecnologías han establecido un entorno globalizado de alta competencia, en el que se debe cumplir el precio y el plazo (VILAÇA y OLIVEIRA, 2011). En “Cualquier proceso de producción, independientemente de lo bien diseñado o mantenido que esté, siempre estará sujeto a una variabilidad natural o inherente, que es el resultado del efecto acumulativo de muchas causas pequeñas e inevitables, llamadas causas comunes” (MONTGOMERY, 2004, p.154). Por lo tanto, la reducción de la anormalidad en las familias de variables es de suma importancia en el proceso estadístico.
Según Souza y Rigão (2005), el CEP actúa preventivamente sobre el proceso utilizando la estadística como elemento base para evaluar sus cambios. Estas características permiten al CEP asistir en el monitoreo del proceso y permite tomar acciones de manera dirigida a resolver problemas, ayudando en la estabilización del proceso y evitando la producción de artículos no conformes (HORA y COSTA, 2009; MAYER, 2004).
El objetivo de este trabajo es utilizar técnicas estadísticas en software para identificar, corregir y eliminar anomalías presentes en los problemas de las ciencias de la educación. La importancia de los gráficos de control del software estadístico en el control de anomalías.
El objetivo principal del control estadístico de procesos es detectar rápidamente la ocurrencia de causas atribuibles en los cambios de proceso, de modo que se pueda realizar una investigación de procesos y acciones correctivas antes de que se fabriquen muchas unidades no conformes (MONTGOMERY, 2013, p.280).
Por lo tanto, el software estadístico es relevante en el proceso de identificación y eliminación de la variabilidad.
La función del control estadístico de procesos en los gráficos de software es evidenciar las modulaciones que ocurrieron durante el procesamiento y desarrollar gráficos estadísticos que puedan proporcionar un parámetro más preciso, ayudando en prácticas que puedan mejorar los puntos predominantes de fabricación, además de reconocer, corregir, eliminar o adaptar procesos con anormalidad, dando un parámetro más preciso, para que se puedan aplicar mejoras en la línea de producción (OLIVEIRA, 2015, p.22).
Los cuadros de control del software estadístico permiten encontrar la variabilidad demostrada a través de los gráficos, permitiendo una mejor visualización del proceso, con el fin de demostrar posibles defectos, para la aplicación de correcciones más eficientes, en la búsqueda de la mejora continua.
Incluso con el progreso en el proceso a través del control de calidad, todavía hay causas de variabilidad en el proceso, es decir, cuando hay una oscilación alrededor de la media o el punto ideal de la especificación, se requiere un monitoreo constante del comportamiento de producción. “A través del análisis de los datos recolectados y la caracterización de la causa de inestabilidad o variabilidad del sistema, utilizados en gráficos de control, herramientas de control estadístico de procesos como resultado para obtener una mejora continua del proceso” (JURAN y GRYNA, 1992).
Todos los procesos exhiben variabilidad, es decir, cuanto mayor es la variabilidad, mayor es el descontrol sobre los resultados producidos y los resultados deseados. (MONTGOMERY, 1997).
Para mejorar la calidad de un producto es necesario hacer uso de software estadístico:
En un entorno competitivo, la mejora continua de los procesos permite monitorizar, controlar y mejorar los procesos productivos siempre que se detecte alguna anomalía. Si existe un carácter preventivo, estas acciones contribuyen a minimizar las pérdidas y aumentar la productividad (BORTOLOTTI, 2009, p.02).
Tales técnicas estadísticas que utilizan software minitab contribuyen al análisis de diversos productos, detectando y reduciendo posibles anomalías, asegurando existencias dentro de parámetros de calidad. “Uno de los principales resultados del estudio de calidad industrial fue el uso generalizado de métodos estadísticos de control de procesos para eliminar causas especiales en los procesos y reducir las causas comunes de variación” (MONTGOMERY, 1997). En este contexto, el control estadístico de procesos es una herramienta extremadamente importante para la aplicación de técnicas estadísticas en la reducción de la variación. El control estadístico de procesos se puede definir como un conjunto de siete herramientas de solución de problemas para lograr la estabilidad del proceso, además de mejorar su capacidad. (FERREIRA et. al., 2008).
Los gráficos de control del software estadístico ayudan en la identificación y estabilidad de las causas de variabilidad de los procesos, sirviendo de base para decisiones y acciones correctivas de control, reduciendo la variabilidad y evitando datos de muestra fuera de control.
El control estadístico de procesos es una poderosa colección de herramientas para la recopilación, análisis e interpretación de datos, con el objetivo de mejorar la calidad mediante la eliminación de causas especiales de variación, y se puede utilizar para la mayoría de los procesos. (MONTGOMERY, 2004, p.279-281).
El estudio sobre gráficos de control en software estadístico contribuye al análisis de aplicaciones en ciencias de la educación en la reducción de la variabilidad en las muestras analizadas, generando mejores resultados en el control de calidad.
2. MATERIALES Y MÉTODOS
2.1 MATERIALES
Los materiales utilizados para controlar la variabilidad en las aplicaciones de ciencias de la educación fueron los gráficos de control en Minitab Software.
2.2 MÉTODOS
Para llevar a cabo el estudio, se utilizó el método cuantitativo y la tabla de control del software minitab para reducir la variabilidad en las aplicaciones de ciencias de la educación. La metodología busca la validación de datos mediante el uso de datos estadísticos. El estudio tuvo la siguiente distribución: Elección de la aplicación a analizar, determinación de los límites inferior y superior en parámetros medios y amplitud, distribución de muestras y verificación de sus puntos, análisis de problemas mediante gráficos de control y corrección de causas especiales a partir de los análisis de muestras fuera de control.
“El método cuantitativo busca la validación de datos a través del uso de datos estadísticos, con análisis de un gran número de casos representativos. Busca cuantificar los datos y aplicar alguna forma de análisis estadístico” (OLIVEIRA, 2011). El enfoque cuantitativo se utiliza con frecuencia en estudios descriptivos, que buscan clasificar la relación entre variables y la relación causal entre fenómenos.
Richardson (1999, p.70) conceptualiza:
el enfoque cuantitativo, como su nombre lo indica, se caracteriza por el uso de la cuantificación tanto en las modalidades de recogida de información como en el tratamiento de las mismas mediante técnicas estadísticas, desde las más simples como porcentaje, media, desviación estándar, hasta las más complejas, como coeficiente de correlación, análisis de regresión, etc. Representa, en principio, la intención de garantizar la exactitud de los resultados y evitar distorsiones del análisis y la interpretación, permitiendo así un margen de seguridad en relación con las inferencias.
Según Michel (2005, p. 31), el enfoque cuantitativo es una metodología de investigación social que utiliza la cuantificación en las modalidades de recolección de información y su tratamiento a través de técnicas estadísticas, como porcentaje medio, desviación estándar, coeficiente de correlación, análisis de regresión, entre otras. Los gráficos de control son una herramienta beneficiosa que aporta mejoras y aseguramiento de la calidad de los residuos aumentando los costes, la desaparición de la chatarra y la resolución de diversos problemas de producción relacionados con métodos específicos, etc. (ROSA, 2009).
Los cuadros de control fueron utilizados por variables y atributos como técnicas en la construcción de gráficos en aplicaciones probabilizadoras y estadísticas, donde se observó una mejora de la estabilidad en relación con la variabilidad de los defectos de la muestra. Para encontrar una posible causa de variabilidad y verificar si el proceso está bajo control, los gráficos se utilizaron para controlar las anomalías en los puntos de muestreo. A través de los gráficos fue posible identificar y comparar la variabilidad en cuestiones de ciencias estadísticas.
Hizo uso del software minitab como herramienta de análisis de datos. A partir de los resultados entre los límites de control fue posible resolver defectos y mejorar la calidad. Se eligieron los gráficos de control de la media, amplitud y desviación estándar para controlar las variaciones de la media en estadística.
El instrumento tuvo como objetivo identificar, analizar, comparar, corregir y reducir la variabilidad en las aplicaciones de ciencias de la educación que hizo el uso de Minitab que es un programa informático propietario dirigido a fines estadísticos (MINITAB, 2016). “Es una herramienta que nos permite realizar cálculos estadísticos complejos y visualizar los resultados, haciendo que el análisis de datos sea accesible para el usuario ocasional y conveniente para el usuario más experimentado” (PEREIRA y PATRÍCIO, 2016).
Para mejorar la calidad, se utiliza tecnología de software estadístico:
Las herramientas estadísticas además de priorizar las aplicaciones propuestas según el grado de importancia, hacen la identificación y ayudan en la acción sobre los problemas para la eliminación de posibles causas. Posibilitar a la institución un mayor grado de estabilidad en las aplicaciones analizadas (WERKEMA, 2006, p.32).
Estratificación: “La estratificación consiste en dividir los sectores en subsectores según factores deseados, los cuales se denominan factores de estratificación, es decir, por el proceso de dividir el todo heterogéneo en subgrupos homogéneos” (VIEIRA, 1999).
Hoja deverificación: Para Werkema (2006), la hoja de verificación es un formulario que tiene en su alcance criterios para ser analizado, con el fin de facilitar la recopilación y el llenado de datos. Es una herramienta utilizada para ayudar en la recopilación de datos y debe ser adecuada para que la recopilación sea efectiva. Por lo tanto, la hoja de verificación debe especificar claramente el tipo de datos a recopilar, la operación a realizar, la fecha de recolección, el analista y cualquier otra información que sea útil para identificar la causa del mal desempeño funcional (CARPINETTI, 2010; MONTGOMERY, 2009). Según Vieira (1999), el tipo de hoja de control dependerá de cuáles serán sus objetivos, siendo estos: cómo aumentar la proporción de elementos no conformes; atributo inspect; indicar dónde se encuentra el defecto en el producto final; plantear las causas de los defectos; analizar la distribución de una variable; y supervisar un proceso de fabricación.
Gráfico de Pareto: Es la herramienta que realiza la distribución de frecuencia de datos, señalando el defecto que se produce con mayor frecuencia, y pueden ser estos de orden porcentual o real. Recordando que un defecto con mayor frecuencia puede no ser el problema principal o más crítico del proceso (CARPINETTI, 2010; MONTGOMERY, 2009). Vieira (1999) dice que el gráfico de Pareto se utiliza para identificar las causas de problemas como productos manufacturados que requieren retrabajo, gastos innecesarios, accidentes de trabajo, averías de equipos, errores y retrasos en la entrega, entre otros.
Diagrama de causa yefecto: También conocido como Diagrama de Ishikawa tiene la función de identificar y analizar las causas que promueven un efecto no deseado. Es un diagrama eficaz para identificar la raíz del problema (CARPINETTI, 2010; MONTGOMERY, 2009). Werkema (2006) afirma que el Diagrama de Causa y Efecto es una herramienta utilizada para presentar la relación entre el efecto o problema y la causa que podría alterar el resultado. El Diagrama de Causa y Efecto organiza la información de manera que la hace más clara para facilitar el análisis e identificación de las causas del problema, permitiendo tomar acciones correctivas para eliminar la causa del problema (TRIVELLATO, 2010).
Histograma: Según Werkema (1995), un histograma se puede definir como un gráfico de barras en el que el eje horizontal, subdividido en varios pequeños
intervalos, muestra los valores asumidos por una variable de interés.
Diagrama de dispersión: El diagrama de dispersión se encarga de ayudar a identificar las relaciones entre un defecto y una causa, es decir, tiene como objetivo identificar la relación entre dos variables o incluso la relación de una tercera causa. Las relaciones entre las variables pueden ser: positivas, negativas o inexistentes (CARPINETTI, 2010; MONTGOMERY, 2009).
Gráfico decontrol: Según Werkema (2006), cualquier activo tangible o intangible, cuando se elabora y/o se realiza, tiene una variación derivada del proceso. Se sabe que estas variaciones deben reducirse estrictamente. Para Werkema (2006), los gráficos de control se utilizan para monitorear la variabilidad, distinguir los tipos de variación y evaluar la estabilidad del proceso, ya sea que esté bajo control o no. Sin embargo, el proceso puede variar de causas comunes o causas especiales.
Los gráficos de control fueron creados por Shewhart, y están compuestos por límite central o medio (LC), límite inferior (LI) y límite superior (LS). Su función principal es indicar si el proceso está bajo control o no, es decir, si el proceso está fabricando productos de acuerdo con las especificaciones o no. El análisis del proceso se realiza a partir de la verificación del gráfico de control, observando si los puntos trazados en el mismo se encuentran entre los límites superior e inferior de especificación (CARPINETTI, 2010; MONTGOMERY, 2009).
Gráficos de control: Sirve para analizar las variaciones de proceso de causas comunes, y detectar causas especiales, es una herramienta llamada Gráficos o Gráficos de control. Analizar la capacidad de un proceso es una parte vital de un programa de calidad global. Entre los principales usos de datos de un análisis de capacidad de proceso destacan (MONTGOMERY, 2004):
2.2.1 NORMAS ESTADÍSTICAS PARA IDENTIFICAR CAUSAS ESPECIALES
Sugiere un conjunto de reglas de decisión para distinguir patrones no aleatorios en gráficos de control. Específicamente, sugiere que se concluya que el proceso está fuera de control si (MONTGOMERY, 2004):
1er caso: identifique seis, ocho o más puntos por encima o por debajo de la línea central. Posibles causas: cambio en el proceso de ajuste de la máquina, método o material diferente, descomposición de un componente en la máquina, rotura de la máquina y amplia variación en el material recibido.
2º caso: encuentra seis, siete o más puntos arriba o abajo. Posibles causas: desgaste gradual de la herramienta, desgaste del equipo o desgaste relacionado con el instrumento de medición.
3º caso: comprobar el desplazamiento de la media. Posibles causas: nuevo método, nueva máquina en la mejora de la calidad y un nuevo lote de material.
4º caso: puntos fuera de los límites de control. Posibles causas: error de medición o tipificación, rotura de la herramienta o instrumento de medición no regulado, que no permite la identificación de la medición.
5º caso: periodicidad de puntos. Posibles causas: falta de uniformidad en la materia prima recibida, rotación de operadores, plantillas e instrumentos, y diferencia entre turnos.
2.2.2 GRÁFICOS DE CONTROL DE VARIABLES Y ATRIBUTOS
Los gráficos de control por variables están destinados a informar sobre la mejora de la calidad, la capacidad del proceso, la toma de decisiones con respecto a la especificación del producto, el proceso de producción y las decisiones sobre las piezas recién producidas. Se aplican donde las características de calidad se pueden medir cuantitativamente. Pueden ser, por ejemplo, dimensiones de piezas, volumen, peso, entre otros. Así, se percibe su amplio ámbito de aplicación, ya que varios tipos de procesos tienen este tipo de características (MAGALHÃES, 2011).
“Los gráficos de control para variables son más utilizados que los gráficos de control para atributos, porque tienen información más concreta, trabajando con muestras pequeñas, lo que permite identificar más rápidamente las causas que afectan la estabilidad del proceso” (REBELATO, 2006). “Los cuadros de control para variables son gráficos para medias, utilizados para controlar el valor promedio del rendimiento del proceso, cuadro de amplitud o gráfico de desviación estándar, siendo el gráfico de amplitud más utilizado, porque, en la mayoría de los casos, no se conoce la desviación estándar del proceso” (CASTRO, 2012).
Los gráficos de control se pueden clasificar en dos grupos: gráficos de control para variables: registra las características de calidad que se miden a escala cuantitativa. Y los gráficos de control por atributos: registra las características de calidad, midiéndose en una escala cualitativa, por ejemplo, se considera conforme y no conforme (SIQUEIRA, 1997). Así, según Spiegel y Stephens (2007), los términos ‘variables’ y ‘atributos’ se asocian con el tipo de datos recogidos del proceso.
2.2.3 GRÁFICO DE CONTROL PARA MEDIO (BARRA X) Y AMPLITUD ( )
El gráfico promedio ![]() se utiliza para controlar el promedio del proceso (centralidad) y el gráfico de amplitud
se utiliza para controlar el promedio del proceso (centralidad) y el gráfico de amplitud ![]() para controlar la variabilidad del proceso considerado (IPEK et al., 1999).
para controlar la variabilidad del proceso considerado (IPEK et al., 1999).
Expresiones para calcular los límites de control de ![]() y R.
y R.
Gráfico de control ![]() . La línea central y los límites de control superior e inferior para el gráfico de control
. La línea central y los límites de control superior e inferior para el gráfico de control ![]() son:
son:
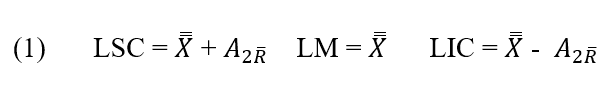
Gráfico de control R. La línea central y los límites de control superior e inferior para el gráfico de control R son:
![]()
2.2.4 GRÁFICO MEDIO (BARRA X) Y DESVIACIÓN ESTÁNDAR (S)
El gráfico de control para la media (gráfico de barras X) se utiliza para controlar la media del proceso, mientras que el gráfico de control (gráfico de desviación estándar S) se utiliza para controlar la variabilidad del proceso. Cuando el tamaño de la muestra (subgrupo) es menor o igual a diez, los gráficos R y S tendrán el mismo aspecto. Sin embargo, cuando el tamaño de la muestra crece, el gráfico S se vuelve más preciso que el gráfico R, y debe usarse (SIQUEIRA, 1997).
Gáfico de control ![]() . La línea central y los límites de control superior e inferior para el gráfico de control
. La línea central y los límites de control superior e inferior para el gráfico de control ![]() son:
son:
![]()
Gráfico de control S: 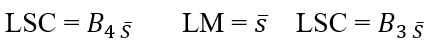
2.2.4.1 GRÁFICOS DE CONTROL POR ATRIBUTOS
Las tarjetas de atributos se utilizan para controlar el análisis de defectos. Estos gráficos son especialmente útiles para rastrear materias primas y productos terminados, y también se utilizan para analizar comentarios de calidad en cartas de consumidores. Un atributo es una característica de un producto, un proceso o cualquier otra población que se puede contar, pero no se puede describir, por lo que sus valores se incrementan (RODRIGUES, 1998). Son gráficos que nos permiten identificar cómo se comportan los conjuntos de muestras en torno a umbrales, tendencias y cambios de nivel. En las variables, se nota rápidamente cuando los datos no siguen una distribución aleatoria. En las tablas de control de atributos, las unidades se clasifican como perfectas o defectuosas según los criterios establecidos. Por tanto, la probabilidad de que se produzca una unidad defectuosa es constante y, en consecuencia, la distribución muestral correspondiente es binomial (CHAVES y TEIXEIRA, 1997). Las tarjetas de atributos se utilizan para controlar el análisis de defectos. Estos gráficos son especialmente útiles en el control de materias primas y productos terminados, y también se utilizan en el análisis de comentarios sobre calidad y características expresados cualitativamente, es decir, cuando estas características analizadas no están representadas numéricamente, se pueden clasificar según o no cumple (SOUZA, 2005). Se trata de medidas representativas que resultan de contar el número de elementos del producto en una escala discreta que presentan una característica particular de interés. Las mediciones se realizan mediante inspección visual y se registran las características no medibles. Se puede decir gráfico de control por variable aleatoria discreta con función de densidad de probabilidad de Poisson (LAGO, 1999).
Las matemáticas de las tarjetas de atributos no requieren tablas. Pueden aplicarse a sistemas en los que las medidas consisten en aprobar o desaprobar o a procesos en los que es muy difícil o imposible obtener medidas de variables (RODRIGUES, 1998).
La información estadística de las mediciones por atributos en la resolución de problemas de ciencias de la educación se clasifica en productos con anomalías o defectos. Uno de los principales objetivos del análisis de medición por atributo es identificar, detectar y corregir defectos, la calidad puede definirse como el conjunto de atributos que hacen que un bien o servicio sea plenamente apto para el uso para el que fue concebido (MONTGOMERY, 1985). Las cuatro gráficas de control por atributos en anomalías y defectos, utilizadas según Montgomery (2004), son las siguientes: Gráficas de controles por atributos que son: gráfica p (proporciones disconformes), gráfica np (unidades disconformes), C cuadro (número de incumplimientos por unidad) y Letra u (tasa de incumplimiento por unidad).
2.2.5 GRÁFICO P (PROPORCIONES NO CONFORMES)
Para Werkema (2006), el gráfico p se utiliza cuando la característica de la calidad de interés está representada por la proporción de artículos defectuosos producidos por el proceso analizado.
Gráfico de control P:
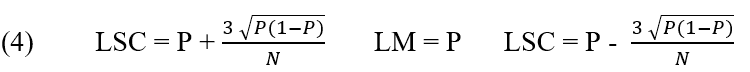
2.2.6 GRÁFICO NP (UNIDADES NO CONFORMES)
La carta no indica el número de defectos por muestra y se utiliza para controlar el número de productos defectuosos en cada lote y garantizar que el proceso esté bajo control (RODRIGUES, 1998).
La línea central y los límites de control superior e inferior para el gráfico np son:
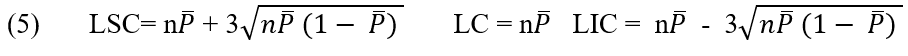
2.2.7 GRÁFICO C NÚMERO DE (NO CONFORME POR UNIDAD)
El gráfico c se utiliza para determinar si el número de defectos en un solo elemento está dentro de los límites de control definidos. Puede considerarse como inspección final (RODRIGUES, 1998). El gráfico c es más apropiado cuando los defectos se dispersan en un medio continuo, como: número de fallas por área de tela, número de imperfecciones por longitud de piso; y cuando un producto puede tener más de un tipo de defecto (RIBEIRO y CATEN, 2012).
Por lo tanto, los límites de control del gráfico C se calcularán utilizando las ecuaciones:
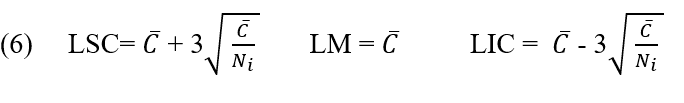
2.2.8 TASA DE INCUMPLIMIENTO GRÁFICO U POR UNIDAD
El gráfico u se utiliza para controlar defectos en una unidad de producción (MONTGOMERY, 1997). La tabla u se recomienda cuando el producto está compuesto por varias partes y muchas características de calidad que deben ser inspeccionadas y también cuando el tamaño de la unidad de producto es variable (CORTIVO, 2005).
La línea central y los límites de control superior e inferior para el gráfico U son:
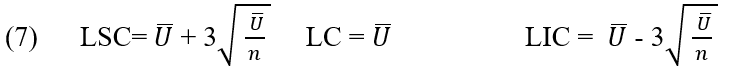
2.2.9 REGRESIÓN LINEAL MÚLTIPLE
El análisis de regresión múltiple es una técnica que se utiliza para investigar la relación entre una variable dependiente y un conjunto de variables independientes (MONTGOMERY y RUNGER, 2009). La técnica permite la estimación de valores futuros para la variable dependiente, dado un conjunto de datos de entrada para las variables independientes (PEDRINI y CATEN, 2009; DOWNING y CLARK, 2002)
El modelo base de regresión lineal múltiple donde ![]() para j=0,1,2…..k son coeficientes de regresión, Y es la variable dependiente de los regresores
para j=0,1,2…..k son coeficientes de regresión, Y es la variable dependiente de los regresores ![]() y el valor y es el error aleatorio de la ecuación. (MONTGOMERY, 2015).
y el valor y es el error aleatorio de la ecuación. (MONTGOMERY, 2015).
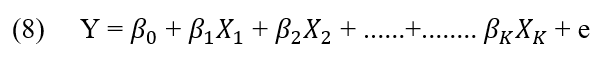
El proceso se estudia para comprender las necesidades de analizar las aplicaciones de las ciencias de la educación y sus pasos del proceso. Se plantean fuentes de análisis, las aplicaciones que se analizan en el mismo, son la variabilidad los principales factores que influyen en él. Identificar el tipo de gráfico de control más apropiado para analizar los datos mediante software minitab. Con el método de control estocástico del proceso se buscó la estructuración de la investigación con el fin de ayudar al progreso de la misma.
3. RESULTADOS Y DISCUSIÓN
3.1 EL USO DE GRÁFICOS DE CONTROL DE MINITAB PARA REDUCIR LA VARIABILIDAD
Después de recopilar y trazar los datos en aplicaciones de ingeniería, se construyeron algunos gráficos para variables y gráficos para atributos en los cuadros de control del software Minitab para monitorear las pérdidas debidas a variaciones en la producción. Para el análisis de los resultados, el rango de tolerancia compuesto por los componentes fue determinado por los siguientes componentes: Límite de control superior LSC, LC de línea media y Límite de control inferior LIC.
Se observó que después de identificar, eliminar y reducir las causas de variabilidad trajo la posibilidad de mejorar la calidad de los productos. A través del análisis de los resultados obtenidos en las aplicaciones estadísticas se presentará el control de estabilidad en las causas de defectos en los puntos muestral en las gráficas, y se realizó el control del proceso en muestra con el fin de controlar la variabilidad. Los gráficos de control presentaron los siguientes resultados entre los parámetros estadísticos: Cálculo de la media del proceso, Cálculo de la desviación estándar, Cálculo de los límites de control LSC, LIC y amplitud en las siguientes aplicaciones:
3.2 PROBABILIDAD Y APLICACIONES ESTADÍSTICAS EN INGENIERÍA POR GRÁFICO DE CONTROL EN SOFTWARE MINITAB EN REDUCCIÓN DE VARIABILIDAD
Construcciones gráficas en aplicaciones de estadística descriptiva ejecutadas por el gráfico de control en Minitab Software.
01) Los datos se refieren a un proceso de mecanizado de pines, en el que los diámetros se miden mediante el muestreo de 5 piezas en 25 lotes. Revise el proceso con Minitab Software.
Tabla 1: Mediciones del diámetro del pasador
| Lote | Medidas | ||||||
| 1 | 2,08495 | 2,09203 | 1,01425 | 0,47627 | 1,75308 | ||
| 2 | 2,44288 | 1,84913 | 1,02012 | 1,5103 | 0,5167 | ||
| 3 | 2,08819 | 0,34567 | 0,67246 | 2,14641 | 0,51528 | ||
| 4 | 1,42411 | 1,04348 | 1,15683 | 0,9108 | 1,23562 | ||
| 5 | 1,43307 | 0,22926 | 1,51612 | 0,82627 | 1,29935 | ||
| 6 | 1,2113 | 0,63715 | 0,97815 | 2,30782 | 1,0003 | ||
| 7 | 2,14731 | 1,95837 | 0,95294 | 1,35384 | 0,73037 | ||
| 8 | 2,02444 | 1,60384 | 1,64667 | 1,66449 | 0,92746 | ||
| 9 | 1,4743 | 1,93916 | 1,06107 | 1,55396 | 0,8049 | ||
| 10 | 1,09096 | 2,09033 | 0,62161 | 1,45256 | 1,77208 | ||
| 11 | 1,90879 | 1,274 | 1,46827 | 1,36343 | 1,06161 | ||
| 12 | 0,81791 | 1,89952 | 1,24044 | 0,72729 | 1,44959 | ||
| 13 | 0,58784 | 1,57195 | 0,73316 | 1,05367 | 3,29273 | ||
| 14 | 2,12184 | 0,90374 | 0,59773 | 1,63101 | 0,82706 | ||
| 15 | 1,2819 | 0,89479 | 1,05394 | 1,25779 | 0,99451 | ||
| 16 | 0,82836 | 0,16347 | 2,12864 | 1,69732 | 0,90752 | ||
| 17 | 0,14026 | 1,0432 | 0,76948 | 1,72083 | 3,95445 | ||
| 18 | 2,19158 | 0,87777 | 0,955 | 1,50304 | 1,1604 | ||
| 19 | 0,93195 | 1,82231 | 1,2179 | 1,72608 | 1,45375 | ||
| 20 | 0,84523 | 2,79753 | 2,30041 | 0,47693 | 0,58081 | ||
| 21 | 1,84098 | 2,37729 | 1,89976 | 1,2079 | 3,2343 | ||
| 22 | 1,15648 | 2,5689 | 0,90064 | 3,7548 | 1,24616 | ||
| 23 | 2,21913 | 0,91997 | 2,15777 | 1,48548 | 0,25288 | ||
| 24 | 1,41393 | 0,71069 | 0,63707 | 1,71835 | 1,52855 | ||
| 25 | 1,5938 | 1,19839 | 0,88228 | 1,23019 | 0,41643 | ||
Fuente: Acción (2019)
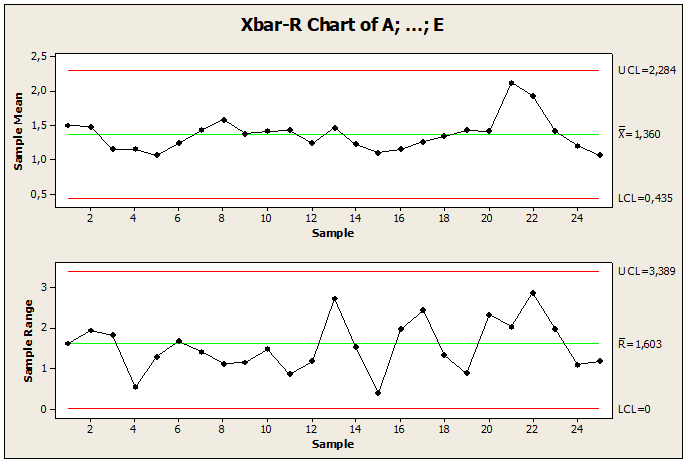
Figura 01: Gráfico de control de pin defectuoso fuera de control
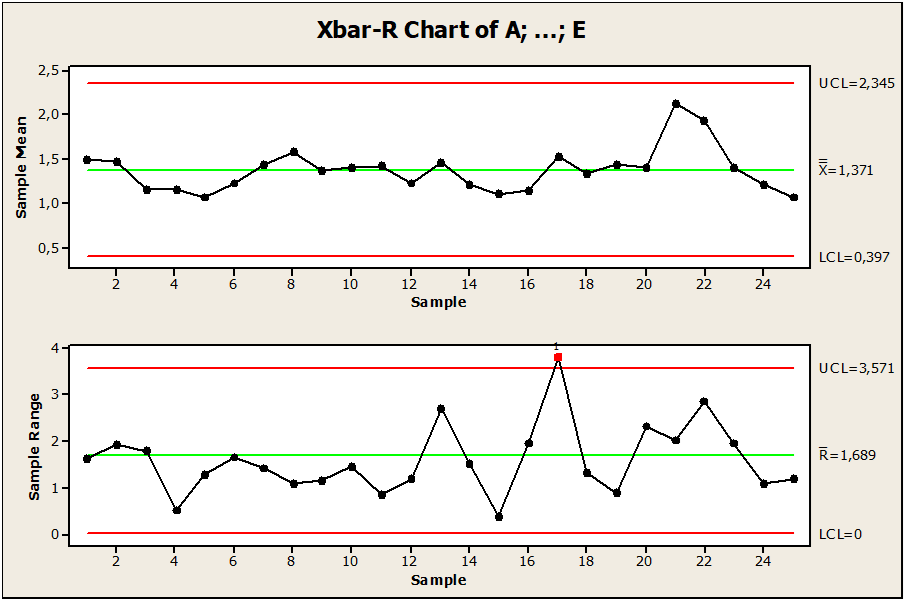
Los datos de muestra presentan un proceso de mecanizado de pines observado en 25 lotes de pines. Como se muestra en la Figura 01. Observamos que hay variación entre el punto 17 por encima del límite superior de control lsc, donde el punto está fuera del límite de control. Su límite central es igual a 1.68, límite de control superior con el valor 3.57 y límite inferior igual a 0.0, esto implica que el punto 17 en el valor pin 3.95445 está influenciado por la variabilidad. Por lo tanto, para mantener el proceso bajo control, se recomendó eliminar, cambiar valores o construir un nuevo gráfico.
Figura 02: Gráfico de control con los límites ajustados
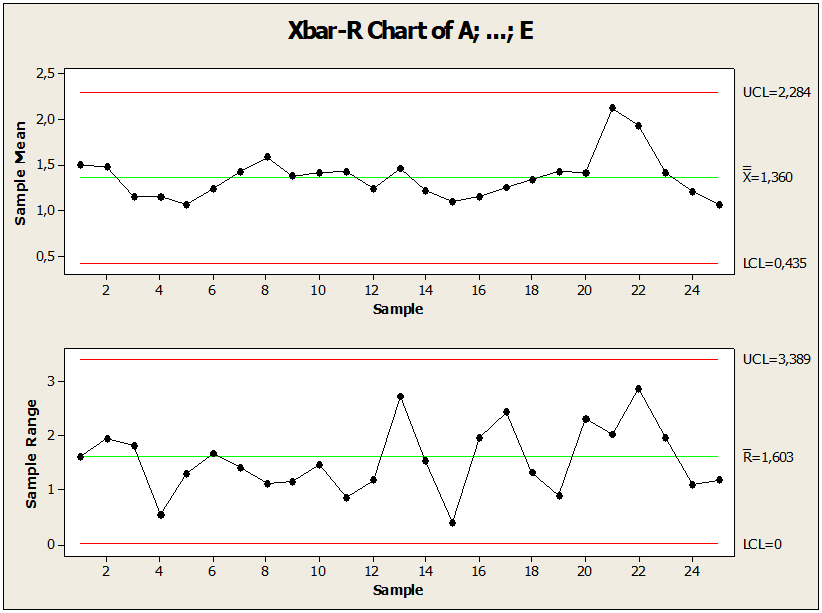
Después de comprobar la anomalía, Figura 02. El gráfico muestra el punto bajo control en relación con la media, donde hubo modificación para mantener el proceso bajo control. En la muestra del punto 17 del valor de no conformidad 3.95445, cambió a 2.55445. Este cambio realizado por el gráfico de control seguido de reglas estadísticas redujo la variabilidad y se ajustó el punto fuera del límite de control. Concluimos que todas estas medidas estadísticas mantuvieron el proceso estable. Después de identificar, analizar, corregir, reducir y controlar el proceso de muestras no conformes, fue posible comparar los resultados obtenidos con los resultados anteriores entre el proceso: Proceso fuera de control, LC igual a 1,68, desviación estándar igual a 0,69 y amplitud del valor límite 3,81 un punto por encima del límite. LSC. Proceso bajo control LC igual a 1,60, desviación estándar igual a y 0,66 Amplitud del valor límite 3,61. Después de la comparación con los valores calculados en la 1ª y 2ª prueba, hubo una mejora en los parámetros estadísticos.
Figura 03: Muestra los diámetros de los pines
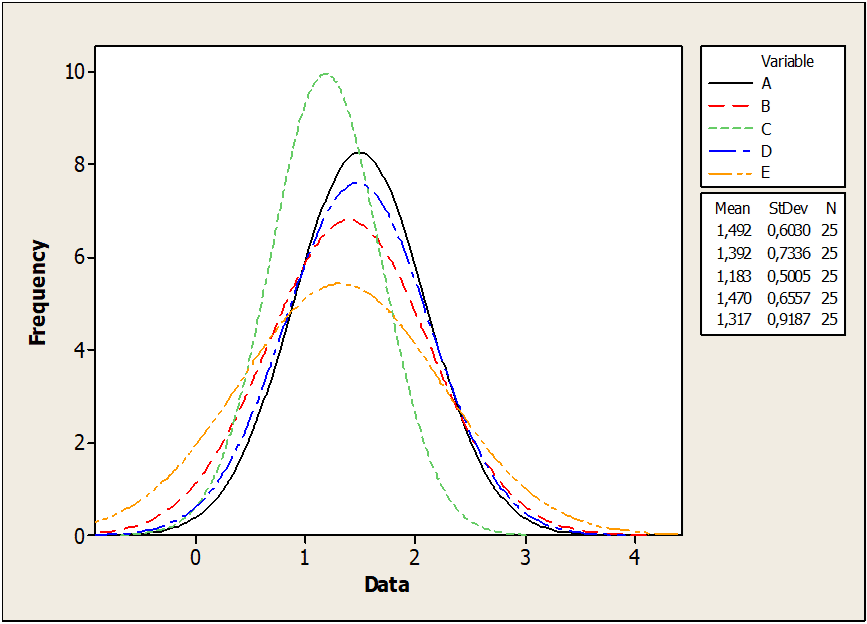
La Figura 03 muestra una curva de dispersión de diámetros de pasador en subgrupos de E con mayor precisión que la curva de dispersión de los subgrupos D. La desviación estándar para muestras del subgrupo E (0.91) es mucho mayor que las muestras del subgrupo D. (0.50). Por lo tanto, la distribución ajustada para el subgrupo E es aplanada y más precisa.
02) Se realizó un estudio para determinar el aumento de defectos en las puertas de acero inoxidable de los equipos de cocina producidos en una empresa metalúrgica. Durante el estudio, los defectos a continuación aparecieron con sus ocurrencias y costos asociados. Construya los respectivos diagramas de Pareto.
Tabla 2: piezas defectuosas
| Tipo de defectos | Nº. de piezas defectuosas | Costo unitario reparación/chatarra | |
| Soldadura mal ejecutada | 55 | 50 | |
| Perforación deficiente | 9 | 50 | |
| Defectos de flexión | 274 | 5 | |
| Embalaje | 15 | 50 | |
| Mala calidad de la placa | 16 | 50 | |
| Cortes | 126 | 30 | |
| Otro | 12 | 50 |
Fuente: Core Formation -Nufec (2006)
Figura 04: Números de piezas defectuosas
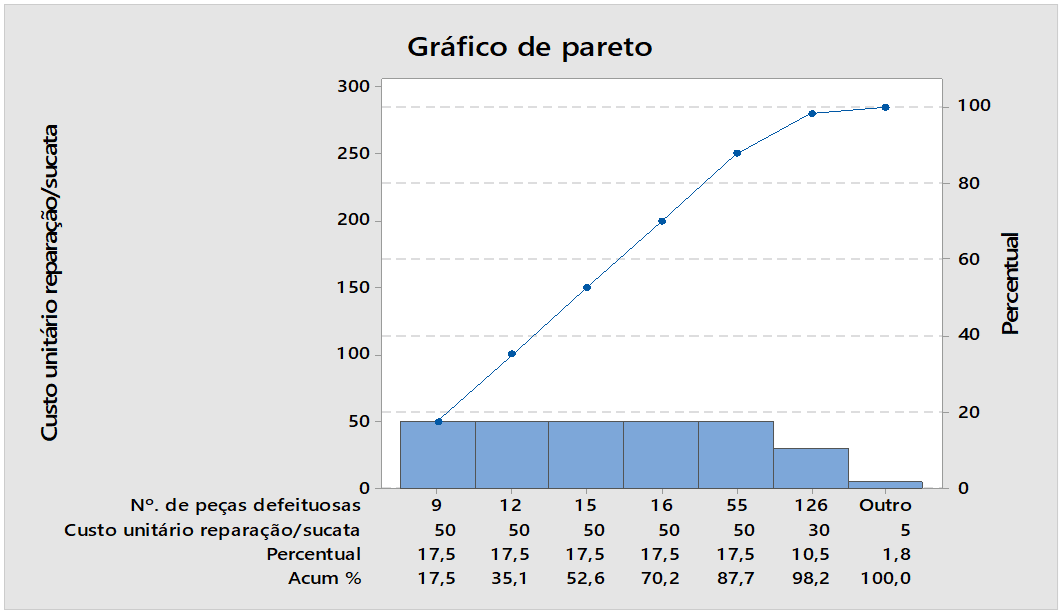
La Figura 04 muestra los resultados de los números de piezas defectuosas, porcentaje, la mayor fuente 9 piezas defectuosas que corresponde a un porcentaje del 17,5 %. Al analizar la figura, se percibe la presencia de concentración de causas de especial variabilidad que requieren corrección por el gráfico de control del software Minitab.
Figura 05: Proceso de números de piezas defectuosos fuera de control
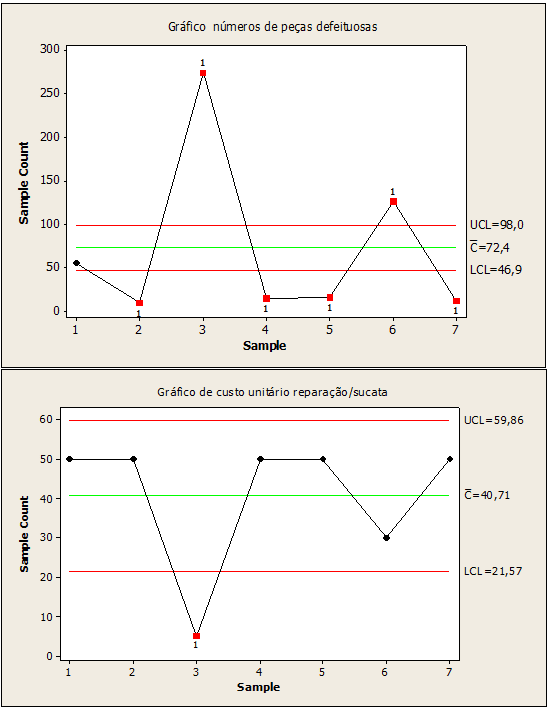
Se verificó que la figura 05, referidas a piezas defectuosas, mostraba variabilidad en los puntos 2,3,4,5,6,7 con valores (9.274,15,16.126,12). Por otro, coste unitario en la reparación de la chatarra puntual con variabilidad 3 con un valor igual a 5. Se concluye que hay causas especiales en estos puntos, y hay una necesidad de corrección.
Figura 06: Proceso de números de piezas defectuosos bajo control
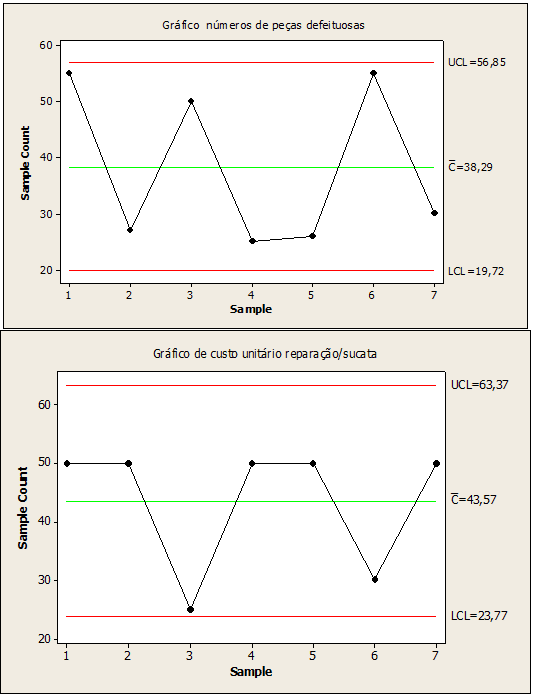
En la figura 06, los valores utilizados en lugar de los valores de los puntos fuera de control 2,3,4,5,6,7, seguidos son 27,50,25,26,55,30 para piezas defectuosas y 25 para la reparación de chatarra de costo unitario en el punto 3. Estos datos de reemplazo generados por la tabla de control mejoraron el proceso estocástico manteniéndose bajo control, reduciendo la variabilidad en la fabricación de portales de acero inoxidable, manteniendo estable la calidad del producto.
03) Un molde de extrusión se utiliza para producir varillas de aluminio. El diámetro de las cañas es una característica crítica de la calidad. La siguiente tabla muestra los valores x y r para 20 muestras de cinco cañas cada una. Las especificaciones en los bastones son 0.5035 +/- 0.0010 pulgadas. Los valores de los datos son los últimos tres dígitos de la medida, es decir, 34.2 se lee como 0.50342.
a) Usando todos los datos, encuentre los límites de control para los gráficos X y R, construya el gráfico y trace los datos.
b) Utilizar los límites de los intentos de control de elementos (a) para identificar puntos fuera de control. Si es necesario, revise sus límites de control, teniendo en cuenta que cualquier muestra fuera de los límites de control puede ser eliminada.
Tabla 3: Muestras de uñas
| Muestra | R | Muestra | R | ||
| 1 | 34,2 | 3 | 11 | 35,4 | 8 |
| 2 | 31,6 | 4 | 12 | 34,0 | 6 |
| 3 | 31,8 | 4 | 13 | 36,0 | 4 |
| 4 | 33,4 | 5 | 14 | 37,2 | 7 |
| 5 | 35,0 | 4 | 15 | 35,2 | 3 |
| 6 | 32,1 | 2 | 16 | 33,4 | 10 |
| 7 | 32,6 | 7 | 17 | 35,0 | 4 |
| 8 | 33,8 | 9 | 18 | 34,4 | 7 |
| 9 | 34,8 | 10 | 19 | 33,9 | 8 |
| 10 | 38,6 | 4 | 20 | 34,0 | 4 |
Fuente: Montgomery (2013)
Figura 07: Muestras de varillas fuera de control
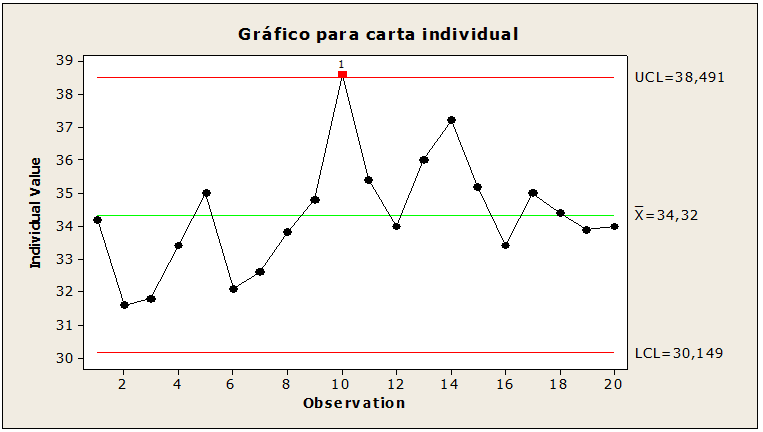
Control estadístico para 20 muestras de cinco varillas cada una. Al interpretar la figura 07, los valores del límite superior fueron 38,49, la media 34,32, la desviación estándar 1,72, el límite inferior 30,14 con el punto 10 del valor 38, 6 por encima del límite superior dando indicaciones de causas especiales que pueden ser correctas. Se sugiere una corrección en este punto para que se ajusten los límites.
Figura 08: Muestras de uñas bajo control
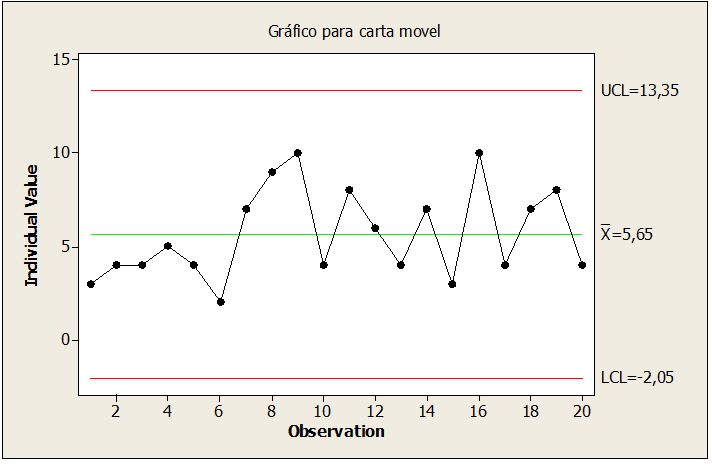
Al corregir el punto de la figura 08, se ajustó el punto 10, reduciendo el valor de la muestra a 36,6, manteniendo el proceso estable y bajo control en la fabricación del diámetro de las varillas de aluminio.
Figura 09: Muestras de tallo de capacidad de proceso
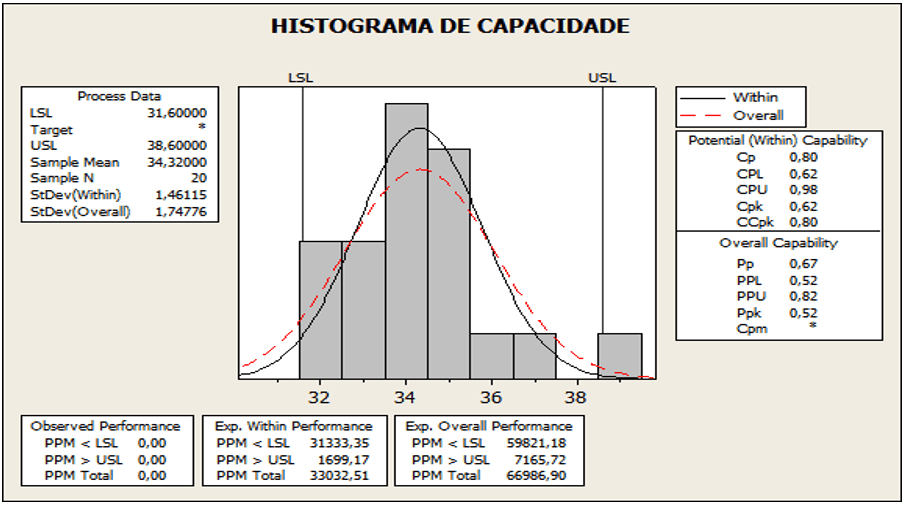
Según el análisis de la Figura 09, presenta el valor para Cpk igual a 0,49, media 5,65, desviación estándar 2,434 y valor p 0,025. Resultado de CPk fuera de los límites, si Ppk < CPk. La media obtenida fue de 5,65, con desplazamiento a la LSE. El CPk 0.49 inferior a los valores establecidos que implica 1.33 está fuera del límite estable.
Figura 10: Porcentaje de defectos
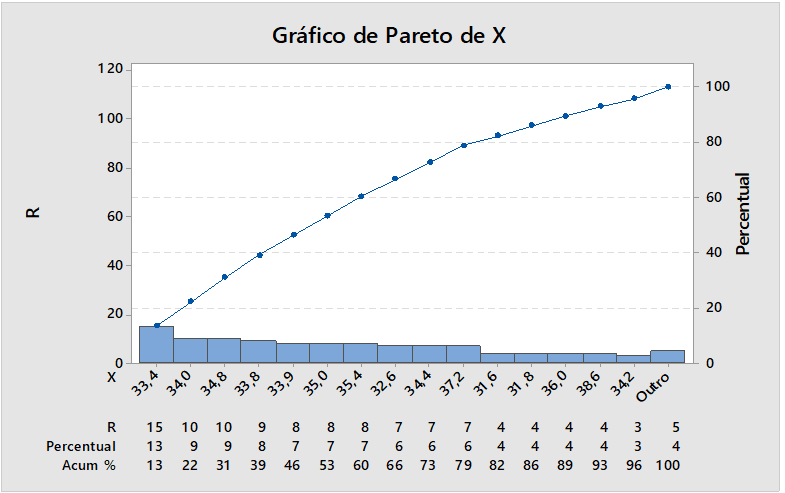
Figura 10. El gráfico de pareto proporciona el porcentaje de las muestras analizadas de defectuosos producidos en este proceso, porcentaje, la mayor fuente de 15 piezas defectuosas que corresponde a un porcentaje del 13%. Es necesario eliminar la variación.
Observando las cifras, se verificó que en la Figura 07, el punto 10 está fuera del límite de control, presentando anormalidad en el diámetro de las varillas que puede ser correcta. Ya en la figura 09, el cpk está fuera de los límites. Sin embargo, la figura 10, tiene un defecto en las varillas. Siguiente figura 08. Después de interpretar, analizar y eliminar las causas especiales en el punto del diámetro se mantuvo estable.
La Figura 11 muestra los gráficos de control para las medias, la desviación estándar y el número de no conformidades medidas mediante el muestreo de 5 piezas en 25 lotes. A través de los gráficos presentados podemos observar que hay un punto fuera del límite de control y se distribuye alrededor de la media, así como nos permitió observar el orden de la magnitud de las desviaciones del proceso y finalmente permitió encontrar los puntos de causas especiales, donde presenta un punto fuera del límite. A través de estos análisis, encontramos que existe variabilidad de causa especial en el punto 17 LSC, donde el punto está fuera del límite de control, lo que requiere correcciones y reducción de la variabilidad. Esta anormalidad fue detectada por la tabla de control de Minitab Software en la 1ª prueba donde el proceso fue necesario para estabilizarse. Entonces, para mantener el proceso bajo control, se aplicó la 2ª prueba para complementar la 1ª prueba con el fin de crear un nuevo gráfico de control que tenga el proceso bajo control.
Se recomendaron tres situaciones al construir el gráfico de límites bajo control: eliminar la observación del valor 3.95445, cambiar los valores de no conformidad o construir un nuevo gráfico. La 2ª prueba de la Figura 12. Mostrar la corrección, comparación y reducción de variaciones en la construcción de un nuevo gráfico con el punto bajo control en relación a la media, con modificación en el punto de muestreo con el fin de mantener el proceso bajo control. El valor de la muestra 3,95445 cambió el valor 2,55445. Después de controlar el proceso, fue posible comparar los resultados obtenidos con los resultados anteriores entre los procesos. En comparación con los valores del cálculo de la muestra en el proceso bajo control, la media presentó el valor igual a 1,60, la desviación estándar 0,66 y la amplitud del valor límite 3,66. Mientras que el proceso fuera de control significa igual a 1.68, desviación estándar 0.69 y amplitud límite con valor 3.81.
Figura 11: Carta fuera de control
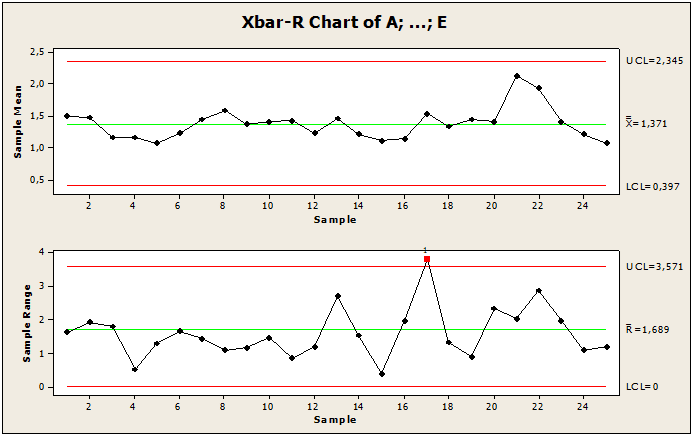
Figura 12: Carta bajo control
Los resultados obtenidos en este estudio muestran las tablas de control como una herramienta eficaz para reducir la variabilidad en las aplicaciones de las ciencias de la educación al encontrar la estabilidad del proceso y mejorar la calidad.
4. CONCLUSIÓN
A través de los gráficos de control del software Minitab, fue posible trazar y analizar cambios en la distribución de la muestra en el proceso estadístico informando puntos críticos con variabilidad en aplicaciones de las ciencias de la educación. A través del análisis de los gráficos de control podemos percibir que las aplicaciones estadísticas presentaron variabilidad.
El gráfico es una herramienta utilizada para controlar la anormalidad mediante pruebas estadísticas y se encontró variabilidad en algunos puntos de muestra de aplicaciones estadísticas. Por lo tanto, era necesario hacer inferencias en el control de variables con puntos fuera de control. Se verificó por la 1ª prueba que los subgrupos que son inusuales en comparación con otros subgrupos presentaban anomalías, y hubo necesidad de aplicar la 2ª prueba para corregir y mantener el proceso bajo control.
Los gráficos permiten verificar las variaciones y estabilizar las variables entre los parámetros medios, las desviaciones estándar y la amplitud. Los gráficos permitieron aproximar los puntos de muestreo fuera de los límites y ajustar los defectos entre límites, ayudando en la mejora continua del proceso, permitiendo percibir defectos y controlar las causas de variación anormal entre los parámetros limitados del cuadro bajo comparación de las muestras en las pruebas de verificación.
Analizando los gráficos con el fin de establecer límites para futuras inspecciones sería necesario eliminar la variabilidad espacial y después de cambiar las muestras construir un nuevo gráfico en minitab se hace factible en la eliminación de estos puntos para el cálculo de los límites revisados.
Los objetivos establecidos en esta investigación se lograron con éxito al permitir el uso de técnicas estadísticas para identificar y eliminar anomalías que no se ajustan a los problemas estadísticos. Tales técnicas permitieron la inferencia en aplicaciones de ingeniería a través de muestras. Las acciones redujeron la ocurrencia de variabilidad en Minitab Software y, por lo tanto, mantuvieron el proceso estocástico estable y bajo control. Este tema expuso que es posible recopilar, analizar e interpretar datos a través de gráficos de control, ya que a través de esta herramienta es posible verificar anomalías en problemas estadísticos.
Se encuentra que el software estadístico es capaz de cumplir con las especificaciones en el control de procesos. Se verificó la necesidad de utilizar Minitab para prevenir posibles causas de variabilidad. Finalmente, con el presente estudio de variabilidad, fue posible percibir y comprender la contribución de los recursos de los gráficos de control mediante la aplicación del software en la reducción de la anormalidad en las aplicaciones de la ciencia estadística.
REFERENCIAS
BORTOLOTTI, S. L. V. et al. Análise da qualidade do produto final no processo de envase de azeitonas verdes. Tecnol. & Hum., Curitiba, ano 23, n. 36, jan/jun. 2009. Disponível em: https://revistas.utfpr.edu.br/rth/article/viewFile/6238/3889
CARPINETTI, L. C. R. Gestão da Qualidade, Conceitos e Técnicas. São Paulo: Atlas S.A., 2010.
CARPINETTI, L. C. R. Gestão da Qualidade: Conceitos e Técnicas. São Paulo: Atlas, 2010.
CARPINETTI, L. C. R. Gestão da Qualidade: Conceitos e Técnicas. São Paulo: Atlas, 2010.
CASTRO, D. R. C. et al. A aplicabilidade dos gráficos de controle nas empresas como modelo de inspeção para a avaliação da qualidade. In: XXXII Encontro Nacional de Engenharia de Produção. Bento Gonçalves, RS, 2012. Disponível em: http://www.abepro.org.br/biblioteca/enegep2012_tn_stp_158_921_20804.pdf
CHAVES, J. B. P. Controle de Qualidade na Indústria de Alimentos. Viçosa,
MG, (s.n.), 1997.
CHAVES, J. B. P.; TEIXEIRA, M. A. Controle Estatístico de Qualidade:
inspeção por amostragem/ mapas de controle. DTA/UFV. Viçosa, MG: (s.n.), p. 162,
1997.
CORTIVO, Z. D. Aplicação do Controle Estatístico de Processo em sequências curtas de produção e análise estatística de processo através do planejamento econômico. Curitiba: Universidade Federal do Paraná, 2005.
FERREIRA, J. M.; OLIVEIRA, M. S. de. Controle estatístico da qualidade. Lavras: UFLA/FAEPE, p.87, 2008.
GADELHA, G. R. de O.; MORAIS, G. H. N. Análise do Processo de Desperdício de Embalagens em uma Indústria Alimentícia: Aplicação das Quatro Primeiras Etapas do MASP. Fortaleza-SC: XXXV ENEGEP, 2015.
GADELHA, G. R. de O.; MORAIS, G. H. N. Análise do Processo de Desperdício de Embalagens em uma Indústria Alimentícia: Aplicação das Quatro Primeiras Etapas do MASP. Fortaleza-SC: XXXV ENEGEP, 2015.
HORA, H. R. M., COSTA, H. G. Tomada de decisão no MASP: uma contribuição para decisões utilizando a matriz AHP. XXIX Encontro Nacional de Engenharia de Produção. Salvador. ENEGEP, 2009.
IPEK, H. et al. The application of statistical process control. Minerals Engineering, Vol. 12, Issue 7, p. 827-835, 1999. ISSN 0892-6875. Disponível em: https://doi.org/10.1016/S0892-6875(99)00067-9.
JURAN, J. M.; GRYNA, F. M. Controle da Qualidade: Métodos Estatísticos Clássicos Aplicados à Qualidade. São Paulo, Ed. Makron, 1992.
LAGO NETO, J. C. do. O efeito da autocorrelação em gráficos de controle para variável contínua: Um estudo de caso. Florianópolis, 1999.
MAGALHÃES, M. S. de; MOURA NETO, F. D. Economic-statistical design of variable parameters non-central chi-square control chart. Production, v. 21, n. 2, p. 259–270, 2011.
MICHEL, M. H. Metodologia e Pesquisa Científica em Ciências Sociais: Um Guia Prático para Acompanhamento da Disciplina e Elaboração de Trabalhos Monográficos. São Paulo: Atlas, 2005.
MINITAB. Conheça o Minitab para Windows. 1º. ed. São Paulo: Editora Minitab
Inc., 2010.
MONTGOMERY, D. C. Estatística Aplicada e Probabilidade para Engenheiros. Tradução e revisão técnica Verônica Calado. Rio de Janeiro, LTC, 2015.
MONTGOMERY, D. C. Introdução Ao Controle Estatístico Da Qualidade. 4. ed. Rio de Janeiro: LTC, 2009.
MONTGOMERY, D. C. Introdução ao Controle Estatístico de Qualidade. 3. ed. Rio de Janeiro: LTC, 1997.
MONTGOMERY, D. C. Introdução ao Controle Estatístico de Qualidade. 4. ed. Rio de Janeiro: LTC, 2004.
MONTGOMERY, D. C. Introdução ao Controle Estatístico de Qualidade. 3. ed. Rio de Janeiro: LTC, 2013.
MONTGOMERY, D. C. Introdução ao controle estatístico de qualidade. Rio de Janeiro: LTC, 2016.
OLIVEIRA, T. S.; LIMA, R. H. P. Aplicação do controle estatístico de processo na mensuração da variabilidade em uma usina de etanol. Anais. INGEPRO Inovação, Gestão e Produção, v. 3, n. 6, p. 022-033, 2015.
OLIVEIRA, V. F. de. Mobilidade e acessibilidade urbana: uma análise socioespacial a partir dos bairros Jardim Morada do Sol e Conjunto Habitacional Ana Jacinta, em Presidente Prudente. Faculdade de Ciências e Tecnologia – FCT, Unesp, 2011.
PALLADINI, E. P. et al. Gestão da Qualidade: Teoria e Casos. 2. Ed. São Paulo: Atlas, 2010.
PEDRINI, D. C. Proposta de um método para aplicação de gráficos de controle de regressão no monitoramento de processos. Universidade Federal do Rio Grande do Sul: UFRGS, 2009.
PEREIRA, A.; PATRÍCIO, T. Guia prático de utilização: análise de dados para Ciências Sociais e Psicologia. 8.ª ed. Lisboa : Sílabo, 2013.
REBELATO, M. G. et al. Estudo sobre a aplicação de gráficos de controle em processos de saturação de papel. XIII SIMPEP. Bauru, SP: 2006.
RIBEIRO, J. L.; CATEN, C. T. Controle estatístico de processos: Apostila de Curso. Porto Alegre: UFRGS, 2012.
RICHARDSON, R. J. Pesquisa social: métodos e técnicas. 3 ed. São Paulo: Atlas, 1999.
RICHARDSON, R. J. Pesquisa social: métodos e técnicas. São Paulo: Atlas, 1999.
RODRIGUES, G. P. Controle Estatístico de Qualidade e de Processo na Indústria de Alimentos. Universidade Federal de Viçosa, MG, p. 152,1998.
ROSA, L. C. Introdução ao Controle Estatístico de Processos. Santa Maria, Ed. Da UFSM, 2009.
SIQUEIRA, L. G. P. Controle Estatístico de Processos – Equipe Grifo – Série Qualidade Brasil. São Paulo: Pioneira, 1997.
SOUZA, A. M., RIGÃO, M. H. Identificação de variáveis fora de controle em processos produtivos multivariados. Revista Produção, São Paulo, V.15 no.1, p.74-86, abr. 2005.
SOUZA, R. Case Research in Operations Management. EDEN Doctoral Seminar on Research Methodology in Operations Management, Brussels, Belgium, 2005.
SPIEGEL, M. R.; STEPHENS, L. J. Schaum’s esboço de teoria e problemas de estatística: Aprenda a si mesmo. 4ª ed., Rio de Janeiro: LTC, 2007.
TRIVELLATO, A. A. Aplicação das sete ferramentas básicas da qualidade no ciclo PDCA para melhoria contínua: estudo de caso numa empresa de autopeças. Trabalho de conclusão de curso, Universidade de São Paulo, 2010.
VIEIRA, S. Estatística para a qualidade: como avaliar com precisão a qualidade em produtos e serviços. Rio de Janeiro: Elsevier, 1999.
VILAÇA, A. C.; OLIVEIRA, R. C. B. Utilização do Controle Estatístico de Processo para Avaliação de Peso de Massas para Pastel. FAZU em Revista, Uberaba, n. 8, p. 137-146. 2011.
WERKEMA, M. C. C. Avaliação de sistemas de medição. 2.ed. Belo Horizonte: Werkema. 2012.
WERKEMA, M. C. C. Ferramentas estatísticas básicas para o gerenciamento de processos. Belo Horizonte: Werkema, 2006.
YIN, R. K. Estudo de caso: planejamento e métodos. 2. Ed. Porto Alegre: Bookman, 2001.
[1] Maestría en Ingeniería de Procesos – PPGEP / ITEC-UFPA.
[2] Doctor en Ingeniería de Recursos Naturales por la Universidad Federal de Pará.
Enviado: Abril de 2021.
Aprobado: Junio de 2021.