REVISIÓN POR PARES
D’AGOSTINO, José Rubens Buccolo[1]
D’AGOSTINO, José Rubens Buccolo. Patrones de repeticiones en la división por números primos. Revista Científica Multidisciplinar Núcleo do Conhecimento. Año 08, Ed. 01, vol. 01, págs. 96-109. Enero 2023. ISSN:2448-0959, Enlace de acceso: https://www.nucleodoconhecimento.com.br/olimpiada-de-matematica/por-numeros-primos, DOI: 10.32749/nucleodoconhecimento.com.br/olimpiada-de-matematica/por-numeros-primos
RESUMEN
El tema de esta peer review explora las posibilidades de repetir patrones que involucran números primos. Para ello se demuestran análisis de división de números naturales por números primos. Adicionalmente, se realizan comparaciones entre intervalos de dividendos, así como entre cocientes, utilizando algoritmos y hojas de cálculo. Y finalmente, se presentan gráficamente los eventos que demuestran prueba de autenticidad.
Palabras llave: Patrones primos, Indexación de números primos, Factorización y números primos, Arquitectura de números primos, Física cuántica y números primos.
1. INTRODUCCIÓN
Esta peer review resulta de la observación de operaciones matemáticas largas y el desarrollo secuencial de algoritmos, necesarios para mostrar consistencia en las conexiones entre números primos. En la metodología utilizada, las respuestas se distribuyen sistemáticamente en hojas de cálculo de acuerdo con la aparición de nuevos resultados, lo que permite que nuevos hechos computados amplíen las posibilidades de llegar a las respuestas evolutivas buscadas. Tal dirección de pasos encarna una forma de investigación insustituible cuando ocurren descubrimientos inesperados, es decir, un camino que necesita estar basado en datos sólidos que hasta entonces se desconocían. Por tanto, con cada nueva información que aparece, es necesario crear algoritmos específicos, que validen de forma segura los nuevos datos que se añaden a la investigación.
A continuación, se presentarán secuencialmente hojas de cálculo y gráficos, comprobando la existencia de correlaciones en la secuencia de números primos. Creo que de los casos demostrados en esta investigación surgen más interrogantes que incitan a los estudiosos y que también pueden ser aplicados a otras ciencias.
2. DEMOSTRACIÓN DE LA EXISTENCIA DE PATRONES DE REPETICIÓN EN LA DIVISIÓN POR NÚMEROS PRIMOS
Los descubrimientos sobre los números primos y sus aplicaciones siempre sorprenden, y este es precisamente el tema central de esta peer review, que se presenta a continuación.
Considerando que todo número natural (n) es divisible al menos una vez por un número primo (p), resultando un cociente entero (q), podemos crear una ecuación definiendo intervalos enteros (I), es decir:
(n2/p1=q2) – (n1/p1=q1) = I
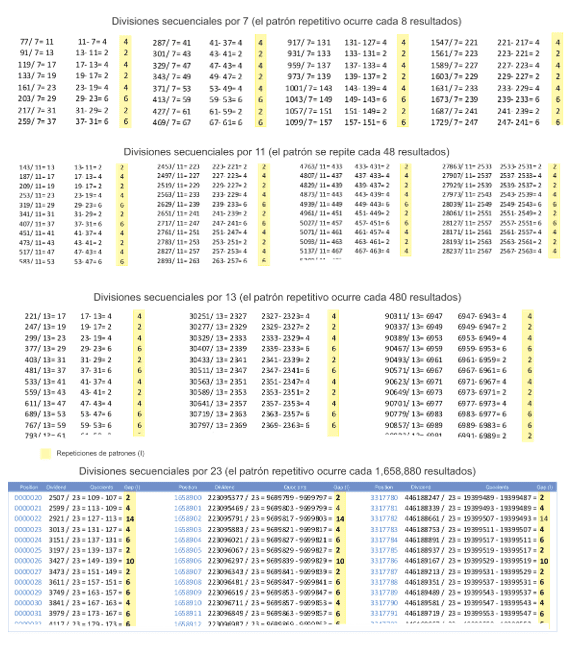
Por tanto, dividiendo secuencialmente números naturales (n1,n2,n3…) por el mismo número primo (p) y restando posteriormente los cocientes enteros resultantes de estas divisiones (q2-q1), definiremos una secuencia de intervalos (I), como se muestra horizontalmente en la tabla a continuación, Figura 1. Note que en la secuencia de divisiones por 7, que está marcada en amarillo, podemos observar la ocurrencia de patrones de repetición, que cada ocho celdas se repiten hasta el infinito.
Figura 1. Hoja de cálculo con patrones de repeticiones de intervalo (I) entre cocientes

En las divisiones por 2 a 7, de esta tabla, podemos observar que existen patrones de intervalo (I), los cuales se repiten con una frecuencia de (p1, p2, p3, p4) así: Uno (I) para división por 2 y por 3; Dos (I) para la división por 5; y Ocho (I) para división por 7, etc.
Hay secuencias transversales con valores repetidos también marcados en esta tabla, podremos entender por qué suceden al final de esta peer review.
3. TODOS LOS NÚMEROS PRIMOS CREAN UN PATRÓN REPETITIVO CUANDO SON DIVISORES SECUENCIALES
En las siguientes tablas, en la Fig. 2, podemos ver que los patrones de repetición tienden a repetirse hasta el infinito. Así, sabiendo que (I) es el intervalo entre la sucesión de cocientes, estos resultados nos muestran que existen patrones de repetición, a partir de: Ocho (I) para división por 7; Cuarenta y ocho (I) para división por 11; Cuatrocientos ochenta (I) para la división por 13 y Un millón seiscientos cincuenta y ocho mil ochocientos ochenta (I) para la división por 23.
Figura 2. Tablas que contienen patrones parciales de divisiones por diferentes números primos
4. CUALQUIER NÚMERO PRIMO, CUANDO ES DIVISOR GENERA UN ÍNDICE DE DISTANCIA NUMÉRICA ENTRE LOS CORRESPONDIENTES DIVIDENDOS
Durante más de dos mil años, las tablas que contienen números primos han captado nuestra atención. Recientemente, con el desarrollo de Algoritmos que generan grandes tablas, se ha hecho posible visualizar nuevos fundamentos en el comportamiento de estos peculiares números. Uno de los conceptos inusuales es que en la división secuencial de cualquier número natural (D) por el mismo número primo (P), luego de un período aleatorio, ocurre un patrón de repetición entre los intervalos del cociente (I). Cuando se encuentran estos patrones que se repiten, es posible reconocer la existencia de un índice para cada número primo, que es un intervalo constante entre los dividendos correspondientes. A continuación se muestra un diagrama que representa el comportamiento de estos índices (Figura 3).
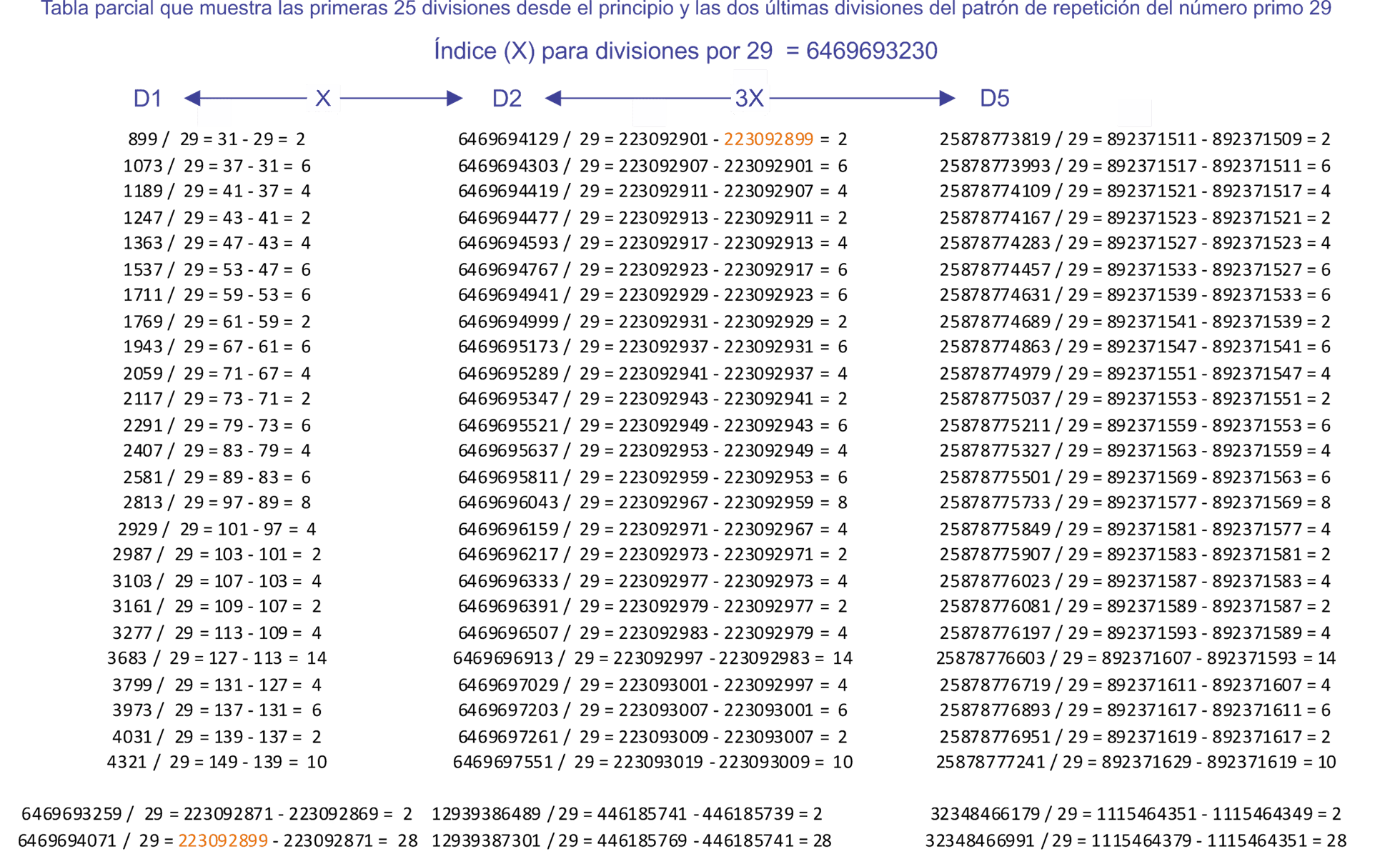
Figura 3. Diagrama que muestra que existe un índice (X) entre los dividendos correspondientes (D) para las divisiones por un solo número primo

Si consideramos que los patrones de repetición (P) son un divisor primo que define una sucesión acotada, entonces nos daremos cuenta de que (P) representa una espiral que se expande hasta el infinito, partiendo de un centro común.
Al comparar las columnas de la tabla anterior, podemos ver que los dividendos (D1) si se restan de los dividendos correspondientes (D2), definen el mismo valor del índice (X), que se expande en línea recta con perfecta homogeneidad en todas las direcciones hacia el infinito.
5. SIEMPRE HAY CORRESPONDENCIAS EN LA SECUENCIA DE DIVISIONES POR LOS MISMOS NÚMEROS PRIMOS
Observamos en la lectura de esta peer review que hay mucha correspondencia en las divisiones por números primos. En la siguiente tabla, se marcan los intervalos entre dividendos, así como entre divisiones por un mismo número primo, asegurándose así de que ambos son patrones de repetición que se proyectan sincrónicamente hasta el infinito.

Figura 4. Patrón repetido completo para el número primo 13, que se muestra horizontalmente

6. TABLAS QUE MUESTRAN LA EXISTENCIA DE PATRONES DE REPETICIÓN, ASÍ COMO LA EXISTENCIA DE UN ÍNDICE PARA CADA UNO DE LOS NÚMEROS PRIMOS, QUE PERMANECE IGUAL HASTA EL INFINITO
El descubrimiento de que hay un índice para cada número primo, que vincula un dividendo específico (D) a sus pares mayores, continuando hasta el infinito, también revela otro patrón sorprendente, ya que estos índices (X) están directamente relacionados con él, la suma de los intervalos (I) que ocurren con su número primo anterior (P), definiendo así otro patrón: Suma(P2(I)) = P1(X), como podemos ver al final de la siguiente tabla. (Figura 5)

Figura 5. Tabla con números primos, cantidad de intervalos, suma total de intervalos e índices entre dividendos

En las cuatro tablas siguientes hay referencias a los Índices (X) que se presentaron en la Figura 5 a partir de la división por los números primos 29 a 41.
A pesar de la certeza de que existen patrones de división por números primos, que se muestran en las tablas y gráficos anteriores, queda la duda de si es posible tener una sola ecuación que permita definir los siguientes patrones de repetición, con divisiones por números primos mayores que 29. Aun así, usando algoritmos, podemos encontrar el último dividendo de cualquier patrón repetitivo, verificando así que realmente hay infinitos patrones repetitivos en subsiguientes divisiones por cualquier número primo. Sin embargo, para divisiones superiores al número 41 es necesario utilizar equipos más potentes para lograr los resultados necesarios. Por lo tanto, aún es necesario crear largas tablas de intervalos entre cocientes de divisiones por números primos, hasta que dichos patrones repetitivos ocurran naturalmente, si queremos conocer cantidades de intervalos existentes, sus valores específicos y sus detalles geométricos.
Aunque las divisiones entre números primos se calculan progresivamente, pudiendo así probar la existencia de correspondencias entre los dividendos y permitiendo identificar el índice relativo a cada número primo, todavía parece que no hay forma de calcular patrones de intervalos entre cocientes sin producir tablas completas.
7. LOS NÚMEROS ENTEROS DIVIDIDOS SECUENCIALMENTE POR EL MISMO NÚMERO PRIMO RESULTARAN EN UNA SECUENCIA PERIÓDICA DE COCIENTES NÚMEROS PRIMOS
Como ejemplos de este efecto, tenga en cuenta que los primeros cuatro dividendos, divididos por el Prime 7, son 49, 77, 91, 119 que resultan en los cocientes 7, 11, 13, 17. Luego, para divididos por 11, son 121, 143, 187, 209 resultando en los cocientes 11, 13, 17, 19. Al igual que los divididos por 13 son 169, 221, 247, 299, lo que resulta en los cocientes 13, 17, 19, 23. y los divididos por 29, que son 841, 899, 1073, 1189, lo que resulta en la secuencia de cocientes primos 29, 31, 37, 41. Continuando así hasta el infinito.
Estas sucesiones periódicas de cocientes son la causa de las posiciones transversales de repetición de intervalos de igual valor que se muestran en la figura 1.
Otro detalle importante de estos patrones de repetición es que ocurren igual para dividendos positivos y negativos, reflejando perfectamente los patrones de intervalos entre los cocientes, y también generan los mismos índices.
8. CONCLUSIONES
Con la llegada de los nuevos procesadores, es posible crear tablas con un gran número de celdas y así poder visualizar secuencias con divisiones extraordinarias que pueden generar patrones repetitivos de intervalos entre cocientes, definiendo así un hecho matemático más. Por supuesto, no solo las máquinas pueden encontrar nuevos resultados matemáticos, sino que detrás de ellos está la necesidad de que los académicos desarrollen algoritmos. Por tanto, la intuición y la observación humana son, en estos casos, imprescindibles para que se produzcan nuevos descubrimientos en la ciencia. Y algunos de estos descubrimientos largamente esperados incluso se relacionan con las peculiaridades de los números primos.
En esta peer review, espero haber demostrado que hay patrones intrigantes de repetición entre intervalos de dividendos cuando se dividen por el mismo número primo. Al mismo tiempo, estos patrones dan evidencia de la existencia de un índice específico para cada número primo que se proyecta hacia el infinito. Quizás la posible revelación de estos eventos también puede encontrar soluciones matemáticas que involucren o ayuden a otras ciencias, cumpliendo así otro paso importante en los descubrimientos científicos.
NOTA
La traducción del material del inglés al español fue responsabilidad del autor.
[1] Licenciatura en Diseño Industrial. ORCID: 0000-0002-7149-9780.
Enviado: Diciembre de 2022.
Aprobado: Diciembre de 2022.




4 comentarios
Hola José Ruben buccolo D’agostin
Soy Daniel Mercado desde Puerto Rico un aficionado y artístico de los números por varios años. Leí tu investigación y resulta está alineada y coincide con mis estudios y mis análisis. Estos patrones que involucran números primos lo llamé “La estructura de los primos” que es lo mismo decir el Largo Estructural de los Primos (lep) para poder visualizarlo diseñé colores visuales al que llamé tipologías numerales coloreando los valores separando aquellos números compuestos de lo que no son números compuestos. Llevo investigando y coloreando los comportamientos de los números usando como referencia la tabla de multiplicación. La Figura1 mostrado en tu estudio lo tengo coloreado representándolo en la “Tipología de números primos” adquiriéndolo por la estructura que representa el número. La ocurrencia de patrones de repetición de la Figura1 por 5 que tienes dos y los valores que esto representa en una ecuación lineal sería lo siguiente: n2+(6-(n2-n1)) ó nk +(6-(n(k) – n(k-1))) ó si deseas probarlo en hoja de cálculo suponer que la celda A1 = 5 y la celda A2 = 7 entonces para celda A3 = A2 + (6-(A2 – A1)) y recorra la fórmula en la columna A y observará que los saltos corresponde a 4 y 2. Para hallar los valores de una ecuación lineal para los restos de los números tienden a complicarse al crecer su tamaño.
También formulé que el largo de esa estructura para número primo (lepk) es lepk = (pk-1)-1)*(lepk-1).
Tomamos como ejemplo p = 11, el largo de estructura para pk 11 = (7-1) x (8) = 6*8 =48
Para pk 13 = (11-1)x48 = 480
Te proveo mi lista:
para pk = 5 es 2
para pk = 7 es 8
para pk = 11 es 48
para pk = 13 es 480
para pk = 17 es 5760
para pk = 19 es 92160
para pk = 23 es 1658880
para pk = 29 es 36495360
para pk = 31 es 1021870080
para pk = 37 es 30656102400
para pk = 41 es 1103619686400
para pk = 43 es 44144787456000
para pk = 47 es 1854081073152000
para pk = 53 es 85287729364992000
para pk = 59 es 4434961926979580000
para pk = 61 es 257227791764816000000
para pk = 67 es 15433667505889000000000
para pk = 71 es 1018622055388670000000000
para pk = 73 es 71303543877207000000000000
para pk = 79 es 5133855159158900000000000000
para pk = 83 es 400440702414394000000000000000
para pk = 86 es 32836137597980300000000000000000
para pk = 97 es 2791071965828330000000000000000000
para pk = 101 es 267942882799520000000000000000000000
etc.
Me despido, en caso de querer contactarme para conocer mis diseños y estudios lo puede hacer ya que veo que está altamente alineado a tu investigación.
Hola Daniel Mercado, gracias por tu comentario.
Es muy interesante que lleguemos, por diferentes caminos, a una secuencia numérica similar en relación a los números primos. Su ecuación demostró que las divisiones por el mismo número primo, tienen una lógica creciente por la cantidad de intervalos entre cocientes, formando así patrones de repetición.
En mi caso, como habrás notado, descubrí estas secuencias creando tablas y comparando resultados. Afortunadamente, mi trabajo práctico logró revelar tal cadencia de intervalos que eventualmente no se podía percibir de otra manera, lo que permitió la visualización de ecuaciones, como las que ejecutaste con calidad.
Mis estudios comenzaron con algoritmos, los cuales desarrollé, para crear tablas secuenciales de números primos hasta quintillones y al observar detalles pude ver que había repeticiones de patrones para cada división por un mismo número primo, teniendo en cuenta que los dividendos (secuencia de números naturales) no eran divisibles por un primo menor. Lo que me permitió crear una tabla y comparar los intervalos entre cocientes. Esta tabla está en la Figura 1.
De hecho, mi intuición desde 2019 era que podía haber patrones de repeticiones en los intervalos entre los cocientes, en las divisiones por números primos, y no entre sus secuencias crecientes, y al final mis algoritmos y conocimientos de creación de hojas de cálculo acabaron mostrando que esto sucede. Me sorprendió que no se mencionaran estos patrones repetitivos o que se hayan publicado artículos desde que creé la hoja de trabajo en la Figura 1. Lo que me obligó a continuar mi investigación de forma independiente hasta la publicación de este artículo en diciembre de 2022.
En el desarrollo de mi trabajo también pude visualizar que para cada número primo, al ser un divisor, determina un solo índice que se alinea al infinito en los intervalos entre los dividendos (secuencia de números naturales), cuando las columnas de patrones de repetición se colocan, a un lado del otro.
Imagino que estos índices tienen alguna aplicación para facilitar los cálculos matemáticos, ya que podemos calcular divisiones con números pequeños y a partir de los resultados, que tienen pocos dígitos, aplicando estos índices podemos encontrar valores más grandes en proporciones aritméticas. Como muestra el gráfico de la figura 3.
Esta figura también me llama la atención y he estado investigando la posibilidad de crear gráficas similares para números primos después del 7. Pero, en estos casos, creo que los valores de los intervalos se dan con una frecuencia algo aleatoria, por lo tanto, tener la secuencia completa de intervalos, todavía existe la necesidad de calcular cada división secuencialmente.
Me gustaría analizar las geometrías de diferentes números primos superponiéndolos, pensando también que esto puede traer algo utilizable gráficamente.
Me complace ver que mi trabajo también puede ser útil en el desarrollo de sus proyectos. De la misma forma que imagino que conocer vuestros diseños y estudios me puede ayudar en un futuro. Por lo tanto, también me gustaría saber más sobre su trabajo, así como poder intercambiar más ideas sobre otras estadísticas que presentan mis algoritmos. Aprecio tu atención,
José D’Agostino
Hola, distinguido profesor José D’Agostino
Lamento también mi demora para responderte. No logré ver en mi correo electrónico si este web me haya informado nuestros escritos aquí ya publicados. Aprecio mucho y con honor por tomar de tu tiempo para responderme profesor. Es muy cierto que estos números nos trae las posibilidades de hacer graficas. Te maravillaría verlo en 2D. Antes de resaltar y compartir nuestros trabajos. Para conocernos mejor; ¿Quisiera saber, con todo y el respeto que te mereces distinguido profesor qué harías si lograra desentrañar el misterio de la distribución de los números primos?
También agradezco mucho tu atención.
Estimado Daniel Mercado, creo que si hay académicos, en el área de investigación universitaria, que estén interesados en ofrecer espacio para alguna publicación más científica, continuando con nuevos hallazgos relacionados con los números primos, puede traer una oportunidad para desarrollar algunos trabajo, sumando simultáneamente esfuerzos. Sin embargo, sería mejor aprovechar otros medios, como WhatsApp, para seguir comunicando sobre estos asuntos. De hecho, existe un criterio más complicado para hacerlo a través del portal de la revista. Si está interesado y desea enviarme algún material gráfico, además de mensajes, utilice el número de teléfono 0055(12) 997733075. No dude en contactarme si es necesario.