ARTÍCULO ORIGINAL
SOUZA JÚNIOR, Elias Pereira De [1]
SOUZA JÚNIOR, Elias Pereira De. “Diferencia entre cuadrados” en el Teorema de Pitágoras. Revista Científica Multidisciplinar Núcleo do Conhecimento. Año 05, Ed. 10, Vol. 06, págs. 05-13. Octubre de 2020. ISSN: 2448-0959, Enlace de acceso: https://www.nucleodoconhecimento.com.br/olimpiada-de-matematica/el-teorema-de-pitagoras
RESUMEN
Este artículo tiene como objetivo mostrar aplicaciones del contenido del Teorema de Pitágoras en la construcción del conocimiento en el aula, centrándose en una técnica algebraica para la “diferencia entre cuadrados”. Primero, el artículo explora la introducción y aplicación del Teorema de Pitágoras como nuevo contenido en el aula dentro de un ejemplo contextualizado. Por lo tanto, el teorema fue demostrado por el maestro, y los estudiantes son guiados a cuestionar y razonar métodos alternativos para obtener resultados además del clásico teorema de Pitágoras demostrado. Pronto empezaron a surgir algunos métodos, posibilidades de resolución para el ejemplo inicial, una de estas formas fue la noción geométrica de Teorema, sin embargo, los estudiantes continuaron sus investigaciones. La parte crucial de la clase fue el razonamiento del procedimiento algebraico que llamó la atención de diferente manera durante las investigaciones de los estudiantes, fue la “diferencia entre cuadrados” como solución al Teorema dentro del conjunto de números naturales, ya que, no todos los conjuntos numéricos respondieron la relación. Y en este punto, se crean reflexiones para los estudiantes sobre cómo explorar las matemáticas e investigarlas de diferentes maneras, ya que la intención era explorar la diversidad de las matemáticas y agudizar la sensibilidad de los estudiantes para hacer nuevos descubrimientos. El Teorema de Pitágoras es bien conocido y aplicado, se puede encontrar fácilmente en varias publicaciones matemáticas, pero hacer que los estudiantes trasciendan fórmulas y procedimientos es enseñar a pensar.
Palabras clave: Educación, modelado, docencia, Pitágoras, aprendizaje.
1. INTRODUCCIÓN
El tema presentado en este artículo fue elegido debido a una experiencia desarrollada en el aula, que tuvo como objetivo explorar las formas de relacionar y aplicar el Teorema de Pitágoras en su forma algebraica y geométrica según el estudio de triángulos con énfasis en el triángulo rectángulo, explorando la idea del Teorema de Pitágoras en la visión del alumno, logrando así formar diversas posibilidades de resolución de problemas relacionados con el Teorema, entre ellos la “diferencia entre cuadrados”.
Sin embargo, este artículo también buscó relatar una experiencia vivida en la escuela, a través de la recolección de información y cálculos observados, buscando comprender la importancia de la construcción del conocimiento por parte del alumno, marcando así una diferencia en el proceso de enseñanza-aprendizaje. Porque, en la formación del conocimiento de los estudiantes, se vuelve indispensable la práctica directa, investigativa o incluso lúdica en el aula, en la que se cree que de esta práctica surgen desafíos, dudas o certezas si este es el camino que el alumno quiere recorrer. seguir, cómo hacer y qué no hacer para proceder, buscando así la comprensión ideal en la resolución de problemas. En esta clase 36 alumnos de primer grado de bachillerato participaron en la clase “A” del Colégio Sagrada Família, Brasília DF
Por tanto, se aplican varias perspectivas de estudio al Teorema de Pitágoras. Luego, se mostrará una propuesta simple en la que se interpreta el Teorema, relacionándolo con la diferencia entre cuadrados. De esta forma, resulta un hecho interesante a mostrar, incluso desde el punto de vista educativo.
1.1 LA PROPUESTA DE CLASE Y EL TEOREMA DE PYTHAGORAS
Incitar al alumno a buscar la solución de un problema o incluso fomentar la investigación en el aula, de diferentes formas y posibilidades, es utilizar una metodología diferente, es decir, es aplicar la modelización matemática. En consecuencia, hace del aula un campo de investigación y práctica pronto, un lugar más interesante y atractivo para los estudiantes, y marca la diferencia.
La Educación Matemática va más allá de lo tradicional, es innovar por la diversidad de acciones permitiendo innumerables métodos de enseñanza y aprendizaje. Porque, desafiar al alumno a encontrar soluciones a los problemas por sí solo es abrir posibilidades para nuevos descubrimientos, como un hilo en el que se están descubriendo las matemáticas en varios contextos aplicables, D’ambrosio (1998), habló sobre las ideas mencionadas anteriormente.
Entonces, la propuesta que se hizo a los estudiantes se basó en el siguiente problema, una escalera de 12 metros de largo se apoya debajo de una pared. La base de las escaleras está a 8 metros de la pared, como se muestra en la figura siguiente. Luego se pidió a los estudiantes que determinaran la altura de la pared.
Figura 1: aplicación del triángulo rectángulo

De manera intuitiva, se instruyó a los estudiantes para que intentaran encontrar el valor de la medida de la pared utilizando la definición fundamental de cualquier triángulo, un contenido que ya había sido estudiado en años anteriores, sirviendo de base para introducir otros contenidos. En general, para construir un triángulo es posible comprobar la condición de existencia de triángulos, que es que la medida de cada lado es menor que la suma de las medidas de los otros dos y mayor que el valor absoluto de la diferencia entre estos. medidas, aplicando un patrón geométrico. Se observa el siguiente patrón:
Figura 2: Condición de existencia de un triángulo
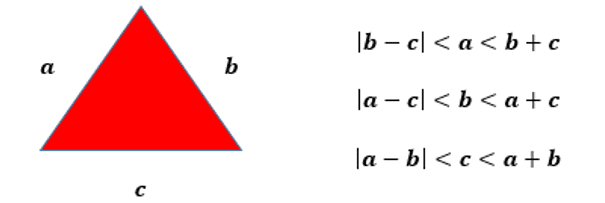
Los estudiantes llegaron a algunos valores posibles y pertinentes para calcular la medida de la escalera, como un lado del triángulo. Sin embargo, para aplicar el Teorema de Pitágoras es necesario que el triángulo tenga al menos uno de sus ángulos que mida 90º. Por tanto, el siguiente paso fue demostrar el teorema de Pitágoras.
1.2 DEMOSTRACIÓN DEL TEOREMA DE PYTHAGORAS
En el proceso de aprendizaje posterior a la investigación inicial de los triángulos y su existencia, el siguiente paso fue agudizar la curiosidad de los estudiantes para formalizar algunas curiosidades y conclusiones iniciales. Entonces, en esta parte de la clase los estudiantes relacionaron varios cuadrados con sus respectivas áreas tratando de encontrar patrones con la mediación del profesor. Pronto, los estudiantes comenzaron a ver las propiedades que Pitágoras usó para el teorema, que se basa en la suma de las áreas de los polígonos que forman una figura construida de triángulos rectángulos congruentes, es decir, comparar las áreas como se muestra a continuación. cifras.
Figura 3 Demostración del teorema de Pitágoras
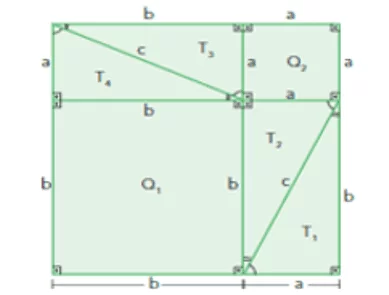
Figura 4 Demostración del teorema de Pitágoras
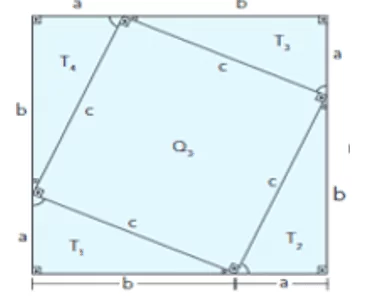
Considere que los 2 lados más pequeños de un triángulo se llaman colectores y el lado más largo de un triángulo rectángulo es la hipotenusa. Tenga en cuenta que las figuras se construyeron utilizando cuatro triángulos rectángulos congruentes iguales a “a” y “b” y la hipotenusa “c” formando cuadrados más grandes con lados iguales a (a + b). Si se eliminan los cuatro triángulos rectángulos congruentes de las dos figuras, las figuras restantes tienen la misma área. Por lo tanto, hay
En la figura 3:
- Suma de las áreas de los cuatro triángulos rectángulos = (T1 + T2 + T3 + T4)
- Área restante Q1 + Q2 = a2 + b2
En la figura 4:
- Suma de las áreas de los cuatro triángulos rectángulos = (T1 + T2 + T3 + T4)
- Área restante = Q3 = c2
Entonces, c2 = a2 + b2
Esta relación se puede aplicar a cualquier triángulo rectángulo. “C” es el lado más grande del triángulo llamado hipotenusa, “a” y “b” el lado del triángulo como se muestra arriba.
1.3 REANUDANDO EL EJEMPLO INICIAL
Después de demostrar el teorema, quedó claro para los estudiantes que la pregunta es una aplicación del teorema de Pitágoras, en el que los lados se llaman catéteres y el lado más grande del triángulo opuesto al ángulo de se llama hipotenusa. Por lo tanto, la relación pitagórica se puede escribir de esta manera:
(Hipotenusa) ² = (Cateto 1) ² + (cateto 2) ²
Figura 5: triángulo rectángulo
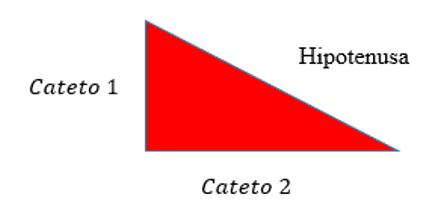
Consecuentemente:
Los estudiantes aplicaron la lista anterior de la siguiente manera:
- La hipotenusa es equivalente a la escalera (12 m)
- La distancia entre la escalera y la pared es una pierna (8 m)
- La altura de la pared es el otro lado, en este caso “x”
aplicando el teorema:
![]()
Restando 8² de ambos lados de la igualdad
![]()
![]()
En este punto, un estudiante hizo una pregunta sobre la resta de cuadrados: – “¿solo podemos resolver esta resta después de resolver los cuadrados?”
Por lo tanto, comenzaron las investigaciones de otras formas de restar cuadrados.
1ra solución:
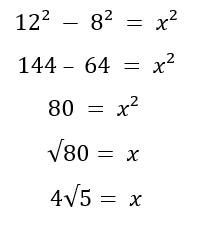
2da solución:
El maestro junto con los estudiantes observaron un patrón. Vea abajo:
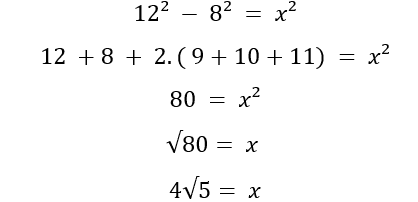
En este punto, se notó un patrón para la diferencia entre cuadrados, en el que los números pertenecen al conjunto de números naturales, en la forma
![]()
Ejemplo:
a = 23 y b = 19, aplicando …
Tomando la prueba:
![]() La igualdad es cierta para los números
La igualdad es cierta para los números
![]()
Después de probar las operaciones sobre el conjunto de números naturales, también se aplicó a algunos otros conjuntos, como el conjunto de números enteros que también funcionaban y los reales, que en el último caso algunos números no lograron establecer la verdadera igualdad, fijando así esta aplicación para números naturales.
2. COMPROBACIÓN DE LA RELACIÓN
Relación de la diferencia entre cuadrados:
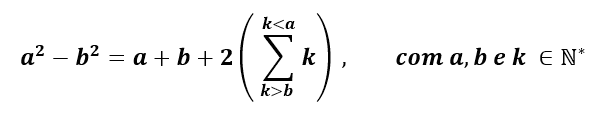
Considerar
a2 + b2 con a y b pertenecientes a números naturales mayores que cero, considerando a > b, tenemos la siguiente proposición para a y b:
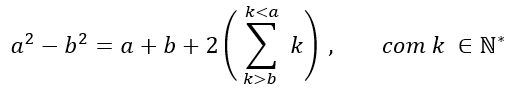
Pronto si
![]()
Entonces
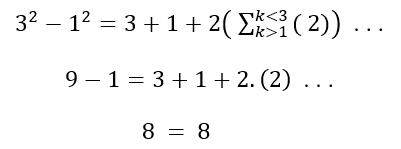
Ahora, considerando m como cualquier número natural.
Si a y b son verdaderas, para a y b, ∈
![]()
, entonces a = b + m, también será cierto, para m ∈
![]()
Tomando m = 1, para
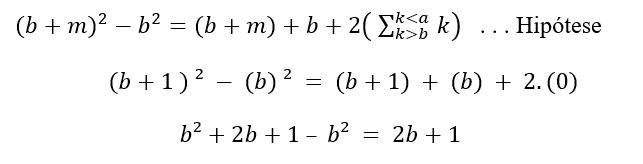
Pronto,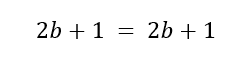
Por tanto, la relación
![]()
, es válido para cualquier
![]()
¡Cómo quería demostrar!
Esta demostración se mostró rápidamente a los estudiantes que se sorprendieron por la aplicación que se les había ocurrido, encontrando así una relación diferente con el Teorema de Pitágoras en la “diferencia entre cuadrados”.
3. CONCLUSIÓN
El objetivo de incitar a los estudiantes a encontrar diferentes formas de resolver problemas es construir conocimientos utilizando las competencias y habilidades ya adquiridas, proporcionando la base para nuevos aprendizajes y descubrimientos. Este artículo es un ejemplo de esto, ya que el profesor dio las instrucciones básicas y los estudiantes estaban investigando formas de resolver el problema.
Lo que lo hace más interesante, es que en medio de las investigaciones, puede haber varias formas de llegar a un resultado. Ver estos caminos y orientarlos hace que la educación matemática sea diferente y placentera para los estudiantes, lo que justifica el modelado matemático.
Luego, siguiendo las aplicaciones del Teorema de Pitágoras en el ejemplo inicial, el docente con los alumnos discutió las formas de resolver la diferencia entre cuadrados, dejando siempre claro que la construcción del conocimiento es la parte fundamental de la clase, el docente es el el mediador y los estudiantes hacen descubrimientos.
En uno de los procesos en los que el alumno planteó la pregunta sobre el cálculo de la diferencia entre cuadrados en la resolución del problema, la clase con el docente pudo afirmar que el método observado para restar cuadrados es válido en algunos puntos relevantes.
Por tanto, el docente demostró la aplicabilidad de la operación descubierta dentro del conjunto de números naturales, resolviendo la cuestión de la aplicabilidad de la operación, dejando claro el método al alumno y a la clase. Pronto, terminamos la pregunta y resolvimos otros ejemplos con el método descubierto. El regreso del alumno a clase fue el siguiente renglón “hemos descubierto una nueva fórmula, que mola”, para un profesor de palabras exactas no hay forma de que un renglón pueda ser más llamativo así.
El alumno pidió orientación para estudiar sumas y demostraciones. Que un chico de primer grado de Bachillerato, el desarrollo futuro de este alumno lo dejo en la imaginación de quienes lean este artículo.
4. REFERENCIAS
DANTE, Luiz Roberto. MATEMÁTICA: Contexto e Aplicações volume único / Luiz Roberto Dante, Fernando Viana – – 4. Edição – – São Paulo: Ática, 2018.
HEFEZ, Abramo. Indução Matemática:\induçãofinal”. Estilo OBMEP – Rio de Janeiro – Departamento de Matemática Aplicada Universidade Federal Fluminense, 2009. Disponível em: http://www.obmep.org.br/docs/apostila4.pdf. Acesso em: 04 maio de 2020. D’Ambrósio, U.Etnomatemática. São Paulo: Ática, 1998.
SANTOS. Marconi Coelho dos. Teorema de Pitágoras: suas diversas demonstrações. Campina Grande (PB):UEPB, 2011. 42f. Monografia (Especialização em Educação Matemática para professores do Ensino Médio) {Universidade Estadual da Paraíba, Centro de Ciências e Tecnologia, Campina Grande, 2011.
VIANA, M. C. V.; SILVA, C. M. Concepções de Professores de Matemática sobre a utilização da História da Matemática no processo de Ensino-Aprendizagem. In: ENCONTRO NACIONAL DE HISTÓRIA DA MATEMÁTICA, 9., 2007, Belo Horizonte. Pôsteres… Belo Horizonte, 2007. Disponível: https://www2.unifap.br/matematicaead/_les/2016/03/TCC-REVISADO.pdf Acesso em: 04 maio de 2020.
[1] Postgrado en Matemáticas.
Recibido: Septiembre de 2020.
Aprobado: Octubre de 2020.