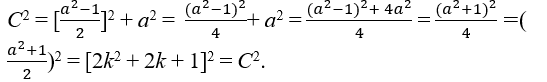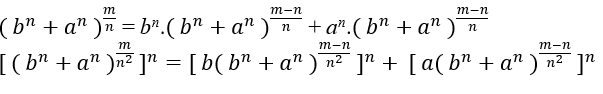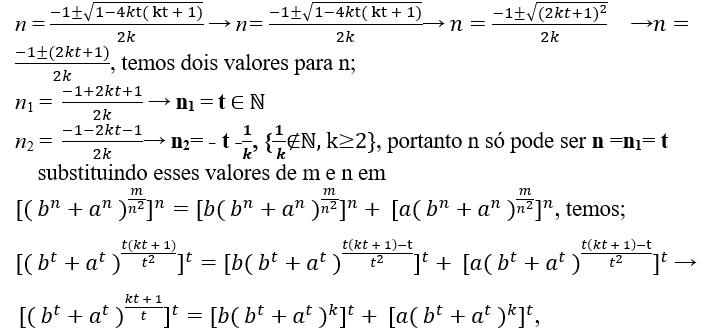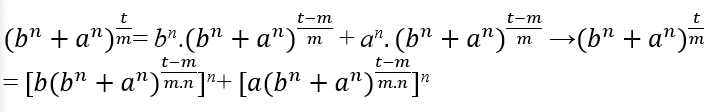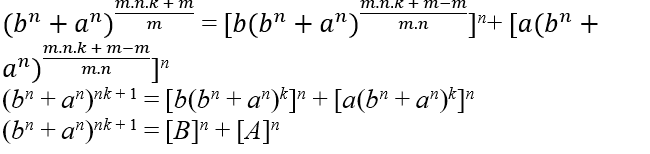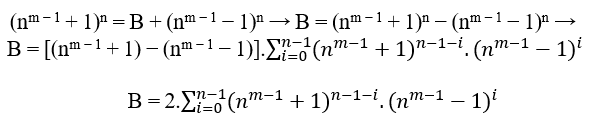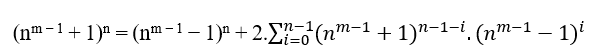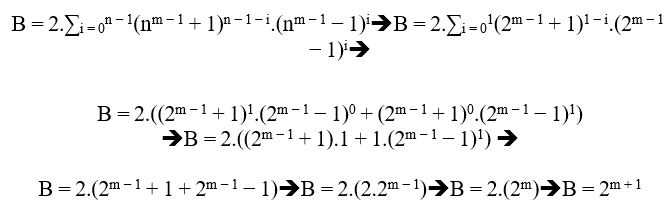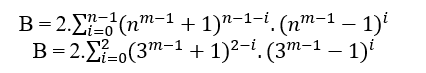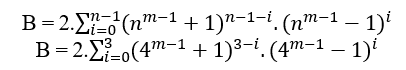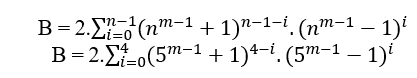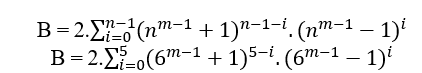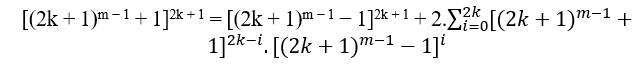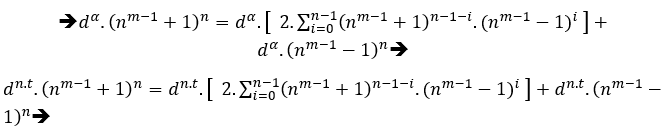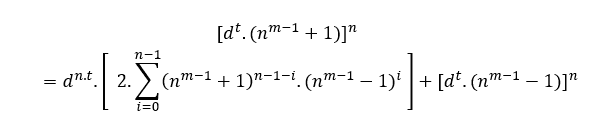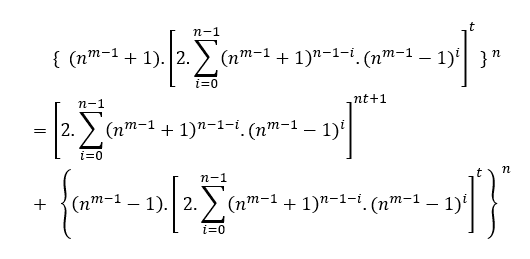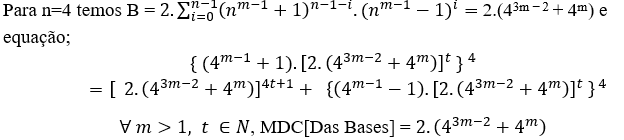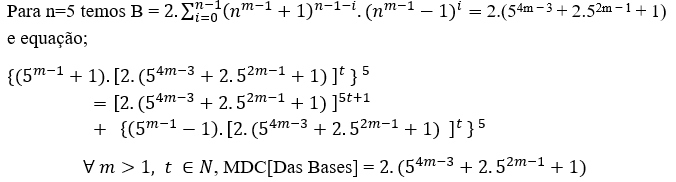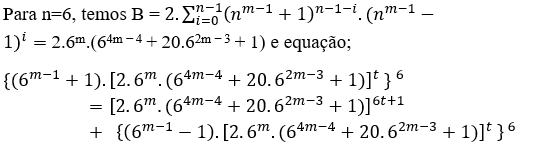Demostración de Beal Conjecture

ARTIGO ORIGINAL

SOUSA, Francisco Rafael Macena de ^[1]

SOUSA, Francisco Rafael Macena de. Demostración de la conjetura de Beal. Revista Científica Multidisciplinar Núcleo do Conhecimento. año 04, Ed. 11, Vol. 05, páginas 132-173. Noviembre de 2019. ISSN: 2448-0959, Enlace de acceso: https://www.nucleodoconhecimento.com.br/matematica/conjectura-de-beal

DECLARACIÓN DE CONJETURA

Si a^x + b^y á c^z , donde a, b, c, x, y y z son enteros positivos y x, y, z ≥ 3, entonces a, b y c tienen un factor primo común, lo que significa que a, b y c son divisibles por el mismo número primo. O bien, la ecua^ción a^x + p^or á cz no tiene solución para enteros positivos con x, y, z ≥ 3 y mdc (a, b, c) a 1.

RESUMEN

Este artículo contiene demostraciones utilizando principios de álgebra y teoría de números, con respecto a la conjetura fue anunciado por Andrew Beal un banquero y entusiasta de la teoría de números propuso un desafío para aquellos que prueban o presentan contraejemplo a tal problema que generaliza el último teorema de fermat, cn á bn + ^un, con n ≥ 3, esto fue demostrado por el matemático inglés Andrew Wiles utilizando como base una conjetura hecha por los matemáticos Yutaka Taniyama y Goro Shimu , esta demostración realizada por Wiles pocos matemáticos entenderán por el alto nivel o complejidad, también se utilizará el Teorema Sebá, "Sebastiáo Vieira do Nascimento (Sebá)", graduado en Economía por la UFPB, maestro en ingeniería del mismo, profesor completo de UFCG, su teorema probado se basa en ese cm á bn + un, con m y n prim^o ent^re sí, este es mdc (m. n) , la conjetura fue propuesta por el propio Beal en 1993, pero sólo fue bien conocida incluso por la comunidad matemática en 1997 después de que R. D. Mauldin publicara el artículo una Generalización del último teorema de Fermat: La conjetura de Beal y el problema del premio en la revista Noticesofthe American Society Mathematical Society.

Palabras clave: Conjetura, Andrew Beal, el último teorema de Fermat.

1. INTRODUCCIÓN

Este artículo tiene como objetivo probar la Conjetura de Beal, propuesta por Andrew Beal un banquero, empresario, inversor, jugador de póquer y matemático aficionado que tiene fascinación en la teoría de números, desafió a cualquier matemático en el mundo a probar o dar un contraejemplo a su Conjetura que fue propuesto desde 1993 hasta la actualidad, no se presentó ninguna demostración que generalice la conjetura incluyendo fermat's Last Theorem , este artículo contiene conocimientos matemáticos que cualquier persona que llegó a tener el segundo grado de la escuela secundaria completa y tiene facilidad en las propiedades matemáticas es posible entender las demostraciones iniciales, ya para aquellos que tienen una educación superior en exacto y más allá de estos será fácil de entender de principio a fin, la conjetura se basa en enteros positivos o soluciones en números naturales con los exponentes más grandes iguales a 3 (tres) y sus bases mayores o igual a 1 (uno) , si es así se demostrará que en realidad el mdc (c, b , a) a C > 1, donde esta C es el factor primo común que divide a, b y c, con el ≤ b o a ≥ b, de tal manera que sea posible tener c^omo e^cuaci^ón cz por + ax, x, y, z ≥ 3, exponentes, caso contradictorio poseerá como m (c, b, , a ) a 1 y x, y, z ≥ 3, este es el único valor que divide c, b, a es 1 (a), es decir, a,b y c son primos entre sí.

Para llegar a la demostración era necesario crear nuevos teoremas, pero para que el teorema sea realmente válido, así como la conjetura debe ser probada en el curso de los teoremas se crean a partir de principios y propiedades en la teoría de números, el mayor desafío en este artículo como cualquier otro que implica números primos esos números que sólo tiene dos divisores en los naturales que es 1 (uno) y a sí mismo (número primo) , porque todavía es algo que la teoría de los números todavía no ha sido capaz de encontrar una manera más rápida de factorizar números gigantes, sin embargo en la teoría de números tenemos como hipótesis y también demostró que cualquier X un número compuesto, podemos escribir – es un producto de varios poderes de números primos iguales o distintos, incluyendo cuando tiene exponentes 0 (cero) o 1 (uno). La idea de esta conjetura es simplemente facilitar el encuentro de factores primos.

2. BREVE HISTORIA A CONJETURA

2.1 FERMAT Y SU TEOREMA

Comienza con Pierre Fermat que vivió en la Francia del siglo XVIII, un funcionario en la ciudad francesa de Toulouse, las matemáticas para él era su pasatiempo favorito, lo interesante es que Fermat tenía mayor fama debido a sus costumbres de presentar a otros matemáticos problemas que desafiaron a las mentes más grandes de la época, donde a menudo dejaban sus contemporáneos perplejos en un intento de resolverlos. Fermat tuvo la idea de crear una propuesta similar al famoso teorema de Pitágoras que es bien conocido hoy en este siglo, pero no tenía soluciones en los naturales, esta proposición fue más allá de su tiempo y ganó fama a lo largo del siglo, por no encontrar una solución o contraejemplo, por ello ganó su nombre y por ser su último reto tuvo como nombre el último teorema de Fermat , la ecuación de su fama es cn á bn + un^, donde a, b, c y n ∈ N, con n ≥ 3, según él tuvo la manifestación, murió sin que nadie supiera cuál era su supuesta respuesta, debido a esto se hizo conocido como su último teorema. El mérito del descubrimiento de esta proposición debía a su primogénito, vio varias notas de Fermat en un cierto libro de Aritmetics que pertenecía, ya que su padre tenía el hábito de hacer borradores o anotaciones en libros. Después del hallazgo del hijo, las notas o descubrimientos fueron publicados en un libro Arithmetica de Diofanto que contenía observaciones del padre, en 1670 el libro contenía 48 observaciones, pero a lo largo del camino generaciones de matemáticos y físicos estaban dando soluciones a sus desafíos, sin embargo tenía uno que la mayoría pensaba que era el último, debido a esto tenía un nombre tan desafiante. En su libro contenía la siguiente declaración: "He descubierto una maravillosa demostración de esta propuesta que, sin embargo, no encaja en los márgenes de este libro" (FERMAT. 1607 – 1665)².

2.2 YUTAKA TANIYAMA, GORO SHIMURA Y ANDREW WILES

En 1954, Yutaka Taniyama y Goro Shimura, jóvenes matemáticos japoneses, se hicieron amigos porque se interesaron en el mismo libro, el mismo artículo y los mismos cálculos, esta conjetura Taniyama-Shimura permitió a Wiles realizar el sueño de su hijo, empleando un esfuerzo intelectual y una determinación que era difícil de creer como era posible para un ser humano. La conjetura que los dos presentaron sirvió como un camino a su solución definitiva al problema, sin embargo el matemático Yutaka Taniyama tomó su propia vida en 1958, por lo que retrasó aún más el desarrollo de la solución, al desarrollo de la conjetura en si no fue hecho intencionalmente para resolver el último teorema de Fermat, sin embargo fue lo que realmente sucedió más tarde Wiles se dio cuenta de que tal base que ayudó a la prueba – , para quien pudiera imaginar que el trabajo de dos estudiantes de finales del siglo XX podría ser utilizado en algo que resolviera uno de los mayores misterios de la historia de las matemáticas. Pero fue Andrew Wiles quien terminó demostrando el último teorema de Fermat, Wiles es un profesor universitario de Princeton que comenzó su interés en el problema cuando era niño en su ciudad natal tenía una biblioteca pública, pero fue sólo durante 1986 que realmente comenzó a comenzar su trabajo de resolver el teorema de sus sueños, según Wiles que su investigación se hizo en completo secreto , porque en su ser sabía que encontraría la solución, pero no era el momento de afirmar tal cosa a la comunidad académica, la intuición lo es todo a un apasionado en la teoría de los números, sin embargo la intuición muestra el camino, pero probar si está bien o mal lleva tiempo y dedicación, tal vez temiendo la presión que sufriría frente a un problema tan famoso y la solución difícil era demasiado arriesgado afirmar una solución inicial tan posible , al analizar la conjetura de los dos japoneses, Andrew Wiles señaló que tal teorema podía ser una manera de resolver, sin embargo la conjetura tenía que probarse primero antes de demostrar lo que había buscado tanto desde que era un niño, en su mente estaba tan claro que Wiles podía soñar con la solución del teorema todo dependía de la prueba de la conjetura de los dos estudiantes , sin embargo Wiles no demostró el último teorema de Fermat, sino más bien la conjetura Taniyama-Shimura, lo que implicará prueba – allí.

Finalmente, el 23 de junio de 1993, en una conferencia celebrada en el Instituto Isaac Newton de Ciencias Matemáticas en Cambridge, Andrew Wiles, 356 años después de la presentación del teorema, hizo su anuncio de su demostración, pero contenía un pequeño defecto en su solución, Wiles se retira durante un año con el fin de corregir tal error y presentar su nueva demostración refundida , después de la corrección y revisión del mismo error detectado, tomó unos meses para evaluar su solución, su demostración tuvo 200 páginas, y después de un largo período de ansiedad, su descubrimiento o demostración fue finalmente aceptada, pero tan compleja que sólo unas pocas personas en todo el mundo fueron capaces de entenderlo, y Wiles (después de recibir un premio por valor de 50.000.00 de libras de la Fundación Wolfshlke) , entra como el matemático que demostró el teorema más intrigante y desafiante en la historia de las matemáticas, y así concluye uno de los mayores problemas no encontrados o demostrados que desafiaron a los grandes matemáticos antes y durante, por lo que el último teorema de Fermat no tiene soluciones con enteros positivos con n ≥ ³3.

2.3 ANDREW BEAL Y SU CONJETURA QUE RECIBIÓ SU NOMBRE

Andrew Beal (nacido el 29 de noviembre de 1952), banquero, empresario, inversor, jugador de póquer y matemático aficionado y entusiasta de una de las mejores áreas que es la teoría de números. Beal también es conocido por la conjetura de Beal mientras investiga las generalizaciones del último teorema de Fermat, de 1993 a 1997, Beal ofreció un premio monetario por una prueba revisada por pares de esta conjetura o un contra-ejemplo, porque en 1993 tenía un valor de $5,000 el valor del premio aumentó varias veces y actualmente es $1,000,000.00 para la persona que lo demuestra o presenta un ejemplo contradictorio en otras palabras un contra-ejemplo para aquellos que generalizan El último teorema de Fermat. Según las propias declaraciones del banquero, en un anuncio de prensa de la Sociedad Americana de Matemáticas, el objetivo del valor millonario es "inspirar a las mentes jóvenes para reflexionar sobre el tema y hacerlas cada vez más interesadas en el estudio de las matemáticas^"4.

3. DESARROLLO A LA CONJETURA DE BEAL

Para demostrar que se necesitarán tres nuevos teoremas (T.M, S.T.M e T.G.M), debido a que el Teorema de Sebá es un caso particular de conjetura de Beal, esto también se mostrará más adelante.

3.1 MACENA O T.M

Dadas dos ecuaciones Eq¹:cz ^por + ax y _Eq2^:cm ^á cm con soluciones enteras positivas y tiene como base común c ≠ 0, con c, b, z, z, y m ∈ N, m > z es posible determinar una nueva ecuaci_ón Eq3 que tiene tanto el formato de Eq1 como Eq₂. Esto significa que si Eq3 no satisface E_q1 no tiene soluciones positivas completas. Ejemplo₁ es la ecuación Eq1 → c2 a b2 ⁺ a2 ^y Eq2 _→ cm c^m con c ≠ 0 y m ∈ N, sabemos que Eq1 tiene soluciones enteras porque es el propio teorema de Pitágoras, sólo tiene que comprobar usando los triples póthagóricos, al igual que _Eq2 también tiene soluciones enteras que se probará por delante. Dicho esto, entonces es posible determinar una ecuación Eq3 que tiene el fo_rmato Eq1 y Eq₂. Como c ≠ 0 possamos usar os seguintes passos em Eq₁ → c² = b² + a² → 1 = c^− 2.(b² + a²)(I) Eq₁ → c² = b² + a² →  c=(b²+a²)^1/2(II)
Próximo passo é usar Eq₂, pois possamos escrever Eq₂ da seguinte forma c^m = c^m.1 ao substituir (I) temos c^m = c^m.c⁻².(b² + a²) → c^m = c^m−2.(b² + a²) → c^m = b².c^m−2 + a².c^m−2(III) Substituindo (II) em (III);
= b². + a². → = . Seja m−2 múltiplo de 4 isto é m−2 = 4.n, com n ∈ ℕ, então temos que m = 4.n + 2, ao substituir temos; (b² + a²)^2.n + 1 = [b(b² + a²)ⁿ]² +[a(b²+a²)ⁿ]²

(b² + a²)^2n + 1= [B]² + [A]² agora só resta verificar se (b² + a²)^2n + 1 é do tipo C²,pela triplas pitagórica essa igualdade é satisfeita logo (b² + a²)^2.n + 1 = (c²)^2.n + 1 = c^{2.(2.n + 1)}= [c^2.n + 1]² = [C]²
Portanto C² = [B]² + [A]² o mesmo formato de Eq₁ para concluir deve ter propriedade de Eq₂C² = [B]² + [A]² → (b² + a²)^2n + 1 = [b(b² + a²)ⁿ]² + [a(b²+ a²)ⁿ]² → (c²)^2n + 1= [b(c²)ⁿ]² + [a(c²)ⁿ]² →
c^4n + 2 = [b.c²ⁿ]2 + [a.c²ⁿ]2 → c^4n + 2 = b²c⁴ⁿ + a²c⁴ⁿ → c^4n + 2 = c⁴ⁿ.(b² + a²) → c⁴ⁿ⁺²=c⁴ⁿ.(c²) → c⁴ⁿ⁺²=c⁴ⁿ⁺² →c^m=c^m . Então foi verificado que é possível encontra uma Eq₃ que tenha as duas propriedades então a Eq₃ para essas duas equações é; Eq₃ → (b²+a²)2ⁿ⁺¹=[b(b²+a²)ⁿ]²+[a(b²+a²)ⁿ]²

3.1.1 CATA T.M

Seja Eq₁: c^z = b^y + a^x e Eq₂: c^m = c^m, com m > z, a, b, c, x, y, z , m ∈ ℕ e c ≠ 0.
Prueba de E_q2:

De hecho, 1 a 1, multiplicando ambos lados por c ∈ N* tenemos 1.c a 1.c, al multiplicar de nuevo por el mismo c tenemos c2 a c2, multiplicando lógicamente por m veces tendremos;
cm á ^{c(₁1 + ₁2 + ₁3 + … + 1_m − 1 + 1_m) = m}} = c^m. Por lo tanto se muestra a E_q2.

Como c ≠ 0, possamos usar os seguintes artifícios:

c^z = b^y + a^x → 1 = c^− z.(b^y + a^x)( I ) elemento neutro da multiplicação
c^z = b^y + a^x → c =(b^y+a^x)^1/z( II )

A Eq₂ pode ser escrita da seguinte maneira c^m = c^m.1 , ao substituir (I) nessa equação é obtido:

c^m = c^m.1 → c^m = c^m.c ^− z.(b^y + a^x) → c^m = c^m − z.(b^y + a^x) → c^m = b^y.c^m − z + a^x.c^m − z
Ao substituir ( II ) resulta em;

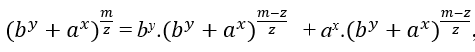, colocando os expoentes y e x em evidências

Para que ∈ ℕ o MMC( zy , zx )= zxy, então m – z deve ser múltiplo de zxy, portanto m – z = zxy.k, com k ∈ ℕ. Isolando m e substituindo na equação resulta:

(b^y + a^x)^xyk + 1 = [b.(b^y + a^x)^xk]^y + [a.(b^y + a^x)^yk]^x

Portanto essa é a nova equação;
Eq₃:(b^y + a^x)^xyk + 1 = [b.(b^y + a^x)^xk]^y + [a.(b^y + a^x)^yk]^x → C^xyk + 1 = B^y + A^x
Pelo princípio da comparação ou formato C^xyk + 1 = B^y + A^x é equivalente a c^z = b^y + a^x, é a própria estrutura da conjectura de Beal.

Logo satisfez a Eq₁ falta mostra que também tem o formato de Eq₂: c^m = c^m

(b^y + a^x)^xyk + 1 = [b.(b^y + a^x)^xk]^y+ [a.(b^y + a^x)^yk]^x, como c^z = b^y + a^x temos;
(c^z)^xyk + 1 = [b.(c^z)^xk]^y + [a.(c^z)^yk]^x → c^z.^{(xyk + 1)} = [b.c^z.xk]^y + [a.c^z.yk]^x → c^zxyk + z = b^y.c^zxyk + a^x.c^zxyk →  como
m = zxyk + z
c^m = b^y.c^zxyk + a^x.c^zxyk → c^m = c^zxyk.(b^y + a^x) → c^m = c^zxyk.(c^z) → c^m = c^zxyk + z = c^m.

Por lo tanto probado desde E_q3 satisfecho E_q1 y E_q2.

Dados:

C^Z= B^y + A^x

C = b^y + a^x, B = b.(b^y + a^x)^xk, A = a.(b^y + a^x)^yk e Z = xyk + 1

MDC(C, B, A) = MDC(b^y + a^x, b.(b^y + a^x)^xk, a.(b^y + a^x)^yk) = b^y + a^x = c^z = C.

MDC(Z, y, x) = MDC(xyk + 1, y, x) = 1

OBS:

Se k for zero temos;
(b^y + a^x)^xyk + 1 = [b.(b^y + a^x)^xk]^y + [a.(b^y + a^x)^yk]^x → (b^y + a^x)¹ = [b.(b^y + a^x)⁰]^y + [a.(b^y + a^x)⁰]^x, como b^y + a^x = c^z ≠ 0 portanto (b^y + a^x)⁰ = 1
(b^y + a^x)¹ = [b.1]^y + [a.1]^x → b^y + a^x = b^y + a^x

Se caso o m fosse igual a z a equação Eq₁ e Eq₂ seria igual, por sua vez seria igual a Eq₃

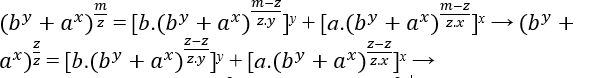
(b^y + a^x)¹ = [b.(b^y+a^x)⁰]^y + [a.(b^y+a^x)⁰]^x →  b^y + a^x = [b.1]^y + [a.1]^x.

Si el caso x-y-k-1 tenemos un cuadrado perfect^o
(po^{r + ax)xyk} + [b.(b^y + a^x)^xk]¹ á [a.(b^y + a^x)^yk]^y + x ^→ (b1 + ^a1)1 + 1[b.(b¹ + a¹)¹] x 1[a.(b¹ + a¹)¹] + 1 →
(b + a)2[b.(b + a)] a [a.(b + a)]+ → (b + a)² a b.(b + a) + a.(b + a) á b2 + ba + a2 á b2 + 2a^b + a2 á (b ⁺ a)2
Ejemp^lo2 Compr_obando con los números de la ecuación Eq₃, ser b-3, a-2 y n-1 que tenemos;

(b2 + ^a2)2n + [b(b² + a²)ⁿ]¹ x 2[a(b² + a²)ⁿ] + 2 → (32 ^{+ 22) 2,1} + [3(3² + 2²)¹]¹ x 2[2(3² + 2²)¹] + 2 →
(9 + 4)3[3(9 + 4)] x 2[2(9 + 4)] + 2 → 133 [3.13]^a 2 [2.13]⁺ 2 → ¹33 a ³92 + ²62 → 2187 a 1521 + 676 → 2187 a 2187

3.2 MOSTRANDO CADA CASO POR T.M

Para mostrar la validez de este teorema también es necesario mostrar las posibilidades o posibles valores de z, y, x y m ∈ N, si no contradice ningún teorema ya demostrado por matemáticos como (teorema de Pitágoras " por varios matemáticos", el teorema de Sebá " por Sebastian " y el último teorema de fermat " por Andrew Wiles " y así sucesivamente el T.M es válido y será una herramienta para probar la Conjetura De Beal.

3.2.1 TEMA PYTHagoras

Esto es cuando z-y-x-2
Supongamos que E_q1 → ^c2 a b² + a², tiene soluciones completas, para c, a, b, m ∈ N, c ≠ 0 y E_q2 → ^cm a ^cm es posible encontrar un Eq3 que satisfaga las dos ecuaciones anteriores, si esto ocurre pronto E_q1 → c-√(^b2+^a2 )∈ N.
Esta demostración ya se ha mostrado en el ejempl_o 1, sólo es necesario mostrar que el uso actual del triple pitagórico está satisfecho con la condición c-√(^b2+^a2) ∈ N.
La hipótesis es c2 ^a b2 ⁺ a2, Tesis C² a C².
Usando la Hipótesis c2 a b2 ⁺ a2 a^ñadiendo en ambos lados por 2b + 1 ∈ N, un cuadrado perfecto se obtiene en un lado, c2 + 2b + 1 á b2 + 2b + ¹ + a2 → c2 + 2b ⁺ 1 á (b + 1)2 + a2, s^abemos que en un triáng^ulo de^recho la hipotenusa es mayor que cualquiera de los catetos en particular c > b > a, entonces existe la posibilidad de c á b 1 , darse cuenta de que se trata de una solución adecuada para resolver la ecuación c2 + 2b + 1 á (b + 1)2 + a2 → c2 + 2b + 1 á c2 + a2 → 2b ⁺ 1 a2 al aislar b, se ^obtien^e y co^mo , darse cuenta de qu^e tanto b como c para ser un entero basta (a) ser impar porque los tiempos impares impares impares sigue siendo impar, por lo tanto una condición de 2k + 1 para ser impar con k ∈ , así lo hemos hecho;

→ 2 x 2 + 2 k + 1)2, por lo que tenemos C a 2k2 + 2k + 1, B a 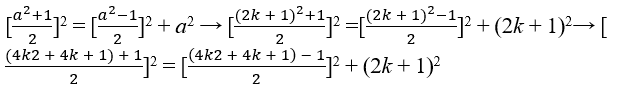2k2[2k² + 2k + 1] + 2[2k² + 2k]^k y A a 2k + 1 ^∈ N, son los triples pit^agóricos (2k2 + 2k + ^1, 2k2 + 2k, 2k + 1), comprobando los triples de la tesis (2k2 ⁺ 2k + 1, 2k2 + ²k, 2k + 1), comprobando la tesis de lasis

3.2.2 PARA EL CASO DEL ÚLTIMO TEOREMA DE FERMAT

Esto es cuando z-y-x-n
Supongamos que E_q1 → ^cn a ^bn + ^a, tiene solución para n≥3, con c, a, b, m ∈ N, c ≠ 0 y Eq2 → cm a cm^, es posible encontrar un Eq3 que satisfaga las dos ecuaciones anteriores, si esto ocurre pronto E_q1 → c a n√^bn+^an ∈ N.
Como c ≠ 0 possamos escrever Eq₁, da seguinte forma;

Eq₁ → cⁿ = bⁿ + aⁿ → 1 = c ^− n.(bⁿ + aⁿ)(I) elemento neutro da multiplicação
Eq₁ → cⁿ = bⁿ + aⁿ → c = ( bⁿ+aⁿ )^1/n(II)
Verifique que a Eq₂ pode ser escrita da seguinte forma sem alterar seus valores c^m = c^m.1, ao substituir (I) em Eq₂, temos;
c^m = c^m.c ^− n.(bⁿ + aⁿ) → c^m = c^m − n.(bⁿ + aⁿ) → c^m = bⁿ.c^m − n + aⁿ.c^m − n(III)

Substituído (II) em (III)

Perceba que o formato é o mesmo que Eq₁, basta verificar se m − n é múltiplo de n², se sim então possamos escrever m − n = n².k com k ∈ ℕ, isolando m temos m = n².k + n isso é uma equação do 2ª grau;
m = n².k + n ⇒ kn² + n − m = 0, com isso possamos encontrar valores para m e n por Bhaskara.

, para que n seja natural obrigatoriamente  -1±√1-4km deve ser múltiplo de 2k, então;
-1±√1-4km = 2k.t, com t ∈ ℕ
-1±√1-4km = 2k.t → ±√1-4km= 2k.t + 1 elevando ambos ao quarado temos 1 + 4km = (2k.t + 1)²→ 4km = (2k.t + 1)² − 1 perceba que é a diferença de dois quadrado então;
4km = (2k.t + 1 − 1).(2k.t + 1 + 1) → 4km = (2k.t).(2k.t + 2) → 4km = 4.(k.t).(k.t + 1) → km = k.t.(k.t + 1) →
m = t( kt + 1), então substituindo esse valor de m em n =  -1±√1-4km temos;

logo (b^t+ a^t)^kt + 1 = B^t + A^t, perceba kt + 1 não é múltiplo de t, pois mdc( kt + 1 , t ) = 1, isso é “kt + 1” e “t” são primos entre, e por Andrew Wiles é impossível b^t + a^t = c^t (Ultimo Teorema de Fermat), para t > 2.
Porque kt + 1 ≠ t.α, con 2 < α ∈ N, por lo tanto no satisface e_q1, por lo que Eq1 no tiene soluciones, como se dice en T.M.
Todavia C =^kt+1√B^t+A^t ∈ ℕ, EQSebá, Teorema de Sebá, verificando a igualdade;
C = ^kt+1√B^t+A → C = ^kt+1√[b (b^t+a^t )^k]^t+ [a( b^t+a^t )^k]^t  →C = ^kt+1√b^t( b^t+a^t )^kt + a^t ( b^t+a^t )^kt → ^kt+1√( b^t+a^t )^kt.( b^t+a^t ) → C = ^kt+1√( b^t+a^t )^kt+1 → C = b^t + a^t.

3.2.3 TEMA SEBÁ

c^m a bⁿ+ y^, con mdc(m,n)-1
Demostración de Sebastiáo Vieira do Nascimento ( Sebá )
Teorema: La ecuación Cm – An + Bn admite soluciones naturales para m y n primos entre sí.
Prueba:
Sé la ecuación;
( 1 )^cm á ^bn + ^an, siendo a, b, c, n y m enteros positivos. Multiplicando ambos os membros da equação ( 1 ) por (bⁿ + aⁿ)^m
obtém-se:
( 2 )c^m*(bⁿ + aⁿ)^m = (bⁿ + aⁿ)*(bⁿ + aⁿ)^m, Substituindo o valor de da (1) em (2), obtém-se:
(bⁿ + aⁿ)^m + 1 = (bⁿ + aⁿ)*(bⁿ + aⁿ)^m
ou
( 3 )(bⁿ + aⁿ)^m + 1 = bⁿ(bⁿ + aⁿ)^m + aⁿ(bⁿ + aⁿ)^m
Se escolhermos valores para a e b tal que a ≤ b ou a≥b, e substituirmos na (3), obtém-se valores inteiros positivos para A, B e C.

Ejemplo: Divida un cuadrado en dos cubos de varias maneras diferentes. Seja a equação:
( 4 )C² = B³ + A³, Considere a equação:
c² = b³ + a³, Multiplicando ambos os membros da equação acima por (b³ + a³)^m, onde m e n  ∈ ℕ, temos:

c²(b³ + a³)^m = (b³ + a³)(b³ + a³)^m
( 5 )(b³ + a³)^m + 1 = b³(b³ + a³)^m + a³(b³ + a³)^m

Comparando a equação (5) com a equação (4), devemos decompor m em potências de 3 e m + 1 em potências de 2. Esto sólo será posible si m y m + 1 son, respectivamente, múltiplos de 3 y 2. Logo:
m = 6k – 3 e m + 1 = 6k – 2, Assim, a equação (5) fica:

(b³ + a³)^6k − 2 = b³(b³ + a³)^6k − 3 + a³(b³ + a³)^6k − 3
[(b³ + a³)^3k − 1]² = [b(b³ + a³)^2k − 1]³ + [a(b³ + a³)^2k − 1]³, Logo, as soluções da equação dada são obtidas fazendo:

C = (b³ + a³)^3k − 1, B = b(b³ + a³)^2k − 1 e A = a(b³ + a³)^2k − 1, onde k ∈ N*, a e b ∈ ℕ.
Pruebas con la T.M Isso é quando z=m e y=x=n
Suponhamos que Eq₁ → c^m = bⁿ + aⁿ, possui solução para m e n primo entre si isso é mdc(m,n)=1, com c, a, b, t, m e n ∈ ℕ, c ≠ 0 e Eq₂ → c^t = c^t é possível encontrar uma Eq₃ que satisfaça as duas equações anteriores, se isso ocorrer logo Eq₁ → c =^m√bⁿ+aⁿ ∈ ℕ.

Como c ≠ 0 possamos usar os seguintes métodos;
c^m = bⁿ + aⁿ → 1 = c^− m*(bⁿ + aⁿ), (I) elemento neutro da multiplicação
c^m= bⁿ + aⁿ → c = (bⁿ+aⁿ)^1/m, (II)
Possamos escrever Eq₂ da seguinte forma c^t = c^t.1, substituindo ( I ) em Eq₂ temos;

c^t = c^t.c^− m.(bⁿ + aⁿ) → c^t = c^t − m.(bⁿ + aⁿ) → c^t = bⁿc^t − m + aⁿc^t − m, ao substituir (II) temos;

Para que 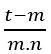seja natural t − m deve ser múltiplo de n e m, logo t − m = m.n.k, com k ∈ ℕ, isolando t temos t = m.n.k + m, ao substituir na equação é obtido;

Resta mostrar que nk + 1 é múltiplo de m, se sim ele é da forma nk + 1 = m.α, com α ∈ ℕ ou bⁿ + aⁿ = C^m
Caso ocorra algum desses dois caso temos C^m = Bⁿ + Aⁿ então estará mostrada que Eq₁ tem solução.

Tenemos que t – m á m.n.k dividiendo ambos por m, se obtiene a 1 n.k añadiendo 1 en ambos lados , n.k + 1, ya que t es múltiplo de m, por lo ∈ N, con esto podemos utilizar los siguientes pasos;

Como n.k + 1 y nk + 1 m.α esto es m.α → α , si α es natural, entonces debe ser natural, si sólo si t es también múltiplo de ^m2, pero t no es múltiplo de m2, porque es de la forma t a m.n.k + m, incluso si k era igual a m, sería de la forma t á n.m2 + m á m.(nk ⁺ 1) ≠ m2. (NK+1), por lo que NK+1 no es múltiplo de T, por lo que mdc (NK+1,T)-1, son primos entre sí.

Sólo queda para comprobar sⁱ bn ^{+ u}n ^cm.
Sabemos que nk + 1 não é múltiplo de n, pois o mdc(nk + 1, n) = 1 e como a igualdade da equação (bⁿ + aⁿ)^nk + 1 = [b(bⁿ + aⁿ)^k]ⁿ + [a(bⁿ + aⁿ)^k]ⁿ é satisfeita já mostrada anteriormente na EQ_Sebá, pelo princípio do formato ou comparação temos que:

C^nk + 1= Bⁿ + Aⁿ equivale a c^m = bⁿ + aⁿ, logo;

(bⁿ + aⁿ)^nk + 1 = Bⁿ + Aⁿ → (c^m)^nk + 1 = c^{m.(nk + 1)} = [c^nk + 1]^m = C^m = Bⁿ + Aⁿ

Com isso foi satisfeita a Eq₁, falta mostrar Eq₂ → c^t = c^t, perceba que:
(bⁿ + aⁿ)^nk + 1 = Bⁿ + Aⁿ → (bⁿ + aⁿ)^nk + 1 = [b(bⁿ + aⁿ)^k]ⁿ + [a(bⁿ + aⁿ)^k]ⁿ →
(c^m)^nk + 1 = [b(c^m)^k]ⁿ + [a(c^m)^k]ⁿ → c^{m.(nk + 1)} = [b(c^m)^k]ⁿ + [a(c^m)^k]ⁿ
como t= m.( nk + 1 );
c^t = bⁿ(c^m)^nk+ aⁿ(c^m)^nk → c^t = (c^m)^nk(bⁿ + aⁿ) → c^t = (c^m)^nk(c^m) → c^t = (c^m)^nk + 1 → c^t = c^{m.(nk + 1)} = c^t, Então provado pois Eq₃ tem propriedades tanto de Eq₁ como Eq₂.

3.2.4 EN CASO DE QUE SEAN MÚLTIPLES POR T.M

Caso (1): para el múltiplo y de x esto es y xk con k ∈ N
Be Eq₁: c^z á b^xk + a^x y Eq₂ :c^m á cm^, con m > z y c ≠ 0 se puede encontrar una nueva Ecuación Eq3_, que tiene propiedades de Eq1 y Eq2 s_i Eq3 no _tiene propiedad del logotipo _Eq1 Eq1, _no tiene soluciones completas.

Como c ≠ 0, temos;
c^z = b^xk + a^x → 1 = c ^− z.(b^xk + a^x), (I) elemento neutro da multiplicação
c^z = b^xk + a^x → c = (b^xk+a^x)^1/z, (II)

Possamos escrever Eq₂ da seguinte maneira usando ( I );
c^m = c^m.c^− z.(b^xk + a^x) → c^m = c^m − z.(b^xk + a^x) → c^m = b^xk.c^m − z + a^x.c^m − z, ao substituir (II) temos;

Colocando os xk e x em evidência temos;
, note que o mmc (zxk, zx) e para que ∈ ℕ, obrigatoriamente z – m deve ser múltiplo de zxk isso é m − z = zxk.α com α ∈ ℕ, com isso temos;

(b^xk + a^x)^{xk.α + 1} = [b.(b^xk + a^x)^α]^xk + [a.(b^xk + a^x)^k.α]^x, note que essa equação pode ser escrita da seguinte forma;

(b^xk + a^x)^{xk.α + 1} = [b^k.(b^xk + a^x)^k.α]^x + [a.(b^xk + a^x)^k.α]^x, isso é Teorema de Sebá portanto já provado logo C^{xk.α + 1} = B^xk + A^x equivalente a C^m = B^x + A^x pois MDC(xk.α + 1 , xk )=MDC(xk.α + 1 , x)= MDC(m,x)=1, portanto primo entre si, por sua vez equivalente Eq₁.

Verificando Eq₂ que é c^m = c^m
(b^xk + a^x)^{xk.α + 1} = [b.(b^xk + a^x)^α]^xk+ [a.(b^xk+ a^x)^k.α]^x, como b^xk + a^x = c^z temos; (c^z)^{xk.α + 1} = [b.(c^z)^α]^xk + [a.(c^z)^k.α]^x → c^{zxk.α + z} = [b.c^zα]^xk + [a.c^zk.α]^x como m = zxk.α + z
c^m = b^xk.c^xzkα + a^x.c^xzk.α → c^m = c^xzkα(b^xk + a^x) → c^m = c^xzkα(c^z) → c^m = c^{xzkα + z} = c^m.
Pronto satisfecho E_q1 y Eq₂, por lo tanto probado.
Caso (2): para x múltiplo de y isso é x = yk com k ∈ ℕ
Essa demonstração é análoga em relação ao Caso (1), chegara que Eq₃ é;
(b^y + a^yk)^{yk.α + 1} = [b.(b^y + a^yk)^k.α]^y + [a.(b^y + a^yk)^α]^yk →
(b^y + a^yk)^{yk.α + 1} = [b.(b^y + a^yk)^k.α]^y + [a.(b^y + a^yk)^kα]^y → C^{yk.α + 1} = B^y + A^y equivalente C^m = B^y + A^y por sua vez equivalente Eq₁: c^z = b^y + a^yk com k, α ∈ ℕ .
Caso (3): para múltiples z de x esto es z á xk y MDC(z,x,y) -1, con k ∈ N

Be E_q1: ^cxk po^r + a^x, podemos escribir Eq1 del siguiente formato E_q1: ^por c^xk – a^x, y Eq2 _será sobre la base de b en lugar de c, con b ≠ 0 y c > a, lo_goti^po Eq²: bm á bm, con m > y, por lo que es posible Eq3 que tiene propiedad eq₁ y Eq₂, si no satisface Eq1 e_ntonces Eq₁ no tiene soluciones completas positivas.

Como b ≠ 0 temos;
b^y = c^xk − a^x → 1 = b ^− y(c^xk − a^x), (I) elemento neutro da multiplicação
b^y = c^xk − a^x → b = (c^xk-a^x)^1/y, (II)
Eq₂ pode ser escrito da seguinte maneira b^m = b^m.1, substituído (I) em Eq₂ temos;
b^m = b^m.b^− y(c^xk − a^x) → b^m = b^m − y(c^xk − a^x) → b^m = c^xk.b^m − y− a^x.b^m − y, substituindo (II)temos;

, isolando xk e x temos;
MMC( xyk , x )= xyk, para que  ∈ ℕ, m – y deve ser múltiplo de xyk, isso é m − y = xyk.α, com α ∈ ℕ, com esses dados temos;

(c^xk − a^x)^xkα + 1 = [c.(c^xk − a^x)^α]^xk − [a.(c^xk − a^x)^k.α]^x, note que possamos organizar da seguinte forma;

(c^xk − a^x)^xkα + 1 = [c.(c^xk − a^x)^α]^xk − [a.(c^xk − a^x)^k.α]^x → [c.(c^xk − a^x)^α]^xk = (c^xk − a^x)^xkα + 1 + [a.(c^xk − a^x)^k.α]^x, portanto z pode ser múltiplo de x, e seu MDC( z , x , y ) = 1

Como z = xk, temos;
[c.(c^z − a^x)^α]^z = (c^z − a^x)^zα + 1 + [a.(c^z − a^x)^k.α]^x, com isso temos;

C = c.(c^z − a^x)^α, B = c^z − a^x e A = a.(c¹ − a^x)^k.α, logo C^z= B^zα + 1 + A^x, com z=xk, isso é equivalente a Eq₁, resta mostrar que também é Eq₂: b^m = b^m.

[c.(c^z − a^x)^α]^z = (c^z − a^x)^zα + 1 + [a.(c^z − a^x)^k.α]^x, como b^y = c^z − a^xez = xk, temos;

[c.(b^y)^α]^xk = (b^y)^xkα + 1 + [a.(b^y)^k.α]^x → c^xk.(b^y)^xkα = b^{xykα + y} + a^x.(b^y)^xk.α, como m = xykα + y, temos;

c^xk.b^xykα = b^m + a^x.b^xyk.α → c^xk.b^xykα − a^x.b^xyk.α = b^m → b^xykα.(c^xk − a^x) = b^m → b^xykα.(b^y) = b^m → b^{xykα + y} = b^m
→ b^m = b^m

Portanto como Eq₃ satisfez Eq₁ e Eq₂, logo Eq₁ possui soluções nos inteiros positivos.
Caso (4) para z múltiples de y esto es z – yk con k ∈ N
Esta demostración es análoga en relación con el caso (3), alcanzan el mismo formato que la ec_uación Eq3, pero con b en lugar de a, e y en lugar de[c.(c^yk − b^y)^α] ^x;

[b.(c^yk − b^y)^k.α]^yk á + ⁽cyk á b^{x)yk +} 1, con α ∈ N.
Caso (5): para múltiples z de x e y esto es z – xyk con MDC(z, x, y) – MDC(x, y)≥1, y k ∈ N
Be Eq₁: c^xyk por + ax y Eq2_: cm á cm^, con c ≠ 0 y k ∈ N, se puede encontrar una nueva Ecuación Eq3, que tiene propiedades de Eq1 y Eq2 s_i Eq3 no _tiene propiedad del logotipo _Eq1 Eq1 n_o tiene soluciones completas.

Como c ≠ 0 temos;
c^xyk = b^y + a^x → 1 = c ^− xyk*(b^y + a^x), (I) elemento neutro da multiplicação

Possamos escrever Eq₂ da seguinte maneira usando ( I );
c^m = c^m.c^− xyk.(b^y + a^x) → c^m = c^{m − xyk}.(b^y + a^x) → c^m = b^y.c^{m − xyk} + a^x.c^{m − xyk} , ao substituir (II) temos;

, Colocando y e x evidência temos;

O MMC(xy²k , x²yk )=x²y²k, para que 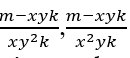 ∈ ℕ, obrigatoriamente m – xyk deve ser múltiplo de x²y²k isso é m − xyk = x²y²k.α, com α ∈ ℕ, logo temos;

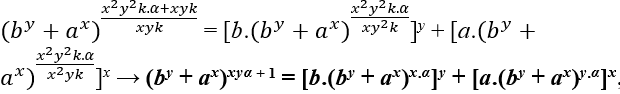Veja que xyα + 1 não é múltiplo de xy, pois MDC(xy.α + 1 , xy ) = 1, logo Eq1 não tem soluções inteiras positivas para z múltiplo de x e y.
Para p^or + ^ax por el principio de comparación mostrado anteriormente es igual ^{a cxyk} + 1 por ⁺ ax y como z xyk, tenemos ^{cz +} 1 p^or + ^ax. Por lo tanto z +1 no es múltiplo de x e y, por lo q_ue Eq1 no tiene solución en enteros positivos.
Caso ( 6 ): para z múltiplo de x, e y múltiplo de x é z = xk e y = xt, com k ≥ t e MDC(z,x,y)=x , e k, t ∈ ℕ
Seja Eq₁: c^xk = b^xt + a^x e Eq₂: c^m = c^m, com c ≠ 0 e k, t ∈ ℕ, é possível encontrar uma nova equação Eq₃, que tenha propriedades de Eq₁ e Eq₂ caso Eq₃ não tenha propriedade de Eq₁ logo Eq₁ não tem soluções inteiras.

Como c ≠ 0 temos;
c^xk = b^xt + a^x → 1 = c^− xk*(b^xt + a^x), , (I) elemento neutro da multiplicação
c^xk = b^xt + a^x → c = (b^xt + a^x)^1/xk (II)

Possamos escrever Eq₂ da seguinte maneira usando ( I );
c^m = c^m.c^− xk.(b^xt + a^x) → c^m = c^m − xk.(b^xt + a^x) → c^m = b^xt.c^m − xk + a^x.c^m − xk, ao substituir (II) temos;

, isolando xt e x temos;
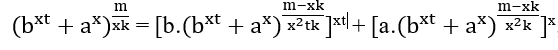, MMC(x²tk,x²k)=x²tk, para que  ∈ ℕ é necessário que m – xk seja múltiplo de  x²tk, isso é m − xk = x²tk.α, com α ∈ ℕ, substituindo esses valores é obtido;

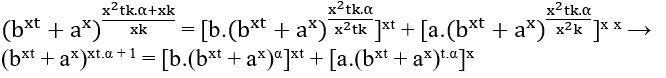como xt.α + 1 não é múltiplo de x, resta olhar para b^xt + a^x, perceba que inicialmente Eq₁ é c^xk = b^xt + a^x → (c^k)^x = (b^t)^x + a^x Ultimo teorema de Fermat.
Debido _a que Eq3 no satisfi_e Eq1, por lo ta_nto Eq1 no tiene una solución completa positiva cuando z es múltiplo de x, y múltiplo de x.

Caso ( 7 ): para z múltiplo de y, e x múltiplo de y é z = yk e x = yt, com k ≥ t e MDC(z,x,y)=y , e k, t ∈ ℕ
Essa demonstração é análoga em relação ao Caso (6), pois recai em Ultimo teorema de Fermat.

Caso ( 8 ): para z múltiplo de y e x, x ou y múltiplo um do outro, isso é z = xyk e x = yt ou z = xyk e y = xt, com k ≥ t e MDC(z,x,y)=y ou MDC(z,x,y)=x , e k, t ∈ ℕ
Essa demonstração é análoga em relação ao Caso (6) e (7), pois recai em Ultimo teorema de Fermat.

Obs: c^xyk = b^xt + a^x → (c^yk)^x = (b^t)^x + a^x e c^xyk = b^y + a^yt → (c^xk)^y = b^y + (a^t)^y, ambos Último Teorema de Fermat.
Conclusión en caso de que los exponentes sean múltiples:
No hay solución para enteros positivos, en los casos (5), ( 6 ), ( 7 ) y ( 8 )

3.3 SEGÚN MACENA O S.T.m

Dado n ≥ 2 el grado del primer miembro de la ecuación, siempre es posible determinar un ^{B (nm} – 1 ⁺ 1) ^{n (nm} á 1 ^x 1)n, y si MDC(a, B, c) – 1 entonces n tiene grado par, si el MDC(a, B, c) á 2.t ≥ 2 entonces el grado n es impar, en ambos casos un s^atículo , ^en particular para cualquier n par o impar tenemos el MDC(a,B,c) – c donde c es de la forma ²n – 1.
Para probar este teorema tendrás que encontrar una herramienta antes de probarla.
Herramienta:
Para encontrar la herramienta primero debemos analizar cómo se comporta el binomio de Newton desde el grado 2.

(x + y)² = 1.x² + 2.x.y + 1.y², isso é 1 2 1.
(x + y)³ = 1.x³ + 3.x².y + 3.x.y² + 1.y³, isso é 1 33 1.
(x + y)⁴ = 1.x⁴ + 4.x³.y + 6.x².y² + 4.x.y³ + 1.y⁴, isso é 1 4 6 4 1.
(x + y)⁵ = 1.x⁵ + 5.x⁴.y + 10.x³.y² + 10.x².y³ + 5.x.y⁴ + 1.y⁵, isso é 15101051.
*
*

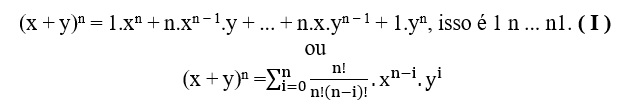
Agora subtraindo xⁿ ou yⁿ em ambos os lados de ( I ), é obtido;

(x + y)ⁿ − xⁿ = n.x^n − 1.y + … + n.x.y^n − 1 + yⁿ( I I)
ou
(x + y)ⁿ − yⁿ = 1.xⁿ + n.x^n − 1.y + … + n.x.y^{n 1(I})

Por la diferencia de dos poderes del mismo grado podemos escribir (x + y)n x xn, de l^a siguiente manera;

De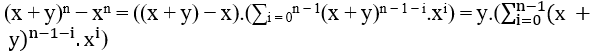l mismo modo, también podemos escribir (x + y)n ^a yn, de la siguiente manera;

Con esto tenemos dos nuevas ecuaciones diferenciando sólo en x e y.

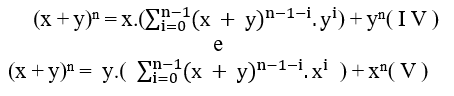
Añadiendo ( I V ) y ( V ) tenemos;

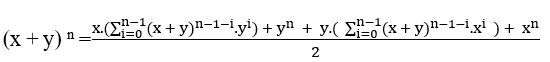
Para que sea divisible por 2, sólo y ser igual a x esto es y – x o x – y, con lo que tenemos

Dividiend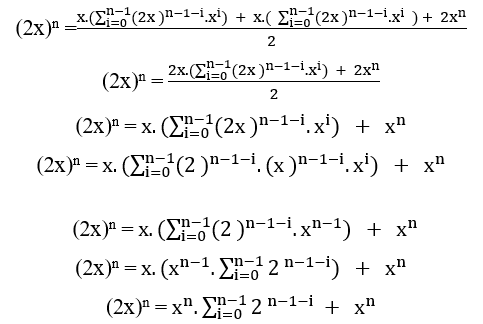o por el factor común que es xn que ten^emos;

El elemento ( VI ) es la herramienta que se utilizará para probar el teorema.

Provando os casos de n ser par ou ímpar:

Seja m ≥ 2, é possível obter equações do formato cⁿ = B + aⁿ, onde o MDC(c,B,a) = 1 se o grau n for par, e MDC(c, B, a) = 2.t ≥ 2, com t ∈ N^*, se o grau n é ímpar.

Método si la base es 2, se utilizará para completar cuadrados, si es 3 estará completando cubos, y así sucesivamente, hasta que la base n utilizará completar el poder del umpisth.

Ser b una base, con b ∈ N*, por lo que dar iniciativa tenemos;

Para b 2 tenemos;

2m x ²m de hecho esto es válido, podemos escribir de la siguiente manera 2m a ²m.1, ^darse cuenta de que la siguiente igualdad es válida.
2^m = 2^m.(2 − 1) → 2^m = 2^m + 1 − 2^m → 2.2^m − 1 = 2^m + 1 − 2.2^m − 1, para completar o quadrado do primeiro membro basta somarmos em ambos os lados2^{2(m − 1)} + 1, com isso resulta em;

2.2^m − 1 + 2^{2(m − 1)} + 1 = 2^m + 1 − 2.2^m − 1 + 2^{2(m − 1)} + 1 → (2^{2(m − 1)} + 2.2^m − 1 + 1) = 2^m + 1 + (2^{2(m − 1)} − 2.2^m − 1 + 1) , portanto temos dois quadrados perfeitos, e com isso uma nova equação;

(2 ^{m – 1}+ 1 )² = 2 ^{m + 1}+ (2 ^{m – 1}– 1 )²( 1 )

O seu MDC(2^m − 1 + 1, 2, 2^m − 1 − 1) = 1

Veja que só depende de uma variável no caso m, Veja os exemplos usando os números.

Para m = 2

(2^m − 1 + 1)² = 2^m + 1 + (2^m − 1 − 1)²
(2¹ + 1)² = 2³ + (2¹ − 1)²
(2 + 1)² = 2³ + (2 − 1)²
3² = 2³ + 1²
9 = 8 + 1

Para m = 3

(2^m − 1 + 1)² = 2^m + 1 + (2^m − 1 − 1)²
(2² + 1)² = 2⁴ + (2² − 1)²
(4 + 1)² = 2⁴ + (4 − 1)²
5² = 2⁴ + 3²
5² = 4² + 3²
25 = 16 + 9

Para m = 4

(2^m − 1 + 1)² = 2^m + 1 + (2^m − 1 − 1)²
(2³ + 1)² = 2⁵ + (2³ − 1)²
(8 + 1)² = 2⁵ + (8 − 1)²
9² = 2⁵ + 7²
(3²)² = 2⁵ + 7²
3⁴ = 2⁵ + 7²
81 = 32 + 49

Para m = 5

(2^m − 1 + 1)² = 2^m + 1 + (2^m − 1 − 1)²
(2⁴ + 1)² = 2⁶ + (2⁴ − 1)²
(16 + 1)² = 2⁶ + (16 − 1)²
17² = 2⁶ + 15²
289 = 64 + 225

Para m = 6

(2^m − 1 + 1)² = 2^m + 1 + (2^m − 1 − 1)²
(2⁵ + 1)² = 2⁷ + (2⁵ − 1)²
(32 + 1)² = 2⁷ + (32 − 1)²
33² = 2⁷ + 31²
1089 = 128 + 961

E assim por diante.

Para b 3, tenemos;

De hech^o, esto es válido, podemos escribir de la siguiente manera 3m a 3m.¹, da^rnos cuenta de que la siguiente igualdad es válida.
3^m = 3^m.1 → 3^m = 3^m.(3 − 2) → 3^m = 3^m + 1 − 2.3^m → 3.3^m − 1 = 3^m + 1 − 3.2.3^m − 1, para completar o cubo no primeiro lado da igualdade basta somarmos 3^{3(m − 1)} + 3.3^{2(m − 1)} + 1em ambos os lados, com isso resulta em;
3.3^m − 1 + 3^{3(m − 1)} + 3.3^{2(m − 1)} + 1 = 3^m + 1 − 2.3^m + 3^{3(m − 1)} + 3.3^{2(m − 1)} + 1 → (3^{3(m − 1)} + 3.3^{2(m − 1)} + 3.3^m − 1 + 1) = 3^m + 1 + 3^{3(m − 1)} + 3.3^{2(m − 1)} +  − 3.2.3^m − 1 + 1 → (3^m − 1 + 1)³ = 3^m + 1 + 3^{3(m − 1)} + 3.3^{2(m − 1)} − 2.3^m + 1, deve existir algum k ∈ ℕ, que somado e subtraído que gerem um cubo perfeito no segundo lado da igualdade assim como ocorreu no exemplo anterior sendo assim temos;
(3^m − 1 + 1)³ = [3^m + 1 + 3^{3(m − 1)} + 3.3^{2(m − 1)} − 2.3^m + 1 + k] − k, para determinar k, basta 3^m + 1 + 3^{3(m − 1)} + 3.3^{2(m − 1)} − 2.3^m + 1 + k = (3^m − 1 − 1)³;

3^m + 1 + 3^{3(m − 1)} + 3.3^{2(m − 1)} − 2.3^m + 1 + k = 3^{3(m − 1)} − 3.3^{2(m − 1)} + 3.3^m − 1 − 1
3^m + 1 + 3.3^{2(m − 1)} − 2.3^m + 1 + k =  − 3.3^{2(m − 1)} + 3.3^m − 1 − 1
k =  − 3^m + 1 − 3.3^{2(m − 1)} − 3.3^{2(m − 1)} + 3.3^m − 1 + 2.3^m − 1 − 1
k =  − 3^m + 1 − 6.3^{2(m − 1)} + 3.3^m − 1 + 2.3^m − 2
k =  − 3^m + 1 − 2.3.3^{2(m − 1)} + 3^m + 2.3^m − 2
k =  − 3^m + 1 − 2.3^{2(m − 1) + 1} + 3.3^m − 2
k =  − 3^m + 1 − 2.3^2m − 1 + 3.3^m − 2
k =  − 3^m + 1 − 2.(3^2m − 1 + 1) + 3.3^m
k =  − 3^m + 1 − 2.(3^2m − 1 + 1) + 3^m + 1
k =  − 2.(3^2m − 1 + 1)

Logo

− k = 2.(3^2m − 1 + 1)
Com isso temos outra equação
(3^m − 1 + 1)³ = [3^m + 1 + 3^{3(m − 1)} + 3.3^{2(m − 1)} − 2.3^m + 1 + k] − k
(3^m − 1 + 1)³ = (3^m − 1 − 1)³ + 2.(3^2m − 1 + 1)

(3^m − 1 + 1)³ = 2.(3^2m − 1 + 1) + (3^m − 1 − 1)³( 2 )

Como 3^m − 1 + 1 , 2.(3^2m − 1 + 1) e 3^m − 1 − 1, são pares pois potência de 3 é sempre impar somando 1 ou subtraindo 1 dessa potência isso nos dar um par.
Portanto o MDC(3^m − 1 + 1, 2.(3^2m − 1 + 1), 3^m − 1 − 1) = 2.t ≥ 2, com t ∈ N^*. Exemplo em números:

Para m = 2 temos;

(3^m − 1 + 1)³ = 2.(3^2m − 1 + 1) + (3^m − 1 − 1)³
(3¹ + 1)³ = 2.(3³ + 1) + (3¹ − 1)³
(4)³ = 2.(28) + (2)³
4³ = 2.28 + 2³, MDC( 4 , 2.28 , 2 ) = 2
64 = 56 + 8

Para m = 3 temos;

(3^m − 1 + 1)³ = 2.(3^2m − 1 + 1) + (3^m − 1 − 1)³
(3² + 1)³ = 2.(3⁵ + 1) + (3² − 1)³
(10)³ = 2.(244) + (8)³
10³ = 2.244 + 8³
1000 = 488 + 512

E assim por diante.

O método mais rápido de encontrarmos essas equações é usando cⁿ =B +aⁿ onde c = n^m − 1+1 e a = n^m − 1−1, isso é;

Então a equação geral é;

Se n é de grau 2 temos;

Portanto;
(n^m − 1 + 1)ⁿ = B + (n^m − 1 − 1)ⁿ

(2^m − 1 + 1)² = 2^m + 1 + (2^m − 1 − 1)²( 1 )

MDC(2^m − 1 + 1, 2, 2^m − 1 − 1) = 1, com m ≥ 2.

Se n é de grau 3 temos;

B = 2.((3^m − 1 + 1)².(3^m − 1 − 1)⁰ + (3^m − 1 + 1)¹.(3^m − 1 − 1)¹ + (3^m − 1 + 1)⁰.(3^m − 1 − 1)²)

B = 2.((3^m − 1 + 1)² + (3^m − 1 + 1).(3^m − 1 − 1) + (3^m − 1 − 1)²)

B = 2.((3^{2(m − 1)} + 2.3^m − 1 + 1) + 3^{2(m − 1)} − 1 + (3^{2(m − 1)} − 2.3^m − 1 + 1))

B = 2.(2.3^{2(m − 1)} + 1 + 3^{2(m − 1)})

B = 2.(3^{2(m − 1)}(2 + 1) + 1)

B = 2.(3^{2(m − 1)}(3) + 1)

B = 2.(3^{2(m − 1) + 1} + 1)

B = 2.(3^2m − 1 + 1)

Portanto;

(n^m − 1 + 1)ⁿ = B + (n^m − 1 − 1)ⁿ

(3^m − 1 + 1)³ = 2.(3^2m − 1 + 1) + (3^m − 1 − 1)³( 2 )

MDC(3^m − 1 + 1, 2.(3^2m − 1 + 1), 3^m − 1 − 1) = 2.t ≥ 2, com t ∈ N^* e m ≥ 2

Se n é de grau 4 temos;

B = 2.((4^m − 1 + 1)³.(4^m − 1 − 1)⁰ + 4^m − 1 + 1)².(4^m − 1 − 1)¹ + 4^m − 1 + 1)¹.(4^m − 1 − 1)² + 4^m − 1 + 1)⁰.(4^m − 1 − 1)³)

B = 2.(4^3m − 2 + 4^m) ou B = 2^2m + 1.(2^{4(m − 1)} + 1) ou B = 2^6m − 3 + 2^2m + 1 ou B = 8^2m − 1 + 2^2m + 1

Fazendo os cálculos corretamente chegara em;

B = 2.(43m − 2 + 4m) ou B = 22m + 1.(24(m − 1) + 1) ou B = 26m − 3 + 22m + 1 ou B = 82m − 1 + 22m + 1

Portanto temos;

(n^m − 1 + 1)ⁿ = B + (n^m − 1 − 1)ⁿ
(4^m − 1 + 1)⁴ = 2.(4^3m − 2 + 4^m) + (4^m − 1 − 1)⁴( 3 )
O MDC(4^m − 1 + 1, 2.(4^3m − 2 + 4^m), 4^m − 1 − 1) = 1, com m ≥ 2

ou

(2^{2(m − 1)} + 1)⁴ = 2^2m + 1.(2^{4(m − 1)} + 1) + (2^{2(m − 1)} − 1)⁴
O MDC(2^{2(m − 1)} + 1, 2^2m + 1.(2^{4(m − 1)} + 1), 2^{2(m − 1)} − 1) = 1, com m ≥ 2

ou

(2^{2(m − 1)} + 1)⁴ = 2^6m − 3 + 2^2m + 1 + (2^{2(m − 1)} − 1)⁴
O MDC(2^{2(m − 1)} + 1, 2^6m − 3, 2^2m + 1, 2^{2(m − 1)} − 1) = 1, com m ≥ 2

Se n é de grau 5 temos;

B = 2((5^m − 1 + 1)^4 − 0.(5^m − 1 − 1)⁰ + (5^m − 1 + 1)^4 − 1.(5^m − 1 − 1)¹ + (5^m − 1 + 1)^4 − 2.(5^m − 1 − 1)² + (5^m − 1 + 1)^4 − 3.(5^m − 1 − 1)³ + (5^m − 1 + 1)^4 − 4.(5^m − 1 − 1)⁴)

B = 2((5^m − 1 + 1)⁴ + (5^m − 1 + 1)³.(5^m − 1 − 1) + (5^m − 1 + 1)².(5^m − 1 − 1)² + (5^m − 1 + 1).(5^m − 1 − 1)³ + (5^m − 1 − 1)⁴)

Fazendo os cálculos chegará que B vale;

B = 2.(5^4m − 3 + 2.5^2m − 1 + 1)

Portanto a equação para o grau 5 é;

(5^m − 1 + 1)⁵ = 2.(5^4m − 3 + 2.5^2m − 1 + 1) + (5^m − 1 − 1)⁵( 4 )

MDC(5^m − 1 + 1, 2.(5^4m − 3 + 2.5^2m − 1 + 1), 5^m − 1 − 1) = 2.t ≥ 2, com t ∈ N^* e m ≥ 2.

Se n é de grau 6 temos;

B = 2.((6^m − 1 + 1)^5 − 0.(6^m − 1 − 1)⁰ + (6^m − 1 + 1)^5 − 1.(6^m − 1 − 1)¹ + (6^m − 1 + 1)^5 − 2.(6^m − 1 − 1)² + (6^m − 1 + 1)^5 − 3.(6^m − 1 − 1)³ + (6^m − 1 + 1)^5 − 4.(6^m − 1 − 1)⁴ + (6^m − 1 + 1)^5 − 5.(6^m − 1 − 1)⁵)

B = 2.((6^m − 1 + 1)⁵ + (6^m − 1 + 1)⁴.(6^m − 1 − 1) + (6^m − 1 + 1)³.(6^m − 1 − 1)² + (6^m − 1 + 1)².(6^m − 1 − 1)³ + (6^m − 1 + 1).(6^m − 1 − 1)⁴ + (6^m − 1 − 1)⁵)

Fazendo os cálculos corretamente vai chegar em;

B = 2.(6^5m − 4 + 20.6^3m − 3 + 6^m), ou B = 2.6^m.(6^4m − 4 + 20.6^2m − 3 + 1) e a equação é;

(6^m − 1 + 1)⁶ = 2.6^m.(6^4m − 4 + 20.6^2m − 3 + 1) + (6^m − 1 − 1)⁶( 5 )

Com MDC(6^m − 1 + 1, 2.6^m.(6^4m − 4 + 20.6^2m − 3 + 1), 6^m − 1 − 1) = 1, com m ≥ 2

Então perceba que foi satisfeitas as condições de ( 1 ) até ( 5 ) para os casos onde n é par e n é ímpar.

Para probar esta ecuación debemos mostrar para el caso general no sólo de (1) a ( 5 ) sino de (1) a (n).

Para n pares:
Sea n .2k con k ∈ N*, por los ejemplos anteriores se obtiene el MDC(a,B,c)-1, el Reemplazado en B;

Por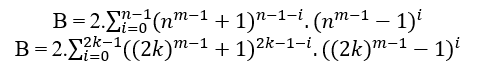 la definición de Par el B ya es un par, entonces es divisible por 2, sigue siendo marcar c y a. Si c y a son impares entonces el MDC (c,B,a) es 1, si c y b es incluso entonces el MDC(c,B,a) es 2.t ≥ 2, con t ∈ N*.

Como c á n^{m á 1} + 1 y a á nm ^{á 1 á} 1 de la ecuación ^cn – B + a cuando se reemplazan los valores de n y B que t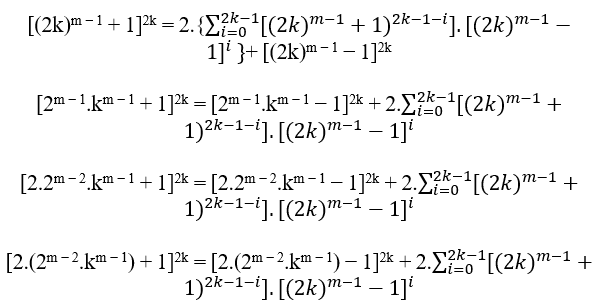enemos;

Así que ^{2. (}2m ^{s 2.k}m 1) + 1 como 2. ^{(2m s} 2^{.km 1}) – 1, son impares, por lo que a y c son impares, con esto el único valor que divide a, B y c es 1.

Para n Impar:
Si n a 2k + 1 con k ∈ N*, por los ejemplos anteriores se obtiene el MDC(a,B,c)-1, el Reemplazado en B;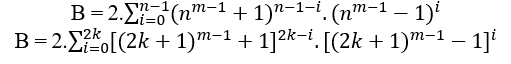

Al establecer el par el B ya es un par, entonces es divisible por 2, queda marcar c y a. Si c y a son impares entonces el MDC(c,B,a) es 1, si c y b es incluso entonces el MDC(c,B,a) es 2.t ≥ 2, con t ∈ N*.

Como c = n^m − 1 + 1 e a = n^m − 1 − 1 da equação cⁿ = B + aⁿ ao substituir os valores de n e B temos;

Como 2k + 1 é impar se elevarmos ao quadrado também é ímpar:
(2k + 1)² = 4k² + 4k + 1 = 2.(2k² + 2k) + 1
Se somarmos 1 em ambos os lados ou subtraímos 1 isso é um par?
(2k + 1)² + 1 = 2.(2k² + 2k) + 2 = 2.[2k² + 2k + 1] é um par, e (2k + 1)² − 1 = 2.(2k² + 2k) − 2 = 2.[2k² + 2k − 1] es una pareja.

Como 2k + 1 é ímpar se elevarmos ao cubo também é ímpar:
(2k + 1)³ = 8k³ + 12k² + 6k + 1 = 2.(4k³ + 6k² + 3k) + 1
Se somarmos 1 em ambos os lados ou subtraímos 1 isso é um par?
(2k + 1)³ + 1 = 2.(4k³ + 6k² + 3k) + 2 = 2.[4k³ + 6k² + 3k + 1] é um par, e (2k + 1)³ − 1 = 2.(4k³ + 6k² + 3k) − 2 = 2.[4k³ + 6k² + 3k − 1] es una pareja.

Como 2k + 1 é ímpar se elevarmos a quarta potência também é ímpar:
(2k + 1)⁴ = 16k⁴ + 32k³ + 6k + 1 = 2.(8k⁴ + 16k³ + 3k²) + 1
Se somarmos 1 em ambos os lados ou subtraímos 1 isso é um par?
(2k + 1)⁴ + 1 = 2.(8k⁴ + 16k³ + 3k²) + 2 = 2.[8k⁴ + 16k³ + 3k² + 1]é um par, e (2k + 1)⁴ − 1 = 2.(8k⁴ + 16k³ + 3k²) − 2 = 2.[8k⁴ + 16k³ + 3k² − 1]é um par .

se continuar sempre será um par portanto (2k + 1)^m − 1 + 1 e (2k + 1)^m − 1 − 1 é par e como B também é par, logo o menor valor que divide c,B e a é 2, logo MDC(a, B, c) = 2.t ≥ 2, com t ∈ N^*

Portanto temos as duas Equações principais:

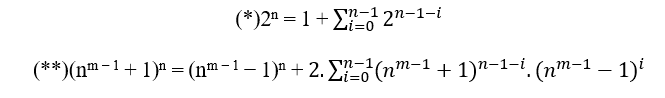
3.3.1 CATA S.T.m

Para probar S.T.M sólo queda mostrar que, independientemente de la n, ya sea par o impar, tenemos MDC(a,B,c) , donde c ^á 2n – 1 ya se ha demostrado que (**) tiene diferente MDC si n es incluso así como n es impar. Mas se usarmos a ferramenta (*) que foi gerada a partir do binômio de Newton, ao fazer x = y foi reduzido para a seguinte equação;

Como ao isolarmos temos;

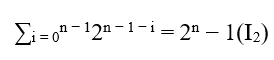
Ao substituir (I2) e (I1) é obtido;

(2x)ⁿ = xⁿ.(2ⁿ− 1) + xⁿ

Para que o primeiro lado da equação seja escrito como a soma de duas potências do segundo lado da equação, e como o fator comum é xⁿ, todavia como não foi definido qual valor de x, então basta x ser escrito como 2ⁿ − 1, dito isso a equação só irá depender do grau n, portanto temos;

(2x)ⁿ = xⁿ.(2ⁿ− 1) + xⁿ
(2.(2ⁿ − 1))ⁿ = (2ⁿ − 1)ⁿ.(2ⁿ − 1) + (2ⁿ − 1)ⁿ

Portanto outra equação que só depende de uma variável.

(2.(2ⁿ − 1))ⁿ = (2ⁿ − 1)^n + 1 + (2ⁿ − 1)ⁿ

Dados para essa nova Equação;
a = 2.(2ⁿ − 1), B = (2ⁿ − 1)^n + 1 e c = 2ⁿ − 1

MDC(a,B,c)=MDC(2.(2ⁿ − 1), (2ⁿ − 1)^n + 1, 2ⁿ − 1) = 2ⁿ − 1 = c
para n par
Isso é n=2k com k ∈ N^*

MDC(2.(2^2k − 1), (2^2k − 1)^2k + 1, 2^2k − 1) = 2^2k − 1 = c

para n impar
Isso é n= 2k + 1 com k ∈ N^*

MDC(2.(2^2k + 1 − 1), (2^2k + 1 − 1)^2k + 2, 2^2k + 1 − 1) = 2^2k + 1 − 1 = c

De fato está provado pois foi atendida todas as afirmações que o S.T.M propôs.
Teste com números;
Para n = 2 temos;

(2.(2ⁿ − 1))ⁿ = (2ⁿ − 1)^n + 1 + (2ⁿ − 1)ⁿ
(2.(2² − 1))² = (2² − 1)^2 + 1 + (2² − 1)²
(2.(3))² = 3³ + 3²
6² = 3³ + 3²
36 = 27 + 9

Para n = 3 temos;

(2.(2ⁿ − 1))ⁿ = (2ⁿ − 1)^n + 1 + (2ⁿ − 1)ⁿ
(2.(2³ − 1))³ = (2³ − 1)^3 + 1 + (2² − 1)³
(2.(7))³ = 7⁴ + 7³
14³ = 7⁴ + 7³
2744 = 2401 + 343

No momento S.T.M  aparentemente duas equações, porém só uma está no formato da Conjectura que é;

(2^m − 1 + 1)² = 2^m + 1 + (2^m − 1 − 1)²
MDC(2^m − 1 + 1, 2, 2^m − 1 − 1) = 1, com m ≥ 2.  “Não está, pois contém 2 como expoente”

e

(2.(2ⁿ − 1))ⁿ = (2ⁿ − 1)^n + 1 + (2ⁿ − 1)ⁿ
MDC(2.(2ⁿ − 1), 2ⁿ − 1, 2ⁿ − 1) = 2ⁿ − 1, com n ≥ 2. " si n>2 entonces pertenece a Beal Conjecture"

3.4 OTRAS ECUACIONES GENERADAS POR EL MÉTODO DE S.T.M.

F₁: ⇒  (2^m − 1 + 2^k − 1)² = 2^k(m + 1) + (2^m − 1 − 2^k − 1)²
É a geral da ( 1 ).
MDC(2^m − 1 + 2^k − 1, 2, 2^m − 1 − 2^k − 1) = 1, com k = 1 e m ≥ 2.
ou
MDC(2^m − 1 + 2^k − 1, 2, 2^m − 1 − 2^k − 1) = 2, com m ≥ 2 e m > k > 1.
Escriba si m a 4, entonces k puede ser 3.2 y 1.

F₂: ⇒  (2^m − 1.k^m + k)² = (2k)^m + 1 + (2^m − 1.k^m − k)²
Essa é a equação geral da anterior .
MDC(2^m − 1.k^m + k, 2k, 2^m − 1.k^m − k) = k, com m ≥ 2 e k ∈ N^*.

F₃: ⇒  (2^m + k^m + 2)² = (2k)^m + 2 + (2^m − k^m + 2)²
ou
(2^m + k^m + 2)² = (2k)^m + 2 + (k^m + 2 − 2^m)²
Se m = 0 e k for par temos; MDC(1 + k², 2k, |1 − k²|) = 1, com k ∈ N^*.
Se m = 0 e k for ímpar temos; MDC(1 + k², 2k, |1 − k²|) = 2α ≥ 2, com k, α ∈ N^*.
Se k for ímpar temos; MDC(2^m + k^m + 2, 2k, |2^m − k^m + 2|) = 1, com m ≥ 1 e k ∈ N^*.
Se k for par temos; MDC(2^m + k^m + 2, 2k, |2^m − k^m + 2|) = 2α ≥ 2, com m ≥ 1 e k, α ∈ N^*.

Formula Geral do Formato C² = B + A² ⇒ C² = b^m + A²
G₁: ⇒  (a^m + 2^m − 2.t^m)² = (2.a.t)^m + (a^m − 2^m − 2.t^m)²
Dados:
C = a^m + 2^m − 2.t^m, b = 2.a.t e A = |a^m − 2^m − 2.t^m|

( i ) Se a é ímpar e m > 2 o MDC(C,b,A)=1, ∀t ∈ N^*.

( ii ) Si a es impar con m a 2 y t a Even, el MDC(C,b,A)-1 .

( iii ) Si a es impar con m a 2 y t un Impar, el MDC(C, b, A) a 2o ≥ 2 con α ∈ ^N*.

( iv ) Si a es par y m > 2, el MDC (C, b, A) a 2o ≥ 2, ∀t, α ∈ ^N*.

( v ) Si a está emparejado con m a 2 y t un Impar el MDC(C, b, A) a 1, t ∈ ^N*.

( vi ) Si a está emparejado con m a 2 y t a Par, el MDC (C, b, A) a 2o ≥ 2, t, α ∈ ^N*.

Cómo surgió cada fórmula o ecuación:
La idea surgió debido a la conjetura Fermat-Catalán, porque al tener Cz – By + Ax^, sólo tiene una cantidad finita de soluciones en las que A, B y C son enteros positivos sin factores primos comunes y x, y y z son enteros positivos que satisfacen ()/() < 1, porque todas las soluciones tendrán 2 como uno de los exponentes. Debido a esto sería posible que la fijación del exponente 2 en la diferencia cuadrada tendría resultados satisfactorios en el formato de la conjetura? Cuando se utiliza el mismo método de S.T.M, foi surgindo novas equações com soluções nos inteiros positivos.

F₁: Seja (2^r + 2^s)² = B + (2^r − 2^s)² ⇒ B = (2^r + 2^s)² − (2^r − 2^s)², com B, r, s ∈ ℕ onde r > s, r e s variáveis não definidas no momento.

B = (2^r + 2^s)² − (2^r − 2^s)² → B = (2^r + 2^s − 2^r + 2^s).(2^r + 2^s + 2^r − 2^s) → B = (2^s + 2^s).(2^r + 2^r) → B = 2^s + 1.2^r + 1 → B = 2^{s + r + 2}

Ao adaptar s e r nas variáveis m e k como S.T.M, temos que m > k subtraindo 1 em ambos os lados temos m − 1 > k − 1 ao compara r > s, temos que r = m − 1 e s = k − 1, com isso temos B = 2^{k − 1 + m − 1 + 2} → B = 2^{m + k − 2 + 2} → B = 2^m + k, portanto a equação é;

F₁: ⇒ (2^m − 1 + 2^k − 1)² = 2^m + k + (2^m − 1 − 2^k − 1)²

Se k for 1, então MDC(2^m − 1 + 2^1 − 1, 2, 2^m − 1 − 2^1 − 1) = MDC(2^m − 1 + 2⁰, 2, 2^m − 1 − 2⁰) = MDC(2^m − 1 + 1, 2, 2^m − 1 − 1) = 1, ∀m ∈ N^*

Exemplo ao usar essa equação que tem MDC=1, com m = 2, 3, 5, 6. ; m no puede ser 1 porque k era 1.

Para m = 2
(2^2 − 1 + 1)² = 2^2 + 1 + (2^2 − 1 − 1)² → 3² = 2³ + 1² → 9 = 8 + 1

Para m = 3
(2^3 − 1 + 1)² = 2^3 + 1 + (2^3 − 1 − 1)² → 5² = 2⁴ + 3² → 25 = 16 + 9

Para m = 4
(2^4 − 1 + 1)² = 2^4 + 1 + (2^4 − 1 − 1)² → 9² = 2⁵ + 7² → 3⁴ = 2⁵ + 7² → 81 = 32 + 49

Para m = 5
(2^5 − 1 + 1)² = 2^5 + 1 + (2^5 − 1 − 1)² → 17² = 2⁶ + 15² → 289 = 64 + 225

Para m = 6
(2^6 − 1 + 1)² = 2^6 + 1 + (2^6 − 1 − 1)² → 33² = 2⁷ + 31² → 1089 = 128 + 961

Se k > 1, então MDC(2^m − 1 + 2^k − 1, 2, 2^m − 1 − 2^k − 1) = 2, ∀m, k ∈ N^*, onde m > k

Exemplo se m = 5, então k varia entre 2 até 4.

(2^m − 1 + 2^k − 1)² =2^m + k + (2^m − 1 − 2^k − 1)²→ (2^5 − 1 + 2^k − 1)² =2^5 + k + (2^5 − 1 − 2^k − 1)²→ (2⁴ +2^k − 1)² =2^5 + k + (2⁴ − 2^k − 1)²

Para k = 2
(2⁴ + 2^2 − 1)² = 2^5 + 2 + (2⁴ − 2^2 − 1)² → (2⁴ + 2¹)² = 2⁷ + (2⁴ − 2¹)²
→ 18² = 2⁷ + 14² → 324 = 128 + 196

Para k = 3
(2⁴ + 2^3 − 1)² = 2^5 + 3 + (2⁴ − 2^3 − 1)² → (2⁴ + 2²)² = 2⁸ + (2⁴ − 2²)²
→ 20² = 2⁸ + 12² → 400 = 256 + 144

Para k = 4
(2⁴ + 2^4 − 1)² = 2^5 + 4 + (2⁴ − 2^4 − 1)² → (2⁴ + 2³)² = 2⁹ + (2⁴ − 2³)²
→ 24² = 2⁹ + 8² → 24² = 2⁹ + 2⁶ → 576 = 512 + 64

F₂: Seja (2^s.k^r + k)² = B + (2^s.k^r − k)² ⇒ B = (2^s.k^r + k)² − (2^s.k^r − k)², com B, k, r, s ∈ ℕ onde r > s, r e s variáveis não definidas no momento.

B = (2^s.k^r + k)² − (2^s.k^r − k)² → B = (2^s.k^r + k − 2^s.k^r + k).(2^s.k^r + k + 2^s.k^r − k) → B = (2k).(2^s + 1.k^r) → B = 2k.2^s + 1.k^r → B = 2^s + 2.k^r + 1, Para que B seja escrito como uma potência basta s + 2 = r + 1, isso resulta que B = (2k)^r + 1 ou B = (2k)^s + 2, Porém para que isso seja verdade r deve ser maior que s isso é r > s.

Hipótese s + 2 = r + 1 ⇒ s = r − 1  e tese r > s

Temos que s + 1 > s somando 1 em ambos os lados s + 2 > s + 1 ⇒ r + 1 = s + 2 > s + 1 > s ⇒ r + 1 > s por sua vez r + 1 > r portanto r > s, perceba que ao usar a Hipótese onde s = r − 1 ⇒ r = s + 1 e substituir em r > s é satisfeita a desigualdade s + 1 > s.

Portanto B = (2k)^r + 1 = (2k)^s + 2 = (2k)^r + 1, logo a equação é;
(2^r − 1.k^r + k)² = (2k)^r + 1 + (2^r − 1.k^r − k)², para que tudo expoente fique em função da mesma variável m, basta r ser igual a m, isso é r = m. Com isso já temos outra equação;

F₂: ⇒ (2^m − 1.k^m + k)² = (2k)^m + 1 + (2^m − 1.k^m − k)²

Se k é 1, isso é a própria equação de F₁ do MDC=1;

(2^m − 1.1^m + 1)² = (2.1)^m + 1 + (2^m − 1.1^m − 1)² → (2^m − 1 + 1)² = 2^m + 1 + (2^m − 1 − 1)²

Se k > 1 tem como MDC = k

MDC(2^m − 1.k^m + k, 2k, 2^m − 1.k^m − k) = k, ∀m, k ∈ N^*.

Para k = 2

(2^m − 1.k^m + k)² = (2k)^m + 1 + (2^m − 1.k^m − k)²
(2^m − 1.2^m + 2)² = (4)^m + 1 + (2^m − 1.2^m − 2)²
(2^2m − 1 + 2)² = 4^m + 1 + (2^2m − 1 − 2)²
Se m = 1
(2^{2.1 − 1} + 2)² = 4^1 + 1 + (2^{2.1 − 1} − 2)² → 4² = 4² + 0² → 16 = 16
Se m = 2
(2^{2.2 − 1} + 2)² = 4^2 + 1 + (2^{2.2 − 1} − 2)² → (2³ + 2)² = 4³ + (2³ − 2)² → 10² = 4³ + 6² → 100 = 64 + 36
Se m = 3
(2^{2.3 − 1} + 2)² = 4^3 + 1 + (2^{2.3 − 1} − 2)² → (2⁵ + 2)² = 4⁴ + (2⁵ − 2)² → 34² = 4⁴ + 30² → 1156 = 256 + 900
*
*
*
E assim por diante …

Para k = 3
(2^m − 1.k^m + k)² = (2k)^m + 1 + (2^m − 1.k^m − k)²
(2^m − 1.3^m + 3)² = 6^m + 1 + (2^m − 1.3^m − 3)²
Se m = 1
(2^1 − 1.3¹ + 3)² = 6^1 + 1 + (2^1 − 1.3¹ − 3)²
(2⁰.3 + 3)² = 6² + (2⁰.3 − 3)² → 6² = 6² + 0²
Se m = 2
(2^2 − 1.3² + 3)² = 6^2 + 1 + (2^2 − 1.3² − 3)²
(2¹.9 + 3)² = 6³ + (2¹.9 − 3)² → 21² = 6³ + 15² → 441 = 216 + 225
Se m = 3
(2^3 − 1.3³ + 3)² = 6^3 + 1 + (2^3 − 1.3³ − 3)^2Nn
(2².27 + 3)² = 6⁴ + (2².27 − 3)² → 111² = 6⁴ + 105² → 12321 = 1296 + 11025
*
*
*

E assim por diante …
F₃: Seja (2^s + k^r)² = B + (2^s − k^r)² ⇒ B = (2^s + k^r)² − (2^s − k^r)², com B, r, s ∈ ℕ onde r > s, r e s variáveis não definidas no momento.

B = (2^s + k^r)² − (2^s − k^r)² → B = (2^s + k^r − 2^s + k^r).(2^s + k^r + 2^s − k^r) → B = 2.k^r.2^s + 1 → B = 2^s + 2.k^r, nesse caso para que B seja uma potência basta r = s + 2. De hecho r > s porque s + 2 > r s + 1 > s ⇒ r > s al colocar el exponente en una función de m, sólo s á m este nos da r á m + 2.

Logotipo B ^{a 2s} + ².kr á (2^k)r á (2k^{)m +} 2.

Portanto a nova equação é;

F₃: ⇒ (2^m + k^m + 2)² = (2k)^m + 2 + (2^m − k^m + 2)², com k ∈ N^* e m ≥ 0.
Si k es 1 para ∀m ∈ N^* el MDC a 1 o Si m es 0 a ∀k ∈ N* ^también el MDC a 1.
Se não ocorre nenhum desses casos F₃ Possui MDC = 2α ≥ 2, ∀α ∈ N^*

A lógica é a mesma para G₁,“Já que ela é a geral ”;

Pois ao fazer B = (a^r + 2^s.t^r )² − (a^r − 2^s.t^r)² → B = (a^r + 2^s.t^r  − a^r  + 2^s.t^r).(a^r + 2^s.t^r  + a^r- 2^s.t^r) →

.De forma simples basta s + 2 = r ou s = r – 2, como r é m fazendo a conversão temos s = m – 2, isso é;
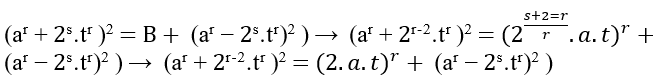G₁: ⇒  (a^m + 2^m − 2.t^m)² = (2.a.t)^m + (a^m − 2^m − 2.t^m)²
Dados:
C = a^m + 2^m − 2.t^m, B = 2.a.t e A = |a^m − 2^m − 2.t^m|

( i ) Se a é ímpar e m > 2 o MDC(C,b,A)=1, ∀t ∈ N^*.

( ii ) Si a es impar con m a 2 y t a Even, el MDC(C,b,A)-1 .

( iii ) Si a es impar con m a 2 y t un Impar, el MDC(C, b, A) a 2o ≥ 2 con α ∈ ^N*.

( iv ) Si a es par y m > 2, el MDC (C, b, A) a 2o ≥ 2, ∀t, α ∈ ^N*.

( v ) Si a está emparejado con m a 2 y t un Impar el MDC(C, b, A) a 1, t ∈ ^N*. ( vi ) Si a está emparejado con m a 2 y t a Par, el MDC (C, b, A) a 2o ≥ 2, t, α ∈ ^N*.

4. FÓRMULAS GENERADAS POR T.M E S.T.M CON SOLUCIONES EN NATURAL

Dados básicos; a,b,c,x,y,z,A,B,C,α e k ∈ N

Fórmula₁: C^z = C^{xyk + 1} = B^y+ A^x, mdc(x,y,z)=1

( b^y + a^x )^xyk + 1  = [ b( b^y + a^x)^xk]^y + [ a( b^y + a^x )^yk]^x

Dados:
C =b^y+ a^x,  B =b(b^y+ a^x)^xk  e  A = a( b^y+ a^x )^yk,  MDC(C, B, A) = C.

Fórmula₂: C^z = C^{xk + 1} = B^x+ A^x, ouC^z = C^{yk + 1} = B^y+ A^y, mdc(z,x)= mdc(z,x) = 1

( b^x + a^x )^xk + 1  = [ b( b^x + a^x )^k ]^x + [ a( b^x + a^x )^k ]^x

OU

( b^y + a^y )^yk + 1  = [ b( b^y + a^y )^k]^y + [ a( b^y + a^y )^k ]^y

Dados:
C =b^x+ a^x, B =b(b^x+ a^x)^k e A = a(b^x+ a^x )^k, MDC(C, B, A) = C.

OU

C =b^y+ a^y, B =b(b^y+ a^y)^k e A = a( b^y+ a^y )^k, MDC(C, B, A) = C.

 

Fórmula₃: C^z = C^xk = B^{xkα+ 1}+A^x, ouC^z=C^yk = B^{ykα+ 1}+A^y, mdc( z, y , x ) = 1

[ c( c^xk− a^x )^α]^xk = ( c^xk− a^x )^xkα+1 +[ a(c^xk−a^x)^kα]^x

OU

[ c( c^yk− b^y )^α]^yk = [ b( c^yk− b^y )^kα]^y + ( c^yk− b^y )^ykα+1

Dados:
C = c(c^xk − a^x), B = c^xk − a^x e A = a.(c^xk −a^x), MDC(C,B,A)= B.

OU

C = c(c^yk − b^y),  B = b(c^yk − b^y) e A = c^yk − b^y,  MDC(C,B,A)= A.

Fórmula₄:

(2.(2ⁿ − 1))ⁿ = (2ⁿ − 1)^n + 1 + (2ⁿ − 1)ⁿ

ou

(2ⁿ⁺¹ − 2)ⁿ = (2ⁿ − 1)^n + 1 + (2ⁿ − 1)ⁿ

Dados;
a = 2.(2ⁿ − 1), B = (2ⁿ − 1)^n + 1 e c = 2ⁿ − 1, MDC(a B,c)=MDC(2.(2ⁿ − 1), (2ⁿ − 1)^n + 1, 2ⁿ − 1) = 2ⁿ − 1 = c

Fórmula₅:

G₁: ⇒ (a^m + 2^m − 2.t^m)² = (2.a.t)^m + (a^m − 2^m − 2.t^m)²
Dados:
C = a^m + 2^m − 2.t^m, B = 2.a.t e A = |a^m − 2^m − 2.t^m|, Com t ≠ 2.a

( i ) Se a é ímpar e m > 2 o MDC(C,b,A)=1, ∀t ∈ N^*.

( ii ) Si a es impar con m a 2 y t a Even, el MDC(C,b,A)-1 .

( iii ) Si a es impar con m a 2 y t un Impar, el MDC(C, b, A) a 2o ≥ 2 con α ∈ ^N*.

( iv ) Si a es par y m > 2, el MDC (C, b, A) a 2o ≥ 2, ∀t, α ∈ ^N*.

( v ) Si a está emparejado con m a 2 y t un Impar el MDC(C, b, A) a 1, t ∈ ^N*.   ( vi ) Si a está emparejado con m a 2 y t a Par, el MDC (C, b, A) a 2o ≥ 2, t, α ∈ ^N*.

Em Particular

c² = 2^{m + 1} + b², MDC(a,b,c)=1

(2^m−1+1)²=2^m+1+(2^m−1−1)²
c=2^m−1+1, b=2 e a=2^m−1−1, MDC(a,b,c)=1

5. T.G.M O TEOREMA GENERAL MACENA

Dada cualquier ecuación válida de los enteros positivos en forma de potencia, o generado por T.M o S.T.M cuando se multiplica p^or d á una potencia, donde d es una base adecuada de transformación en la suma de dos potencias, y α es un exponente entero positivo múltiple de los exponentes de las otras bases o mmc de los exponentes multiplicado por t *^, por lo tanto resulta en una potencia escrita en la suma de otros dos poderes con un factor común d o múltiplo de d múltiples.

Exemplo:
, com B>A e m ≥ n ≥ 2, onde α=mmc(1,m,n).t, t ϵ N*
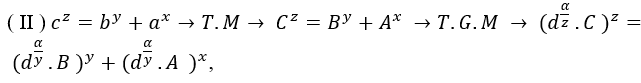, onde α=mmc(z,y,x).t, t ϵ N*
, onde α=mmc(n,1,n).t, t ϵ N*
( IV ) C²=B+A²→ Geralpor S.T.M→ ( a^m  +  2^m − 2.t^m )²  =  ( 2.a.t )^m  + ( a^m − 2^m − 2.t^m )²→T.G.M →
, donde α .mmc(2,m,2).β, β ε N*
Con esto siempre tenemos un factor común en el formato de la Conjetura si los exponentes x,y,z≥3, independientemente de la ecuación abordada.
"Con la excepción de ( IV ) que tendrá grado 2 siempre al menos en una de las bases".

5.1 PRUEBA T.G.M

Para probar este teorema es necesario probar los artículos. ( I ), ( II ), ( III ) y ( IV ).

Provando item ( I ) Seja qualquer equação do tipo , com B,ao multiplicar por uma potência , d não definida no momento, porém , isso é d^m.n.t , logo temos;

como d não está definido basta d ser iguala C isso é 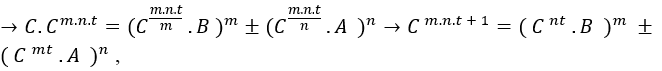, onde C é o fator comum da equação, pois
Exemplo em números;

C₁ = B^m+A^m→ 29 =3³ + 2², pelo teorema d=C₁=29 eα= mmc(1,3,2).t = 6t,  →29^6t+1 = 3³ . 29^6t + 2². 29^6t

29^6t+1 =( 3.29^2t )³ + ( 2.29^3t )² , se t=1 temos 29⁷=2523³+48778², mdc( 29 , 2523 , 48778 ) = 29 ,se t = 2 temos 29¹³=2121843³+1189646642², mdc(29, 2121843 , 1189646642 ) = 29 e assim por diante com t ≥3
C₂ = B^m-Aⁿ→ 23 =3³-2², pelo teorema d=C₂=23eα=mmc(1,3,2).t = 6t,→23^6t+1 =3³.23^6t-2².23^6t→
23^6t+1 =(3.23^2t)³ – (2.23^3t)²→, se t=1 temos 23⁷=1587³-24334²,mdc( 23 , 1587 , 24334 ) = 23,se t = 2 temos 23¹³=839523³-296071778², mdc(23, 839523 , 296071778 ) = 23 e assim por diante com t ≥3.
Provando item ( II ) Seja qualquer equação do tipo  c^z=b^y+a^x com soluções nos inteiros positivos, por T.M chegaremos em uma equação equivalente com as seguintes bases;
C =b^y+a^x, B =b(b^y+a^x )^xk e A =a( b^y+a^x )^yk, com equação C^xyk+1=B^y+A^x→C^z=B^y+A^x
Ao multiplicar por uma potência d^α , d não definida no momento, porém α=mmc(z,y,x).t , tϵN*, isso é d^zyx.t , logo temos;
d^zyx.t .C^z= d^zyx.t.B^y+d^zyx.t .A^x→(d^yx.t .C )^z= (d^zx.t .B )^y+(d^zy.t .A )^x→ Como mdc( C , B , A ) = C então

MDC[(d^yx.t .C ),(d^zx.t .B ),(d^zy.t .A ) ] ≥ d^t .C , em particular se d = C temos C^z(yxt+1)= (C^zx.t .B )^y+(C^zy.t .A )^x
MDC[ C , (C^zx.t .B ), (C^zy.t .A ) ] = C. Expandir usando todos los datos de la ecuación es;

• ^dyx.t . b^y+a^x  }^z= {d^zx.t .b( b^y+a^x )^xk}^y+{d^zy.t .a( b^y+a^x )^yk}^x
Como z= xyk + 1
{d^yx.t .( b^y+a^x ) }^xyk+1= {d^(xyk+1)x.t .b(b^y+a^x )^xk}^y+{d^(xyk+1)y.t .a( b^y+a^x )^yk}^x
Exemplo em números
x=y=2, t=k=1 e b=a=3 e d=5
{5⁴ .( 3²+3² ) }⁵= {5¹⁰ .3( 3²+3² )²}²+{5¹⁰ .3( 3²+3² )²}²
{5⁴ .18 }⁵= {5¹⁰ .3.18²}²+{5¹⁰ .3.18²}²
11250⁵=9492187500²+9492187500²
MDC(11250 ,9492187500,9492187500)=11250
Provando item ( III ) Seja qualquer equação do tipo cⁿ=B+aⁿ,com soluções nos inteiros positivos, por S.T.M, temos uma vasta quantidade de equações porém B é sempre , ao multiplicar a equação pela potencia d^α, d não definida no momento, com α = mmc(n,1,n).t, t ϵ N*, temos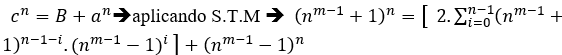

Como temos;

→Como d não está definido basta d=B isso é;

Ou

Exemplos;
( 1 )

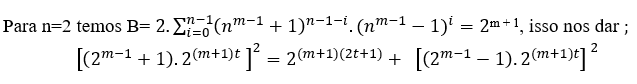
Sem = 2, temos → (3.2^3t )²=2^3(2t+1)+ 2^6t, ∀ t ∈N, MDC[(3.2^3t),2,2]=2
Se m = 3, temos →(5.2^4t )²=2^4(2t+1)+(3.2^4t)², ∀ t ∈N, MDC[(5.2^4t),2,(5.2^4t)]=2
[…]
( 2 )

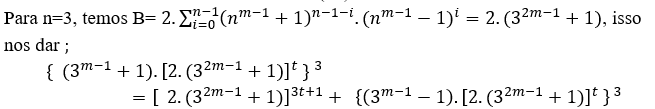Sem = 2, temos →{4.56^t}³=56^3t+1+ {2.56^t } ³, ∀ t ∈N, MDC[(4.56^t),56,2.56^t]= 56
Se m=3, temos →{10.488^t} ³=488^3t+1+ {8.488^t }³, ∀ t ∈N,MDC[(10.488^t),488,8.488^t] = 488
[…]
( 4 )

( 5 )

( 6 )

∀ m > 1, t ∈ N, MDC[Das Bases] = 2.6^m. (6^4m-4 + 20. 6^2m-3 +1)

( 7 )
E assim por diante
.
.
.
( … )

NOTA: Hasta ahora los puntos ( I ), ( II ) y ( III ) sólo permanecen ( IV )

Elemento de prueba ( IV ) Ser cualquier ecuación de tipo c2-B+a2^, con ^soluciones en los enteros positivos, utilizando los medios de S.T.M, tenemos;
^C2-B+C²→General por S.T.M→( a^m +  2^m − 2.t^m )²  =  ( 2.a.t )^m  + ( a^m − 2^m − 2.t^m )², ao multiplicar pela potencia d^α, com d não definido no momento, porém α = mdc(2,m,2).β , β ϵ N*, dessa vez usa β devido que a equação já possui t, dito isso temos;

d^α.(a^m  +  2^m − 2.t^m )²  =  d^α.( 2.a.t )^m  + d^α.( a^m − 2^m − 2.t^m )²
[d^mβ.( a^m  +  2^m − 2.t^m )]²  = [d^2β.( 2.a.t )]^m  + [d^mβ( a^m − 2^m − 2.t^m )]² [d^mβ .( a^m  +  2^m − 2.t^m )]² = [2at.d^2β ]^m  + [d^mβ ( a^m − 2^m − 2.t^m )]²

En este caso d puede ser cualquier número que pertenezca a los enteros positivos excepto cero, (d-N*).
Ejemplo en números;

a2, d-5et-m-β 3

[5⁹ .( 2³  +  2¹.3³)]²  = [12.5⁶]3 + [5⁹ .( 2³  -  2¹.3³)]²
[ 5⁹ .( 62 )]²  = [12.5⁶]³ + [5⁹ .( -46)]²
[121093750]²  = [187500]³+ [ -89843750 ]²
121093750²  = 187500³ + (- 89843750 )²

MDC[121093750 ,187500 ,| – 89843750 |] = 31250

OBS: Já o MDC(Das Bases ) ≥ d^β, esse 31250 = 2.d^2β>d^β

La idea es la misma para cualquier ecuación con la suma de 2 potencias.

Así que estás demostrando T.G.M

Curiosidad:( 1.0 )

5 = 3 + 2 → multiplicado pela base 3 → 5.3 = 3² + 2.3 → como 3 = 5 – 2 → substitui no primeiro membro 5(5 – 2)=3² + 2.3 → 5² – 2.5 = 3² + 2.³ → isolando 5² = 3² + 2.( 3 + 5 ) →
5² = 3² + 2.( 8 ) → 5² = 3² + 2.( 23 ) → 5² = 3² + 2⁴.

( 1.1 )

5³ = 5³ → 5³ = 5.5² → possamos escrever 5 = 2² + 1, pondo no segundo membro →
5³ = (2² + 1).5^{2 →} 53 = 2².5² + 5² → 5³= 10² + 5².

"NOTA: Esta curiosidad es otro artículo que publicaré en el futuro, ABC Conjecture"

6. PROBAR LA CONJETURA DE BEAL

(1a Condición) Dada la ecuación cz po^r + a^x, con soluciones en los enteros positivos, con á z , y, x ≥ 3 / c, b , un ≠ 0, a continuación, a, b y c tienen un factor primo común, lo que significa que a, b y c son divisibles por el mismo número primo.

O

(2a Condición) La ecuación a x + b y á c z no tiene solución para enteros positivos con x,y,z ≥ 3 y mdc(a,b,c)

Inicio de la prueba

A (2a Condición ) Es imposible obtener números en los enteros positivos con mdc(a,b,c) á1, y exponentes x,y,z ≥ 3, por dos razones ya mostradas:

1a — Se ha demostrado que la Conjetura Fermat-Catalán sólo tiene una cantidad finita de soluciones, actualmente sólo hay 10 ecuaciones encontradas, en las que a, b, y c son enteros positivos sin factores primos comunes y x, y, y z son integrales positivos satisfactorios, porque todas las soluciones tendrán 2 como uno de los exponentes, esto ya se adhiere a la hipótesis de mdc(a). ,b,c) 1, y los exponentes x,y,z ≥ 3.

LOS 10 ENCONTRADOS SON; Imagen tomada del sitio de wikipedia.

2o — Si votas por la parte S.T.M tenga en cuenta que cuando las ecuaciones tienen el mdc(bases)-1, siempre tiene un exponente 2, incluso variando los otros exponentes, y como S.T.M ha sido probado, así como la Conjetura Fermat – El catalán afirma que al menos uno de los exponentes debe ser 2, entonces pega la hipótesis por la simple razón de contener un exponente 2 en una de las bases.

Así que sólo queda otra condición por probar.

El (1a Condición) ya es posible a través de T.M, S.T.M e T.G.M, todos tienen factores comunes en ambas bases sólo para mostrar que tiene un factor primo común que divide ambas bases con los exponentes x,y,z ≥ 3.

PROVA:

Dados;

Seja p um número primo, e F^p = p^u um fator primo comum p, e pi ≠pi+1, i índice, primos distintos e os expoentes Ui ≥ Ui+1≥0, i índice, expoentes distintos ou não, então C um número natural pode ser inscrito como;

C = Fp = p^u, ou C = p1^u1.p2^u2 ou C = p1^u1.p2^u2. p3^u3 .p4^u4 …pi^ui .pi+1^ui+1… Fatores primos comum, como c^z = b^y + a^x, e pelo algum método de T.M, S.T.M e T.G.M, é obtido C^z = B^y + A^x, então;

C^z =(F^p )^z = p^z.u↔B^y + A^x = p^z.u, ou C^z =( p1^u1 ) .p2^u2 )^z =p1^z.u1 .p2^z.u2 ↔B^y + A^x = p1^z.u1 .p2^z.u2 ou

C^z =(p1^u1.p2^u2. p3^u3 .p4^u4 … pi^ui.pi+1^ui+1…)^z =p1^z.u1 .p2^z.u2. p3^z.u3.p4^z.u4… pi^z.ui.pi^+1z.ui+1…= B^y + A^x

CONSTRUINDO C^{z →} C^z A PARTIR DE Cⁿ.

De hecho, 1 a 1, porque 1 es un elemento neutro de la multiplicación dijo que es c ε N*, cuando se multiplica por ambos lados tenemos 1.c a 1.c→c á c, cuando se multiplica de nuevo por c tenemos c.c c.c→c2 a ^c2→ sⁱ este proceso continúa por n veces hemos → cn a cn, teⁿga eⁿ cuenta si n > z, tenemos ^cn>^cz.

Por lo ^tanto, cn – cn se puede inscribir ^como cⁿ – c^z.cn – z, la hipótesis de la conjetura es que el ^eje cz- by+, tiene un factor primo común que divide las bases c,b y a, con z,y,x ≥ 3, con esto lo tene^mos;

^cn ^– cz.cn ^– z→cn ⁽ by+ ax).cn – z→^cn á ^by. c^{n – z} + a^x.c^{n – z}, entonces si el ^ax c^z by+ tiene soluciones en los enteros positivos, con exponentes mayores o iguales a 3, de hecho cⁿ a p^or. c^{n – z} + a^x.c^{n – z}, tiene un factor que divide ambos porque el mdc(^cn, ^by. c^{n – z}, a^x.c^{n – z}) – cⁿ> 1.

La traducción se demuestra que el ^hacha cz+ by+ tiene tales soluciones, por lo que de hecho está confirmando la hipótesis y esta es una tesis. Pero para llegar a esa declaración tenemos que probar la igualdad, pero esto ya ha sido demostrado por los teoremas T.M, S.T.M e T.G.M, sin embargo, las condiciones de los exponentes eran mayores o iguales a 3 no fueron incluidas, ni las condiciones de los factores primos por lo que concluyen que esto está probado la conjetura de Beal.

Usando T.M temos que a equação c^z= b^y+ a^x, tornasse;

(b^y+a^x)^xyk+1=[b.(b^y+a^x)^xk ]^y+[a.(b^y+a^x)^yk]^x, onde z = xyk + 1, C = b^y+a^x ,
B= b.(b^y+a^x)^xk e A = a.(b^y+a^x)^yk , isso é C^z = B^y + A^x, com mdc (C,B,A) = C >1, para
x,y,z> 2 ou x,y,(xyk+1) > 2.

Por lo tant^o, si Cz – ^By + Ax tiene soluciones en los enteros positivos, ent^onces ^{cz –} cxyk + 1 p^or + ax, simplemente porque tiene el mismo formato o estructura. Dito isso resta mostrar cⁿ, que é;
cⁿ = b^y. c^{n – z} + a^x.c^{n – z} , adaptando para as bases C,B e A temos;

C ⁿ = B^y. C ^{n – z} + A^x.C^{n – z}

(b^y+a^x)ⁿ=[b.(b^y+a^x)^xk ]^y.(b^y+a^x)(n-z)+[a.(b^y+a^x)(yk )]^x.(b^y+a^x)(n-z)
(b^y+a^x)ⁿ=b^y.(b^y+a^x)^{xyk + n- z}+a^x.(b^y+a^x)^{xyk + n- z} , como z = xyk+1,
(b^y+a^x)n=b^y.(b^y+a^x)^{xyk + n- xyk-1} +a^x.(b^y+a^x)^{xyk + n- xyk-1}
(b^y+a^x)ⁿ=b^y.(b^y+a^x)^n-1+a^x.(b^y+a^x)^n-1

“Essa é a equação em funções dos expoentes n,x,y,com bases nos teoremas já mostrados anteriores temos ( n – 1)é um múltiplo de x,y, isso é n – 1 =

xyt ou n = xy.t + 1, o t é apenas para diferenciar de k, já usando”

(b^y+a^x)^xy.t+1=b^y.(b^y+a^x)^xyt +a^x.(b^y+a^x) ^xyt
(b^y+a^x)^xy.t+1=[b.(b^y+a^x)^xt ]^y+[a.(b^y+a^x)^yt]^x
Então como Cⁿ>C^z→Cⁿ-C^z> 0 → (b^y+a^x )^xy.t+1-(b^y+a^x )(x^y.k+1)>0→dividindo por(b^y+a^x ), temos→(b^y+a^x )^xy.t-(b^y+a^x )(x^y.k)>0→dividindo (b^y+a^x )^xy, temos →
(b^y+a^x )^t-(b^y+a^x )^k>0→(b^y+a^x )^t>(b^y+a^x )^k→t > k, ∀ t,k ∈N

Então a equação com todas as variáveis pode ser escrita da seguinte forma;
( EQ₁ )(b^y+a^x)^xy(t+k)⁺¹=[b.(b^y+a^x)x^(t+k) ]^y+[a.(b^y+a^x)(^y(t+k) )]^x

OU

( EQ₂ ) (b^y+a^x)^{xy( t – k )+1)}=[b.(b^y+a^x)^{x( t – k ) ]y}+[a.(b^y+a^x)^{y(t – k)} ]x

Pra chegar nessas duas formulas basta usar T.M, con n-z-xyt→n xyt + z, y como z-xyt, tenemos n á xy (t +k), y como se demostró que t > k, también es válido n á xy( t – k ) ∈N*

Al igual que las otras fórmulas generadas por T.M y algunos también de S.T.M e T.G.M, que tiene el formato Cz – Por +^Ax, ^tiene el mismo comportamiento que ( EQ1)e ₍ EQ2), _a continuación, mostrar las condiciones de los factores primos como al principio de esta prueba está demostrando literalmente todas las condiciones de la conjetura de Beal para el caso afirmativo que es (1a condición ).

(#) Para el caso de un factor primo común en ( EQ₁)e ( E_Q2), se tra^ta de Cz- ^By + ^Ax á pz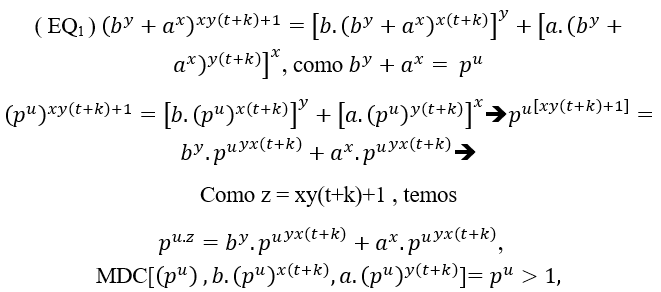.u ;

Por lo tanto, un factor primo común p, porque la igualdad se satisface si continú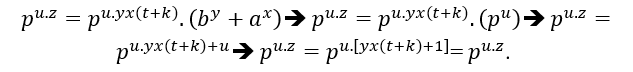a,

Análogamente a ( EQ1 ) tendrá el mismo resultado

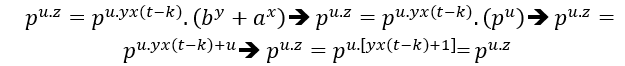(##) Para el caso de 2 factores primos comunes en (EQ1) y (EQ2),
, de hecho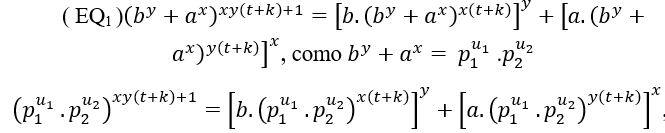, el mdc será el producto de dos poderes de primos distintos, esto es
Comprobación de la igualdad, como z á xy(t+k)+1, tenemos;

cuand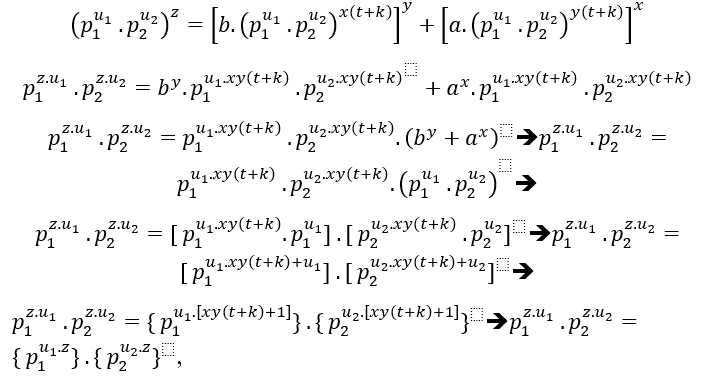o se divide por cualquiera de los factores primos comunes cae en la condición ( ) .
Análogamente a (EQ2);

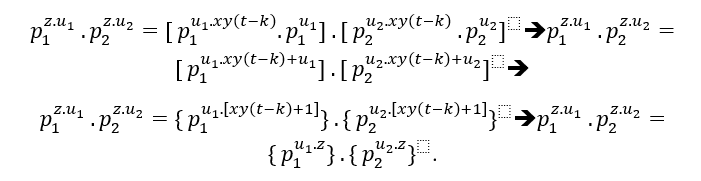( ### ) Para el caso de un factor primo común en (EQ1) y (EQ2), esto es;

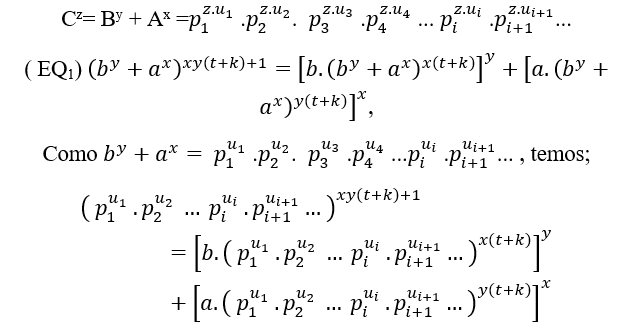
De hecho, tendremos un MDC con varios factores primos comunes, o a partir de 3, poderes de primos distintos entre sí, eso es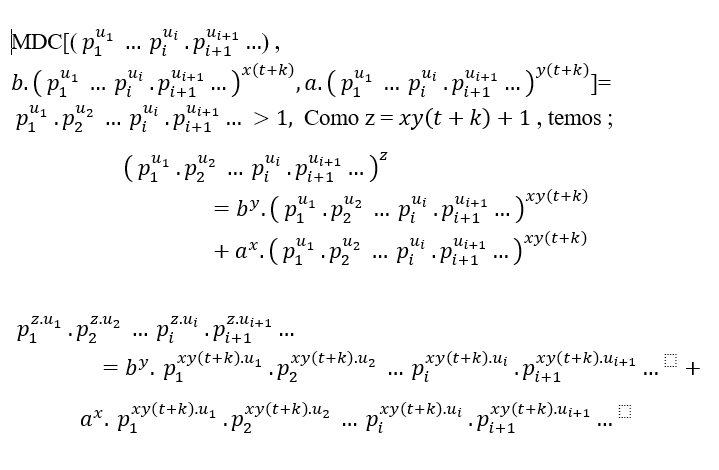
_________

_________

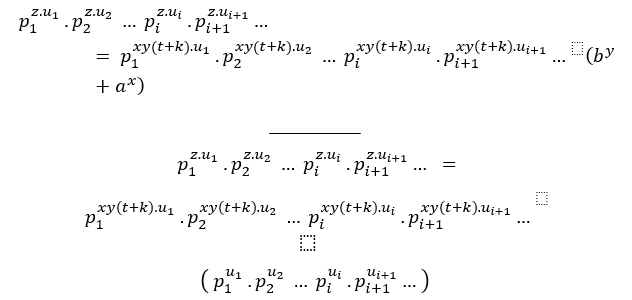
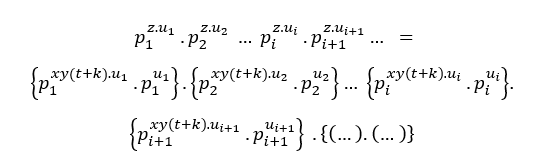
Al igual que la condición (-), tenemos;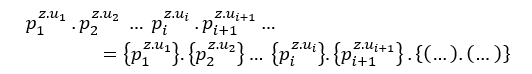

Cada vez que se divide por un factor primo común se reducirán hasta que se convierta sólo en un factor primo común.
Análogamente a (EQ2), tam_bién está satisfecho;

Po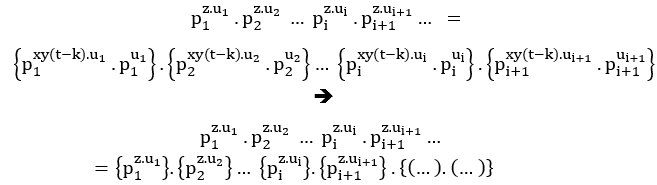r lo tanto, conjetura probada!

7. CONSIDERACIONES FINALES

Este artículo fue propuesto como una prueba objetiva general – allí la conjetura de Beal, cuando se utilizan los teoremas T.M, S.T.M e T.G.M combinado con las aplicaciones en la teoría de números en realidad era posible demostrar, sin embargo no era posible encontrar una estafa – ejemplo, sin embargo, cuando se utilizan los medios en el curso del desarrollo debe haber notado que cada paso era esencial para el otro de todos modos en relación con los teoremas presentados sin la T.M no podía usar T.G.M, sem o T.G.M o S.T.M no podría ser utilizado para la conjetura De Beal si no tuviera T.M o S.T.M e T.G.M sería algo muy vago, en otras palabras, no apoyaba la demostración de tal conjetura.
En el mejor de los casos sin los otros teoremas como el Teorema de Pitágoras, el último teorema de Fermat, el Teorema de Sebá y la conjetura de Fermat– Catalán la T.M sería algo muy vago y tomaría mucho más tiempo para ser probado, sólo por poseer tales teoremas de la T.M es una extensión y al mismo tiempo lo que soporta los teoremas citados, en otras palabras T.M era la pieza que faltaba para la finalización.

8. REFERÊNCIAS

BEAL, Andrew. Site: Wiki de Poker. 2008. Disponível em:<https://poker.fandom.com/wiki/Andrew_Beal> Acesso em: 03 de Junho de 2018.

FERMAT, biografias de Matemáticos. Site: Só Matemática. 1998-2019. Disponível em: <https://www.somatematica.com.br/biograf/fermat.php> Acesso em: 18 de Maio de 2018.

KILHIAN, (Sebastião Vieira do Nascimento, “Sebá”). A Conjectura de Beal – Casos Particulares. Site: O baricentro da Mente. 28/04/2012. Disponível em: <https://www.obaricentrodamente.com/2014/11/a-conjectura-de-beal-casos-particulares.html> Acesso em: 27 de Maio de 2018.

TANIYAMA e SHIMURA, Teorema de Shimura-taniyama-Wil. Editada pela última vez em 5 de setembro de 2017 Site: Wikipédia. Disponível em:<https://pt.wikipedia.org/wiki/Teorema_de_Shimura-Taniyama-Weil> Acesso em: 16 de Junho de 2018.

WILES, Biografia de matemáticos. Site: Só Matemática. 1998-2019. Disponível em: <https://www.somatematica.com.br/biograf/andrew.php > Acesso em: 15 de Maio de 2018.

9. FONTES DE PESQUISA

Site: O Baricentro da Mente. Título: A conjectura de Beal casos particulares. URL: <https://www.obaricentrodamente.com/2014/11/a-conjectura-de-beal-casos-particulares.html> Acesso em: 05 de Maio de 2018.
Site: O Baricentro da Mente. Título: Método de resolução das equações de Sebá. URL: <https://www.obaricentrodamente.com/2012/04/metodo-de-resolucao-das-equacoes-de.html> Acesso em: 05 de Maio de 2018.
Site: Folha de São Paulo. Título: Livro narra solução de teorema que confundiu teóricos por 358 anos. URL: <https://www1.folha.uol.com.br/fsp/ciencia/fe25109801.htm> Acesso em: 10 de Maio de 2018.
Site: Wikipedia. Título: Conjectura de Beal. URL:
<https://pt.wikipedia.org/wiki/Conjectura_de_Beal> Acesso em: 24 de Maio de 2018.
Site: ICM. Título: Detalhes do Autor "Sebastião Vieira do nascimento ( Sebá )". URL:
<https://www.lcm.com.br/site/livros/detalhesAutor?id=A01644> Acesso em: 27 de Setembro de 2019.
Site: Morfismo. Título: Conjectura de Beal. URL:
<https://morfismo.wordpress.com/2013/11/25/conjectura-de-beal/> Acesso em: 28 de Julho de 2018.
Site: DocSity. Título: Fermat, Notas de estudos de Física. URL:
<https://www.docsity.com/pt/fermat-6-1/4705276/> Acesso em: 01 de Setembro de 2019.
Site: Wikipedia. Título: Conjectura de Fermat-Catalan. URL:
<https://pt.wikipedia.org/wiki/Conjectura_de_Fermat-Catalan> Acesso em: 23 de Setembro de 2019.

^[1] Graduación en matemáticas.

Enviado: Agosto, 2019.

Aprobado: Noviembre, 2019.