ARTICOLO ORIGINALE
BELLAS, Leonardo Dias [1]
BELLAS, Leonardo Dias. Calcolo della proporzione numerica. Revista Científica Multidisciplinar Núcleo do Conhecimento. Anno 05, Ed. 12, Vol. 02, pp. 144-162. dicembre 2020. ISSN: 2448-0959, Collegamento di accesso: https://www.nucleodoconhecimento.com.br/olimpiadi-di-matematica/proporzione-numerica
RIEPILOGO
Nel 2011, un’osservazione logica matematica è stata fatta da questo autore ed è stata studiata da allora, questa logica riguarda che tutti i numeri possono essere rappresentati da un numero sequenziale da 1 a 9. Tuttavia, fu fatta la scoperta di ciò di cui si trattava questa logica e un altro calcolo esistente della Sequenza di Fibonacci era correlato. Detto questo, questo studio è stato sviluppato per registrare informazioni di questa logica riguardo a questa scoperta scientifica del calcolo della proporzione numerale, e sulla logica della proporzione numerale e sulla sua relazione con altre scoperte e concetti scientifici che sono stati sviluppati da altri matematici in precedenza. Per discutere e dimostrare queste osservazioni matematiche che non erano state osservate in precedenza e fornire una nuova opzione di calcolo più efficiente, poiché qualsiasi numero può essere rappresentato da numeri sequenziali da 1 a 9. Così, attraverso il calcolo e la logica della proporzione numerale possiamo identificarlo, oltre a dimostrare la sua applicabilità in matematica e scienze attuali.
Parola chiave: Rapporto numerico, sequenza di Fibonacci
1. INTRODUZIONE
L’intenzione di questo studio è quella di dimostrare questa scoperta matematica sulle proporzioni numeriche e mostrare la sua applicabilità nella matematica attuale. Attraverso calcoli matematici e dimostrazioni, il calcolo della proporzione numerica sarà spiegato e applicato trattando che qualsiasi numero può essere rappresentato da un numero sequenziale da 1 a 9. Questa sequenza da 1 a 9 è una sequenza sequenziale, in quanto si ripete all’infinito e in sequenza. E così mostrare il suo rapporto con un altro calcolo già eseguito, quello della sequenza di Fibonacci che è un coefficiente infinito di due misure successive. Il numero irrazionale chiamato (PHI) è ottenuto, con un valore approssimativo di 1,618 che è anche noto come rapporto aureo o proporzione d’oro, secondo il matematico Leonardo de Pisa.
2. LOGICA DELLE PROPORZIONI NUMERALI
Quando si dimostra il calcolo del rapporto numerico, dobbiamo fare alcune osservazioni matematiche, come l’esempio della logica del rapporto numerico. Come esemplificato nella tabella seguente:
Tavolo uno. Calcolo delle proporzioni logica e numerica

Fonte: autore.
Così possiamo osservare che tutti gli interi, decimali o cifre da 0,000000…0001 a Infinito, quando aggiunti alla loro ultima variabile è sequenziale da 1 a 9, cioè la somma delle cifre di qualsiasi numero, essendo zero neutro, è sequenziale da 1 a 9 Infinitamente. Quindi con questa logica possiamo osservare che tutti i numeri possono essere rappresentati da un numero sequenziale da 1 a 9, segue un modo più semplice per esprimere quella logica.
Figura 1: Logica delle proporzioni numerali

Fonte: autore.
3. CALCOLO DELLE PROPORZIONI NUMERALI
Ora passiamo al calcolo delle proporzioni numerali. In questo caso ho usato l’alfabeto romano, ma è possibile utilizzare un altro alfabeto o un altro simbolo / codice.
Figura 2: Calcolo delle proporzioni numerali

Fonte: autore.
Possiamo osservare che indipendentemente dal fatto che usiamo numeri interi o numeri di proporzione numerica, identifichiamo che in entrambi i calcoli i risultati sono gli stessi. Tuttavia, è osservabile che usare la logica delle proporzioni numerali per raggiungere il risultato è più semplice. Poiché non è necessario utilizzare l’intero alfabeto infinito di Interi, solo la sequenza da 1 a 9. Questo calcolo è come se si rompesse l’infinito di interi in una sequenza da 1 a 9 (numerale). Perché qualsiasi numero è sequenziale da 1 a 9.
Diamo un’occhiata al nome João, per l’intero si trova il numero 1015115 e nella logica numerica è il numero 1616. Pertanto, abbiamo osservato che sia il numero 1015115 che 1616, e la somma delle cifre fino alla loro ultima variabile è uguale a 5, quindi possiamo fare una scala dei numeri, facilitando le operazioni con grande volume, sequenziando e identificando ogni elemento da 1 a 9.
Possiamo anche applicare il calcolo della proporzione numerica a queste osservazioni, nei milioni di seguito:
Notando anche in miliardi:
Possiamo anche osservare nelle decime:
Qui nei dizymas possiamo osservare meglio l’infinito che va da 9 a 1.
La base, o il principio alla base di questo ragionamento, è registrare la scoperta di questo calcolo della proporzione numerale che dimostra che tutti i numeri possono essere rappresentati da un numero sequenziale da 1 a 9 all’infinito. Essere chiaramente osservato nella logica e nel calcolo della proporzione numerica, qui presentato. Quindi applicheremo i suoi significati con esempi di matematica e logica.
Pertanto, possiamo anche osservare l’infinito da 1 a 9.
4. INFINITO E LOGICA DEL RAPPORTO NUMERICO
L’esempio seguente è l’esempio identificando Infinity nella logica delle proporzioni numerali:
Figura 3: Logica delle proporzioni numeriali infinite
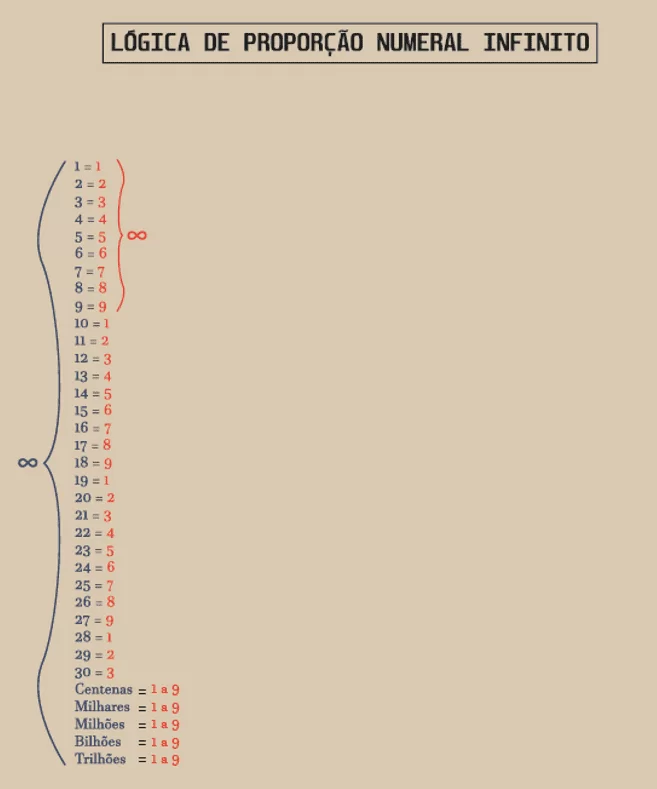
Guardando il grafico sopra è possibile andare all’infinito, sia in numeri interi che in numeri numerali. E come detto prima si suddivide l’intero numero in numeri, e guardandolo così, dove è più facile trovare o contare all’infinito? Contare tutti i numeri, passare attraverso migliaia, milioni, miliardi, trilioni ecc. o contare solo da 1 a 9? Osservando la logica calcolando le proporzioni numerali sequenziali da 1 a 9, è più facile e semplice trovare e contare all’infinito.
5. APPLICAZIONI DI CALCOLO DELLE PROPORZIONI NUMERALI
Il calcolo della proporzione numerica può essere molto utile, qualche tempo fa è stata effettuata una scoperta scientifica di un nuovo sistema binario, che è una scoperta molto importante di un sistema per il funzionamento dell’elettronica come computer, smartphone, videogiochi ecc. È molto più efficiente e sicuro dell’attuale sistema. Questo studio è stato pubblicato sulla stessa rivista scientifica e il link sarà nei riferimenti di questo lavoro. Ma conoscere questo calcolo del rapporto numerico ha aiutato a scoprire il sistema Binario 2, e ha dato la base per identificare le differenze logiche tra i sistemi binari, come in questo caso di seguito dove il calcolo del rapporto numerico può essere applicato. (BELLAS, 2019)
Figura 4: Sequenza binaria del sistema

Fonte: Autore
Quindi osservando le due logiche dei sistemi binari e usando il calcolo del rapporto numerico identifichiamo una logica in ogni sistema, abbiamo nel sistema binario 1, una sequenza di 6 ripetizioni 1, 2, 4, 8, 7, 5. E la logica del sistema binario 2, è una sequenza di 2 ripetizioni 3 e 6. Nelle due logiche binarie i numeri raddoppiano all’infinito, ma nel sistema binario 1, si piega all’infinito in una sequenza di 6 valori e nel sistema binario 2, si piega all’infinito in una sequenza di 2 valori. Quindi il sistema binario 2 ha più logica matematica ed è più efficiente del sistema binario 1, matematicamente e logicamente.
Una delle definizioni logiche è, quando un’informazione si ripete o ha sequenza. Nel caso del sistema binario 1 si ripete o ha sequenza in una logica a 6 fattori, già nel sistema binario 2 si ripete o ha sequenza in una logica di 2 fattori, quindi il sistema binario 2 è più semplice, è più logico. Due fattori logici sono più semplici di 6 fattori logici.
C’è un video su Youtube, con il titolo ”O Segredo dos números 3, 6 e 9” – Fatti sconosciuti. In questo video si riferisce alle osservazioni di Nikola Tesla riguardanti i numeri 3 e 6, ma questo video non è servito come riferimento per la realizzazione delle scoperte scientifiche di questo lavoro e anche quello del sistema binario 2, quando questo studio ha iniziato a essere sviluppato e del sistema binario, quindi anche le osservazioni dei numeri 3 e 6, così come il calcolo e la logica della proporzione numerica , sono stati eseguiti in modo diverso e prima dell’accesso alle informazioni di quella proposta da parte di Nikola Tesla in questo video.
Tesla trovò il rapporto tra le cifre 3 e 6, ma non lo correlava a un codice binario, non si riferiva a un sistema binario e programmazione, e non sviluppò un calcolo del rapporto numerico, ma Tesla osservò la relazione del sistema binario con Fibonacci e trovò il sequenziale logico 1, 2, 4, 8, 7, 5 del sistema binario 1 e trovò anche sequenziale 3 e 6 , ma non lo ha relazionato con un sistema binario, ma è stato lo scienziato che si è avvicinato di più alla ricerca di un nuovo sistema binario. (TESLA, Youtube)
E nella scoperta del sistema binario 2, le scansioni sequenziali 3 e 6 non sono state la prima osservazione fatta sul sistema binario 2, queste informazioni fanno parte così come molte altre fatte durante la scoperta scientifica del sistema binario 2, come il codice binario, il pixel rotondo, la scoperta di neutroni nella programmazione binaria e anche l’identificazione dell’1 (uno) uguale a Pi , e altre differenze tra il tipo di circuiti aperti e chiusi nei sistemi binari e le differenze nella programmazione binaria.
Tuttavia, questo video aiuta nelle fondazioni negli aspetti logici a fare le osservazioni scientifiche, matematiche, logiche e fisiche di questo studio. In sintesi per fare i risultati di questi studi, le informazioni sulla sequenza logica dei numeri 3 e 6 di Tesla erano sconosciute, e guardando il video di Tesla, osservò i numeri 3 e 6 in un modo diverso da come è stato osservato in questo studio, in questi risultati scientifici qui presenti, le scansioni sequenziali 3 e 6 sono state osservate calcolando il rapporto numerico.
Questo video è stato successivamente osservato la scoperta e la pubblicazione del sistema binario 2 e anche successivamente la pubblicazione del processo brevettuale nel INPI (Istituto Nazionale di Proprietà Industriale), ma per la qualità del materiale, perché il soggetto ha gli stessi riferimenti, ed è stato ben citato da uno dei migliori fisici della scienza moderna, e anche per cercare una maggiore osservazione sull’argomento , questo video è molto utile.
Segue questa citazione di Tesla per rappresentare la grandezza di ciò che è capire in matematica e fisica l’ampiezza della conoscenza che è quella di comprendere il significato dei numeri 3 e 6. ” Se conoscessi la magnificenza dei numeri 3, 6 e 9, allora avrei la chiave dell’Universo” (TESLA, Youtube)
Figura 5: Citare Nikola Tesla 3 e 6.

Possiamo dire che osservare l’infinito da 1 a 9 e quindi capire che tutti i numeri possono essere rappresentati da questa sequenza di infinito, ha anche una grande magnificenza.
Sistema binario 2 è la più importante scoperta scientifica tecnologica oggi, in quanto è una tecnologia avanzata, un computer con tecnologia Sistema binario 2 è molto superiore a un computer con l’attuale tecnologia Sistema binario, e questo calcolo è una delle equazioni più complesse che abbiamo.
Ci sono diverse differenze tecniche che dimostrano la superiorità del sistema binario 2 al sistema binario 1, di seguito saranno citati alcuni come esempi:
1 – Differenza nel tipo di Circuito Fisico, nel Sistema Binario 1 il circuito si apre, cioè è un circuito interrotto e nel Sistema Binario 2 il circuito è chiuso, cioè è un circuito continuo, questo genera una grande differenza di superiorità nelle prestazioni e nella risposta del Sistema. Il circuito continuo è più efficiente di un circuito interrotto.
2 – Un’altra differenza tecnica è che nel circuito Sistema binario 1 funziona solo con due elementi fisici e logici di programmazione negativa e positiva, mentre il Sistema binario 2 funziona con tre elementi di programmazione fisica e logica il negativo, neutro e il positivo, con questi tre elementi nella programmazione il circuito si chiude a causa del neutro, portando così una prestazione e un risultato superiori , anche incidendo sulla sicurezza del sistema. Un modo per esprimersi tecnicamente nel senso di sicurezza della programmazione binaria, è che un sistema binario senza il circuito neutro è aperto, quindi la sua porta è aperta è insicura, e nel sistema binario con il neutro il circuito è chiuso, quindi di conseguenza la sua porta è chiusa, quindi il sistema binario 2 ha più sicurezza.
3 – Altri aspetti sono nella programmazione della logica fisica dei Sistemi, nel sistema binario 1 funziona solo con 1 π (un PI) senza neutro, mentre nel sistema binario 2 la logica fisica del sistema funziona con 2 π (due PI) con neutro, questo porta una grande differenza nel tipo di realtà virtuale dei sistemi, nel sistema binario 1 il pixel è quadrato e nel sistema binario 2 il pixel è rotondo , influenzando direttamente il tipo di realtà, dimensione e grafica del sistema, portando più qualità, definizione, velocità, agilità e logica, aumentando anche l’elaborazione e la capacità nel volume dei dati, quindi una maggiore efficienza negli aspetti logici nella programmazione del Sistema Binario 2. 2 π (due PI) con neutro è maggiore di 1 π (un PI) senza neutro.
4 – E un’altra importante ragione tecnica è la differenza tra codici binari e sequenze logiche di sistemi, come spiegato in precedenza nel sistema binario 1 è una sequenza logica a sei fattori e il sistema binario 2 è una sequenza logica a due fattori, e questa differenza nelle sequenze e nei codici binari influisce direttamente sia sul volume di elaborazione dei dati che sulla velocità di risposta del sistema binario 2 che è più agile e logico matematicamente e Fisicamente. Sequenziale 3 e 6 è più logico ed efficiente di 1, 2, 4,8, 7, 5.
Ci sono altre differenze tecniche e altre informazioni, ma questi esempi sopra sono quelli che dimostrano le principali differenze tra i sistemi, e l’insieme di queste differenze tecniche tra i sistemi binari dimostra la qualità superiore di un sistema rispetto all’altro sistema.
La scoperta della programmazione del sistema binario 2 è una delle programmazione logiche che abbiamo in uno dei gradi più complessi e alti che esistano fino ad oggi, e fare osservazioni matematiche, logiche e fisiche usando solo 0 (zero) e 1 (uno), cioè vedere i sistemi in zero e uno, è una grande sfida.
In relazione ai circuiti e alla programmazione dei sistemi binari, un modo corretto in cui possiamo esprimere, è che un computer che pensa a zeri e uno, quindi la scoperta scientifica del sistema binario 2, è la scoperta di un modo nuovo o più efficiente per un computer di pensare a zeri e uno.
Sistema binario 2 è la tecnologia più avanzata che esiste oggi. I sistemi binari sono sistemi, poiché svolgono varie funzioni, sono circuiti logici e anche programmazione, il Sistema Binario 2 è un nuovo sistema più efficiente e sicuro per il funzionamento dell’elettronica, e differenzia una programmazione binaria dall’altra attraverso la disposizione logica di zeri e uno.
Tuttavia, questo studio è per dimostrare la scoperta del calcolo della proporzione numerica, se si desidera ulteriori informazioni sul sistema binario 2, l’articolo è in riferimenti a questo lavoro.
Il sistema binario 2 funziona con le leggi del rapporto numerico, elabora i tuoi dati da 1 a 9, essendo quindi molto più efficiente. Il sistema binario 2 funziona anche rispettando le leggi di Fibonacci, e questo studio ha riferimento e relazione anche nel calcolo della proporzione numerica, perché sono praticamente la stessa cosa, i due sono un coefficiente di infinito, è stato scoperto solo un nuovo modo matematico di calcolare, esprimere e osservare parte delle leggi di Fibonacci. Queste osservazioni vengono eseguite qui chiamate calcolo della proporzione numerica.
Dopo un lungo periodo di studio e ricerca, e risultati di osservazioni al di sopra del calcolo della proporzione numerica, è stata trovata una relazione tra questa scoperta e un altro studio, quello della sequenza di Fibonacci (PHI). La logica della proporzione numerica da 1 a 9 all’Infinito è direttamente collegata alle leggi di Fibonacci, che segue anche le leggi matematiche,
che attraverso le misure della serie di Fibonacci, quando si analizza il coefficiente di due misure successive, si ottiene il numero irrazionale chiamato (PHI), con un valore approssimativo di 1,618. E questa congiuntura di misure basate su questo numero è chiamata Golden Ratio, o Golden Ratio, che si trova, quindi, nei fiori, negli alberi, nelle onde, nelle galassie, nei gusci, negli uragani, nella faccia simmetrica dell’essere umano, nelle articolazioni ossee e nelle caratteristiche degli esseri umani, nel loro battito cardiaco e nel loro DNA. Anche nella rifrazione della luce fornita dagli elettroni degli atomi, nelle vibrazioni, in altre manifestazioni più (TANURE, online, s/p).
E spiega perché la sequenza va da 1 a 9. Di seguito possiamo vedere che il quadrante successivo è il doppio di tutti i precedenti, ad esempio, il 2 è il doppio di [1], il 3 è il doppio di [1 e 2 ], 4 è il doppio di [1, 2 e 3], 5 è il doppio di [1, 2, 3 e 4] e così via. Ed è sempre sequenziale da 1 a 9, dove 9 è il doppio di tutti i suoi predecessori, ripetendo così la logica dell’Infinito: 1 2 3 4 5 6 7 8 9, 1 2 3 4 5 6 7 8 9, 1 2 3 4 5 6 7 8 9. Sempre la cifra successiva il doppio del numero dei suoi predecessori. Di seguito è riportato un modo per esprimere la sequenza di Fibonacci
Figura 6: Sequenza Fibonacci-PHI
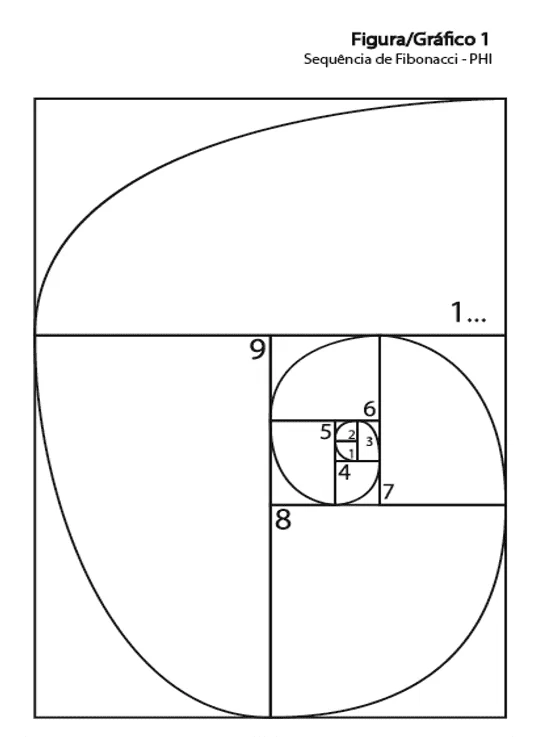
Fonte: Author’s
Guardando il grafico sopra concludiamo che:
9 x PHI = 1 Infinito (Nove volte la misura di fibonacci è uguale a un Infinito) o
9 x 1,618 = 1 unità Infinity o 1.
OR 1 infinito = 1 unità (un infinito è uguale a un’unità)
Ad esempio, se si trova matematicamente la misura di Fibonacci che rappresenta l’infinito in una conchiglia, questa conchiglia è rappresentata dall’essere 1 unità, perché questo coefficiente di infinito è presente o firmato matematicamente in questa unità.
La misura della proporzione numerica o sequenza di Fibonacci che è rappresentata da un coefficiente e da una logica di proporzione per calcolare e trovare l’infinito, perché se trovi questo coefficiente o calcolo presente in qualsiasi elemento, galassia, pianta o animale, quell’essere o elemento è rappresentato dall’essere 1 (uno) unità nelle leggi di Fibonacci.
Tutti gli elementi e gli esseri sono firmati matematicamente, fisicamente e naturalmente con questo coefficiente dell’Infinito.
C’è un Infinito matematicamente firmato in ogni unità.
Un’altra citazione trovata sulla sequenza di Fibonacci parla della logica del rapporto come esemplificato di seguito:
è una successione di numeri che seguono uno schema.
La sequenza di Fibonacci non è altro che l’ordine degli interi, che normalmente si discosta da zero e uno in cui ogni numero successivo corrisponde alla somma delle due cifre precedenti. Questa continuità può essere vista in vari fenomeni della natura.
La sequenza di Fibonacci fu chiamata così dal matematico italiano Leonardo de Pisa, noto anche come Fibonacci. Nel 1202, da questa sequenza numerica, il matematico riportò l’avanzata di una popolazione di conigli.
Fibonacci Formula
La successione di Fibonacci è una successione di interi iniziata per zero e uno, in cui ogni termine successivo corrisponde alla somma dei due numeri precedenti:
0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584… (Sequenza di Fibonacci – Educa + Brasile).
E qui possiamo notare la differenza dei metodi di osservazione tra il calcolo di Fibonacci, e questo calcolo matematico e logico della proporzione numerica. Sia la logica della proporzione numerale che la sequenza di Fibonacci sono la stessa cosa, ma questo coefficiente infinito può essere osservato in questi due modi distinti. Poiché Fibonacci era un riferimento per sviluppare questa scoperta della Logica della Proporzione Numerale, perché nelle due osservazioni hanno lo stesso coefficiente di infinito, solo il modo di essere osservati cambia, quindi battezzeremo anche il calcolo di questa sequenza da 1 a 9 di questo studio di Fiboleo, per la ragione della relazione tra i nomi degli autori di queste osservazioni.
Sequenziale da 1 a 9 come dimostrato nei calcoli presenti in questo studio, logica delle proporzioni numerali e calcolo della proporzione numerica.
Ecco ulteriori informazioni dalle citazioni della sequenza di Fibonacci nelle ricerche su Internet:
Questo metodo è applicato nell’analisi dei mercati finanziari, nella teoria dei giochi e nell’informatica, nonché nelle configurazioni biologiche e naturali. Modelli naturali. La sequenza di Fibonacci può essere osservata anche nei fenomeni naturali). (Sequenza di Fibonacci – Educa + Brasile).
Qui in questa citazione possiamo vedere che parla di informatica, è anche dove il calcolo della proporzione numerica è stato applicato per identificare un nuovo sistema binario, come esemplificato in precedenza in questo studio.
Dai un’occhiata ad altre citazioni sul calcolo, di seguito alcune di esse:
Girasole: I chicchi di girasole hanno semi disposti in un doppio set a spirale. Il più delle volte è 21 in senso orario e altri 34 in senso antiorario.
Pigna: dopo la crescita della frutta, i semi formano una doppia spirale con otto in senso orario e altri 13 in senso antiorario.
Shell shell: ogni parte del guscio ha la dimensione della somma dei due predecessori. È noto che un coha ha tre lati principali, quindi supponendo che un lato metri 2 (1 + 1), e l’altro 5 (3 + 2) il terzo sarà 8 (5 + 3). (Sequenza di Fibonacci: Educa + Brasile).
Quindi la logica del Rapporto Numerico, che è sequenziale da 1 a 9, è un coefficiente dell’Infinito e quindi possiamo eseguire la stessa osservazione in fibonacci sequenziale, che è anche un coefficiente infinito. Ma imparare questo calcolo è molto efficiente per le operazioni in cui ha un alto volume di numeri di cifre, perché possiamo identificarli in una sequenza logica più semplice, tutti i numeri sono rappresentati da numeri sequenziali da 1 a 9 all’infinito.
CONCLUSIONE
La conclusione di questo studio ha lo scopo di registrare la scoperta del calcolo della proporzione numerica e della logica della proporzione numerica, e di correlare questa scoperta del calcolo della proporzione numerica con il calcolo di Fibonacci, oltre a dimostrare la sua applicabilità in matematica e specialmente nei sistemi binari e per quanto riguarda la sua applicazione in relazione all’infinito.
Questo studio può fornire la base per nuove scoperte scientifiche, come è già accaduto, e per la ricerca. Può aiutare le persone a pensare a nuovi modi di gestire i numeri, ed è un nuovo modo più semplice di calcolare sequenziando tutti i valori a Infinity da 1 a 9. Nella logica della proporzione numerica, l’infinito è rotto da 1 a 9. Anche per presentare nuove informazioni, un nuovo modo di osservare, esprimere, trovare, calcolare e decifrare l’Infinito.
RIFERIMENTO
BELLAS, L.D. Sistema Binário 2 – Código Fechado. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 02, Vol. 05, pp. 110-151. Fevereiro de 2019. ISSN: 2448-0959. Disponível em: https://www.nucleodoconhecimento.com.br/tecnologia/sistema-binario-2-codigo-fechado
TANURE, A.C. Proporção Áurea e Sequência Fibonacci. Pagasus Portal. Disponível em: http://pegasus.portal.nom.br/proporcao-aurea-e-sequencia-de-fibonacci/
TESLA, N. Os segredos dos números 3, 6 e 9. Youtube – Fatos Desconhecidos https://www.youtube.com/watch?v=c2M9ZfZ5h5A&t=682s
Sequência de Fibonacci. Educa+Brasil. Disponível em: https://www.educamaisbrasil.com.br/enem/matematica/sequencia-de-fibonacci
[1] Laureato in Economia Aziendale con specializzazione in Commercio Estero.
Inviato: Maggio, 2020.
Approvato: dicembre 2020.