ORIGINALER ARTIKEL
BELLAS, Leonardo Dias [1]
BELLAS, Leonardo Dias. Berechnung des Zahlenanteils. Revista Científica Multidisciplinar Núcleo do Conhecimento. Jahrgang 05, Ed. 12, Vol. 02, S. 144-162. Dezember 2020. ISSN: 2448-0959, Zugangslink: https://www.nucleodoconhecimento.com.br/mathematischen-olympiaden/zahlenanteils
ZUSAMMENFASSUNG
Im Jahr 2011 wurde eine mathematische logische Beobachtung von diesem Autor gemacht und wurde seitdem untersucht, diese Logik betrifft, dass alle Zahlen durch eine sequenzielle Zahl von 1 bis 9 dargestellt werden können. Die Entdeckung dessen, worum es bei dieser Logik ging, wurde jedoch gemacht und eine weitere bestehende Berechnung der Fibonacci-Sequenz war im Zusammenhang. Das heißt, diese Studie wurde entwickelt, um Informationen dieser Logik über diese wissenschaftliche Entdeckung der Numeral Proportion Calculation und über die Numeral Proportion Logic und ihre Beziehung zu anderen wissenschaftlichen Entdeckungen und Konzepten, die zuvor von anderen Mathematikern entwickelt wurden, aufzuzeichnen. Um diese zuvor nicht beobachteten mathematischen Beobachtungen zu diskutieren und zu demonstrieren und eine neue Möglichkeit einer effizienteren Berechnung zu bieten, da jede Zahl durch sequenzielle Ziffern von 1 bis 9 dargestellt werden kann. So können wir dies durch die Berechnung und Logik von Numeral Proportion identifizieren, zusätzlich zu seiner Anwendbarkeit in Mathematik und aktueller Wissenschaft.
Schlagwort: Zahlenverhältnis, Fibonacci-Sequenz
1. EINFÜHRUNG
Die Absicht dieser Studie ist es, diese mathematische Entdeckung über numerische Proportionen zu demonstrieren und ihre Anwendbarkeit in der aktuellen Mathematik zu zeigen. Durch mathematische Berechnungen und Demonstrationen wird die Berechnung des Ziffernanteils erklärt und angewendet, indem behandelt wird, dass eine beliebige Zahl durch eine sequenzielle Zahl von 1 bis 9 dargestellt werden kann. Diese Sequenz von 1 bis 9 ist eine sequenzielle Sequenz, da sie sich unendlich und sequenziell wiederholt. Und so zeigen Sie seine Beziehung zu einer anderen Berechnung bereits durchgeführt, die der Fibonacci-Sequenz, die ein unendlicher Koeffizient von zwei aufeinander folgenden Maßnahmen ist. Die irrationale Zahl genannt (PHI) wird erhalten, mit einem ungefähren Wert von 1.618, die auch als goldenes Verhältnis oder goldenes Verhältnis bekannt ist, nach Mathematiker Leonardo de Pisa.
2. NUMERAL ASPECT RATIO LOGIC
Wenn wir die Berechnung des Zahlenverhältnisses demonstrieren, müssen wir einige mathematische Beobachtungen machen, wie z. B. das Beispiel der Logik des Zahlenverhältnisses. Wie in der nachstehenden Tabelle dargestellt:
Tabelle eins. Berechnung des Logik- und Ziffernseitenverhältnisses

Quelle: Autor.
So können wir beobachten, dass alle ganzen Zahlen, Dezimalstellen oder Ziffern von 0.000000…0001 bis Infinity, wenn sie zu ihrer letzten Variablen addiert werden, sequenziell von 1 bis 9 ist, d.h. die Summe der Ziffern einer beliebigen Zahl, die neutral Null ist, ist sequenziell von 1 bis 9 Unendlich. Mit dieser Logik können wir also beobachten, dass alle Zahlen durch eine sequenzielle Zahl von 1 bis 9 dargestellt werden können, folgt einem einfacheren Weg, diese Logik auszudrücken.
Abbildung 1: Logik des Numeralen Seitenverhältnisses

Quelle: Autor.
3. NUMERAL ASPECT RATIO BERECHNUNG
Gehen wir nun zur Berechnung des Zahlenaspektverhältnisses. In diesem Fall habe ich das römische Alphabet verwendet, aber ein anderes Alphabet oder ein anderes Symbol/Code kann verwendet werden.
Abbildung 2: Berechnung des Numeralen Seitenverhältnisses

Quelle: Autor.
Wir können beobachten, dass unabhängig davon, ob wir ganzzahlige Zahlen oder Zahlen zahlen, erkennen, dass in beiden Berechnungen die Ergebnisse identisch sind. Es ist jedoch zu beobachten, dass die Verwendung der Logik des Zahlenaspektverhältnisses, um das Ergebnis zu erreichen, einfacher ist. Da Sie nicht das gesamte Unendliche Alphabet der Ganzzahlen verwenden müssen, nur die Sequenz von 1 bis 9. Diese Berechnung ist, als ob Sie die Unendlichkeit der ganzzahligen in einer Sequenz von 1 bis 9 (Anzahl) gebrochen haben. Denn eine beliebige Zahl ist sequenziell von 1 bis 9.
Schauen wir uns den Namen João an, durch die ganze Zahl sitzt die Zahl 1015115 und in der Zahlenlogik ist die Zahl 1616. So haben wir beobachtet, dass sowohl die Zahl 1015115 als auch 1616 und die Summe der Ziffern bis zu ihrer letzten Variablen gleich 5 ist, so dass wir eine Skala der Zahlen erstellen können, die Operationen mit großem Volumen erleichtert, jedes Element von 1 bis 9 sequenziert und identifiziert.
Wir können auch die Berechnung des Zahlenverhältnisses in diesen Beobachtungen anwenden, in der Anzahl von Millionen unten:
Auch in Milliardenhöhe:
Wir können auch in Diplets beobachten:
Hierin den Dizymen können wir das Unendliche, das von 9 auf 1 geht, besser beobachten.
Die Grundlage, oder das Prinzip, das dieser Argumentation zugrunde liegt, besteht darin, die Entdeckung dieser Berechnung des Numeralproportions aufzuzeichnen, aus der hervorgeht, dass alle Zahlen durch eine fortlaufende Zahl von 1 bis 9 unendlich dargestellt werden können. Deutlich beobachtet in der Logik und Berechnung des Ziffernanteils, hier dargestellt. So werden wir seine Bedeutungen mit Beispielen von Mathematik und Logik anwenden.
Daher können wir auch unendlich e.A. von 1 bis 9 beobachten.
4. INFINITY UND DIE LOGIC VON NUMERAL RATIO
Das folgende Beispiel ist das Beispiel, indem Infinity in der Logik des Ziffernseitenverhältnisses identifiziert wird:
Abbildung 3: Unendliche Logik des Zifferns eitenverhältnisses
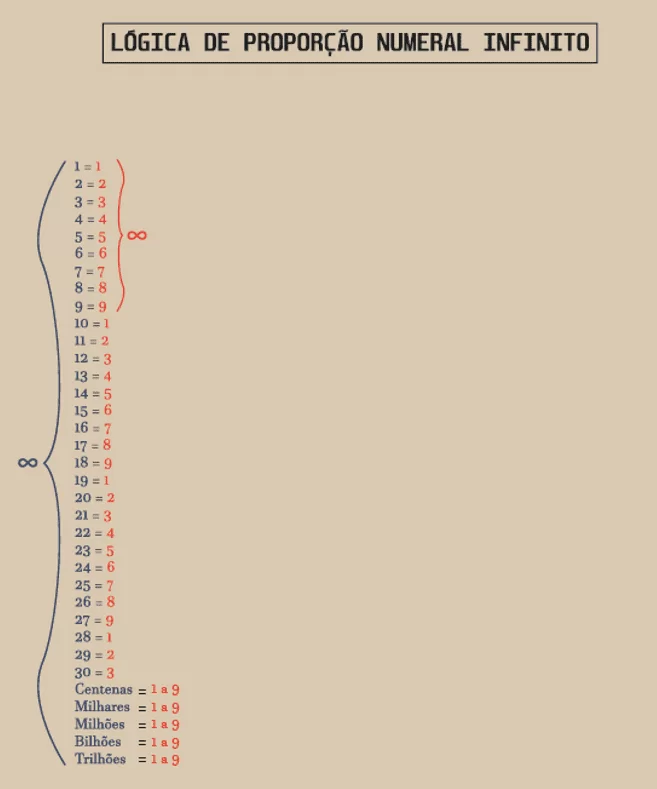
Wenn man sich das Diagramm oben anschaut, ist es möglich, ins Unendliche zu gehen, sowohl in ganzen Zahlen als auch in Zahlen. Und wie bereits erwähnt, zerlegen Sie die ganzen Zahlen in Ziffern, und wenn Sie es so betrachten, wo ist es einfacher, zu finden oder bis ins Unendliche zu zählen? Zählen Sie die ganze Zahl, gehen Sie durch Tausende, Millionen, Milliarden, Billionen usw. oder zählen Sie nur von 1 bis 9? Durch die logikbeobachtete Berechnung des sequenziellen Zahlenseitenverhältnisses von 1 bis 9 ist es einfacher und einfacher, das Verhältnis zu unendlich zu finden und zu zählen.
5. NUMERAL ASPECT RATIO ANWENDUNGEN
Die Berechnung der Numeralproportion kann sehr nützlich sein, vor einiger Zeit wurde eine wissenschaftliche Entdeckung eines neuen binären Systems durchgeführt, die eine sehr wichtige Entdeckung eines Systems für den Betrieb von Elektronik wie Computer, Smartphones, Videospiele usw. ist. Es ist viel effizienter und sicherer als das aktuelle System. Diese Studie wurde in derselben wissenschaftlichen Zeitschrift veröffentlicht, und der Zusammenhang wird in den Referenzen dieser Arbeit sein. Aber das Wissen um diese Berechnung des Zahlenverhältnisses half, das Binary 2-System zu entdecken, und gab die Grundlage für die Identifizierung logischer Unterschiede zwischen binären Systemen, wie in diesem Fall unten, wo die Berechnung des Zahlenverhältnisses angewendet werden kann. (BELLAS, 2019)
Abbildung 4: Binäre Systemsequenz

Wenn wir also die beiden Logiken binärer Systeme betrachten und die Berechnung des Zahlenverhältnisses verwenden, identifizieren wir eine Logik in jedem System, wir haben im binären System 1 eine Sequenz von 6 Wiederholungen 1, 2, 4, 8, 7, 5. Und die Logik des binären Systems 2, ist eine Sequenz von 2 Wiederholungen 3 und 6. In den beiden binären Logiken verdoppeln sich die Zahlen bis ins Unendliche, aber im binären System 1 faltet es sich in einer Sequenz von 6 Werten in die Unendlichkeit und im binären System 2 faltet man sich in einer Sequenz von 2 Werten in die Unendlichkeit. So hat binäres System 2 mehr mathematische Logik und ist effizienter als binäres System 1, mathematisch und logisch.
Eine der logischen Definitionen ist, wenn eine Information wiederholt wird oder eine Sequenz hat. Im Falle von Binärsystem 1 wiederholt es oder hat Sequenz in einer 6-Faktor-Logik, bereits im binären System 2 wiederholt es oder hat Sequenz in einer Logik von 2 Faktoren, so dass das Binäre System 2 einfacher ist, ist es logischer. Zwei logische Faktoren sind einfacher als 6 logische Faktoren.
Es gibt ein Video auf Youtube mit dem Titel ” O Segredo dos números 3, 6 e 9 ” – Unknown Facts. In diesem Video bezieht es sich auf Nikola Teslas Beobachtungen in Bezug auf die Zahlen 3 und 6, aber dieses Video diente nicht als Referenz für die Realisierung der wissenschaftlichen Entdeckungen dieser Arbeit und auch die des Binären Systems 2, als diese Studie begann entwickelt und das Binäre System, so auch die Beobachtungen der Zahlen 3 und 6, sowie die Berechnung und Logik des numerischen Anteils , wurden auf eine andere Weise und vor dem Zugriff auf die Informationen dieses Vorschlags von Nikola Tesla in diesem Video durchgeführt.
Tesla fand das Verhältnis der Ziffern 3 und 6, aber nicht in Beziehung zu einem binären Code, bezieht sich nicht auf ein binäres System und Programmierung, und entwickelte keine numerische Verhältnis Berechnung, aber Tesla beobachtete die Beziehung des Binärsystems mit Fibonacci und fand die logische sequentielle 1, 2, 4, 8, 7, 5 des binären Systems 1 und fand auch sequenzielle 3 und 6 , aber bezog es nicht auf ein binäres System, aber er war der Wissenschaftler, der am nächsten kam, um ein neues binäres System zu finden. (TESLA, Youtube)
Und bei der Entdeckung von Binäres System 2, sequenzielle Scans 3 und 6 waren nicht die erste Beobachtung über binäres System 2 gemacht, diese Information ist Teil sowie zahlreiche andere während der wissenschaftlichen Entdeckung von binärem System 2 gemacht, wie Binärcode, rundepixel, Neutron enkotonung in binäre Programmierung und auch die Identifizierung der 1 (ein) gleiche Pi , und andere Unterschiede zwischen der Art der offenen und geschlossenen Schaltungen in binären Systemen und Unterschiede in der binären Programmierung.
Dieses Video hilft jedoch bei Grundlagen in logischen Aspekten, um die wissenschaftlichen, mathematischen, logischen und physikalischen Beobachtungen dieser Studie zu machen. Zusammenfassend, um die Ergebnisse dieser Studien zu machen, waren die Informationen über die logische Abfolge von Teslas Zahlen 3 und 6 unbekannt, und als er Teslas Video sah, beobachtete er die Zahlen 3 und 6 auf eine andere Weise als in dieser Studie beobachtet wurde, in diesen hier vorliegenden wissenschaftlichen Erkenntnissen wurden sequenzielle Scans 3 und 6 durch Berechnung des Zahlenverhältnisses beobachtet.
Dieses Video wurde später die Entdeckung und Veröffentlichung des binären Systems 2 und auch später die Veröffentlichung des Patentverfahrens in der INPI (Nationales Institut für gewerbliches Eigentum), aber für die Qualität des Materials beobachtet, weil das Thema die gleichen Referenzen hat, und wurde gut von einem der besten Physiker in der modernen Wissenschaft zitiert, und auch eine größere Beobachtung zu diesem Thema zu suchen , ist dieses Video sehr nützlich.
Es folgt diesem Zitat von Tesla, um die Größe dessen darzustellen, was es ist, in Mathematik und Physik die Breite des Wissens zu verstehen, die die Bedeutung der Zahlen 3 und 6 zu verstehen ist. ” Wenn du die Pracht der Zahlen 3, 6 und 9 wüsstest, dann hättest du den Schlüssel zum Universum” (TESLA, Youtube)
Abbildung 5: Zitat Nikola Tesla 3 und 6.

Wir können sagen, dass die Beobachtung der Unendlichkeit von 1 bis 9 und damit das Verständnis, dass jede und alle Zahlen durch diese Folge der Unendlichkeit dargestellt werden können, auch eine große Pracht hat.
Binäres System 2 ist die wichtigste technologische wissenschaftliche Entdeckung heute, da es eine fortschrittliche Technologie ist, ein Computer mit Binäres System 2 Technologie ist viel besser als ein Computer mit aktuellen Binäres System Technologie, und diese Berechnung ist eine der komplexesten Gleichungen, die wir haben.
Es gibt mehrere technische Unterschiede, die die Überlegenheit von Binäres System 2 zu Binäres System 1 demonstrieren, unten werden einige als Beispiele zitiert:
1 – Unterschied in der Art der physikalischen Schaltung, im Binärsystem 1 wird die Schaltung geöffnet, das heißt, es ist ein unterbrochener Stromkreis und im Binärsystem 2 ist der Schaltkreis geschlossen, das heißt, es ist ein kontinuierlicher Kreislauf, dies erzeugt einen großen Unterschied der Überlegenheit in der Leistung und Reaktion des Systems. Der Durchlaufkreis ist effizienter als ein unterbrochener Schaltkreis.
2 – Ein weiterer technischer Unterschied ist, dass im Binärsystem 1 Schaltung funktioniert nur mit zwei physikalischen und logischen Elementen der Programmierung der negativen und positiven, während das Binäre System 2 arbeitet mit drei physikalischen und logischen Programmierelemente die negative, neutrale und die positive, mit diesen drei Elementen in der Programmierung wird die Schaltung wegen der neutralen geschlossen, so dass eine überlegene Leistung und Ergebnis , einschließlich der Auswirkungen auf die Systemsicherheit. Eine Möglichkeit, sich technisch im Sinne der Sicherheit der binären Programmierung auszudrücken, ist, dass ein binäres System ohne den neutralen Kreislauf offen ist, so dass seine Tür offen ist unsicher, und im binären System mit dem neutralen ist der Schaltkreis geschlossen, so dass folglich seine Tür geschlossen ist, so dass das Binärsystem 2 mehr Sicherheit hat.
3 – Andere Aspekte ist in der Programmierung der physikalischen Logik der Systeme, im binären System 1 funktioniert es nur mit 1 π (ein PI) ohne neutral, während im binären System 2 die physikalische Logik des Systems mit 2 π (zwei PI) mit neutral arbeitet, bringt dies einen großen Unterschied in der Art der virtuellen Realität der Systeme, im Binärsystem 1 ist das Pixel quadratisch und im binären System 2 ist das Pixel rund , direkt auf die Art der Realität, Dimension und Grafik des Systems, bringt mehr Qualität, Definition, Geschwindigkeit, Agilität und Logik, auch erhöhung der Verarbeitung und Kapazität im Datenvolumen, wodurch eine größere Effizienz in den logischen Aspekten in der Programmierung des Binärsystems 2. 2 π (zwei PI) mit neutral ist größer als 1 π (ein PI) ohne neutral.
4 – Und ein weiterer wichtiger technischer Grund ist der Unterschied zwischen binären Codes und logischen Sequenzen von Systemen, wie weiter oben in Binäres System1 erklärt ist eine sechs-Faktor logische Sequenz und Binäres System 2 ist eine Zwei-Faktor-logische Sequenz, und dieser Unterschied in Sequenzen und binären Codes direkt wirkt sich sowohl auf die Datenverarbeitungslautstärke und die Antwortgeschwindigkeit von Binäres System 2, die agiler und logischer ist und Physisch. Sequenzielle 3 und 6 ist logischer und effizienter als 1, 2, 4,8, 7, 5.
Es gibt andere technische Unterschiede und andere Informationen, aber diese Beispiele oben sind diejenigen, die die Hauptunterschiede zwischen den Systemen zeigen, und die Menge dieser technischen Unterschiede zwischen binären Systemen zeigen die überlegene Qualität eines Systems als das andere System.
Die Entdeckung der binären System 2 Programmierung ist eine der logischen Programmierung, die wir in einem der komplexesten und hohen Grade haben, die bisher existiert, und mathematische, logische und physikalische Beobachtungen mit nur 0 (Null) und 1 (eins), das heißt, Systeme in Null und eins zu sehen, ist eine große Herausforderung.
In Bezug auf die Schaltkreise und programmierung von binären Systemen, eine richtige Art und Weise, die wir ausdrücken können, ist, dass ein Computer, den er an Nullen und Einsen denkt, so dass die wissenschaftliche Entdeckung des binären Systems 2, eine Entdeckung eines neuen Weges oder effizienterweise für einen Computer ist, um an Nullen und Einsen zu denken.
Binäres System 2 ist die fortschrittlichste Technologie, die es heute gibt. Binäre Systeme sind Systeme, weil sie verschiedene Funktionen ausführen, sie sind logische Schaltungen und auch Programmierung, das Binäre System 2 ist ein neues System effizienter und sicherer für den Betrieb der Elektronik, und unterscheidet eine binäre Programmierung von der anderen durch die logische Anordnung von Nullen und Einsen.
Jedoch, Diese Studie soll die Entdeckung der Berechnung des Numeralproportions demonstrieren, wenn Sie mehr Informationen über das Binärsystem 2 wollen, ist der Artikel in Verweisen auf diese Arbeit.
Binäres System 2 arbeitet mit den Gesetzen des Zahlenverhältnisses, es verarbeitet Ihre Daten von 1 bis 9 und ist damit viel effizienter. Binäres System 2 funktioniert auch unter Beachtung der Gesetze von Fibonacci, und diese Studie hat Bezug und Beziehung auch in der Berechnung der Numeralproportion, weil sie praktisch die gleiche Sache sind, die beiden sind ein Koeffizient der Unendlichkeit, nur eine neue mathematische Art der Berechnung, Ausdruck und Beobachtung Teil der Gesetze von Fibonacci wurde entdeckt. Diese Beobachtungen werden hier als Berechnung des Numeralproportions bezeichnet.
Nach einer langen Zeit der Studie und Forschung, und Leistungen der Beobachtungen über der numerischen Proportion Berechnung, wurde eine Beziehung zwischen dieser Entdeckung und einer anderen Studie, die der Fibonacci-Sequenz (PHI) gefunden. Die Logik des Ziffernanteils von 1 bis 9 bis Unendlichist ist direkt mit den Gesetzen von Fibonacci verbunden, die auch mathematischen Gesetzen folgt,
dass durch die Messungen der Fibonacci-Serie bei der Analyse des Koeffizienten von zwei aufeinanderfolgenden Kennzahlen die irrationale Zahl (PHI) mit einem ungefähren Wert von 1,618 ermittelt wird. Und diese Konjunktisierung von Maßnahmen, die auf dieser Zahl basieren, wird Golden Ratio genannt, oder Golden Ratio, das daher in Blumen, Bäumen, Wellen, in Galaxien, Muscheln, Hurrikanen, im symmetrischen Gesicht des Menschen, in ihren Knochengelenken und in den Merkmalen des Menschen, in seinem Herzschlag und in seiner DNA zu finden ist. Auch in der Brechung des Lichts, das von den Elektronen der Atome, in Schwingungen, in anderen weiteren Manifestationen (TANURE, online, s/p) bereitgestellt wird.
Und es erklärt, warum die Sequenz von 1 bis 9 ist. Unten können wir sehen, dass der nächste Quadrant das Doppel aller vorherigen ist, zum Beispiel ist die 2 das Doppel der [1], die 3 das Doppel der [1 und 2 ], 4 ist doppelt so groß wie [1, 2 und 3], 5 ist doppelt so groß wie [1, 2, 3 und 4] und so weiter. Und es ist immer sequentiell von 1 bis 9, wobei 9 doppelt so groß ist wie alle seine Vorgänger, wodurch die Logik von Infinite wiederholt wird: 1 2 3 4 5 6 7 8 9, 1 2 3 4 5 6 7 8 9, 1 2 3 4 5 6 7 8 9. Immer die nächste Ziffer doppelt so viele wie ihre Vorgänger. Unten finden Sie eine Möglichkeit, die Fibonacci-Sequenz auszudrücken
Abbildung 6: Fibonacci-PHI-Sequenz
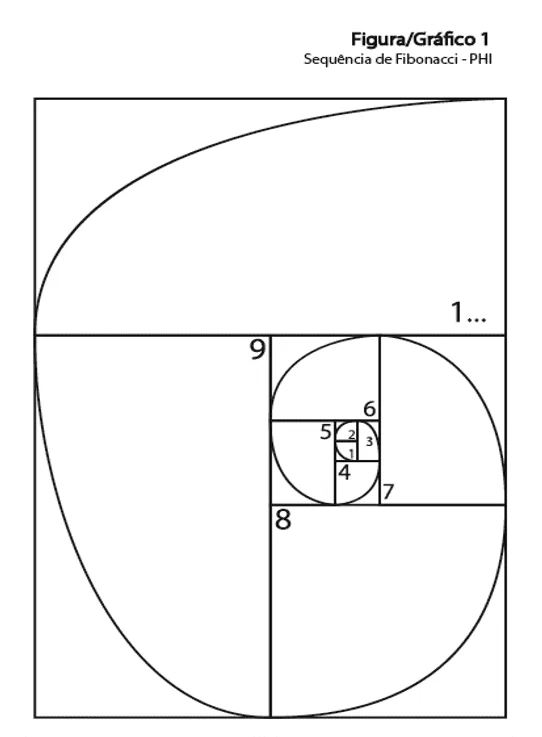
Wenn wir uns das obige Diagramm ansehen, kommen wir zu dem Schluss, dass:
9 x PHI = 1 Infinity (Neunmal entspricht das Fibonacci-Maß einer Unendlichkeit) oder
9 x 1.618 = 1 Unendlichkeit oder 1 Einheit.
ODER 1 Unendlichkeit = 1 Einheit (eine Unendlichkeit entspricht einer Einheit)
Wenn Sie z. B. das Fibonacci-Maß, das die Unendlichkeit in einer Muschel darstellt, mathematisch finden, wird diese Muschel durch 1 Einheit dargestellt, da dieser Unendlichkeitskoeffizient in dieser Einheit vorhanden oder mathematisch signiert ist.
Das Maß des Numeralanteils oder der Fibonacci-Sequenz, die durch einen Koeffizienten und eine Logik des Proportions dargestellt wird, um unendlich zu berechnen und zu finden, denn wenn Sie diesen Koeffizienten oder diese Berechnung in einem Element, einer Galaxie, pflanze oder tierisch finden, wird dieses Wesen oder Element durch eine Einheit in den Gesetzen von Fibonacci dargestellt.
Alle Elemente und Wesen sind mathematisch, physisch und natürlich mit diesem Koeffizienten der Unendlichkeit signiert.
In jeder Einheit befindet sich eine mathematisch signierte Unendlichkeit.
Ein weiteres Zitat über Fibonacci Sequenz findet sich über die Ratio-Logik, wie unten veranschaulicht:
ist eine Abfolge von Zahlen, die einem Muster folgen.
Die Fibonacci-Sequenz ist nichts anderes als die Reihenfolge der ganzzahligen Zahlen, die normalerweise von Null abweicht und eine, in der jede nächste Zahl der Summe der vorherigen beiden Ziffern entspricht. Diese Kontinuität zeigt sich in verschiedenen Naturphänomenen.
Die Fibonacci-Sequenz wurde von dem italienischen Mathematiker Leonardo de Pisa, auch bekannt als Fibonacci, benannt. Im Jahre 1202 berichtete der Mathematiker aus dieser numerischen Sequenz über den Vormarsch einer Kaninchenpopulation.
Fibonacci Formel
Die Fibonacci-Nachfolge ist eine Folge von ganzen Zahlen, die mit Null und eins begonnen werden, wobei jeder nachfolgende Begriff der Summe der vorherigen beiden Zahlen entspricht:
0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584… (Fibonacci-Sequenz – Educa + Brasilien).
Und hier können wir den Unterschied der Beobachtungsmethoden zwischen der Fibonacci-Berechnung und dieser mathematischen und logischen Berechnung des Ziffernanteils feststellen. Sowohl die Numeral Proportion Logic als auch die Fibonacci Sequence sind dasselbe, aber dieser unendliche Koeffizient kann auf diese beiden unterschiedlichen Arten beobachtet werden. Da Fibonacci ein Verweis war, um diese Entdeckung der Logik des Numeral Proportion zu entwickeln, weil sie in den beiden Beobachtungen den gleichen Koeffizienten der Unendlichkeit haben, ändert sich nur die Art und Weise, beobachtet zu werden, so dass wir auch die Berechnung dieser Sequenz von 1 bis 9 dieser Studie von Fiboleo taufen werden, wegen der Beziehung zwischen den Namen der Autoren dieser Beobachtungen.
Sequenziell von 1 bis 9, wie in den berechnungen in dieser Studie nachgewiesen, Die Berechnung der Numeralproportionen und der Berechnung des Numeralproportions.
Hier sind weitere Informationen aus Fibonacci Sequenz Zitate in Internet-Suchen:
Diese Methode wird in der Analyse von Finanzmärkten, Spieltheorie und Informatik sowie biologischen und natürlichen Konfigurationen angewendet. Natürliche Modelle. Die Fibonacci-Sequenz kann auch bei Naturphänomenen beobachtet werden). (Fibonacci-Sequenz – Educa + Brasilien).
Hier in diesem Zitat können wir sehen, dass es über Informatik spricht, es ist auch, wo die Numeralproportion Berechnung angewendet wurde, um ein neues binäres System zu identifizieren, wie zuvor in dieser Studie gezeigt.
Schauen Sie sich weitere Angebote über die Berechnung, unten einige von ihnen:
Sonnenblume: Die Sonnenblumenkerne haben Samen, die in einer Doppelspirale angeordnet sind. Meistens sind es 21 im Uhrzeigersinn und weitere 34 gegen den Uhrzeigersinn.
Tannenzapfen: Nach Fruchtwachstum bilden die Samen eine Doppelspirale mit acht im Uhrzeigersinn und weiteren 13 gegen den Uhrzeigersinn.
Shell-Shell: Jeder Teil der Schale hat die Größe der Summe der beiden Vorgänger. Es ist bekannt, dass ein Koha drei Hauptseiten hat, so dass eine Seite Meter 2 (1 + 1), und die andere 5 (3 + 2) die dritte wird 8 (5 + 3). (Fibonacci-Sequenz: Educa + Brasilien).
Die Numerische Verhältnis-Logik, die eine sequenzielle von 1 bis 9 ist, ist also ein Koeffizient der Unendlichkeit und so können wir die gleiche Beobachtung in Fibonacci sequenziell durchführen, was auch ein unendlicher Koeffizient ist. Aber diese Berechnung zu lernen ist sehr effizient für Operationen, bei denen sie ein hohes Volumen von Ziffernhatzahlen hat, weil wir sie in einer einfacheren logischen Reihenfolge identifizieren können, alle und alle Zahlen werden durch die fortlaufenden Zahlen 1 bis 9 unendlich dargestellt.
FAZIT
Die Schlussfolgerung dieser Studie zielt darauf ab, die Entdeckung der Berechnung des Numeralanteils und der Logik des Numeralanteils zu erfassen und diese Entdeckung der Berechnung des Numeralproportions mit der Fibonacci-Berechnung in Beziehung zu setzen, neben dem Nachweis ihrer Anwendbarkeit in der Mathematik und insbesondere in binären Systemen und hinsichtlich ihrer Anwendung in Bezug auf die Unendlichkeit.
Diese Studie könnte, wie bereits geschehen, die Grundlage für neue wissenschaftliche Entdeckungen und für die Forschung liefern. Es kann Menschen helfen, neue Wege zu denken, um mit Zahlen umzugehen, und es ist eine einfachere neue Möglichkeit, zu berechnen, indem alle Werte auf Unendlichvon von 1 bis 9 sequenziert werden. In der Logik des Ziffernanteils wird die Unendlichkeit von 1 bis 9 gebrochen. Auch um neue Informationen zu präsentieren, eine neue Art, wie man das Unendliche beobachtet, ausdrückt, findet, berechnet und entschlüsselt.
VERWEIS
BELLAS, L.D. Sistema Binário 2 – Código Fechado. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 02, Vol. 05, pp. 110-151. Fevereiro de 2019. ISSN: 2448-0959. Disponível em: https://www.nucleodoconhecimento.com.br/tecnologia/sistema-binario-2-codigo-fechado
TANURE, A.C. Proporção Áurea e Sequência Fibonacci. Pagasus Portal. Disponível em: http://pegasus.portal.nom.br/proporcao-aurea-e-sequencia-de-fibonacci/
TESLA, N. Os segredos dos números 3, 6 e 9. Youtube – Fatos Desconhecidos https://www.youtube.com/watch?v=c2M9ZfZ5h5A&t=682s
Sequência de Fibonacci. Educa+Brasil. Disponível em: https://www.educamaisbrasil.com.br/enem/matematica/sequencia-de-fibonacci
[1] Abschluss in Betriebswirtschaft mit Spezialisierung auf Außenhandel.
Eingesandt: Mai 2020.
Genehmigt: Dezember 2020.






