ARTICLE ORIGINAL
BELLAS, Leonardo Dias [1]
BELLAS, Leonardo Dias. Calcul de la proportion numérique. Revista Científica Multidisciplinar Núcleo do Conhecimento. An 05, Ed. 12, Vol. 02, pp. 144-162. décembre 2020. ISSN: 2448-0959, Lien d’accès: https://www.nucleodoconhecimento.com.br/olympiades-mathematiques/proportion-numerique
RÉSUMÉ
En 2011, une observation logique mathématique a été faite par cet auteur et a été étudiée depuis lors, cette logique concerne que tous les nombres peuvent être représentés par un chiffre séquentiel de 1 à 9. Cependant, la découverte de ce qu’était cette logique a été faite et un autre calcul existant de la séquence de Fibonacci a été lié. Cela dit, cette étude a été développée pour enregistrer des informations sur cette logique concernant cette découverte scientifique du calcul de la proportion numérique, et sur la logique de proportion numérique et sa relation avec d’autres découvertes et concepts scientifiques qui ont été développés par d’autres mathématiciens auparavant. Afin de discuter et de démontrer ces observations mathématiques qui n’avaient pas été précédemment observées et de fournir une nouvelle option de calcul plus efficace, puisque n’importe quel nombre peut être représenté par des chiffres séquentiels de 1 à 9. Ainsi, grâce au calcul et à la logique de Numeral Proportion, nous pouvons l’identifier, en plus de démontrer son applicabilité en mathématiques et en sciences actuelles.
Mot-clé: Rapport numérique, Séquence Fibonacci
1. INTRODUCTION
L’intention de cette étude est de démontrer cette découverte mathématique sur les proportions numériques et de montrer son applicabilité dans les mathématiques actuelles. Par des calculs mathématiques et des démonstrations, le calcul de la proportion numérique sera expliqué et appliqué en traitant que n’importe quel nombre peut être représenté par un chiffre séquentiel de 1 à 9. Cette séquence de 1 à 9 est une séquence séquentielle, car elle se répète infiniment et séquentiellement. Et ainsi montrer sa relation avec un autre calcul déjà effectué, celui de la séquence de Fibonacci qui est un coefficient infini de deux mesures successives. Le nombre irrationnel appelé (PHI) est obtenu, avec une valeur approximative de 1.618 qui est également connu sous le nom de rapport d’or ou proportion d’or, selon le mathématicien Leonardo de Pisa.
2. LOGIQUE DE RAPPORT D’ASPECT NUMÉRIQUE
Lors de la démonstration du calcul du rapport numérique, nous devons faire quelques observations mathématiques, comme l’exemple de la logique du rapport numérique. Comme l’illustre le tableau ci-dessous :
Table 1. Calcul du rapport de logique et d’aspect numérique

Source: auteur.
Ainsi, nous pouvons observer que tous les entiers, décimales ou chiffres de 0,000000…0001 à l’Infini, lorsqu’ils sont ajoutés à leur dernière variable est séquentielle de 1 à 9, c’est-à-dire, la somme des chiffres de n’importe quel nombre, étant neutre zéro, est séquentielle de 1 à 9 Infiniment. Ainsi, avec cette logique, nous pouvons observer que tous les nombres peuvent être représentés par un chiffre séquentiel de 1 à 9, suit une façon plus simple d’exprimer cette Logique.
Figure 1 : Logique de rapport d’aspect numérique

Source: auteur.
3. CALCUL DU RAPPORT D’ASPECT NUMÉRIQUE
Passons maintenant au calcul du rapport d’aspect numérique. Dans ce cas, j’ai utilisé l’alphabet romain, mais un autre alphabet ou un autre symbole / code peut être utilisé.
Figure 2 : Calcul du rapport d’aspect numérique

Source: auteur.
Nous pouvons observer que, peu importe si nous utilisons des nombres d’entiers ou des nombres de proportions numériques, nous identifions que dans les deux calculs, les résultats sont les mêmes. Cependant, il est observable que l’utilisation de la logique de rapport d’aspect numérique pour atteindre le résultat est plus simple. Parce que vous n’avez pas à utiliser l’alphabet infini entier d’Entiers, seulement la séquence de 1 à 9. Ce calcul est comme si vous avez brisé l’infini des entiers dans une séquence de 1 à 9 (Numeral). Parce que n’importe quel nombre est séquentiel de 1 à 9.
Regardons le nom João, par l’entier se trouve le numéro 1015115 et dans la logique numérique est le nombre 1616. Ainsi, nous avons observé que le nombre 1015115 et 1616, et la somme des chiffres jusqu’à leur dernière variable est égale à 5, afin que nous puissions faire une échelle des nombres, facilitant les opérations avec un grand volume, séquençage et l’identification de chaque élément de 1 à 9.
Nous pouvons également appliquer le calcul de proportion numérique à ces observations, en millions ci-dessous:
Notant également en milliards:
Nous pouvons également observer dans les dîmes:
Ici, dans les dizymes, nous pouvons mieux observer l’infini allant de 9 à 1.
La base, ou le principe qui sous-tend ce raisonnement, est d’enregistrer la découverte de ce calcul de proportion numérique démontrant que tous les nombres peuvent être représentés par un nombre séquentiel de 1 à 9 infiniment. Être clairement observé dans la logique et le calcul de la proportion numérique, présenté ici. Nous allons donc appliquer ses significations avec des exemples de mathématiques et de logique.
Par conséquent, nous pouvons également observer l’infini de 1 à 9.
4. L’INFINI ET LA LOGIQUE DU RAPPORT NUMÉRIQUE
L’exemple suivant est l’exemple en identifiant Infinity dans la logique du rapport d’aspect numérique :
Figure 3 : Logique infinie de rapport d’aspect numérique
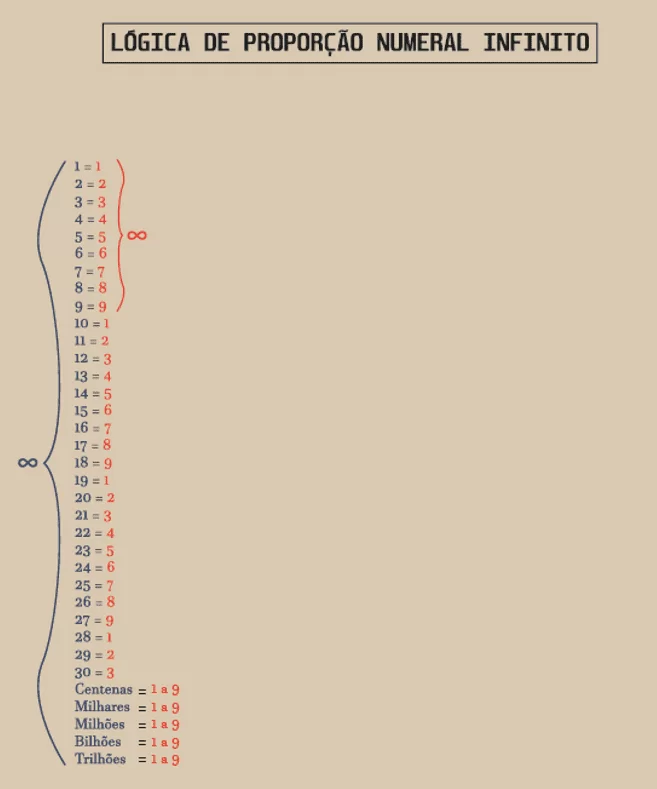
Source: auteur
En regardant le graphique ci-dessus, il est possible d’aller à l’infini, à la fois en nombre entier et en chiffres numériques. Et comme indiqué précédemment, vous décomposez tous les nombres en chiffres, et en le regardant comme ceci, où est-il plus facile de trouver ou de compter à l’infini? Compter l’ensemble des chiffres, passer par des milliers, des millions, des milliards, des billions, etc. ou compter seulement de 1 à 9? En observant logiquement en calculant le rapport d’aspect numérique séquentiel de 1 à 9, il est plus facile et plus simple de trouver et de compter à l’infini.
5. APPLICATIONS DE CALCUL DU RAPPORT D’ASPECT NUMÉRIQUE
Le calcul de la proportion numérique peut être très utile, il ya quelque temps a été effectué une découverte scientifique d’un nouveau système binaire, qui est une découverte très importante d’un système pour le fonctionnement de l’électronique tels que les ordinateurs, smartphones, jeux vidéo, etc. Il est beaucoup plus efficace et sécurisé que le système actuel. Cette étude a été publiée dans cette même revue scientifique, et le lien sera dans les références de ces travaux. Mais connaissant ce calcul de ratio numérique a contribué à découvrir le système Binary 2, et a donné la base pour identifier les différences logiques entre les systèmes binaires, comme dans ce cas ci-dessous où le calcul du rapport numérique peut être appliqué. (BELLAS, 2019)
Figure 4 : Séquence du système binaire

Donc, en regardant les deux logiques des systèmes binaires et en utilisant le calcul du rapport numérique, nous identifions une logique dans chaque système, nous avons dans le système binaire 1, une séquence de 6 répétitions 1, 2, 4, 8, 7, 5. Et la logique du système binaire 2, est une séquence de 2 répétitions 3 et 6. Dans les deux logiques binaires les nombres doublent à l’infini, mais dans le système binaire 1, il se plie à l’infini dans une séquence de 6 valeurs et dans le système binaire 2, vous pliez à l’infini dans une séquence de 2 valeurs. Ainsi, le système binaire 2 a plus de logique mathématique et est plus efficace que le système binaire 1, mathématiquement et logiquement.
L’une des définitions logiques est, quand une information se répète ou a une séquence. Dans le cas du système binaire 1, il répète ou a une séquence dans une logique de 6 facteurs, déjà dans le système binaire 2, il répète ou a une séquence dans une logique de 2 facteurs, de sorte que le système binaire 2 est plus simple, il est plus logique. Deux facteurs logiques sont plus simples que 6 facteurs logiques.
Il ya une vidéo sur Youtube, avec le titre «O Segredo dos números 3, 6 e 9» – Faits inconnus. Dans cette vidéo, il se réfère aux observations de Nikola Tesla concernant les numéros 3 et 6, mais cette vidéo n’a pas servi de référence pour la réalisation des découvertes scientifiques de ce travail et aussi celle du système binaire 2, lorsque cette étude a commencé à être développée et le système binaire, ainsi que les observations des nombres 3 et 6, ainsi que le calcul et la logique de la proportion numérique , ont été effectués d’une manière différente et avant l’accès à l’information de cette proposition par Nikola Tesla dans cette vidéo.
Tesla a trouvé le rapport des chiffres 3 et 6, mais ne l’a pas lié à un code binaire, ne se rapportait pas à un système binaire et la programmation, et n’a pas développé un calcul de ratio numérique, mais Tesla a observé la relation du système binaire avec Fibonacci et a trouvé la séquentielle logique 1, 2, 4, 8, 7, 5 du système binaire 1 et a également trouvé séquentiel 3 et 6 , mais ne l’a pas lié à un système binaire, mais il était le scientifique qui est venu le plus près de trouver un nouveau système binaire. (TESLA, Youtube)
Et dans la découverte du système binaire 2, les scans séquentiels 3 et 6 n’ont pas été la première observation faite sur le système binaire 2, cette information fait partie ainsi que de nombreux autres effectués lors de la découverte scientifique du système binaire 2, tels que le code binaire, pixel rond, découverte neutronique dans la programmation binaire et aussi l’identification de la 1 (une) égale Pi , et d’autres différences entre le type de circuits ouverts et fermés dans les systèmes binaires et les différences dans la programmation binaire.
Cependant, cette vidéo aide dans les fondations dans les aspects logiques pour faire les observations scientifiques, mathématiques, logiques et physiques de cette étude. En résumé, pour faire les résultats de ces études, les informations sur la séquence logique des numéros 3 et 6 de Tesla étaient inconnues, et en regardant la vidéo de Tesla, il a observé les nombres 3 et 6 d’une manière différente de la façon dont il a été observé dans cette étude, dans ces résultats scientifiques présents ici, les scans séquentiels 3 et 6 ont été observés en calculant le rapport numérique.
Cette vidéo a ensuite été observée la découverte et la publication du système binaire 2 et plus tard la publication du processus de brevet dans le INPI (Institut national de la propriété industrielle), mais pour la qualité du matériau, parce que le sujet a les mêmes références, et a été bien cité par l’un des meilleurs physiciens de la science moderne, et aussi de chercher une plus grande observation sur le sujet , cette vidéo est très utile.
Il suit cette citation de Tesla pour représenter l’ampleur de ce qu’il est de comprendre en mathématiques et en physique l’étendue des connaissances qui est de comprendre le sens des nombres 3 et 6. ” Si vous connaissiez la magnificence des numéros 3, 6 et 9, alors vous auriez la clé de l’Univers » (TESLA, Youtube)
Figure 5 : Citation Nikola Tesla 3 et 6.

Nous pouvons dire que l’observation de l’infini de 1 à 9 et donc la compréhension que tous les nombres peuvent être représentés par cette séquence de l’infini, a une grande magnificence ainsi.
Système binaire 2 est la découverte scientifique technologique la plus importante aujourd’hui, car il s’agit d’une technologie de pointe, un ordinateur avec système binaire 2 technologie est beaucoup supérieure à un ordinateur avec la technologie actuelle du système binaire, et ce calcul est l’une des équations les plus complexes que nous avons.
Il existe plusieurs différences techniques qui démontrent la supériorité du système binaire 2 au système binaire 1, ci-dessous seront cités certains comme exemples:
1 – Différence dans le type de circuit physique, dans le système binaire 1 le circuit est ouvert, c’est-à-dire, il s’agit d’un circuit interrompu et dans le système binaire 2 le circuit est fermé, c’est-à-dire, c’est un circuit continu, cela génère une grande différence de supériorité dans les performances et la réponse du système. Le circuit continu est plus efficace qu’un circuit interrompu.
2 – Une autre différence technique est que dans le système binaire 1 circuit ne fonctionne qu’avec deux éléments physiques et logiques de la programmation du négatif et positif, tandis que le système binaire 2 fonctionne avec trois éléments de programmation physique et logique le négatif, neutre et positif, avec ces trois éléments dans la programmation du circuit devient fermé en raison de la neutre, apportant ainsi une performance supérieure et le résultat , y compris affecter la sécurité du système. Une façon de s’exprimer techniquement dans le sens de la sécurité de la programmation binaire, c’est qu’un système binaire sans le circuit neutre est ouvert, de sorte que sa porte est ouverte est précaire, et dans le système binaire avec le neutre le circuit est fermé, de sorte que par conséquent sa porte est fermée, de sorte que le système binaire 2 a plus de sécurité.
3 – D’autres aspects est dans la programmation de la logique physique des systèmes, dans le système binaire 1, il ne fonctionne qu’avec 1 π (un PI) sans neutre, tandis que dans le système binaire 2 la logique physique du système fonctionne avec 2 π (deux PI) avec neutre, ce qui apporte une grande différence dans le type de réalité virtuelle des systèmes, dans le système binaire 1 le pixel est carré et dans le système binaire 2 le pixel est rond , affectant directement le type de réalité, la dimension et les graphiques du système, apportant plus de qualité, définition, vitesse, agilité et logique, augmentant également le traitement et la capacité dans le volume de données, donc une plus grande efficacité dans les aspects logiques dans la programmation du système binaire 2. 2 π (deux PI) avec neutre est supérieur à 1 π (un PI) sans neutre.
4 – Et une autre raison technique importante est la différence entre les codes binaires et les séquences logiques des systèmes, comme expliqué précédemment dans le système binaire 1 est une séquence logique à six facteurs et le système binaire 2 est une séquence logique à deux facteurs, et cette différence dans les séquences et les codes binaires affecte directement à la fois le volume de traitement des données et la vitesse de réponse du système binaire 2 qui est plus agile et logique mathématiquement et Physiquement. Séquentiel 3 et 6 est plus logique et efficace que 1, 2, 4,8, 7, 5.
Il existe d’autres différences techniques et d’autres informations, mais ces exemples ci-dessus sont ceux qui démontrent les principales différences entre les systèmes, et l’ensemble de ces différences techniques entre les systèmes binaires démontrent la qualité supérieure d’un système par rapport à l’autre système.
La découverte de la programmation du système binaire 2 est l’une des émissions logiques que nous avons dans l’un des degrés les plus complexes et élevés qui existe à ce jour, et de faire des observations mathématiques, logiques et physiques en utilisant seulement 0 (zéro) et 1 (un), c’est-à-dire, voir les systèmes en zéro et un, est un grand défi.
En ce qui concerne les circuits et la programmation des systèmes binaires, une bonne façon que nous pouvons exprimer, c’est qu’un ordinateur qu’il pense des zéros et des uns, de sorte que la découverte scientifique du système binaire 2, est une découverte d’une nouvelle façon ou plus efficace pour un ordinateur de penser à zéros et ceux.
Système binaire 2 est la technologie la plus avancée qui existe aujourd’hui. Les systèmes binaires sont des systèmes, parce qu’ils exécutent diverses fonctions, ils sont des circuits logiques et aussi la programmation, le système binaire 2 est un nouveau système plus efficace et sûr pour le fonctionnement de l’électronique, et différencie une programmation binaire de l’autre par l’arrangement logique des zéros et des uns.
Toutefois, cette étude est de démontrer la découverte du calcul de la proportion numérique, si vous voulez plus d’informations sur le système binaire 2, l’article est en référence à ce travail.
Système binaire 2 fonctionne avec les lois du rapport numérique, il traite vos données de 1 à 9, étant ainsi beaucoup plus efficace. Système binaire 2 fonctionne également en respectant les lois de Fibonacci, et cette étude a la référence et la relation aussi dans le calcul de la proportion numérique, parce qu’ils sont pratiquement la même chose, les deux sont un coefficient de l’infini, seule une nouvelle façon mathématique de calculer, d’exprimer et d’observer une partie des lois de Fibonacci a été découvert. Ces observations sont effectuées ici appelées calcul de la proportion numérique.
Après une longue période d’étude et de recherche, et des réalisations d’observations supérieures au calcul de la proportion numérique, une relation a été trouvée entre cette découverte et une autre étude, celle de la séquence de Fibonacci (PHI). La logique de la proportion numérique de 1 à 9 à l’Infini est directement liée aux lois de Fibonacci, qui suit également les lois mathématiques,
que par les mesures de la série Fibonacci, lors de l’analyse du coefficient de deux mesures successives, le nombre irrationnel appelé (PHI) est obtenu, avec une valeur approximative de 1.618. Et cette conjoncture de mesures basées sur ce nombre s’appelle le Rapport d’Or, ou Rapport d’Or, qui se trouve, par conséquent, dans les fleurs, les arbres, les vagues, dans les galaxies, les coquilles, les ouragans, dans la face symétrique de l’être humain, dans leurs articulations osseuses et dans les caractéristiques des humains, leur rythme cardiaque et dans leur ADN. Aussi dans la réfraction de la lumière fournie par les électrons des atomes, dans les vibrations, dans d’autres manifestations plus (TANURE, en ligne, s/ p).
Et cela explique pourquoi la séquence est de 1 à 9. Ci-dessous, nous pouvons voir que le quadrant suivant est le double de tous les précédents, par exemple, le 2 est le double du [1], le 3 est le double du [1 et 2 ], 4 est le double de [1, 2 et 3], 5 est le double de [1, 2, 3 et 4] et ainsi de suite. Et il est toujours séquentiel de 1 à 9, 9 étant le double de tous ses prédécesseurs, répétant ainsi la logique de l’Infini: 1 2 3 4 5 6 7 8 9, 1 2 3 4 5 6 7 8 9, 1 2 3 4 5 6 7 8 9. Toujours le chiffre suivant double le nombre de ses prédécesseurs. Voici un moyen d’exprimer la séquence de Fibonacci
Figure 6 : Séquence Fibonacci-PHI
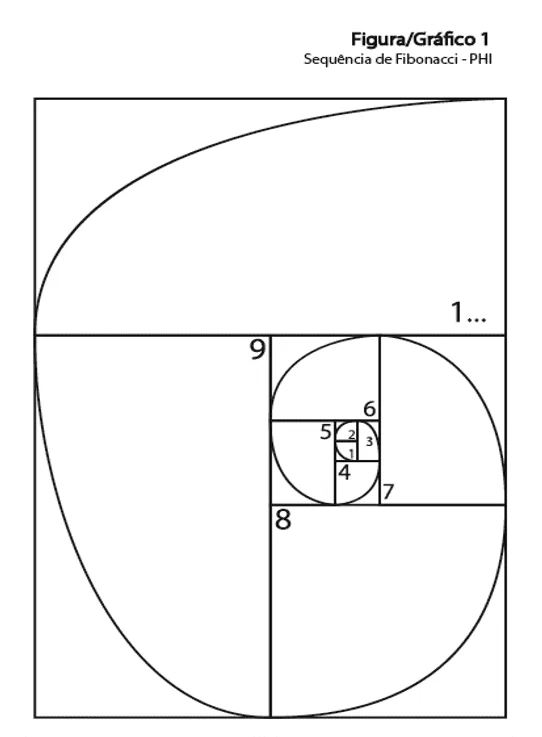
En regardant le tableau ci-dessus, nous concluons que:
9 x PHI = 1 Infini (Neuf fois la mesure fibonacci égale à une Infini) ou
9 x 1.618 = 1 Infini ou 1 unité.
OU 1 infini = 1 Unité (Une infinité équivaut à une unité)
Par exemple, si vous trouvez mathématiquement la mesure Fibonacci qui représente l’infini dans un coquillage, ce coquillage est représenté par 1 unité, parce que ce coefficient d’infini est présent ou mathématiquement signé dans cette unité.
La mesure de la proportion numérique ou de la séquence de Fibonacci qui est représentée par un coefficient et une logique de proportion pour calculer et trouver l’infini, parce que si vous trouvez ce coefficient ou calcul présent dans n’importe quel élément, galaxie, plante ou animal, cet être ou élément est représenté en étant 1 (une) unité dans les lois de Fibonacci.
Tous les éléments et les êtres sont signés mathématiquement, physiquement et naturellement avec ce coefficient de l’Infini.
Il y a une Infini mathématiquement signée dans chaque unité.
Une autre citation trouvée au sujet de la séquence de fibonacci parle de la logique de rapport telle qu’illustrée ci-dessous :
est une succession de nombres qui suivent un modèle.
La séquence de Fibonacci n’est rien de plus que l’ordre des entiers, qui s’écarte normalement de zéro et un dans lequel chaque nombre suivant correspond à la somme des deux chiffres précédents. Cette continuité peut être observée dans divers phénomènes de la nature.
La séquence de Fibonacci a été nommée par le mathématicien italien Leonardo de Pisa, également connu sous le nom de Fibonacci. En 1202, à partir de cette séquence numérique, le mathématicien rapporta l’avance d’une population de lapins.
Formule Fibonacci
La succession fibonacci est une séquence d’entiers commencée par zéro et une, dans laquelle chaque terme ultérieur correspond à la somme des deux numéros précédents :
0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584… (Séquence Fibonacci – Educa + Brésil).
Et ici, nous pouvons remarquer la différence de méthodes d’observation entre le calcul Fibonacci, et ce calcul mathématique et logique de la proportion numérique. La logique de proportion numérique et la séquence de Fibonacci sont la même chose, mais ce coefficient infini peut être observé de ces deux manières distinctes. Comme Fibonacci était une référence pour développer cette découverte de la Logique de la Proportion Numérique, parce que dans les deux observations ils ont le même coefficient d’infini, seulement la façon d’être observé change, donc nous allons également baptiser le calcul de cette séquence de 1 à 9 de cette étude par Fiboleo, pour la raison de la relation entre les noms des auteurs de ces observations.
Séquentiel de 1 à 9 comme prouvé dans les calculs présents dans cette étude, logique de proportion numérique et calcul de proportion numérique.
Voici plus d’informations de fibonacci citations séquence dans les recherches sur Internet:
Cette méthode est appliquée dans l’analyse des marchés financiers, de la théorie des jeux et de l’informatique, ainsi que dans les configurations biologiques et naturelles. Modèles naturels. La séquence de Fibonacci peut également être observée dans les phénomènes naturels). (Séquence Fibonacci – Educa + Brésil).
Ici, dans cette citation, nous pouvons voir qu’il parle d’informatique, c’est aussi là que le calcul de la proportion numérique a été appliqué pour identifier un nouveau système binaire, comme illustré plus tôt dans cette étude.
Consultez d’autres citations sur le calcul, ci-dessous certains d’entre eux:
Tournesol : Les grains de tournesol ont des graines disposées en double spirale. La plupart du temps, il est 21 dans le sens des aiguilles d’une montre et un autre 34 dans le sens inverse des aiguilles d’une montre.
Cône de pin : après la croissance des fruits, les graines forment une double spirale avec huit dans le sens des aiguilles d’une montre et 13 autres dans le sens inverse des aiguilles d’une montre.
Coquille : chaque partie de la coquille a la taille de la somme des deux prédécesseurs. Il est connu qu’un coha a trois côtés principaux, donc en supposant qu’un côté mètres 2 (1 + 1), et l’autre 5 (3 + 2) le troisième sera de 8 (5 + 3). (Séquence Fibonacci: Educa + Brésil).
Ainsi, la logique du rapport numérique, qui est séquentielle de 1 à 9, est un coefficient de l’Infini et nous pouvons donc effectuer la même observation en séquentiel fibonacci, qui est aussi un coefficient infini. Mais l’apprentissage de ce calcul est très efficace pour les opérations où il a un volume élevé de chiffres, parce que nous pouvons les identifier dans une séquence logique plus simple, tous les nombres sont représentés par des nombres séquentiels 1 à 9 infiniment.
CONCLUSION
Conclusion de cette étude vise à enregistrer la découverte du calcul de la proportion numérique et la logique de la proportion numérique, et de relier cette découverte du calcul de la proportion numérique avec le calcul Fibonacci, en plus de démontrer son applicabilité en mathématiques et en particulier dans les systèmes binaires et en ce qui concerne son application par rapport à l’infini.
Cette étude pourrait fournir une base pour de nouvelles découvertes scientifiques, comme cela s’est déjà produit, et pour la recherche. Il peut aider les gens à penser de nouvelles façons de traiter les nombres, et c’est une nouvelle façon plus simple de calculer en séquençant toutes les valeurs à l’infini de 1 à 9. Dans la logique de la proportion numérique, l’infini est brisé de 1 à 9. Aussi pour présenter de nouvelles informations, une nouvelle façon d’observer, d’exprimer, de trouver, de calculer et de déchiffrer l’Infini.
RÉFÉRENCE
BELLAS, L.D. Sistema Binário 2 – Código Fechado. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 02, Vol. 05, pp. 110-151. Fevereiro de 2019. ISSN: 2448-0959. Disponível em: https://www.nucleodoconhecimento.com.br/tecnologia/sistema-binario-2-codigo-fechado
TANURE, A.C. Proporção Áurea e Sequência Fibonacci. Pagasus Portal. Disponível em: http://pegasus.portal.nom.br/proporcao-aurea-e-sequencia-de-fibonacci/
TESLA, N. Os segredos dos números 3, 6 e 9. Youtube – Fatos Desconhecidos https://www.youtube.com/watch?v=c2M9ZfZ5h5A&t=682s
Sequência de Fibonacci. Educa+Brasil. Disponível em: https://www.educamaisbrasil.com.br/enem/matematica/sequencia-de-fibonacci
[1] Diplômé en administration des affaires avec spécialisation en commerce extérieur.
Envoyé : Mai 2020.
Approuvé : décembre 2020.






