Démonstration de la conjecture du nombre impair imparfait

ARTICLE ORIGINAL

SANTOS, Adecio da Silva ^[1]

SANTOS, Adecio da Silva. Démonstration de la conjecture du nombre impair imparfait. Revista Científica Multidisciplinar Núcleo do Conhecimento. 04 année, Ed. 05, Vol. 07, pp. 176-185. mai 2019. ISSN : 2448-0959. Lien d’accès: https://www.nucleodoconhecimento.com.br/olympiades-mathematiques/nombre-impair

RÉSUMÉ

Parmi environ 48 problèmes ouverts (Conjectures) de mathématiques dans le domaine de la théorie des nombres, la conjecture nombres impairs parfaits à prouver dans cet article. La méthode que nous avons utilisée pour le test a été la démonstration par la réduction à l’absurdité. Et nous avons délibérément modifié le nom du problème pour imperfect Odd Number Conjecture, parce que nous l’avons trouvé plus compatible avec la solution trouvée. En outre, nous laissons dans l’annexe une liste de plusieurs problèmes ouverts des mathématiques.

Mots-clés: Conjecture, Démonstration, Odd Perfect.

1. INTRODUCTION

La génération du XXIe siècle est pleine d’innovations technologiques, qui nous permettent de connaître pratiquement le monde entier, et de communiquer « instantanément » de n’importe où sur la planète.

Les mathématiques ont joué un rôle très important dans la construction dans l’ensemble de notre société actuelle. Sa précision et l’exactitude de ses résultats ne laissent aucune marge d’erreur. Mais si tu le laisses immobile, c’est délibéré.

Une science comme celle-ci si riche et souveraine a une particularité, elle ne permet pas à l’ego ou à l’arrogance d’avoir beaucoup d’espace dans l’esprit de ses érudits, parce que autant qu’elle peut être respectée, voire admirée, à notre époque actuelle, il y a encore des problèmes mathématiques que personne dans l’histoire n’a jamais été en mesure de les prouver encore.

Environ 417 problèmes ne sont pas résolus dans les domaines les plus variés des mathématiques. Le lecteur intéressé à les connaître peut vérifier la référence (1). Mais nous soulignons que certains d’entre eux ne peuvent jamais être démontrés, bien qu’ils soient vrais, cela est garanti par les théoriques d’incomplétivité de Gödel.

Notre article expose la preuve d’un de ces problèmes ouverts de mathématiques, à savoir la Conjecture de The Perfect Odd Numbers, mais nous l’avons rebaptisé la Conjecture du Nombre Impair Imparfait parce que nous trouvons cette phrase plus cohérente avec notre résultat.

Nous avons utilisé à la fois la méthode de démonstration par réduction à l’absurdité, la propriété de la trichotomie et un résultat dans le texte que nous appelons propriété: (P), en plus de certaines manipulations algébriques.

À la fin, nous laissons, à l’ANNEXE A, une liste très éclectique de diverses conjectures mathématiques.

2. CADRE THÉORIQUE

Dans cette partie, nous donnons crédit aux références qui ont contribué de manière significative à la préparation de notre article.

Qui étaient la référence (2), parce qu’elle nous a fourni la base d’un raisonnement logique mathématique afin que nous puissions trouver le résultat final de l’œuvre soutenue par des arguments logiquement cohérents. Cette référence nous a également fait marcher du début à la fin de la démonstration à travers les principes de non-contradiction et les troisièmes exclus qui étaient nos deux « jambes » jusqu’à ce que nous atteignions notre résultat.

Il était également important de faire référence (3) parce qu’il a fourni une maturité à travers ses exercices afin que nous puissions avoir un chemin de la façon d’attaquer le problème en cours d’analyse dans cet article par la méthode de démonstration par la réduction à l’absurdité.

Enfin, nous laissons les références (4), (5) et la liste des problèmes de l’ANNEXE A au lecteur intéressé à en apprendre davantage sur la Conjecture des nombres impairs parfaits, en plus d’autres conjectures de la théorie des nombres et plus de problèmes des différents domaines des mathématiques.

3. CONJECTURE D’UN NOMBRE IMPAIR IMPARFAIT

Le domaine des études mathématiques connu sous le nom de théorie des nombres a environ 48 problèmes ouverts. Parmi ceux-ci, il y a ce que nous appellera la Conjecture du Nombre Impair Imparfait. Cependant, ce problème est mieux connu sous le nom de Conjecture nombres impairs parfaits. Et il indique qu’il n’y a pas de nombre impair parfait. Cependant, nous avons modifié le nom de la conjecture à dessein, parce que nous l’avons trouvé plus conforme à notre résultat.

Selon le portail, www.matematica.br: « Un nombre est dit parfait s’il est égal à la somme de ses propres diviseurs. Un nombre positif de diviseurs N eux-mêmes sont tous des diviseurs integer positifs de N, sauf le N lui-même. » (6)

À ce jour, des nombres parfaits et même sont connus. Les mathématiciens qui ont le plus étudié ce thème étaient Euclide, Euler et Descartes. En outre, il est également connu une formule pour tous les nombres parfaits même. Il a d’abord été étudié par Euclide et a ensuite été achevé par Euler.

Des explications résumées de ce qui précède se trouvent dans plusieurs articles universitaires. Mais selon Jeane Barbosa Ferreira et Marcos Ferreira de Melo:

Euclide fait valoir que si « q » est un nombre premier tel que 2_q-1 qui est également premier, alors la formule n = 2^q-1(2^q-1) génère des nombres parfaits même. Longtemps après, Euler (1707-1783) a prouvé que chaque numéro de paire parfait est obtenu par la recette ci-dessus, établissant ainsi la réciprocité du theorème d’Euclide. Il est à noter que les premiers numéros de la forme 2^q-1 sont connus comme cousins de Mersenne. (7)

C’est pourquoi les nombres impairs parfaits conjecture existe. Depuis l’analyse des nombres parfaits, même est bien avancé. Le premier mathématicien qui a mentionné la conjecture des nombres impairs parfaits était Descartes. Et jusqu’à cet article, personne n’avait encore prouvé ou réfuté l’allégation.

Notre article présente une preuve de la Conjecture de Perfect Odd Numbers, et pour cela nous utilisons la définition du nombre parfait, un résultat montré dans le texte que nous appelons propriété (P), la propriété de la trichotomie et quelques manipulations algébriques. Tout cela dans une construction logique basée sur la technique de démonstration par réduction à l’absurdité.

Nous laissons en dessous de l’expression de la conjecture et de sa démonstration.

De plus, s’il y a une erreur dans la preuve, nous aimerions que les lecteurs approfondissent leurs études afin de les montrer et de les corriger. Chaque contribution est la bienvenue.

Conjecture imparfaite de nombre impair : Il n’y a aucun nombre impair parfait.

DÉMONSTRATION: Premièrement, nous prouvons que tout entier naturel parfait, N, a la propriété (P): 1+d₁+d₂+d₃+…+d_n-1, Où 1< d₁< d₂< d₃< …<d_n-1<d_n sont tous les diviseurs stricts de N.

En fait, notez que N = 1+d₁+d₂+d₃+…+d_n-1+d_n, parce que N est un nombre parfait. Supposons maintenant, absurdement, que 1+d₁+d₂+d₃+…+d_{n-1 <} d_n et en ajoutant, dans les deux membres de l’inégalité précédente, le terme dn on retrouve l’expression suivante 1+d₁+d₂+d₃+…+d_n-1+(d_n)<d_n+(d_n)⇒1+d₁+d₂+d₃+…+d_n-1+(d_n)<2d_n.Alors nous devons d_n<1+d₁+d₂+d₃+…+d_n-1+(d_n)<2d_n⇒d_n<N<2d_n⇒1<<2. Cependant, comme dn divise N nous trouvons le nature l entre 1 et 2. Ce qui est absurde!

D’un autre côté, supposons que c’est absurde, mais seulement cette fois que l’inégalité est d_n<1+d₁+d₂+d₃+…+d_n-1. Maintenant, en ajoutant, dans les deux membres de l’inégalité précédente, le terme dn on trouve  d_n+(d_n)<1+d₁+d₂+d₃+…+d_n-1+d_n ce qui implique dans 2d_n<1+d₁+d₂+d_n+…+d_n-1+(d_n), C’est ,2d_n<N (I) . Notez également que
≤d_n⇒N≤d₁.d_n (II), car d_nest le plus grand diviseur de N. Donc de (I) et (II) est
 2d_n<N≤d₁.d_n, en divisant tous les membres de la dernière inégalité par d_n nous avons
2<≤d₁ (III), mais comment d₁ est le plus petit diviseur de N autre que 1 et est un diviseur de N inégalité (III) nous fournit que  =d₁⇒N=d₁.d_n est-ce  2<d₁, donc cela signifie que tous les diviseurs de sont impairs, car s’il y avait un diviseur d’être pair, alors 2=d₁, ce qui est absurde dans notre hypothèse. De là, nous avons 4 (quatre) situations à analyser:

1ère situation: d₁ divide d_i ∀i= 1,2,3,4,…,n, car d₁ est le plus petit diviseur de N. Et cela implique que d_i=d₁ⁱ ∀=1,2,3,4,…,n, parce que s’il y en avait d_i autre que le pouvoir d₁ alors cela générerait un nouveau diviseur de N autre que d_i ∀=1,2,3,4,…,n, ce qui est absurde. Donc, cette situation signifie que 1+d₁²+d₁³+d₁⁴+…+d₁ⁿ=N=d_{1 .} d_n=d₁.d₁ⁿ=d₁ⁿ⁺¹, mais par la formule de la somme d’un P.G fini on a 1+d₁²+d₁³+d₁⁴+…+d₁ⁿ=1+d₁²., C’est ,1+d₁².=d₁ⁿ⁺¹⇒1+= d₁ⁿ⁺¹⇒= d₁ⁿ⁺¹⇒ d₁-1+d₁ⁿ⁺¹–d₁² = (d₁-1).d₁ⁿ⁺¹=d₁ⁿ⁺²–d₁ⁿ⁺¹ ⇒d₁-1+d₁ⁿ⁺¹–d₁²=d₁ⁿ⁺² – d₁ⁿ⁺¹, alors nous devons d₁+2d₁ⁿ⁺¹ – d₁² –d₁ⁿ⁺² =1⇒d₁(1+2d₁ⁿ–d₁–d₁ⁿ⁺¹)=1⇒d₁ divise 1, absurde!

2ème situation: d₁ divise certains d_j et d’autres ne s’arrêtent pas j=1, 2, 3, 4,…,n. Alors nous devons N=1+(d₁+d_j1+d_j2+…+d_jk) + (d_i1 +…+d_im ), où d₁ ,d_j1 ,d_j2 ,…,djk sont les nombres divisibles par d₁ e d_i1 ,…,d_im ils ne sont pas. Et les chiffres 1,d₁ ,d_j1 ,d_j2 ,…,d_jk ,d_i1 ,…,d_im sont tous les diviseurs stricts de N.

Disons que la plus haute puissance _de D1 qui divise N est ^d1n. Ainsi, nous pouvons réécrire tous les diviseurs eux-mêmes de la façon dont:

1, (d₁, d₁², …, d₁ⁿ), (d₁d_i1, d₁d_i2, …, d₁d_im), (d₁²d_i1, d₁²d_i2, …, d₁²d_im), …, (d₁ⁿd_i1, d₁ⁿd_i2, …. d₁ⁿd_im), (d_i1,d_i2, …, d_im).

Par conséquent, avec cette nouvelle écriture, nous devons ajouter les diviseurs de N propre est:

N=1+(d₁+d₁²+…+d₁ⁿ) + (d₁d_i1+…+d₁d_im) +(d₁²d_i1+…+d₁²d_im)+ … …+(d₁ⁿd_i1+…+d₁ⁿd_im) + (d_i1+d_i2+…+d_im)

= 1+(d₁+d₁²+…+d₁ⁿ)+(d₁+d₁²+…+d₁ⁿ)d_i1+…+(d₁+d₁²+…+d₁ⁿ)d_im++(d_i1+d_i2+…+d_im)

=1+(d₁+d₁²+…+d₁ⁿ) + (d₁+d₁²+…+d₁ⁿ)(d_i1+…+d_im)+(d_i1+…+d_im)

=1+(d₁+d₁²+…+d₁ⁿ) +(d₁+d₁²+…+d₁ⁿ+1) . (d_i1+…+d_im)

=(1+d₁+d₁²+…+ d₁ⁿ) . (1+d_i1+…+d_im)

Mas N=d₁.d_n=(1+d₁+d₁2+…+d₁n) . (1+d_i1+…+d_im), et cela implique que

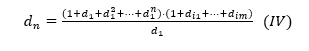
D’autre part, d_n=d₁^{n .} d_im^* (V) , onde d_im^* est le plus grand nombre parmi d_i1, …, d_im.

Enfin, par (IV) et (V) on a:mais cela nous donne que N = (1+d₁+d₁²+…+d₁ⁿ) . (1+d_i1+…+d_im) = d₁ⁿ⁺¹ . d_im * , c’est à dire ^{, d}1n +1, serait un diviseur de n lui-même qui ne serait pas sur notre liste de diviseurs propres de N. Qu’est-ce qu’un, ABSURDE!

3ème situation _: d1 ne partage aucun d_j, mais a des facteurs premiers en commun avec certain_s dj pour j=2, 3, 4,…, n. Cela implique que ces principaux facteurs dans la division commune N et serait plus petit que _d1 qui est le plus petit, absurde diviseur N!

Situation 4: d1 ne divise pas de d_j, d’ailleurs, d₁ et d_j n’ont pas de facteurs premiers en commun pour tous les j =2, 3, 4, …, n.

Donc, comme N =d₁ . d_n, Nous devons d₂, d₃, d₄, …, d_n-1 diviser d_n, parce qu’ils ne partagent pas d₁ par le fait d’être d₁ le plus petit diviseur de N. Maintenant, remarquez que ≠ d₁ ∀i= 1,3,4,5…,n , parce que si= d_i pour certains d_i, cela impliquerait que d_n=d₂ . d_i⇒ N=d₁ . d₂ . d_i, mais comme d₁ n’a pas de facteurs premiers en commun avec aucun di nous sommes obligés d’accepter d₁ . d₂ e d₁ . d_i comme de nouveaux diviseurs de N, non-sens! Parce que tous les diviseurs n ont déjà été répertoriés, et la même chose par notre 4ème situation n’est pas divisible par d₁. C’est-à-dire, il est même différent de tous di, mais cela, aussi, générerait un autre nombre qui n’est pas sur la liste de tous les diviseurs de N, une autre absurdité!

Par conséquent, par trichotomie, nous n’avons que le choix 1+d₁+d₂+d₃+…+d_n-1=d_n.

Enfin, supposons, absurdement, qu’il y ait un nombre impair parfait, disons 2k+1. Maintenant, nous allon_s 1<I₁<I₂<I₃<…<I_2n étant tous les diviseurs 2k +1 eux-mêmes. Notez que I₁,I₂,I₃,…,I_2n sont des nombres impairs et dans une quantité même de nombres, parce que la somme d’une quantité même de nombres impairs est égal et plus 1 résultats dans un impair.

Mais par la propriété (P), que nous avons prouvé est valable pour chaque nombre parfait, nous avons à 1+I₁+I₂+I₃+…+I_2n-1=I_2n. Maintenant, notez que ce 1+I₁+I₂+I₃+…+I_2n1 est égal, car c’est la somme d’une quantité même de nombres impairs (nous considérons le 1 étant impair) et I_2n est étrange. C’est-à-dire, nous trouvons un nombre naturel qui est même et étrange simultanément, ABSURDE!

Par conséquent, il n’y a pas de nombre naturel impair parfait.

4. CONSIDÉRATIONS FINALES

Notre article présente une démonstration de la conjecture de nombres impairs parfaits, mais le changement de nom de Conjecture étrange imparfaite due à est plus compatible avec notre résultat. Mais les mathématiques ont au-delà de cela beaucoup d’autres problèmes ouverts. Et l’objectif principal de notre travail est d’encourager les lecteurs à essayer également de résoudre des problèmes plus ouverts dans la région. Atteindre avec cela l’augmentation des chercheurs dans les domaines les plus variés des mathématiques dans notre pays.

Dans la plupart, nous attendons des suggestions pour l’amélioration de notre article, des critiques constructives, aussi. Et que notre article fournit la continuation pour beaucoup d’autres travaux académiques.

5.  RÉFÉRENCES

1. Portal do openproblemgarden. Disponível em: http://www.openproblemgarden.org/op/odd

_perfect_number. Acesso em 22 de abril de 2019.

2. ALENCAR FILHO, Edgard de. Iniciação à Lógica Matemática. 18 Ed. São Paulo: Nobel, 1975.

3. LIMA, Elon Lages Análise Real. vol. 1 Coleção Matemática Universitária, SBM,. Rio de Janeiro, 2001.

4. Canal A Matemaníaca por Julia Jaccoud. Disponível em: https://www.youtube.com/watch?v=

CHZBYfAmkcE. Acesso em 21 de abril de 2019.

5. Portal do Impa. Disponível em https://impa.br/noticias/problemas-do-milenio-da-geometria-a-fisica-quantica/. Acesso em 21 de abril de 2019.

6. Portal da matematica. Disponível em:http: //www.matematica.br/historia/nperfeitos.html. Acesso em 21 de abril de 2019.

7. Portal da ufc. Disponível em: http://www.periodicos.ufc.br/eu/article/view/15284/15570 Acesso em 22 de abril de 2019.

ANNEXE A

LISTE DES CONJECTURES MATHÉMATIQUES

1. P contre NP

2. Conjecture de Hodge

3. Hypothèse de Riemann

4. Existence de Yang-Mills et gamme de masse

5. Existence et douceur de Navier-Stokes

6. Conjecture de Birch et Swinnerton-Dyer

7. Conjecture de Beal

8. Conjecture de Fermat-Catalan

9. Conjecture de Goldbach

10. Conjecture de Collatz

11. Conjecture d’Erdös

12. Conjecture du nombre de carrés magiques

13. Conjecture d’Andrica

14. Conjecture des cousins ​​jumeaux

15. La conjecture de Legendre

16. Problème de fin heureuse

17. Problème de cercle de Gauss

18. Problème inverse de Galois

19. Conjecture de Littlewood

20. Longues progressions arithmétiques de l’arc-en-ciel

21. Progressions arithmétiques monotones de 4 fins

22. La conjecture du double cap

23. Conjecture de Beneš

24. Longueur de produit surréaliste

25. Projets de couverture combinatoire

26. Un point zéro dans un mapping linéaire

27. Conjecture de partition large

28. Numéros de Ramsey diagonaux

29. La conjecture de base additive

30. Les nombres de Fermat sont-ils tous carrés libres?

^[1] Diplômé et master en mathématiques.

Soumis: Avril, 2019.

Approuvé : mai 2019.