Dimostrazione della congettura del numero dispari imperfetto

ARTICOLO ORIGINALE

SANTOS, Adecio da Silva ^[1]

SANTOS, Adecio da Silva. Dimostrazione della congettura del numero dispari imperfetto. Revista Científica Multidisciplinar Núcleo do Conhecimento. anno 04, Ed. 05, Vol. 07, pp. 176-185. maggio 2019. ISSN: 2448-0959. Link di accesso: https://www.nucleodoconhecimento.com.br/olimpiadi-di-matematica/numero-dispari

RIEPILOGO

Tra i circa 48 problemi aperti (congetture) della matematica nell’area della teoria dei numeri, la congettura dei numeri dispari perfetti da dimostrare in questo articolo. Il metodo che abbiamo usato per il test è stato la dimostrazione per riduzione all’assurdità. E abbiamo volutamente modificato il nome del problema per La congettura imperfetta dei numeri dispari, perché l’abbiamo trovato più coerente con la soluzione trovata. Inoltre lasciamo in allegato un elenco di diversi problemi aperti della matematica.

Parole chiave: Congettura, Dimostrazione, Dispari perfetto.

1. INTRODUZIONE

La generazione del XXI secolo è piena di innovazioni tecnologiche, che ci permettono di conoscere praticamente l’intero globo e comunicare “istantaneamente” da qualsiasi parte del pianeta.

La matematica giocò un ruolo molto importante nella costruzione nel suo insieme della nostra società attuale. La sua accuratezza e accuratezza dei suoi risultati non lascia alcun margine di errore. Ma se lo lasci immobile, è intenzionale.

Una scienza come questa così ricca e sovrana ha una particolarità, non permette all’ego o all’arroganza di avere molto spazio nella mente dei suoi studiosi, perché per quanto possa essere rispettata, anche ammirata, ai nostri tempi ci sono ancora problemi matematici che nessuno nella storia è mai stato in grado di dimostrarli.

Circa 417 problemi sono irrisolti nei più svariati campi della matematica. Il lettore interessato a conoscerli può controllare il riferimento (1). Ma sottolineiamo che alcuni di essi non possono mai essere dimostrati, anche se sono veri, questo è garantito dai teoremi di incompletezza di Gödel.

Il nostro articolo espone la dimostrazione di uno di questi problemi aperti della matematica, vale a dire la congettura dei numeri dispari perfetti, ma l’abbiamo rinominata congettura del numero dispari imperfetto perché troviamo questa frase più coerente con il nostro risultato.

Abbiamo usato sia per il metodo di dimostrazione per riduzione all’assurdità, la proprietà della trichotomia e un risultato nel testo che chiamiamo proprietà: (P), oltre ad alcune manipolazioni algebriche.

Alla fine lasciamo, nell’ALLEGATO A, un elenco molto eclettico di varie congetture matematiche.

2. QUADRO TEORICO

In questa parte diamo credito ai riferimenti che hanno contribuito in modo significativo alla preparazione del nostro articolo.

Che erano il riferimento (2), perché ci forniva la base del ragionamento logico matematico in modo da poter trovare il risultato finale del lavoro supportato da argomenti logicamente coerenti. Questo riferimento ci ha fatto anche camminare dall’inizio alla fine della manifestazione attraverso i principi di Non-Contraddizione e del Terzo Escluso che erano le nostre due “gambe” fino a raggiungere il nostro risultato.

Era anche importante fare riferimento (3) perché forniva una maturità attraverso i suoi esercizi in modo da poter avere un percorso su come attaccare il problema in analisi in questo articolo con il metodo dimostrativo per riduzione all’assurdità.

Infine, lasciamo i riferimenti (4), (5) e l’elenco dei problemi nell’ALLEGATO A al lettore interessato a saperne di più sulla congettura dei numeri dispari perfetti, oltre ad altre congetture della teoria dei numeri e più problemi dei vari campi della matematica.

3. CONGETTURA DI NUMERO DISPARI IMPERFETTO

Il campo degli studi matematici noto come Teoria dei Numeri ha circa 48 problemi aperti. Tra questi c’è quella che chiameremo la congettura del numero dispari imperfetto. Tuttavia, questo problema è meglio conosciuto come Congettura dei numeri dispari perfetti. E afferma che non esiste un numero dispari perfetto. Tuttavia, abbiamo modificato il nome della congettura intenzionalmente, perché l’abbiamo trovata più coerente con il nostro risultato.

Secondo il portale www.matematica.br: “Un numero è detto perfetto se è uguale alla somma dei propri divisori. Un numero positivo N divisori stessi sono tutti divisori interi positivi di N tranne la N stessa. (6)

Ad oggi, sono noti numeri pari perfetti. I matematici che studiarono maggiormente questo tema furono Euclide, Eulero e Cartesio. Inoltre, è anche conosciuta una formula per tutti i numeri pari perfetti. Fu studiato per la prima volta da Euclide e fu successivamente completato da Eulero.

Spiegazioni riassunte di quanto sopra si trovano in diversi documenti accademici. Ma secondo Jeane Barbosa Ferreira e Marcos Ferreira de Melo:

Euclide sostiene che se “q” è un numero primo come 2_q-1 che è anche primo, allora la formula n = 2^q-1(2^q-1)  genera numeri pari perfetti. Molto tempo dopo, Eulero (1707-1783) dimostrò che ogni numero di coppia perfetto è ottenuto dalla ricetta di cui sopra, stabilendo così il reciproco del teorema di Euclide. Vale la pena notare che i numeri primi della form^a 2q-1 sono noti come cugini di Mersenne. (7)

Ecco perché esiste la congettura perfetta dei numeri dispari. Poiché l’analisi dei numeri pari perfetti è a buon punto. Il primo matematico che menzionava la congettura dei numeri dispari perfetti fu Cartesio. E fino a questo articolo, nessuno aveva ancora provato o confutato l’affermazione.

Il nostro articolo presenta una prova della congettura di Perfect Odd Numbers, e per questo usiamo la definizione di numero perfetto, un risultato mostrato nel testo che chiamiamo proprietà (P), la proprietà della trichotomia e alcune manipolazioni algebriche. Tutto questo in una costruzione logica basata sulla tecnica della dimostrazione per riduzione all’assurdo.

Lasciamo sotto l’espressione della congettura e della sua dimostrazione.

Inoltre, se c’è qualche errore nelle prove, vorremmo che i lettori approfondisce i loro studi per mostrarlo e risolverlo. Ogni contributo è benvenuto.

Congettura imperfetta del numero dispari: non esiste un numero dispari perfetto.

DIMOSTRAZIONE: Per prima cosa dimostriamo che ogni numero naturale perfetto, N, ha la proprietà (P): 1+d₁+d₂+d₃+…+d_n-1, dove 1< d₁< d₂< d₃< …<d_n-1<d_n sono tutti i divisori propri di N.

In effetti, nota quello N= 1+d₁+d₂+d₃+…+d_n-1+d_n, perché N è un numero perfetto. Supponiamo, ora, assurdamente, che 1+d₁+d₂+d₃+…+d_{n-1 <} d_n e aggiungendo, in entrambi i membri della precedente disuguaglianza, il termine dn troviamo la seguente espressione 1+d₁+d₂+d₃+…+d_n-1+(d_n)<d_n+(d_n)⇒1+d₁+d₂+d₃+…+d_n-1+(d_n)<2d_n. Quindi dobbiamo d_n<1+d₁+d₂+d₃+…+d_n-1+(d_n)<2d_n⇒d_n<N<2d_n⇒1<<2. Tuttavia, poiché dn divide N troviamo il naturale tra 1 e 2. Il che è ASSURDO!

D’altra parte, supponiamo che sia assurdo, ma solo questa volta la disuguaglianza lo è
d_n<1+d₁+d₂+d₃+…+d_n-1. Ora, aggiungendo, in entrambi i membri della precedente disuguaglianza, il termine d_n abbiamo trovato d_n+(d_n)<1+d₁+d₂+d₃+…+d_n-1+d_n che implica in 2d_n<1+d₁+d₂+d_n+…+d_n-1+(d_n), questo è,2d_n<N (I) . Nota anche quello
≤d_n⇒N≤d₁.d_n (II), perché d_n è il massimo divisore di N. Quindi di (I) e (II) è
2d_n<N≤d₁.d_n, dividendo tutti i membri dell’ultima disuguaglianza per d_n noi abbiamo
2<≤d₁ (III), ma come d₁ è il più piccolo divisore di N diverso da 1 e è un divisore di N disuguaglianza (III) ce lo fornisce =d₁⇒N=d₁.d_n è questo 2<d₁, quindi questo significa che tutti i divisori di sono dispari, perché se ci fosse un divisore di essere anche allora 2=d₁, che è assurdo nella nostra ipotesi. Da qui abbiamo 4 (quattro) situazioni da analizzare:

1ª situação: d₁ divide d_i ∀i= 1,2,3,4,…,n, perché d₁ è il più piccolo divisore di N. E questo lo implica d_i=d₁ⁱ ∀=1,2,3,4,…,n, perché se ce ne fossero d_i diverso dal potere d₁ allora questo genererebbe un nuovo divisore di N diverso da d_i ∀=1,2,3,4,…,n, il che è assurdo. Quindi questa situazione significa quello 1+d₁²+d₁³+d₁⁴+…+d₁ⁿ=N=d_{1 .} d_n=d₁.d₁ⁿ=d₁ⁿ⁺¹, ma dalla formula della somma di un P.G finito abbiamo
1+d₁²+d₁³+d₁⁴+…+d₁ⁿ=1+d₁²., questo è,1+d₁².=d₁ⁿ⁺¹⇒1+= d₁ⁿ⁺¹⇒= d₁ⁿ⁺¹⇒ d₁-1+d₁ⁿ⁺¹–d₁² = (d₁-1).d₁ⁿ⁺¹=d₁ⁿ⁺²–d₁ⁿ⁺¹ ⇒d₁-1+d₁ⁿ⁺¹–d₁²=d₁ⁿ⁺² – d₁ⁿ⁺¹, allora dobbiamo d₁+2d₁ⁿ⁺¹ – d₁² –d₁ⁿ⁺² =1⇒d₁(1+2d₁ⁿ–d₁–d₁ⁿ⁺¹)=1⇒d₁ divide 1, assurdo!

2a situazione: d₁ divide alcuni d_j e altri non si fermano j=1, 2, 3, 4,…,n. Quindi dobbiamo N=1+(d₁+d_j1+d_j2+…+d_jk) + (d_i1 +…+d_im ), dove d₁ ,d_j1 ,d_j2 ,…,d_jk sono i numeri divisibili per d₁ e d_i1 ,…,d_im non sono. E i numeri 1,d₁ ,d_j1 ,d_j2 ,…,d_jk ,d_i1 ,…,d_im sono tutti i divisori propri di N.

Diciamo che la più alta potenza _di d1 che divide N è _d¹n. Quindi possiamo riscrivere tutti i divisori stessi di come:

1, (d₁, d₁², …, d₁ⁿ), (d₁d_i1, d₁d_i2, …, d₁d_im), (d₁²d_i1, d₁²d_i2, …, d₁²d_im), …, (d₁ⁿd_i1, d₁ⁿd_i2, …. d₁ⁿd_im), (d_i1,d_i2, …, d_im).

Pertanto, con questa nuova scrittura, dobbiamo aggiungere i divisori di N è:

N=1+(d₁+d₁²+…+d₁ⁿ) + (d₁d_i1+…+d₁d_im) +(d₁²d_i1+…+d₁²d_im)+ … …+(d₁ⁿd_i1+…+d₁ⁿd_im) + (d_i1+d_i2+…+d_im)

= 1+(d₁+d₁²+…+d₁ⁿ)+(d₁+d₁²+…+d₁ⁿ)d_i1+…+(d₁+d₁²+…+d₁ⁿ)d_im++(d_i1+d_i2+…+d_im)

=1+(d₁+d₁²+…+d₁ⁿ) + (d₁+d₁²+…+d₁ⁿ)(d_i1+…+d_im)+(d_i1+…+d_im)

=1+(d₁+d₁²+…+d₁ⁿ) +(d₁+d₁²+…+d₁ⁿ+1) . (d_i1+…+d_im)

=(1+d₁+d₁²+…+ d₁ⁿ) . (1+d_i1+…+d_im)

Mas N=d₁.d_n=(1+d₁+d₁2+…+d₁n) . (1+d_i1+…+d_im), e questo implica quello

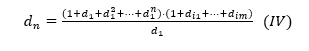
D’altra parte, d_n=d₁^{n .} d_im^* (V) , onde d_im^* è il numero più alto tra d_i1, …, d_im.

Infine, con (IV) e (V) abbiamo:ma questo ci dà che N =(1+d₁+d₁²+…+d₁ⁿ) . (1+d_i1+…+d_im) = d₁ⁿ⁺¹ . d_im^* , cioè , d1n+₁^, sarebbe un divisore di n stesso che non sarebbe nella nostra lista di divisori propri di N. Che cos’è un, ASSURDO!

3a situazione_: d₁ non condivide al_cun dj, ma ha fattori primi in comune con qualche d_j per j=2, 3, 4,…, n. Ciò implica che questi fattori primi nella divisione comune N e sarebbero più piccoli di d₁, che è il più piccolo, assurdo divisore N!

4a situazione: d₁ non divide alcun d_j, inoltre, d₁ e d_j non hanno fattori primi in comune per tutti j=2, 3, 4, …, n.

Quindi, come N=d₁ . d_n, dobbiamo d₂, d₃, d₄, …, d_n-1 dividere d_n, perché non condividono d₁ dal fatto di essere d₁ o più piccolo divisore di N. Ora, notalo≠ d₁ ∀i= 1,3,4,5…,n , perchè se= d_i per alcuni d_i, questo implicherebbe quello d_n=d₂ . d_i⇒ N=d₁ . d₂ . d_i, ma poiché d₁ non ha fattori primi in comune con nessun di siamo obbligati ad accettare d₁ . d₂ e d₁ . d_i come nuovi divisori di N, sciocchezze! Perché tutti e n divisori sono già stati elencati, e lo stesso per la nostra 4a situazione non è divisibile per d₁. Cioè, è anche diverso da tutti di, ma anche questo genererebbe un altro numero che non è nell’elenco di tutti i divisori di N, un’altra sciocchezza!

Pertanto, per tricotomia, abbiamo solo la scelta 1+d₁+d₂+d₃+…+d_n-1=d_n.

Infine, supponiamo, assurdamente, che ci sia un numero dispari perfetto, diciamo 2k +1. Ora, facciamo 1<I₁<_I2<_I3<…_<I2n sono tutti i divisori 2k+1 stessi. Si noti che I₁,I₂,I₃,…,I_2n sono numeri dispari e in una quantità pari di numeri, perché la somma di una quantità pari di numeri dispari è pari e più 1 risulta in uno dispari.

Ma per la proprietà (P), che abbiamo dimostrato è valida per ogni numero perfetto, dobbiamo 1 + I1 + I2 ₊ I₃ + …+ I2_n-1 = _I2n. Ora, nota che questo 1 ₊ I1 + I2 + _{I3 +} …+ I2n-1 è pari, in quanto è la somma di una quantità pari di numeri dispari (consideriamo l’1 dispari) e I_2n è dispari. Cioè, troviamo un numero naturale che è pari e strano contemporaneamente, ASSURDO!

Pertanto, non esiste un numero naturale dispari perfetto.

4. CONSIDERAZIONI FINALI

Il nostro articolo presenta una dimostrazione della congettura di Perfect Odd Numbers, ma la ridenominazione di Congettura dispari imperfetta dovuta è più coerente con il nostro risultato. Ma la matematica ha al di là di questo molti altri problemi aperti. E l’obiettivo principale del nostro lavoro è incoraggiare i lettori a cercare anche di risolvere problemi più aperti nella zona. Raggiungere con questo l’aumento dei ricercatori nei più svariati campi della matematica nel nostro paese.

Nella maggior parte dei casi ci aspettiamo suggerimenti per il miglioramento del nostro articolo, anche critiche costruttive. E che il nostro articolo fornisce la continuazione per molte altre opere accademiche.

5.  RIFERIMENTI

1. Portal do openproblemgarden. Disponível em: http://www.openproblemgarden.org/op/odd

_perfect_number. Acesso em 22 de abril de 2019.

2. ALENCAR FILHO, Edgard de. Iniciação à Lógica Matemática. 18 Ed. São Paulo: Nobel, 1975.

3. LIMA, Elon Lages Análise Real. vol. 1 Coleção Matemática Universitária, SBM,. Rio de Janeiro, 2001.

4. Canal A Matemaníaca por Julia Jaccoud. Disponível em: https://www.youtube.com/watch?v=

CHZBYfAmkcE. Acesso em 21 de abril de 2019.

5. Portal do Impa. Disponível em https://impa.br/noticias/problemas-do-milenio-da-geometria-a-fisica-quantica/. Acesso em 21 de abril de 2019.

6. Portal da matematica. Disponível em:http: //www.matematica.br/historia/nperfeitos.html. Acesso em 21 de abril de 2019.

7. Portal da ufc. Disponível em: http://www.periodicos.ufc.br/eu/article/view/15284/15570 Acesso em 22 de abril de 2019.

ANEXO A

ELENCO DELLE CONIETTURE MATEMATICHE

1. P contro NP

2. Congettura di Hodge

3. Ipotesi di Riemann

4. Esistenza di Yang-Mills e gamma di massa

5. Esistenza e levigatezza di Navier-Stokes

6. Congettura di Birch e Swinnerton-Dyer

7. Congettura di Beal

8. Congettura di Fermat-catalana

9. Congettura di Goldbach

10. Congettura di Collatz

11. Congettura di Erdös

12. Congettura del numero di quadrati magici

13. Congettura di Andrica

14. Congettura di cugini gemelli

15. La congettura di Legendre

16. Problema a lieto fine

17. Problema del cerchio di Gauss

18. Problema inverso di Galois

19. Congettura di Littlewood

20. Lunghe progressioni aritmetiche dell’arcobaleno

21. Progressioni aritmetiche monotone di 4 finali

22. La congettura del double cap

23. Congettura di Beneš

24. Lunghezza del prodotto surreale

25. Progetti di copertura combinatoria

26. Un punto zero in una mappatura lineare

27. Congettura della partizione larga

28. Numeri Ramsey diagonali

29. La congettura della base additiva

30. Tutti i numeri di Fermat sono quadrati gratuiti?

^[1] Laureato e master in matematica.

Inviato: Aprile, 2019.

Approvato: Maggio, 2019.