Demonstration der Vermutung der unvollkommenen UngeradenZahl

ORIGINAL-ARTIKEL

SANTOS, Adecio da Silva ^[1]

SANTOS, Adecio da Silva. Demonstration der Vermutung der unvollkommenen UngeradenZahl. Revista Científica Multidisciplinar Núcleo do Conhecimento. 04-Jahr, Ed. 05, Vol. 07, S. 176-185. Mai 2019. ISSN: 2448-0959. Zugangslink: https://www.nucleodoconhecimento.com.br/mathematischen-olympiaden/ungerade-zahl

ZUSAMMENFASSUNG

Unter etwa 48 offenen Problemen (Vermutungen) der Mathematik im Bereich der Zahlentheorie, die Perfect Odd Numbers Conjecture in diesem Artikel bewiesen werden. Die Methode, die wir für den Test verwendet haben, war die Demonstration durch Reduktion auf Absurdität. Und wir haben den Namen des Problems absichtlich für Imperfect Odd Number Conjecture geändert, weil wir es konsistenter mit der gefundenen Lösung fanden. Darüber hinaus hinterlassen wir im Anhang eine Liste von mehreren offenen Problemen der Mathematik.

Schlüsselwörter: Vermutung, Demonstration, Odd Perfect.

1. EINFÜHRUNG

Die Generation des 21. Jahrhunderts ist voller technologischer Innovationen, die es uns ermöglichen, praktisch den ganzen Globus zu kennen und “sofort” von überall auf dem Planeten zu kommunizieren.

Die Mathematik spielte eine sehr wichtige Rolle beim Aufbau unserer heutigen Gesellschaft. Seine Genauigkeit und Genauigkeit seiner Ergebnisse lässt keinen Spielraum für Fehler. Aber wenn Sie es still lassen, ist es zielgerichtet.

Eine Wissenschaft wie diese, die so reich und souverän ist, hat eine Besonderheit, sie lässt Weich oder Arroganz nicht viel Raum in den Köpfen ihrer Gelehrten haben, denn so sehr sie respektiert, ja bewundert werden kann, gibt es in unserer heutigen Zeit immer noch mathematische Probleme, die noch niemand in der Geschichte beweisen konnte.

Rund 417 Probleme sind in den unterschiedlichsten Bereichen der Mathematik ungelöst. Der Leser, der sie kennt, kann die Referenz (1) einsehen. Aber wir betonen, dass einige von ihnen nie nachgewiesen werden können, obwohl sie wahr sind, wird dies durch Gödels Unvollständigkeitstheoreme garantiert.

Unser Artikel enthüllt den Beweis eines dieser offenen Probleme der Mathematik, nämlich die Vermutung der perfekten seltsamen Zahlen, aber wir haben es in die Vermutung der Unvollkommenen Odd Number umbenannt, weil wir diesen Satz mit unserem Ergebnis kohärenter finden.

Wir verwendeten sowohl für die Methode der Demonstration durch Reduktion auf Absurdität, die Eigenschaft der Trichotomie und ein Ergebnis in dem Text, den wir Eigenschaft nennen: (P), zusätzlich zu einigen algebraischen Manipulationen.

Am Ende hinterlassen wir in ANHANG A eine sehr eklektische Liste verschiedener mathematischer Vermutungen.

2. THEORETISCHEN RAHMEN

In diesem Teil würdigen wir die Referenzen, die wesentlich zur Vorbereitung unseres Artikels beigetragen haben.

Das waren die Referenzen (2), weil sie uns die Grundlage mathematischer logischer Argumentation lieferten, so dass wir das Endergebnis der Arbeit finden konnten, die durch logisch kohärente Argumente gestützt wurde. Diese Bezugnahme ließ uns auch vom Anfang bis zum Ende der Demonstration durch die Prinzipien der Nicht-Widerspruch und der Dritten Ausgeschlossenen gehen, die unsere beiden “Beine” waren, bis wir unser Ergebnis erreichten.

Es war auch wichtig, (3) darauf hinzuweisen, weil es durch seine Übungen eine Reife bot, so dass wir einen Weg haben konnten, wie wir das in diesem Artikel analysierte Problem durch die Demonstrationsmethode durch Reduktion auf Absurdität angreifen konnten.

Schließlich überlassen wir die Referenzen (4), (5) und die Liste der Probleme in ANHANG A dem Leser, der mehr über die Vermutung von Perfect Odd Numbers erfahren möchte, zusätzlich zu anderen Vermutungen der Zahlentheorie und mehr Problemen der verschiedenen Bereiche der Mathematik.

3. CONJECTURE VON IMPERFECT ODD NUMBER

Das Feld der Mathematik-Studien bekannt als Zahlentheorie hat etwa 48 offene Probleme. Unter diesen ist das, was wir die Vermutung der Unvollkommenen odd Number nennen werden. Jedoch, Dieses Problem ist besser bekannt als The Perfect Odd Numbers Conjecture. Und es heißt, dass es keine perfekte ungerade Zahl gibt. Wir haben den Namen der Vermutung jedoch absichtlich geändert, weil wir ihn mit unserem Ergebnis konsistenter fanden.

Laut dem Portal www.matematica.br: “Eine Zahl wird als perfekt bezeichnet, wenn sie der Summe ihrer eigenen Trennwände entspricht. Eine positive Zahl N Teiler selbst sind alle positive ganzzahlige Teiler von N außer dem N selbst.” (6)

Bis heute sind perfekte gerade Zahlen bekannt. Die Mathematiker, die dieses Thema am meisten studierten, waren Euklid, Euler und Descartes. Darüber hinaus ist es auch eine Formel für alle perfekten geraden Zahlen bekannt. Es wurde zuerst von Euklid studiert und später von Euler abgeschlossen.

Zusammengefasste Erläuterungen zu den oben genannten finden sich in mehreren wissenschaftlichen Arbeiten. Aber nach Jeane Barbosa Ferreira und Marcos Ferreira de Melo:

Euclid argumentiert, dass, wenn “q” eine Primzahl wie 2_q-1 ist, die auch Primzahl ist, dann erzeugt die Formel n = 2^q-1(2^q-1) perfekte gerade Zahlen. Lange danach bewies Euler (1707-1783), dass jede perfekte Paarzahl durch das obige Rezept erhalten wird, wodurch der Gegenverkehr von Euklids Satz festgestellt wurde. Es ist erwähnenswert, dass die Primzahlen der Form 2^q-1 als Mersennes Cousins bekannt sind. (7)

Deshalb gibt es die perfekte, ungerade Zahlenvermutung. Da die Analyse der perfekten geraden Zahlen weit fortgeschritten ist. Der erste Mathematiker, der die Vermutung der Perfect Odd Numbers erwähnte, war Descartes. Und bis zu diesem Artikel hatte noch niemand die Behauptung bewiesen oder widerlegt.

Unser Artikel stellt einen Beweis für die Vermutung von Perfect Odd Numbers dar, und dafür verwenden wir die Definition der perfekten Zahl, ein Ergebnis, das im Text, den wir Eigenschaft (P) nennen, das Eigentum der Trichotomie und einige algebraische Manipulationen angezeigt wird. All dies in einer logischen Konstruktion, die auf der Technik der Demonstration durch Reduktion auf Absurdität basiert.

Wir lassen die Äußerung der Vermutung und ihre Demonstration unter.

Darüber hinaus möchten wir, wenn es einen Fehler in den Beweisen gibt, dass die Leser tiefer in ihre Studien gehen, um sie zu zeigen und zu beheben. Jeder Beitrag ist willkommen.

Unvollkommene Odd Number-Vermutung: Es gibt keine perfekte ungerade Zahl.

DEMONSTRATION: Zuerst beweisen wir, dass jede perfekte natürliche Zahl N die Eigenschaft hat (P):1+d₁+d₂+d₃+…+d_n-1, onde 1< d₁< d₂< d₃< …<d_n-1<d_n sind alle richtigen Teiler von N.

Beachten Sie in der Tat, dass N = 1+d₁+d₂+d₃+…+d_n-1+d_n, weil N eine perfekte Zahl ist. Nehmen wir jetzt absurderweise an, dass 1+d₁+d₂+d₃+…+d_{n-1 <} d_n und indem wir in beiden Mitgliedern der vorherigen Ungleichung den Begriff dn hinzufügen, finden wir den folgenden Ausdruck 1+d₁+d₂+d₃+…+d_n-1+(d_n)<d_n+(d_n)⇒1+d₁+d₂+d₃+…+d_n-1+(d_n)<2d_n. Also müssen wir d_n<1+d₁+d₂+d₃+…+d_n-1+(d_n)<2d_n⇒d_n<N<2d_n⇒1<<2. Jedoch, wie d_n trennt N finden wir das Natürliche zwischen 1 und 2. Das ist ABSURD!

Nehmen wir andererseits an, es sei absurd, aber nur diesmal ist diese Ungleichheit
d_n<1+d₁+d₂+d₃+…+d_n-1. Fügen wir nun in beiden Mitgliedern der vorherigen Ungleichung den Begriff dn hinzu, den wir finden d_n+(d_n)<1+d₁+d₂+d₃+…+d_n-1+d_n was impliziert in 2d_n<1+d₁+d₂+d_n+…+d_n-1+(d_n), das ist, 2d_n<N (I) . Beachten Sie auch das ≤d_n⇒N≤d₁.d_n (II), weil d_n ist der größte Teiler von N. Also von (I) und (II) ist 2d_n<N≤d₁.d_n, Teilen Sie alle Mitglieder der letzten Ungleichung durch d_n, die wir haben 2<≤d₁ (III), aber wie d₁ ist der kleinste Teiler von N außer 1 und ist ein Teiler der N-Ungleichung (III) liefert uns das =d₁⇒N=d₁.d_n ist das  2<d₁, Das bedeutet also, dass alle Teiler von ungerade sind, denn wenn es einen Teiler des Seins gab, dann auch dann 2=d₁, Das ist absurd in unserer Annahme. Von hier aus haben wir 4 (vier) Situationen zu analysieren:

1. Situation: d₁ teilt sich d_i ∀i= 1,2,3,4,…,n, weil d₁ der kleinste Teiler von N ist. Und das impliziert das d_i=d₁ⁱ ∀=1,2,3,4,…,n, denn wenn es welche gäbe d_i anders als Macht d₁ dann würde dies einen neuen Teiler von N erzeugen, der nicht d_i ∀=1,2,3,4,…,n, das ist absurd. Diese Situation bedeutet das also 1+d₁²+d₁³+d₁⁴+…+d₁ⁿ=N=d_{1 .} d_n=d₁.d₁ⁿ=d₁ⁿ⁺¹, aber nach der Formel der Summe eines endlichen P.G. haben wir
1+d₁²+d₁³+d₁⁴+…+d₁ⁿ=1+d₁²., das ist,1+d₁².=d₁ⁿ⁺¹⇒1+= d₁ⁿ⁺¹⇒= d₁ⁿ⁺¹⇒ d₁-1+d₁ⁿ⁺¹–d₁² = (d₁-1).d₁ⁿ⁺¹=d₁ⁿ⁺²–d₁ⁿ⁺¹ ⇒d₁-1+d₁ⁿ⁺¹–d₁²=d₁ⁿ⁺² – d₁ⁿ⁺¹, dann müssen wir d₁+2d₁ⁿ⁺¹ – d₁² –d₁ⁿ⁺² =1⇒d₁(1+2d₁ⁿ–d₁–d₁ⁿ⁺¹)=1⇒d₁ teilt 1, absurd!

2. Situation: d₁ teilt einige d_j und andere hören nicht auf j=1, 2, 3, 4,…,n. Wir haben also N = 1 + (d₁+d_j1+d_j2+…+d_jk) + (d_i1 +…+d_im ), wo d₁ ,d_j1 ,d_j2 ,…,d_jk sind die Zahlen teilbar durch d₁ e d_i1 ,…,d_im Sie sind nicht. Und die Zahlen 1,d₁ ,d_j1 ,d_j2 ,…,d_jk ,d_i1 ,…,d_im sind alle richtigen Teiler von N.

Nehmen wir an, die höchste Kraft von d₁, die N trennt, ist ^d1n. So können wir alle Trennwände selbst wie:

1, (d₁, d₁², …, d₁ⁿ), (d₁d_i1, d₁d_i2, …, d₁d_im), (d₁²d_i1, d₁²d_i2, …, d₁²d_im), …, (d₁ⁿd_i1, d₁ⁿd_i2, …. d₁ⁿd_im), (d_i1,d_i2, …, d_im).

Daher müssen wir mit diesem neuen Schreiben die Trennwände von Ns eigenen hinzufügen:

N=1+(d₁+d₁²+…+d₁ⁿ) + (d₁d_i1+…+d₁d_im) +(d₁²d_i1+…+d₁²d_im)+ … …+(d₁ⁿd_i1+…+d₁ⁿd_im) + (d_i1+d_i2+…+d_im)

= 1+(d₁+d₁²+…+d₁ⁿ)+(d₁+d₁²+…+d₁ⁿ)d_i1+…+(d₁+d₁²+…+d₁ⁿ)d_im++(d_i1+d_i2+…+d_im)

=1+(d₁+d₁²+…+d₁ⁿ) + (d₁+d₁²+…+d₁ⁿ)(d_i1+…+d_im)+(d_i1+…+d_im)

=1+(d₁+d₁²+…+d₁ⁿ) +(d₁+d₁²+…+d₁ⁿ+1) . (d_i1+…+d_im)

=(1+d₁+d₁²+…+ d₁ⁿ) . (1+d_i1+…+d_im)

Mas N=d₁.d_n=(1+d₁+d₁2+…+d₁n) . (1+d_i1+…+d_im), und das impliziert das

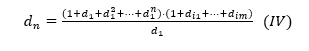
Andererseits, d_n=d₁^{n .} d_im^* (V) , wo d_im^* ist die größte Zahl unter d_i1, …, d_im.

Schließlich haben wir durch (IV) und (V):aber das gibt uns, dass N =(1+d₁+d₁²+…+d₁ⁿ) . (1+d_i1+…+d_im) = d₁ⁿ⁺¹ . d_im^* ,dh , d1n+1_, wäre ein Divisor von n selbst, der nicht auf unserer Liste der Teiler eigene von N. Was ist ein, ABSURD!

3. Situation: d₁ teilt keinen d_J, hat aber Primfaktoren gemeinsam mit einigen d_j für j=2, 3, 4,…, n. Dies impliziert, dass diese Hauptfaktoren in der gemeinsamen Teilung N und wäre kleiner als d1, die der kleinste, absurde N-Teiler ist!

Situation 4: d₁ teilt keine dj, _außerdem haben d₁ u_nd dj keine Primfaktoren gemeinsam für alle j=2, 3, 4, …, n.

So wie N=d₁ . d_n, Wir müssen d₂, d₃, d₄, …, d_n-1 Teilen d_n, weil sie d₁ nicht teilen, weil d₁ der kleinste Teiler von N ist. Beachten Sie nun, dass ≠ d₁ ∀i= 1,3,4,5…,n , pois se = d_i für einige d_i würde dies das implizieren d_n=d₂ . d_i⇒ N=d₁ . d₂ . d_i, aber da d₁ keine Hauptfaktoren gemeinsam hat, sind wir v_erpflichtet, d1 zu akzeptier_en. d₂ e d₁ . d_i als neue Trennwände von N, Unsinn! Da alle n Teiler bereits aufgeführt sind, und das gleiche durch unsere 4. Situation ist nicht durch d1 teilb_ar. Das heißt, es ist sogar anders als alle di, aber auch dies würde eine andere Zahl generieren, die nicht auf der Liste aller Trennwände von N steht, ein weiterer Unsinn!

Daher haben wir durch Trichotomie nur die Wahl 1+d₁+d₂+d₃+…+d_n-1=d_n.

Nehmen wir schließlich, absurderweise, dass es eine perfekte ungerade Zahl gibt, sagen wir 2k+1. Nun, lassen Sie uns 1<I₁<I₂<I₃<…<I_2n sind alle 2k+1-Teiler selbst. Beachten Sie, dass I₁,I₂,I₃,…,I_2n ungerade Zahlen und in einer geraden Anzahl von Zahlen sind, weil die Summe einer geraden Anzahl von ungeraden Zahlen gerade ist und plus 1 zu einem ungeraden Ergebnis führt.

Aber durch die Eigenschaft (P), die wir für jede perfekte Zahl gültig haben, müssen wir 1+I₁+I₂+I₃+…+I_2n-1=I_2n.  Beachten Sie nun, das_s di_ese 1+I₁+I₂+I₃+…+I_2n-1 gerade ist, da es die Summe einer geraden Anzahl ungerader Zahlen ist (wir halten die 1 für ungerade) undI_2n ist seltsam. Das heißt, wir finden eine natürliche Zahl, die gleich und seltsam gleichzeitig ist, ABSURD!

Daher gibt es keine perfekte ungerade natürliche Zahl.

4. ABSCHLIEßENDE ÜBERLEGUNGEN

Unser Artikel stellt eine Demonstration der Vermutung von Perfect Odd Numbers dar, aber die Umbenennung von Imperfect Odd Conjecture aufgrund ist konsistenter mit unserem Ergebnis. Aber die Mathematik hat über diese vielen anderen offenen Probleme hinaus. Und das Hauptziel unserer Arbeit ist es, die Leser zu ermutigen, auch zu versuchen, offenere Probleme in der Region zu lösen. Damit wird der Anstieg der Forscher in den unterschiedlichsten Bereichen der Mathematik in unserem Land erreicht.

In den meisten erwarten wir Vorschläge zur Verbesserung unseres Artikels, konstruktive Kritik, auch. Und dass unser Artikel Fortsetzung für viele andere akademische Arbeiten bietet.

5.  REFERENZEN

1. Portal do openproblemgarden. Disponível em: http://www.openproblemgarden.org/op/odd

_perfect_number. Acesso em 22 de abril de 2019.

2. ALENCAR FILHO, Edgard de. Iniciação à Lógica Matemática. 18 Ed. São Paulo: Nobel, 1975.

3. LIMA, Elon Lages Análise Real. vol. 1 Coleção Matemática Universitária, SBM,. Rio de Janeiro, 2001.

4. Canal A Matemaníaca por Julia Jaccoud. Disponível em: https://www.youtube.com/watch?v=

CHZBYfAmkcE. Acesso em 21 de abril de 2019.

5. Portal do Impa. Disponível em https://impa.br/noticias/problemas-do-milenio-da-geometria-a-fisica-quantica/. Acesso em 21 de abril de 2019.

6. Portal da matematica. Disponível em:http: //www.matematica.br/historia/nperfeitos.html. Acesso em 21 de abril de 2019.

7. Portal da ufc. Disponível em: http://www.periodicos.ufc.br/eu/article/view/15284/15570 Acesso em 22 de abril de 2019.

ANHANG A

LISTE DER MATHEMATISCHEN KONJEKTUREN

1. P gegen NP

2. Hodge Vermutung

3. Riemann-Hypothese

4. Existenz von Yang-Mühlen und Massenbereich

5. Existenz und Glätte von Navier-Stokes

6. Conjectura de Birch e Swinnerton-Dyer

7. Beal Vermutung

8. Fermat-katalanische Vermutung

9. Goldbach-Vermutung

10. Collatz-Vermutung

11. Erdös-Vermutung

12. Vermutung der Anzahl der magischen Quadrate

13. Andrica Vermutung

14. Zwillingscousin-Vermutung

15. Conjectura de Legendre

16. Happy-End-Problem

17. Gauß-Kreis-Problem

18. Galois inverses Problem

19. Littlewood-Vermutung

20. Lange arithmetische Abläufe des Regenbogens

21. Monotone arithmetische Progressionen von 4 Endungen

22. Die Doppelkappen-Vermutung

23. Beneš-Vermutung

24. Surreale Produktlänge

25. Kombinatorische Deckungsprojekte

26. Ein Nullpunkt in einer linearen Abbildung

27. Breite Partitionsvermutung

28. Diagonale Ramsey-Zahlen

29. Die additive Basisvermutung

30. Sind alle Fermat-Zahlen quadratisch frei?

^[1] Abschluss und Master in Mathematik.

Eingereicht: April 2019.

Genehmigt: Mai 2019.