Demonstração da conjectura do número ímpar imperfeito

ARTIGO ORIGINAL

SANTOS, Adecio da Silva ^[1]

SANTOS, Adecio da Silva. Demonstração da conjectura do número ímpar imperfeito. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 05, Vol. 07, pp. 176-185. Maio de 2019. ISSN: 2448-0959.

RESUMO

Escolhemos, dentre cerca de 48 problemas (Conjecturas) em aberto da matemática na área de Teoria dos Números, a Conjectura dos Números Ímpares Perfeitos para ser provada neste artigo. O método que utilizamos para a prova foi o de demonstração por redução ao absurdo. E modificamos, propositadamente, o nome do problema para Conjectura do Número Ímpar Imperfeito, pois achamos mais coerente com a solução encontrada. Além disto deixamos no ANEXO A uma listas de vários problemas em aberto de matemática.

Palavras–chave: Conjectura, Demostração, Ímpar Perfeito.

1. INTRODUÇÃO

A geração do século XXI está repleta de inovações tecnológicas, as quais nos possibilita conhecer praticamente o globo inteiro, além de nos comunicarmos “instantaneamente” de qualquer lugar do planeta.

A matemática teve uma participação muito importante na construção como um todo de nossa sociedade atual. A sua exatidão e rigorosidade dos seus resultados não deixa qualquer margem de erro. Porém caso deixe ainda assim é proposital.

Uma ciência como esta tão rica e soberana possui uma particularidade, ela não permite que o ego ou a arrogância tenham muito espaço na mente de seus estudiosos, pois por mais que ela possa ser respeitada, até mesmo admirada, em nossos tempos atuais ainda existem problemas de matemática que ninguém nunca na história conseguiu prova-los ainda.

Aproximadamente 417 problemas estão sem solução nos mais variados campos da matemática. O leitor interessado em conhece-los pode verificar a referência (1). Mas ressaltamos que alguns deles nunca possam ser demonstrados, embora sejam verdadeiros, isto é garantido pelos Teoremas da Incompletude de Gödel.

Nosso artigo expõe a prova de um destes problemas em aberto da matemática, a saber a Conjectura dos Números Ímpares Perfeitos, mas o rebatizamos de Conjectura do Número Ímpar Imperfeito pois achamos mais coerente essa frase com nosso resultado.

Usamos para tanto o método de demonstração por redução ao absurdo, a propriedade da tricotomia e um resultado no texto que chamamos de propriedade: (P), além de algumas manipulações algébricas.

Ao final deixamos, no ANEXO A, uma lista bem eclética de várias conjecturas matemáticas.

2. REFERENCIAL TEÓRICO

Neste parte damos crédito as referências que contribuíram significativamente para a elaboração de nosso artigo.

As quais foram a referência (2), pois esta nos forneceu a base do raciocínio lógico matemático para podermos encontrar o resultado final do trabalho sustentado por argumentações logicamente coerentes. Esta referência também nos fez andar do início ao final da demonstração através dos princípios da Não Contradição e do Terceiro Excluído que foram nossas duas “pernas” até chegarmos em nosso resultado.

Também foi importante a referência (3) pois esta forneceu uma maturidade através de seus exercícios para podermos ter um caminho de como atacar o problema em análise neste artigo pelo método de demonstração por redução ao absurdo.

Por fim deixamos as referências (4), (5) e a lista de problemas do ANEXO A para o leitor interessado em saber mais sobre a Conjectura dos Números Ímpares Perfeitos, além de outras conjecturas de Teoria dos Números e mais problemas dos variados campos da matemática.

3. CONJECTURA DO NÚMERO ÍMPAR IMPERFEITO

A área de estudos da matemática conhecida como Teoria dos Números possuí cerca de 48 problemas em aberto. Dentre estes encontra-se o que chamaremos de Conjectura do Número Ímpar Imperfeito. Porém, este problema é mais conhecido como Conjectura dos Números Ímpares Perfeitos. E a mesma afirma que não existe um número ímpar perfeito. Todavia modificamos o nome da conjectura propositadamente, pois achamos mais coerente com nosso resultado.

Segundo o portal www.matematica.br: “Um número se diz perfeito se é igual à soma de seus divisores próprios. Divisores próprios de um número positivo N são todos os divisores inteiros positivos de N exceto o próprio N.” (6)

Até hoje só se conhece números perfeitos pares. Os matemáticos que mais estudaram esse tema foram Euclides, Euler e Descartes. Além disso já se sabe, também, uma fórmula para todos os números pares perfeitos. A mesmo foi estudada primeiro por Euclides e posteriormente foi concluída por Euler.

Explicações resumidas sobre o comentado acima são encontradas em vários trabalhos acadêmicos. Mas de acordo com Jeane Barbosa Ferreira e Marcos Ferreira de Melo:

Euclides argumenta que se “q” é um número primo tal 2_q-1 que também é primo, então a fórmula n = 2^q-1(2^q-1) gera números perfeitos pares. Muito tempo depois, Euler (1707-1783) provou que todo número perfeito par é obtido pela receita acima, estabelecendo assim a recíproca do teorema de Euclides. Vale apena observar que os números primos da forma 2^q-1 são conhecidos como primos de Mersenne. (7)

Por isso a razão da existência da Conjectura dos Números Ímpares Perfeitos. Visto que a análise dos números pares perfeitos está bem avançada. O primeiro matemática que mencionou a conjectura dos Números Ímpares Perfeitos foi Descartes. E até este artigo, ninguém ainda havia provado ou refutado a afirmação.

Nosso artigo expõe uma prova da Conjectura dos Números Ímpares Perfeitos, e para tanto utilizamos a definição de número perfeito, um resultado mostrado no texto que chamamos de propriedade (P), a propriedade da tricotomia e algumas manipulações algébrica. Tudo isto em uma construção lógica baseada na técnica de demonstração por redução ao absurdo.

Deixamos a baixo o enunciado da conjectura e sua demonstração.

No mais, caso tenha algum erro na prova, gostaríamos que os leitores aprofundassem seus estudos em prol de mostrar e consertar lo. Toda contribuição é bem vinda.

Conjectura do Número Impar Imperfeito: Não existe um número ímpar perfeito.

DEMONSTRAÇÃO: Primeiro provemos que todo número natural perfeito, N, possui a propriedade (P):1+d₁+d₂+d₃+…+d_n-1, onde 1< d₁< d₂< d₃< …<d_n-1<d_n são todos os divisores próprios de N.

De fato, note que N= 1+d₁+d₂+d₃+…+d_n-1+d_n, pois N é um número perfeito. Suponhamos, agora, por absurdo, que 1+d₁+d₂+d₃+…+d_{n-1 <} d_n e adicionando, em ambos os membros da desigualdade anterior, o termo d_n encontramos a expressão seguinte 1+d₁+d₂+d₃+…+d_n-1+(d_n)<d_n+(d_n)⇒1+d₁+d₂+d₃+…+d_n-1+(d_n)<2d_n. Daí temos que d_n<1+d₁+d₂+d₃+…+d_n-1+(d_n)<2d_n⇒d_n<N<2d_n⇒1<<2. Porém, como d_n divide N encontramos o natural  entre 1 e 2. O que é um ABSURDO!

Por outro lado, vamos supor por absurdo, mas só que dessa vez que a desigualdade seja d_n<1+d₁+d₂+d₃+…+d_n-1. Agora, adicionando, em ambos os membros da desigualdade anterior, o termo d_n encontramos d_n+(d_n)<1+d₁+d₂+d₃+…+d_n-1+d_n o que implica em 2d_n<1+d₁+d₂+d_n+…+d_n-1+(d_n), ou seja,2d_n<N (I) . Observe, ainda, que ≤d_n⇒N≤d₁.d_n (II), pois d_n é o maior divisor de N. Então de (I) e (II) fica 2d_n<N≤d₁.d_n, dividindo todos os membros da última desigualdade por dn temos 2<≤d₁ (III), mas como d₁ é o menor divisor de N diferente de 1 e é um divisor de N a desigualdade (III) nos fornece que =d₁⇒N=d₁.d_n e que  2<d₁, portanto isto acarreta que todos os divisores de são ímpares, pois caso existisse algum divisor de sendo par então 2=d₁, o que é um absurdo em nossa suposição. A partir daqui temos 4 (quatro) situações para analisarmos:

1ª situação: d₁ divide d_i ∀i= 1,2,3,4,…,n, pois d₁ é o menor divisor de N. E isto implica que d_i=d₁ⁱ ∀=1,2,3,4,…,n, pois caso existisse algum d_i que não fosse potência de d₁ então isto geraria um novo divisor de N diferente de d_i ∀=1,2,3,4,…,n, o que é um absurdo. Então esta situação acarreta que 1+d₁²+d₁³+d₁⁴+…+d₁ⁿ=N=d_{1 .} d_n=d₁.d₁ⁿ=d₁ⁿ⁺¹, mas pela fórmula da soma de uma P.G finita temos 1+d₁²+d₁³+d₁⁴+…+d₁ⁿ=1+d₁²., ou seja,1+d₁².=d₁ⁿ⁺¹⇒1+= d₁ⁿ⁺¹⇒= d₁ⁿ⁺¹⇒ d₁-1+d₁ⁿ⁺¹–d₁² = (d₁-1).d₁ⁿ⁺¹=d₁ⁿ⁺²–d₁ⁿ⁺¹ ⇒d₁-1+d₁ⁿ⁺¹–d₁²=d₁ⁿ⁺² – d₁ⁿ⁺¹, dai temos que d₁+2d₁ⁿ⁺¹ – d₁² –d₁ⁿ⁺² =1⇒d₁(1+2d₁ⁿ–d₁–d₁ⁿ⁺¹)=1⇒d₁ divide 1, absurdo!

2ª situação: d₁ divide alguns d_j e outros não para j=1, 2, 3, 4,…,n. Então temos que N=1+(d₁+d_j1+d_j2+…+d_jk) + (d_i1 +…+d_im ), onde d₁ ,d_j1 ,d_j2 ,…,djk são os números divisíveis por d₁ e d_i1 ,…,d_im não são. E os números 1,d₁ ,d_j1 ,d_j2 ,…,d_jk ,d_i1 ,…,d_im são todos os divisores próprios de N.

Digamos que a maior potência de d₁ que divide N seja d₁ⁿ . Então, podemos reescrever todos os divisores próprios de como:

1, (d₁, d₁², …, d₁ⁿ), (d₁d_i1, d₁d_i2, …, d₁d_im), (d₁²d_i1, d₁²d_i2, …, d₁²d_im), …, (d₁ⁿd_i1, d₁ⁿd_i2, …. d₁ⁿd_im), (d_i1,d_i2, …, d_im).

Portanto, com essa nova escrita, temos que a somando dos divisores próprios de N fica:

N=1+(d₁+d₁²+…+d₁ⁿ) + (d₁d_i1+…+d₁d_im) +(d₁²d_i1+…+d₁²d_im)+ … …+(d₁ⁿd_i1+…+d₁ⁿd_im) + (d_i1+d_i2+…+d_im)

= 1+(d₁+d₁²+…+d₁ⁿ)+(d₁+d₁²+…+d₁ⁿ)d_i1+…+(d₁+d₁²+…+d₁ⁿ)d_im++(d_i1+d_i2+…+d_im)

=1+(d₁+d₁²+…+d₁ⁿ) + (d₁+d₁²+…+d₁ⁿ)(d_i1+…+d_im)+(d_i1+…+d_im)

=1+(d₁+d₁²+…+d₁ⁿ) +(d₁+d₁²+…+d₁ⁿ+1) . (d_i1+…+d_im)

=(1+d₁+d₁²+…+ d₁ⁿ) . (1+d_i1+…+d_im)

Mas N=d₁.d_n=(1+d₁+d₁^{2+…+d₁n) . (1+d_i1+…+d_im), e isto implica que}

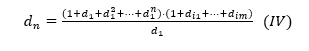
Por outro lado, d_n=d₁^{n .} d_im^* (V) , onde d_im^* é o maior número dentre os d_i1, …, d_im.

Finalmente, por (IV) e (V) temos:mas isto nos fornece que N=(1+d₁+d₁²+…+d₁ⁿ) . (1+d_i1+…+d_im) = d₁ⁿ⁺¹ . d_im^* ,ou seja, , d₁ⁿ⁺¹, seria um divisor próprio de N que não estaria em nossa lista de divisores próprios de N. O que é um, ABSURDO!

3ª situação: d₁ não divide nenhum d_j, mas possui fatores primos em comum com alguns d_j para j=2, 3, 4,…, n. Isto implica que estes fatores primos em comum dividem N e seriam menores que d₁ que é o menor divisor de N, absurdo!

4ª situação: d₁ não divide nenhum d_j, além disso, d₁ e d_j não possuem fatores primos em comum para todo j=2, 3, 4, …, n.

Então, como N=d₁ . d_n, temos que d₂, d₃, d₄, …, d_n-1 dividem d_n, pois os mesmos não dividem d₁ pelo fato de ser d₁ o menor divisor de N. Agora, note que ≠ d₁ ∀i= 1,3,4,5…,n , pois se = d_i para algum d_i, isto implicaria que d_n=d₂ . d_i⇒ N=d₁ . d₂ . d_i, mas como d₁ não possui fatores primos em comum com nenhum d_i somos obrigados a aceitar d₁ . d₂ e d₁ . d_i como novos divisores de N, absurdo! Pois todos os divisores de N já foram listados, e os mesmos pela nossa 4ª situação não são divisíveis por d₁. Ou seja, é mesmo diferente de todo d_i, mas isto, também, geraria outro número que não está na lista de todos os divisores de N, outro absurdo!

Logo, pela tricotomia, só nos resta a escolha 1+d₁+d₂+d₃+…+d_n-1=d_n.

Finalmente, suponhamos, por absurdo, que exista um número impar perfeito, digamos 2k+1. Agora, denotemos 1<I₁<I₂<I₃<…<I_2n sendo todos os divisores próprios de 2k+1. Observe que I₁,I₂,I₃,…,I_2n são números ímpares e em uma quantidade par de números, pois a soma de uma quantidade par de números ímpares é par e mais 1 resulta em um ímpar.

Mas pela propriedade (P), a qual provamos que é válida para todo número perfeito, temos que 1+I₁+I₂+I₃+…+I_2n-1=I_2n. Ora, note isto 1+I₁+I₂+I₃+…+I_2n-1 é par, pois é a soma de uma quantidade par de números ímpares (consideramos o 1 sendo ímpar) e I_2n é impar. Ou seja, encontramos um número natural que é par e ímpar simultaneamente, ABSURDO!

Portanto, não existe nenhum número natural ímpar perfeito.

4. CONSIDERAÇÕES FINAIS

Nosso artigo expõe uma demonstração da Conjectura dos Números Ímpares Perfeitos, porém a rebatizamos de Conjectura do Ímpar Imperfeito devido está mais coerente com nosso resultado. Mas a matemática possui além deste muitos outros problemas em aberto. E o principal objetivo de nosso trabalho é encorajar os leitores a também tentarem resolver mais problemas em aberto da área. Alcançando com isto o aumento dos pesquisadores nos mais variados campos da matemática em nosso país.

No mais esperamos sugestões para a melhoria de nosso artigo, criticas construtivas, também. E que nosso artigo propicie continuação para muitos outros trabalhos acadêmicos.

5.  REFERÊNCIAS

1. Portal do openproblemgarden. Disponível em: http://www.openproblemgarden.org/op/odd

_perfect_number. Acesso em 22 de abril de 2019.

2. ALENCAR FILHO, Edgard de. Iniciação à Lógica Matemática. 18 Ed. São Paulo: Nobel, 1975.

3. LIMA, Elon Lages Análise Real. vol. 1 Coleção Matemática Universitária, SBM,. Rio de Janeiro, 2001.

4. Canal A Matemaníaca por Julia Jaccoud. Disponível em: https://www.youtube.com/watch?v=

CHZBYfAmkcE. Acesso em 21 de abril de 2019.

5. Portal do Impa. Disponível em https://impa.br/noticias/problemas-do-milenio-da-geometria-a-fisica-quantica/. Acesso em 21 de abril de 2019.

6. Portal da matematica. Disponível em:http: //www.matematica.br/historia/nperfeitos.html. Acesso em 21 de abril de 2019.

7. Portal da ufc. Disponível em: http://www.periodicos.ufc.br/eu/article/view/15284/15570 Acesso em 22 de abril de 2019.

ANEXO A

LISTA DE CONJECTURAS MATEMÁTICAS

1. P versus NP

2. Conjectura de Hodge

3. Hipótese de Riemann

4. Existência de Yang-Mills e intervalo de massa

5. Existência e suavidade de Navier-Stokes

6. Conjectura de Birch e Swinnerton-Dyer

7. Conjectura de Beal

8. Conjectura de Fermat-Catalan

9. Conjectura (forte) de Goldbach

10. Conjectura de Collatz

11. Conjectura de Erdös

12. Conjectura do Número de Quadrados Mágicos

13. Conjectura de Andrica

14. Conjectura dos primos gêmeos

15. Conjectura de Legendre

16. Problema do final feliz

17. Problema do círculo de Gauss

18. Problema inverso de Galois

19. Conjectura de Littlewood

20. Progressões aritméticas longas do arco-íris

21. Progressões Aritméticas Monotônicas de 4 Terminações

22. A conjectura do double cap

23. Conjectura de Beneš

24. Comprimento do produto surreal

25. Projetos de cobertura combinatória

26. Um ponto zero em um mapeamento linear

27. Conjectura ampla da partição

28. Números de Ramsey na diagonal

29. A conjectura da base aditiva

30. Todos os números da Fermat são livres de quadrados?

^[1]Graduado e mestre em matemática.

Enviado: Abril, 2019.

Aprovado: Maio, 2019.