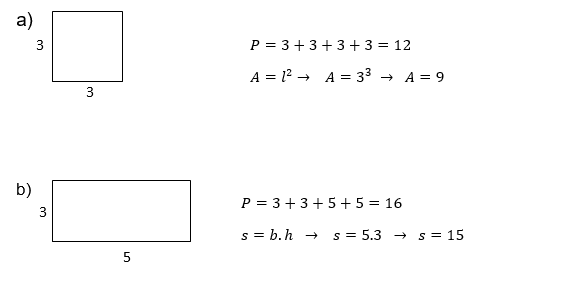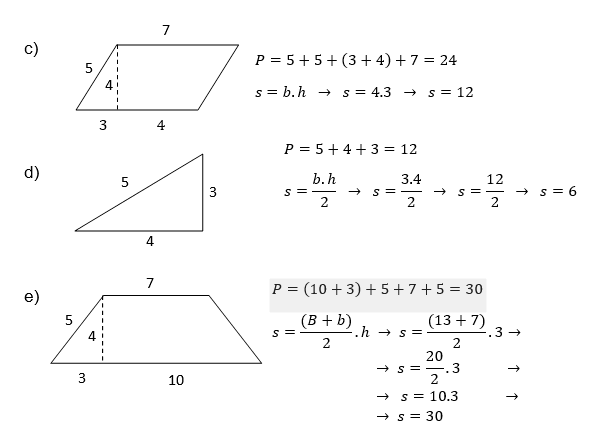FREIRE, Amanda Freitas [1], RODRIGUES, Fabiana Soares [2], AQUINO, Maria Rosane Souza [3], SOARES, Maria Vanessa [4], GOIS, David Denis Pires de [5], VIANA, José Damião [6]
FREIRE, Amanda Freitas; et.al. El uso del Geoplano en la enseñanza de la geometría: cálculo de área y perímetro. Revista científica multidisciplinaria base de conocimiento. año 03, Ed. 06, vol. 03, págs. 119-135, junio de 2018. ISSN:2448-0959
Resumen
Esta investigación lleva como tema central la enseñanza de cálculo de área y perímetro de figuras en la geometría del plano, utilizando como recurso el Geoplano. Se defiende, en este artículo, la idea de que mediante el uso de materiales manipulables es posible facilitar el contenido de enseñanza y aprendizaje, del mismo modo desarrollar el razonamiento y el interés de los estudiantes en la solución de problemas. En este artículo se presentará con un campo de carácter cualitativo, que se produjo en la serie final de la escuela primaria, en el octavo grado de la escuela "C" estado periodista Edson Régis, en el barrio de São Cristóvão en la ciudad de Arcoverde-PE, un Taller realizado por el programa institucional de iniciación a la docencia (PIBID). Durante el taller se observó una participación efectiva en clase y también una mejora en el rendimiento de los estudiantes.
Palabras clave: enseñanza de las matemáticas, geometría plana, Geoplano.
Introducción
Hoy en día, vivimos en una especie de esto cada vez más centrado en los avances tecnológicos, y la reunión es necesaria para las distintas acciones humanas desde simples a cosas complejas. El conocimiento matemático es de suma importancia para el individuo se relaciona con la sociedad y el medio ambiente en que vive. Este conocimiento hoy en día no presentan en la vida cotidiana de muchos estudiantes, por las dificultades para establecer relaciones de lo aprendido con situaciones del día a día. BNCC (Base de currículo común nacional) informa sobre este respecto que los estudiantes tienen que establecer los conocimientos adquiridos con hechos cotidianos y describe lo siguiente:
Es importante destacar que esta asociación entre el mundo físico que nos rodea y el mundo desconocido de las matemáticas puede estar relacionada con un doble. Por ejemplo, mientras que un rectángulo paralelepípedo actúa como un modelo abstracto para la caja de zapatos de objeto físico, el modelo abstracto de la esfera de la figura geométrica espacial, podemos asociar el objeto de fútbol del mundo físico (Brasil, 2015) .
El objetivo de esta investigación es destacar la importancia del uso de recursos en el aprendizaje de las matemáticas para el aprendizaje y la enseñanza de la geometría plana, específicamente el cálculo de área y perímetro. Así que en el mundo físico o inmaterial matemáticas está presente en todo lo que nos rodea, por lo que es importante su conocimiento. En el aula la complejidad matemática asociada con el día a día, se hace más presente, una vez que las cuestiones y preguntas presentadas no están representados de una manera en la que el estudiante puede tocar y posar con algo físico. Estos temas se presentan de una manera sólo imaginaria. Así que cuando hay alguna característica que permite que el profesor puede exponer en su forma física para el estancamiento y las cuestiones planteadas, el docente se convierte en más atractivo y fácil de entender para el estudiante.
Salir de estas dificultades surgen algunas preguntas: ¿Cómo hacer más atractiva a los estudiantes educación matemática? ¿El uso del Geoplano como herramienta de enseñanza facilitaría el aprendizaje de los estudiantes? ¿Como educadores podemos hacer la enseñanza y aprendizaje más versátil? Es crucial que los profesores hacen uso de los conocimientos que el alumno ya posee y dejando ese punto puede hacer que las conexiones con las matemáticas. Nada es más útil utilizar las instrucciones aprendidas en problemas que surgen en la sociedad. Con esto hemos desarrollado esta investigación mediante el programa institucional de iniciación a la enseñanza[7] (PIBID) del municipio de la Superior Educación de Arcoverde (EFSA), con el fin de introducir al alumno a un hecho a mano con recursos didácticos de matemáticas. Sugerimos el Geoplano como una herramienta para la enseñanza y el aprendizaje del cálculo de área y perímetro de figuras planas, para los alumnos de la serie final de la escuela primaria II, específicamente el año 8 periodista Edson Régis ubicado en Arcoverde-PE y. Ya que con esta función podemos explorar conceptos básicos de geometría plana o geometría no-euclidiana tales como: punto, línea y plano.
Las primeras geométricas ideas que se originó con la capacidad humana de buscar alternativas para resolver problemas prácticos:
Buscando el origen del desarrollo de la geometría en los primeros días, con el hombre primitivo, podemos imaginar que las configuraciones de espacio de conocimiento, formas y tamaños han originado, posiblemente con la capacidad humana para observar y reflexionar sobre la desplazamientos, con la construcción de estrategias de caza y alimentos de los cultivos, con la creación de herramientas y utensilios, con el fin de satisfacer sus necesidades básicas. Para garantizar la vivienda, con la división del trabajo, fueron surgiendo otras necesidades y la producción de ampliación de conocimientos geométricos. La necesidad de construcción, delimitar la tierra condujo a la noción de figuras y curvas y posiciones como vertical, perpendicular, paralelo (GH, 2008, p. 7).
Metodología
Se trata de una investigación con enfoque cualitativo, que se utilizó una técnica de investigación de campo. Como un instrumento de recolección de datos fueron utilizados cuestionarios, entrevistas y observación.
En busca de respuestas a las preguntas presentadas en la introducción, llevamos a cabo diversas actividades tales como entrevistas con profesores y estudiantes y un taller utilizando el Geoplano. En primer lugar, fue entrevistado profesor del regente del octavo grado "C" y pronto después de la serie que precede, un cuestionario fue elaborado que contiene cinco preguntas: ¿Sabe usted el Geoplano? ¿Utilizar algún tipo de recurso para la enseñanza de la geometría? ¿Cuáles son las dificultades encontradas durante estas clases? ¿Durante la clase, ha presentado las principales figuras geométricas planas? Cómo enseñan el cálculo de áreas y perímetros.
Con respecto a los estudiantes, se aplicó un cuestionario a treinta estudiantes con cinco preguntas, algunas de ellas son: ¿Sabe usted el Geoplano? ¿Clase de geometría el profesor utiliza a algún tipo de material utilizable? ¿Sabes qué es perímetro? ¿Y el área? ¿Sabes cómo calcular el perímetro y el área de estas figuras?
Para analizar las respuestas, uno se da cuenta de la gran dificultad en el contenido, el período de gracia para cumplir con el Geoplano y algunas figuras planas. Basado en las respuestas que se llevó a cabo un taller utilizando el Geoplano, abordar el cálculo de área y perímetro.
¿Después del taller, entrevista con los estudiantes para evaluar el desempeño, que contiene tres preguntas: el Geoplano podría ser utilizado en geometría? ¿Esta característica facilita el cálculo de área y perímetro? ¿Hubo dificultad en el manejo del Geoplano?
Este estudio pretende encontrar respuestas a las preguntas establecen y verificar la importancia del Geoplano como facilitador del proceso enseñanza-aprendizaje de cálculo de área y perímetro.
Enseñanza de las matemáticas
Futuros docentes en matemáticas se enfrentan a situaciones de preocupación en el proceso de enseñanza-aprendizaje. En el aula el maestro debe enseñar una gran cantidad de contenido en un corto plazo, debe transmitir este conocimiento que tomó cientos de años en unas pocas horas de clase, siendo estos pasan la mayor parte del tiempo de manera abrupto y difícil de abstraer y causar obstrucciones en la comprensión de los estudiantes.
Olvidar que también ese objetivo del proceso educativo es que los estudiantes tengan la mayor utilización posible, pero esta meta está lejos de ser alcanzado, porque muchos maestros se preocupan más con la cantidad de contenido que esto aplique la cantidad el conocimiento es receptivo por el estudiante.
La construcción del conocimiento matemático depende mucho de la manera en que se tratan, los conceptos deben ser transferidos de una manera más cercana a la realidad física, trayendo ejemplos de la vida cotidiana y también utilizando los conocimientos adquiridos por los estudiantes fuera de el campo de la escuela. Los profesores sería la responsabilidad de su clase de planificar con antelación, basado en las necesidades y dificultades de su alumno, en el cual su objetivo es suministrar la falta de sus estudiantes.
Junior Saint (2011), establece que:
La educación matemática debe concebirse como un proceso más amplio de la construcción, en los que es necesario tener un plan para abordar los problemas que presentan, y es posible alcanzar los objetivos propuestos de una manera mecánica.
Matemáticas en las noticias
Es conocido que las matemáticas surgieron desde el momento en que el hombre necesitaba contar. Desde ese momento el hombre fue la creación de estrategias de contar poder crear los primeros símbolos matemáticos con el paso del tiempo, las cantidades fueron representadas por las expresiones, gestos, palabras y símbolos, cada uno de que la gente tenía su forma representación.
Matemáticas a lo largo de la historia ha estado sufriendo varias evoluciones para llegar a lo que hoy conocemos. Actualmente esta disciplina juega un papel esencial en la vida del hombre, es su uso y el conocimiento en esta área ofrece al individuo la oportunidad de construir un futuro mucho mejor. La falta de este conocimiento restringe los seres humanos para resolver problemas de la vida cotidiana, para entrar en el mercado laboral y adquirir nuevos conocimientos en diversas áreas que utiliza las matemáticas como disciplina es indispensable.
Este contexto nos permite analizar esta disciplina en muchos aspectos, trayendo al aula, examinaremos las dificultades de aprendizaje encontradas por los estudiantes.
Dentro de este campo hay diferentes contenidos en los que se encuentran varios problemas de aprendizaje, una de las disciplinas de las matemáticas en el que hay grandes dificultades es la geometría.
Geometría plana o geometría no-euclidiana
Euclides en su libro "El elemento" dividido en 13 volúmenes, donde 10 que se dedicó a su creación y teoría del número 03, buscaba en tres los geométricos, que son:
- El punto (es que no tiene partes)
- La recta (longitud sin espesor)
- El plan (es el que tiene longitud y anchura)
Éstas se toman sin definición porque son palabras primitivas.

En el contexto de la geometría plana se estudian los polígonos y figuras planas, como el rectángulo, cuadrado, paralelogramo, triángulo, trapecio, entre otros.
Polígono es un plan limitado de segmentos rectos, saliendo de él, podemos encontrar dos tipos: regular, con lados y ángulos congruentes e irregulares, con lados y ángulos congruentes, en este estudio podemos encontrar conceptos primitivos de la geometría plana, que es calcular área y perímetro, calcular el perímetro de figuras planas se hace por la suma de sus partes. Sabemos que un cuadrado tiene cuatro lados mide ?, pronto tenemos la siguiente expresión:, donde es el perímetro y ? es el lado de la Plaza, es decir, el perímetro es el contorno de una superficie dada, ya sea regular o no.
El área de un polígono es ya un poco más complicado, porque no será el contorno de la figura, pero el número que ocupa en el plan, el área se da generalmente por la letra puede ser determinado con una expresión que va según la figura que representa , vamos a ver algunas fotos y cómo calcular sus respectivas áreas y perímetros.
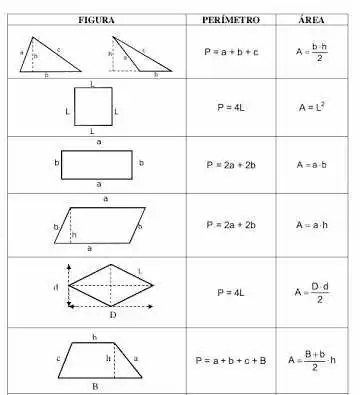
Ejemplos:
Calcular áreas de figuras a continuación:
A partir de este punto que podemos ver que la realidad del estudiante está llena de figuras geométricas planas, entonces ese estudiante encontrará problemas de diversas complejidades, por lo que el conocimiento geométrico es importante a la formación intelectual el estudiante porque le proporcionará conocimientos y habilidades que te ayudarán conseguirán situados y resolver ciertos problemas en el entorno en el cual se inserta.
Según el currículo nacional parámetros – PCN (Brasil, 1998), los conceptos geométricos son una parte importante del currículo de matemáticas en la secundaria, porque a través de esta el estudiante desarrolla un tipo especial de pensamiento que le permite comprender y representar el mundo en que vive. Si esto funcionó desde el mundo físico, permite a los estudiantes a hacer conexiones entre las matemáticas y otras áreas del conocimiento.
Es comprensible que según la PNC el aprendizaje de la geometría es de suma importancia en todos los niveles de educación. Sin embargo los profesores por varias razones no se preocupan por la enseñanza de la geometría y tan poco en las características de búsqueda que facilitan la enseñanza-aprendizaje y para hacer ese aprendizaje más dinámico, sin desviarse del contexto. Observar que algunos autores para desarrollar los libros de texto puesto que el contenido en los últimos capítulos, haciendo cumplimiento de tiempos por los educadores.
GEOPLANO
El nombre viene del conjunto Geo, Geoplano significado geometría y plan, que significa superficie plana por lo tanto, Geoplano. Palabra es que primero fue utilizado en 1961, por el profesor Caleb Gattegno, del Instituto de la educación, Universidad de Londres (KNIJNIK, BASSO; KLÜSENER, 1996; Menezes, 2008).

El Geoplano es que un pedazo de madera de superficie plana con clavos roscados la misma distancia uno del otro. Hay algunos tipos de Geoplano: cuadrado, Circular, el Trelissado y la Oficina Oval. La Plaza es el más ampliamente utilizado, Plaza madera superficie dividida compuesto tan a cuadros por clavos equidistantes. Es una confección simple, que ayuda a los estudiantes a superar sus dificultades y al mismo tiempo aprender a manipularlo, también puede ser utilizado como un juego matemático que facilita la comprensión del estudiante en la relación lúdica. Esta característica permite a los estudiantes a adquirir nuevas experiencias y también hace posible su forma física, dejando el modo tan abstracto, imaginario a través de la construcción de figuras y tiene un truco adicional basado en conteo de pines de izquierda a derecho, filas y columnas, dentro y fuera de la obra que más dinámica, porque a diferencia de otros juegos el Geoplano tiene flexibilidad, así que los estudiantes pueden hacer y deshacer en cualquier momento con tu profesor.
Según Sharma (2009, p. 8) señala que:
En el juego, arriesgar, probar, probar, inventar, todos libres del fantasma de una evaluación punitiva y la castración. El profesor que utiliza el juego tiene la función de organizar y sistematizar estas actividades para permitir a los estudiantes a caminar en busca de nuevos conocimientos (…).
Sin embargo, se da cuenta que con la introducción del Geoplano, puede promover la enseñanza de la geometría plana una manera diferente de acercarse y representan diversos contenidos del acondicionamiento físico, tales como: cálculo de área y perímetro de polígonos.
Investigación de campo
Después de la identificación del Geoplano como recurso útil y capaz de promover un aprendizaje significativo, tres cuestionarios, dos eran para la recogida de datos y otro para la recogida de resultados.
Según el cuestionario que el profesor respondió que nunca se utiliza cualquier recurso didáctico manipulados y desconoce el Geoplano. La serie anterior en su informe afirma que el uso de otros materiales manipulables, como el Geoplano. Éstos trajeron polémica porque según la entrevista con los estudiantes, afirmaban no conocer el material.
El contenido trabajado, eran cálculos de áreas y perímetros de figuras planas, antes de aplicar el taller tenemos también una entrevista con la clase, hemos detectado una gran dificultad para que puedan reconocer el Geoplano, pocos polígonos, calcular áreas y perímetros, como se muestra en los siguientes resultados.
¿1) conoce el GEOPLANO?
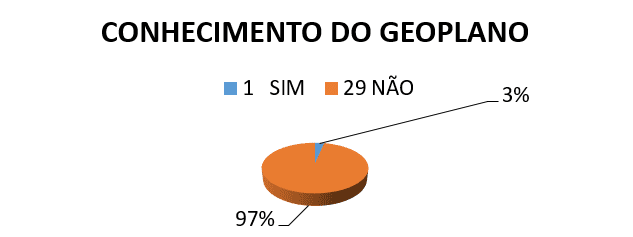
¿GEOMETRÍA 2 º) las clases al profesor tiene ya utilizan algunos tipo de MATERIAL utilizable?
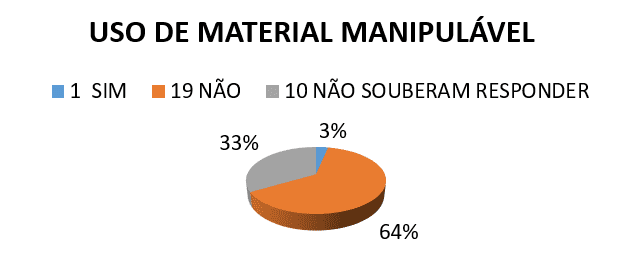
¿3) sabes qué es perímetro o área?

4) que cifras por debajo de ¿sabes?
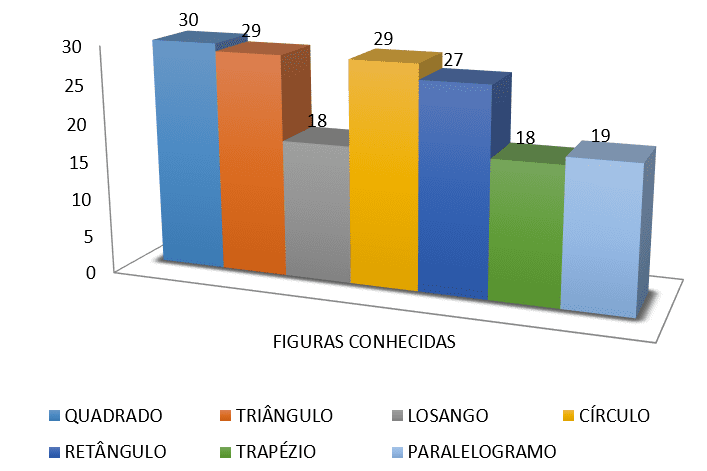
¿5) sabes calcular el perímetro o el área de algunas de estas figuras?

Mediante el análisis de los datos obtenidos, se realizó la necesidad de realizar un taller, en el que se presentó el Geoplano como recurso para la enseñanza y el aprendizaje. A través de este taller buscamos Mostrar tan versátil como el manejo de esta característica.
Dividido en cinco grupos de seis alumnos, cada grupo recibió dos Geoplanos, un cuadrado, un círculo y una cierta cantidad de elástico. En un primer momento después de ser entregados a los estudiantes de Geoplanos, que han tenido durante un tiempo la libertad de manejar y construir figuras según la imaginación de cada uno.
Con el uso de diapositivas, hubo un acercamiento que muestra los principales polígonos regulares. Poco después, desafió a los estudiantes para realizar cálculos de perímetros y áreas de varios polígonos, usando el Geoplano y la malla a cuadros. Este desafío trajo un movimiento participativo por parte de los estudiantes, en el caso de algo diferente de su vida cotidiana. El Geoplano cuando usa encantos, despierta interés y que versatilidad a la clase.
Smole, Diniz y Cándido destacan:
Una de las grandes ventajas de la Geoplano es, a diferencia de la hoja de papel, tiene movilidad, es "dinámico", y la flexibilidad con que puede hacer y deshacer la construcción permite que el niño se acostumbra a ver figuras en diversas posiciones, note si un dado una oportunidad para la solución de un problema es conveniente y corregirlo de inmediato si es necesario. (2003, p. 112).
Durante el taller a través de comentarios, se observó que había una mejora en el rendimiento de los estudiantes al realizar los cálculos propuestos, también una participación efectiva en la clase.



Como evaluación de aprendizaje, hubo la necesidad de realizar otro cuestionario con los alumnos para la confirmación de los resultados obtenidos como se muestra en los gráficos.
¿1 º) el GEOPLANO podría ser utilizado en geometría?

¿2 º) esta característica facilita calcular área y perímetro?

¿3) tasa de su desempeño en el manejo del GEOPLANO?
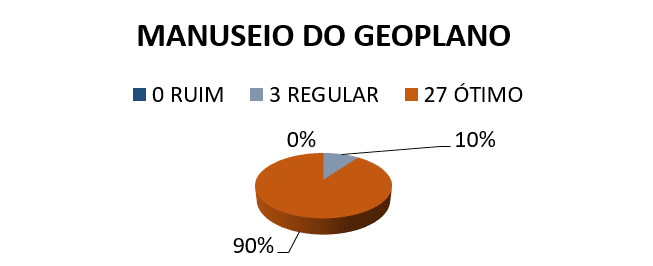
Según los resultados obtenidos a través de la encuesta realizada con los estudiantes después del taller, se observó que había un acuerdo eficaz por parte de los estudiantes de algunos resultados. La primera y la segunda carta muestra que 100% de los estudiantes de acuerdo con el uso del Geoplano en geometría, puesto que esta característica facilita calcular área y perímetro. Aún analizando los resultados es posible notar que esta característica es fácil de manejar, porque el tercer gráfico presenta una calificación alta en relación con el rendimiento de los estudiantes al manipular el Geoplano, 10% de los estudiantes encuentra su habitual manejo y rendimiento 90% gran.
Por lo tanto el aprendizaje de los estudiantes fue significativo durante la ejecución del taller, el mismo demostró compromiso, curiosidad, entusiasmo y dedicación, resolver los problemas propuestos usando el Geoplano y la malla a cuadros.
Consideraciones finales
Los recursos, cuando bien diseñados, proporcionan a los estudiantes la construcción de conocimiento matemático, para que este trabajo hemos decidido elegir el Geoplano, porque será de un conocimiento previo de esta herramienta para el educador, que puede ofrecer para educar de una forma diferente de ampliar su desarrollo cognitivo, proporcionando situaciones concretas y sistematizadas.
Por lo tanto, esta función se utilizará como un método de enseñanza en que los estudiantes pueden experimentar situaciones de aprendizaje diferentes símbolos de trabajo, resolver problemas que involucran el perímetro y área de polígonos, en los que sean capaces de hacer un análisis real Lo que es experimentado. De tal modo, el Geoplano, elegido para tal encaja perfectamente en estas actividades, porque según el currículo nacional parámetros, los juegos de una manera generalmente son portadores de un aspecto relevante, que es un reto que conduce al alumno, es decir, es un gran forma de animarlo a afrontar nuevas situaciones que pueden poner en práctica sus aprendizajes, perder el miedo a aprender matemáticas.
Según Rego y Rego (2013).
… Mediante experimentos con material concreto, el estudiante desarrolla un gusto por el placer del descubrimiento, a enfrentar retos y superarlos, desarrollo de hábitos y costumbres que pueden conducir más adelante a ser un individuo y actuar.
Se puede concluir que a través de juegos, recursos didácticos y facilitadores de herramientas de enseñanza y aprendizaje es posible que educadores hacen clases de matemáticas más versátil, atractivo para los estudiantes.
Referencias
Brasil. Ministerio de educación. Plan de estudios común: Matemáticas: MEC, 2015, p. 116.
Brasil. Departamento de Fundamental la educación. Plan de estudios nacional: Parámetro de matemáticas. Brasilia: MEC/SEF.1998.
GH, Claudia Maria. Geometría: espacio y forma. Unochapecó: Chapecó; Coordinación de educación a distancia, 2008.
MARKHAM, j. e. (Ed.). Conocimiento, interdisciplinaria y actividades de enseñanza con juegos de matemáticas: una propuesta metodológica. Recife: UFRPE, 2008. (Serie de contexto matemático)
REGO, R. G; REGO. R. M. Matematicativa. 4. Ed. Vista. Londres 2013 (formación del profesorado) p. 25
SANTOS JUNIOR, V. B. D. La movilización de contenidos matemáticos en actividades prácticas en el contexto de juego con Licenciandos de matemáticas. Tesis (Maestría en enseñanza de las Ciencias y matemáticas)-programa de posgrado en Educación de Ciencias y matemáticas, Departamento de educación, Universidad Federal Rural de Pernambuco. Recife, 2011. P. 22-36
SHARMA, Mónica Menezes. La actividad lúdica en el aula de matemáticas: acción y reflexión. Disponible en <http: sbem.com.br/files/ix/enem/minicurso/trabalhos="">.</http:> Consultado el 20 de octubre de 2009.
SMOLE, Kátia Cristina Stocco; DINIZ, Maria Ignez de Souza Vieira; Candido, Patricia Terezinha. Figuras y formas. Porto Alegre: New Haven, 2003. (colección matemática 0 a 6, v. 3).
[1] Graduarse en el curso de grado en matemáticas de la CESA.
[2] Graduarse en el curso de grado en matemáticas de la CESA.
[3] Graduarse en el curso de grado en matemáticas de la CESA.
[4] Graduarse en el curso de grado en matemáticas de la CESA.
[5] Graduarse en el curso de grado en matemáticas de la CESA.
[6] Asesor. Profesor del CESA.
[7] Del PIBID es un programa del Gobierno Federal que quiere fomentar la formación de docentes en nivel superior para la educación básica, contribuyendo a la mejora de la profesión docente. Más acceso a la información:<HTTP: www.capes.gov.br/educacao-basica/capespibid=""></HTTP:>