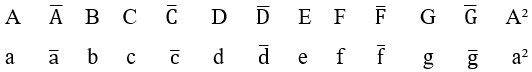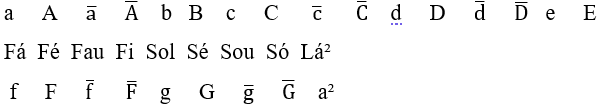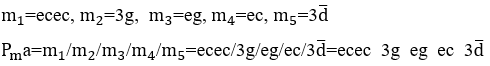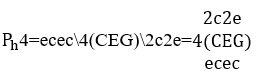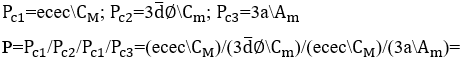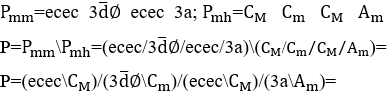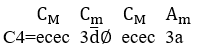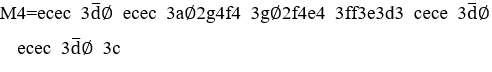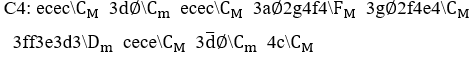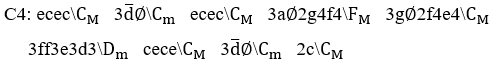La estructura matemática de la música

ARTÍCULO ORIGINAL

VIANA, Arnóbio Araújo ^[1]

VIANA, Arnóbio Araújo. La estructura matemática de la música. Revista Científica Multidisciplinar Núcleo do Conhecimento. Año. 07, ed. 08, vol. 02, pág. 196-220. Agosto 2022. ISSN: 2448-0959, Enlace de acceso: https://www.nucleodoconhecimento.com.br/olimpiada-de-matematica/matematica-de-la-musica, DOi: 10.32749/nucleodoconhecimento.com.br/olimpiada-de-matematica/matematica-de-la-musica

RESUMEN

Teniendo en cuenta que la composición musical es una estructura matemática sonora, este artículo demuestra el desarrollo de la Estructura Matemática de la Música, difundiendo un lenguaje sonoro más comprensible y adaptado a la tecnología actual de los estudios científicos relacionados con la Ciencia de la Música. Por lo tanto, el objetivo de esta investigación fue desarrollar un lenguaje algebraico para estructurar matemáticamente la Música, utilizando únicamente letras, números y símbolos para escribir los sonidos de las notas musicales de forma alfanumérica, representando sus principales características sonoras, tales como: frecuencia (f) , amplitud (a) y tiempo de duración (t), en una sola expresión para identificar una onda de sonido. El lenguaje desarrollado permite una ortografía con lectura sencilla y permite el estudio de los fenómenos musicales en general sobre una plataforma con representaciones gráficas en el sistema de coordenadas cartesianas de las estructuras de los agrupamientos melódicos, con las notas musicales en melodía y los grupos armónicos con las notas. en armonía, promoviendo así la Estructura Matemática de la Música.

Palabras claves: Célula Musical, Melodía, Armonía, Ritmo.

1. INTRODUCCIÓN

Esta investigación fue posible gracias al desarrollo de las operaciones de Armonización o H y su Melodiación inversa o M, establecidas en el artículo “la operación de armonización (H) y su operación de melodía inversa (M)” (VIANA, 2022).

En el citado artículo se define que la Operación H (\), entre ondas sonoras de notas musicales, forman una agrupación armónica, cuya armonía (h) es el efecto sonoro del resultado de una combinación entre ellas  . En este caso, estas ondas están interconectadas simultáneamente en el espacio-tiempo, es decir, sus tiempos iniciales son iguales y sus tiempos finales también son iguales. Estas ondas de notas musicales iguales forman una agrupación armónica de un solo sonido o una armonía al unísono  (VIANA, 2022).

Su operación inversa M (\), se define entre ondas sonoras de notas musicales que forman una agrupación melódica, cuya melodía es el efecto sonoro del resultado del arreglo entre ellas  . En este caso, estas ondas están continuamente interconectadas en el espacio-tiempo, es decir, el tiempo final de una onda es igual al tiempo inicial de la siguiente y así sucesivamente, donde las ondas de notas musicales iguales forman una agrupación melódica de sonidos repetidos . De esta forma, las agrupaciones musicales formadas y organizadas en el espacio-tiempo, constituirán una composición musical, compuesta de melodía, armonía y ritmo (VIANA, 2022).

Por lo tanto, el objetivo de esta investigación fue desarrollar un lenguaje algebraico para estructurar matemáticamente la Música, utilizando únicamente letras, números y símbolos para escribir los sonidos de las notas musicales de forma alfanumérica, representando sus principales características sonoras, tales como: frecuencia (f) , amplitud (a) y tiempo de duración (t), en una sola expresión para identificar una onda de sonido.

2. REPRESENTACIÓN DE UNA NOTA MUSICAL

Para representar algebraicamente el sonido de una nota musical en esta investigación son necesarias tres características fundamentales: la frecuencia del sonido (f); la amplitud (a); y el tiempo de duración (t), formando la expresión  “”, llamado, en este estudio, la Célula Musical.

Se le dio esta nomenclatura porque representa cualquier onda sonora o no sonora, o incluso cualquier atributo que compone la estructura de una canción, siendo la nota musical la célula sonora más importante de la Música, y la pausa musical, la no sonora más importante. celda de sonido a la Música.Música, considerada una nota musical silenciosa o sin sonido, donde la frecuencia de amplitud cero   está representado por un cero negado como tu cifra   en este Lenguaje Algebraico Musical.

2.1 REPRESENTACIÓN DE LA FRECUENCIA MUSICAL

La frecuencia (f), en general, es la característica más importante de cualquier vibración y es provocada por un sismo en cualquier medio, que producirá una serie de frecuencias. Cuando en la Operación H natural entre ellos, se forma una armonía, la cual determina la frecuencia resultante de esta sacudida  . Además, el que tenga el sonido más bajo o la oscilación más baja entre ellos  , es la más importante de todas, llamada Frecuencia Fundamental , siendo la característica responsable del sonido que escuchamos y que nos permite distinguir un sonido grave o de baja frecuencia de un sonido agudo o de alta frecuencia.

Actualmente representada en Música, basada en la obra de Guest (2020, p. 33 a 41), por las primeras siete letras del Alfabeto Latino A, B, C, D, E, F y G, llamados cifrados, que representan respectivamente las notas musicales Lá, Si, Dó, Ré, Mi, Fá y Sol, donde en mayúsculas indicarán las armonías de acompañamientos instrumentales o Acordes Musicales que, en este estudio, también representarán las notas musicales agrupadas en armonía, resultado de la Operación “H” entre ellas  . Las letras minúsculas representarán las notas musicales agrupadas en melodía, resultado de la Operación “M” entre ellas  .

La octava nota musical del abecedario mencionado anteriormente es la repetición de la primera nota , com uma frequência duas vezes mais alta, identificada por um índice numérico dois ao lado superior da sua cifra   y, si este índice se posicionara por debajo  , esta nota se llamaría la octava baja, con su frecuencia a la mitad de la primera nota, lo que significa que sus frecuencias están disminuyendo  .

Por lo tanto, una escala de notas musicales en octava se puede representar entre paréntesis con su índice indicativo arriba   o octava baja con su índice indicativo debajo .

Entre las ocho notas musicales principales , sin embargo, existen otras cinco notas intermedias, actualmente representadas con el símbolo de sostenido    junto con su cifra en una escala creciente en Lá , separados por espacios de frecuencia llamados semitonos .

Sin embargo, en este estudio, la palabra “Sharp” se reemplaza por la letra “u” y tu símbolo   por una barra sobre el cifrado , para proporcionar un nombre monosilábico o monosilábico, que puede ser cantado por cualquier persona en el estudio de solfeo de estas notas musicales. De esta manera, la nota musical Lá agudo    tambien es la nota Lau , Dó agudo    la nota Dou , Ré agudo   la nota Reu , Fá agudo la nota Fau   y Sol agudo la nota Sou .

Sin embargo, también hay doce notas musicales en el medio, entre las trece notas de la escala de semitono creciente en Lá , separados por espacios de frecuencia llamados Microtom , utilizado, normalmente, por músicos del Continente Oriental, quienes, en este estudio, presentan sus nombres con sus cifras, originadas con la primera letra de la nota antes de su posición en la escala ascendente en Lá , unido a una vocal (a, e, i, o, u), excluyendo aquellos que repiten los nombres de notas existentes.

Por ejemplo, la primera nota de microtono “”  entre las notas Lá y Lau , tener tu nombre “Lé”, formado con la letra L de la nota Lá (a), más la vocal “e” de la secuencia “a, (e), i, o, u”, excluyendo la vocal “a” de la nota Lá y tu numero es el mismo que el de la nota Lá (a), pero en mayúscula (A) cuando está en melodía, así como el nombre de la siguiente nota de microtono “”  entre las notas Lau y Si , tener tu nombre “Li”, formado con la letra L de la nota Lau , más la vocal “i” de la secuencia “a, e, (i), o, u”, excluyendo las vocales “a” y “e” de las notas Lá y Lé, su número es el mismo que el de la nota Lau , pero en mayúscula y, el nombre de la duodécima nota musical    entre la nota Sou y Lá octava  , es “Só” , siendo formado por la letra “S” de Sou y “o” de la secuencia de vocales “a, e, i, (o), u”, excluyendo las vocales “a” existente en Sá, “e” existente en Sé, “i” existente en Si, dejando la vocal “o”. Tu número es el mismo que el de la nota Sou , pero en mayúscula  . Así se llamaban microtonos a las notas musicales, por debajo de la escala de semitonos y la escala de microtonos en Lá.

Escala musical de semitonos en Lá

Lá  Lau  Si  Dó  Dou  Ré  Reu  Mi  Fá  Fau  Sol  Sou  Lá2

Escala musical de microtonos en Lá

Lá Lé Lau Li Si Sá Dó Dá Dou Dé Ré Rá Reu Ri Mi Má

2.2 TONO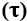, SEMITONO 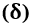Y MICROTONO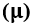

Cualquiera que sea la escala musical, sus notas musicales están separadas en melodía por espacios de intervalos de frecuencia , que puede presentar tres medidas a diferentes frecuencias, denominadas Tono , Semitono e Microtono , siendo el semitono determinado a través de su escala de trece notas musicales , que es una serie de un PG o Progresión Geométrica, (SILVA, s.d.).

En este caso, un PG musical (PGM), donde la decimotercera nota es el doble de la primera . Por lo tanto, se puede aplicar la fórmula del N-ésimo término de un PG   y calcula tu razón , dónde y , resultando en un intervalo de uno semitono , siendo el Tono calculado por la potencia cuadrada de un semitono   y el microtono calculado por la raíz cuadrada de un semitono .

Estos valores también pueden ser determinados por la fórmula general de los intervalos de frecuencia dónde “n” igual a uno da como resultado el intervalo de un semitono “n” igual a dos    resulta en el rango de un tono “n” igual a la mitad    da como resultado el rango de un microtono   De esta forma, la frecuencia de una nota musical se puede calcular a través de la fórmula del Término General de un PG   donde el primer termino   es la frecuencia fundamental estándar de la nota musical Lá   y el segundo termino   es la frecuencia de la siguiente nota musical , Por lo tanto, la frecuencia fundamental de la nota Si es el producto entre la nota Lá por Tom , así como el producto entre la frecuencia de la nota Si por el semitono, da como resultado la frecuencia de la nota Dó y el producto de la frecuencia de la nota Dó por el microtono, da como resultado la frecuencia de la nota Dá y así sucesivamente para cualquier nota musical.

Sin embargo, vale la pena recordar que estas frecuencias son valores aproximados, ya que el Tono , el semitono    y el microtono   son números irracionales o infinitos, como el número pi   Además, para una mejor comprensión operativa de los intervalos de frecuencia en una escala lineal, un semitono se considera igual a un medio tono    un microtono es igual a un cuarto de tono   y un semitono igual a medio microtono .

2.3 REPRESENTACIÓN DEL TIMBRE MUSICAL

Cuando la frecuencia fundamental   se toma del conjunto de frecuencias armónicas, que componen cualquier frecuencia   las frecuencias restantes formarán el Timbre   del latín Timpanum, que es una característica secundaria de la frecuencia resultante , pero eso nos permite distinguir distintos sonidos con la misma frecuencia fundamental.

Esta característica se considera opcional en el Lenguaje Algebraico Musical, dejando en manos del ejecutante la elección del instrumento a utilizar en la emisión de las notas musicales. Sin embargo, el Timbre se puede representar mediante un número entero natural acentuado con una tilde  adjunto al cifrado de la nota musical   o al principio de la ortografía   para cada melodía o venir antes de un paréntesis solo para algunas notas musicales , dónde   la parte de la melodía que indica el instrumento a utilizar está subtitulada (= instrumento).

2.4 REPRESENTACIÓN DE AMPLITUD MUSICAL

la amplitud (a) de una nota musical   se mide por su intensidad sonora en decibeles , que puede variar desde cero hasta un límite audible soportable por el ser humano (HELERBROCK, s.d.), siendo la característica que nos permite distinguir un sonido débil de un sonido fuerte.

Normalmente, se utiliza el rango de intensidad de sonido entre cuarenta y sesenta decibelios    como el rango de intensidad normal para que cualquier nota musical sea escuchada por los seres humanos y, por debajo de este rango, el cifrado de la nota se identifica con un acento grave y, por encima de este rango con un acento agudo. Además, si se necesita una intensidad específica para cualquier valor, solo un acento circunflejo en ese valor adjunto al cifrado de la nota  , indicando esta intensidad multiplicada por diez  , también puede ir antes de un paréntesis para varias notas musicales   . Una flecha adjunta a una nota musical indicará que su intensidad de sonido está aumentando   descendiendo   o creciente-decreciente y viceversa .

2.5 REPRESENTACIÓN DEL TIEMPO DE DURACIÓN MUSICAL

el tiempo de duracionde una célula musical  , nota o silencio, es la característica que nos permite distinguir un sonido de corta duración de un sonido de larga duración, siendo representado por un número entero natural positivo  , que en un arreglo melódico ante la cifra de una célula musical , representa una duración igual o mayor a un segundo . En este contexto, los más utilizados son los de segundo  , dos segundos , tres segundos , cuatro segundos y pocos otros durante esta duración .

Debido a las medidas más utilizadas en un ritmo musical, en este estudio, el período estándar se limita a cuatro segundos  y, cuando ese mismo entero viene en un arreglo melódico después de la cifra de una celda musical    representará una duración igual o inferior a un segundo constituyendo un número fraccionario a la Música.

Insinuando “n” como número denominador de una fracción, cuyo numerador es la unidad  , siendo las duraciones más utilizadas medio segundo , un tercio de segundo  , un cuarto de segundo  , un sexto de segundo  , un octavo de segundo   y no más de una novena de segundo de duración , porque el sonido deja de ser auditivo para el ser humano cuando es igual o inferior a una décima de segundo  . Por tanto, tanto el tiempo de duración en segundos como en fracciones de segundo se pueden representar en una misma celda musical. Por ejemplo,   es la nota Ré tres segundos de duración,   es la nota Ré un tercio de segundo de largo y   es la nota Ré un segundo, medio y cuarto de segundo de largo.

Cuando un tiempo de duración   ven con un acento agudo o grave  , significa que es instantáneo o igual a un noveno de segundo , con el resto de la duración real en pausa musical. En este caso, el acento agudo indica una amplitud con intensidad fuerte y el acento bajo indica una amplitud con intensidad débil. Por ejemplo,   es la nota Dó con fuerte intensidad de sonido en la duración instantánea y haga una pausa por el resto de la duración de medio segundo.

Cuando una duración va seguida de dos puntos significa una breve interrupción en la composición musical, permitiendo a los músicos interactuar con el público, reiniciando en cualquier momento, normalmente en la misma medida de la interrupción.

Cuando una duración va acompañada de puntos suspensivos   significa que después de su término, se prolonga en pausa musical por otro tiempo determinado, pudiendo terminar en el mismo compás o en otro compás diferente. Por ejemplo, es la nota Sol con una duración de un segundo, y puede terminar en el mismo compás o en cualquier otro compás.

Cuando una nota musical comienza en un compás y termina en otro sin perder su continuidad sonora, su cifra en el siguiente compás se identifica con un apóstrofe. Por ejemplo, la nota Dó con tres segundos , siendo dos segundos    en una medida y un segundo   en el siguiente latido .

3. OPERACIONES ENTRE CÉLULAS MUSICALES

Las operaciones entre celdas musicales forman agrupaciones de notas y silencios musicales, llamados monomios musicales y cuando un tiempo de duración venir entre dos células musicales , siempre pertenecerá a la primera celda y el segundo tiene una duración posterior. En este caso, es un segundo implícito y solo una coma antes de esa duración te hará pertenecer a la segunda celda haciendo que el primero dure por un segundo implícito. Por ejemplo,   es la nota do con medio segundo y la nota mi con un segundo de duración y   es la nota Dó con un segundo y la nota Mi dos segundos de duración.

3.1 OPERACIÓN “M” ENTRE CÉLULAS MUSICALES

Cuando dos o más celdas musicales cualesquiera están en operación M, forman un monomio algebraico melódico m, cuyo resultado es una melodía entre ellas, donde el tiempo de duración final de la primera nota es igual al tiempo de duración inicial de la segunda nota , así como el tiempo de duración final de la segunda nota es igual al tiempo de duración inicial de la tercera nota . Por ejemplo, notas musicales Dó, Mi, Sol, Mi, Dó, todo un segundo de duración   en la Operación M forman un monomio melódico de domisolmidó melody   y, cualquier cambio de posición de una de estas notas, en esta operación, formará otro resultado con otra melodía  .

3.2 OPERACIÓN “H” ENTRE CÉLULAS MUSICALES

Cuando dos o más notas musicales rítmicas o notas de igual duración   mantenerse en funcionamiento , forman un monomio algebraico armónico h, cuyo resultado es una armonía entre ellos, donde sus tiempos iniciales de duración son todos iguales , así como sus tiempos finales de duración .

Notas musicales iguales, en esta operación, dan como resultado un monomio al unísono o una sola nota musical y, cuando estas notas son arrítmicas o de distinta duración, formarán diversas armonías según la operación M. Por ejemplo, la operación H entre y entre . En este caso, la nota Sol con menor duración formar la primera armonía domisol , dejando la nota Mi con menor duración formando la armonía domi   en melodía con armonía domisol, dejando la nota Dó un segundo largo  en melodía con armonía domi.

3.3 OPERACIÓN “M” ENTRE MONOMIS MUSICALES

Cuando dos o más monomios musicales están en operación, formarán un polinomio melódico , donde sus monomios están separados por espacios en blanco, lo que implica que los operadores   entre ellos, pudiendo formarse: sólo por monomios melódicos en una sola melodía , sólo por monomios armónicos en una melodía de armonías   y compuesto de monomios melódicos y armónicos .

Estos monomios deben ser rítmicos o tener períodos iguales  , determinado por la suma de los tiempos de duración de sus células musicales , propiedad denominada en este estudio Principio del Ritmo, la cual permite que cualquier sistema permanezca en equilibrio durante su existencia y, aunque ocurra una eventual arritmia en su estructura o si uno de estos períodos es diferente a los demás, el período siguiente seguirá siendo el mismo como el anterior período de equilibrio para corregir el desequilibrio ocasional. Sin embargo, una secuencia de arritmias en la estructura rítmica puede provocar el colapso del ritmo de este polinomio.

Cuando los monomios de este polinomio son arrítmicos, deben estar modulados en un ritmo en una estructura rítmica binaria , ternario  , cuaternario o cualquier otro , ajustando los períodos arrítmicos en rítmica y solo el primer y el último monomio de un ritmo pueden estar incompletos de notas musicales, respectivamente, subtendiendo la pausa musical antes y después de estas notas completando los períodos de estos monomios, como se muestra en los ejemplos a continuación.

a) Operación con los monomios rítmicos  

polinomio melódico cuaternario

b) Operación con los monomios arrítmicos

polinomio melódico arrítmico

Módulo rítmico ternario

polinomio melódico ternario

3.4 OPERACIÓN “H” ENTRE MONOMIS MUSICALES

Cuando dos o más monomios musicales están en operación , forman un polinomio armónico . Así, los monomios quedan en la misma forma operativa, separados por sus operadores   o pueden tener la forma de una matriz de columnas 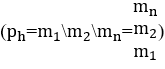, solo puede estar formado por monomios melódicos en armonía , solo por monomios armónicos   y compuesto de monomios melódicos y armónicos . A continuación se muestra un ejemplo de la Operación   entre tres monomios musicales rítmicos.

A continuación se muestra un ejemplo de la Operación entre tres monomios musicales rítmicos.

Monomios melódicos

Forma operativa:

Forma de matriz:

El monomio armónico   puede ser reemplazada por su forma de acorde de Dó mayor (ALMADA, 2012). De esta forma, su duración está implícita y es igual a la duración de los monomios melódicos de esta operación   o puede ceñirse a su duración específica si es diferente de la duración del monomio melódico, que determina el período del compás. Por ejemplo, si  .

3.5 OPERACIÓN “M” ENTRE POLINOMIS MUSICALES

Cuando dos o más polinomios musicales rítmicos están en operación M,pueden formar varios tipos de nuevos polinomios musicales monorrítmicos. Cuando todos los polinomios presentan el mismo ritmo, en caso contrario, forman polinomios polirrítmicos, siendo los más utilizados en Música, los formados únicamente por polinomios armónicos que son compuestos rítmicos , como ejemplo a continuación.

Dada la forma polinomios compuestos:

Forma operativa:

Forma de matriz:

Dónde:

3.6 OPERACIÓN “H” ENTRE POLINOMIS MUSICALES

Cuando dos o más polinomios musicales rítmicos están en operación , pueden formar varios tipos de nuevos polinomios musicales, siendo los más utilizados en Música los formados entre polinomios melódicos solo con monomios melódicos rítmicos, con polinomios melódicos solo con monomios armónicos rítmicos  , en este caso, los monomios de los polinomios operativos   deben ser rítmicas entre sí, como se muestra en el siguiente ejemplo.

Dada la forma de los polinomios melódicos

Forma operativa:

Forma de matriz:

4. GRÁFICOS DE UN POLÍNOMA MUSICAL

Los monomios musicales se pueden trazar en un gráfico en los ejes de coordenadas cartesianas. Para ello, se deben ubicar en el eje de ordenadas o en su línea vertical las frecuencias o cifras de sus notas musicales, y en el eje de abscisas o en su línea horizontal, el tiempo de duración de dichas notas. Luego, conectando estos puntos con segmentos de línea para un monomio melódico, se forma el gráfico de línea melódica.

Sin embargo, para un monomio armónico, donde sus duraciones son simultáneas, simplemente marque la duración de su nota musical tónica o la nota principal del acorde de acompañamiento musical en el gráfico lineal del monomio melódico, justo arriba de la figura para una armonía de la mayor y una poco más bajo para una armonía del modo menor, formando el gráfico de la Línea Armónica, de acuerdo con los ejemplos que se enumeran a continuación.

a)

Gráfico 1. Escala musical en Dó en ritmo binario.

 

 

b)

Gráfico 2. Melodía sencilla en ritmo cuaternario.

c)

Gráfico 3. Melodía con armonía.

5. ARMONÍA DEL ACOMPAÑAMIENTO MUSICAL

Dada cualquier melodía , puede determinar la armonía de su acompañamiento musical aplicando el módulo armónico    desarrollado en este estudio. En cada compás de esta melodía, que transforma las notas musicales melódicas en armónicas, mediante la operación   entre ellas , cuya armonía resultante se ajusta a una armonía de acordes de acompañamiento de modo mayor o menor existente (ALMADA, 2012), como un ejemplo de la melodía a continuación.

Armonía de:

Ajuste de   por el valor de Dó mayor:

Ajuste de  al acorde de Dó menor en función de

Ajuste de por el valor de Fá mayor:

Ajuste de por el valor de Dó mayor:

Ajuste de por el valor de Ré menor:

Armonía sencilla de:

Operación  entre y

La armonía que acompaña   es una armonía simple. En el ejemplo anterior, las armonías encontradas en los módulos armónicos se ajustaron con los acordes mayores y menores existentes más adecuados, teniendo en cuenta la influencia de la nota tónica del acorde de Dó la mayor de las melodias . Como quedó demostrado, en algunos compases, las notas musicales de corta duración quedaron sin acordes musicales, sin perjudicar la armonía de la melodia .

5.1 MELODÍA DE ACOMPAÑAMIENTO MUSICAL

Estas armonías de acompañamiento musical se pueden convertir en una melodía de acompañamiento. Para hacer esto, simplemente aplique el Módulo melódico a estas armonías  , que transforma una armonía en varias melodías a través de la Operación entre tus notas armónicas, que por una tríada o tres notas musicales en armonía , dará como resultado seis melodías distintas .

Debido a la permutación entre estas tres notas musicales para formar los arreglos de notas en las melodías   y por una tétrada o cuatro notas musicales , dará como resultado veinticuatro melodías distintas, debido a que la permutación de cuatro es igual a 24 arreglos melódicos . A partir de ahí basta elegir una de estas melodías para el acompañamiento musical del monomio melódico de esta armonía, subtitulándola por separado. En este caso, el tiempo de duración de cada nota viene determinado por el inverso del número de notas musicales por segundo , que por una tríada o tres notas musicales , es un tercio de un segundo largo  , como ejemplo a continuación.

Acorde de Dó mayor:

melodías

Subtitular:

Gráfico 4. Melodía &4 con una melodía de acompañamiento.

 

6. MEDIDAS DE MONOMIS MUSICALES

Los monomios musicales de una melodía o de una armonía en general brindarán dos tipos de medidas musicales importantes para la Música, una denominada Período Musical, que mide la duración de un monomio melódico  , armónico y compuesta de melódico con armónico , escalado en segundos ; y otro llamado Textura Musical , que mide la aparición de notas musicales en la estructura de un monomio melódico , armónico o compuesta , escalado en notas musicales . La relación entre la textura melódica y el período melódico   determina la dinámica melódica de las notas musicales en la estructura de un monomio melódico.

6.1 PERIODO Y TEXTURA DE UN MONOMIUM MELODICO

Un monomio melódico presenta sus notas musicales continuamente distribuidas en el espacio-tiempo, formando un Período Melódico  , determinado por la suma de los tiempos de duración de sus notas musicales , escalado en segundos . La Textura Melódica , está determinado por el número de notas musicales en su etapa melódica.

La relación entre la textura melódica y el período melódico determina la dinámica melódica de las notas musicales por segundo en la estructura de este monomio, como se muestra a continuación.

1) Monomio melódico

Periodo melódico:

Textura melódica: cuatro notas musicales

Dinámica melódica: melodía lenta

2) Monomio melódico

Periodo melódico:

Textura melódica: dieciséis notas musicales

Dinámica melódica: melodía muy rápida

6.2 PERÍODO Y TEXTURA DE UN MONOMIUM ARMÓNICO

Un monomio armónico presenta sus notas musicales interconectadas al mismo tiempo y suelen ser rítmicas o de la misma duración. Por lo tanto, su Período Armónico es igual al tiempo de duración de cualquier nota musical en su estructura , escalado en segundos .

Sin embargo, puede ocurrir que un monomio armónico sea arrítmico o presente sus notas musicales con duraciones diferentes. En este caso se producirán varias armonías diferentes, con diferentes periodos armónicos y la melodía entre ellas da como resultado el periodo armónico total de este monomio  . Además, la Textura Armónica  , está determinada por el número de notas musicales en armonía en el período armónico, como se muestra a continuación.

1) Monomio armónico rítmico

Periodo armónico:

Textura armónica:

2) Monomio armónico arrítmico

Periodo armónico:

Textura armónica arrítmica:

6.3 PERÍODO Y TEXTURA DE UN POLINOMIO MELÓDICO

Un polinomio melódico rítmico es aquel en el que sus monomios tienen períodos iguales. De esta forma, el producto del número de barras para su periodo , determina el tiempo de duración de este polinomio  , escalado en segundos o minutos.

Aunque este polinomio se compusiera con melodías y armonías, el cálculo de su duración sería el mismo, mientras que su textura melódica total queda el número de notas musicales en ese Tiempo de Duración.

La relación de esta textura melódica total con el tiempo de duración total forma la dinámica melódica   de notas musicales en este polinomio, siendo escalado en notas musicales por segundo.

Cuando el polinomio melódico está compuesto por una armonía, su Textura Armónica total está determinado por la media aritmética de las texturas armónicas de todos sus monomios armónicos de sus barras  , como se muestra abajo.

Tiempo de duración del polinomio

Período melódico de

Números de barra:

Tiempo de duración total:

Textura melódica completa:

Dinámica melódica: (Melodía con dinámica lenta)

Todas las texturas armónicas son iguales a:

Textura armónica total: (Textura sencilla)

7. PLAGIO ENTRE POLINOMIS MELÓDICOS

Normalmente, los plagios son igualdades que se dan entre monomios melódicos y polinomios melódicos   y, cómo estos monomios están formados por notas musicales distribuidas de forma continua que graficadas en un gráfico en el sistema de coordenadas cartesianas, muestran sus líneas melódicas, las cuales pueden compararse entre sí, mostrando sus similitudes o diferencias, se considera plagio a quienes presentan sus líneas melódicas, es decir, que coinciden en el gráfico , colocándolos uno encima del otro, o incluso transportando las notas musicales de los monomios considerados plagio al tono de las notas de los monomios originales. A continuación se muestra un ejemplo de monomios de plagio.

Monomios melódicos iguales: e .

Gráfico 5. Monomios melódicos .

 

7.1 PORCENTAJE DE PLAGIO

Cuando una parte continua de un polinomio melódico es plagio de otra, es decir, tiene un porcentaje de plagio o igualdad en relación al polinomio original, las similitudes identificadas pueden calcularse mediante la fórmula , dónde   es el número de monomios melódicos o compases con plagio, y es el número total de monomios o compases del polinomio original, sin las repeticiones melódicas. Por ejemplo, dada una melodía con cincuenta compases y, entre ellos, diez compases consecutivos fueron plagiados en otra melodía, entonces:

8. ESTRUCTURA DE UN RITMO

El ritmo es un fenómeno que ocurre en la duración de cualquier sistema, dividiéndose en partes iguales para mantenerse en equilibrio. Así sucede en el ritmo de una melodía, donde su duración   se divide en partes de periodos iguales, denominadas medidas, que se vinculan continuamente en función de la Operación , además, cada medida también se divide en partes iguales de periodos más pequeños, llamados unidades de tiempo  , que además están continuamente interconectados en función de la Operación   .

Se sabe que la duración de cualquier período , tiene una duración inicial    y final , pronto, . Además, esta duración inicial   consiste en un latido audible o no audible, causado por un impulso , dado por una fuerza por una duración instantánea, permaneciendo en silencio por el resto de su duración  , por lo tanto, el período de cualquier compás está formado por su tiempo inicial   en sintonía con tu tiempo de silencio .

En un solo compás, además del compás de tu período con tu tiempo de silencio , aún existe, en su interior, debido a la Operación  , los latidos de las unidades de tiempo, con sus tiempos de silencio  , cuyo resultado hace que el primer latido sea dos veces más fuerte que los demás  , y el efecto de sonido se llama la Cadencia Rítmica de la Medida  , que tiene una velocidad de pulsación llamada Tempo Rítmico del Compás, siendo inversamente proporcional al período de esta unidad de tiempo , escalado en latidos por segundo o latidos por minuto .

En este contexto, cuanto menor sea la duración de esta unidad de tiempo, mayor será el tempo rítmico de estos latidos, lo que proporciona dos movimientos rítmicos en un cuerpo físico en su área de operación, uno de los cuales se denomina Regencia Rítmica. , donde un cuerpo sin salir de su posición de reposo, sigue el movimiento del Tempo Rítmico de estos latidos, y otro llamado Danza Rítmica  , donde un cuerpo se mueve desde su posición de reposo a otras posiciones distintas, dependiendo del tempo rítmico de estos latidos.

8.1 LEY DE LA ACENTUACIÓN TÓNICA DE LAS BARRAS

La propiedad de que el primer tiempo de la unidad de tiempo de una medida es más fuerte que los otros tiempos en la misma medida originó la Ley de Acentuación Tónica de los Compases que marca, de manera incisiva, toda nota musical que ocupa esa primera posición en los compases de un ritmo. También acentuando cualquier sílaba de cualquier palabra que ocupe esa posición, modificando o no su acentuación ortográfica, cualquiera que sea la lengua hablada del mundo. En el caso de un silencio colocado en esta posición y una nota musical en la posición siguiente, se produce un efecto musical llamado Contratempo.

8.2 ESTRUCTURA DE UNA BRÚJULA COMPUESTA

Un compás se llama compuesto cuando en su período se produce más de una cadencia rítmica distinta  , formado por otras unidades de tiempo distintas  . En este caso, la barra compuesta puede ser melódica o armónica.

En la Medida Compuesta Melódica, las cadencias rítmicas de las unidades de tiempo dependen de la Operación , dando como resultado una cadencia rítmica melódica  . Entre ellos se origina un tempo rítmico melódico , una regencia rítmica melódica y una danza rítmica melódica .

En la Medida del Compuesto Armónico, las cadencias rítmicas de las diferentes unidades de tiempo están en función de la Operación , resultando en una Cadencia Rítmica Armónica entre ellos  .

A condición de que , la Cadencia Rítmica resultante está determinada por la unidad de tiempo de menor duración  , en este caso, el Tempo rítmico armónico resultante viene dado por el período de la unidad de tiempo más pequeña  , con su conducción armónica rítmica normalmente una función del tempo rítmico de la unidad de tiempo más grande   y su rítmica danza armónica dependiendo del tempo rítmico mayor y menor .

8.3 RITMO ARMÓNICO

La cadencia rítmica de un compás suele ser melódica  , debido a que sus unidades de tiempo son una función de la Operación . Sin embargo, esta cadencia puede ser armónica con los periodos de sus unidades de tiempo en función de la Transacción   , dando como resultado una sola unidad de tiempo, con su cadencia rítmica melódica . Por ejemplo, cuando un grupo de personas guarda silencio durante un tiempo determinado o cuando varios relojes están sincronizados.

9. CONSIDERACIONES FINALES

Este artículo tuvo como objetivo desarrollar un lenguaje algebraico para estructurar matemáticamente la Música, utilizando únicamente letras, números y símbolos para escribir los sonidos de las notas musicales de forma alfanumérica, representando sus principales características sonoras, tales como: frecuencia , amplitud   y tiempo de duracion  , en una sola expresión para identificar una onda de sonido.

Al final, parece que las Matemáticas de la Música solo fueron posibles con el desarrollo de la Operación   y su operación inversa, proporcionando las agrupaciones de ondas sonoras de notas musicales, respectivamente en las formaciones de armonías de acompañamientos instrumentales y melodías que aparecen en cada momento en la inspiración de un compositor, haciendo más sencillo el estudio de la música, con un lenguaje sonoro más comprensible y adaptado a la actualidad tecnología de los estudios científicos de la Ciencia de la Música. Finalmente, con la demostración de la Estructura Matemática de la Música, se puede decir que una composición musical es una estructura matemática del sonido.

REFERENCIA

ALMADA, Carlos. Harmonia Funcional. Editora Unicamp, 2ª Edição, 2012.

GUEST, Ian. Harmonia – Método Prático. Editora Luminar. Vol. 1, p. 33 a 41, 2020.

HELERBROCK, Rafael. Intensidade do som. Mundo da educação, s.d. Disponível em: https://mundoeducacao.uol.com.br/fisica/velocidade-intensidade-som.htm. Acesso em: 22  de julho de 2022.

SILVA, Luiz Paulo Moreira. Progressão geométrica. Brasil Escola, s.d. Disponível em: https://brasilescola.uol.com.br/matematica/progressao-geometrica.htm. Acesso em? 22 de julho de 2022.

VIANA, Arnóbio Araújo. A operação harmonização (H) e sua inversa operação melodiação (M). Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 07, Ed. 03, Vol. 03, pp. 144-171. Março de 2022. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/operacao-harmonizacao, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/operacao-melodiacao. Acesso em: 22 de julho de 2022.

^[1] Graduado en Ingeniería Eléctrica, op. Electrónica de la Universidad Federal de Pará-UFPA. ORCID: 0000-0001-7010-9114.

Enviado: Julio de 2022.

Aprobado: Agosto de 2022.