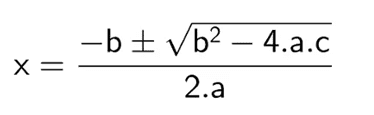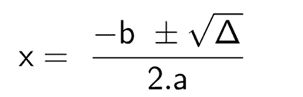ARTÍCULO ORIGINAL
PEDREIRA, Sinvaldo Martins [1]
PEDREIRA, Sinvaldo Martins. El fracaso de Bhaskara. Revista Científica Multidisciplinar Núcleo do Conhecimento. Año. 07, ed. 02, vol. 02, pág. 178-186. Febrero 2022. ISSN: 2448-0959, Enlace de acceso: https://www.nucleodoconhecimento.com.br/olimpiada-de-matematica/fracaso-de-bhaskara
RESUMEN
Este trabajo tiene como objetivo mostrar que debido a fallas en el sistema aritmético, las reglas universitarias basadas en un estándar erróneo pueden generar resultados incorrectos, como la regla de la ecuación cuadrática, que puede propagar una falsa certeza de exactitud, por el simple hecho de ser de seguir. paradigmas seculares, sin una amplia observancia contextual de la realidad involucrada, porque cuando se trata de ciencias exactas, siempre debemos tener una visión holística, considerando ampliamente todos los factores involucrados, ya que una acción presente tiene consecuencias en el futuro y cuando nos basamos en fallan los sistemas, terminamos teniendo una falsa sensación de éxito, ya que seguimos todos los pseudo preceptos al pie de la letra. Sin embargo, surge un nuevo sistema que pone a prueba la contundencia del camino aritmético a seguir.
Palabras clave: Fracasos, Precisión, Sistema, Holístico.
1. INTRODUCCIÓN
En primer lugar, este trabajo no pretende menospreciar el genio de Bhaskara, sino mostrar que debido a una falla conceptual en el sistema aritmético, incluso los genios pueden cometer errores.
La ecuación cuadrática se estandarizó presentándose de la siguiente forma: ax² + bx + c = 0, donde su solución era una incógnita, por lo que la solución al problema vino con la fórmula:
Pero para simplificar la resolución, encuentre primero el delta;
Δ = b² – 4ac
Posteriormente, el resultado de delta se une a la ecuación:
Finalmente, al ser una ecuación cuadrática, X tiene dos resultados:
X = X, y X = X,,
Ejemplo I:
X² + 10 X – 56 = 0 A = 1, B = 10, C = – 56
Δ = 10² – (4. 1 .- 56)
Δ = 100 – (- 224)
Δ = 324
X = –10 ± √324
2.1
X, = –10 + 18 => X, = 8 => X, = 4
2 2
X,, = –10 – 18 => X,, = – 28 => X,,= – 14
2 2
Entonces las respuestas son: X, = 4 y X,, = -14
Ejemplo II:
X² – 10 X – 56 = 0 A = 1, B = -10, C = – 56
Δ = -10² – ( 4. 1 .- 56)
Δ = 100 – (- 224)
Δ = 324
X = -10 ± √324
2.1
X, = 10 + 18 => X, = 28 => X, = 14
2 2
X,, = 10 – 18 => X,, = – 8 => X,, = – 4
2 2
Entonces las respuestas son: X, = 14 y X,, = – 4
2. HOLISMO
2.1 HOLISMO I
Como se mencionó anteriormente, usemos un poco de holismo; toda ecuación cuadrática proviene de una distributiva, donde:
1º caso
(a + b)² => (a + b) . (a + b) = a² + 2ab + b² Nota: tanto a como b son estrictamente positivos según la regla.
2º caso
(a – b)² => (a – b) . (a – b) = a² – 2ab + b² Nota: a positivo y b negativo según la regla.
2.2 HOLISMO II
En el término oculto, toda suma y toda resta tiene un resultado, por lo que
a + b = c, consecuencia (a + b)² = c², entonces; a² + 2ab + b² = c²
a – b = c, consecuencia (a – b)² = c², entonces; a² – 2ab + b² = c²
2.3 HOLISMO III
Evidenciando términos, pongamos en evidencia los términos de la ecuación;
I. a = X, b = 5, c = 9
Pronto; (a + b)² = c² => (X + 5)² = 9² => X² + 2 . 5X + 25 = 81 => X² + 10X + 25 – 81 = 0 => X² + 10X – 56 = 0
II. a = X, b = – 5, c = 9
Pronto; (a – b)² = c² => (X – 5)² = 9² => X² – 2 . 5X + 25 = 81 => X² – 10X + 25 – 81 = 0
=>X² – 10X – 56 = 0
2.4 HOLISMO IV
Correspondencia:
I. X² + 10X – 56 = 0
A = X², B = 10X, C = -56, entonces A = a², B = 2. 5X, C = 25 – 81, implica A = a², B = 2 . ab, C = b² – (c²),
II. X² – 10X – 56 = 0
A = X², B = – 10X, C = -56, entonces A = a², B = – 2 . 5X, C = 25 – 81, implica A = a², B = – 2 . ab, C = b² – (c²),
3. RACIONALIZACIÓN
I. Si en (a + b)² = c² => a² + 2ab + b²- (c²) = 0
A = a², B = 2 ab , C = b² – (c²), Nota: (B = 2 ab) por regla a y b son estrictamente positivos, In X² + 10X – 56 = 0
A = X² , B = 10X, C = -56, Nota: (B = 10X) por regla X es estrictamente positivo.
Entonces en X² + 10X – 56 = 0 la única raíz posible es 4, porque -14 va en contra de la regla matemática.
II. Si en (a – b)² = c² => a² – 2ab + b²- (c²) = 0, (a = X, b = – 5, c = 9)
A = a², B = – 2 ab, C = b² – (c²), Nota: (B = – 2 ab) por regla general si b es negativa, a tiene que ser estrictamente positiva.
En X² – 10X – 56 = 0
A = X² , B = -10X, C = -56, Nota: (B = – 10X) por regla X es estrictamente positiva.
Entonces en X² – 10X – 56 = 0, la única raíz posible de X es 14, porque – 4 va en contra de la regla matemática.
4. ORDENAMIENTO
4.1 CASO I
Si (X² + 10X – 56 = 0) = (a² – 2ab + b²- (c²)) entonces:
A = X² y A = a², implica (X = a)
B = 10X y B = 2ab, implica (10X = 2ab)
C = -56 y C = + b²- (c²), implica (- 56 = b² – (c²))
Encontrando la raíz, primero encuentra el valor de b:
si A = X y A + a, B = 10X donde B = 2ab, ponemos b en evidencia
10X = 10a, implica 10a = 2ab => b = 10a/ 2a => b = 5
Segundo, se encuentra el valor de c;
Si C = -56 y C = + b²- (c²), ponemos c en evidencia
-56 = b²- (c²) implica -56 = 5²- (c²) => c² = 25 + 56 => c² = 81 => c = 9
Finalmente, se encuentra el valor de la raíz;
Entonces (a + b)² = c², implica (a + b) = c
Si ((a + b)² = c² ) = ((X + b)² = c²), implica (X + b) = c, es decir:
X + 5 = 9 => X = 9 – 5 => X = 4
4.2 CASO II
Si (X² – 10X – 56 = 0) = (a² – 2ab + b²- (c²)) entonces:
A = X² y A = a², implica (X = a)
B = – 10X y B = – 2ab, implica (- 10X = 2ab)
C = -56 y C = b²- (c²), implica (- 56 = b² – (c²))
Encontrando la raíz, primero encuentra el valor de b:
si A = X y A = a, B = – 10X donde B = – 2ab, ponemos b en evidencia
– 10X = – 10a, implica – 10a = – 2ab => – b = – 10a/ 2a => – b = – 5
Según el valor de c:
Si C = – 56 y C = – b²- (c²), ponemos c en evidencia
– 56 = – b²- (c²) implica – 56 = – 5²- (c²) => c² = 25 + 56 => c² = 81 => c = 9
Finalmente, se encuentra el valor de la raíz:
Entonces (a – b)² = c², implica (a – b) = c
Si ((a – b)² = c² ) = ((X – b)² = c²) , implica (X – b) = c, es decir:
X – 5 = 9 => X = 9 + 5 => X = 14
5. PARADOJA
Como se demuestra en los dos ejemplos, no fue necesario usar la fórmula de Bhaskara para resolver ninguna de las ecuaciones cuadráticas.
Tanto (X² + 10X – 56 = 0) como (X² – 10X – 56 = 0) se resolvieron sin utilizar dicho recurso matemático, destacando que en ambos solo existe una raíz posible.
Sin embargo, a pesar de haberse demostrado la falla en la fórmula de Bhaskara, aún existe una falla de mayor grado sistémico, que es la regla de los signos, pues como lo ve y normaliza Pedreira (2016), un número negativo al cuadrado sigue siendo negativo, ya que las proporciones tienen características neutrales, simplemente multiplicando o dividiendo algo; ej.: 3 x *3 = *9 (donde (*) antes de un número indica que es negativo, para no confundirlo con el signo (–) que indica una resta), quedando el fallo de cambio de signo al cambiar el lado de la igualdad, que se puede resolver con la regla de la Base y los Componentes, donde la Base (B) es igual a la suma de los Componentes y el Componente (C) es igual a la diferencia de la Base por uno o más Componentes,
Ej.: B = 15 C = 8 y 7, 15 = 8 + 7 => 15 – 8 = 7 => 8 = 15 – 7 => 8+7 = 15 => 15 – (8 + 7) = 0
6. HACIENDO UNA COMPARACIÓN
La ecuación (a + b)² = c² siempre terminará en una incógnita de la forma: a² + 2ab +b² – (c²) = 0 y esto termina exigiendo una segunda etapa de elaboración aritmética para resolver el problema, como se ve antes de. Mientras que si usamos la Regla de Base y Componentes (BC), la solución es lineal y continua;
Ej.: (a + b)² = c², por la regla BC: c (a + b) = c² => ca + cb = c²
7. EN LA PRÁCTICA:
7.1 EJEMPLO I
Regla actual: ( X + 8)² = 144 => ( X + 8) . (X + 8) = 144 => X² + 2 . 8 X + 64 = 144 =>
X² + 16X + 64 – 144 = 0 => X² + 16X – 80 = 0 (desconocido)
Regla base y componentes: (X + 8)² = 144 => 12 . X + 12 . 8 = 144 => 12X + 96 = 144 =>
12X = 144 – 96 => 12X = 48 => X = 48/12 => X = 4 (resultado directo)
7.2 EJEMPLO II
Regla actual: ( X – 5)² = 49 => ( X – 5) . (X – 5) = 49 => X² + 2 . – 5 . X + 25 = 49 =>
X² + 10X + 25 – 49 = 0 => X² + 10X – 14 = 0 (desconocido)
Regla base y componentes: (X – 5)² = 49 => 7 . X-7. 5 = 49 => 7X – 35 = 49 =>
7X = 49 +35 => 7X = 84 => X = 84/7 => X = 12 (resultado directo)
7.3 EJEMPLO III: OTRAS POSIBILIDADES
Regla actual: ( X + 6)² = – 121 (sin solución): debido a la regla actual en una ecuación cuadrática en la forma (a + b)² = c², c² siempre será positivo, porque todo número positivo o negativo siendo elevado a una potencia par, se vuelve positivo.
Regla base y componentes: (X + 6)² = *121 => 11X + 11 . 6 = *121 => 11X = *121 – 66 => 11X = *187 => X = *187/11 => X = *17 (tiene solución): debido a la regla de Base y Componentes para considerar los números ya sean multiplicadores o divisores como razones geométricas (RG) y RGs tienen carácter neutro, independientemente de que esté elevado a alguna potencia, par o impar, si es positivo seguirá siendo positivo, si es negativo (*) seguirá siendo negativo.
8. CONSIDERACIONES FINALES
Se ha comprobado que aún dentro de las reglas que se utilizan actualmente, la fórmula de la ecuación cuadrática siempre da como respuesta dos raíces, desencadenando una eterna dualidad de exactitud, lo que es en sí mismo una paradoja, falla derivada del hecho de que no considerar términos ocultos en su solución, es decir, cuando consideramos el distributivo: (a + b)² => (a + b) . (a + b) = a² + 2ab + b² , omitimos la igualdad (c²) y esto acaba generando una oscuridad en su resolución, provocando un lapso sistémico.
Aún subsanando este lapsus, el sistema actual sigue siendo limitado, pues cuando usamos la regla de Base y componentes, aumentamos infinitamente las posibilidades de las operaciones, ya que cuando consideramos las razones geométricas como neutras, las ecuaciones elevadas a cualquier potencia tendrán el signo de su numerador, ya sea positivo o negativo.
REFERENCIAS
PEDREIRA, S. M. O Valor dos Números. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 01, Vol. 08. pp. 05-16. setembro de 2016. Disponível em: https://www.nucleodoconhecimento.com.br/matematica/o-valor-dos-numeros.
PEDREIRA, S. M. Reestruturando os Números. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 09, Vol. 06, pp. 115-120. Setembro de 2019. Disponível em: https://www.nucleodoconhecimento.com.br/matematica/reestruturando-os-numeros.
SILVA, L. P. M. Fórmula de Bhaskara. Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/formula-bhaskara.htm. Acesso em 15 de dezembro de 2021.
[1] Licenciado en Logística, 4to semestre en Química, Matemático Aficionado.
Enviado: Diciembre de 2021.
Aprobado: Febrero de 2022.