ORIGINALER ARTIKEL
SOUZA JÚNIOR, Elias Pereira De [1]
SOUZA JÚNIOR, Elias Pereira De. “Unterschied zwischen Quadraten” im Satz von Pythagoras. Revista Científica Multidisciplinar Núcleo do Conhecimento. Jahr 05, Ed. 10, Vol. 06, pp. 05-13. Oktober 2020. ISSN: 2448-0959, Zugangslink: https://www.nucleodoconhecimento.com.br/mathematischen-olympiaden/satz-von-pythagoras
ABSTRAKT
Dieser Artikel soll Anwendungen des Inhalts des Satzes von Pythagoras bei der Konstruktion von Wissen im Klassenzimmer zeigen, wobei ein Schwerpunkt auf einer algebraischen Technik für den “Unterschied zwischen Quadraten” liegt. Zunächst wird die Einführung und Anwendung des Satzes von Pythagoras als neuer Unterrichtsinhalt in einem kontextualisierten Beispiel untersucht. Daher wurde der Satz vom Lehrer demonstriert, und die Schüler werden dazu gebracht, zusätzlich zu dem demonstrierten klassischen Satz des Pythagoras alternative Methoden zur Erzielung von Ergebnissen zu hinterfragen und zu begründen. Bald tauchten einige Methoden auf, Auflösungsmöglichkeiten für das erste Beispiel, eine dieser Formen war der geometrische Begriff des Satzes, jedoch setzten die Studenten ihre Untersuchungen fort. Der entscheidende Teil der Klasse war die Begründung des algebraischen Verfahrens, das bei den Untersuchungen der Schüler auf andere Weise auffiel, es war der „Unterschied zwischen Quadraten“ als Lösung für den Satz innerhalb der Menge der natürlichen Zahlen, da dies nicht der Fall war Alle numerischen Sätze beantworteten die Beziehung. An diesem Punkt werden Reflexionen für die Schüler erstellt, wie sie Mathematik erforschen und auf unterschiedliche Weise untersuchen können, da die Vielfalt der Mathematik erforscht und die Sensibilität der Schüler für neue Entdeckungen geschärft werden soll. Der Satz von Pythagoras ist bekannt und angewendet. Er kann leicht in verschiedenen mathematischen Literaturen gefunden werden. Um die Schüler dazu zu bringen, Formeln und Verfahren zu überschreiten, muss man lehren, wie man denkt.
Schlüsselwörter: Bildung, Modellierung, Lehren, Pythagoras, Lernen.
1. EINLEITUNG
Das in diesem Artikel vorgestellte Thema wurde aufgrund einer im Klassenzimmer entwickelten Erfahrung ausgewählt, die darauf abzielte, die Art und Weise der Beziehung und Anwendung des Satzes von Pythagoras in seiner algebraischen und geometrischen Form gemäß der Untersuchung von Dreiecken mit Schwerpunkt auf dem rechten Dreieck zu untersuchen die Idee des Satzes von Pythagoras aus Sicht des Schülers, wodurch es gelang, verschiedene Möglichkeiten zur Lösung von Problemen im Zusammenhang mit dem Satz zu bilden, darunter den “Unterschied zwischen Quadraten”.
In diesem Artikel wurde jedoch auch versucht, über eine in der Schule gelebte Erfahrung durch das Sammeln von Informationen und beobachteten Berechnungen zu berichten, um die Bedeutung der Wissenskonstruktion durch den Schüler zu verstehen und so den Lehr-Lern-Prozess zu verbessern. Denn bei der Bildung des Wissens der Schüler wird es unabdingbar, im Klassenzimmer direkt, recherchierend oder sogar ludisch zu üben, wobei angenommen wird, dass sich aus dieser Praxis Herausforderungen, Zweifel oder Gewissheiten ergeben, wenn dies der Weg ist, den der Schüler gehen möchte Folgen Sie, wie zu tun ist und was nicht, um fortzufahren, und suchen Sie so das ideale Verständnis für die Problemlösung. In dieser Klasse nahmen 36 Schüler der ersten Klasse der High School an der Klasse “A” von Colégio Sagrada Família, Brasília DF teil
Daher werden verschiedene Studienperspektiven auf den Satz von Pythagoras angewendet. Dann wird ein einfacher Vorschlag gezeigt, in dem der Satz interpretiert wird und der sich auf die Differenz zwischen Quadraten bezieht. Dies führt zu einer interessanten Tatsache, die auch unter dem Gesichtspunkt der Bildung gezeigt werden muss.
1.1 DER KLASSENVORSCHLAG UND DAS PYTHAGORAS-THEOREM
Den Schüler dazu anzuregen, nach einer Lösung eines Problems zu suchen oder sogar die Forschung im Klassenzimmer auf unterschiedliche Weise und mit unterschiedlichen Möglichkeiten zu fördern, bedeutet, eine andere Methodik anzuwenden, dh mathematische Modellierung anzuwenden. Folglich macht es das Klassenzimmer bald zu einem Forschungs- und Praxisfeld, zu einem interessanteren und attraktiveren Ort für Studenten und macht den Unterschied.
Der Mathematikunterricht geht über das Traditionelle hinaus. Er soll durch die Vielfalt der Maßnahmen, die unzählige Lehr- und Lernmethoden ermöglichen, innovativ sein. Denn den Schüler herauszufordern, nur Lösungen für Probleme zu finden, bedeutet, Möglichkeiten für neue Entdeckungen zu eröffnen, wie zum Beispiel einen Thread, in dem Mathematik in verschiedenen anwendbaren Kontexten entdeckt wird. D’ambrosio (1998) sprach über die oben genannten Ideen.
Der Vorschlag an die Schüler basierte also auf dem folgenden Problem: Eine Leiter mit einer Länge von 12 Metern wird unter einer Wand getragen. Die Basis der Treppe ist 8 Meter von der Wand entfernt, wie in der folgenden Abbildung gezeigt. Die Schüler wurden dann gebeten, die Höhe der Wand zu bestimmen.
Abbildung 1: Anwendung des rechtwinkligen Dreiecks

Intuitiv wurden die Schüler angewiesen, den Wert der Wandmessung anhand der grundlegenden Definition für jedes Dreieck zu ermitteln. Dieser Inhalt wurde bereits in den vergangenen Jahren untersucht und diente als Grundlage für die Einführung anderer Inhalte. Um ein Dreieck zu bilden, ist es im Allgemeinen möglich, den Zustand der Existenz von Dreiecken zu überprüfen. Dies ist das Maß beider Seiten, das kleiner als die Summe der Maße der beiden anderen und größer als der absolute Wert der Differenz zwischen diesen ist Maßnahmen, Anwenden eines geometrischen Musters. Das folgende Muster wird beobachtet:
Abbildung 2: Existenzbedingung eines Dreiecks
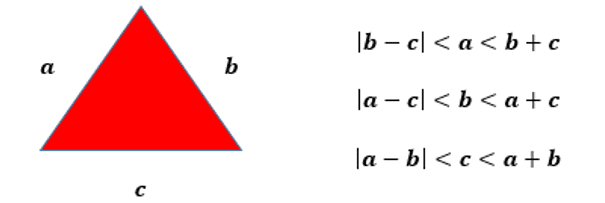
Die Schüler kamen zu einigen möglichen und relevanten Werten, um das Treppenmaß als eine Seite des Dreiecks zu berechnen. Um jedoch den Satz von Pythagoras anzuwenden, muss das Dreieck mindestens einen seiner Winkel von 90 ° haben. Daher bestand der nächste Schritt darin, den Satz von Pythagoras zu demonstrieren.
1.2 DEMONSTRATION DES PYTHAGORAS-THEOREMS
Im Lernprozess nach der ersten Untersuchung der Dreiecke und ihrer Existenz bestand der nächste Schritt darin, die Neugier der Schüler zu schärfen, einige Kuriositäten und erste Schlussfolgerungen zu formalisieren. In diesem Teil der Klasse haben die Schüler mehrere Quadrate mit ihren jeweiligen Bereichen verknüpft und versucht, mit der Vermittlung des Lehrers Muster zu finden. Bald begannen die Schüler, die Eigenschaften zu erkennen, die Pythagoras für den Satz verwendete, der auf der Summe der Flächen der Polygone basiert, die eine aus kongruenten rechtwinkligen Dreiecken konstruierte Figur bilden, dh die Flächen wie im Folgenden gezeigt zu vergleichen Zahlen.
Abbildung 3 Demonstration des Satzes von Pythagoras
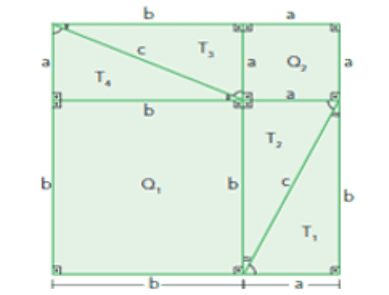
Abbildung 4 Demonstration des Satzes von Pythagoras
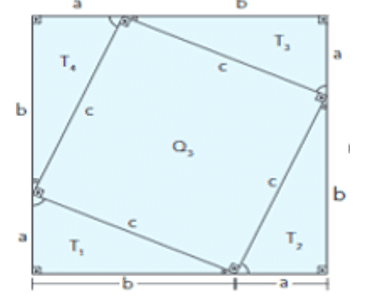
Bedenken Sie, dass die 2 kleinsten Seiten eines Dreiecks als Kollektoren bezeichnet werden und die längste Seite eines rechtwinkligen Dreiecks die Hypotenuse ist. Es ist zu beachten, dass die Figuren unter Verwendung von vier kongruenten rechtwinkligen Dreiecken konstruiert wurden, die gleich “a” und “b” sind, und der Hypotenuse “c”, die größere Quadrate mit Seiten gleich (a + b) bilden. Wenn die vier kongruenten rechtwinkligen Dreiecke der beiden Figuren entfernt werden, haben die übrigen Figuren die gleiche Fläche. Daher gibt es
In Abbildung 3:
- Summe der Flächen der vier rechtwinkligen Dreiecke = (T1 + T2 + T3 + T4)
- Verbleibender Bereich Q1 + Q2 = a2 + b2
In Abbildung 4:
- Summe der Flächen der vier rechtwinkligen Dreiecke = (T1 + T2 + T3 + T4)
- Verbleibende Fläche = Q3 = c2
Also ist c2 = a2 + b2
Diese Beziehung kann auf jedes rechtwinklige Dreieck angewendet werden. “C” ist die größte Seite des Dreiecks, die als Hypotenuse bezeichnet wird, “a” und “b” die Seite des Dreiecks, wie oben gezeigt.
1.3 WIEDERAUFNAHME DES ERSTEN BEISPIELS
Den Schülern wurde klar, nachdem der Satz demonstriert wurde, dass die Frage eine Anwendung des Satzes von Pythagoras ist, bei dem die Seiten als Katheter bezeichnet werden und die größte Seite des Dreiecks, die dem Winkel gegenüber liegt, als Hypotenuse bezeichnet wird. Somit kann die pythagoreische Beziehung folgendermaßen geschrieben werden:
(Hypotenuse) ² = (Kateto 1) ² + (Kateto 2) ²
Abbildung 5: rechtwinkliges Dreieck
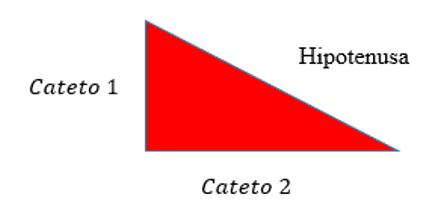
Deshalb:
Die Schüler haben die obige Liste wie folgt angewendet:
- Die Hypotenuse entspricht der Leiter (12 m)
- Der Abstand zwischen Leiter und Wand beträgt ein Bein (8 m)
- Die Höhe der Wand ist die andere Seite, in diesem Fall “x”
Anwendung des Satzes:
![]()
Subtrahieren von 8² von beiden Seiten der Gleichheit
![]()
![]()
Zu diesem Zeitpunkt stellte ein Schüler eine Frage zur Subtraktion von Quadraten: – “Können wir diese Subtraktion erst lösen, nachdem wir die Quadrate gelöst haben?”
Daher begannen Untersuchungen anderer Möglichkeiten zum Subtrahieren von Quadraten.
1. Lösung:
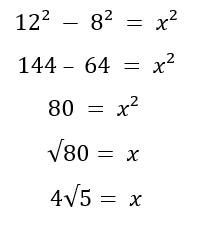
2. Lösung:
Ein Muster wurde vom Lehrer zusammen mit den Schülern beobachtet. Siehe unten:
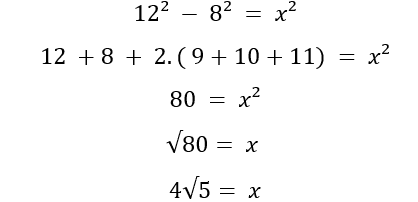
Zu diesem Zeitpunkt wurde ein Muster für den Unterschied zwischen Quadraten, in denen die Zahlen zur Menge der natürlichen Zahlen gehören, in der Form festgestellt
![]()
Beispiel:
a = 23 und b = 19, anwendbar …
Den Test machen:
![]()
Gleichheit gilt für Zahlen
![]()
Nach dem Testen der Operationen an der Menge der natürlichen Zahlen wurde sie auch auf einige andere Mengen angewendet, wie z. B. die Menge der ganzen Zahlen, die ebenfalls funktionierten, und die realen, wobei im letzteren Fall einige Zahlen keine echte Gleichheit herstellten und somit festlegten diese Anwendung für natürliche Zahlen.
2. BEWEIS DER BEZIEHUNG
Verhältnis für die Differenz zwischen Quadraten:
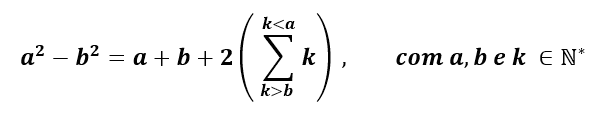
Erwägen
a2 + b2 mit a und b, die zu natürlichen Zahlen größer als Null gehören, unter Berücksichtigung von a > b haben wir den folgenden Satz für a und b:
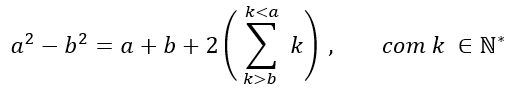
Bald wenn
![]()
Dann
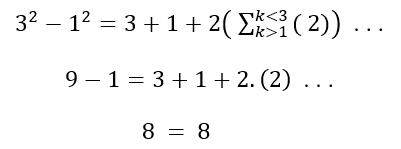
Betrachten wir nun m als eine natürliche Zahl.
Wenn a und b wahr sind, gilt für a und b ∈
![]()
, dann gilt auch a = b + m für m ∈
![]()
Nehmen Sie m = 1, z
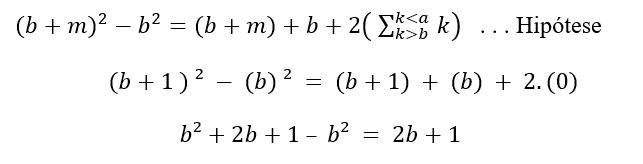
Bald,
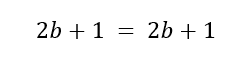
Daher die Beziehung
![]()
gilt für alle
![]()
Wie ich demonstrieren wollte!
Diese Demonstration wurde sofort den Schülern gezeigt, die von der Anwendung, die sie entwickelt hatten, überrascht waren, und so eine andere Beziehung zum Satz von Pythagoras im “Unterschied zwischen Quadraten” fanden.
3. SCHLUSSFOLGERUNG
Das Ziel, die Schüler dazu zu bewegen, verschiedene Wege zur Lösung von Problemen zu finden, besteht darin, Wissen unter Verwendung der bereits erworbenen Kompetenzen und Fähigkeiten aufzubauen und die Grundlage für neues Lernen und neue Entdeckungen zu schaffen. Dieser Artikel ist ein Beispiel dafür, da der Lehrer grundlegende Anweisungen gab und die Schüler nach Wegen suchten, um das Problem zu lösen.
Was es interessanter macht, ist, dass es inmitten von Untersuchungen mehrere Möglichkeiten gibt, ein Ergebnis zu erzielen. Wenn man diese Wege sieht und sie führt, wird der Mathematikunterricht für die Schüler anders und angenehm, was eine mathematische Modellierung rechtfertigt.
In Anlehnung an die Anwendung des Satzes von Pythagoras im ersten Beispiel diskutierte der Lehrer mit den Schülern die Möglichkeiten, den Unterschied zwischen Quadraten zu lösen, und machte dabei immer klar, dass die Konstruktion von Wissen der grundlegende Teil der Klasse ist, der Lehrer der Mediator und Studenten machen Entdeckungen.
In einem der Prozesse, in denen der Schüler die Frage nach der Berechnung der Differenz zwischen Quadraten bei der Lösung des Problems stellte, konnte die Klasse mit dem Lehrer feststellen, dass die beobachtete Methode zum Subtrahieren von Quadraten in einigen relevanten Punkten gültig ist.
Daher demonstrierte der Lehrer die Anwendbarkeit der Operation, die innerhalb der Menge natürlicher Zahlen entdeckt wurde, und löste die Frage nach der Anwendbarkeit der Operation, um die Methode dem Schüler und der Klasse klar zu machen. Bald beendeten wir die Frage und lösten andere Beispiele mit der entdeckten Methode. Die Rückkehr des Schülers in die Klasse war die folgende Zeile: “Wir haben eine neue Formel entdeckt, die cool ist.” Für einen Lehrer mit exakten Wörtern gibt es keine Möglichkeit, dass eine Zeile so auffälliger sein kann.
Der Student bat um Anleitung, um Summen und Demonstrationen zu studieren. Dass ein Junge aus der ersten Klasse der High School, die zukünftige Entwicklung dieses Schülers, überlasse ich in der Vorstellung derer, die diesen Artikel lesen.
4. REFERENZEN
DANTE, Luiz Roberto. MATEMÁTICA: Contexto e Aplicações volume único / Luiz Roberto Dante, Fernando Viana – – 4. Edição – – São Paulo: Ática, 2018.
HEFEZ, Abramo. Indução Matemática:\induçãofinal”. Estilo OBMEP – Rio de Janeiro – Departamento de Matemática Aplicada Universidade Federal Fluminense, 2009. Disponível em: http://www.obmep.org.br/docs/apostila4.pdf. Acesso em: 04 maio de 2020. D’Ambrósio, U.Etnomatemática. São Paulo: Ática, 1998.
SANTOS. Marconi Coelho dos. Teorema de Pitágoras: suas diversas demonstrações. Campina Grande (PB):UEPB, 2011. 42f. Monografia (Especialização em Educação Matemática para professores do Ensino Médio) {Universidade Estadual da Paraíba, Centro de Ciências e Tecnologia, Campina Grande, 2011.
VIANA, M. C. V.; SILVA, C. M. Concepções de Professores de Matemática sobre a utilização da História da Matemática no processo de Ensino-Aprendizagem. In: ENCONTRO NACIONAL DE HISTÓRIA DA MATEMÁTICA, 9., 2007, Belo Horizonte. Pôsteres… Belo Horizonte, 2007. Disponível: https://www2.unifap.br/matematicaead/_les/2016/03/TCC-REVISADO.pdf Acesso em: 04 maio de 2020.
[1] Nachdiplom in Mathematik.
Eingereicht: September 2020.
Genehmigt: Oktober 2020.


