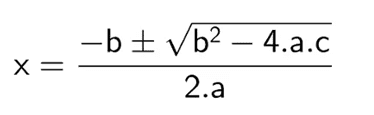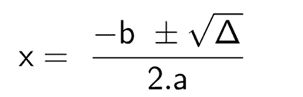ORIGINALER ARTIKEL
PEDREIRA, Sinvaldo Martins [1]
PEDREIRA, Sinvaldo Martins. Bhaskaras Versagen. Revista Científica Multidisciplinar Núcleo do Conhecimento. Jahr. 07, Hrsg. 02, Bd. 02, p. 178-186. Februar 2022. ISSN: 2448-0959, Zugangslink: https://www.nucleodoconhecimento.com.br/mathematischen-olympiaden/bhaskaras-versagen
RESUMO
Diese Arbeit soll zeigen, dass universitäre Regeln, die auf einem falschen Standard basieren, aufgrund von Fehlern im Rechensystem falsche Ergebnisse erzeugen können, wie z säkulare Paradigmen, ohne eine breite kontextbezogene Betrachtung der jeweiligen Realität, denn wir müssen im Umgang mit exakten Wissenschaften immer eine ganzheitliche Betrachtung haben, die alle beteiligten Faktoren im Großen und Ganzen berücksichtigt, da eine gegenwärtige Handlung Konsequenzen für die Zukunft hat und wenn wir uns darauf stützen Systeme fehlerhaft, haben wir am Ende ein falsches Erfolgsgefühl, da wir alle Pseudo Regeln buchstabengetreu befolgen. Es entsteht jedoch ein neues System, das die Eindringlichkeit des zu beschreibenden arithmetischen Weges auf die Probe stellt.
Schlüsselwörter: Misserfolge, Genauigkeit, System, Ganzheitlich.
1. EINLEITUNG
Zunächst einmal soll diese Arbeit Bhaskaras Genie nicht schmälern, sondern zeigen, dass aufgrund eines konzeptuellen Fehlers im arithmetischen System selbst Genies Fehler machen können.
Die quadratische Gleichung wurde standardisiert, indem sie in der folgenden Form dargestellt wurde: ax² + bx + c = 0, wobei ihre Lösung eine Unbekannte war, sodass die Lösung des Problems mit der Formel kam:
Aber um die Auflösung zu vereinfachen, finden Sie zuerst das Delta;
Δ = b² – 4ac
Anschließend wird das Ergebnis von Delta mit der Gleichung verbunden:
Da es sich schließlich um eine quadratische Gleichung handelt, hat X zwei Ergebnisse:
X = X, und X = X,,
Beispiel I:
X² + 10 X – 56 = 0 A = 1, B = 10, C = – 56
Δ = 10² – (4. 1 .- 56)
Δ = 100 – (- 224)
= 324
X = -10 ± √324
2.1
X, = –10 + 18 => X, = 8 => X, = 4
2 2
X,, = -10 – 18 => X,, = – 28 => X,,= – 14
2 2
Die Antworten lauten also: X, = 4 und X,, = -14
Beispiel II:
X² – 10 X – 56 = 0 A = 1, B = -10, C = – 56
Δ = -10² – ( 4. 1 .- 56)
Δ = 100 – (- 224)
= 324
X = -10 ± √324
2.1
X, = 10 + 18 => X, = 28 => X, = 14
2 2
X,, = 10 – 18 => X,, = – 8 => X,, = – 4
2 2
Die Antworten lauten also: X, = 14 und X,, = – 4
2. HOLISMUS
2.1 HOLISMUS I
Lassen Sie uns, wie bereits erwähnt, ein wenig Holismus anwenden; jede quadratische Gleichung kommt von einer distributiven, wobei:
1º Fall
(a + b)² => (a + b) . (a + b) = a² + 2ab + b² Beob: Sowohl a als auch b sind gemäß der Regel streng positiv.
2º Fall
(a – b)² => (a – b) . (a – b) = a² – 2ab + b² Beob: a positiv und b negativ gemäß der Regel.
2.2 HOLISMUS II
Im verborgenen Term hat also jede Addition und jede Subtraktion ein Ergebnis
a + b = c, Folge (a + b)² = c², dann; a² + 2ab + b² = c²
a – b = c, Folge (a – b)² = c², dann; a² – 2ab + b² = c²
2.3 HOLISMUS III
Terme beweisen, lassen Sie uns die Terme der Gleichung beweisen;
I. a = X, b = 5, c = 9
Demnächst; (a + b)² = c² => (X + 5)² = 9² => X² + 2 . 5X + 25 = 81 => X² + 10X + 25 – 81 = 0 => X² + 10X – 56 = 0
II. a = X, b = – 5, c = 9
Demnächst; (a – b)² = c² => (X – 5)² = 9² => X² – 2 . 5X + 25 = 81 => X² – 10X + 25 – 81 = 0
=>X² – 10X – 56 = 0
2.4 HOLISMUS IV
Korrespondenz:
I. X² + 10X – 56 = 0
A = X² , B = 10X, C = -56, also A = a², B = 2 . 5X, C = 25 – 81, impliziert A = a², B = 2 . ab, C = b² – (c²),
II. X² – 10X – 56 = 0
A = X², B = – 10X, C = -56, also A = a², B = – 2 . 5X, C = 25 – 81, impliziert A = a², B = – 2 . ab, C = b² – (c²),
3. RACIONALIZANDO
I. Wenn in (a + b)² = c² => a² + 2ab + b²- (c²) = 0
A = a², B = 2 ab , C = b² – (c²), Beob: (B = 2 ab) nach Regel sind a und b streng positiv, In X² + 10X – 56 = 0
A = X² , B = 10X, C = -56, Beob.: (B = 10X) nach Regel ist X strikt positiv.
Also in X² + 10X – 56 = 0 ist die einzig mögliche Wurzel 4, weil -14 gegen die mathematische Regel verstößt.
II. Wenn in (a – b)² = c² => a² – 2ab + b²- (c²) = 0, (a = X, b = – 5, c = 9)
A = a², B = – 2 ab, C = b² – (c²), Beob.: (B = – 2 ab) in der Regel, wenn b negativ ist, muss a strikt positiv sein.
Bei X² – 10X – 56 = 0
A = X² , B = -10X, C = -56, Beob.: (B = – 10X) nach Regel ist X strikt positiv.
In X² – 10X – 56 = 0 ist die einzig mögliche Wurzel von X also 14, weil – 4 gegen die mathematische Regel verstößt.
4. BESTELLUNG
4.1 FALL I
Wenn (X² + 10X – 56 = 0) = (a² – 2ab + b²- (c²)) dann:
A = X² und A = a², impliziert (X = a)
B = 10X und B = 2ab, impliziert (10X = 2ab)
C = -56 und C = + b²- (c²), impliziert (- 56 = b² – (c²))
Finden Sie die Wurzel, finden Sie zuerst den Wert von b:
wenn A = X und A + a, B = 10X, wobei B = 2ab, setzen wir b in Beweis
10X = 10a, impliziert 10a = 2ab => b = 10a/ 2a => b = 5
Zweitens wird der Wert von c gefunden;
Wenn C = -56 und C = + b²- (c²), setzen wir c in Beweis
-56 = b²- (c²) impliziert -56 = 5²- (c²) => c² = 25 + 56 => c² = 81 => c = 9
Schließlich wird der Wert der Wurzel gefunden;
Also (a + b)² = c², impliziert (a + b) = c
Wenn ((a + b)² = c² ) = ((X + b)² = c²), impliziert dies (X + b) = c, das heißt:
X + 5 = 9 => X = 9 – 5 => X = 4
4.2 FALL II
Wenn (X² – 10X – 56 = 0) = (a² – 2ab + b²- (c²)) dann:
A = X² und A = a², impliziert (X = a)
B = – 10X und B = – 2ab, impliziert (- 10X = 2ab)
C = -56 und C = b²- (c²), impliziert (- 56 = b² – (c²))
Finden Sie die Wurzel, finden Sie zuerst den Wert von b:
wenn A = X und A = a, B = – 10X, wobei B = – 2ab ist, setzen wir b in Beweis
– 10X = – 10a, impliziert – 10a = – 2ab => – b = – 10a/ 2a => – b = – 5
Nach dem Wert von c:
Wenn C = – 56 und C = – b²- (c²), setzen wir c in Beweis
– 56 = – b²- (c²) impliziert – 56 = – 5²- (c²) => c² = 25 + 56 => c² = 81 => c = 9
Schließlich wird der Wert der Wurzel gefunden:
Also (a – b)² = c², impliziert (a – b) = c
Wenn ((a – b)² = c² ) = ((X – b)² = c²) , impliziert dies (X – b) = c, das heißt:
X – 5 = 9 => X = 9 + 5 => X = 14
5. PARADOX
Wie in den beiden Beispielen gezeigt, war es nicht notwendig, die Formel von Bhaskara zu verwenden, um irgendeine der quadratischen Gleichungen zu lösen.
Sowohl (X² + 10X – 56 = 0) als auch (X² – 10X – 56 = 0) wurden gelöst, ohne eine solche mathematische Ressource zu verwenden, wobei betont wurde, dass es in beiden Fällen nur eine mögliche Wurzel gibt.
Obwohl der Fehler in Bhaskaras Formel nachgewiesen wurde, gibt es jedoch immer noch einen Fehler von größerem systemischem Ausmaß, nämlich die Vorzeichenregel, denn wie von Pedreira (2016) gesehen und normalisiert, bleibt eine negative Zahl zum Quadrat negativ, da sie geometrisch ist Verhältnisse haben neutrale Eigenschaften, sie multiplizieren oder dividieren einfach etwas; B.: 3 x *3 = *9 (wobei (*) vor einer Zahl angibt, dass sie negativ ist, um sie nicht mit dem Vorzeichen (–) zu verwechseln, das eine Subtraktion anzeigt), wodurch das Vorzeichen beim Ändern von nicht geändert werden kann Seite der Gleichheit, die mit der Basis- und Komponenten Regel gelöst werden kann, wobei Basis (B) gleich der Summe der Komponenten und Komponente (C) gleich der Differenz von Basis um eine oder mehrere Komponenten ist,
Beispiel: B = 15 C = 8 und 7, 15 = 8 + 7 => 15 – 8 = 7 => 8 = 15 – 7 => 8+7 = 15 => 15 – (8 + 7) = 0
6. EINEN VERGLEICH MACHEN
Die Gleichung (a + b)² = c² endet immer in einer Unbekannten in der Form: a² + 2ab +b² – (c²) = 0, und dies erfordert schließlich eine zweite Stufe der arithmetischen Ausarbeitung, um das Problem zu lösen, wie wir gesehen haben Vor. Wenn wir dagegen die Basis- und Komponenten Regel (BC) verwenden, ist die Lösung linear und stetig;
Bsp.: (a + b)² = c², nach der BC-Regel: c (a + b) = c² => ca + cb = c²
7. IN DER PRAXIS:
7.1 BEISPIEL I
Aktuelle Regel: ( X + 8)² = 144 => ( X + 8) . (X + 8) = 144 => X² + 2 . 8 . X + 64 = 144 =>
X² + 16X + 64 – 144 = 0 => X² + 16X – 80 = 0 (unbekannt)
Grundregel und Komponenten: (X + 8)² = 144 => 12 . X + 12 . 8 = 144 => 12X + 96 = 144 =>
12X = 144 – 96 => 12X = 48 => X = 48/12 => X = 4 (direktes Ergebnis)
7.2 BEISPIEL II
Aktuelle Regel: ( X – 5)² = 49 => ( X – 5) . (X – 5) = 49 => X² + 2 . – 5 . X + 25 = 49 =>
X² + 10X + 25 – 49 = 0 => X² + 10X – 14 = 0 (unbekannt)
Grundregel und Komponenten: (X – 5)² = 49 => 7 . X-7 . 5 = 49 => 7X – 35 = 49 =>
7X = 49 +35 => 7X = 84 => X = 84/7 => X = 12 (direktes Ergebnis)
7.3 BEISPIEL III: ANDERE MÖGLICHKEITEN
Aktuelle Regel: ( X + 6)² = – 121 (keine Lösung): Aufgrund der aktuellen Regel in einer quadratischen Gleichung in der Form (a + b)² = c², wird c² immer positiv sein, weil jede positive oder negative Zahl zu einer gleichmäßigen Potenz erhoben, wird es positiv.
Grundregel und Komponenten: (X + 6)² = *121 => 11X + 11 . 6 = *121 => 11X = *121 – 66 => 11X = *187 => X = *187/11 => X = *17 (hat eine Lösung): aufgrund der Regel von Basis und Komponenten, um die Zahlen zu berücksichtigen entweder Multiplikatoren oder Divisoren wie geometrische Verhältnisse (RG) und RGs haben einen neutralen Charakter, egal ob sie potenziert werden, gerade oder ungerade, wenn sie positiv sind, bleiben sie positiv, wenn sie negativ sind (*) es wird weiterhin negativ sein.
8. SCHLUSSBETRACHTUNGEN
Es ist erwiesen, dass die Formel der quadratischen Gleichung auch innerhalb der derzeit verwendeten Regeln immer zwei Wurzeln als Antwort gibt, was eine ewige Dualität der Genauigkeit auslöst, die an sich ein Paradoxon ist, dieses Versagen ergibt sich aus der Tatsache, dass wir dies nicht tun berücksichtige versteckte Terme in seiner Lösung, das heißt, wenn wir den distributiven betrachten: (a + b)² => (a + b) . (a + b) = a² + 2ab + b² , lassen wir die Gleichheit (c²) weg und dies führt zu einer Unklarheit in seiner Auflösung, was zu einem systemischen Fehler führt.
Selbst wenn wir diesen Fehler korrigieren, ist das derzeitige System immer noch begrenzt, denn wenn wir die Regel der Basis und der Komponenten verwenden, erweitern wir die Möglichkeiten der Operationen unendlich, denn wenn wir geometrische Verhältnisse als neutral betrachten, haben Gleichungen mit beliebiger Potenz das Vorzeichen von deren Zähler, egal ob positiv oder negativ.
VERWEISE
PEDREIRA, S. M. O Valor dos Números. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 01, Vol. 08. pp. 05-16. setembro de 2016. Disponível em: https://www.nucleodoconhecimento.com.br/matematica/o-valor-dos-numeros.
PEDREIRA, S. M. Reestruturando os Números. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 09, Vol. 06, pp. 115-120. Setembro de 2019. Disponível em: https://www.nucleodoconhecimento.com.br/matematica/reestruturando-os-numeros.
SILVA, L. P. M. Fórmula de Bhaskara. Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/formula-bhaskara.htm. Acesso em 15 de dezembro de 2021.
[1] Diplom-Logistiker, 4º Semester Chemie, Hobby-Mathematiker.
Gesendet: Dezember 2021.
Genehmigt: Februar 2022.