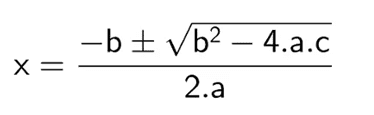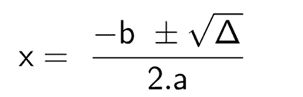ARTICLE ORIGINAL
PEDREIRA, Sinvaldo Martins [1]
PEDREIRA, Sinvaldo Martins. L’échec de Bhaskara. Revista Científica Multidisciplinar Núcleo do Conhecimento. An. 07, éd. 02, Vol. 02, p. 178-186. Février 2022. ISSN : 2448-0959, Lien d’accès: https://www.nucleodoconhecimento.com.br/olympiades-mathematiques/lechec-de-bhaskara
RÉSUMÉ
Ce travail vise à montrer qu’en raison de failles dans le système arithmétique, des règles universitaires basées sur une mauvaise norme peuvent générer des résultats incorrects, comme la règle de l’équation quadratique, qui peut propager une fausse certitude d’exactitude, pour le simple fait d’être à suivre paradigmes séculaires, sans une large observation contextuelle de la réalité en cause, car lorsqu’il s’agit de sciences exactes, il faut toujours avoir une vue holistique, en considérant largement tous les facteurs en jeu, car une action présente a des conséquences dans le futur et quand on se base sur systèmes défectueux, nous finissons par avoir un faux sentiment de réussite, puisque nous suivons tous les pseudo-préceptes à la lettre. Cependant, un nouveau système émerge, mettant à l’épreuve la force de la voie arithmétique à suivre.
Mots clés : Échecs, Précision, Système, Holistique.
1. INTRODUCTION
Tout d’abord, ce travail n’est pas destiné à minimiser le génie de Bhaskara, mais à montrer qu’en raison d’une faille conceptuelle dans le système arithmétique, même les génies peuvent faire des erreurs.
L’équation quadratique a été normalisée en se présentant sous la forme suivante : ax² + bx + c = 0, où sa solution était une inconnue, donc la solution au problème est venue avec la formule :
Mais pour simplifier la résolution, trouvez d’abord le delta ;
Δ = b² – 4ac
Par la suite, le résultat de delta est joint à l’équation :
Enfin, comme il s’agit d’une équation quadratique, X a deux résultats :
X = X, et X = X,,
Exemple I :
X² + 10 X – 56 = 0 A = 1, B = 10, C = – 56
Δ = 10² – (4. 1 .- 56)
Δ = 100 – (- 224)
Δ = 324
X = -10 ± √324
2.1
X, = –10 + 18 => X, = 8 => X, = 4
2 2
X,, = –10 – 18 => X,, = – 28 => X,,= – 14
2 2
Donc les réponses sont : X, = 4 et X,, = -14
Exemple II :
X² – 10 X – 56 = 0 A = 1, B = -10, C = – 56
Δ = -10² – ( 4. 1 .- 56)
Δ = 100 – (- 224)
Δ = 324
X = -10 ± √324
2.1
X, = 10 + 18 => X, = 28 => X, = 14
2 2
X,, = 10 – 18 => X,, = – 8 => X,, = – 4
2 2
Donc les réponses sont : X, = 14 et X,, = – 4
2. HOLISME
2.1 HOLISME I
Comme mentionné précédemment, utilisons un peu de holisme ; toute équation quadratique provient d’une équation distributive, où :
1er cas
(a + b)² => (a + b) . (a + b) = a² + 2ab + b² Remarque : a et b sont strictement positifs selon la règle.
2ème cas
(a – b)² => (a – b) . (a – b) = a² – 2ab + b² Remarque : a positif et b négatif selon la règle.
2.2 HOLISME II
Dans le terme caché, chaque addition et chaque soustraction a un résultat, donc
a + b = c, conséquence (a + b)² = c², alors ; a² + 2ab + b² = c²
a – b = c, conséquence (a – b)² = c², alors ; a² – 2ab + b² = c²
2.3 HOLISME III
Mise en évidence des termes, mettons les termes de l’équation en évidence ;
I. a = X, b = 5, c = 9
Bientôt; (a + b)² = c² => (X + 5)² = 9² => X² + 2 . 5X + 25 = 81 => X² + 10X + 25 – 81 = 0 => X² + 10X – 56 = 0
II. a = X, b = – 5, c = 9
Bientôt; (a – b)² = c² => (X – 5)² = 9² => X² – 2 . 5X + 25 = 81 => X² – 10X + 25 – 81 = 0
=>X² – 10X – 56 = 0
2.4 HOLISME IV
Correspondance:
I. X² + 10X – 56 = 0
A = X² , B = 10X, C = -56, donc A = a², B = 2 . 5X, C = 25 – 81, implique A = a², B = 2 . ab, C = b² – (c²),
II. X² – 10X – 56 = 0
A = X², B = – 10X, C = -56, donc A = a², B = – 2 . 5X, C = 25 – 81, implique A = a², B = – 2 . ab, C = b² – (c²),
3. RATIONALISER
I. Si dans (a + b)² = c² => a² + 2ab + b²- (c²) = 0
A = a², B = 2 ab , C = b² – (c²), Remarque : (B = 2 ab) par règle a et b sont strictement positifs, In X² + 10X – 56 = 0
A = X² , B = 10X, C = -56, Remarque : (B = 10X) par règle X est strictement positif.
Donc dans X² + 10X – 56 = 0 la seule racine possible est 4, car -14 va à l’encontre de la règle mathématique.
II. Si dans (a – b)² = c² => a² – 2ab + b²- (c²) = 0, (a = X, b = – 5, c = 9)
A = a², B = – 2 ab, C = b² – (c²), Remarque : (B = – 2 ab) en règle générale si b est négatif, a doit être strictement positif.
En X² – 10X – 56 = 0
A = X² , B = -10X, C = -56, Remarque : (B = – 10X) par règle X est strictement positif.
Donc dans X² – 10X – 56 = 0, la seule racine possible de X est 14, car – 4 va à l’encontre de la règle mathématique.
4. COMMANDE
4.1 CAS I
Si (X² + 10X – 56 = 0) = (a² – 2ab + b²- (c²)) alors :
A = X² et A = a², implique (X = a)
B = 10X et B = 2ab, implique (10X = 2ab)
C = -56 et C = + b²- (c²), implique (- 56 = b² – (c²))
En trouvant la racine, trouvez d’abord la valeur de b :
si A = X et A + a, B = 10X où B = 2ab, on met b en évidence
10X = 10a, implique 10a = 2ab => b = 10a/ 2a => b = 5
Deuxièmement, la valeur de c est trouvée ;
Si C = -56 et C = + b²- (c²), on met c en évidence
-56 = b²- (c²) implique -56 = 5²- (c²) => c² = 25 + 56 => c² = 81 => c = 9
Enfin, la valeur de la racine est trouvée ;
Donc (a + b)² = c², implique (a + b) = c
Si ((a + b)² = c² ) = ((X + b)² = c²), cela implique (X + b) = c, soit :
X + 5 = 9 => X = 9 – 5 => X = 4
4.2 CAS II
Si (X² – 10X – 56 = 0) = (a² – 2ab + b²- (c²)) alors :
A = X² et A = a², implique (X = a)
B = – 10X et B = – 2ab, implique (- 10X = 2ab)
C = -56 et C = b²- (c²), implique (- 56 = b² – (c²))
En trouvant la racine, trouvez d’abord la valeur de b :
si A = X et A = a, B = – 10X où B = – 2ab, on met b en évidence
– 10X = – 10a, implique – 10a = – 2ab => – b = – 10a/ 2a => – b = – 5
Selon la valeur de c :
Si C = – 56 et C = – b²- (c²), on met c en évidence
– 56 = – b²- (c²) implique – 56 = – 5²- (c²) => c² = 25 + 56 => c² = 81 => c = 9
Enfin, la valeur de la racine est trouvée :
Donc (a – b)² = c², implique (a – b) = c
Si ((a – b)² = c² ) = ((X – b)² = c²) , cela implique (X – b) = c, soit :
X – 5 = 9 => X = 9 + 5 => X = 14
5. PARADOXE
Comme démontré dans les deux exemples, il n’était pas nécessaire d’utiliser la formule de Bhaskara pour résoudre l’une des équations quadratiques.
(X² + 10X – 56 = 0) et (X² – 10X – 56 = 0) ont été résolus sans utiliser une telle ressource mathématique, soulignant que dans les deux il n’y a qu’une seule racine possible.
Cependant, bien que la faille de la formule de Bhaskara ait été démontrée, il y a toujours une faille d’un degré systémique plus important, qui est la règle des signes, car comme vu et normalisé par Pedreira (2016), un nombre négatif au carré reste négatif, puisque la géométrie les ratios ont des caractéristiques neutres, se contentant de multiplier ou de diviser quelque chose ; ex : 3 x *3 = *9 (où (*) devant un nombre indique qu’il est négatif, pour ne pas le confondre avec le signe (–) qui indique une soustraction), laissant le défaut de changer de signe lors du changement de côté de l’égalité, qui peut être résolu avec la règle de la base et des composants, où la base (B) est égale à la somme des composants et le composant (C) est égal à la différence de la base par un ou plusieurs composants ,
Ex. : B = 15 C = 8 et 7, 15 = 8 + 7 => 15 – 8 = 7 => 8 = 15 – 7 => 8+7 = 15 => 15 – (8 + 7) = 0
6. FAIRE UNE COMPARAISON
L’équation (a + b)² = c² aboutira toujours à une inconnue sous la forme : a² + 2ab +b² – (c²) = 0 et cela finit par exiger une deuxième étape d’élaboration arithmétique pour résoudre le problème, comme on le voit avant de. Alors que si nous utilisons la Règle de Base et Composantes (BC), la solution est linéaire et continue ;
Ex. : (a + b)² = c², par la règle BC : c (a + b) = c² => ca + cb = c²
7. EN PRATIQUE:
7.1 EXEMPLE I
Règle actuelle : ( X + 8)² = 144 => ( X + 8) . (X + 8) = 144 => X² + 2 . 8 . X + 64 = 144 =>
X² + 16X + 64 – 144 = 0 => X² + 16X – 80 = 0 (inconnu)
Règle de base et composantes : (X + 8)² = 144 => 12 . X + 12 . 8 = 144 => 12X + 96 = 144 =>
12X = 144 – 96 => 12X = 48 => X = 48/12 => X = 4 (résultat direct)
7.2 EXEMPLE II
Règle actuelle : ( X – 5)² = 49 => ( X – 5) . (X – 5) = 49 => X² + 2 . – 5 . X + 25 = 49 =>
X² + 10X + 25 – 49 = 0 => X² + 10X – 14 = 0 (inconnu)
Règle de base et composantes : (X – 5)² = 49 => 7 . X-7. 5 = 49 => 7X – 35 = 49 =>
7X = 49 +35 => 7X = 84 => X = 84/7 => X = 12 (résultat direct)
7.3 EXEMPLE III : AUTRES POSSIBILITÉS
Règle actuelle : ( X + 6)² = – 121 (pas de solution) : en raison de la règle actuelle dans une équation quadratique sous la forme (a + b)² = c², c² sera toujours positif, car tout nombre positif ou négatif étant élevé à une puissance paire, il devient positif.
Règle de base et composantes : (X + 6)² = *121 => 11X + 11 . 6 = *121 => 11X = *121 – 66 => 11X = *187 => X = *187/11 => X = *17 (a une solution) : en raison de la règle de Base et Composants pour considérer les nombres les multiplicateurs ou les diviseurs tels que les rapports géométriques (RG) et les RG ont un caractère neutre, qu’il soit élevé à une puissance, paire ou impaire, s’il est positif, il continuera à être positif, s’il est négatif (*) il restera négatif.
8. CONSIDÉRATIONS FINALES
Il a été prouvé que même dans les règles actuellement utilisées, la formule de l’équation quadratique donne toujours comme réponse deux racines, déclenchant une éternelle dualité d’exactitude, ce qui est en soi un paradoxe, cet échec provenant du fait que nous ne considérer les termes cachés dans sa solution, c’est-à-dire lorsque l’on considère la distributive : (a + b)² => (a + b) . (a + b) = a² + 2ab + b² , on omet l’égalité (c²) et cela finit par générer une obscurité dans sa résolution, provoquant une défaillance systémique.
Même en corrigeant ce lapsus, le système actuel reste encore limité, car lorsqu’on utilise la règle de Base et des composantes, on augmente à l’infini les possibilités d’opérations, puisque lorsqu’on considère les rapports géométriques comme neutres, les équations élevées à n’importe quelle puissance auront le signe de leur numérateur, qu’il soit positif ou négatif.
RÉFÉRENCES
PEDREIRA, S. M. O Valor dos Números. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 01, Vol. 08. pp. 05-16. setembro de 2016. Disponível em: https://www.nucleodoconhecimento.com.br/matematica/o-valor-dos-numeros.
PEDREIRA, S. M. Reestruturando os Números. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 09, Vol. 06, pp. 115-120. Setembro de 2019. Disponível em: https://www.nucleodoconhecimento.com.br/matematica/reestruturando-os-numeros.
SILVA, L. P. M. Fórmula de Bhaskara. Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/formula-bhaskara.htm. Acesso em 15 de dezembro de 2021.
[1] Diplômé en Logistique, 4ème semestre en Chimie, Mathématicien amateur.
Envoyé : Décembre 2021.
Approuvé : Février 2022.