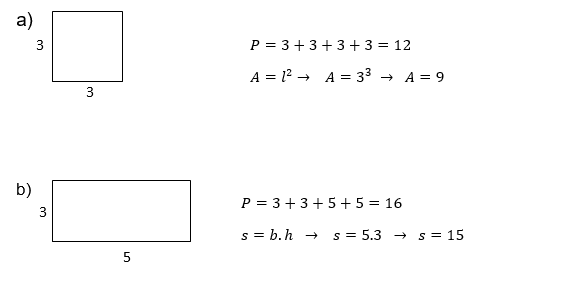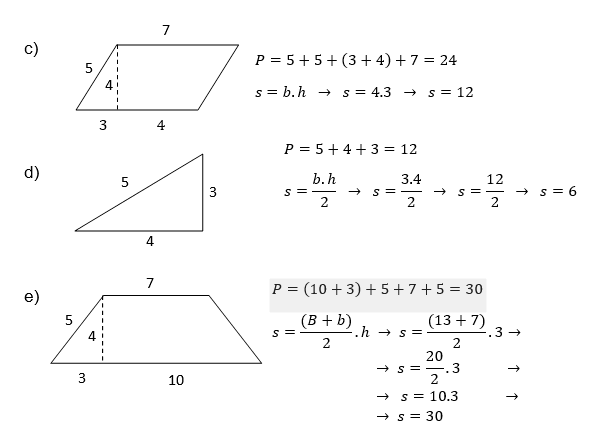FREIRE, Amanda Freitas [1], RODRIGUES, Fabiana Soares [2], AQUINO, Maria Rosane Souza [3], SOARES, Maria Vanessa [4], GOIS, David Denis Pires de [5], VIANA, José Damião [6]
FREIRE, Amanda Freitas; et.al. L’utilisation de la Géoplan dans l’enseignement de la géométrie : calculer l’aire et le périmètre. Revue scientifique pluridisciplinaire de la base de connaissances. 03 ans, Ed. 06, vol. 03, pp. 119-135, juin 2018. ISSN:2448-0959
Résumé
Cette recherche apporte comme thème central de l’enseignement du calcul d’aire et le périmètre des figures de la géométrie plane, en utilisant comme ressource le Géoplan. Se défend, dans cet article, l’idée que, grâce à l’utilisation de matériaux manipulables, est possible faciliter le contenu de l’enseignement/apprentissage, de la même façon développer le raisonnement et l’intérêt des étudiants pour résoudre les problèmes. Dans cet article seront présentés avec un domaine de caractère qualitatif, qui a eu lieu dans la dernière série de l’école primaire, qui s’est tenue à la huitième année de l’école « C » État journaliste Edson Régis, dans le quartier de São Cristóvão dans la ville de Arcoverde-PE, un atelier organisé par le programme institutionnel de l’Initiation à l’enseignement (PIBID). Au cours de l’atelier, on a noté une participation effective dans la classe et aussi une amélioration de la performance des élèves.
Mots clés : enseignement des mathématiques, géométrie plane, Géoplan.
Introduction
Aujourd'hui, nous vivons dans une sorte de ce plus en plus axé sur les progrès technologiques, et la réunion est nécessaire pour les différentes actions humaines des plus simples aux choses complexes. La connaissance mathématique est d’une importance capitale pour l’individu est liée à la société et l’environnement dans lequel il vit. Cette connaissance aujourd'hui ne présentent dans la vie quotidienne de beaucoup d’étudiants, de difficultés à établir des relations qu’appris avec des situations quotidiennes. La BNCC (Base nationale de Curriculum commun) des rapports sur ce sujet que les élèves doivent établir les connaissances acquises avec les événements quotidiens et décrit ce qui suit :
Il est important de souligner que cette association entre le monde physique qui nous entoure et dans le monde inconnu des mathématiques peut être liée à un double. Par exemple, alors qu’un rectangle de parallélépipède agit comme un modèle abstrait pour la boîte à chaussures objet physique, au modèle abstrait de sphère figure géométrique spatiale, nous pouvons associer l’objet du football du monde physique (Brésil, 2015) .
L’objectif de cette recherche est de mettre en évidence l’importance de l’utilisation des ressources dans l’apprentissage des mathématiques de l’enseignement et l’enseignement de la géométrie plane, plus précisément le calcul de l’aire et le périmètre. Alors soyez dans le monde physique ou immatériel mathématiques est présent dans tout autour de nous, il est donc important à votre connaissance. En classe la complexité en mathématiques associé avec le jour le jour, il devient plus présent, une fois les enjeux et questions présentées ne sont pas représentées de manière dans laquelle les étudiants peuvent toucher et posent avec quelque chose de physique. Ces questions sont présentées d’une manière seulement imaginaire. Alors quand est-il une fonctionnalité qui permet à l’enseignant peut exposer dans votre forme physique à l’impasse et les questions soulevées, l’enseignement devient plus attrayante et facile à comprendre pour l’étudiant.
Laissant ces difficultés se posent quelques questions : Comment faire l’éducation mathématique plus attrayant pour les étudiants ? L’utilisation de la Géoplan comme outil d’enseignement faciliterait l’apprentissage des élèves ? Comment nous en tant qu’éducateurs pouvons rendre l’enseignement plus polyvalent ? Il est essentiel que les enseignants les connaissances que l’étudiant possède déjà et laissant ce point peut être faite que connu des connexions avec les mathématiques. Rien n’est plus utile d’utiliser les instructions apprises dans les problèmes qui se posent sur la société. Avec cela, nous avons élaboré cette recherche à travers le programme institutionnel de l’Initiation à l’en[7]seignement (PIBID) de la municipalité de Superior éducation de Arcoverde (EFSA), afin d’introduire l’étudiant à une Math conçu avec ressources pédagogiques. Nous suggérons le Géoplan comme un outil pour l’enseignement/apprentissage de calcul d’aire et périmètre des figures de l’avion, pour les élèves de la série finale de l’école primaire II, plus précisément la 8e année journaliste Edson Régis situées en Arcoverde-PE et. Étant donné que grâce à cette fonctionnalité, nous pouvons découvrir les concepts fondamentaux de la géométrie plane ou la géométrie non euclidienne tels que : point, ligne et plan.
Le premier géométriques des idées a débuté avec la capacité humaine à rechercher des solutions de rechange pour résoudre des problèmes pratiques :
Cherchant l’origine du développement de la géométrie dans les premiers jours, avec l’homme primitif, on peut imaginer que les configurations de l’espace de connaissances, de formes et de tailles ont provenu, éventuellement avec la capacité humaine à observer et à réfléchir sur la déplacements, avec la construction de stratégies pour la chasse et de la nourriture des cultures, avec la création d’outils et ustensiles, afin de satisfaire leurs besoins fondamentaux. Pour sécuriser le logement, à la Division du travail, autres besoins se font jour et la production de l’élargissement des connaissances géométriques. La nécessité d’un renforcement, délimitent le terrain a conduit à la notion de chiffres, de courbes et de postes de vertical, perpendiculaire, parallèle (GH, 2008, p. 7).
Méthodologie
Il s’agit d’une recherche avec une approche qualitative, qui a utilisé une technique de recherche sur le terrain. Comme un instrument de collecte de données ont été utilisé des questionnaires, d’entrevues et observation.
À la recherche de réponses aux questions présentées dans l’introduction, nous effectuons diverses activités telles que des entrevues avec les enseignants et étudiants et un atelier en utilisant le Géoplan. At a tout d’abord, a été interviewé, professeur du régent de huitième année « C » et peu de temps après la série qui le précède, un questionnaire a été élaboré contenant cinq questions : vous connaissez le Géoplan ? Vous utilisez un type de ressource pour l’enseignement de la géométrie ? Quelles sont les difficultés rencontrées au cours de ces classes ? Au cours de la classe, vous avez présenté les principales figures géométriques plat ? Comment enseignez-vous le calcul d’aires et de périmètres.
En ce qui concerne les élèves, un questionnaire a été appliqué à trente élèves avec cinq questions, certains d'entre eux sont : vous connaissez le Géoplan ? Classe Geometry l’enseignant a utilisé une sorte de matériau utilisable ? Vous savez quel est le périmètre ? Et région ? Vous savez comment calculer le périmètre et l’aire de ces chiffres ?
Pour analyser les réponses, on réalise la grande difficulté dans le contenu, le délai de grâce pour rencontrer le Géoplan et quelques chiffres plats. Basé sur les réponses a organisé un atelier à l’aide du Géoplan, aborder le calcul de l’aire et le périmètre.
Après l’atelier, interview avec les élèves pour évaluer les performances, contenant trois questions : le Géoplan pourrait être utilisé en géométrie ? Cette fonctionnalité facilite le calcul de l’aire et le périmètre ? Il y avait des difficultés à manipuler le Géoplan ?
Cette étude vise à trouver des réponses aux questions énoncées et vérifier l’importance de la Géoplan comme facilitateur du processus enseignement-apprentissage du calcul aire et le périmètre.
Enseignement des mathématiques
Futurs enseignants en mathématiques sont confrontés à des situations préoccupantes dans le processus enseignement-apprentissage. Dans la salle de classe, l’enseignant doit enseigner une vaste quantité de contenu en peu de temps, doit transmettre cette connaissance qui a eu des centaines d’années en quelques heures de classe, étant ces passé la plupart du temps de manière abrupt et difficile d’abstraction et de causer des blocages dans la compréhension des étudiants.
Oublier que cet objectif du processus éducatif est également que les étudiants peuvent avoir la plus grande utilisation possible, mais cet objectif est loin d’être atteint, car beaucoup d’enseignants est plus concernés par la quantité de contenu que de la quantité appliquée cela la connaissance est réceptive par l’étudiant.
La construction de la connaissance mathématique dépend beaucoup de la façon dont elles s’adressent, les concepts doivent être transférés d’une manière plus proche de la réalité physique, apportant des exemples de la vie quotidienne et aussi en utilisant les connaissances acquises par les élèves à l’extérieur le terrain de l’école. Les enseignants seraient de la responsabilité de votre leçon de planification à l’avance, basé sur les besoins et les difficultés de votre élève, dans lequel votre objectif est de fournir l’absence de vos élèves.
Saint Junior (2011), stipule que :
L’enseignement des mathématiques doit être considérée comme un processus plus large de construction, dans lequel il est nécessaire d’avoir un plan pour régler les problèmes posés, et il est possible d’atteindre les objectifs proposés de manière mécanique.
Mathématiques dans l’actualité
On sait que les mathématiques ont émergé dès lors que l’homme avait besoin de compter. Depuis ce moment, l’homme a été la création des stratégies de compter pour pouvoir créer les symboles mathématiques de la premières avec le passage du temps, les quantités étaient représentées par les expressions, les gestes, les mots et les symboles, chacun de qui les gens a votre chemin représentation.
Mathématiques tout au long de l’histoire subit diverses évolutions pour arriver à ce que nous connaissons aujourd'hui. Actuellement cette discipline joue un rôle essentiel dans la vie de l’homme, est l’utilisation et les connaissances dans ce domaine vous propose à l’individu la possibilité de construire un avenir nettement mieux. L’absence de cette connaissance limite les humains pour résoudre les problèmes de la vie quotidienne, pour entrer dans le marché du travail et pour acquérir de nouvelles connaissances dans divers domaines qui utilise les mathématiques en tant que discipline est indispensable.
Ce contexte permet d’analyser cette discipline dans de nombreux aspects, ce qui porte à la salle de classe, nous allons examiner les difficultés d’apprentissage rencontrées par certains étudiants.
Dans ce domaine, il y a un contenu différent dans lequel ils sont trouvent plusieurs troubles d’apprentissage, une des disciplines des mathématiques dans lequel il y a des grandes difficultés est la géométrie.
Géométrie plane ou la géométrie non euclidienne
Euclid dans votre livre « The Element » divisée en 13 volumes, où 10 qu’il se consacre à votre création et théorie des nombres 03, recherché sur trois principes géométriques, ils sont :
- Le point (est que vous n’avez pas parties)
- La ligne droite (longueur sans épaisseur)
- Le plan (est tout ce que qui a longueur et largeur)
Celles-ci est considérées comme aucune définition parce qu’ils sont des mots primitifs.

Dans le cadre de la géométrie plane, nous étudierons les polygones et les figures plates, tels que rectangle, carré, parallélogramme, triangle, trapèze, entre autres.
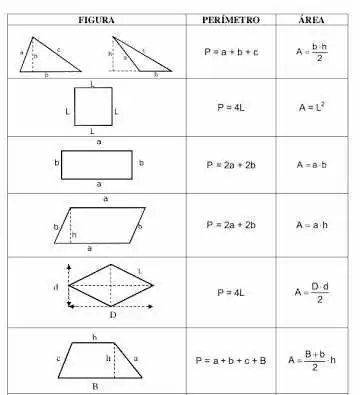
Polygone est un plan limité pour des segments de droites, laissant, on trouve deux types : régulières, avec les côtés et les angles congrus et irrégulières, avec les côtés et les angles congruents, dans cette étude nous pouvons trouver des concepts primitifs de la géométrie plat, qui est le calcul aire et périmètre, calculer le périmètre des figures de l’avion est fait par la somme de ses parties. Nous savons qu’un carré a quatre côtés mesurant ?, bientôt, nous avons l’expression suivante :, où est le périmètre et ? est le côté de la place, autrement dit, le périmètre est le contour d’une surface donnée, que ce soit régulier ou non.
L’aire d’un polygone est déjà un peu plus compliqué, parce qu’il ne sera pas le contour de la figure, mais le nombre qu’il occupe dans le plan, la zone est généralement donné par la lettre peut être déterminée avec une expression qui se déroule selon la figure qu’il représente , nous allons voir quelques photos et comment calculer leurs domaines respectifs et les périmètres.
Exemples :
Calculer les aires des figures ci-dessous :
À partir de ce point, que nous pouvons voir que la réalité de l’étudiant est pleine de figures géométriques plat, puis cet étudiant vous rencontrerez des problèmes de complexités diverses, ainsi les connaissances géométriques devient importante à la formation intellectuelle l’étudiant parce qu’il vous fournira des compétences et capacités qui vous aidera à obtenir situées et résoudre certains problèmes dans l’environnement dans lequel il est inséré.
Selon le national curriculum paramètres – NCP (Brésil, 1998), les concepts géométriques constituent une partie importante du programme d’études de mathématiques à l’école secondaire, parce que par ce biais l’étudiant développe un type spécial de réflexion qui vous permet de comprendre et représenter le monde dans lequel il vit. Si cela a fonctionné du monde physique, permet aux étudiants d’établir des liens entre les mathématiques et autres domaines de la connaissance.
Il est compréhensible que, selon le SNPC apprentissage de la géométrie est d’une importance primordiale à tous les niveaux de l’éducation. Cependant les enseignants pour plusieurs raisons ne soucient pas de l’enseignement de la géométrie et si peu dans des fonctions de recherche qui facilitent l’enseignement-apprentissage et faire que l’apprentissage plus dynamique, sans dévier du contexte. Observant que certains auteurs à développer leurs manuels mis ce contenu dans les derniers chapitres, rendant la conformité barrée par les éducateurs.
GÉOPLAN
Le nom vient de la commune Geo, Géoplan sens géométrie et plan, ce qui signifie surface plane donc Géoplan. Mot, c’est qu’il a été tout d’abord utilisé en 1961, par le professeur Caleb Gattegno, de l’Institute of education, University of London (KNIJNIK, BASSO ; KLÜSENER, 1996 ; Menezes, 2008).

Le Géoplan est qu'un morceau de bois plat surface avec clous tapé la même distance de l’autre. Il existe certains types de Géoplan : carré, circulaire, le Trelissado et le bureau ovale. Le carré est le plus largement utilisé, en bois surface split composé alors quadrillé square par clous équidistants. C’est une confection simple, qui aide les élèves à surmonter leurs difficultés et en même temps apprendre à manipuler, il peut également être utilisé comme un jeu mathématique qui facilite la compréhension de l’étudiant en relation ludique. Cette fonctionnalité permet aux étudiants d’acquérir de nouvelles expériences et aussi rend possible de votre forme physique, quitter le mode tellement abstrait, imaginaire, par le biais de construction des figures et avoir un gadget supplémentaire basée sur le nombre de broches de gauche à droit, les lignes et les colonnes à l’intérieur et à l’extérieur de l’ouvrage porteur plus dynamique, car contrairement aux autres jeux du Géoplan a souplesse, donc les étudiants peuvent faire et à défaire à tout moment avec votre professeur.
Selon Sharma (2009, p. 8) fait remarquer que :
Dans le jeu, vous pouvez prendre des risques, essayer, essayer, inventer, tout est gratuit le fantôme d’une évaluation punitive et neutre. L’enseignant qui utilise le jeu a pour mission d’organiser et de systématiser ces activités pour permettre aux étudiants de marcher à la recherche de nouvelles connaissances (…).
Cependant se rend compte qu’avec l’introduction de la Géoplan, peut favoriser l’enseignement de la géométrie plane une façon différente d’aborder et représentent les différents contenus de remise en forme, telles que : calculer l’aire et le périmètre des polygones.
Recherches sur le terrain
Après l’identification de la Géoplan comme une ressource utile et capable de promouvoir l’apprentissage significatif, trois questionnaires, deux ont été pour la collecte de données et l’autre pour la collecte des résultats.
Selon le questionnaire que le professeur a répondu que jamais utilisé n’importe quelle ressource didactique manipulé et ignore le Géoplan. La série précédente dans vos États de rapport qui fait utilise d’autres matières manipulables, y compris le Géoplan. Ces apporté controversée, car selon l’interview avec les élèves, ils prétendaient ne pas connaître le matériel.
Le contenu a travaillé, étaient calculs d’aires et de périmètres de figures plates, avant que nous appliquons l’atelier nous aussi une entrevue avec la classe, nous avons détecté une grande difficulté pour eux de reconnaître le Géoplan, peu de polygones, calculer Aires et périmètres, comme le montre les résultats suivants.
1er) je vous savoir le GÉOPLAN ?
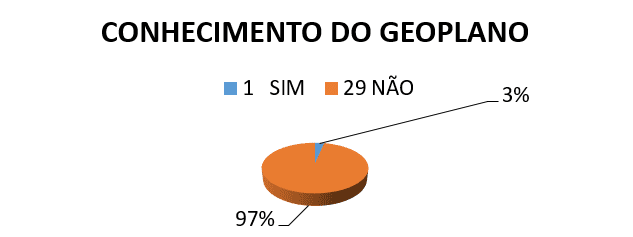
CLASSES de géométrie 2e) le professeur a déjà utilisé certains type de matériau utilisable ?
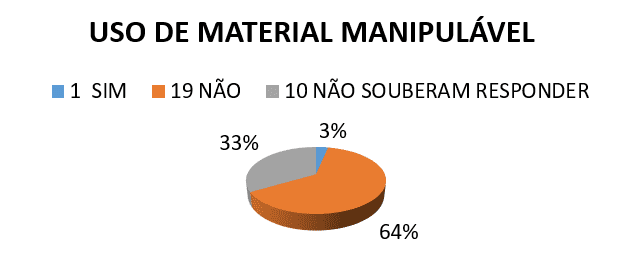
3ème) vous savez quel est le périmètre ou région ?

4) dont les chiffres ci-dessous vous connaissez ?
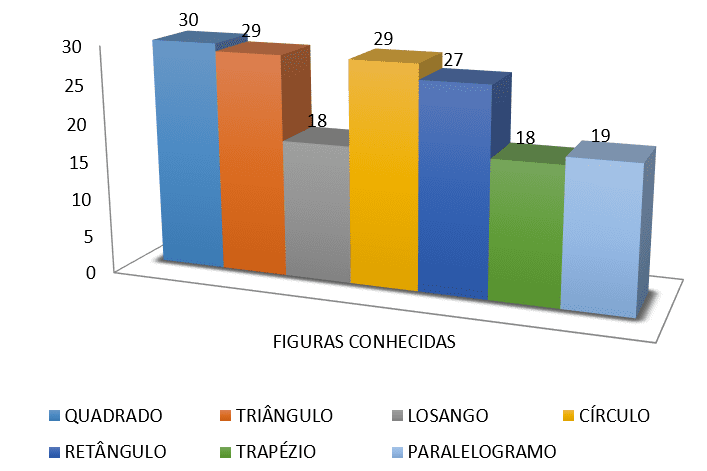
5) vous savez calculer le périmètre ou la région de certains de ces chiffres ?

En analysant les données obtenues, on se rend compte qu’il fallait organiser un atelier, dans lequel le Géoplan a été présenté comme une ressource pour l’enseignement et l’apprentissage. Grâce à cet atelier, nous recherchons spectacle si polyvalent que cette fonction de gestion.
Divisés en cinq groupes de six élèves, chaque groupe a reçu deux Geoplanos, un carré, un cercle et une certaine quantité d’élastique. Dans un premier temps, après avoir offert aux élèves de Geoplanos, ils ont eu pendant un certain temps la liberté de gérer et construire des figures selon l’imagination de chacun.
À l’aide de diapositives, il y avait une approche montrant les principaux polygones réguliers. Peu après, mis au défi les étudiants d’effectuer des calculs de périmètres et aires de polygones différents utilisant le Géoplan et maille damier. Ce défi a apporté un mouvement participatif de la part des étudiants, dans le cas de quelque chose de différent de votre quotidien. Le Géoplan lorsque utilisé les charmes, suscite l’intérêt et apporter la polyvalence en classe.
Élance, Diniz et Cândido mettent en évidence que :
Un des grands avantages de la Géoplan est, contrairement à la feuille de papier, il a la mobilité, est « dynamique », et la flexibilité avec laquelle ils peuvent faire et à défaire la construction permet à l’enfant s’habituer à voir les figures dans plusieurs positions, vous remarquerez si un étant donné une chance que j’ai fait pour la solution d’un problème est adapté et rectifier tout de suite si nécessaire. (2003, p. 112).
Au cours de l’atelier par le biais de commentaires, il a été noté qu’il y avait une amélioration de la performance des élèves lors du calcul proposé, également une participation effective dans la classe.



Comme l’évaluation des apprentissages, il est nécessaire d’effectuer un autre questionnaire avec les élèves pour la confirmation des résultats obtenus, comme illustré dans le graphique.
1e) le GÉOPLAN pourrait servir en géométrie ?

2ème) cette fonctionnalité facilité calculer l’aire et le périmètre ?

3e) taux leur PERFORMANCE dans le traitement du GÉOPLAN ?
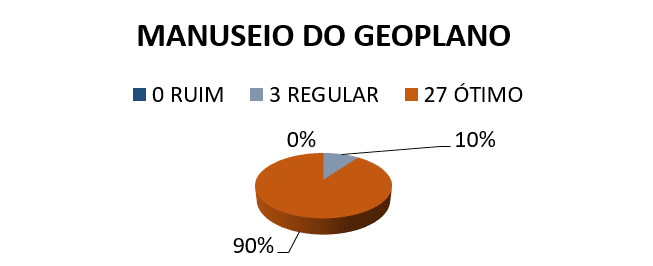
Selon les résultats obtenus par le biais de l’enquête menée avec les étudiants après l’atelier, on a remarqué qu’il y avait un accord effectif de la part d’étudiants pour quelques résultats. Le premier et le deuxième graphique montre que 100 % des étudiants d’accord avec l’utilisation de la Géoplan en géométrie, étant donné que cette fonction facilite le calcul aire et le périmètre. Toujours analyser les résultats, qu'il est possible de noter que cette fonctionnalité est facile à manipuler, car le troisième diagramme présente une note élevée en ce qui concerne les performances des élèves lorsque vous manipulez le Géoplan, 10 % des étudiants trouvé votre comportement ordinaire et les performances 90 % grande.
C’est pourquoi l’apprentissage des élèves était significative lors de l’exécution de l’atelier, le même a montré d’enthousiasme, curiosité et engagement, dévouement, résoudre les problèmes a proposé d’utiliser le Géoplan et maille damier.
Considérations finales
Les ressources, lorsque bien conçu, offrent aux élèves la construction de la connaissance mathématique, ce travail, nous avons décidé de choisir le Géoplan, car il sera d’une connaissance préalable de cet outil pour l’éducateur qui peut offrir pour éduquer une autre façon d’élargir votre développement cognitif, fournissant des situations concrètes et systématisées.
Par conséquent, cette fonctionnalité sera utilisée comme une méthode d’enseignement dans lequel les élèves peuvent vivre des situations d’apprentissage différents symboles de travail, résoudre des problèmes portant sur le périmètre et aire des polygones, où ils seront en mesure de faire une analyse réelle Ce qui est actuellement connu. Ainsi, le Géoplan, choisi pour ces s’inscrit parfaitement dans ces activités, car selon le programme national de paramètres, les jeux d’une manière généralement sont porteurs d’un aspect pertinent, c’est un défi qui mène à l’étudiant, c'est-à-dire, c’est un grand façon de l’encourager à affronter des situations nouvelles, où ils peuvent mettre en pratique leurs apprentissages, perdre votre peur de l’apprentissage des mathématiques.
Conformément à la Rego & Rego (2013).
… Grâce à des expériences avec du matériel concret, l’étudiant développe un goût pour le plaisir de la découverte, à relever les défis et les surmonter, en développant des US et coutumes qui peut conduire plus tard être un particulier et capable d’agir.
Il peut être conclu que par le biais de jeux, ressources pédagogiques et animateurs des outils d’enseignement/apprentissage n’est possible qu’éducateurs leçons de math plus polyvalents, attrayant pour les étudiants.
Références
Brésil. Ministère de l’éducation. Tronc commun : Mathématiques : MEC, 2015, p. 116.
Brésil. Département de fondamentaux éducation. Programme d’études national : Paramètre de Math. Brasilia : MEC/SEF.1998.
GH, Claudia Maria. Géométrie : l’espace et la forme. Unochapecó : Chapecó ; Coordination de l’enseignement à distance, 2008.
MARKHAM, j. e. (s. la dir. de). Connaissances, interdisciplinaires et activités pédagogiques avec des jeux mathématiques : une proposition méthodologique. Recife : UFRPE, 2008. (Série de contexte mathématique)
REGO, R. G ; REGO. R. M. Matematicativa. 4. Ed. Vue. Londres 2013 (formation des enseignants) p. 25
SANTOS JUNIOR, V. B. D. La mobilisation des matières mathématiques dans des activités pratiques dans le contexte du jeu avec Licenciandos de mathématiques. Thèse (master dans l’enseignement des sciences et mathématiques)-programme d’études supérieures en sciences et en mathématiques de l’éducation, ministère de l’éducation, Université fédérale rurale du Pernambouc. Recife, 2011. P. 22-36
SHARMA, Monica Menezes. L’activité ludique en classe de mathématiques : action et réflexion. Disponibles dans <http: sbem.com.br/files/ix/enem/minicurso/trabalhos="">.</http:> Consulté le 20 octobre 2009.
ÉLANCE, Kátia Cristina Stocco ; DINIZ, Maria Ignez de Souza Vieira ; Candide, Patricia Terezinha. Formes et figures. Porto Alegre : New Haven, 2003. (v, de la Collection mathématique de 0 à 6. 3).
[1] Avoir obtenu son diplôme dans le cadre de la licence en mathématiques de la CESA.
[2] Avoir obtenu son diplôme dans le cadre de la licence en mathématiques de la CESA.
[3] Avoir obtenu son diplôme dans le cadre de la licence en mathématiques de la CESA.
[4] Avoir obtenu son diplôme dans le cadre de la licence en mathématiques de la CESA.
[5] Avoir obtenu son diplôme dans le cadre de la licence en mathématiques de la CESA.
[6] Conseiller. Professeur de CESA.
[7] Le PIBID est un programme du gouvernement fédéral qui veut encourager la formation des enseignants de niveau supérieur pour l’éducation de base, qui contribuent à l’amélioration de la profession enseignante. Plus accès à l’information :<HTTP: www.capes.gov.br/educacao-basica/capespibid=""></HTTP:>