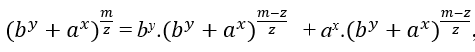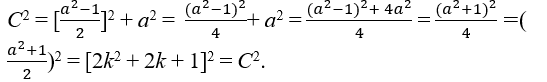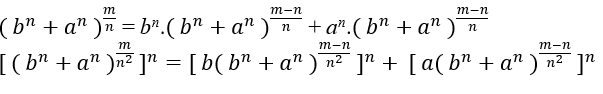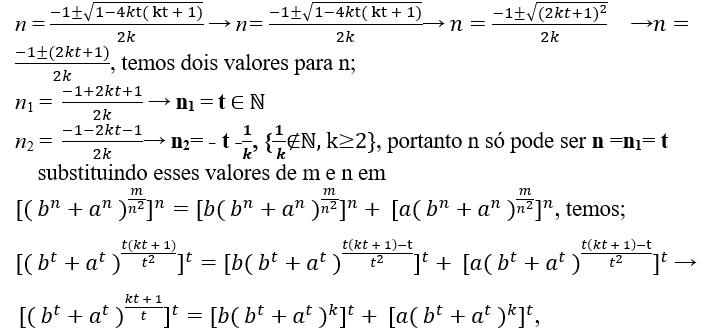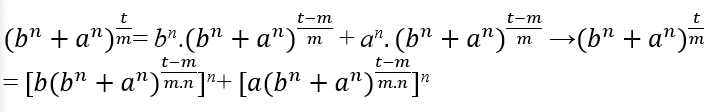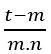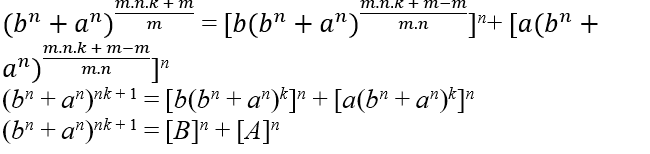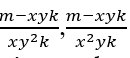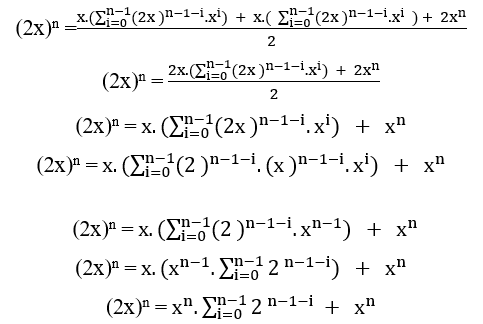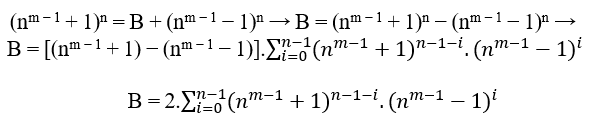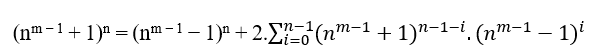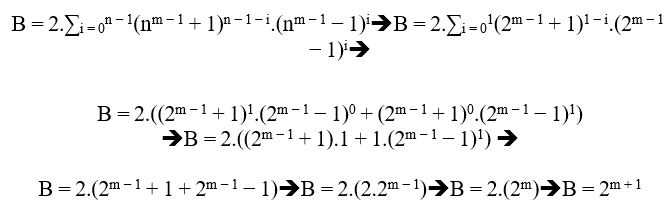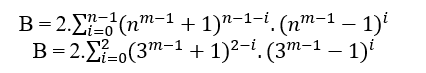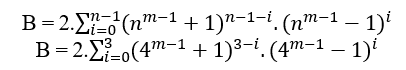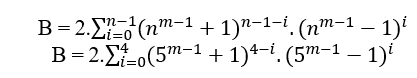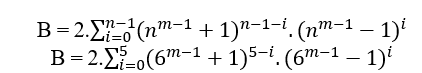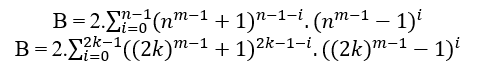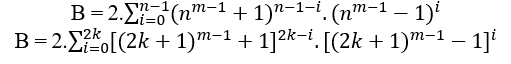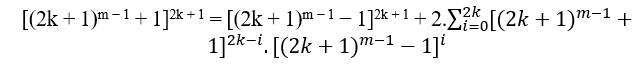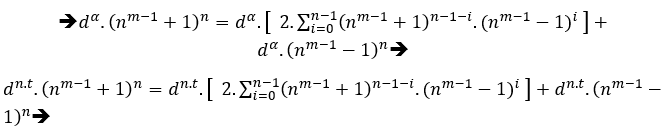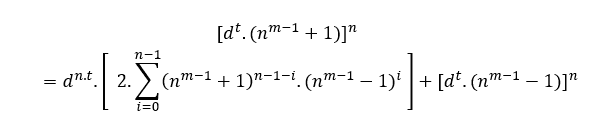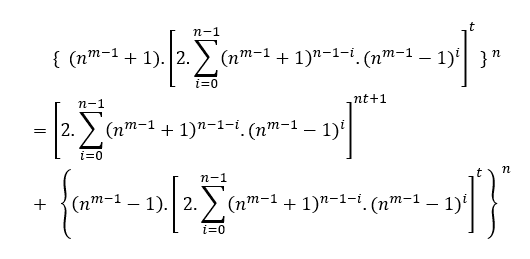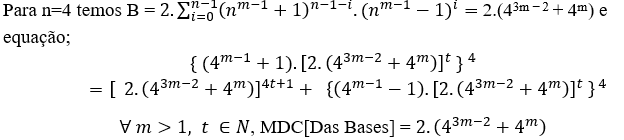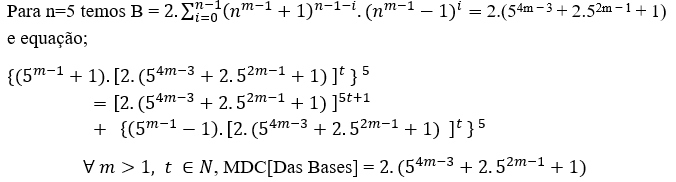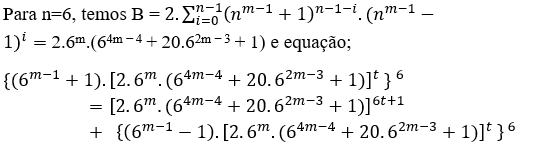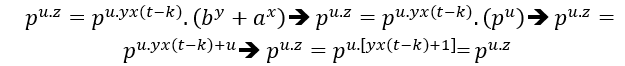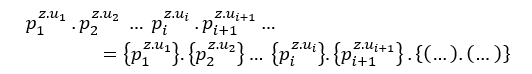ARTICLE ORIGINAL
SOUSA, Francisco Rafael Macena de [1]
SOUSA, Francisco Rafael Macena de. Démonstration de la Conjecture de Beal. Revista Científica Multidisciplinar Núcleo do Conhecimento. 04 année, Ed. 11, vol. 05, pp. 132-173. novembre 2019. ISSN: 2448-0959, Lien d’accès: https://www.nucleodoconhecimento.com.br/olympiades-mathematiques/conjecture-de-beal
DÉCLARATION DE CONJECTURE
Si ax + by = cz , où a, b, c, x, y et z sont des entiers positifs et x, y, z ≥ 3, puis a, b et c ont un facteur premier commun, ce qui signifie que a, b et c sont divisibles par le même nombre premier. Ou, l’équation ax + by = cz n’a pas de solution pour les entiers positifs avec x, y, z ≥ 3 et mdc (a, b, c) = 1.
RÉSUMÉ
Cet article contient des démonstrations utilisant les principes de l’algèbre et de la théorie des nombres, en ce qui concerne la conjecture a été annoncé par Andrew Beal un banquier et passionné de théorie des nombres a proposé un défi pour ceux qui prouvent ou présentent contre-exemple à un tel problème qui généralise le dernier théorème de fermat, cn = bn + an,, avec n ≥ 3, cela a été démontré par le mathématicien anglais Andrew Wiles en utilisant comme base une conjecture faite par les mathématiciens Yutaka Taniyama et Goro Shimu , cette démonstration faite par Wiles peu de mathématiciens comprendront par le haut niveau ou la complexité, sera également utilisé le Theorème de Sebá, « Sebastião Vieira do Nascimento (Sebá) », diplômé en économie par l’UFPB, maître en ingénierie de la même, professeur titulaire de l’UFCG, son theorème éprouvé est basé sur ce cm = bn + an, avec m et n prime entre eux, c’est mdc (m, n) = 1 , la conjecture a été proposée par Beal lui-même en 1993, mais elle n’était bien connue que par la communauté mathématique en 1997 après que R. D. Mauldin a publié l’article une généralisation du dernier theorème de Fermat : La conjecture de Beal et le problème de prix dans le Journal Noticesofthe American Mathematical Society.
Mots-clés: Conjecture, Andrew Beal, Fermat’s Last Theorem.
1. INTRODUCTION
Cet article vise à prouver la conjecture de Beal, proposé par Andrew Beal un banquier, entrepreneur, investisseur, joueur de poker et mathématicien amateur qui a fascination dans la théorie des nombres, il a mis au défi tout mathématicien dans le monde de prouver ou de donner un contre-exemple à sa Conjecture qui a été proposé de 1993 à nos jours, aucune démonstration n’a été présentée qui généralise la conjecture, y compris fermat Dernier Theorem , cet article contient des connaissances mathématiques que toute personne qui est venu pour avoir la deuxième année de l’école secondaire complète et a facilité dans les propriétés mathématiques est possible de comprendre les démonstrations initiales, déjà pour ceux qui ont une éducation supérieure en exact et au-delà de ceux-ci seront faciles à comprendre du début à la fin, la conjecture est basée sur des entiers positifs ou des solutions en nombre naturel avec les plus grands exposants égaux à 3 (trois) et leurs bases supérieures ou égales à 1 (un) , si c’est le cas, il sera démontré qu’en fait le mdc (c, b, a) = C > 1, où ce C est le principal facteur commun qui divise a, b et c, avec le ≤ b ou un ≥ b, de telle sorte qu’il est possible d’avoir comme équation cz = by + ax, x, y, z ≥ 3, exposants, cas contradictoire possédera comme mdc (c, b , a ) = 1 et x, y, z ≥ 3, c’est la seule valeur qui divise c, b, a est 1 (a), en d’autres termes a,b et c sont des nombres premiers entre eux.
Pour arriver à la démonstration, il était nécessaire de créer de nouveaux théoriques, mais pour que le theorème soit réellement valide ainsi que la conjecture doit être prouvé au cours des théoriques sont créés à partir de principes et de propriétés dans la théorie des nombres, le plus grand défi dans cet article que tout autre qui implique des nombres premiers ces nombres qui a seulement deux diviseurs dans les naturels qui est 1 (un) et lui-même (nombre premier) , parce que c’est encore quelque chose que la théorie des nombres n’a pas encore été en mesure de trouver un moyen plus rapide de prendre en compte les nombres géants, mais dans la théorie des nombres que nous avons comme hypothèse et a également prouvé que tout X un nombre composé, nous pouvons écrire – il X comme un produit de divers pouvoirs de nombres premiers égaux ou distincts, y compris quand il a exposants 0 (zéro) ou 1 (un). L’idée de cette conjecture est simplement de faciliter la rencontre de facteurs premiers.
2. BRÈVE HISTOIRE À CONJECTURA
2.1 FERMAT ET SON THEORÈME
Tout commence avec Pierre Fermat qui a vécu dans la France du XVIII e siècle, fonctionnaire dans la ville de Français de Toulouse, les mathématiques pour lui était son passe-temps favori, ce qui est intéressant, c’est que Fermat avait une plus grande renommée en raison de ses coutumes de présenter à d’autres mathématiciens des problèmes qui ont défié les plus grands esprits de l’époque, où ils ont souvent laissé ses contemporains perplexes dans une tentative de les résoudre. Fermat a eu l’idée de créer une proposition similaire au célèbre théorème de Pythagore qui est bien connu aujourd’hui dans ce siècle, mais n’avait pas de solutions dans les naturels, cette proposition est allé au-delà de son temps et a gagné la gloire tout au long du siècle, pour ne pas trouver une solution ou contre-exemple, à cause de cela a gagné son nom et pour être son dernier défi avait comme nom le dernier théorème de Fermat , l’équation de sa renommée est cn = bn + an, où a, b, c e n ∈ N, avec n ≥ 3, selon lui avait la démonstration, est mort sans que personne ne sache quelle était sa réponse supposée, à cause de cela est devenu connu comme son dernier theorème. Le mérite de la découverte de cette proposition due à son premier-né, il a vu plusieurs notes de Fermat dans un certain livre d’Aritmétiques qui appartenait, car son père avait l’habitude de faire des brouillons ou des annotations dans les livres. Après la découverte du fils, les notes ou découvertes ont été publiées dans un livre Arithmetica de Diofanto contenant des observations du père, en 1670 le livre contenait 48 observations, mais le long du chemin des générations de mathématiciens et de physiciens donnaient des solutions à leurs défis, cependant avait celui que la plupart pensaient était le dernier, à cause de cela avait un nom si difficile. Dans son livre, il contenait la déclaration suivante: « J’ai découvert une merveilleuse démonstration de cette proposition qui, cependant, ne rentre pas dans les marges de ce livre » (FERMAT. 1607 – 1665)2.
2.2 YUTAKA TANIYAMA, GORO SHIMURA ET ANDREW WILES
En 1954, Yutaka Taniyama et Goro Shimura, jeunes mathématiciens japonais, sont devenus amis parce qu’ils se sont intéressés au même livre, au même article et aux mêmes calculs, cette conjecture Taniyama-Shimura a permis à Wiles de réaliser le rêve de son garçon, en utilisant un effort intellectuel et une détermination difficiles à croire que possible à un être humain. La conjecture que les deux ont présentée a servi de chemin à leur solution définitive au problème, mais le mathématicien Yutaka Taniyama s’est enlevé la vie en 1958, de sorte qu’il a encore retardé le développement de la solution, au développement de la conjecture dans la question de savoir si elle n’a pas été intentionnellement faite pour résoudre le dernier théorème de Fermat, mais c’est ce qui s’est réellement passé plus tard Wiles réalisé qu’une telle base qui a aidé la preuve – là certainement ce théorème , pour qui pourrait imaginer que le travail de deux étudiants de la fin du XXe siècle pourrait être utilisé dans quelque chose qui a résolu l’un des plus grands mystères de l’histoire des mathématiques. Mais c’est Andrew Wiles qui a fini par démontrer le dernier theorème de Fermat, Wiles est un professeur d’université de Princeton qui a commencé son intérêt pour le problème comme un enfant dans sa ville natale avait une bibliothèque publique, mais ce n’est qu’en 1986 qu’il a vraiment commencé son travail de résoudre le theorème de ses rêves, selon Wiles que ses recherches ont été faites dans le plus grand secret , car dans son être, il savait qu’il trouverait la solution, mais il n’était pas temps d’affirmer une telle chose à la communauté universitaire, l’intuition est tout à un passionné dans la théorie des nombres, mais l’intuition montre la voie, mais prouver si elle est bonne ou mauvaise prend du temps et le dévouement, peut-être craindre la pression qui souffrirait face à un problème aussi célèbre et solution difficile était trop risqué pour affirmer une telle solution initiale possible , en analysant la conjecture des deux Japonais, Andrew Wiles a noté qu’un tel theorème pouvait être un moyen de résoudre, mais la conjecture devait être prouvée d’abord avant de démontrer ce qu’il avait tant cherché depuis qu’il était enfant, dans son esprit il était si clair que Wiles pouvait rêver de la solution du théom tout dépendait de la preuve de la conjecture des deux étudiants , cependant Wiles n’a pas démontré le dernier theorème de Fermat, mais plutôt la conjecture Taniyama-Shimura, qui impliquera la preuve – là.
Enfin, le 23 juin 1993, lors d’une conférence tenue au Sir Isaac Newton Institute for Mathematical Sciences à Cambridge, Andrew Wiles, 356 ans après la présentation du theorème, a fait son annonce de sa démonstration, mais contenait une petite faille dans sa solution, Wiles se retire pour un an afin de corriger une telle erreur et de présenter sa nouvelle démonstration remaniée , après la correction et l’examen de la même erreur détectée, il a fallu quelques mois pour évaluer sa solution, sa démonstration avait 200 pages, et après une longue période d’anxiété, sa découverte ou sa démonstration a finalement été acceptée, mais si complexe que seules quelques personnes dans le monde entier ont été en mesure de le comprendre, et Wiles (après avoir reçu un prix d’une valeur de 50.000.00 livres de la Fondation Wolfskehl) , il entre en tant que mathématicien qui a démontré le théorem le plus intrigant et le plus difficile de l’histoire des mathématiques, et conclut ainsi l’un des plus grands problèmes non rencontrés ou démontrés qui ont défié les grands mathématiciens avant et pendant, de sorte que le Dernier Theorème de Fermat n’a pas de solutions avec des entiers positifs avec n ≥ 33.
2.3 ANDREW BEAL ET SA CONJECTURE QUI A REÇU SON NOM
Andrew Beal (né le 29 novembre 1952), banquier, entrepreneur, investisseur, joueur de poker et mathématicien amateur et passionné de l’un des meilleurs domaines qu’est la théorie des nombres. Beal est également connu pour la conjecture de Beal tout en enquêtant sur les généralisations du dernier theorème de Fermat, de 1993 à 1997, Beal a offert un prix en argent pour une preuve évaluée par des pairs de cette conjecture ou un contre-exemple, parce qu’en 1993, il avait une valeur de 5 000 $, la valeur du prix a augmenté à plusieurs reprises et est actuellement de 1 000 000 $ pour la personne qui le prouve ou présente un exemple contradictoire en d’autres termes un contre-exemple pour ceux qui généralisent Le dernier theorème de Fermat. Selon les propres déclarations du banquier, dans une annonce de presse de l’American Mathmatical Society, le but de la valeur millionnaire est d’«inspirer les jeunes esprits à réfléchir sur la question et de les rendre de plus en plus intéressés par l’étude des mathématiques » 4.
3. DÉVELOPPEMENT À LA CONJECTURE DE BEAL
Pour démontrer qu’il faudra trois nouveaux théoriques (T.M, S.T.M e T.G.M), parce que le Theorème de Sebá est un cas particulier de la conjecture de Beal, cela sera également montré plus tard.
3.1 MACENA OU T.M
Compte tenu de deux équations Eq1:cz = by + ax e Eq2:cm = cm avec des solutions entières positives et a comme base commune c ≠ 0, avec c, b, a, z, y, x et m ∈ N, m > z, il est possible de déterminer une nouvelle Equation Eq3 qui a à la fois le format d’Eq1 ainsi que Eq2. Cela signifie que si Eq3 ne satisfait pas Eq1, il n’a pas de solutions positives complètes. Exemple1 est l’équation Eq1 → c2 = b2 + a2 et Eq2 → cm = cm avec c ≠ 0 et m ∈ ℕ,, nous savons que Eq1 a des solutions entières parce qu’il est le propre théorème de pythagore, il suffit de vérifier en utilisant les triples pythagoriques, tout comme Eq2 a également des solutions complètes qui seront prouvées à l’avance. Cela dit, il est alors possible de déterminer une équation Eq3 qui a à la fois le format Eq1 et Eq2. Comme c ≠ 0 nous pouvons utiliser les étapes suivantes dans Eq1 → c2 = b2 + a2 → 1 = c− 2.(b2 + a2)(I) Eq1 → c2 = b2 + a2 → c=(b2+a2)1/2(II)
La prochaine étape consiste à utiliser Eq2, parce que nous pouvons écrire Eq2 par ici cm = cm.1 lors du remplacement (I) nous avons cm = cm.c−2.(b2 + a2) → cm = cm−2.(b2 + a2) → cm = b2.cm−2 + a2.cm−2(III) Remplacement de (II) dans (III);
![]()
= b2.
+ a2.
→
=
. Soit m – 2 un multiple de 4 soit m – 2 = 4.n, avec n ∈ ℕ, alors nous devons
m = 4.n + 2, lors du remplacement, nous avons; (b2 + a2)2.n + 1 = [b(b2 + a2)n]2 +[a(b2+a2)n]2
(b2 + a2)2n + 1 = [B]2 + [A]2 maintenant nous devons juste vérifier (b2 + a2)2n + 1 c’est comme C2,par les triplets de Pythagore, cette égalité est bientôt satisfaite (b2 + a2)2.n + 1 = (c2)2.n + 1 = c2.(2.n + 1) = [c2.n + 1]2 = [C]2
Por conséquent C2 = [B]2 + [A]2 le même format Eq1 para concluir deve ter propriedade de Eq2C2 = [B]2 + [A]2 → (b2 + a2)2n + 1 = [b(b2 + a2)n]2 + [a(b2 + a2)n]2 → (c2)2n + 1 = [b(c2)n]2 + [a(c2)n]2 → c4n + 2 = [b.c2n]2 + [a.c2n]2 → c4n + 2 = b2c4n + a2c4n → c4n + 2 = c4n.(b2 + a2) → c4n+2=c4n.(c2) → c4n+2=c4n+2 →cm=cm . Il a donc été vérifié qu’il est possible de trouver un Eq3 qui a les deux propriétés donc Eq3 pour ces deux équations est Eq3 → (b2+a2)2n+1=[b(b2+a2)n]2+[a(b2+a2)n]2
3.1.1 DÉGUSTATION T.M
Être Eq1: cz = by + ax et Eq2: cm = cm, avec m > z, a, b, c, x, y, z , m ∈ ℕ et c ≠ 0.
Prouver Eq2:
En fait 1 = 1, multipliant les deux côtés par c ∈ N* nous avons 1.c = 1.c, en multipliant à nouveau par le même c nous avons c2 = c2, se multipliant logiquement par m fois nous aurons ;
cm = c{(11 + 12 + 13 + … + 1m − 1 + 1m) = m} = cm. Par conséquent montré à Eq2.
Como c ≠ 0, possamos usar os seguintes artifícios:
cz = by + ax → 1 = c − z.(by + ax)( I ) élément neutre de multiplication
cz = by + ax → c =(by+ax)1/z( II )
La Eq2 peut s’écrire comme suit cm = cm.1 , en remplaçant (I) dans cette équation, on obtient:
cm = cm.1 → cm = cm.c − z.(by + ax) → cm = cm − z.(by + ax) → cm = by.cm − z + ax.cm − z
Le remplacement de (II) entraîne;
, mettre les exposants y et x en évidence![]()
Pour quoi
![]() ∈ ℕ o MMC( zy , zx )= zxy, alors m – z doit être un multiple de zxy, par conséquent m – z = zxy.k, com k ∈ ℕ. Isoler m et remplacer dans l’équation donne les résultats:
∈ ℕ o MMC( zy , zx )= zxy, alors m – z doit être un multiple de zxy, par conséquent m – z = zxy.k, com k ∈ ℕ. Isoler m et remplacer dans l’équation donne les résultats:
(by + ax)xyk + 1 = [b.(by + ax)xk]y + [a.(by + ax)yk]x
Voici donc la nouvelle équation;
Eq3:(by + ax)xyk + 1 = [b.(by + ax)xk]y + [a.(by + ax)yk]x → Cxyk + 1 = By + Ax
Pelo princípio da comparação ou formato Cxyk + 1 = By + Ax c’est équivalent à cz = by + ax, c’est la structure même de la conjecture de Beal.
Bientôt, il a satisfait le Eq1 manque montre qu’il a également le format de Eq2: cm = cm
(by + ax)xyk + 1 = [b.(by + ax)xk]y + [a.(by + ax)yk]x, comme cz = by + ax nous avons;
(cz)xyk + 1 = [b.(cz)xk]y + [a.(cz)yk]x → cz.(xyk + 1) = [b.cz.xk]y + [a.cz.yk]x → czxyk + z = by.czxyk + ax.czxyk → comme
m = zxyk + z
cm = by.czxyk + ax.czxyk → cm = czxyk.(by + ax) → cm = czxyk.(cz) → cm = czxyk + z = cm.
Donc prouvé depuis Eq3 satisfait Eq1 et Eq2.
Dé:
CZ = By + Ax
C = by + ax, B = b.(by + ax)xk, A = a.(by + ax)yk e Z = xyk + 1
MDC(C, B, A) = MDC(by + ax, b.(by + ax)xk, a.(by + ax)yk) = by + ax = cz = C.
MDC(Z, y, x) = MDC(xyk + 1, y, x) = 1
OBS:
Si k pour zéro, nous avons;
(by + ax)xyk + 1 = [b.(by + ax)xk]y + [a.(by + ax)yk]x → (by + ax)1 = [b.(by + ax)0]y + [a.(by + ax)0]x, comme by + ax = cz ≠ 0 pár conséquent (by + ax)0 = 1
(by + ax)1 = [b.1]y + [a.1]x → by + ax = by + ax
Si m était égal à z l’équation Eq1 et Eq2 serait égal, à son tour serait égal à Eq3
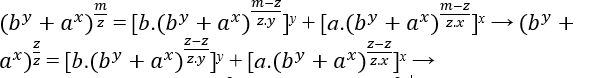
(by + ax)1 = [b.(by+ax)0]y + [a.(by+ax)0]x → by + ax = [b.1]y + [a.1]x.
Si le cas x=y=k=1 nous avons un carré parfait
(par + hache)xyk + 1[b.(by + ax)xk] = y[a.(by + ax)yk] + x → (b1 + a1)1 + 1 [b.(b1 + a1)1]= 1 [a.(b1 + a1)1]+ 1 + 1 →
(b + a[b.(b + a)])2 =[a.(b + a)] + → (b + a)2 = b.(b + a) + a.(b + a) = b2 + ba + ab + a2 = b2 + 2ab + a2 = (b + a)2
Exemple2 Vérification avec chiffres de l’équation Eq3, être b=3, a=2 et n=1 que nous avons;
(b2 + a2)2[b(b2 + a2)n]n + [a(b2 + a2)n]1 = 2 + 2 → (32 + 22)2,1 [3(32 + 22)1]+ 1 [2(32 + 22)1]= 2 + 2 →
(9 + 4[3(9 + 4)])3 =[2(9 + 4)] 2 + 2 → 13[3.13]3 = [2.13]2 + 2 → 133 = 392 + 262 → 2187 = 1521 + 676 → 2187 = 2187
3.2 MONTRANT CHAQUE CAS PAR T.M
Pour montrer la validité de ce théorème, il est également nécessaire de montrer les possibilités ou les valeurs possibles de z, y, x et m ∈ ℕ, s’il ne contredit aucun théorème déjà démontré par des mathématiciens tels que (théorème de Pythagore ” par plusieurs mathématiciens « , théorème de Sebá ” par Sebastian ” et dernier théorème de Fermat ” par Andrew Wiles ” et ainsi de suite) puis le T.M est valide et sera un outil pour prouver la conjecture de Beal.
3.2.1 THÈME PYTHAGORAS
C’est alors que z=y=x=2
Supposons que Eq1 → c2 = b2 + a2, a des solutions entières, pour c, a, b, m ∈ ℕ, c ≠ 0 et Eq2 → cm = cm il est possible de trouver un Eq3 qui satisfait les deux équations précédentes, si cela se produit bientôt Eq1 → c=√(b2+a2) ∈ ℕ.
Cette démonstration a déjà été montrée dans l’exemple1, il est seulement nécessaire de montrer qu’effectivement l’utilisation du triple pythagorique est satisfaite de la condition c=√(b2+a2) ∈ ℕ.
L’hypothèse est c2 = b2 + a2, thèse C2 = C2.
Utilisation de l’hypothèse c2 = b2 + a2 ajoutant des deux côtés par 2b + 1 ∈ ℕ, un carré parfait est obtenu d’un côté, c2 + 2b + 1 = b2 + 2b + 1 + a2 → c2 + 2b + 1 = (b + 1)2 + a2, nous savons que dans un triangle droit l’hypoténuse est plus grande que n’importe laquelle des catétos en particulier c > b > a, alors il ya la possibilité de c = b + 1 , se rendre compte qu’il s’agit d’une solution appropriée pour résoudre l’équation c2 + 2b + 1 = (b + 1)2 + a2 → c2 + 2b + 1 = c2 + a2 → 2b + 1 = a2 lors de l’isolement b, est obtenu et comme , se rendre
compte
, que les deux b et c pour être un entier suffisent (a) être bizarre parce que les temps impairs impairs reste étrange, donc un = 2k + 1 condition pour être bizarre avec k ∈ , c’est ce que nous avons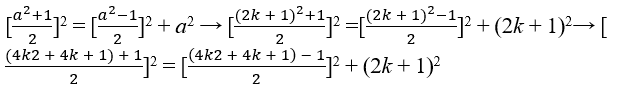
→ [2k2 + 2k + 1]2 = [2k2 + 2k]2 + (2k + 1)2, donc nous avons C = 2k2 + 2k + 1, B = 2k2 + 2k e A = 2k + 1 ∈ ℕ, sont les triples pythagoriens (2k2 + 2k + 1, 2k2 + 2k, 2k + 1), vérifier la thèse
3.2.2 POUR LE CAS DU DERNIER THEORREM DE FERMAT
C’est alors que z=y=x=n
Supposons que Eq1 → cn = bn + an, une solution pour n≥3, avec c, a, b, m ∈ N, c ≠ 0 et Eq2 → cm = cm il est possible de trouver un Eq3 qui satisfait les deux équations précédentes, si cela se produit bientôt Eq1 → c = n√bn+an ∈ ℕ.
Comme c ≠ 0 nous pouvons écrire Eq1, par ici;
Eq1 → cn = bn + an → 1 = c − n.(bn + an)(I) élément neutre de multiplication
Eq1 → cn = bn + an → c = ( bn+an )1/n(II)
Vérifiez que le Eq2 peut s’écrire comme suit sans changer ses valeurs cm = cm.1, à remplacer (I) dans Eq2, nous avons;
cm = cm.c − n.(bn + an) → cm = cm − n.(bn + an) → cm = bn.cm − n + an.cm − n(III)
Remplacé (II) dans (III)
Sachez que le format est le même que Eq1, juste vérifier si m − n est multiple de n2, si oui alors on peut écrire m − n = n2.k avec k ∈ ℕ, isoler m nous avons m = n2.k + n c’est une équation de 2ª grau;
m = n2.k + n ⇒ kn2 + n − m = 0, avec cela, nous pouvons trouver des valeurs pour m et n par Bhaskara.
, pour qu’il ne soit pas nécessairement naturel -1 ± √1-4 km doit être un multiple de 2k, alors;
-1±√1-4km = 2k.t, com t ∈ ℕ
-1±√1-4km = 2k.t → ±√1-4km= 2k.t + 1 élever les deux au quart que nous avons 1 + 4km = (2k.t + 1)2 → 4km = (2k.t + 1)2 − 1 réalisez que c’est alors la différence de deux carrés;
4km = (2k.t + 1 − 1).(2k.t + 1 + 1) → 4km = (2k.t).(2k.t + 2) → 4km = 4.(k.t).(k.t + 1) → km = k.t.(k.t + 1) →
m = t( kt + 1), puis en remplaçant cette valeur de m dans n = -1±√1-4km nous avons;
bientôt (bt + at)kt + 1 = Bt + At, prendre conscience de kt + 1 n’est pas un multiple de t, car mdc( kt + 1 , t ) = 1, C’est “kt + 1” et “t” sont cousins entre, et par Andrew Wiles c’est impossible bt + at = ct (Dernier théorème de Fermat), pour t > 2.
Parce que kt + 1 ≠ t.α, avec 2 < α ∈ N, ne satisfait donc pas Eq1, donc Eq1 n’a pas de solutions, comme il est dit en T.M.
Toutefois C =kt+1√Bt+At ∈ ℕ, EQSebá, Théorème de Seba, vérifiant l’égalité;
C = kt+1√Bt+A → C = kt+1√[b (bt+at )k]t+ [a( bt+at )k]t →C = kt+1√bt( bt+at )kt + at ( bt+at )kt → kt+1√( bt+at )kt.( bt+at ) → C = kt+1√( bt+at )kt+1 → C = bt + at.
3.2.3 THÈME SEBÁ
cm = bn+ an, avec mdc(m,n)=1
Démonstration de Sebastião Vieira do Nascimento ( Sebá )
Theorème: L’équation Cm = An + Bn admet des solutions naturelles pour m et n nombres premiers les uns aux autres.
Preuve:
Soyez l’équation;
( 1 )cm = bn + an, étant a, b, c, n et m integers positifs. Multiplicando ambos os membros da equação ( 1 ) por (bn + an)m
vous obtenez:
( 2 )cm*(bn + an)m = (bn + an)*(bn + an)m, Remplacement de la valeur de da (1) dans (2), vous obtenez:
(bn + an)m + 1 = (bn + an)*(bn + an)m
ou
( 3 )(bn + an)m + 1 = bn(bn + an)m + an(bn + an)m
Si nous choisissons des valeurs pour a et b telles que a ≤ b ou a≥b, et substituons dans (3), des valeurs entières positives sont obtenues pour A, B et C.
Exemple : Divisez un carré en deux cubes de plusieurs façons différentes. Soyez l’équation:
( 4 )C2 = B3 + A3, Considérez l’équation:
c2 = b3 + a3, Multiplier les deux membres de l’équation ci-dessus par (b3 + a3)m, où m et n ∈ ℕ, nous avons:
c2(b3 + a3)m = (b3 + a3)(b3 + a3)m
( 5 )(b3 + a3)m + 1 = b3(b3 + a3)m + a3(b3 + a3)m
Comparaison de l’équation (5) avec l’équation (4), il faut décomposer m en puissances de 3 et m + 1 en puissances de 2. Cela ne sera possible que si m et m + 1 sont, respectivement, des multiples de 3 et 2. bientôt:
m = 6k – 3 e m + 1 = 6k – 2, Ainsi, l’équation (5) est:
(b3 + a3)6k − 2 = b3(b3 + a3)6k − 3 + a3(b3 + a3)6k − 3
[(b3 + a3)3k − 1]2 = [b(b3 + a3)2k − 1]3 + [a(b3 + a3)2k − 1]3, Par conséquent, les solutions de l’équation donnée sont obtenues en faisant:
C = (b3 + a3)3k − 1, B = b(b3 + a3)2k − 1 et A = a(b3 + a3)2k − 1, où k ∈ N*, a et b ∈ ℕ.
Prouver en utilisant le T.M C’est quand z=m et y=x=n
Supposer que Eq1 → cm = bn + an, a une solution pour m et n premiers l’un à l’autre
mdc(m,n)=1, avec c, a, b, t, m et n ∈ ℕ, c ≠ 0 e Eq2 → ct = ct tu peux en trouver un Eq3 qui satisfait les deux équations précédentes, si cela se produit bientôt
Eq1 → c =m√bn+an ∈ ℕ.
Comme c ≠ 0 nous pouvons utiliser les méthodes suivantes;
cm = bn + an → 1 = c − m*(bn + an), (I) élément neutre de multiplication
cm = bn + an → c = (bn+an)1/m, (II)
Nous pouvons écrire Eq2 par ici ct = ct.1, remplacer ( I ) dans Eq2 nous avons;
ct = ct.c − m.(bn + an) → ct = ct − m.(bn + an) → ct = bnct − m + anct − m, lors du remplacement (II) nous avons;
Pour quoi
être naturel t – m doit être un multiple de n et m, alors t – m = m.n.k, avec k ∈ ℕ, en isolant t on a t = m.n.k + m, lors du remplacement dans l’équation, il est obtenu;
Il reste à montrer que nk + 1 est un multiple de m, si oui il est de la forme nk + 1 = m.α, avec α ∈ ℕ ou bn + an = Cm
Si l’un de ces deux se produit, si nous avons Cm = Bn + An, alors il sera montré que Eq1 a une solution.
Nous devons t − m = m.n.k diviser les deux par m, il est obtenu
− 1 = n.k ajoutant 1 des deux côtés
=n.k + 1, comme t est multiple de m, donc
∈ ℕ, avec cela, nous pouvons utiliser les étapes suivantes;
Comme
=n.k + 1 et nk + 1 = m.α c’est
= m.α→ α =
, si α est naturel alors
il devrait être naturel, si ce n’est que si t est également multiple de m2, mais t n’est pas multiple de m2, parce qu’il est de la forme t = m.n.k + m, même si k était égal à m, il serait de la forme t = n.m2 + m = m.(nk + 1) ≠ m2. (NK+1), donc NK+1 n’est pas multiple de T, donc mdc ( nk + 1, t )=1, sont des nombres premiers entre eux.
Il ne reste plus qu’à vérifier si bn + an =Cm.
Sabemos que nk + 1 não é múltiplo de n, pois o mdc(nk + 1, n) = 1 e como a igualdade da equação (bn + an)nk + 1 = [b(bn + an)k]n + [a(bn + an)k]n é satisfeita já mostrada anteriormente na EQSebá, pelo princípio do formato ou comparação temos que:
Cnk + 1 = Bn + An équivaut à cm = bn + an, bientôt;
(bn + an)nk + 1 = Bn + An → (cm)nk + 1 = cm.(nk + 1) = [cnk + 1]m = Cm = Bn + An
Avec ça, le Eq1, émission manquante Eq2 → ct = ct, réaliser que:(bn + an)nk + 1 = Bn + An → (bn + an)nk + 1 = [b(bn + an)k]n + [a(bn + an)k]n →
(cm)nk + 1 = [b(cm)k]n + [a(cm)k]n → cm.(nk + 1) = [b(cm)k]n + [a(cm)k]n
como t= m.( nk + 1 );
ct = bn(cm)nk + an(cm)nk → ct = (cm)nk(bn + an) → ct = (cm)nk(cm) → ct = (cm)nk + 1 → ct = cm.(nk + 1) = ct, Donc prouvé parce que Eq3 a des propriétés à la fois Eq1 et Eq2.
3.2.4 AU CAS OÙ ILS SONT MULTIPLES PAR T.M
Cas (1): pour plusieurs y de x c’est y = xk avec k ∈ N
Soyez Eq1: cz = bxk + ax e Eq2 :cm = cm, avec m > z et c ≠ 0 vous pouvez trouver une nouvelle Equation Eq3, qui a des propriétés d’Eq1 et Eq2 si Eq3 n’a pas la propriété du logo Eq1 Eq1, n’a pas de solutions complètes.
Comme c ≠ 0, nous avons;
cz = bxk + ax → 1 = c − z.(bxk + ax), (I) élément neutre de multiplication
cz = bxk + ax → c = (bxk+ax)1/z, (II)
Nous pouvons écrire Eq2 comme suit en utilisant ( I );
cm = cm.c − z.(bxk + ax) → cm = cm − z.(bxk + ax) → cm = bxk.cm − z + ax.cm − z, ao substituir (II) temos;
![]() Colocando os xk e x em evidência temos;
Colocando os xk e x em evidência temos;
![]() , note que o mmc (zxk, zx) e para que
, note que o mmc (zxk, zx) e para que ![]() ∈ ℕ, obrigatoriamente z – m deve ser múltiplo de zxk isso é m − z = zxk.α com α ∈ ℕ, com isso temos;
∈ ℕ, obrigatoriamente z – m deve ser múltiplo de zxk isso é m − z = zxk.α com α ∈ ℕ, com isso temos;
![]() (bxk + ax)xk.α + 1 = [b.(bxk + ax)α]xk + [a.(bxk + ax)k.α]x, note que essa equação pode ser escrita da seguinte forma;
(bxk + ax)xk.α + 1 = [b.(bxk + ax)α]xk + [a.(bxk + ax)k.α]x, note que essa equação pode ser escrita da seguinte forma;
(bxk + ax)xk.α + 1 = [bk.(bxk + ax)k.α]x + [a.(bxk + ax)k.α]x, isso é Teorema de Sebá portanto já provado logo Cxk.α + 1 = Bxk + Ax equivalente a Cm = Bx + Ax pois MDC(xk.α + 1 , xk )=MDC(xk.α + 1 , x)= MDC(m,x)=1, portanto primo entre si, por sua vez equivalente Eq1.
Verificando Eq2 que é cm = cm
(bxk + ax)xk.α + 1 = [b.(bxk + ax)α]xk + [a.(bxk + ax)k.α]x, como bxk + ax = cz temos; (cz)xk.α + 1 = [b.(cz)α]xk + [a.(cz)k.α]x → czxk.α + z = [b.czα]xk + [a.czk.α]x como m = zxk.α + z
cm = bxk.cxzkα + ax.cxzk.α → cm = cxzkα(bxk + ax) → cm = cxzkα(cz) → cm = cxzkα + z = cm.
Bientôt satisfait Eq1 et Eq2, donc prouvé.
Caso (2): para x múltiplo de y isso é x = yk com k ∈ ℕ
Essa demonstração é análoga em relação ao Caso (1), chegara que Eq3 é;
(by + ayk)yk.α + 1 = [b.(by + ayk)k.α]y + [a.(by + ayk)α]yk →
(by + ayk)yk.α + 1 = [b.(by + ayk)k.α]y + [a.(by + ayk)kα]y → Cyk.α + 1 = By + Ay equivalente Cm = By + Ay por sua vez equivalente Eq1: cz = by + ayk com k, α ∈ ℕ .
Cas (3): pour plusieurs z de x c’est z = xk et MDC (z,x,y)=1, avec k ∈ N
Soyez Eq1: cxk = par + hache, nous pouvons écrire Eq1 du format suivant Eq1: par = cxk − hache, et Eq2 sera sur la base de b au lieu de c, avec b ≠ 0 et c > a, logo Eq2: bm = bm, avec m > y, il est donc possible Eq3 qui a à la fois eq1 et Eq2 propriété, si elle ne satisfait pas Eq1 puis Eq1 n’a pas de solutions positives complètes.
Comme b ≠ 0 nous avons;
by = cxk − ax → 1 = b − y(cxk − ax), (I) élément neutre de multi
by = cxk − ax → b = (cxk-ax)1/y, (II)
Eq2 peut s’écrire comme suit bm = bm.1, substitué (I) dans Eq2 nous avons;
bm = bm.b − y(cxk − ax) → bm = bm − y(cxk − ax) → bm = cxk.bm − y − ax.bm − y, en remplaçant (II) nous avons;
, isoler xk et x que nous avons;
![]()
MMC( xyk , x )= xyk, pour quoi
∈ ℕ, m – y doit être un multiple de xyk, C’est m − y = xyk.α, avec α ∈ ℕ, avec ces données que nous avons;
![]()
(cxk − ax)xkα + 1 = [c.(cxk − ax)α]xk − [a.(cxk − ax)k.α]x, notez que nous pouvons organiser comme suit;
(cxk − ax)xkα + 1 = [c.(cxk − ax)α]xk − [a.(cxk − ax)k.α]x → [c.(cxk − ax)α]xk = (cxk − ax)xkα + 1 + [a.(cxk − ax)k.α]x, donc z peut être un multiple de x, et son MDC( z , x , y ) = 1
Comme z = xk, nous avons;
[c.(cz − ax)α]z = (cz − ax)zα + 1 + [a.(cz − ax)k.α]x, avec cela, nous avons;
C = c.(cz − ax)α, B = cz − ax e A = a.(c1 − ax)k.α, bientôt Cz = Bzα + 1 + Ax, avec z=xk, c’est équivalent à Eq1, il reste à montrer que c’est aussi Eq2: bm = bm.
[c.(cz − ax)α]z = (cz − ax)zα + 1 + [a.(cz − ax)k.α]x, comme by = cz − axez = xk, nous avons;
[c.(by)α]xk = (by)xkα + 1 + [a.(by)k.α]x → cxk.(by)xkα = bxykα + y + ax.(by)xk.α, comme m = xykα + y, nous avons;
cxk.bxykα = bm + ax.bxyk.α → cxk.bxykα − ax.bxyk.α = bm → bxykα.(cxk − ax) = bm → bxykα.(by) = bm → bxykα + y = bm
→ bm = bm
Alors comment Eq3 satisfait Eq1 et Eq2, bientôt Eq1 a des solutions sur des entiers positifs.
Cas (4) pour plusieurs z de y c’est z = yk avec k ∈ ℕ
Cette démonstration est analogue par rapport à Case (3), ils atteignent le même format que l’équation Eq3, mais avec b à la place d’un, et y à la place de x;
[c.(cyk − by)α]yk = [b.(cyk − by)k.α]y + (cyk − bx)ykα + 1, avec α ∈ N.
Case (5): pour plusieurs z de x et y c’est z = xyk avec MDC(z, x, y) = MDC(x, y)≥1, e k ∈ ℕ
Soyez Eq1: xyk = by + ax et Eq2: cm = cm, avec c ≠ 0 et k ∈ N, vous pouvez trouver une nouvelle Equation Eq3, qui a des propriétés d’Eq1 et Eq2 si Eq3 n’a pas la propriété du logo Eq1 Eq1 n’a pas de solutions complètes.
Comme c ≠ 0 nous avons;
cxyk = by + ax → 1 = c − xyk*(by + ax), (I) élément neutre de multiplication
![]()
Nous pouvons écrire Eq2 comme suit en utilisant( I );
cm = cm.c − xyk.(by + ax) → cm = cm − xyk.(by + ax) → cm = by.cm − xyk + ax.cm − xyk , lors du remplacement (II) nous avons;
, Mettre les preuves y et x que nous avons;
O MMC(xy2k , x2yk )=x2y2k, pour quoi
∈ ℕ, obligatoirement m – xyk doit être un multiple de x2y2k c’ est m − xyk = x2y2k.α, avec α ∈ ℕ, bientôt nous avons;
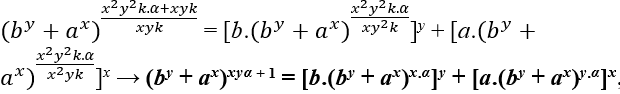 Regarde ça xyα + 1 n’est pas un multiple de xy, car MDC(xy.α + 1 , xy ) = 1, brientôt Eq1 n’a pas de solutions entières positives pour z multiple de x et y.
Regarde ça xyα + 1 n’est pas un multiple de xy, car MDC(xy.α + 1 , xy ) = 1, brientôt Eq1 n’a pas de solutions entières positives pour z multiple de x et y.
Car by + ax hache par le principe de comparaison montré précédemment égale cxyk + 1 = by + ax et comme z = xyk, nous avons cz + 1 = by + ax. Par conséquent z +1 n’est pas multiple de x et y, donc Eq1 n’a pas de solution dans les entiers positifs.
Cas ( 6 ): pour z multiple de x, et y multiple de x est z = xk et y = xt, avec k ≥ t e
MDC(z,x,y)=x , et k, t ∈ ℕ
être Eq1: cxk = bxt + ax e Eq2: cm = cm, com c ≠ 0 e k, t ∈ ℕ,il est possible de trouver une nouvelle équation Eq3, qui a des propriétés de Eq1 et Eq2 cas Eq3 n’a pas la propriété Eq1 donc Eq1 n’a pas de solutions complètes.
Comme c ≠ 0 nous avons;
cxk = bxt + ax → 1 = c − xk*(bxt + ax), , (I) élément neutre de multiplication
cxk = bxt + ax → c = (bxt + ax)1/xk (II)
Nous pouvons écrire Eq2 comme suit en utilisant( I );
cm = cm.c − xk.(bxt + ax) → cm = cm − xk.(bxt + ax) → cm = bxt.cm − xk + ax.cm − xk, lors du remplacement (II) nous avons;
, isoler xt et x nous avons;
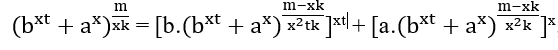 , MMC(x2tk,x2k)=x2tk, pour quoi
, MMC(x2tk,x2k)=x2tk, pour quoi
∈ ℕ il faut que m – xk soit un multiple de x2tk, c’ est m − xk = x2tk.α, avec α ∈ ℕ, le remplacement de ces valeurs est obtenu;
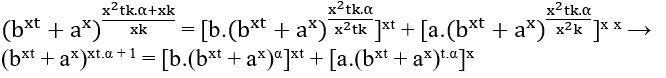 comme xt.α + 1 n’est pas un multiple de x, il reste à regarder bxt + ax, réaliser qu’au départ Eq1 ses cxk = bxt + ax → (ck)x = (bt)x + ax Dernier théorème de Fermat.
comme xt.α + 1 n’est pas un multiple de x, il reste à regarder bxt + ax, réaliser qu’au départ Eq1 ses cxk = bxt + ax → (ck)x = (bt)x + ax Dernier théorème de Fermat.
Parce que Eq3 n’a pas satisfait Eq1, donc Eq1 n’a pas de solution globale positive lorsque z est multiple de x, et y multiple de x.
Cas ( 7 ): pour z multiple de y, et x multiple de y ses z = yk et x = yt, avec k ≥ t et MDC(z,x,y)=y , et k, t ∈ ℕ
Cette démonstration est analogue au cas (6), car elle relève du dernier théorème de Fermat.
Cas ( 8 ): pour z multiple de y et x, x ou y multiple l’un de l’autre, c’est-à-dire z = xyk et x = yt ou z = xyk et y = xt, avec k ≥ t et MDC(z,x,y)=y ou MDC(z,x,y)=x , et k, t ∈ ℕ
Cette démonstration est analogue aux cas (6) et (7), car elle tombe dans le dernier théorème de Fermat.
Obs: cxyk = bxt + ax → (cyk)x = (bt)x + ax e cxyk = by + ayt → (cxk)y = by + (at)y, le dernier théorème de Fermat.
Conclusion au cas où les exposants sont multiples :
Il n’y a pas de solution pour les entiers positifs, dans les cas (5), ( 6 ), ( 7 ) et ( 8 )
3.3 SELON MACENA OU S.T.M
Étant donné n ≥ 2 le degré du premier membre de l’équation, il est toujours possible de déterminer un B=(nm − 1 + 1)n−(nm − 1 − 1)n, et si MDC(a, B, c) = 1 puis n a même degré, si le MDC(a, B, c) = 2,t ≥ 2, puis le n degré est impair, dans les deux cas satisfaire an = B + cn,, en particulier pour tout n même ou impair, nous avons le MDC(a,B,c) = c où c est de la forme 2n − 1.
Pour prouver ce theorème, vous devrez trouver un outil avant de le prouver.
Outil:
Pour trouver l’outil d’abord, nous devons analyser comment newton binomial se comporte à partir de la 2e année.
(x + y)2 = 1.x2 + 2.x.y + 1.y2, isso é 1 2 1.
(x + y)3 = 1.x3 + 3.x2.y + 3.x.y2 + 1.y3, isso é 1 33 1.
(x + y)4 = 1.x4 + 4.x3.y + 6.x2.y2 + 4.x.y3 + 1.y4, isso é 1 4 6 4 1.
(x + y)5 = 1.x5 + 5.x4.y + 10.x3.y2 + 10.x2.y3 + 5.x.y4 + 1.y5, isso é 15101051.
*
*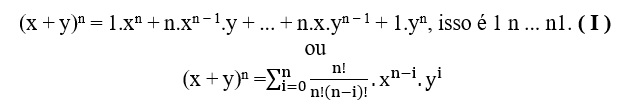
Maintenant soustraire xn ou yn des deux côtés de (I), il est obtenu;
(x + y)n − xn = n.xn − 1.y + … + n.x.yn − 1 + yn( I I)
ou
(x + y)n − yn = 1.xn + n.xn − 1.y + … + n.x.yn − 1 ( I I)
Par la différence de deux pouvoirs du même degré, nous pouvons écrire (x + y)n − xn, comme suit;
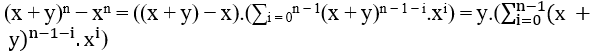 Demême, nous pouvons également écrire (x + y)n − yn, comme suit;
Demême, nous pouvons également écrire (x + y)n − yn, comme suit;
Avec cela,nous avons deux nouvelles équations différeciant seulement en x et y.
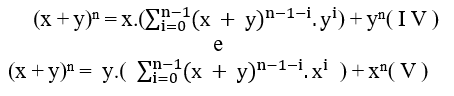
Ajout ( I V ) et ( V ) nous avons;![]()
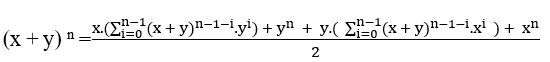
Pour qu’il
,soit divisible par 2, juste y être égal à x c’est y = x ou x = y, avec que nous avons
Division par le facteur commun qui est xn nous avons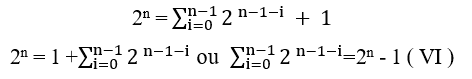 ;
;
L’élément ( VI ) est l’outil qui sera utilisé pour prouver le theorème.
Provando os casos de n ser par ou ímpar:
Être m ≥ 2, il est possible d’obtenir des équations du format cn = B + an, où MDC(c,B,a) = 1 si le degré n est pair, et MDC(c, B, a) = 2.t ≥ 2, avec t ∈ N*, si le degré n est impair..
Méthode si la base est de 2, il sera utilisé pour compléter les carrés, si elle est de 3, il sera l’achèvement des cubes, et ainsi de suite, jusqu’à ce que la base n utilisera l’achèvement de la puissance umpisth.
Soyez b une base, avec b ∈ N*, donnant ainsi l’initiative que nous avons ;
Pour b = 2 nous avons;
2m = 2m en fait c’est valable, nous pouvons écrire comme suit 2m = 2m.1, se rendre compte que l’égalité suivante est valide.
2m = 2m.(2 − 1) → 2m = 2m + 1 − 2m → 2.2m − 1 = 2m + 1 − 2.2m − 1, pour compléter le carré du premier membre il suffit d’ajouter des deux côtés 22(m − 1) + 1, cela se traduit par;
2.2m − 1 + 22(m − 1) + 1 = 2m + 1 − 2.2m − 1 + 22(m − 1) + 1 → (22(m − 1) + 2.2m − 1 + 1) = 2m + 1 + (22(m − 1) − 2.2m − 1 + 1) , nous avons donc deux carrés parfaits, et avec cela une nouvelle équation;
(2 m – 1+ 1 )2 = 2 m + 1+ (2 m – 1– 1 )2( 1 )
Votre écran MDC(2m − 1 + 1, 2, 2m − 1 − 1) = 1
Voir que cela ne dépend que d’une variable dans le cas m, voir les exemples utilisant les nombres.
Pour m = 2
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
(21 + 1)2 = 23 + (21 − 1)2
(2 + 1)2 = 23 + (2 − 1)2
32 = 23 + 12
9 = 8 + 1
Pour m = 3
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
(22 + 1)2 = 24 + (22 − 1)2
(4 + 1)2 = 24 + (4 − 1)2
52 = 24 + 32
52 = 42 + 32
25 = 16 + 9
Pour m = 4
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
(23 + 1)2 = 25 + (23 − 1)2
(8 + 1)2 = 25 + (8 − 1)2
92 = 25 + 72
(32)2 = 25 + 72
34 = 25 + 72
81 = 32 + 49
Pour m = 5
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
(24 + 1)2 = 26 + (24 − 1)2
(16 + 1)2 = 26 + (16 − 1)2
172 = 26 + 152
289 = 64 + 225
Pour m = 6
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
(25 + 1)2 = 27 + (25 − 1)2
(32 + 1)2 = 27 + (32 − 1)2
332 = 27 + 312
1089 = 128 + 961
Etc.
Pour b = 3, nous avons;
3m = 3m en fait c’est valable, nous pouvons écrire comme suit 3m = 3m.1,, se rendre compte que l’égalité suivante est valide.
3m = 3m.1 → 3m = 3m.(3 − 2) → 3m = 3m + 1 − 2.3m → 3.3m − 1 = 3m + 1 − 3.2.3m − 1, pour compléter le cube du premier côté de l’égalité, il suffit d’ajouter 33(m − 1) + 3.32(m − 1) + 1 des deux côtés, cela se traduit par;
3.3m − 1 + 33(m − 1) + 3.32(m − 1) + 1 = 3m + 1 − 2.3m + 33(m − 1) + 3.32(m − 1) + 1 → (33(m − 1) + 3.32(m − 1) + 3.3m − 1 + 1) = 3m + 1 + 33(m − 1) + 3.32(m − 1) + − 3.2.3m − 1 + 1 → (3m − 1 + 1)3 = 3m + 1 + 33(m − 1) + 3.32(m − 1) − 2.3m + 1, il doit y en avoir k ∈ ℕ, cela a ajouté et soustrait qu’ils génèrent un cube parfait sur le deuxième côté de l’égalité, tout comme cela s’est produit dans l’exemple précédent, donc nous l’avons fait;
(3m − 1 + 1)3 = [3m + 1 + 33(m − 1) + 3.32(m − 1) − 2.3m + 1 + k] − k, para determinar k, basta 3m + 1 + 33(m − 1) + 3.32(m − 1) − 2.3m + 1 + k = (3m − 1 − 1)3;
3m + 1 + 33(m − 1) + 3.32(m − 1) − 2.3m + 1 + k = 33(m − 1) − 3.32(m − 1) + 3.3m − 1 − 1
3m + 1 + 3.32(m − 1) − 2.3m + 1 + k = − 3.32(m − 1) + 3.3m − 1 − 1
k = − 3m + 1 − 3.32(m − 1) − 3.32(m − 1) + 3.3m − 1 + 2.3m − 1 − 1
k = − 3m + 1 − 6.32(m − 1) + 3.3m − 1 + 2.3m − 2
k = − 3m + 1 − 2.3.32(m − 1) + 3m + 2.3m − 2
k = − 3m + 1 − 2.32(m − 1) + 1 + 3.3m − 2
k = − 3m + 1 − 2.32m − 1 + 3.3m − 2
k = − 3m + 1 − 2.(32m − 1 + 1) + 3.3m
k = − 3m + 1 − 2.(32m − 1 + 1) + 3m + 1
k = − 2.(32m − 1 + 1)
Bientôt
− k = 2.(32m − 1 + 1)
Avec cela, nous avons une autre équation
(3m − 1 + 1)3 = [3m + 1 + 33(m − 1) + 3.32(m − 1) − 2.3m + 1 + k] − k
(3m − 1 + 1)3 = (3m − 1 − 1)3 + 2.(32m − 1 + 1)
(3m − 1 + 1)3 = 2.(32m − 1 + 1) + (3m − 1 − 1)3( 2 )
Comme 3m − 1 + 1 , 2.(32m − 1 + 1) e 3m − 1 − 1, ce sont des paires parce que la puissance de 3 est toujours impaire en ajoutant 1 ou en soustrayant 1 de cette puissance pour nous donner une paire.
Alors le MDC(3m − 1 + 1, 2.(32m − 1 + 1), 3m − 1 − 1) = 2.t ≥ 2, com t ∈ N*. Exemple en chiffres:
Pour m = 2 nous avons;
(3m − 1 + 1)3 = 2.(32m − 1 + 1) + (3m − 1 − 1)3
(31 + 1)3 = 2.(33 + 1) + (31 − 1)3
(4)3 = 2.(28) + (2)3
43 = 2.28 + 23, MDC( 4 , 2.28 , 2 ) = 2
64 = 56 + 8
Pour m = 3 nous avons;
(3m − 1 + 1)3 = 2.(32m − 1 + 1) + (3m − 1 − 1)3
(32 + 1)3 = 2.(35 + 1) + (32 − 1)3
(10)3 = 2.(244) + (8)3
103 = 2.244 + 83
1000 = 488 + 512
Etc.
La méthode la plus rapide pour trouver ces équations consiste à utiliser cn =B +an où c = nm − 1+1 et a = nm − 1−1, c’est;
Si n est le grade 2, nous avons;
Par conséquent;
(nm − 1 + 1)n = B + (nm − 1 − 1)n
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2( 1 )
MDC(2m − 1 + 1, 2, 2m − 1 − 1) = 1, avec m ≥ 2.
Si n est de niveau 3, nous avons;
B = 2.((3m − 1 + 1)2.(3m − 1 − 1)0 + (3m − 1 + 1)1.(3m − 1 − 1)1 + (3m − 1 + 1)0.(3m − 1 − 1)2)
B = 2.((3m − 1 + 1)2 + (3m − 1 + 1).(3m − 1 − 1) + (3m − 1 − 1)2)
B = 2.((32(m − 1) + 2.3m − 1 + 1) + 32(m − 1) − 1 + (32(m − 1) − 2.3m − 1 + 1))
B = 2.(2.32(m − 1) + 1 + 32(m − 1))
B = 2.(32(m − 1)(2 + 1) + 1)
B = 2.(32(m − 1)(3) + 1)
B = 2.(32(m − 1) + 1 + 1)
B = 2.(32m − 1 + 1)
Par conséquent;
(nm − 1 + 1)n = B + (nm − 1 − 1)n
(3m − 1 + 1)3 = 2.(32m − 1 + 1) + (3m − 1 − 1)3( 2 )
MDC(3m − 1 + 1, 2.(32m − 1 + 1), 3m − 1 − 1) = 2.t ≥ 2, com t ∈ N* e m ≥ 2
Si n est de 4e année, nous avons;
B = 2.((4m − 1 + 1)3.(4m − 1 − 1)0 + 4m − 1 + 1)2.(4m − 1 − 1)1 + 4m − 1 + 1)1.(4m − 1 − 1)2 + 4m − 1 + 1)0.(4m − 1 − 1)3)
B = 2.(43m − 2 + 4m) ou B = 22m + 1.(24(m − 1) + 1) ou B = 26m − 3 + 22m + 1 ou B = 82m − 1 + 22m + 1
Faire les calculs correctement arrivés;
B = 2.(43m − 2 + 4m) ou B = 22m + 1.(24(m − 1) + 1) ou B = 26m − 3 + 22m + 1 ou B = 82m − 1 + 22m + 1
Par conséquent nous avons;
(nm − 1 + 1)n = B + (nm − 1 − 1)n
(4m − 1 + 1)4 = 2.(43m − 2 + 4m) + (4m − 1 − 1)4( 3 )
O MDC(4m − 1 + 1, 2.(43m − 2 + 4m), 4m − 1 − 1) = 1, com m ≥ 2
ou
(22(m − 1) + 1)4 = 22m + 1.(24(m − 1) + 1) + (22(m − 1) − 1)4
O MDC(22(m − 1) + 1, 22m + 1.(24(m − 1) + 1), 22(m − 1) − 1) = 1, com m ≥ 2
ou
(22(m − 1) + 1)4 = 26m − 3 + 22m + 1 + (22(m − 1) − 1)4
O MDC(22(m − 1) + 1, 26m − 3, 22m + 1, 22(m − 1) − 1) = 1, avec m ≥ 2
Si n est de degré 5, nous avons;
B = 2((5m − 1 + 1)4 − 0.(5m − 1 − 1)0 + (5m − 1 + 1)4 − 1.(5m − 1 − 1)1 + (5m − 1 + 1)4 − 2.(5m − 1 − 1)2 + (5m − 1 + 1)4 − 3.(5m − 1 − 1)3 + (5m − 1 + 1)4 − 4.(5m − 1 − 1)4)
B = 2((5m − 1 + 1)4 + (5m − 1 + 1)3.(5m − 1 − 1) + (5m − 1 + 1)2.(5m − 1 − 1)2 + (5m − 1 + 1).(5m − 1 − 1)3 + (5m − 1 − 1)4)
En faisant les calculs, il arrivera que B vaut;;
B = 2.(54m − 3 + 2.52m − 1 + 1)
L’équation pour la 5e année est donc;
(5m − 1 + 1)5 = 2.(54m − 3 + 2.52m − 1 + 1) + (5m − 1 − 1)5( 4 )
MDC(5m − 1 + 1, 2.(54m − 3 + 2.52m − 1 + 1), 5m − 1 − 1) = 2.t ≥ 2, com t ∈ N* e m ≥ 2.
Si n est de 6e année, nous avons;
B = 2.((6m − 1 + 1)5 − 0.(6m − 1 − 1)0 + (6m − 1 + 1)5 − 1.(6m − 1 − 1)1 + (6m − 1 + 1)5 − 2.(6m − 1 − 1)2 + (6m − 1 + 1)5 − 3.(6m − 1 − 1)3 + (6m − 1 + 1)5 − 4.(6m − 1 − 1)4 + (6m − 1 + 1)5 − 5.(6m − 1 − 1)5)
B = 2.((6m − 1 + 1)5 + (6m − 1 + 1)4.(6m − 1 − 1) + (6m − 1 + 1)3.(6m − 1 − 1)2 + (6m − 1 + 1)2.(6m − 1 − 1)3 + (6m − 1 + 1).(6m − 1 − 1)4 + (6m − 1 − 1)5)
Faire les calculs correctement arrivera à;
B = 2.(65m − 4 + 20.63m − 3 + 6m), ou B = 2.6m.(64m − 4 + 20.62m − 3 + 1) et l’équation est;
(6m − 1 + 1)6 = 2.6m.(64m − 4 + 20.62m − 3 + 1) + (6m − 1 − 1)6( 5 )
Avec MDC(6m − 1 + 1, 2.6m.(64m − 4 + 20.62m − 3 + 1), 6m − 1 − 1) = 1, avec m ≥ 2
Notez ensuite que les conditions de (1) à (5) ont été satisfaites pour les cas où n est pair et n est impair.
Afin de prouver cette équation, nous devons montrer pour le cas général non seulement de (1) à ( 5 ) mais de (1) à (n).
Pour n paire:
Être n =2k avec k ∈ N*, par les exemples précédents le MDC(a,B,c)=1, le Remplacé en B est obtenu;
Par la définition de Paire le B est déjà une paire, puis il est divisible par 2, il reste à vérifier c et a. Si c et a sont impairs alors le MDC (c,B,a) est 1, si c et b est même alors le MDC(c,B,a) est 2.t ≥ 2, avec t ∈ N*.
Comme c = nm − 1 + 1 et a = nm − 1 − 1 de l’équation cn = B + an lors du remplacement des valeurs de n et B que 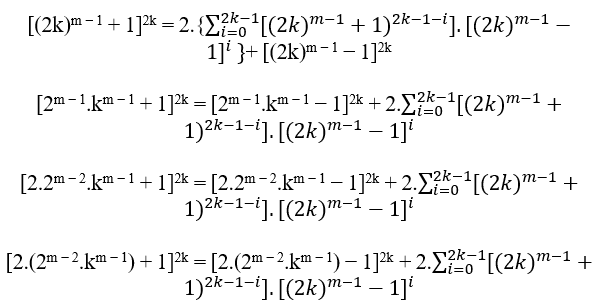
Nous avons 2.(2m − 2.km − 1) + 1 comme 2. 2.(2m − 2.km − 1) + 1 sont impairs, donc a et c sont impairs, avec cela la seule valeur divisant a, B et c est 1.
Pour n Impar:
Que ce soit n = 2k + 1 avec k ∈ N*, par les exemples précédents le MDC(a,B,c)=1, le Remplacé en B est obtenu;
En paramètre paire le B est déjà une paire, puis il est divisible par 2, il reste à vérifier c et a. Si c et a sont impairs alors le MDC(c,B,a) est 1, si c et b est même alors le MDC(c,B,a) est 2.t ≥ 2, avec t ∈ N*.
Comme c = nm − 1 + 1 e a = nm − 1 − 1 de l’équation cn = B + an lors du remplacement des valeurs de n et B nous avons;
Comme 2k + 1 est étrange si on carré c’est aussi impair:
(2k + 1)2 = 4k2 + 4k + 1 = 2.(2k2 + 2k) + 1
Si nous ajoutons 1 des deux côtés ou soustrayons 1, c’est une paire?
(2k + 1)2 + 1 = 2.(2k2 + 2k) + 2 = 2.[2k2 + 2k + 1] é um par, e (2k + 1)2 − 1 = 2.(2k2 + 2k) − 2 = 2.[2k2 + 2k − 1] C’est un couple.
Comme 2k + 1 est étrange si nous montons au cube est également étrange:
(2k + 1)3 = 8k3 + 12k2 + 6k + 1 = 2.(4k3 + 6k2 + 3k) + 1
Si nous ajoutons 1 des deux côtés ou soustrayons 1, est-ce une paire?
(2k + 1)3 + 1 = 2.(4k3 + 6k2 + 3k) + 2 = 2.[4k3 + 6k2 + 3k + 1] é um par, e (2k + 1)3 − 1 = 2.(4k3 + 6k2 + 3k) − 2 = 2.[4k3 + 6k2 + 3k − 1] C’est un couple.
Comme 2k + 1 est étrange si nous élevons la quatrième puissance est également impair:
(2k + 1)4 = 16k4 + 32k3 + 6k + 1 = 2.(8k4 + 16k3 + 3k2) + 1
Si nous ajoutons 1 des deux côtés ou soustrayons 1, est-ce une paire?
(2k + 1)4 + 1 = 2.(8k4 + 16k3 + 3k2) + 2 = 2.[8k4 + 16k3 + 3k2 + 1]c’est une paire, et (2k + 1)4 − 1 = 2.(8k4 + 16k3 + 3k2) − 2 = 2.[8k4 + 16k3 + 3k2 − 1]c’est une paire.
si ça continue, ce sera toujours une paire alors (2k + 1)m − 1 + 1 e (2k + 1)m − 1 − 1 est pair et comme B est pair, donc la plus petite valeur qui divise c, B et a est 2, donc MDC(a, B, c) = 2.t ≥ 2, com t ∈ N*
Par conséquent, nous avons les deux équations principales:
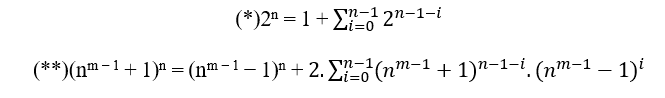
3.3.1 DÉGUSTATION S.T.M
Pour goûter S.T.M reste juste à montrer que indépendamment de la n si elle est même ou étrange, nous avons MDC (a,B,c) = c où c = 2n − 1 a déjà été montré que (**) a MDC différent si n est même ainsi que n est étrange. Mais si nous utilisons l’outil (*) qui a été généré à partir du binôme de Newton, en faisant x = y a été réduit à l’équation suivante;
Comme
en isolant
nous avons;
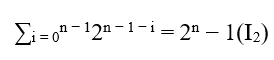
En remplaçant (I2) et (I1), on obtient;
(2x)n = xn.(2n − 1) + xn
Pour que le premier côté de l’équation soit écrit comme la somme de deux puissances du deuxième côté de l’équation, et comme le facteur commun est xn, cependant, comme la valeur de x n’a pas été définie, alors il suffit pour x pour s’écrire 2n – 1, dit ceci, l’équation ne dépendra que du degré n, donc nous avons;
(2x)n = xn.(2n − 1) + xn
(2.(2n − 1))n = (2n − 1)n.(2n − 1) + (2n − 1)n
Donc une autre équation qui ne dépend que d’une variable.
(2.(2n − 1))n = (2n − 1)n + 1 + (2n − 1)n
Données pour cette nouvelle équation;
a = 2.(2n − 1), B = (2n − 1)n + 1 e c = 2n − 1
MDC(a,B,c)=MDC(2.(2n − 1), (2n − 1)n + 1, 2n − 1) = 2n − 1 = c
pour n paire
C’est n=2k avec k ∈ N*
MDC(2.(22k − 1), (22k − 1)2k + 1, 22k − 1) = 22k − 1 = c
pour n impair
C’est n= 2k + 1 avec k ∈ N*
MDC(2.(22k + 1 − 1), (22k + 1 − 1)2k + 2, 22k + 1 − 1) = 22k + 1 − 1 = c
En fait, cela a été prouvé parce que toutes les déclarations proposées par le S.T.M ont reçu une réponse.
Test avec des nombres;
Pour n = 2, nous avons;
(2.(2n − 1))n = (2n − 1)n + 1 + (2n − 1)n
(2.(22 − 1))2 = (22 − 1)2 + 1 + (22 − 1)2
(2.(3))2 = 33 + 32
62 = 33 + 32
36 = 27 + 9
Pour n = 3 nous avons;
(2.(2n − 1))n = (2n − 1)n + 1 + (2n − 1)n
(2.(23 − 1))3 = (23 − 1)3 + 1 + (22 − 1)3
(2.(7))3 = 74 + 73
143 = 74 + 73
2744 = 2401 + 343
Pour le moment, S.T.M semble avoir deux équations, mais une seule est au format Conjecture qu’il est;
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
MDC(2m − 1 + 1, 2, 2m − 1 − 1) = 1, com m ≥ 2. “Ce n’est pas le cas, car il contient 2 comme exposant”
et
(2.(2n − 1))n = (2n − 1)n + 1 + (2n − 1)n
MDC(2.(2n − 1), 2n − 1, 2n − 1) = 2n − 1, com n ≥ 2. « si n>2 appartient alors à Beal Conjecture »
3.4 AUTRES ÉQUATIONS GÉNÉRÉES PAR LA MÉTHODE DE S.T.M.
F1: ⇒ (2m − 1 + 2k − 1)2 = 2k(m + 1) + (2m − 1 − 2k − 1)2
C’est le général ( 1 ).
MDC(2m − 1 + 2k − 1, 2, 2m − 1 − 2k − 1) = 1, avec k = 1 e m ≥ 2.
ou
MDC(2m − 1 + 2k − 1, 2, 2m − 1 − 2k − 1) = 2, avec m ≥ 2 e m > k > 1.
Tapez si m = 4, alors k peut être 3.2 et 1.
F2: ⇒ (2m − 1.km + k)2 = (2k)m + 1 + (2m − 1.km − k)2
C’est l’equation générale de la précédente .
MDC(2m − 1.km + k, 2k, 2m − 1.km − k) = k, avec m ≥ 2 e k ∈ N*.
F3: ⇒ (2m + km + 2)2 = (2k)m + 2 + (2m − km + 2)2
ou
(2m + km + 2)2 = (2k)m + 2 + (km + 2 − 2m)2
Si m = 0 et k pour la paire que nous avons; MDC(1 + k2, 2k, |1 − k2|) = 1, com k ∈ N*.
Si m = 0 e k est étrange que nous ayons; MDC(1 + k2, 2k, |1 − k2|) = 2α ≥ 2, com k, α ∈ N*.
Si k est étrange que nous ayons; MDC(2m + km + 2, 2k, |2m − km + 2|) = 1, com m ≥ 1 e k ∈ N*.
Si k pour la paire que nous avons; MDC(2m + km + 2, 2k, |2m − km + 2|) = 2α ≥ 2, com m ≥ 1 e k, α ∈ N*.
Formule de format général C2 = B + A2 ⇒ C2 = bm + A2
G1: ⇒ (am + 2m − 2.tm)2 = (2.a.t)m + (am − 2m − 2.tm)2
Dé:
C = am + 2m − 2.tm, b = 2.a.t e A = |am − 2m − 2.tm|
( i ) Si a est étrange et m > 2 o MDC(C,b,A)=1, ∀t ∈ N*.
( ii ) Si un est étrange avec m = 2 et t un Même, le MDC (C,b,A)=1 .
( iii ) Si un est impair avec m = 2 et t un Impair, le MDC(C, b, A) = 2α ≥ 2 avec α ∈ N*.
( iv ) Si un est paire et m > 2 le MDC (C, b, A) = 2α ≥ 2, ∀t, α ∈ N*.
( v ) Si un est jumelé avec m = 2 et t un Odd le MDC (C, b, A) = 1, t ∈ N*.
( vi ) Si un est jumelé avec m = 2 et t une paire le MDC (C, b, A) = 2α ≥ 2, t, α ∈ N*.
Comment chaque formule ou équation a vu le jour :
L’idée est née en raison de conjectures Fermat-Catalan, parce que lorsque vous avez Cz = By + Ax, il n’a qu’une quantité limitée de solutions dans lesquelles A, B, et C sont des entiers positifs sans facteurs premiers communs et x, y, et z sont des entiers positifs satisfaisant ()/() < 1, parce que toutes les solutions auront 2 comme l’un des exposants. Pour cette raison, il serait possible que la fixation exposant 2 dans la différence carrée aurait des résultats satisfaisants dans le format de la conjecture? Lorsque vous utilisez la même méthode de S.T.M, de nouvelles équations avec des solutions en nombres entiers positifs sont apparues.
F1: Seja (2r + 2s)2 = B + (2r − 2s)2 ⇒ B = (2r + 2s)2 − (2r − 2s)2, avec B, r, s ∈ ℕ où r > s, r et s variables non définies actuellement.
B = (2r + 2s)2 − (2r − 2s)2 → B = (2r + 2s − 2r + 2s).(2r + 2s + 2r − 2s) → B = (2s + 2s).(2r + 2r) → B = 2s + 1.2r + 1 → B = 2s + r + 2
Lors de l’adaptation de s et r dans les variables m et k comme S.T.M, nous devons m > k soustraire 1 des deux côtés nous avons m − 1 > k − 1 en comparant r > s, nous devons r = m − 1 e s = k − 1, avec ça nous avons B = 2k − 1 + m − 1 + 2 → B = 2m + k − 2 + 2 → B = 2m + k, donc l’équation est;
F1: ⇒ (2m − 1 + 2k − 1)2 = 2m + k + (2m − 1 − 2k − 1)2
Si k for 1, alors MDC(2m − 1 + 21 − 1, 2, 2m − 1 − 21 − 1) = MDC(2m − 1 + 20, 2, 2m − 1 − 20) = MDC(2m − 1 + 1, 2, 2m − 1 − 1) = 1, ∀m ∈ N*
Exemple d’utilisation de cette équation qui a MDC=1, avec m = 2, 3, 5, 6. ; m ne peut pas être 1 parce que k était 1.
Pour m = 2
(22 − 1 + 1)2 = 22 + 1 + (22 − 1 − 1)2 → 32 = 23 + 12 → 9 = 8 + 1
Pour m = 3
(23 − 1 + 1)2 = 23 + 1 + (23 − 1 − 1)2 → 52 = 24 + 32 → 25 = 16 + 9
Pour m = 4
(24 − 1 + 1)2 = 24 + 1 + (24 − 1 − 1)2 → 92 = 25 + 72 → 34 = 25 + 72 → 81 = 32 + 49
Pour m = 5
(25 − 1 + 1)2 = 25 + 1 + (25 − 1 − 1)2 → 172 = 26 + 152 → 289 = 64 + 225
Pour m = 6
(26 − 1 + 1)2 = 26 + 1 + (26 − 1 − 1)2 → 332 = 27 + 312 → 1089 = 128 + 961
Si k > 1, alors MDC(2m − 1 + 2k − 1, 2, 2m − 1 − 2k − 1) = 2, ∀m, k ∈ N*, où m > k
Exemple si m = 5, alors k varie entre 2 até 4.
(2m − 1 + 2k − 1)2 =2m + k + (2m − 1 − 2k − 1)2→ (25 − 1 + 2k − 1)2 =25 + k + (25 − 1 − 2k − 1)2→ (24 +2k − 1)2 =25 + k + (24 − 2k − 1)2
Pour k = 2
(24 + 22 − 1)2 = 25 + 2 + (24 − 22 − 1)2 → (24 + 21)2 = 27 + (24 − 21)2
→ 182 = 27 + 142 → 324 = 128 + 196
Pour k = 3
(24 + 23 − 1)2 = 25 + 3 + (24 − 23 − 1)2 → (24 + 22)2 = 28 + (24 − 22)2
→ 202 = 28 + 122 → 400 = 256 + 144
Pour k = 4
(24 + 24 − 1)2 = 25 + 4 + (24 − 24 − 1)2 → (24 + 23)2 = 29 + (24 − 23)2
→ 242 = 29 + 82 → 242 = 29 + 26 → 576 = 512 + 64
F2: Être (2s.kr + k)2 = B + (2s.kr − k)2 ⇒ B = (2s.kr + k)2 − (2s.kr − k)2, avec B, k, r, s ∈ ℕ où r > s, r et s variables non définies actuellement.
B = (2s.kr + k)2 − (2s.kr − k)2 → B = (2s.kr + k − 2s.kr + k).(2s.kr + k + 2s.kr − k) → B = (2k).(2s + 1.kr) → B = 2k.2s + 1.kr → B = 2s + 2.kr + 1, Pour que B soit écrit comme une puissance suffisante s + 2 = r + 1, il se trouve que B = (2k)r + 1 ou B = (2k)s + 2, Cependant, pour que cela soit vrai, il doit être supérieur à l’art r > s.
Hypothèse s + 2 = r + 1 ⇒ s = r − 1 et thèse r > s
Nous devons s + 1 > s ajouter 1 Sur les deux côtés s + 2 > s + 1 ⇒ r + 1 = s + 2 > s + 1 > s ⇒ r + 1 > s à son tour r + 1 > r par conséquent r > s, réalisez que lorsque vous utilisez l’hypothèse où s = r − 1 ⇒ r = s + 1 et remplacer dans r > s l’inégalité est satisfaite s + 1 > s.
Par conséquent B = (2k)r + 1 = (2k)s + 2 = (2k)r + 1, alors l’équation est;
(2r − 1.kr + k)2 = (2k)r + 1 + (2r − 1.kr − k)2, de sorte que tout est basé sur la même variable m, juste r être égal à m, c’est-à-dire r = m. Avec cela, nous avons déjà une autre équation;
F2: ⇒ (2m − 1.km + k)2 = (2k)m + 1 + (2m − 1.km − k)2
Si k ses 1, c’est l’équation elle-même F1 de MDC=1;
(2m − 1.1m + 1)2 = (2.1)m + 1 + (2m − 1.1m − 1)2 → (2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
Si k > 1 a comme MDC = k
MDC(2m − 1.km + k, 2k, 2m − 1.km − k) = k, ∀m, k ∈ N*.
Pour k = 2
(2m − 1.km + k)2 = (2k)m + 1 + (2m − 1.km − k)2
(2m − 1.2m + 2)2 = (4)m + 1 + (2m − 1.2m − 2)2
(22m − 1 + 2)2 = 4m + 1 + (22m − 1 − 2)2
Se m = 1
(22.1 − 1 + 2)2 = 41 + 1 + (22.1 − 1 − 2)2 → 42 = 42 + 02 → 16 = 16
Se m = 2
(22.2 − 1 + 2)2 = 42 + 1 + (22.2 − 1 − 2)2 → (23 + 2)2 = 43 + (23 − 2)2 → 102 = 43 + 62 → 100 = 64 + 36
Se m = 3
(22.3 − 1 + 2)2 = 43 + 1 + (22.3 − 1 − 2)2 → (25 + 2)2 = 44 + (25 − 2)2 → 342 = 44 + 302 → 1156 = 256 + 900
*
*
*
Etc …
Pour k = 3
(2m − 1.km + k)2 = (2k)m + 1 + (2m − 1.km − k)2
(2m − 1.3m + 3)2 = 6m + 1 + (2m − 1.3m − 3)2
Se m = 1
(21 − 1.31 + 3)2 = 61 + 1 + (21 − 1.31 − 3)2
(20.3 + 3)2 = 62 + (20.3 − 3)2 → 62 = 62 + 02
Se m = 2
(22 − 1.32 + 3)2 = 62 + 1 + (22 − 1.32 − 3)2
(21.9 + 3)2 = 63 + (21.9 − 3)2 → 212 = 63 + 152 → 441 = 216 + 225
Se m = 3
(23 − 1.33 + 3)2 = 63 + 1 + (23 − 1.33 − 3)2Nn
(22.27 + 3)2 = 64 + (22.27 − 3)2 → 1112 = 64 + 1052 → 12321 = 1296 + 11025
*
*
*
Etc…
F3: Être (2s + kr)2 = B + (2s − kr)2 ⇒ B = (2s + kr)2 − (2s − kr)2, avec B, r, s ∈ ℕ où r > s, r et s variables non définies actuellement.
B = (2s + kr)2 − (2s − kr)2 → B = (2s + kr − 2s + kr).(2s + kr + 2s − kr) → B = 2.kr.2s + 1 → B = 2s + 2.kr, dans ce cas pour que B soit une puissance suffisante r = s + 2. En fait r > s parce que s + 2 > r = s + 1 > s ⇒ r > s lors du placement de l’exposant en fonction de m, juste s = m cela nous donner r = m + 2.
Bientôt B = 2s + 2.kr = (2k)r = (2k)m + 2.
La nouvelle équation est donc;
F3: ⇒ (2m + km + 2)2 = (2k)m + 2 + (2m − km + 2)2, avec k ∈ N* et m ≥ 0.
Si k est 1 pour ∀m ∈ N* le MDC = 1 ou Si m est de 0 à ∀k ∈ N* aussi le MDC = 1.
Si aucun de ces cas ne se produit, F3 a MDC = 2α ≥ 2, ∀α ∈ N*
La logique est la même pour G1, “Puisque c’est le général”;
Parce qu’en faisant B = (ar + 2s.tr )2 − (ar − 2s.tr)2 → B = (ar + 2s.tr − ar + 2s.tr).(ar + 2s.tr + ar- 2s.tr) →
Simplement s + 2 = r ou s = r – 2, comme r ses m faire la conversion que nous avons s = m – 2, c’est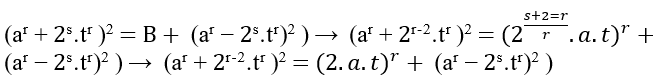 G1: ⇒ (am + 2m − 2.tm)2 = (2.a.t)m + (am − 2m − 2.tm)2
G1: ⇒ (am + 2m − 2.tm)2 = (2.a.t)m + (am − 2m − 2.tm)2
dé:
C = am + 2m − 2.tm, B = 2.a.t e A = |am − 2m − 2.tm|
( i ) Si a est étrange et m > 2 o MDC(C,b,A)=1, ∀t ∈ N*.
( ii ) Si un est étrange avec m = 2 et t un Même, le MDC (C,b,A)=1 .
( iii ) Si un est impair avec m = 2 et t un Impair, le MDC(C, b, A) = 2α ≥ 2 avec α ∈ N*.
iv ) Si un est paire et m > 2 le MDC (C, b, A) = 2α ≥ 2, ∀t, α ∈ N*.
( v ) Si un est jumelé avec m = 2 et t un Odd le MDC (C, b, A) = 1, t ∈ N*. ( vi ) Si un est jumelé avec m = 2 et t une paire le MDC (C, b, A) = 2α ≥ 2, t, α ∈ N*.
4. FORMULES GÉNÉRÉES PAR T.M E S.T.M AVEC DES SOLUTIONS EN NATUREL
Donnee de basea; ,b,c,x,y,z,A,B,C,α e k ∈ N
Formule1: Cz = Cxyk + 1 = By+ Ax, mdc(x,y,z)=1
( by + ax )xyk + 1 = [ b( by + ax)xk]y + [ a( by + ax )yk]x
Dé:
C =by+ ax, B =b(by+ ax)xk e A = a( by+ ax )yk, MDC(C, B, A) = C.
Formule2: Cz = Cxk + 1 = Bx+ Ax, ouCz = Cyk + 1 = By+ Ay, mdc(z,x)= mdc(z,x) = 1
( bx + ax )xk + 1 = [ b( bx + ax )k ]x + [ a( bx + ax )k ]x
OU
( by + ay )yk + 1 = [ b( by + ay )k]y + [ a( by + ay )k ]y
Dé:
C =bx+ ax, B =b(bx+ ax)k e A = a(bx+ ax )k, MDC(C, B, A) = C.
OU
C =by+ ay, B =b(by+ ay)k e A = a( by+ ay )k, MDC(C, B, A) = C.
Formule3: Cz = Cxk = Bxkα+ 1+Ax, ouCz=Cyk = Bykα+ 1+Ay, mdc( z, y , x ) = 1
[ c( cxk− ax )α]xk = ( cxk− ax )xkα+1 +[ a(cxk−ax)kα]x
OU
[ c( cyk− by )α]yk = [ b( cyk− by )kα]y + ( cyk− by )ykα+1
Dé:
C = c(cxk − ax), B = cxk − ax e A = a.(cxk −ax), MDC(C,B,A)= B.
OU
C = c(cyk − by), B = b(cyk − by) e A = cyk − by, MDC(C,B,A)= A.
Formule4:
(2.(2n − 1))n = (2n − 1)n + 1 + (2n − 1)n
OU
(2n+1 − 2)n = (2n − 1)n + 1 + (2n − 1)n
Dé;
a = 2.(2n − 1), B = (2n − 1)n + 1 e c = 2n − 1, MDC(a B,c)=MDC(2.(2n − 1), (2n − 1)n + 1, 2n − 1) = 2n − 1 = c
Formule5:
G1: ⇒ (am + 2m − 2.tm)2 = (2.a.t)m + (am − 2m − 2.tm)2
Dé:
C = am + 2m − 2.tm, B = 2.a.t e A = |am − 2m − 2.tm|, Com t ≠ 2.a
( i ) Si a est étrange et m > 2 o MDC(C,b,A)=1, ∀t ∈ N*.
( ii ) Si un est étrange avec m = 2 et t un Même, le MDC (C,b,A)=1 .
( iii ) Si un est impair avec m = 2 et t un Impair, le MDC(C, b, A) = 2α ≥ 2 avec α ∈ N*.
( iv ) Si un est paire et m > 2 le MDC (C, b, A) = 2α ≥ 2, ∀t, α ∈ N*.
( v ) Si un est jumelé avec m = 2 et t un Odd le MDC (C, b, A) = 1, t ∈ N*.
( vi ) Si un est jumelé avec m = 2 et t une paire le MDC (C, b, A) = 2α ≥ 2, t, α ∈ N*.
En particulier
c2 = 2m + 1 + b2, MDC(a,b,c)=1
(2m−1+1)2=2m+1+(2m−1−1)2
c=2m−1+1, b=2 e a=2m−1−1, MDC(a,b,c)=1
5. T.G.M OU LE GÉNÉRAL THÉOREM MACENA
Compte tenu de toute équation valide des entiers positifs sous forme de puissance, ou généré par T.M ou S.T.M lors de la multiplication par dα un pouvoir, où d est une base adéquate de transformation en la somme de deux pouvoirs, et α est un exposant multiple positive integer des exposants des autres bases ou mmc des exposants multipliés par t *, se traduit donc par un pouvoir écrit dans la somme de deux autres pouvoirs avec un facteur commun d ou multiple de d.
, avec B>A et m ≥ n ≥ 2, où α=mmc(1,m,n).t, t ϵ N*
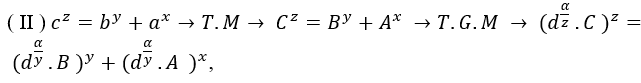
, où α=mmc(z,y,x).t, t ϵ N*
![]() , où α=mmc(n,1,n).t, t ϵ N*
, où α=mmc(n,1,n).t, t ϵ N*
( IV ) C2=B+A2→ Geralpor S.T.M→ ( am + 2m − 2.tm )2 = ( 2.a.t )m + ( am − 2m − 2.tm )2→T.G.M →
![]() , où α =mmc (2,m,2).β, β ε N*
, où α =mmc (2,m,2).β, β ε N*
Avec cela, nous avons toujours un facteur commun dans le format de la Conjecture si les exposants x,y,z≥3, indépendamment de l’équation abordée.
« À l’exception de ( IV ) qui aura grade 2 toujours au moins sur l’une des bases ».
5.1 PROUVER T.G.M
Pour prouver ce theorème, il est nécessaire de prouver les éléments. ( I ), ( II ), ( III ) et ( IV ).
Élément prouvant (I) Si une équation du type
, avec B,
en multipliant par une puissance
, d non défini pour le moment, cependant
, c’ est dm.n.t , bientôt nous avons;
![]() comme d n’est pas défini, il suffit d’être égal à ce que
comme d n’est pas défini, il suffit d’être égal à ce que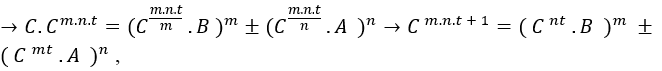 , où C est le facteur commun de l’équation,
, où C est le facteur commun de l’équation, ![]()
Exemple en chiffres;
C1 = Bm+Am→ 29 =33 + 22, par théorème d=C1=29 eα= mmc(1,3,2).t = 6t, →296t+1 = 33 . 296t + 22. 296t
296t+1 =( 3.292t )3 + ( 2.293t )2 , si t=1 nous avons 297=25233+487782, mdc( 29 , 2523 , 48778 ) = 29 , si t = 2 nous avons 2913=21218433+11896466422, mdc(29, 2121843 , 1189646642 ) = 29 etc avec t ≥3
C2 = Bm-An→ 23 =33-22, par théorème d=C2=23eα=mmc(1,3,2).t = 6t,→236t+1 =33.236t-22.236t→
236t+1 =(3.232t)3 – (2.233t)2→, si t=1 nous avons 237=15873-243342,mdc( 23 , 1587 , 24334 ) = 23, si t = 2 nous avons 2313=8395233-2960717782, mdc(23, 839523 , 296071778 ) = 23 etc avec t ≥3.
Élément prouvant ( II ) Si une équation du type cz=by+ax avec des solutions sur des entiers positifs, pour T.M nous arriverons à une équation équivalent avec les bases suivantes;
C =by+ax, B =b(by+ax )xk e A =a( by+ax )yk, com equação Cxyk+1=By+Ax→Cz=By+Ax
En multipliant par une puissance dα , d non défini pour le moment, cependant α=mmc(z,y,x).t , tϵN*, c’est dzyx.t , bientôt nous avons;
dzyx.t .Cz= dzyx.t.By+dzyx.t .Ax→(dyx.t .C )z= (dzx.t .B )y+(dzy.t .A )x→ Comme mdc( C , B , A ) = C alors
MDC[(dyx.t .C ),(dzx.t .B ),(dzy.t .A ) ] ≥ dt .C , en particulier si d = C nous avons Cz(yxt+1)= (Czx.t .B )y+(Czy.t .A )x
MDC[ C , (Czx.t .B ), (Czy.t .A ) ] = C. L’expansion en utilisant toutes les données de l’équation est;
{ dyx.t . by+ax }z= {dzx.t .b( by+ax )xk}y+{dzy.t .a( by+ax )yk}x
Comme z= xyk + 1
{dyx.t .( by+ax ) }xyk+1= {d(xyk+1)x.t .b(by+ax )xk}y+{d(xyk+1)y.t .a( by+ax )yk}x
Exemple en chiffres
x=y=2, t=k=1 e b=a=3 e d=5
{54 .( 32+32 ) }5= {510 .3( 32+32 )2}2+{510 .3( 32+32 )2}2
{54 .18 }5= {510 .3.182}2+{510 .3.182}2
112505=94921875002+94921875002
MDC(11250 ,9492187500,9492187500)=11250
Élément prouvant (III) Si une équation du type cn=B+an,avec des solutions entières positives, par S.T.M, nous avons une grande quantité d’équations mais B est toujours ![]()
, en multipliant l’équation par la puissance dα, d non défini pour le moment, avec α = mmc(n,1,n).t, t ϵ N*, nous avons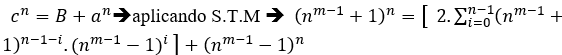
nous avons
![]() →Comme d n’est pas assez défini d=B c’est
→Comme d n’est pas assez défini d=B c’est![]()
Exemples;
( 1 )
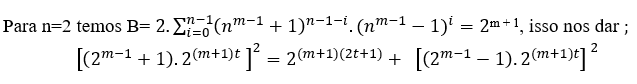
Si m = 2, nous avons → (3.23t )2=23(2t+1)+ 26t, ∀ t ∈N, MDC[(3.23t),2,2]=2
Si m = 3, nous avons →(5.24t )2=24(2t+1)+(3.24t)2, ∀ t ∈N, MDC[(5.24t),2,(5.24t)]=2
[…]
( 2 )
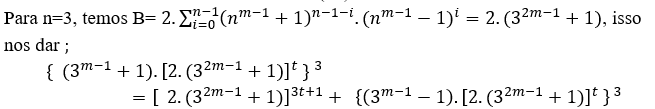 Si m = 2, nous avons →{4.56t}3=563t+1+ {2.56t } 3, ∀ t ∈N, MDC[(4.56t),56,2.56t]= 56
Si m = 2, nous avons →{4.56t}3=563t+1+ {2.56t } 3, ∀ t ∈N, MDC[(4.56t),56,2.56t]= 56
Si m=3, nous avons →{10.488t} 3=4883t+1+ {8.488t }3, ∀ t ∈N,MDC[(10.488t),488,8.488t] = 488
[…]
( 4 )
( 5 )
∀ m > 1, t ∈ N, MDC[Das Bases] = 2.6m. (64m-4 + 20. 62m-3 +1)
( 7 )
Etc.
.
.
.
( … )
NOTE: Jusqu’à présent, les éléments ( I ), ( II ) et ( III ) ne reste que ( IV )
Élément prouvant ( IV ) Être n’importe quelle équation de type c2=B+a2, avec des solutions dans les entiers positifs, en utilisant les moyens de S.T.M, nous l’avons fait;
C2=B+C2→General par S.T.M→( am + 2m − 2.tm )2 = ( 2.a.t )m + ( am − 2m − 2.tm )2, en multipliant par la puissance dα, avec d non défini pour le moment, cependant α = mdc(2,m,2).β , β ϵ N*, cette fois utiliser β parce que l’équation a déjà t, cela dit que nous avons;
dα.(am + 2m − 2.tm )2 = dα.( 2.a.t )m + dα.( am − 2m − 2.tm )2
[dmβ.( am + 2m − 2.tm )]2 = [d2β.( 2.a.t )]m + [dmβ( am − 2m − 2.tm )]2 [dmβ .( am + 2m − 2.tm )]2 = [2at.d2β ]m + [dmβ ( am − 2m − 2.tm )]2
Dans ce cas d peut être n’importe quel nombre appartenant aux entiers positifs sauf zéro, (dεN*).
Exemple en chiffres;
a=2, d=5et=m=β = 3
[59 .( 23 + 21.33)]2 = [12.56]3 + [59 .( 23 - 21.33)]2
[ 59 .( 62 )]2 = [12.56]3 + [59 .( -46)]2
[121093750]2 = [187500]3 + [ -89843750 ]2
1210937502 = 1875003 + (- 89843750 )2
MDC[121093750 ,187500 ,| – 89843750 |] = 31250
REMARQUE: le MDC(Das Bases ) ≥ dβ, cette 31250 = 2.d2β>dβ
L’idée est la même pour n’importe quelle équation avec la somme de 2 puissances.
Donc tu prouves T.G.M
Curiosité:( 1.0 )
5 = 3 + 2 → multiplié par la base 3 → 5.3 = 32 + 2.3 → comme 3 = 5 – 2 → remplace dans le premier membre 5(5 – 2)=32 + 2.3 → 52 – 2.5 = 32 + 2.3 → isoler 52 = 32 + 2.( 3 + 5 ) →
52 = 32 + 2.( 8 ) → 52 = 32 + 2.( 23 ) → 52 = 32 + 24.
( 1.1 )
53 = 53 → 53 = 5.52 → nous pouvons écrire 5 = 22 + 1, mettre le deuxième membre →
53 = (22 + 1).52 → 53 = 22.52 + 52 → 53= 102 + 52.
« NOTE: Cette curiosité est un autre article que je vais publier à l’avenir, ABC Conjecture »
6. PROUVER LA CONJECTURE BEAL
(1ère condition) Compte tenu de l’équation cz = by + ax, avec des solutions dans les entiers positifs, avec { z , y, x ≥ 3 / c, b , un ≠ 0 }, puis a, b et c ont un facteur premier commun, ce qui signifie que a, b et c sont divisibles par le même nombre premier.
Ou
(2ème Condition) Équation a x + b y = c z n’a pas de solution pour les entiers positifs avec x,y,z ≥ 3 et mdc(a,b,c)=1
Démarrage du test
A (2ème Condition ) Il est impossible d’obtenir des nombres dans les entiers positifs avec mdc(a,b,c) =1, et les exposants x,y,z ≥ 3, pour deux raisons déjà montrées :
1er — Il a été démontré que le Conjecture Fermat-Catalan n’a qu’une quantité limitée de solutions, actuellement il n’y a que 10 équations trouvées, dans lesquelles a, b, et c sont des entiers positifs sans facteurs premiers communs et x, y, et z sont des ensembles positifs satisfaisants
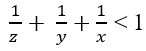
, parce que toutes les solutions auront 2 comme l’un des exposants, cela colle déjà à l’hypothèse de mdc(a) ,b,c) =1, et exposants x,y,z ≥ 3.
LES 10 TROUVÉS SONT; Image tirée du site wikipedia.

2
ème — Si vous votez pour la partie S.T.M notez que lorsque les équations ont le mdc (bases)=1, il a toujours un exposant 2, variant même les autres exposants, et comme S.T.M a été prouvé, tout comme le Conjecture Fermat – Catalan déclare au moins l’un des exposants devrait être 2, puis colle l’hypothèse pour la simple raison de contenir un exposant 2 dans l’une des bases.
Il ne reste donc qu’une seule autre condition à prouver.
La (1ère Condition) est déjà possible grâce à T.M, S.T.M e T.G.M, tous ont des facteurs communs dans les deux bases seulement pour montrer qu’il a un facteur principal commun qui divise les deux bases avec les exposants x,y,z ≥ 3.
PREUVE:
Dé;
Soit p un nombre premier, et Fp = pu un facteur premier commun p, et pi ≠pi+1, i index, cousins et exposants distincts Ui ≥ Ui+1≥0, i index, différents exposants ou non, alors C un nombre naturel peut être entré comme;
C = Fp = pu, ou C = p1u1.p2u2 ou C = p1u1.p2u2. p3u3 .p4u4 …piui .pi+1ui+1… Facteurs premiers communs, tels que cz = by + ax, et par une méthode de T.M, S.T.M e T.G.M, est obtenu Cz = By + Ax, alors;
Cz =(Fp )z = pz.u↔By + Ax = pz.u, ou Cz =( p1u1 ) .p2u2 )z =p1z.u1 .p2z.u2 ↔By + Ax = p1z.u1 .p2z.u2 ou
Cz =(p1u1.p2u2. p3u3 .p4u4 … piui.pi+1ui+1…)z =p1z.u1 .p2z.u2. p3z.u3.p4z.u4… piz.ui.pi+1z.ui+1…= By + Ax
BÂTIMENT Cz → Cz DE Cn.
En fait 1 = 1, parce que 1 est un élément neutre de multiplication dit que c’est c ε N*, lorsqu’il est multiplié des deux côtés, nous avons 1.c = 1.c→c = c, lorsqu’il est multiplié par c nous avons c.c =c.c→c2 = c2→ si ce processus se poursuit pour n fois nous avons → cn = cn, notez si n > z, nous avons cn>cz.
Donc cn = cn peut être inscrit comme cn = cz.cn – z, l’hypothèse de conjecture est que cz= by+ ax, hache, a un facteur principal commun qui divise les bases c,b et a, avec z,y,x ≥ 3, avec ce que nous avons;
cn = cz.cn – z→cn = ( by+ ax).cn – z→cn = by. cn – z + ax.cn – z, puis si cz= by+ ax hache a des solutions dans les entiers positifs, avec des exposants supérieurs ou égaux à 3, en fait cn = by. cn – z + ax.cn – z, a un facteur qui divise à la fois parce que le mdc (cn, by. cn – z, ax.cn – z) = cn> 1.
La traduction est démontrée que cz= by+ ax a de telles solutions de sorte qu’en fait il confirme l’hypothèse et c’est une thèse. Mais pour arriver à cette déclaration, nous devons prouver l’égalité, mais cela a déjà été démontré par les théoriques T.M, S.T.M e T.G.M, cependant, les conditions des exposants étaient supérieures ou égales à 3 n’ont pas été inclus, ni les conditions des principaux facteurs concluant ainsi est prouvé la Conjecture Beal.
Utilisation de T.M temos que a equação cz= by+ ax, tornasse;
(by+ax)xyk+1=[b.(by+ax)xk ]y+[a.(by+ax)yk]x, où z = xyk + 1, C = by+ax ,
B= b.(by+ax)xk e A = a.(by+ax)yk , c’est Cz = By + Ax, avec mdc (C,B,A) = C >1, pour
x,y,z> 2 ou x,y,(xyk+1) > 2.
Donc, si Cz = Par + Ax a des solutions dans les entiers positifs, puis cz = cxyk+1 = by + ax, tout simplement parce qu’il a le même format ou la même structure. Cela dit, il reste à montrer cn, quel est; cn = by. cn – z + ax.cn – z , adaptation pour les bases C, B et A que nous avons;
C n = By. C n – z + Ax.Cn – z
(by+ax)n=[b.(by+ax)xk ]y.(by+ax)(n-z)+[a.(by+ax)(yk )]x.(by+ax)(n-z)
(by+ax)n=by.(by+ax)xyk + n- z+ax.(by+ax)xyk + n- z , comme z = xyk+1,
(by+ax)n=by.(by+ax)xyk + n- xyk-1 +ax.(by+ax)xyk + n- xyk-1
(by+ax)n=by.(by+ax)n-1+ax.(by+ax)n-1
«C’est l’équation en fonctions des exposants n, x, y, basée sur les théorèmes précédemment montrés que nous avons (n - 1) est un multiple de x, y, c’est n – 1 =
xyt ou n = xy.t + 1, t est juste pour différencier de k, en utilisant déjà ”
(by+ax)xy.t+1=by.(by+ax)xyt +ax.(by+ax) xyt
(by+ax)xy.t+1=[b.(by+ax)xt ]y+[a.(by+ax)yt]x
Então como Cn>Cz→Cn-Cz> 0 → (by+ax )xy.t+1-(by+ax )(xy.k+1)>0→partage por(by+ax ), nous avons→(by+ax )xy.t-(by+ax )(xy.k)>0→partage (by+ax )xy, nous avons →
(by+ax )t-(by+ax )k>0→(by+ax )t>(by+ax )k→t > k, ∀ t,k ∈N
Ensuite, l’équation avec toutes les variables peut être écrite comme suit;
( EQ1 )(by+ax)xy(t+k)+1=[b.(by+ax)x(t+k) ]y+[a.(by+ax)(y(t+k) )]x
OU
( EQ2 ) (by+ax)xy( t – k )+1)=[b.(by+ax)x( t – k ) ]y+[a.(by+ax)y(t – k) ]x
Pour accéder à ces deux formules, utilisez simplement T.M, avec n-z=xyt→n= xyt + z, et comme z=xyt, nous avons n = xy (t +k), et comme il a été démontré que t > k, est également valide n = xy ( t – k ) ∈N*
Comme les autres formules générées par T.M et certains aussi de S.T.M e T.G.M, qui a le format Cz = By +Ax, a le même comportement que ( EQ1)e ( EQ2), puis montrant les conditions des facteurs premiers comme au début de ce test prouve littéralement toutes les conditions de la Conjecture Beal pour le cas affirmatif qui est (1ère condition ).
(#) Pour le cas d’un facteur principal commun dans ( EQ1)e( EQ2),isso é Cz= By + Ax = pz.u ;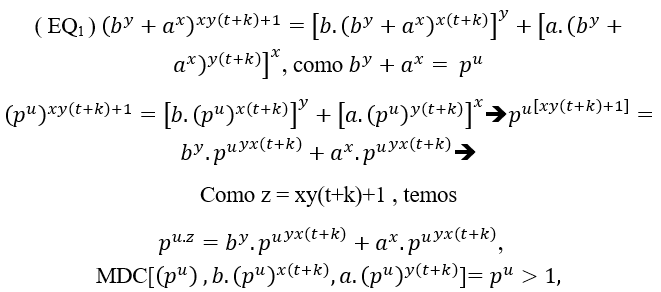
Ainsi, un facteur principal commun p, parce que l’égalité est satisfaite si elle continue,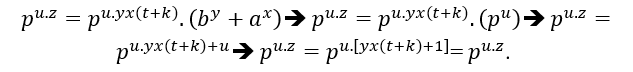
Analoguement à ( EQ1 ) aura le même résultat
(##) Dans le cas de 2 facteurs principaux courants dans (EQ1) et (EQ2), il s’agit
![]() i
i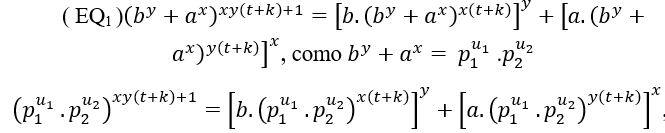 , en fat, le mdc sera le produit de deux pouvoirs de nombres premiers distincts, c’est
, en fat, le mdc sera le produit de deux pouvoirs de nombres premiers distincts, c’est
Vérif![]() ication de l’égalité, comme z = xy(t+k)+1, nous avons;
ication de l’égalité, comme z = xy(t+k)+1, nous avons;
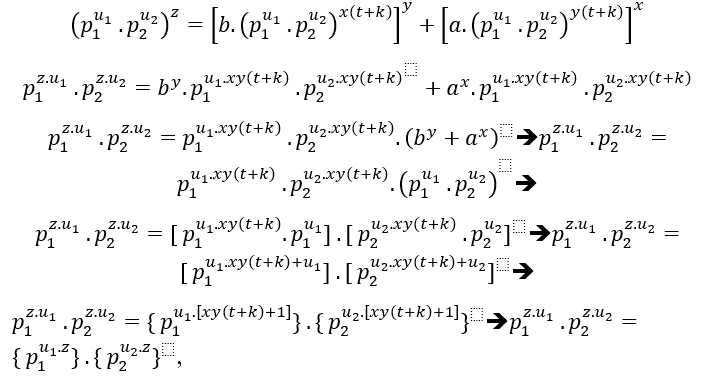 lors de la division par l’un des principaux facteurs communs tombe dans la condition ( # ).
lors de la division par l’un des principaux facteurs communs tombe dans la condition ( # ).
Analogue à (EQ2);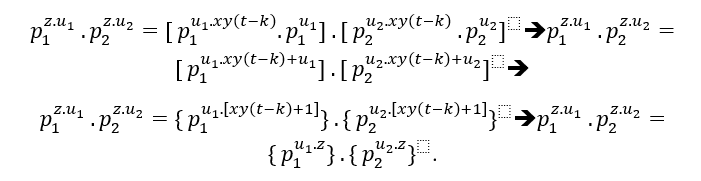 ( ### ) Dans le cas d’un facteur premier commun dans (EQ1) et (EQ2), c’est;
( ### ) Dans le cas d’un facteur premier commun dans (EQ1) et (EQ2), c’est;
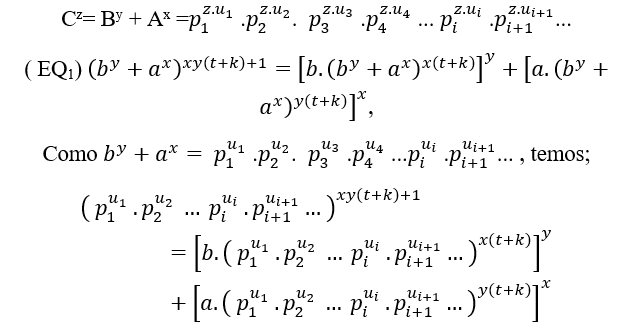
En fait, nous aurons un MDC avec plusieurs facteurs premiers communs, ou à partir de 3, des pouvoirs de nombres premiers distincts les uns des autres, 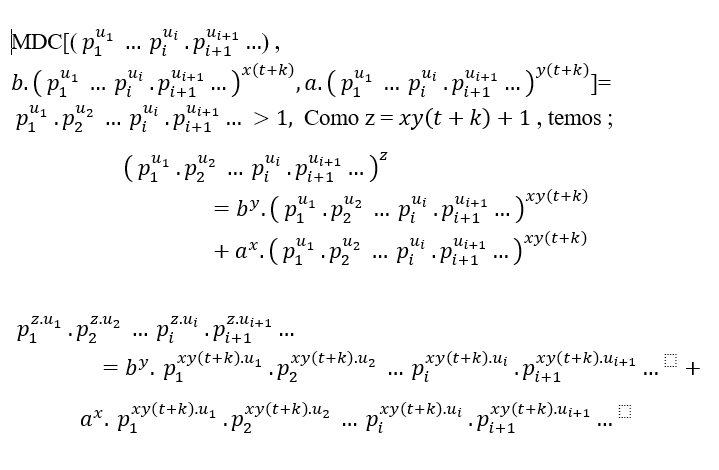 c’est
c’est
_______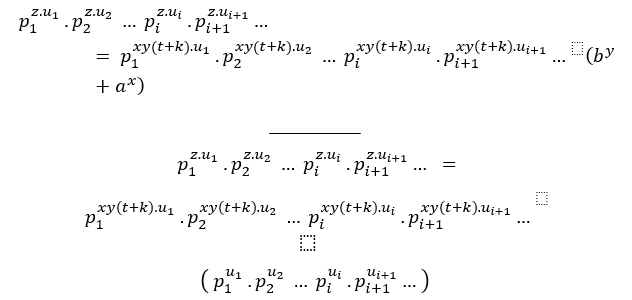 __
__
_________
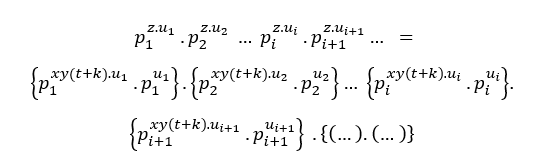
Tout comme la condition (## ), nous avons;
Chaque fois qu’il se divise par un facteur premier commun, ils vont réduire jusqu’à ce qu’il ne devienne qu’un facteur premier commun.
Analogue à (EQ2), il est également satisfait;
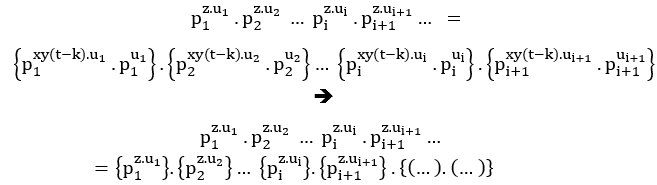 Par conséquent conjecture prouvée!
Par conséquent conjecture prouvée!
7. CONSIDÉRATIONS FINALES
Cet article a été proposé comme une preuve objective générale – il ya la Conjecture Beal, lors de l’utilisation des théoriques T.M, S.T.M e T.G.M combiné avec des applications dans la théorie des nombres, il était effectivement possible de démontrer, mais il n’a pas été possible de trouver un con – exemple, mais lors de l’utilisation des moyens au cours du développement doit avoir remarqué que chaque étape était essentielle pour l’autre de toute façon par rapport aux théoriques présentées sans le T.M ne pouvait pas utiliser T.G.M, sem o T.G.M o S.T.M ne pouvait pas être utilisé pour la conjecture de Beal si elle n’avait pas T.M o S.T.M e T.G.M serait quelque chose de très vague en d’autres termes n’a pas soutenu la démonstration d’une telle conjecture.
Au mieux sans les autres théorèmes tels que Théorème de Pythagore, Le Dernier Théorème de Fermat, Théorème de Sebá et Conjecture de Fermat – Catalan le T.M serait quelque chose de très vague et prendrait beaucoup plus de temps à être prouvé, juste en possédant de tels théoriques le T.M est une extension et en même temps ce qui soutient les théoriques cités, en d’autres termes T.M était la pièce manquante pour l’achèvement.
8. RÉFÉRENCES
BEAL, Andrew. Site: Wiki de Poker. 2008. Disponível em:<https://poker.fandom.com/wiki/Andrew_Beal> Acesso em: 03 de Junho de 2018.
FERMAT, biografias de Matemáticos. Site: Só Matemática. 1998-2019. Disponível em: <https://www.somatematica.com.br/biograf/fermat.php> Acesso em: 18 de Maio de 2018.
KILHIAN, (Sebastião Vieira do Nascimento, “Sebá”). A Conjectura de Beal – Casos Particulares. Site: O baricentro da Mente. 28/04/2012. Disponível em: <https://www.obaricentrodamente.com/2014/11/a-conjectura-de-beal-casos-particulares.html> Acesso em: 27 de Maio de 2018.
TANIYAMA e SHIMURA, Teorema de Shimura-taniyama-Wil. Editada pela última vez em 5 de setembro de 2017 Site: Wikipédia. Disponível em:<https://pt.wikipedia.org/wiki/Teorema_de_Shimura-Taniyama-Weil> Acesso em: 16 de Junho de 2018.
WILES, Biografia de matemáticos. Site: Só Matemática. 1998-2019. Disponível em: <https://www.somatematica.com.br/biograf/andrew.php > Acesso em: 15 de Maio de 2018.
9. RECHERCHE SOURCES
Site: O Baricentro da Mente. Título: A conjectura de Beal casos particulares. URL: <https://www.obaricentrodamente.com/2014/11/a-conjectura-de-beal-casos-particulares.html> Acesso em: 05 de Maio de 2018.
Site: O Baricentro da Mente. Título: Método de resolução das equações de Sebá. URL: <https://www.obaricentrodamente.com/2012/04/metodo-de-resolucao-das-equacoes-de.html> Acesso em: 05 de Maio de 2018.
Site: Folha de São Paulo. Título: Livro narra solução de teorema que confundiu teóricos por 358 anos. URL: <https://www1.folha.uol.com.br/fsp/ciencia/fe25109801.htm> Acesso em: 10 de Maio de 2018.
Site: Wikipedia. Título: Conjectura de Beal. URL:
<https://pt.wikipedia.org/wiki/Conjectura_de_Beal> Acesso em: 24 de Maio de 2018.
Site: ICM. Título: Detalhes do Autor “Sebastião Vieira do nascimento ( Sebá )”. URL:
<https://www.lcm.com.br/site/livros/detalhesAutor?id=A01644> Acesso em: 27 de Setembro de 2019.
Site: Morfismo. Título: Conjectura de Beal. URL:
<https://morfismo.wordpress.com/2013/11/25/conjectura-de-beal/> Acesso em: 28 de Julho de 2018.
Site: DocSity. Título: Fermat, Notas de estudos de Física. URL:
<https://www.docsity.com/pt/fermat-6-1/4705276/> Acesso em: 01 de Setembro de 2019.
Site: Wikipedia. Título: Conjectura de Fermat-Catalan. URL:
<https://pt.wikipedia.org/wiki/Conjectura_de_Fermat-Catalan> Acesso em: 23 de Setembro de 2019.
[1] Diplôme en mathématiques.
Soumis : août 2019.
Approuvé : novembre 2019.