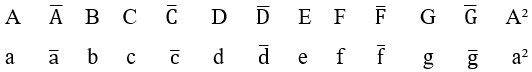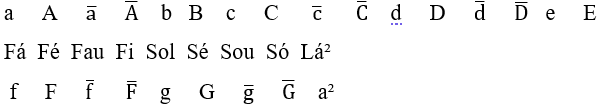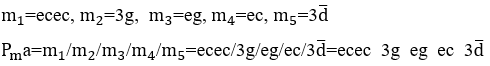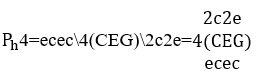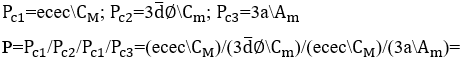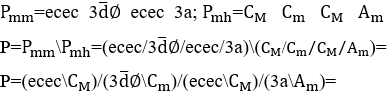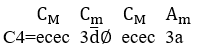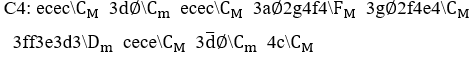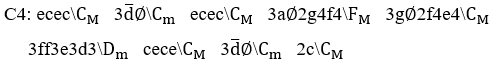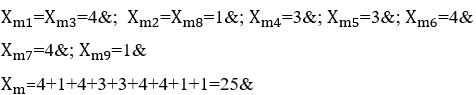La structure mathématique de la musique

ARTICLE ORIGINAL

VIANA, Arnóbio Araújo ^[1]

VIANA, Arnóbio Araújo. La structure mathématique de la musique. Revista Científica Multidisciplinar Núcleo do Conhecimento. An. 07, éd. 08, Vol. 02, p. 196-220. Août 2022. ISSN : 2448-0959, Lien d’accès: https://www.nucleodoconhecimento.com.br/olympiades-mathematiques/mathematique-de-la-musique, DOI: 10.32749/nucleodoconhecimento.com.br/olympiades-mathematiques/mathematique-de-la-musique

RÉSUMÉ

Tenant compte du fait que la composition musicale est une structure mathématique solide, cet article démontre le développement de la structure mathématique de la musique, diffusant un langage sonore plus compréhensible et adapté à la technologie actuelle des études scientifiques liées à la science de la musique. Par conséquent, l’objectif de cette recherche était de développer un langage algébrique pour structurer mathématiquement la musique, en utilisant uniquement des lettres, des chiffres et des symboles pour écrire les sons des notes de musique de manière alphanumérique, représentant ses principales caractéristiques sonores, telles que : fréquence (f) , amplitude (a) et durée (t), en une seule expression pour identifier une onde sonore. Le langage développé permet une orthographe à lecture simple et permet l’étude des phénomènes musicaux en général sur une plate-forme avec des représentations graphiques dans le système de coordonnées cartésien des structures des groupements mélodiques, avec les notes de musique en mélodie et les groupes harmoniques avec les notes en harmonie, promouvant ainsi la Structure Mathématique de la Musique.

Mots clés : Cellule Musicale, Mélodie, Harmonie, Rythme.

1. INTRODUCTION

Cette recherche a été rendue possible par le développement des opérations d’Harmonisation ou H et de sa Mélodie inverse ou M, établies dans l’article « l’opération d’harmonisation (H) et son opération de mélodie inverse (M) » (VIANA, 2022).

Dans l’article précité, il est défini que l’Opération H (\), entre ondes sonores de notes de musique, forme un groupement harmonique, dont l’harmonie (h) est l’effet sonore du résultat d’une combinaison entre elle. Dans ce cas, ces ondes sont interconnectées simultanément dans l’espace-temps, c’est-à-dire que leurs temps initiaux sont égaux et leurs temps finaux sont également égaux. Ces ondes de notes musicales égales forment un groupement harmonique d’un son unique ou une harmonie à l’unisson (VIANA, 2022).

Son opération inverse M (\), est définie entre des ondes sonores de notes musicales qui forment un groupement mélodique, dont la mélodie est l’effet sonore du résultat de l’arrangement entre elles . Dans ce cas, ces ondes sont continuellement interconnectées dans l’espace-temps, c’est-à-dire que le temps final d’une onde est égal au temps initial de l’onde suivante et ainsi de suite, où des ondes de notes de musique égales forment un groupement mélodique de sons répétés . Ainsi, les ensembles musicaux formés et organisés dans l’espace-temps constitueront une composition musicale, composée de mélodie, d’harmonie et de rythme (VIANA, 2022).

Par conséquent, l’objectif de cette recherche était de développer un langage algébrique pour structurer mathématiquement la musique, en utilisant uniquement des lettres, des chiffres et des symboles pour écrire les sons des notes de musique de manière alphanumérique, représentant ses principales caractéristiques sonores, telles que : fréquence (f) , amplitude (a) et durée (t), en une seule expression identifier une onde sonore.

2. REPRÉSENTATION D’UNE NOTE DE MUSIQUE

Pour représenter algébriquement le son d’une note de musique dans cette recherche, trois caractéristiques fondamentales sont nécessaires : la fréquence sonore (f) ; l’amplitude (a); et la durée (t), formant l’expression  “”, appelée, dans cette étude, la Cellule Musicale.

Cette nomenclature a été donnée parce qu’elle représente toute onde sonore ou non sonore, ou même tout attribut qui compose la structure d’une chanson, la note musicale étant la cellule sonore la plus importante pour la musique, et la pause musicale, la non-sonore la plus importante. cellule sonore à la musique La musique, considérée comme une note de musique silencieuse ou sans son, où la fréquence d’amplitude nulle   est représenté par un zéro inversé comme ton chiffre dans ce Langage Algébrique Musical.

2.1 REPRÉSENTATION DE LA FRÉQUENCE MUSICALE

La fréquence (f), en général, est la caractéristique la plus importante de toute vibration et est causée par un tremblement de terre dans n’importe quel milieu, qui produira une série de fréquences. Lors de l’opération H naturelle entre eux, une harmonie se forme, qui détermine la fréquence résultante de cette secousse . De plus, celui avec le son le plus bas ou la plus faible oscillation entre eux , est la plus importante de toutes, appelée Fréquence Fondamentale , étant la caractéristique responsable du son que nous entendons et qui permet de distinguer un son grave ou basse fréquence d’un son aigu ou haute fréquence.

Actuellement représenté dans Musique, d’après l’ouvrage de Guest (2020, p. 33 à 41), par les sept premières lettres de l’alphabet latin A, B, C, D, E, F et G, appelés chiffres, représentant respectivement les notes de musique Lá, Si, Dó, Ré, Mi, Fá et Sol, où en majuscules ils indiqueront les harmonies des accompagnements instrumentaux ou accords musicaux qui, dans cette étude, représenteront également les notes musicales groupées en harmonie, résultat de l’opération “H” entre eux . Les lettres minuscules représenteront les notes de musique regroupées en mélodie, résultat de l’Opération “M” entre eux .

La huitième note de musique de l’alphabet mentionné ci-dessus est la répétition de la première note , deux fois plus souvent, identifié par un index numérique deux sur la face supérieure de son chiffre    et, si cet indice était positionné en dessous , cette note s’appellerait l’octave basse, avec sa fréquence à mi-chemin de la première note, ce qui signifie que ses fréquences diminuent .

Par conséquent, une gamme de notes de musique en octave peut être représentée entre parenthèses avec son index indicatif au-dessus  ou octave grave avec son index indicatif en dessous .

Parmi les huit notes de musique principales , pourtant, il existe cinq autres notes intermédiaires, actuellement représentées par le symbole dièse   aux côtés de son chiffre à une échelle croissante dans Lá , séparés par des espaces de fréquences appelés demi-tons .

Cependant, dans cette étude, le mot « Sharp » est remplacé par la lettre “u” et ton symbole   par une barre oblique sur le chiffre , pour fournir un nom monosyllabique ou à une syllabe, qui peut être chanté par n’importe qui dans l’étude du solfège de ces notes de musique. Ainsi, la note de musique Lá tranchant est aussi la note Lau , Dó tranchant la note Dou , Ré tranchant la note Reu , Fá tranchant la note Fau et Sol tranchant la note Sou .

Pourtant, aussi, il y a douze notes musicales entre les deux, entre les treize notes de l’échelle de demi-ton croissant dans Lá , séparés par des espaces de fréquences appelés Microtom , utilisé, normalement, par les musiciens du Continent oriental, qui, dans cette étude, présentent leurs noms avec leurs chiffres, ont pour origine la première lettre de la note avant leur position dans la gamme ascendante en Lá , joint à une voyelle (a, e, i, o, u), à l’exclusion de ceux qui répètent les noms de notes existantes.

Par exemple, la première note de microton “”  entre les notes Lá et Lau , avoir votre nom “Lé”, formé avec la lettre L de la notice Lá (a), plus la voyelle “e” de la séquence “a, (e), i, o, u”, à l’exclusion de la voyelle “a” de la notice Lá et votre numéro est le même que la note Lá (a), mais en majuscule (A) lorsqu’il est en mélodie, ainsi que le nom de la prochaine note de microtone “”  entre les notes Lau et Si , avoir votre nom “Li”, formé avec la lettre L de la note Lau , plus la voyelle “i” de la séquence “a, e, (i), o, u”, à l’exclusion des voyelles “a” et “e” des notices Lá et Lé, son numéro étant le même que la note Lau , mais en majuscule et, le nom de la douzième note de musique   entre la note Sou et Lá octave , est “Só” , étant formé par la lettre “S” dans Sou et “o” de la séquence vocalique “a, e, i, (o), u”, à l’exclusion des voyelles “a” existant dans Sá, “e” existant dans Sé, “i” existant dans Si, laissant la voyelle “o”. Votre numéro est le même que la note Sou  , mais en majuscule . C’est ainsi que les notes de musique étaient appelées microtons, en dessous de l’échelle des demi-tons et de l’échelle des microtons dans Lá.

Gamme musicale en demi-tons Lá

Lá  Lau  Si  Dó  Dou  Ré  Reu  Mi  Fá  Fau  Sol  Sou  Lá2

Échelle musicale microtone en Lá

Lá Lé Lau Li Si Sá Dó Dá Dou Dé Ré Rá Reu Ri Mi Má

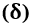2.2 TON, DEMI-TON ET MICROTOM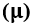

Quelle que soit la gamme musicale, ses notes de musique sont séparées dans la mélodie par des espaces d’intervalles de fréquence  , qui peut présenter trois mesures à des fréquences différentes, appelées Tone , Demi-ton et Microton , étant le demi-ton déterminé par son échelle de treize notes de musique , qui est une série d’un PG ou d’une Progression Géométrique, (SILVA, s.d.).

Dans ce cas, un PG musical (PGM), où la treizième note est le double de la première . Par conséquent, on peut appliquer la formule du Nième Terme d’un PG   et calcule ta raison , où  et , résultant en un intervalle d’un demi-ton  , le ton étant calculé par la puissance carrée d’un demi-ton et le microton calculé par la racine carrée d’un demi-ton .

Ces valeurs peuvent également être déterminées par la formule générale des intervalles de fréquence où”n” égal à un se traduit par un intervalle d’un demi-ton “n” égal à deux    résultats dans la gamme d’un ton “n” égal à la moitié résultats dans la gamme d’un microton   De cette façon, la fréquence d’une note de musique peut être calculée par la formule du terme général d’un PG   où le premier terme   est la fréquence fondamentale standard de la note de musique Lá   et le deuxième terme   est la fréquence de la note de musique suivante . Par conséquent, la fréquence fondamentale de la note Si est le produit entre la note Lá par Tom , ainsi que le produit entre la fréquence de la note Si par le demi-ton, donne la fréquence de la note Dó   et le produit de la fréquence de la note Dó par le microton, se traduit par la fréquence de la note Dá   et ainsi de suite pour n’importe quelle note de musique.

Cependant, il convient de rappeler que ces fréquences sont des valeurs approximatives, car le Tone , le demi-ton   et le Microtone   sont des nombres irrationnels ou infinis, comme le nombre pi . en outre, pour une meilleure compréhension opérationnelle des intervalles de fréquence sur une échelle linéaire, un demi-ton est considéré comme égal à un demi Ton   un microton est égal à un quart de ton  et un demi-ton égal à un demi-microton .

2.3 REPRÉSENTATION DU TIMBRE MUSICAL

Lorsque la fréquence fondamentale est tiré de l’ensemble des fréquences harmoniques, qui composent toute fréquence   les fréquences restantes formeront le Timbre du latin Timpanum, qui est une caractéristique secondaire de la fréquence résultante , mais cela nous permet de distinguer des sons distincts avec la même fréquence fondamentale.

Cette fonctionnalité est considérée comme facultative dans le langage algébrique musical, laissant à l’interprète le soin de choisir l’instrument à utiliser dans l’émission des notes de musique. Cependant, le Timbre peut être représenté par un nombre entier naturel accentué d’un tilde annexé au chiffre de la note de musique  ou au début de l’orthographe pour chaque mélodie ou avant une parenthèse seulement pour certaines notes de musique , où la partie mélodique indiquant l’instrument à utiliser est sous-titrée (=instrument).

2.4 REPRÉSENTATION DE LA GAMME MUSICALE

La largeur (a) d’une note de musique se mesure par son intensité sonore en décibels , qui peut varier de zéro à une limite audible supportable par l’être humain (HELERBROCK, s.d.), étant la caractéristique qui permet de distinguer un son faible d’un son fort.

Normalement, la plage d’intensité sonore comprise entre quarante et soixante décibels est utilisée    comme plage d’intensité normale pour toute note de musique entendue par les êtres humains et, en dessous de cette plage , le chiffre de la note est identifié par un accent grave   et, au-dessus de cette plage   avec un accent aigu. De plus, si une intensité spécifique est nécessaire pour une valeur, juste un accent circonflexe sur cette valeur attachée au chiffrement de note , indiquant cette intensité multipliée par dix, peut également venir avant une parenthèse pour plusieurs notes de musique   . Une flèche attachée à une note de musique indiquera que son intensité sonore augmente descendant ou croissant-décroissant et inversement.

2.5 REPRÉSENTATION DU TEMPS DE DURÉE MUSICALE

Le temps de durée d’une cellule musicale  , note ou silence, est la caractéristique qui nous permet de distinguer un son de courte durée d’un son de longue durée, étant représenté par un nombre entier naturel positif  , que dans un arrangement mélodique devant le chiffre d’une cellule musicale , représente une durée égale ou supérieure à une seconde . Dans ce contexte, les plus utilisés sont ceux d’un second  , deux secondes , trois secondes , quatre secondes et quelques autres sur cette durée .

En raison des mesures les plus utilisées dans un rythme musical, dans cette étude, la période standard est limitée à quatre secondes et, lorsque ce même entier vient dans un arrangement mélodique après le chiffre d’une cellule musicale   il représentera une durée égale ou inférieure à une seconde constituant un nombre fractionnaire à la Musique.

Impliquant “n” comme nombre dénominateur d’une fraction, dont le numérateur est l’unité  , les durées les plus utilisées étant d’une demi-seconde, un tiers de seconde , un quart de seconde , un sixième de seconde , un huitième de seconde et pas plus d’un neuvième de seconde , parce que le son cesse d’être auditif pour l’être humain lorsqu’il est égal ou inférieur à un dixième de seconde . Par conséquent, la durée en secondes et en fractions de seconde peut être représentée dans la même cellule musicale. Par exemple,   c’est la note Ré trois secondes,   c’est la note Ré un tiers de seconde de long et   c’est la note Ré une seconde, une demi et un quart de seconde.

Quand un temps de durée   venir avec un accent aigu ou sérieux , signifie qu’il est instantané ou égal à un neuvième de seconde  , avec le reste de la durée réelle en pause musicale. Dans ce cas, l’accent aigu indique une amplitude de forte intensité et l’accent grave indique une amplitude de faible intensité. Par exemple,   c’est la note Dó à forte intensité sonore dans la durée instantanée   et pause pour le reste de la durée d’une demi-seconde.

Lorsqu’une durée est suivie de deux-points signifie une brève interruption dans la composition musicale, permettant aux musiciens d’interagir avec le public, recommençant à tout moment, normalement dans la même mesure de l’interruption.

Lorsqu’une durée est accompagnée de points de suspension   signifie qu’après sa fin, il se prolonge en pause musicale pendant un autre certain temps, pouvant se terminer dans la même mesure ou dans une autre mesure différente. Par exemple, c’est la note Sol d’une durée d’une seconde, et peut se terminer dans la même mesure ou dans toute autre mesure.

Lorsqu’une note de musique commence dans une mesure et se termine dans une autre sans perdre sa continuité sonore, son chiffre dans la mesure suivante est identifié par une apostrophe. Par exemple, la note C avec trois secondes , être deux secondes   en une mesure et une seconde   dans le prochain bar .

3. OPÉRATIONS ENTRE CELLULES MUSICALES

Les opérations entre cellules musicales forment des groupements de notes et de silences musicaux, appelés monômes musicaux et lorsqu’un temps de durée   venir entre deux cellules musicales , il appartiendra toujours à la première cellule et le second a une durée ultérieure. Dans ce cas, c’est une seconde implicite et seulement une virgule avant cette durée   vous fera appartenir à la deuxième cellule faire durer le premier pendant une seconde implicite . Par exemple,   c’est la note Dó avec une demi-seconde et la note Mi une seconde de long et   c’est la note Dó avec une seconde et la note Mi longue de deux secondes.

3.1 FONCTIONNEMENT « M » ENTRE LES CELLULES MUSICALES

Lorsque deux ou plusieurs cellules musicales fonctionnent M, ils forment un monôme algébrique mélodique m, dont le résultat est une mélodie entre eux  où la durée finale de la première note, où la durée finale de la première note est égal au temps de durée initial de la deuxième note   , ainsi que la durée finale de la deuxième note    est égal au temps de durée initial de la troisième note . Par exemple, des notes de musique Dó, Mi, Sol, Mi, Dó, le tout pendant une seconde   en Opération M former un monôme mélodique de mélodie domisolmidó et, tout changement de position d’une de ces notes, dans cette opération, formera un autre résultat avec une autre mélodie  .

3.2 FONCTIONNEMENT « H » ENTRE LES CELLULES MUSICALES

Lorsque deux notes de musique rythmiques ou plus ou des notes de durée égale   rester en activité , ils forment un monôme algébrique harmonique h, dont le résultat est une harmonie entre eux, où leurs durées initiales sont toutes égales , ainsi que leurs durées finales .

Des notes de musique égales, dans cette opération, donnent un monôme à l’unisson ou une seule note de musique et, lorsque ces notes sont arythmiques ou de durées différentes, elles formeront des harmonies diverses selon l’opération M. Par exemple, l’opération H entre et entrez . Dans ce cas, la note sol la plus courte forment la première harmonie domisol , laissant la note Mi avec une durée plus courte formant l’harmonie domi en mélodie avec harmonie domisol, laissant la note Dó une seconde en mélodie avec harmonie domi.

3.3 OPÉRATION “M” ENTRE MONOMIS MUSICAUX

Lorsque deux ou plusieurs monômes musicaux sont en opération , ils formeront un polynôme mélodique  , où leurs monômes sont séparés par des espaces blancs, impliquant les opérateurs   entre eux, ne pouvant être formés : que par des monômes mélodiques dans une seule mélodie , seulement par des monômes harmoniques dans une mélodie d’harmonieset composé de monômes mélodiques et harmoniques .

Ces monômes doivent être rythmiques ou avoir des périodes égales  , étant déterminé par la somme des temps de durée de leurs cellules musicales , propriété appelée dans cette étude le Principe du Rythme, qui permet à tout système de rester en équilibre durant son existence et, même si une éventuelle arythmie survient dans sa structure ou si l’une de ces périodes est différente des autres, la période suivante restera la même comme la précédente période d’équilibre   pour corriger le déséquilibre occasionnel. Cependant, une séquence d’arythmies dans la structure rythmique peut provoquer l’effondrement du rythme de ce polynôme.

Lorsque les monômes de ce polynôme sont arythmiques, ils doivent être modulés en rythme dans une structure rythmique binaire , ternaire  , quaternaire   ou tout autre , ajustant les périodes arythmiques en rythmique et seuls le premier et le dernier monôme d’un rythme peuvent être incomplets de notes de musique, respectivement, sous-tendant une pause musicale avant et après ces notes complétant les périodes de ces monômes, comme indiqué dans les exemples ci-dessous.

a) Opération   avec les monômes rythmiques

polynôme mélodique quaternaire

b) Opération   avec les monômes arythmiques

polynôme mélodique arythmique

module rythmique ternaire

  polynôme mélodique ternaire

3.4 OPÉRATION « H » ENTRE MONOMIS MUSICAL

Lorsque deux ou plusieurs monômes musicaux sont en opération , ils forment un polynôme harmonique  . Ainsi, les monômes restent sous la même forme opératoire, séparés par leurs opérateurs    ou ils peuvent être sous la forme d’un tableau de colonnes 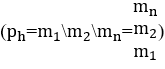, ne peut être formé que par des monômes mélodiques en harmonie , uniquement par des monômes harmoniques   et composé de monômes mélodiques et harmoniques . Ci-dessous un exemple d’opération   entre trois monômes musicaux rythmés.

Ci-dessous un exemple d’opération entre trois monômes musicaux rythmés.

Monômes mélodiques

Forme opérationnelle:

Forme de tableau:

Le monôme harmonique   peut être remplacé par sa forme d’accord dans Dó majeur (ALMADA, 2012). Dessa forma, a sua duração fica subentendre e é igual à duração dos monômios melódicos dessa operação ou il peut s’en tenir à sa durée spécifique si elle est différente de la durée du monôme mélodique, qui détermine la période de la mesure. Par exemple, si  .

3.5 OPÉRATION « M » ENTRE POLYNÔMES MUSICAL

Lorsque deux polynômes musicaux rythmiques ou plus sont en opération M, ils peuvent former divers types de nouveaux polynômes musicaux monorythmiques. Lorsque tous les polynômes présentent le même rythme, sinon, ils forment des polynômes polyrythmiques, étant les plus utilisés en Musique, ceux formés uniquement par des polynômes harmoniques qui sont des composés rythmiques, comme exemple ci-dessous.

Étant donné la forme des polynômes composés:

Forme opérationnelle:

Forme de tableau:

Onde:

3.6 OPÉRATION « H » ENTRE POLYNOMES MUSICAL

Lorsque deux ou plusieurs polynômes musicaux rythmiques sont en opération , ils peuvent former plusieurs types de nouveaux polynômes musicaux, les plus utilisés en Musique étant ceux formés entre polynômes mélodiques uniquement avec des monômes mélodiques rythmiques, avec des polynômes mélodiques uniquement avec des monômes harmoniques rythmiques  , dans ce cas, les monômes des polynômes opératoires doivent être rythmés les uns avec les autres, comme indiqué dans l’exemple ci-dessous.

Étant donné la forme des polynômes mélodiques

Formulaire opérationnel:

Forme de tableau:

4. GRAPHIQUE D’UN POLYNOME MUSICAL

Les monômes musicaux peuvent être tracés sur un graphique sur les axes de coordonnées cartésiennes. Pour cela, les fréquences ou figures de leurs notes de musique doivent être affectées sur l’axe des ordonnées ou leur ligne verticale et, sur l’axe des abscisses ou leur ligne horizontale, le temps de durée de ces notes. Ensuite, en connectant ces points avec des segments de ligne pour un monôme mélodique, le graphique de la Ligne Mélodique est formé.

Cependant, pour un monôme harmonique, où leurs durées sont simultanées, il suffit de tracer la durée de sa note musicale tonique ou la note principale de l’accord d’accompagnement musical sur le graphique linéaire du monôme mélodique, juste au-dessus du chiffre pour une harmonie du majeur et un peu plus bas pour une harmonie du mode mineur, formant le graphique Harmonic Line, selon les exemples listés ci-dessous.

a) dans

Graphique 1. Gamme musicale en do en rythme binaire.

 

 

b)

Graphique 2. Mélodie simple en rythme quaternaire.

c)

Gráfico 3. Melodia com uma harmonia.

5. HARMONIE D’ACCOMPAGNEMENT MUSICAL

Étant donné n’importe quelle mélodie , vous pouvez déterminer l’harmonie de votre accompagnement musical en appliquant le module Harmonic   développé dans cette étude. Dans chaque mesure de cette mélodie, qui transforme les notes musicales mélodiques en harmoniques, par l’opération entre eux , dont l’harmonie résultante est ajustée à une harmonie d’accords d’accompagnement en mode majeur ou mineur existant (ALMADA, 2012), comme exemple de la mélodie ci-dessous.

L’harmonie de:

Ajustement de à l’accord de do majeur:

Ajustement de à l’accord de do mineur en fonction de

Ajustement de à l’accord de Fá majeur:

Ajustement de à l’accord de Dó majeur:

Ajustement de à l’accord de Ré majeur:

Simple harmonie de:

Opération entre et

L’harmonie qui l’accompagne   c’est une simple harmonie. Dans l’exemple ci-dessus, les harmonies trouvées dans les modules harmoniques ont été ajustées avec les accords majeurs et mineurs existants les plus appropriés, en tenant compte de l’influence de la tonique de l’accord de Dó majeur de la mélodie  . Comme démontré, dans certaines mesures, des notes de musique de courte durée ont été laissées sans accords de musique, sans nuire à l’harmonie de la mélodie .

5.1 MÉLODIE D’ACCOMPAGNEMENT MUSICAL

Ces harmonies d’accompagnement musical peuvent être transformées en une mélodie d’accompagnement. Pour cela, appliquez simplement le module mélodique à ces harmonies , qui transforme une harmonie en plusieurs mélodies grâce à l’Opération   entre tes notes harmoniques, que pour une triade ou trois notes de musique en harmonie , se traduira par six mélodies distinctes .

En raison de la permutation entre ces trois notes de musique pour former les arrangements de notes dans les mélodies   et pour une tétrade ou quatre notes de musique , se traduira par vingt-quatre mélodies distinctes, car la permutation de quatre équivaut à 24 arrangements mélodiques . De là, il suffit de choisir une de ces mélodies pour l’accompagnement musical du monôme mélodique de cette harmonie, en la sous-titrant séparément. Dans ce cas, la durée de chaque note est déterminée par l’inverse du nombre de notes de musique par seconde, qui pour une triade ou trois notes de musique , est d’un tiers de seconde de long , comme exemple ci-dessous.

accord de Dó majeur:

mélodies

Sous-titre:

Graphique 4. Mélodie &4 avec une mélodie d’accompagnement.

 

6. MESURES DE MONOMIS MUSICAL

Les monômes musicaux d’une mélodie ou d’une harmonie en général fourniront deux types de mesures musicales importantes pour la Musique, l’une appelée Période Musicale, qui mesure la durée d’un monôme mélodique  , harmonique    et composé de mélodique avec harmonique , mis à l’échelle en quelques secondes ; et un autre appelé Musical Texture , qui mesure l’apparition des notes de musique dans la structure d’un monôme mélodique , harmonique ou composé , mis à l’échelle en notes de musique . Le rapport entre la texture mélodique et la période mélodique détermine la dynamique mélodique des notes de musique dans la structure d’un monôme mélodique.

6.1 PÉRIODE ET TEXTURE D’UN MONOMIUM MÉLODIQUE

un monôme mélodique présente ses notes de musique continuellement réparties dans l’espace-temps, formant une Période Mélodique , déterminé par la somme des temps de durée de ses notes de musique , mis à l’échelle en quelques secondes  . La Texture Mélodique , est déterminé par le nombre   de notes de musique dans sa période mélodique.

Le rapport entre la texture mélodique et la période mélodique  détermine la dynamique mélodique des notes de musique par seconde dans la structure de ce monôme, comme indiqué ci-dessous.

1) Monôme mélodique

Période mélodique:

Texture mélodique: quatro notas musicais

Dynamique mélodique: melodia lenta

2) Monôme mélodique

Période mélodique:

Texture mélodique: seize notes de musique

Dynamique mélodique: mélodie très rapide

6.2 PÉRIODE ET TEXTURE D’UN MONOMIUM HARMONIQUE

Un monôme harmonique   présente ses notes de musique interconnectées en même temps et elles sont généralement rythmées ou de même durée. Par conséquent, sa période harmonique   est égal à la durée de toute note de musique dans sa structure , mis à l’échelle en quelques secondes .

Cependant, il peut arriver qu’un monôme harmonique soit arythmique ou présente ses notes de musique avec des durées différentes. Dans ce cas, plusieurs harmonies différentes se produiront, avec différentes périodes harmoniques et la mélodie entre elles se traduit par la période harmonique totale de ce monôme . De plus, la texture harmonique , est déterminé par le nombre de notes de musique    en harmonie dans la période harmonique, comme indiqué ci-dessous.

1) Monôme harmonique rythmique  

Période harmonique:

Texture harmonique:

2) Monôme harmonique arythmique

Période harmonique:

Texture harmonique arythmique:

6.3 PÉRIODE ET TEXTURE D’UN POLYNOMIUM MÉLODIQUE

Un polynôme mélodique rythmique est celui où ses monômes ont des périodes égales. De cette façon, le produit du nombre   de battements pour sa période , détermine la durée de ce polynôme , échelle en secondes ou en minutes.

Même si ce polynôme est composé de mélodies et d’harmonies, le calcul de sa durée serait le même, tandis que sa texture mélodique totale reste le nombre de notes de musique dans cette durée.

Le rapport de cette texture mélodique totale à la durée totale forme la dynamique mélodique   de notes de musique dans ce polynôme, mis à l’échelle en notes de musique par seconde .

Lorsque le polynôme mélodique est composé d’une harmonie, sa Texture Harmonique totale   est déterminé par la moyenne arithmétique des textures harmoniques de tous ses monômes harmoniques de ses mesures , comme indiqué ci-dessous.

Temps de durée polynomiale

Période mélodique de

Numéros de battements:

Durée totale temps:

Texture mélodique complète:

Dynamique mélodique: (Mélodie avec une dynamique lente)

Toutes les textures harmoniques sont égales à:

Texture harmonique totale: (Texture simple)

7. PLAGIAT ENTRE POLYNOMES MÉLODIQUE

Normalement, les plagiats sont des égalités qui se produisent entre les monômes mélodiques et les polynômes mélodiques   et, comment ces monômes sont formés par des notes de musique   distribués en continu qui tracés sur un graphique dans le système de coordonnées cartésien, montrent leurs lignes mélodiques, qui peuvent être comparées les unes aux autres, montrant leurs similitudes ou leurs différences, ceux qui présentent leurs lignes mélodiques sont considérés comme du plagiat, c’est-à-dire qui coïncident sur le graphique , en les superposant, voire en transportant les notes de musique des monômes considérés comme du plagiat à la tonalité des notes des monômes originaux. Ci-dessous un exemple de monômes de plagiat.

Monômes mélodiques égaux: et .

Graphique 5. Monômes mélodiques .

 

7.1 POURCENTAGE DE PLAGIAT

Lorsqu’une partie continue d’un polynôme mélodique est le plagiat d’un autre, c’est-à-dire qu’elle présente un pourcentage de plagiat ou d’égalité par rapport au polynôme d’origine, les similitudes identifiées peuvent être calculées par la formule , où   est le nombre de monômes mélodiques ou mesures avec plagiat, et est le nombre total de monômes ou de mesures du polynôme d’origine, sans les répétitions mélodiques. Par exemple, étant donné une mélodie de cinquante mesures et, parmi elles, dix mesures consécutives ont été plagiées dans un autre air, donc:

8. STRUCTURE D’UN RYTHME

Le rythme est un phénomène qui se produit dans la durée de tout système, étant divisé en parties égales pour se maintenir en équilibre. C’est ainsi que cela se passe dans le rythme d’une mélodie, où sa durée   est divisé en parties de périodes égales, appelées mesures, qui s’enchaînent continûment en fonction de l’Opération , de plus, chaque mesure est également divisée en parties égales de périodes plus petites, appelées unités de temps qui sont également interconnectés en permanence en fonction de l’Opération, qui sont également interconnectés en permanence en fonction de l’Opération   .

On sait que la durée de toute période, a une durée initiale et final , logo, . De plus, cette durée initiale consiste en un battement audible ou non audible, causé par une impulsion , donnée par une force pendant une durée instantanée, restant silencieux pour le reste de sa durée  , par conséquent, la période de toute mesure est formée par son battement initial   en accord avec votre temps de silence .

En une seule mesure, en plus du rythme de tes règles avec ton temps de silence , existe toujours, à l’intérieur, en raison de l’Opération  , les battements des unités de temps, avec leurs temps de silence  , dont le résultat rend le premier battement deux fois plus fort que les autres , et l’effet sonore s’appelle la cadence rythmique de la mesure  , qui a une vitesse de battement appelée Tempo Rythmique de la Mesure, étant inversement proportionnelle à la période de cette unité de temps , mis à l’échelle en battements par seconde ou battements par minute  .

Dans ce contexte, plus la durée de cette unité de temps est courte, plus le tempo rythmique de ces battements est important, ce qui fournit deux mouvements rythmiques à un corps physique dans sa zone de fonctionnement, dont l’un est appelé Rhythmic Regency  , où un corps sans quitter sa position de repos, suit le mouvement du Tempo Rythmique de ces battements, et un autre appelé Rhythmic Dance  , où un corps passe de sa position de repos à d’autres positions distinctes, selon le tempo rythmique de ces battements.

8.1 LOI D’ACCENTUATION TONIQUE DES BARRES

La propriété du premier temps de l’unité de temps d’une mesure étant plus fort que les autres temps dans la même mesure est à l’origine de la loi d’accentuation tonique des mesures qui marque, de manière incisive, toute note musicale qui occupe cette première position dans les mesures d’un rythme. Accentuant également toute syllabe de tout mot qui occupe cette position, modifiant ou non son accentuation tonique orthographique, quelle que soit la langue parlée du monde. Dans le cas d’un silence placé dans cette position et d’une note de musique dans la position suivante, un effet musical appelé Contratempo se produit.

8.2 STRUCTURE D’UNE COMPAS COMPOSÉE

Une mesure est appelée un composé lorsque plus d’une cadence rythmique distincte se produit dans sa période  , formé par d’autres unités de temps distinctes  . Dans ce cas, la barre composée peut être mélodique ou harmonique.

Dans la mesure composée mélodique, les cadences rythmiques des unités de temps dépendent de l’opération , résultant en une cadence rythmique mélodique  . Entre eux naît un tempo rythmique mélodique  , une régence rythmique mélodique   et une danse rythmique mélodique .

Dans la mesure composée harmonique, les cadences rythmiques des différentes unités de temps et dépendent de l’opération , résultant en une cadence rythmique harmonique entre eux  .

À condition que , la cadence rythmique résultante est déterminée par l’unité de temps avec la durée la plus courte  , dans ce cas, le Tempo rythmique harmonique résultant est donné par la période de la plus petite unité de temps, avec sa conduite harmonique rythmique normalement fonction du tempo rythmique de la plus grande unité de temps   et sa Danse rythmique harmonique   en fonction du tempo rythmique majeur et mineur .

8.3 RYTHME HARMONIQUE

La cadence rythmique d’une mesure est généralement mélodique , du fait que ses unités de temps sont fonction de l’Opération . Cependant, cette cadence peut être harmonique   avec les périodes de ses unités de temps en fonction de l’Opération , résultant en une seule unité de temps, avec sa cadence rythmique mélodique . Par exemple, lorsqu’un groupe de personnes est silencieux pendant un certain temps ou lorsque plusieurs horloges sont synchronisées.

9. CONSIDÉRATIONS FINALES

Cet article visait à développer un langage algébrique pour structurer mathématiquement la musique, en utilisant uniquement des lettres, des chiffres et des symboles pour écrire les sons des notes de musique de manière alphanumérique, représentant ses principales caractéristiques sonores, telles que : la fréquence , amplitude et durée , en une seule expression identifier une onde sonore.

Au final, il apparaît que les Mathématiques de la Musique n’ont été possibles qu’avec le développement de l’Opération   et son opération inverse , fournissant les groupements d’ondes sonores de notes de musique, respectivement dans les formations d’harmonies d’accompagnements instrumentaux et de mélodies qui apparaissent à tout moment dans l’inspiration d’un compositeur, rendant l’étude de la musique plus simple, avec un langage sonore plus compréhensible et adapté à l’actualité technologie des études scientifiques de la Science de la Musique. Enfin, avec la démonstration de la structure mathématique de la musique, on peut dire qu’une composition musicale est une structure mathématique du son.

RÉFÉRENCE

ALMADA, Carlos. Harmonia Funcional. Editora Unicamp, 2ª Edição, 2012.

GUEST, Ian. Harmonia – Método Prático. Editora Luminar. Vol. 1, p. 33 a 41, 2020.

HELERBROCK, Rafael. Intensidade do som. Mundo da educação, s.d. Disponível em: https://mundoeducacao.uol.com.br/fisica/velocidade-intensidade-som.htm. Acesso em: 22  de julho de 2022.

SILVA, Luiz Paulo Moreira. Progressão geométrica. Brasil Escola, s.d. Disponível em: https://brasilescola.uol.com.br/matematica/progressao-geometrica.htm. Acesso em? 22 de julho de 2022.

VIANA, Arnóbio Araújo. A operação harmonização (H) e sua inversa operação melodiação (M). Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 07, Ed. 03, Vol. 03, pp. 144-171. Março de 2022. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/operacao-harmonizacao, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/operacao-melodiacao. Acesso em: 22 de julho de 2022.

^[1] Diplômé en génie électrique, op. Électronique de l’Université Fédérale de Pará-UFPA. ORCID : 0000-0001-7010-9114.

Envoyé : Juillet 2022.

Approuvé : Août 2022.