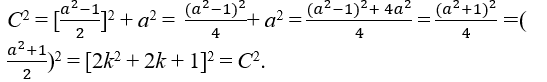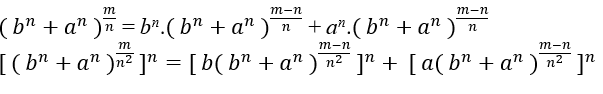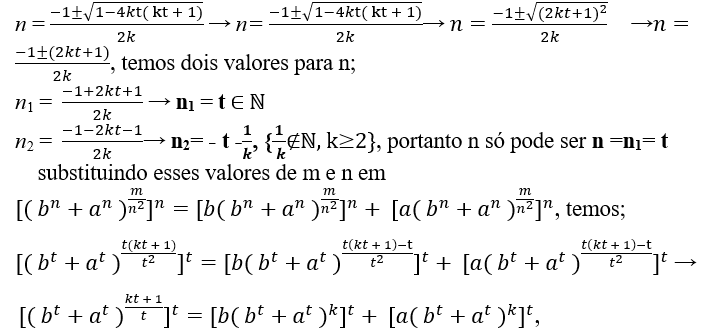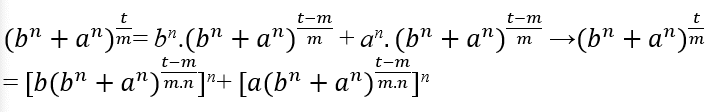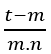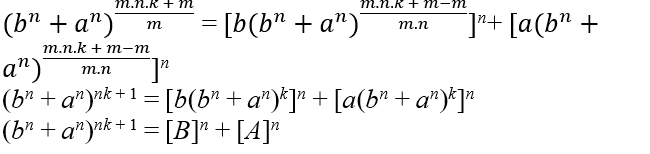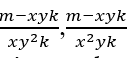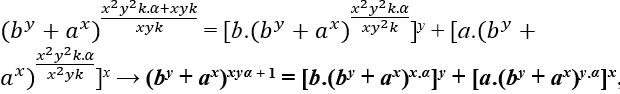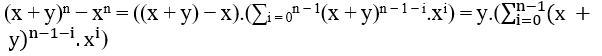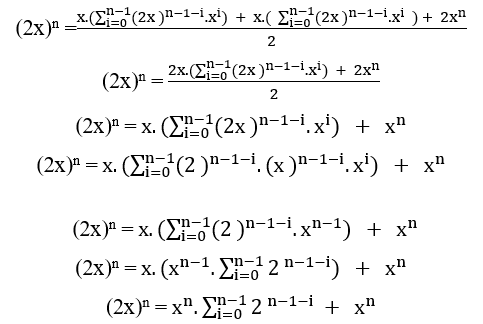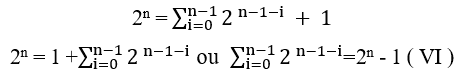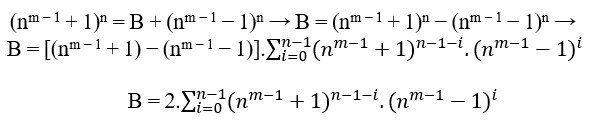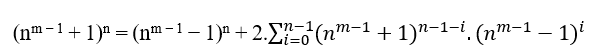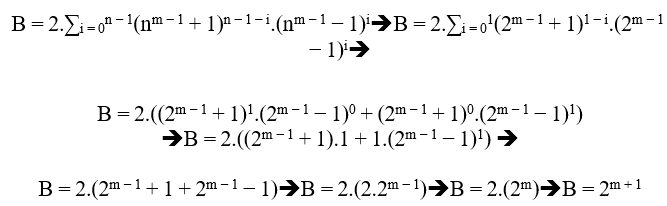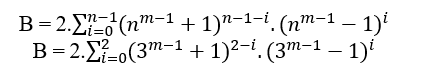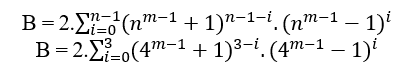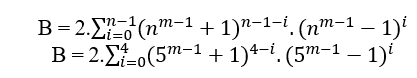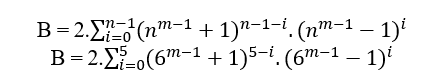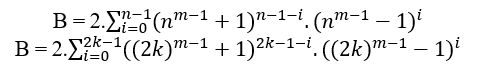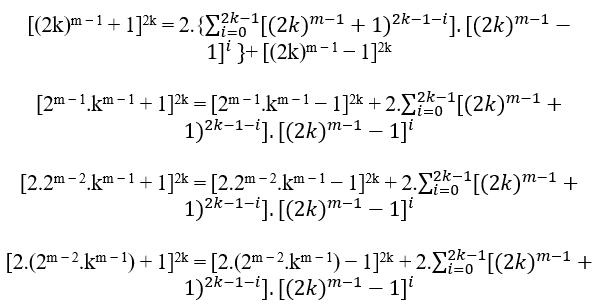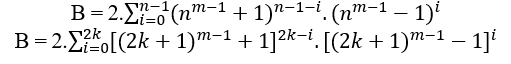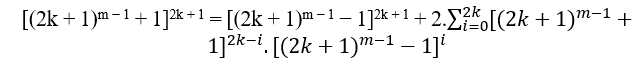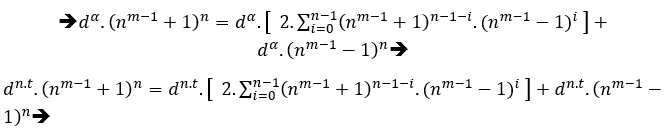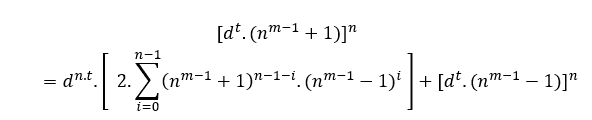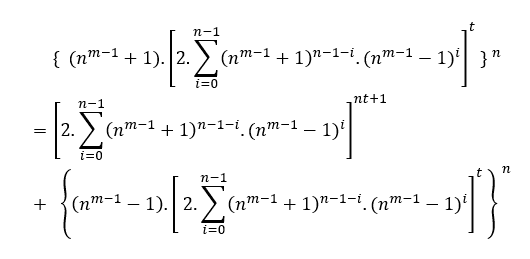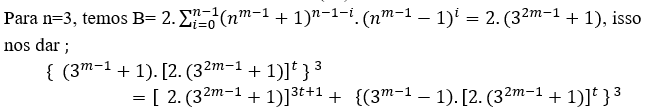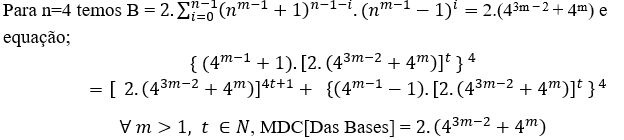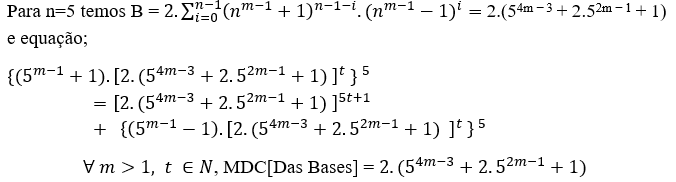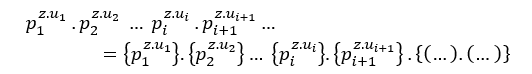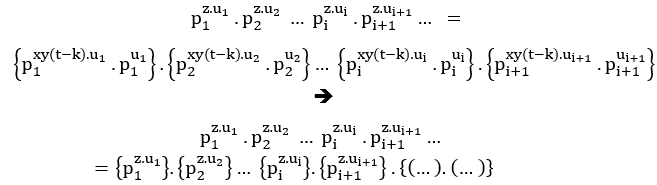ОРИГИНАЛЬНАЯ СТАТЬЯ
SOUSA, Francisco Rafael Macena de [1]
SOUSA, Francisco Rafael Macena de. Демонстрация гипотезы Пала. Revista Científica Multidisciplinar Núcleo do Conhecimento. 04 год, Эд. 11, Vol. 05, стр. 132-173. Ноябрь 2019 года. ISSN: 2448-0959, Ссылка доступа: https://www.nucleodoconhecimento.com.br/matematica/conjectura-de-beal
ЗАЯВЛЕНИЕ ГИПОТЕЗЫ
Если акс ax + by = cz , где a, b, c, x, y e z являются положительными integers и x, y, z ≥ 3, то a, b и c имеют общий премьер-фактор, который означает, что a, b и c делится на одно и то же простое число. Или уравнение ax + by = cz не имеет решения для положительных целых чисел с x, y, z ≥ 3 и mdc (a, b, c) = 1.
РЕЗЮМЕ
Эта статья содержит демонстрации с использованием принципов алгебры и теории числа, относительно гипотезы было объявлено Эндрю Блиал банкир и энтузиаст теории номеров предложил вызов для тех, кто доказать или представить контрпример к такой проблеме, которая обобщает последнюю теорему фермата, cn = bn + an, com n ≥ 3, это было продемонстрировано английский математик Эндрю Уайлс, используя в качестве основы гипотезу, сделанную математиками Yutaka Taniyama и Goro , Эта демонстрация, сделанная Уайлс несколько математиков поймут, на высоком уровне или сложности, также будет использоваться Теорема Себе, “Себастьян виейра-до Nascimento (Себе)”, окончил экономический факультет UFPB, магистр инженерных наук UFPB, полный профессор UFCG, его доказанная теорема основана на том, что cm = bn + an, где люди просты между собой, то есть mdc (m, n) = 1, предположение было предложенный самим Билом в 1993 г., но он был хорошо известен даже математическому сообществу только в 1997 г. после того, как Р. Д. Маулдин опубликовал статью «Обобщение Великой теоремы Ферма: гипотеза Била и проблема приза» в журнале Notices of the American математического общества.
Ключевые слова: Гипотеза, Эндрю Бил, Последняя теорема Фермата.
1. ВВЕДЕНИЕ
Эта статья направлена на то, чтобы доказать гипотезу Пала, предложенную Эндрю Блидом банкиром, предпринимателем, инвестором, игроком в покер и математиком-любителем, который увлекается теорией числа, он бросил вызов любому математику в мире, чтобы доказать или дать контрпример своей гипотезе, которая была предложена с 1993 года по настоящее время, не было представлено никакой демонстрации, которая обобщала бы гипотезу, включая «Последний теорем» фермата , Эта статья содержит математические знания, что любой, кто пришел, чтобы иметь второй класс средней школы полной и имеет легкость в математических свойств можно понять первоначальные демонстрации, уже для тех, кто имеет высшее образование в точном и за их пределами будет легко понять от начала до конца, гипотеза основана на положительных цен или решений в естественных чисел с большими экспонентами равна 3 (три) и их базы больше, чем или равны 1 (один) , если это так, то будет продемонстрировано, что на самом деле mdc (c, b, a) – C > 1, где C – общий простой множитель, который делит a, b и c на a ≤ b или a ≥ b, так что в качестве уравнения можно использовать cz = by + ax, x, y, z ≥ 3, показатели степени, противоречивый случай будет иметь как mdc (c, b, a) = 1 ex, y, z ≥ 3, это единственное значение, которое делит c, b, a равно 1 (единице), другими словами, a, b и c просты между собой.
Чтобы добраться до демонстрации необходимо было создать новые теоремы, но для теоремы на самом деле быть действительным, а также гипотеза должна быть доказана в ходе теоремы создаются из принципов и свойств в теории чисел, самая большая проблема в этой статье, как и любой другой, который включает в себя премьер номера те цифры, которые имеют только два разделителей в естественных, что является 1 (один) и сам (премьер-номер) , потому что это все еще то, что теория чисел еще не удалось найти более быстрый способ фактор гигантских чисел, однако в теории чисел у нас есть в качестве гипотезы, а также доказали, что любой X составной число, мы можем написать – это X как продукт различных полномочий равных или различных премьер чисел, в том числе, когда он имеет экспонентов 0 (ноль) или 1 (один). Идея этой гипотезы заключается в том, чтобы просто облегчить столкновение основных факторов.
2. КРАТКАЯ ИСТОРИЯ ГИПОТЕЗЫ
2.1 ФЕРМАТ И ЕГО ТЕОРЕМА
Она начинается с Пьера Фермата, который жил во Франции 18-го века, государственный служащий во французском городе Тулуза, математика для него было его любимым времяпрепровождением, интересно то, что Фермат имел большую известность благодаря своим обычаям представлять другим математикам проблемы, которые бросали вызов величайшим умам того времени, где они часто покидали его современников в недоумении в попытке их решить. У Фермата была идея создать предложение, похожее на знаменитую теорему Пифагора, которая хорошо известна сегодня в этом столетии, но не имела решений в натуралах, это предложение вышло за рамки его времени и получило известность на протяжении всего столетия, за то, что не нашли решения или контрпример, из-за этого получили свое название и за то, что его последняя задача была, как его имя Последняя теорема Фермата , Уравнение его славы является cn = bn + an, где, a, b, c e n ∈ N, с n ≥ 3, по его словам, была демонстрация, умер, никто не зная, что его предполагаемый ответ, из-за этого стал известен как его последняя теорема. Заслуга открытия этого предложения, причитающегося его первенца, он увидел несколько нот Фермата в определенной книге Аритметики, которая принадлежала, потому что его отец имел привычку делать черновики или аннотации в книгах. После нахождения сына, заметки или открытия были опубликованы в книге Arithmetica de Diofanto, содержащей наблюдения отца, в 1670 году книга содержала 48 наблюдений, но по пути поколения математиков и физиков давали решения своих проблем, однако была одна, что большинство думал, был последним, из-за этого было такое сложное название. В своей книге он содержал следующее заявление: “Я обнаружил замечательную демонстрацию этого предложения, которое, однако, не вписывается в кулуарах этой книги” (FERMAT. 1607 – 1665)2.
2.2 ЮТАКА ТАНИЯМА, ГОРОХО СИМУРА И ЭНДРЮ УАЙЛС
В 1954 г. ютака Танияма и Гороха Симура, молодые японские математики, подружились, потому что заинтересовались одной и той же книгой, той же статьей и теми же расчетами, эта гипотеза Танияма-Симура позволила Уайлсу осуществить мечту своего мальчика, используя интеллектуальные усилия и решимость, в которые трудно было поверить как можно чаще человеку. Гипотеза двух представленных служил путь к их окончательное решение проблемы, однако математик Yutaka Taniyama взял свою собственную жизнь в 1958 году, так что он еще больше задержал разработку решения, к развитию гипотезы в том, было ли это намеренно сделано, чтобы решить последнюю теорему Фермата, однако это было то, что произошло позже Уайлс понял, что такая основа, которая помогла доказательству – там определенно это теорема , ибо кто мог себе представить, что работа двух студентов конца двадцатого века может быть использована в чем-то, что решило одну из величайших загадок в истории математики. Но это был Эндрю Уайлс, который в конечном итоге демонстрации Последней теоремы Фермата, Уайлс профессор Принстонского университета, который начал свой интерес к проблеме, как ребенок в своем родном городе была публичная библиотека, но это было только в 1986 году, что он действительно начал свою работу по решению теоремы своей мечты, в соответствии с Уайлс, что его исследования были сделаны в полной секретности , ибо в своем быту он знал, что найдет решение, но это было не время, чтобы подтвердить такую вещь для академического сообщества, интуиция все страстный в теории числа, однако интуиция показывает путь, но доказать, является ли это правильно или неправильно требует времени и самоотверженности, возможно, опасаясь давления, которое будет страдать перед лицом такой известной проблемы и трудное решение было слишком рискованно, чтобы подтвердить такое возможное первоначальное решение , При анализе гипотезы двух японцев, Эндрю Уайлс отметил, что такая теорема может быть способ решить, однако гипотеза должна быть доказана, прежде чем продемонстрировать, что он искал так много, так как он был ребенком, по его мнению, было так ясно, что Уайлс мог мечтать о решении теоремы все зависит от доказательства гипотезы двух студентов , однако Уайлс не продемонстрировал последнюю теорему Фермата, а скорее гипотезу Танияма-Симура, которая будет подразумевать доказательство – там.
Наконец, 23 июня 1993 года на конференции, состоявшейся в Институте математических наук сэра Исаака Ньютона в Кембридже, Эндрю Уайлс, спустя 356 лет после представления теоремы, сделал свое заявление о своей демонстрации, но содержал небольшой недостаток в своем решении, Уайлс уходит на год, чтобы исправить такую ошибку и представить свою новую демонстрацию , После коррекции и рассмотрения той же ошибки обнаружены, потребовалось несколько месяцев, чтобы оценить его решение, его демонстрация 200 страниц, и после длительного периода тревоги, его открытие или демонстрация была, наконец, принято, но настолько сложным, что лишь немногие люди во всем мире смогли понять это, и Уайлс (после получения приза на сумму 50000,00 фунтов от Фонда Wolfskehl) , он входит в качестве математика, который продемонстрировал наиболее интригующим и сложной теоремы в истории математики, и, таким образом, заключает одну из величайших проблем, не встречались или продемонстрировали, что оспаривается великих математиков до и во время, так что Последняя теорема Фермата не имеет решений с положительными integers с n ≥ 33.
2.3 ЭНДРЮ BEAL И ЕГО ГИПОТЕЗА, КОТОРАЯ ПОЛУЧИЛА ЕГО ИМЯ
Эндрю Ол (родился 29 ноября 1952 года), банкир, предприниматель, инвестор, игрок в покер и математик-любитель и энтузиаст одной из лучших областей, которая является теория номеров. Бл также известен гипотезой Пала, исследуя обобщения последней теоремы Фермата, с 1993 по 1997 год, Бил предложил денежный приз за рецензируемое доказательство этой гипотезы или контрпример, потому что в 1993 году он имел стоимость $ 5000 стоимость приза увеличилась в несколько раз и в настоящее время составляет $ 1,000,000.00 для человека, который доказывает это или представляет противоречивый пример другими словами контр-пример для тех, кто generalize Последняя теорема Фермата. Согласно собственным заявлениям банкира, в пресс-релизе Американского математического общества цель миллионера состоит в том, чтобы «вдохновить молодые умы задуматься над этим вопросом и сделать их все более и более заинтересованными в изучении математики» 4.
3. РАЗВИТИЕ ГИПОТЕЗЫ BEAL
Для демонстрации потребуется три новые теоремы (Т.M, S.T.M e T.G.M), потому что теорема Себа является конкретным случаем гипотезы Пала, это также будет показано позже.
3.1 МАСЕНА ИЛИ Т.M
Учитывая два уравнения Eq1:cz = by + ax и Eq2:cm = cm положительными целыми решениями и имеет общую основу c ≠ 0, с c, b, a, z, y, x и m ∈ N, m > z можно определить новое уравнение Eq3, которое имеет как формат Eq1, так и Eq2. Это означает, что если Eq3 не удовлетворяет Eq1 он не имеет все положительные решения. Примером1 является уравнение Eq1 → c2 = b2 + a2 e Eq2 → cm с c ≠ 0 и м ∈ N, мы знаем, что Eq1 имеет целые решения, потому что это собственная теорема пифагора, просто проверьте использование пифагорических тройных, точно так же, как Eq2 также имеет все решения, которые это будет доказано впереди. Тем не менее, тогда можно определить уравнение Eq3, которое имеет как формат Eq1, так и Eq2. подобно c ≠ 0 мы можем использовать следующие шаги в Eq1 → c2 = b2 + a2 → 1 = c− 2.(b2 + a2)(I) Eq1 → c2 = b2 + a2 → c=(b2+a2)1/2(II)
Следующий шаг – использовать Eq2, потому что мы можем писать Eq2 сюда cm = cm.1 при замене (I) у нас есть cm = cm.c−2.(b2 + a2) → cm = cm−2.(b2 + a2) → cm = b2.cm−2 + a2.cm−2(III) Замена (II) в (III);
![]() = b2.
= b2.![]() + a2.
+ a2.![]() →
→ ![]() =
= ![]() . Быть m−2 несколько из 4 это m−2 = 4.n, с участием n ∈ ℕ, тогда мы должны m = 4.n + 2, при замене имеем; (b2 + a2)2.n + 1 = [b(b2 + a2)n]2 +[a(b2+a2)n]2 (b2 + a2)2n + 1 = [B]2 + [A]2 теперь нам просто нужно проверить, есть ли (b2 + a2)2n + 1 это как C2,пифагоровыми тройками это равенство скоро будет выполнено (b2 + a2)2.n + 1 = (c2)2.n + 1 = c2.(2.n + 1) = [c2.n + 1]2 = [C]2 Следовательно C2 = [B]2 + [A]2 тот же формат Eq1 чтобы сделать вывод, должен владеть Eq2C2 = [B]2 + [A]2 → (b2 + a2)2n + 1 = [b(b2 + a2)n]2 + [a(b2 + a2)n]2 → (c2)2n + 1 = [b(c2)n]2 + [a(c2)n]2 → c4n + 2 = [b.c2n]2 + [a.c2n]2 → c4n + 2 = b2c4n + a2c4n → c4n + 2 = c4n.(b2 + a2) → c4n+2=c4n.(c2) → c4n+2=c4n+2 →cm=cm . Затем было проверено, что можно найти Eq3 который имеет оба свойства, то Eq3 для этих двух уравнений; Eq3 → (b2+a2)2n+1=[b(b2+a2)n]2+[a(b2+a2)n]2
. Быть m−2 несколько из 4 это m−2 = 4.n, с участием n ∈ ℕ, тогда мы должны m = 4.n + 2, при замене имеем; (b2 + a2)2.n + 1 = [b(b2 + a2)n]2 +[a(b2+a2)n]2 (b2 + a2)2n + 1 = [B]2 + [A]2 теперь нам просто нужно проверить, есть ли (b2 + a2)2n + 1 это как C2,пифагоровыми тройками это равенство скоро будет выполнено (b2 + a2)2.n + 1 = (c2)2.n + 1 = c2.(2.n + 1) = [c2.n + 1]2 = [C]2 Следовательно C2 = [B]2 + [A]2 тот же формат Eq1 чтобы сделать вывод, должен владеть Eq2C2 = [B]2 + [A]2 → (b2 + a2)2n + 1 = [b(b2 + a2)n]2 + [a(b2 + a2)n]2 → (c2)2n + 1 = [b(c2)n]2 + [a(c2)n]2 → c4n + 2 = [b.c2n]2 + [a.c2n]2 → c4n + 2 = b2c4n + a2c4n → c4n + 2 = c4n.(b2 + a2) → c4n+2=c4n.(c2) → c4n+2=c4n+2 →cm=cm . Затем было проверено, что можно найти Eq3 который имеет оба свойства, то Eq3 для этих двух уравнений; Eq3 → (b2+a2)2n+1=[b(b2+a2)n]2+[a(b2+a2)n]2
3.1.1 ДЕГУСТАЦИЯ Т.M
Быть Eq1: cz = by + ax e Eq2: cm = cm, c m > z, a, b, c, x, y, z , m ∈ ℕ e c ≠ 0.
Доказательство Eq2:
На самом деле 1 = 1, умножая обе стороны на c ∈ N*, у нас есть 1.c = 1.c, при умножении снова на тот же c у нас есть c2 и c2, логически умножаясь на м раз мы будем иметь; cm = c{(11 + 12 + 13 + … + 1m − 1 + 1m) = m} = cm. Поэтому показано Eq2.
подобно c ≠ 0, мы можем использовать следующие устройства:
cz = by + ax → 1 = c − z.(by + ax)( I ) нейтральный элемент умножения
cz = by + ax → c =(by+ax)1/z( II )
THE Eq2 можно записать следующим образом cm = cm.1 , при замене (I) в этом уравнении получается:
cm = cm.1 → cm = cm.c − z.(by + ax) → cm = cm − z.(by + ax) → cm = by.cm − z + ax.cm − z
Замена (II) приводит к:
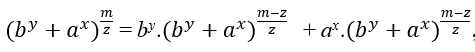 , включение показателей y и x в доказательство
, включение показателей y и x в доказательство
![]()
(by + ax)xyk + 1 = [b.(by + ax)xk]y + [a.(by + ax)yk]x
Итак, это новое уравнение;
Eq3:(by + ax)xyk + 1 = [b.(by + ax)xk]y + [a.(by + ax)yk]x → Cxyk + 1 = By + Ax
По принципу сравнения или формата Cxyk + 1 = By + Ax это эквивалентно cz = by + ax, это сама структура гипотезы Била.
Вскоре это удовлетворило Eq1 Отсутствие показывает, что он также имеет формат Eq2: cm = cm
(by + ax)xyk + 1 = [b.(by + ax)xk]y + [a.(by + ax)yk]x, c cz = by + ax у нас есть; (cz)xyk + 1 = [b.(cz)xk]y + [a.(cz)yk]x → cz.(xyk + 1) = [b.cz.xk]y + [a.cz.yk]x → czxyk + z = by.czxyk + ax.czxyk → c
m = zxyk + z
cm = by.czxyk + ax.czxyk → cm = czxyk.(by + ax) → cm = czxyk.(cz) → cm = czxyk + z = cm.
Поэтому доказано, так как Eq3 удовлетворены Eq1 и Eq2.
CZ = By + Ax
C = by + ax, B = b.(by + ax)xk, A = a.(by + ax)yk e Z = xyk + 1
MDC(C, B, A) = MDC(by + ax, b.(by + ax)xk, a.(by + ax)yk) = by + ax = cz = C.
MDC(Z, y, x) = MDC(xyk + 1, y, x) = 1
OBS:
Если k равно нулю, мы имеем;
(by + ax)xyk + 1 = [b.(by + ax)xk]y + [a.(by + ax)yk]x → (by + ax)1 = [b.(by + ax)0]y + [a.(by + ax)0]x, como by + ax = cz ≠ 0 следовательно (by + ax)0 = 1
(by + ax)1 = [b.1]y + [a.1]x → by + ax = by + ax
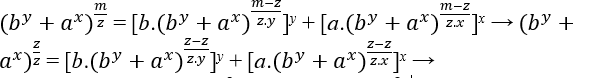
(by + ax)1 = [b.(by+ax)0]y + [a.(by+ax)0]x → by + ax = [b.1]y + [a.1]x.
Если случай x=y=k=1 у нас есть идеальный квадрат
(by + ax)xyk + 1 = [b.(by + ax)xk]y + [a.(by + ax)yk]x → (b1 + a1)1 + 1 = [b.(b1 + a1)1]1 + [a.(b1 + a1)1]1 →
(b + a)2 = [b.(b + a)] + [a.(b + a)] → (b + a)2 = b.(b + a) + a.(b + a) = b2 + ba + ab + a2 = b2 + 2ab + a2 = (b + a)2
Пример2 Проверка с числами уравнение Eq3, быть b=3, a=2 и n=1 у нас есть;
(b2 + a2)2n + 1 = [b(b2 + a2)n]2 + [a(b2 + a2)n]2 → (32 + 22)2.1 + 1 = [3(32 + 22)1]2 + [2(32 + 22)1]2 →(9 + 4)3 = [3(9 + 4)]2 + [2(9 + 4)]2 → 133 = [3.13]2 + [2.13]2 → 133 = 392 + 262 → 2187 = 1521 + 676 → 2187 = 2187
3.2 ОТОБРАЖЕНИЕ КАЖДОГО СЛУЧАЯ ЗА Т.M
Чтобы показать достоверность этой теоремы, необходимо также показать возможности или возможные значения z, y, x и m ∈ N, если это не противоречит какой-либо теореме, уже продемонстрированой математиками, такими как (теорема Пифагора “несколько математиков”, теорема Себа “Себастьян” и последняя теорема Фермата “Эндрю Уайлса” и так далее).M действителен и будет инструментом, чтобы доказать гипотезу Пала.
3.2.1 Пифагор THEME
Это когда z=y=x=2
Предположим, что Eq1 → c2 = b2 + a2 имеет целые решения, для c, a, b, m ∈ N, c ≠ 0 и Eq2 → см. можно найти Eq3, который удовлетворяет двум предыдущим уравнениям, если это происходит вскоре Eq1 → c’√(b2+a2 ) ∈ ℕ.
Эта демонстрация уже была показана в Примере1, нужно только показать, что на самом деле использование пифагора тройной удовлетворяется условие c=√(b2+a2) ∈ ℕ.
Гипотеза c2 = b2 + a2, диссертация C2 – C2.
Используя гипотезу c2 = b2 + a2 добавляя с обеих сторон по 2b + 1 ∈ ℕ, идеальный квадрат получается с одной стороны, c2 + 2b + 1 = b2 + 2b + 1 + a2 → c2 + 2b + 1 = (b + 1)2 + a2, мы знаем, что в правом треугольнике гипотенузы больше, чем любой из катет, в частности c > b > a, то есть возможность c = b + 1, поймите, что это подходящее решение для решения уравнения c2 + 2b + 1 = (b + 1)2 + a2 → c2 + 2b + 1 = c2 + a2 → 2b + 1 = a2 при изоляции b, получено и как , поймите что и b и c для того чтобы быть inte![]() ger дос
ger дос![]() таточно (a) быть нечетным потому что нечетные нечетные времена остают нечетными, поэтому условие a = 2k + 1 для того чтобы быть нечетным с k ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕ , так что у нас есть;
таточно (a) быть нечетным потому что нечетные нечетные времена остают нечетными, поэтому условие a = 2k + 1 для того чтобы быть нечетным с k ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕk ∈ ℕ , так что у нас есть;
→ 2 х 2 ( 2k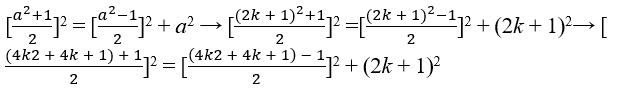 й[2k2 + 2k + 1]2 = [2k2 + 2k]2 + (2k + 1)2 , так что у нас есть C = 2k2 + 2k + 1, B = 2k2 + 2k e A = 2k + 1 ∈ ℕ, являются пифагорийские тройки (2k2 + 2k + 1, 2k2 + 2k, 2k + 1), проверка диссертации
й[2k2 + 2k + 1]2 = [2k2 + 2k]2 + (2k + 1)2 , так что у нас есть C = 2k2 + 2k + 1, B = 2k2 + 2k e A = 2k + 1 ∈ ℕ, являются пифагорийские тройки (2k2 + 2k + 1, 2k2 + 2k, 2k + 1), проверка диссертации
3.2.2 ПО ДЕЛУ ПОСЛЕДНЕЙ ТЕОРЕМЫ ФЕРМАТА
Это когда z=y=x=n
Предположим, что Eq1 → cn = bn + an, имеет решение для n≥3, с c, a, b, m ∈ ℕ, c ≠ 0 e Eq2 → cm = cm. можно найти Eq3, который удовлетворяет двум предыдущим уравнениям, если это произойдет вскоре Eq1 → c = n√bn+an ∈ ℕ
c c ≠ 0 мы можем написать Eq1, сюда;
Eq1 → cn = bn + an → 1 = c − n.(bn + an) (I) нейтральный элемент умножения
Eq1 → cn = bn + an → c = ( bn+an )1/n (II)
Убедитесь, что Eq2 можно записать следующим образом, не меняя его значений cm = cm.1, при замене (I) B Eq2, у нас есть;
cm = cm.c − n.(bn + an) → cm = cm − n.(bn + an) → cm = bn.cm − n + an.cm − n(III)
Заменен (II) B (III)
Поймите, что формат такой же, как Eq1, просто проверьте если m − n кратно n2, если да, то мы можем написать m − n = n2.k c k ∈ ℕ, изолируя m мы имеем m = n2.k + это уравнение 2-й степени;
m = n2.k + n ⇒ kn2 + n − m = 0, с этим мы можем найти значения m и n по Бхаскара.
![]() , для чего n должно быть естественно
, для чего n должно быть естественно
-1±√1-4km должно быть кратно 2k, Так;
-1±√1-4km = 2k.t, com t ∈ ℕ
-1±√1-4km = 2k.t → ±√1-4km= 2k.t + 1 поднимая оба до четверти, у нас есть 1 + 4km = (2k.t + 1)2 → 4km = (2k.t + 1)2 − 1 тогда поймите, что это разница двух квадратов;
4km = (2k.t + 1 − 1).(2k.t + 1 + 1) → 4km = (2k.t).(2k.t + 2) → 4km = 4.(k.t).(k.t + 1) → km = k.t.(k.t + 1) →
m = t( kt + 1), затем заменив это значение m в n = -1±√1-4km temos;
скоро (bt + at)kt + 1 = Bt + At, понимать kt + 1 не делится на t, потому что mdc( kt + 1 , t ) = 1, То есть “kt + 1” e “t” двоюродные братья между собой, и Эндрю Уайлс невозможно bt + at = ct (Последняя теорема Ферма), за t > 2.
Потому что kt + 1≠ t.α, с 2 < α ∈ N, поэтому не удовлетворяет Eq1, поэтому Eq1 не имеет решений, как говорится в Т.M.
тем не мени C =kt+1√Bt+At ∈ ℕ, EQSebá,Теорема Себы, проверка равенства;
C = kt+1√Bt+A → C = kt+1√[b (bt+at )k]t+ [a( bt+at )k]t →C = kt+1√bt( bt+at )kt + at ( bt+at )kt → kt+1√( bt+at )kt.( bt+at ) → C = kt+1√( bt+at )kt+1 → C = bt + at.
3.2.3 ТЕМА SEB
cm = bn+ an, com mdc(m,n)=1
Демонстрация Себастьяно Виейра-де-Насименту (Себе )
Теорема: Уравнение Cm = An + Bn допускает естественные решения для м и премьеры друг к другу.
Доказательство:
Будь уравнением;
( 1 )cm = bn + an, будучи a, b, c, n и m положительными интеграторами. Multiplicando ambos os membros da equação ( 1 ) por (bn + an)m
obtém-se:
( 2 )cm*(bn + an)m = (bn + an)*(bn + an)m, Замена значения da (1) в (2), Вы получаете: (bn + an)m + 1 = (bn + an)*(bn + an)m
или же
( 3 )(bn + an)m + 1 = bn(bn + an)m + an(bn + an)m
Если мы выберем такие значения для a и b, что a ≤ b или a≥b, и подставим в (3), получатся положительные целые значения для A, B и C.
Пример: Разделите квадрат на два куба несколькими способами. Пусть уравнение будет:
( 4 )C2 = B3 + A3, Considere a equação:
c2 = b3 + a3, Multiplicando ambos os membros da equação acima por (b3 + a3)m, onde m e n ∈ ℕ, temos:
c2(b3 + a3)m = (b3 + a3)(b3 + a3)m
( 5 )(b3 + a3)m + 1 = b3(b3 + a3)m + a3(b3 + a3)m
Comparando a equação (5) com a equação (4), devemos decompor m em potências de 3 e m + 1 em potências de 2. Это будет возможно только в том случае, если м и м No 1, соответственно, кратные 3 и 2. Скоро:
m = 6k – 3 e m + 1 = 6k – 2, Таким образом, уравнение (5):
(b3 + a3)6k − 2 = b3(b3 + a3)6k − 3 + a3(b3 + a3)6k − 3
[(b3 + a3)3k − 1]2 = [b(b3 + a3)2k − 1]3 + [a(b3 + a3)2k − 1]3, Следовательно, решения данного уравнения получаются следующим образом:
C = (b3 + a3)3k − 1, B = b(b3 + a3)2k − 1 e A = a(b3 + a3)2k − 1, где k ∈ N*, a e b ∈ ℕ.
Доказательство использования Т.M Вот когда z=m e y=x=n
Предположим, что Eq1 → cm = bn + an, имеет решение для взаимно простых m и n, это
mdc(m,n)=1, com c, a, b, t, m e n ∈ ℕ, c ≠ 0 e Eq2 → ct = ct ты можешь найти один Eq3 который удовлетворяет двум предыдущим уравнениям, если это произойдет в ближайшее время Eq1 → c =m√bn+an ∈ ℕ.
C c ≠ 0 мы можем использовать следующие методы;
cm = bn + an → 1 = c − m*(bn + an), (I) нейтральный элемент умножения
cm = bn + an → c = (bn+an)1/m, (II)
Мы можем написать Eq2 сюда ct = ct.1, замена ( I ) B Eq2 у нас есть;
ct = ct.c − m.(bn + an) → ct = ct − m.(bn + an) → ct = bnct − m + anct − m, при замене (II) у нас есть;
Para que
быть натуральным t – m должно быть кратным n и m, тогда t – m = m.n.k, при k ∈ ℕ, изолируя t, имеем t = m.n.k + m, при замене в уравнении получается;
Осталось показать, что nk + 1 делится на m, если да, то оно имеет вид nk + 1 = m.α, com α ∈ ℕ ou bn + an = Cm
Если произойдет что-либо из этих двух, мы имеем Cm = Bn + An тогда будет показано, что уравнение Eq1 имеет решение.
Мы должныt − m = m.n.k , разделяя оба на м, он получается
− 1 = n.k добавляя 1 с обеих сторон и
= n.k + 1, так как т кратна м, так что
∈ ℕ, при этом мы можем использовать следующие шаги;
подобно
= m.α → α =
, если α натуральное, то
он должен быть естественным, если только если t также кратно m2, но t не кратно m2, так как он имеет вид t = mnk + m, даже если бы k было равно m, он имел бы вид t = n.m2 + m = M. (Nk + 1) ≠ m2 (nk + 1), поэтому nk + 1 не делится на t, поэтому mdc (nk + 1, t) = 1 просты между собой.
Остается выяснить, будет ли bn + an = Cm.
Мы знаем это nk + 1 не делится на n, потому что mdc (nk + 1, n) = 1 и как уравнение равно (bn + an)nk + 1 = [b(bn + an)k]n + [a(bn + an)k]n удовлетворяется уже показано ранее в EQSebá, по принципу формата или сравнения мы должны:
Cnk + 1 = Bn + An равно cm = bn + an, скоро;
(bn + an)nk + 1 = Bn + An → (cm)nk + 1 = cm.(nk + 1) = [cnk + 1]m = Cm = Bn + An
При этом Eq1, пропущенное шоу Eq2 → ct = ct, представь это:
(bn + an)nk + 1 = Bn + An → (bn + an)nk + 1 = [b(bn + an)k]n + [a(bn + an)k]n →
(cm)nk + 1 = [b(cm)k]n + [a(cm)k]n → cm.(nk + 1) = [b(cm)k]n + [a(cm)k]n
como t= m.( nk + 1 );
ct = bn(cm)nk + an(cm)nk → ct = (cm)nk(bn + an) → ct = (cm)nk(cm) → ct = (cm)nk + 1 → ct = cm.(nk + 1) = ct, Это доказано, потому что Eq3 обладает свойствами как Eq1, так и Eq2.
3.2.4 В СЛУЧАЕ, ЕСЛИ ОНИ МНОГОЧИСЛЕННЫ T.M
Случай (1): для y, кратного x, это y = xk с k ∈ ℕ
Будьте Eq1: cz = bxk + ax и Eq2 :cm = cm ,c m > z e c ≠ 0 вы можете найти новый Equation Eq3, который имеет свойства Eq1 и Eq2, если Eq3 не имеет свойства логотипа Eq1 Eq1, не имеет целых решений.
C c ≠ 0, у нас есть;
cz = bxk + ax → 1 = c − z.(bxk + ax), (I) нейтральный элемент умножения
cz = bxk + ax → c = (bxk+ax)1/z, (II)
Мы можем написать Eq2 следующим образом, используя ( I );
cm = cm.c − z.(bxk + ax) → cm = cm − z.(bxk + ax) → cm = bxk.cm − z + ax.cm − z, при замене (II) имеем;
![]()
Помещение xk e x у нас есть доказательства;
![]()
, обратите внимание, что mmc (zxk, zx)а для чего
![]()
∈ ℕ, обязательно z – m должно быть кратным zxk, т. е. m – z = zxk.α, где α ∈ ℕ, и мы имеем;
![]() (bxk + ax)xk.α + 1 = [b.(bxk + ax)α]xk + [a.(bxk + ax)k.α]x, обратите внимание, что это уравнение можно записать следующим образом;
(bxk + ax)xk.α + 1 = [b.(bxk + ax)α]xk + [a.(bxk + ax)k.α]x, обратите внимание, что это уравнение можно записать следующим образом;
(bxk + ax)xk.α + 1 = [bk.(bxk + ax)k.α]x + [a.(bxk + ax)k.α]x, это теорема Себы, так что скоро уже доказано Cxk.α + 1 = Bxk + Ax эквивалентно Cm = Bx + Ax потому как
MDC(xk.α + 1 , xk )=MDC(xk.α + 1 , x)= MDC(m,x)=1, следовательно, двоюродные братья друг другу, что эквивалентно формуле Eq1.
Проверка Eq2 что такое cm = cm
(bxk + ax)xk.α + 1 = [b.(bxk + ax)α]xk + [a.(bxk + ax)k.α]x, нравиться bxk + ax = cz у нас есть; (cz)xk.α + 1 = [b.(cz)α]xk + [a.(cz)k.α]x → czxk.α + z = [b.czα]xk + [a.czk.α]x как m =
zxk.α + z
cm = bxk.cxzkα + ax.cxzk.α → cm = cxzkα(bxk + ax) → cm = cxzkα(cz) → cm = cxzkα + z = cm.
Вскоре удовлетворены Eq1 и Eq2, поэтому доказано.
Случай (2): для x, кратного y, это x = yk с k ∈ ℕ
Эта демонстрация аналогична случаю (1), Eq3 Это;
(by + ayk)yk.α + 1 = [b.(by + ayk)k.α]y + [a.(by + ayk)α]yk →
(by + ayk)yk.α + 1 = [b.(by + ayk)k.α]y + [a.(by + ayk)kα]y → Cyk.α + 1 = By + Ay эквивалент
Cm = By + Ay эквивалент в свою очередь Eq1: cz = by + ayk com k, α ∈ ℕ .
Случай (3): для z, кратного x, это z = xk и MDC (z, x, y) = 1, где k ∈ ℕ
Будьте Eq1: cxk = by + ax, мы можем написать Eq1 из следующего формата Eq1: by = cxk − ax, и Eq2 будет на основе b вместо c, с b ≠ 0 и c > a, логотипом Eq2: bm = bm, с m > y, поэтому возможно Eq3 которое имеет и свойство Eq1 и Eq2, если оно не удовлетворяет Eq1 после этого Eq1 не имеет полное положительное разрешения.
C b ≠ 0 у нас есть;
by = cxk − ax → 1 = b − y(cxk − ax), (I) нейтральный элемент умножения
by = cxk − ax → b = (cxk-ax)1/y, (II)
Eq2 можно записать следующим образом bm = bm.1, заменен (I) в Eq2 у нас есть; bm = bm.b − y(cxk − ax) → bm = bm − y(cxk − ax) → bm = cxk.bm − y − ax.bm − y, заменяя (II) мы имеем;
∈ ℕ, m – y должно быть кратным xyk, то есть m – y = xyk.α, где α ∈ ℕ, с этими данными мы имеем;
![]()
(cxk − ax)xkα + 1 = [c.(cxk − ax)α]xk − [a.(cxk − ax)k.α]x, обратите внимание, что мы можем организовать следующее;
(cxk − ax)xkα + 1 = [c.(cxk − ax)α]xk − [a.(cxk − ax)k.α]x → [c.(cxk − ax)α]xk = (cxk − ax)xkα + 1 + [a.(cxk − ax)k.α]x, поэтому z может быть кратным x, и ваш ЖК-дисплей ( z , x , y ) = 1
Поскольку z = xk, имеем;
[c.(cz − ax)α]z = (cz − ax)zα + 1 + [a.(cz − ax)k.α]x, с этим у нас есть;
C = c.(cz − ax)α, B = cz − ax e A = a.(c1 − ax)k.α, скоро
Cz = Bzα + 1 + Ax, com z=xk, это эквивалентно уравнению Eq1, осталось показать, что это также Eq2: bm = bm.
[c.(cz − ax)α]z = (cz − ax)zα + 1 + [a.(cz − ax)k.α]x, c by = cz − axez = xk, у нас есть;
[c.(by)α]xk = (by)xkα + 1 + [a.(by)k.α]x → cxk.(by)xkα = bxykα + y + ax.(by)xk.α, как m = xykα + y, у нас есть;
cxk.bxykα = bm + ax.bxyk.α → cxk.bxykα − ax.bxyk.α = bm → bxykα.(cxk − ax) = bm → bxykα.(by) = bm → bxykα + y = bm
→ bm = bm
Так как Eq3 довольный Eq1 и Eq2, logo Eq1 имеет решения на натуральных числах. Дело (4) для нескольких z y это z и yk с k ∈ N
Эта демонстрация аналогична по отношению к Case (3), они достигают того же формата, что и уравнение Eq3, но с b вместо a и y вместо x;
[c.(cyk − by)α] x; [b.(cyk − by)k.α]yk и й (cyk – bx) й 1, с α ∈ ℕ.
Корпус (5): для нескольких z x и y это z=xyk с MDC (z, x, y) = MDC (x, y)≥1 и k ∈ ℕ.
Будьте Eq1: cxyk = by + ax e Eq2: cm = cm, com c ≠ 0 e k ∈ ℕ, вы можете найти новый Equation Eq3, который имеет свойства Eq1 и Eq2, если Eq3 не имеет свойства логотипа Eq1 Eq1 не имеет целых решений.
C c ≠ 0 у нас есть;
cxyk = by + ax → 1 = c − xyk*(by + ax), (I) нейтральный элемент умножения
cm = cm.c − xyk.(by + ax) → cm = cm − xyk.(by + ax) → cm = by.cm − xyk + ax.cm − xyk ,
, Подставляя y и x доказательств, которые у нас есть;
MMC(xy2k , x2yk )=x2y2k, для чего
∈ ℕ, обязательно m – xyk должно быть кратно x2y2k То есть m − xyk = x2y2k.α, c α ∈ ℕ, скоро у нас есть;
Видеть, что xyα + 1 не является кратным xy, потому как MDC(xy.α + 1 , xy ) = 1, скоро Eq1 не имеет положительных целочисленных решений для z, кратного x и y.
Дело ( 6 ): для z, кратного x, и y, кратного x, равно z = xk и y = xt, com k ≥ t и MDC(z,x,y)=x , и k, t ∈ ℕ
Быть Eq1: cxk = bxt + ax e Eq2: cm = cm, c c ≠ 0 e k, t ∈ ℕ,
можно найти новое уравнение Eq3, который имеет свойства Eq1 e Eq2 дело Eq3
не владеет Eq1 скоро Eq1 у него нет целых решений.
cxk = bxt + ax → 1 = c − xk*(bxt + ax), (I) нейтральный элемент умножения
cxk = bxt + ax → c = (bxt + ax)1/xk (II)
Мы можем записать Eq2 следующим образом, используя (I);
cm = cm.c − xk.(bxt + ax) → cm = cm − xk.(bxt + ax) → cm = bxt.cm − xk + ax.cm − xk, при замене (II) имеем;
, изолировав xt и x, мы имеем;
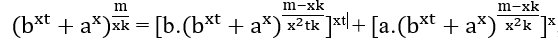 , MMC(x2tk,x2k)=x2tk, para que
, MMC(x2tk,x2k)=x2tk, para que
∈ ℕ необходимо, чтобы м – xk быть кратным x2tk, То есть m − xk = x2tk.α, c α ∈ ℕ, замена этих значений получается;
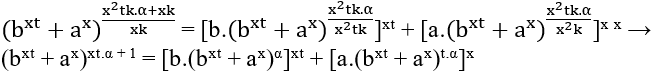 c xt.α + 1 не является кратным x, Остается посмотреть на bxt + ax, понять, что изначально Eq1 é cxk = bxt + ax → (ck)x = (bt)x + ax Последняя теорема Ферма.
c xt.α + 1 не является кратным x, Остается посмотреть на bxt + ax, понять, что изначально Eq1 é cxk = bxt + ax → (ck)x = (bt)x + ax Последняя теорема Ферма.
Поскольку Eq3 не satisfie Eq1, поэтому Eq1 не имеет положительного целого решения, когда z является кратным x, и у кратно x.
Cлучай ( 7 ): заz несколько из y, и x несколько из y Это z = yk e x = yt, с участием k ≥ t e MDC(z,x,y)=y , e k, t ∈ ℕ
Это доказательство аналогично случаю (6), поскольку оно относится к Великой теореме Ферма.
Cлучай ( 8 ): для z, кратного y и x, x или y, кратного друг другу, это z = xyk и x = yt
Вывод в случае, если экспонентов несколько:
Существует нет решения для положительных integers, в случаях (5), ( 6 ), ( 7 ) и ( 8 )
3.3 СОГЛАСНО MACENA ИЛИ S.Т.M
Учитывая n ≥ 2 степень первого члена уравнения, всегда можно определить B=(nm − 1 + 1)n−(nm − 1 − 1)n, что если MDC(a, B, c) = 1 то n имеет четную степень, если MDC (a, B, c) – 2,т ≥ 2, то n градус нечетный, в обоих случаях удовлетворяет an = B + cn, в частности, для любого четного или нечетного n у нас есть MDC(a,B,c) = c, где c имеет форму 2n и 1.
Чтобы доказать эту теорему, вам нужно будет найти инструмент, прежде чем его подтвердить.
Инструмент:
Чтобы найти инструмент, сначала мы должны проанализировать, как биномиальный Ньютон ведет себя с 2 класса.
(x + y)2 = 1.x2 + 2.x.y + 1.y2, То есть 1 2 1.
(x + y)3 = 1.x3 + 3.x2.y + 3.x.y2 + 1.y3,То есть 1 33 1.
(x + y)4 = 1.x4 + 4.x3.y + 6.x2.y2 + 4.x.y3 + 1.y4,То есть 1 4 6 4 1.
(x + y)5 = 1.x5 + 5.x4.y + 10.x3.y2 + 10.x2.y3 + 5.x.y4 + 1.y5, То есть 15101051.
*
*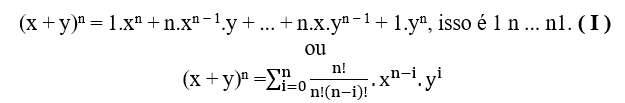
Теперь, вычитая xn или yn из обеих частей (I), получаем;
(x + y)n − xn = n.xn − 1.y + … + n.x.yn − 1 + yn( I I)
ou
(x + y)n − yn = 1.xn + n.xn − 1.y + … n.x.yn N – 1 (I I)
По разнице двух сил одинаковой степени мы можем написать (x + y)n − xn, следующим образом;
ым образом мы также можем написать (x + y)n − yn, следующим образом;
При этом у нас есть два новых уравнения дифференциации только в x и y.
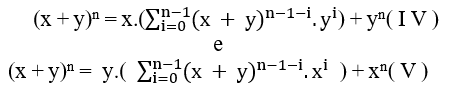
Добавление ( I V ) и ( V ) у нас есть![]()
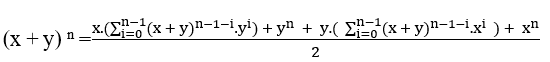 ;
;
Для того,
чтобы быть делится на 2, просто у быть равным х это у й х или х у, с этим у нас есть
Разделение об щим фактором, который xn у нас есть;
Элемент (VI ) является инструментом, который будет использоваться для доказательства теоремы.
Быть m ≥ 2, можно получить уравнения в формате cn = B + an, onde o MDC(c,B,a) = 1 если степень n четная, и MDC(c, B, a) = 2.t ≥ 2, com t ∈ N*, если степень n нечетная.
Метод, если база 2, он будет использоваться для завершения квадратов, если это 3 он будет завершения кубов, и так далее, пока база будет использовать завершения umpisth власти.
Будьте б базы, с b ∈ N*, так что предоставление инициативы у нас есть;
Для b=2 у нас есть;
2m = 2m самом деле это действительно, мы можем написать следующим образом 2m = 2m.1, понимаем, что следующее равенство является действительным.
2m = 2m.(2 − 1) → 2m = 2m + 1 − 2m → 2.2m − 1 = 2m + 1 − 2.2m − 1, чтобы завершить квадрат первого члена, просто добавьте с обеих сторон 22(m − 1) + 1, это приводит к;
2.2m − 1 + 22(m − 1) + 1 = 2m + 1 − 2.2m − 1 + 22(m − 1) + 1 → (22(m − 1) + 2.2m − 1 + 1) = 2m + 1 + (22(m − 1) − 2.2m − 1 + 1) , Итак, у нас есть два полных квадрата, а вместе с ними и новое уравнение;
(2 m – 1+ 1 )2 = 2 m + 1+ (2 m – 1– 1 )2( 1 )
Твой MDC(2m − 1 + 1, 2, 2m − 1 − 1) = 1
Обратите внимание, что в случае m это зависит только от переменной, см. Примеры с числами.
За m = 2
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
(21 + 1)2 = 23 + (21 − 1)2
(2 + 1)2 = 23 + (2 − 1)2
32 = 23 + 12
9 = 8 + 1
За m = 3
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
(22 + 1)2 = 24 + (22 − 1)2
(4 + 1)2 = 24 + (4 − 1)2
52 = 24 + 32
52 = 42 + 32
25 = 16 + 9
За m = 4
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
(23 + 1)2 = 25 + (23 − 1)2
(8 + 1)2 = 25 + (8 − 1)2
92 = 25 + 72
(32)2 = 25 + 72
34 = 25 + 72
81 = 32 + 49
За m = 5
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
(24 + 1)2 = 26 + (24 − 1)2
(16 + 1)2 = 26 + (16 − 1)2
172 = 26 + 152
289 = 64 + 225
За m = 6
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
(25 + 1)2 = 27 + (25 − 1)2
(32 + 1)2 = 27 + (32 − 1)2
332 = 27 + 312
1089 = 128 + 961
Для b = 3, у нас есть;
3m = 3m на самом деле это действительно, мы можем написать следующим образом 3m = 3m.1, понимаем, что следующее равенство является действительным.
3m = 3m.1 → 3m = 3m.(3 − 2) → 3m = 3m + 1 − 2.3m → 3.3m − 1 = 3m + 1 − 3.2.3m − 1, чтобы завершить куб с первой стороны равенства, просто добавьте 33(m − 1) + 3.32(m − 1) + 1 с обеих сторон, это приводит к;
3.3m − 1 + 33(m − 1) + 3.32(m − 1) + 1 = 3m + 1 − 2.3m + 33(m − 1) + 3.32(m − 1) + 1 → (33(m − 1) + 3.32(m − 1) + 3.3m − 1 + 1) = 3m + 1 + 33(m − 1) + 3.32(m − 1) + − 3.2.3m − 1 + 1 → (3m − 1 + 1)3 = 3m + 1 + 33(m − 1) + 3.32(m − 1) − 2.3m + 1, должно быть что-то k ∈ ℕ, это добавляло и вычитало, что они генерируют идеальный куб на второй стороне равенства, как это произошло в предыдущем примере, поэтому мы имеем;
(3m − 1 + 1)3 = [3m + 1 + 33(m − 1) + 3.32(m − 1) − 2.3m + 1 + k] − k, чтобы определить k, просто 3m + 1 + 33(m − 1) + 3.32(m − 1) − 2.3m + 1 + k = (3m − 1 − 1)3;
3m + 1 + 33(m − 1) + 3.32(m − 1) − 2.3m + 1 + k = 33(m − 1) − 3.32(m − 1) + 3.3m − 1 − 1
3m + 1 + 3.32(m − 1) − 2.3m + 1 + k = − 3.32(m − 1) + 3.3m − 1 − 1
k = − 3m + 1 − 3.32(m − 1) − 3.32(m − 1) + 3.3m − 1 + 2.3m − 1 − 1
k = − 3m + 1 − 6.32(m − 1) + 3.3m − 1 + 2.3m − 2
k = − 3m + 1 − 2.3.32(m − 1) + 3m + 2.3m − 2
k = − 3m + 1 − 2.32(m − 1) + 1 + 3.3m − 2
k = − 3m + 1 − 2.32m − 1 + 3.3m − 2
k = − 3m + 1 − 2.(32m − 1 + 1) + 3.3m
k = − 3m + 1 − 2.(32m − 1 + 1) + 3m + 1
k = − 2.(32m − 1 + 1)
Скоро
− k = 2.(32m − 1 + 1)
С этим у нас есть другое уравнение
(3m − 1 + 1)3 = [3m + 1 + 33(m − 1) + 3.32(m − 1) − 2.3m + 1 + k] − k
(3m − 1 + 1)3 = (3m − 1 − 1)3 + 2.(32m − 1 + 1)
(3m − 1 + 1)3 = 2.(32m − 1 + 1) + (3m − 1 − 1)3( 2 )
подобно 3m − 1 + 1 , 2.(32m − 1 + 1) и 3m − 1 − 1, пары, потому что сила 3 всегда странно добавлять 1 или вычитая 1 этой силы, которая дает нам пару.
Так что MDC (3m − 1 + 1, 2.(32m − 1 + 1), 3m − 1 − 1) = 2.t ≥ 2, com t ∈ N*. Пример в цифрахПример в цифрах: ros:
(3m − 1 + 1)3 = 2.(32m − 1 + 1) + (3m − 1 − 1)3
(31 + 1)3 = 2.(33 + 1) + (31 − 1)3
(4)3 = 2.(28) + (2)3
43 = 2.28 + 23, MDC( 4 , 2.28 , 2 ) = 2
64 = 56 + 8
За m = 3 у нас есть;
(3m − 1 + 1)3 = 2.(32m − 1 + 1) + (3m − 1 − 1)3
(32 + 1)3 = 2.(35 + 1) + (32 − 1)3
(10)3 = 2.(244) + (8)3
103 = 2.244 + 83
1000 = 488 + 512
И так далее.
Самый быстрый способ найти эти уравнения – использовать cn =B +an onde c = nm − 1+1 e a = nm − 1−1, isso é;
Если n соответствует степени 2, у нас есть;
Следовательно;
(nm − 1 + 1)n = B + (nm − 1 − 1)n
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2( 1 )
MDC(2m − 1 + 1, 2, 2m − 1 − 1) = 1, c m ≥ 2.
Если n имеет оценку 3, мы имеем;
B = 2.((3m − 1 + 1)2.(3m − 1 − 1)0 + (3m − 1 + 1)1.(3m − 1 − 1)1 + (3m − 1 + 1)0.(3m − 1 − 1)2)
B = 2.((3m − 1 + 1)2 + (3m − 1 + 1).(3m − 1 − 1) + (3m − 1 − 1)2)
B = 2.((32(m − 1) + 2.3m − 1 + 1) + 32(m − 1) − 1 + (32(m − 1) − 2.3m − 1 + 1))
B = 2.(2.32(m − 1) + 1 + 32(m − 1))
B = 2.(32(m − 1)(2 + 1) + 1)
B = 2.(32(m − 1)(3) + 1)
B = 2.(32(m − 1) + 1 + 1)
B = 2.(32m − 1 + 1)
Следовательно;
(nm − 1 + 1)n = B + (nm − 1 − 1)n
(3m − 1 + 1)3 = 2.(32m − 1 + 1) + (3m − 1 − 1)3( 2 )
MDC(3m − 1 + 1, 2.(32m − 1 + 1), 3m − 1 − 1) = 2.t ≥ 2, c t ∈ N* e m ≥ 2
Если n принадлежит к 4 классу, мы имеем;
B = 2.((4m − 1 + 1)3.(4m − 1 − 1)0 + 4m − 1 + 1)2.(4m − 1 − 1)1 + 4m − 1 + 1)1.(4m − 1 − 1)2 + 4m − 1 + 1)0.(4m − 1 − 1)3)
B = 2.(43m − 2 + 4m) или же B = 22m + 1.(24(m − 1) + 1) или же B = 26m − 3 + 22m + 1 ou B = 82m − 1 + 22m + 1
Делая правильные расчеты, пришли;
B = 2.(43m − 2 + 4m) или же B = 22m + 1.(24(m − 1) + 1) или же B = 26m − 3 + 22m + 1 ou B = 82m − 1 + 22m + 1
(nm − 1 + 1)n = B + (nm − 1 − 1)n
(4m − 1 + 1)4 = 2.(43m − 2 + 4m) + (4m − 1 − 1)4( 3 )
MDC(4m − 1 + 1, 2.(43m − 2 + 4m), 4m − 1 − 1) = 1, c m ≥ 2
или же
(22(m − 1) + 1)4 = 22m + 1.(24(m − 1) + 1) + (22(m − 1) − 1)4
MDC(22(m − 1) + 1, 22m + 1.(24(m − 1) + 1), 22(m − 1) − 1) = 1, c m ≥ 2
или же
(22(m − 1) + 1)4 = 26m − 3 + 22m + 1 + (22(m − 1) − 1)4
MDC(22(m − 1) + 1, 26m − 3, 22m + 1, 22(m − 1) − 1) = 1, c m ≥ 2
Если n имеет степень 5, мы имеем;
B = 2((5m − 1 + 1)4 − 0.(5m − 1 − 1)0 + (5m − 1 + 1)4 − 1.(5m − 1 − 1)1 + (5m − 1 + 1)4 − 2.(5m − 1 − 1)2 + (5m − 1 + 1)4 − 3.(5m − 1 − 1)3 + (5m − 1 + 1)4 − 4.(5m − 1 − 1)4)
B = 2((5m − 1 + 1)4 + (5m − 1 + 1)3.(5m − 1 − 1) + (5m − 1 + 1)2.(5m − 1 − 1)2 + (5m − 1 + 1).(5m − 1 − 1)3 + (5m − 1 − 1)4)
Произведя вычисления, придет, что B стоит;
B = 2.(54m − 3 + 2.52m − 1 + 1)
(5m − 1 + 1)5 = 2.(54m − 3 + 2.52m − 1 + 1) + (5m − 1 − 1)5( 4 )
MDC(5m − 1 + 1, 2.(54m − 3 + 2.52m − 1 + 1), 5m − 1 − 1) = 2.t ≥ 2, c t ∈ N* и m ≥ 2.
Se n é de grau 6 temos;
B = 2.((6m − 1 + 1)5 − 0.(6m − 1 − 1)0 + (6m − 1 + 1)5 − 1.(6m − 1 − 1)1 + (6m − 1 + 1)5 − 2.(6m − 1 − 1)2 + (6m − 1 + 1)5 − 3.(6m − 1 − 1)3 + (6m − 1 + 1)5 − 4.(6m − 1 − 1)4 + (6m − 1 + 1)5 − 5.(6m − 1 − 1)5)
B = 2.((6m − 1 + 1)5 + (6m − 1 + 1)4.(6m − 1 − 1) + (6m − 1 + 1)3.(6m − 1 − 1)2 + (6m − 1 + 1)2.(6m − 1 − 1)3 + (6m − 1 + 1).(6m − 1 − 1)4 + (6m − 1 − 1)5)
При правильном выполнении расчетов получим;
B = 2.(65m − 4 + 20.63m − 3 + 6m), ou B = 2.6m.(64m − 4 + 20.62m − 3 + 1) и уравнение; (6m − 1 + 1)6 = 2.6m.(64m − 4 + 20.62m − 3 + 1) + (6m − 1 − 1)6( 5 )
C MDC(6m − 1 + 1, 2.6m.(64m − 4 + 20.62m − 3 + 1), 6m − 1 − 1) = 1, c m ≥ 2
Для того, чтобы доказать это уравнение, мы должны показать для общего случая не только от (1) до ( 5 ), но от (1) до (n).
Для пары n:
Будьте n =2k с k ∈ N*, по предыдущим примерам MDC (a,B,c)=1, замененный в B получен;
По определению Пары B уже пара, то она делится на 2, остается проверить c и a. Если c и a нечетные после этого MDC (c,B,a) 1, если c и b даже после этого MDC (c,B,a) 2.t ≥ 2, с t ∈ N*.
Как с c = nm − 1 + 1 и a = nm − 1 − 1 уравнения cn = B + an при замене значений n и B, которые у нас есть;
Итак, 2.(2m − 2.km − 1) + 1 como 2.(2m − 2.km − 1) − 1, нечетные, так что a и c нечетные, при этом единственное значение, разделяя a, B и c, составляет 1.
Для n Импар:
Независимо от того, n n = 2k + 1 com k ∈ N*, по предыдущим примерам MDC (a,B,c)=1, заменяется в B п олучается;
Установив пару B уже пара, то она делится на 2, остается проверить c и a. Если c и a нечетные после этого MDC (c,B,a) 1, если c и b даже после этого MDC (c,B,a) 2.t ≥ 2, com t ∈ N*.
C c = nm − 1 + 1 и = nm − 1 − 1 уравнения cn = B + an при замене значений n и B имеем;
подобно 2k + 1 нечетно, если возвести в квадрат, оно также нечетное:
(2k + 1)2 = 4k2 + 4k + 1 = 2.(2k2 + 2k) + 1
Если мы прибавим 1 с обеих сторон или вычтем 1, получится ли это пара?
(2k + 1)2 + 1 = 2.(2k2 + 2k) + 2 = 2.[2k2 + 2k + 1] é um par, e (2k + 1)2 − 1 = 2.(2k2 + 2k) − 2 = 2.[2k2 + 2k − 1] Это пара.
подобно 2k + 1 нечетно, если мы поднимаемся на куб, тоже нечетно:
(2k + 1)3 = 8k3 + 12k2 + 6k + 1 = 2.(4k3 + 6k2 + 3k) + 1
Если мы прибавим 1 с обеих сторон или вычтем 1, получится ли это пара?
(2k + 1)3 + 1 = 2.(4k3 + 6k2 + 3k) + 2 = 2.[4k3 + 6k2 + 3k + 1] é um par, e (2k + 1)3 − 1 = 2.(4k3 + 6k2 + 3k) − 2 = 2.[4k3 + 6k2 + 3k − 1] Это пара.
подобно 2k + 1 нечетно, если мы возводим четвертую степень, тоже нечетно:
(2k + 1)4 = 16k4 + 32k3 + 6k + 1 = 2.(8k4 + 16k3 + 3k2) + 1
Если мы прибавим 1 с обеих сторон или вычтем 1, получится ли это пара?
(2k + 1)4 + 1 = 2.(8k4 + 16k3 + 3k2) + 2 = 2.[8k4 + 16k3 + 3k2 + 1]é um par, e (2k + 1)4 − 1 = 2.(8k4 + 16k3 + 3k2) − 2 = 2.[8k4 + 16k3 + 3k2 − 1]это пара.
если он будет продолжаться, это всегда будет пара, поэтому (2k + 1)m − 1 + 1 e (2k + 1)m − 1 − 1 четно, и поскольку B также четно, наименьшее значение, которое делит c,B и Это 2, скоро MDC(a, B, c) = 2.t ≥ 2, c t ∈ N*
Итак, у нас есть два основных уравнения:
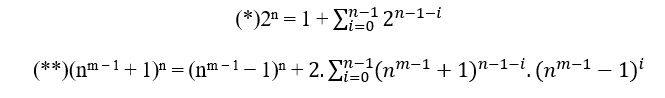
3.3.1 ДЕГУСТАЦИЯ С.Т.M
По вкусу С.T.M просто остается, чтобы показать, что независимо от ли это даже или странно у нас есть MDC (a,B,c)= c onde c = 2n − 1 уже было показано, что (**) имеет различные MDC, если даже, а также странно. Но если мы воспользуемся инструментом (*), который был сгенерирован из бинома Ньютона, при выполнении x = y он был сведен к следующему уравнению;
подобно
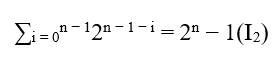
Заменой (I2) и (I1) получается;
(2x)n = xn.(2n − 1) + xn
Чтобы первая часть уравнения была записана как сумма двух степеней второй части уравнения, а поскольку общий множитель равен xn, однако, поскольку значение x не было определено, достаточно записать его как 2n – 1 это уравнение будет зависеть только от степени n, поэтому мы имеем;
(2x)n = xn.(2n − 1) + xn
(2.(2n − 1))n = (2n − 1)n.(2n − 1) + (2n − 1)n
(2.(2n − 1))n = (2n − 1)n + 1 + (2n − 1)n
Данные для этого нового уравнения;
a = 2.(2n − 1), B = (2n − 1)n + 1 e c = 2n − 1
MDC(a,B,c)=MDC(2.(2n − 1), (2n − 1)n + 1, 2n − 1) = 2n − 1 = c
для n даже
То есть n=2k c k ∈ N*
MDC(2.(22k − 1), (22k − 1)2k + 1, 22k − 1) = 22k − 1 = c
для нечетных n
MDC(2.(22k + 1 − 1), (22k + 1 − 1)2k + 2, 22k + 1 − 1) = 22k + 1 − 1 = c
Фактически, это было доказано, потому что на все утверждения, предложенные S.T.M., был дан ответ.
Тест с числами;
Для n = 2 имеем;
(2.(2n − 1))n = (2n − 1)n + 1 + (2n − 1)n
(2.(22 − 1))2 = (22 − 1)2 + 1 + (22 − 1)2
(2.(3))2 = 33 + 32
62 = 33 + 32
36 = 27 + 9
Para n = 3 temos;
(2.(2n − 1))n = (2n − 1)n + 1 + (2n − 1)n
(2.(23 − 1))3 = (23 − 1)3 + 1 + (22 − 1)3
(2.(7))3 = 74 + 73
143 = 74 + 73
2744 = 2401 + 343
На данный момент S.T.M очевидно, два уравнения, но только одно находится в формате гипотезы, что и есть;
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
MDC(2m − 1 + 1, 2, 2m − 1 − 1) = 1, com m ≥ 2. “Это не так, поскольку в нем 2 в качестве показателя степени”
и
(2.(2n − 1))n = (2n − 1)n + 1 + (2n − 1)n
MDC(2.(2n − 1), 2n − 1, 2n − 1) = 2n − 1, c n ≥ 2. “если n>2, то принадлежит Beal Гипотеза”
3.4 ДРУГИЕ УРАВНЕНИЯ, ГЕНЕРИРУЕМЫЕ МЕТОДОМ С.T.M.
F1: ⇒ (2m − 1 + 2k − 1)2 = 2k(m + 1) + (2m − 1 − 2k − 1)2
Это генерал ( 1 ).
MDC(2m − 1 + 2k − 1, 2, 2m − 1 − 2k − 1) = 1, c k = 1 e m ≥ 2.
или же
MDC(2m − 1 + 2k − 1, 2, 2m − 1 − 2k − 1) = 2, c m ≥ 2 e m > k > 1.
Тип, если м No 4, то k может быть 3,2 и 1.
F2: ⇒ (2m − 1.km + k)2 = (2k)m + 1 + (2m − 1.km − k)2
Это общее уравнение предыдущего.
MDC(2m − 1.km + k, 2k, 2m − 1.km − k) = k, c m ≥ 2 e k ∈ N*.
F3: ⇒ (2m + km + 2)2 = (2k)m + 2 + (2m − km + 2)2
или же
(2m + km + 2)2 = (2k)m + 2 + (km + 2 − 2m)2
Если m = 0 e k странно у нас есть; MDC(1 + k2, 2k, |1 − k2|) = 2α ≥ 2, c k, α ∈ N*.
Если k странно у нас; MDC(2m + km + 2, 2k, |2m − km + 2|) = 1, c m ≥ 1 e k ∈ N*.
Если k для пары имеем; MDC(2m + km + 2, 2k, |2m − km + 2|) = 2α ≥ 2, c m ≥ 1 e k, α ∈ N*.
Формула общего формата C2 = B + A2 ⇒ C2 = bm + A2
G1: ⇒ (am + 2m − 2.tm)2 = (2.a.t)m + (am − 2m − 2.tm)2
Игральная кость:
C = am + 2m − 2.tm, b = 2.a.t e A = |am − 2m − 2.tm|
( i ) Если это нечетное и e m > 2 o MDC(C,b,A)=1, ∀t ∈ N*.
( ii ) Если нечетным с м = 2 и т чет, MDC (C,b,A) = 1
( iii ) Если нечетные с м = 2 и т нечетным, MDC (C, b, A) = 2α ≥ 2 com α ∈ N*.
( iv ) Если пара и м > 2 MDC (C, b, A) = 2α ≥ 2, ∀t, α ∈ N*.
( v ) Если a в паре с m = 2 и t нечетным MDC (C, b, A) = 1, t ∈ N*.
( vi ) Если a в паре с м = 2 и т пара MDC (C, b, A) = 2α ≥ 2, t, α ∈ N*.
Как каждая формула или уравнение произошло:
Идея возникла из-за Фермат-каталонская гипотеза, потому что, когда с Cz = By + Ax, он имеет только конечное количество решений, в которых A, B и C являются положительными integers без общих основных факторов и х, у, и z являются положительными интеграторов удовлетворяющих ()/() < 1, потому что все решения будут иметь 2 в качестве одного из показателей. Из-за этого вполне возможно, что фиксация экспонента 2 в квадратной разнице будет иметь удовлетворительные результаты в формате гипотезы? При использовании того же метода С.T.M, foi surgindo novas equações com soluções nos inteiros positivos.
F1: Быть (2r + 2s)2 = B + (2r − 2s)2 ⇒ B = (2r + 2s)2 − (2r − 2s)2, c B, r, s ∈ ℕ где r > s, r e s переменные в настоящее время не определены.
B = (2r + 2s)2 − (2r − 2s)2 → B = (2r + 2s − 2r + 2s).(2r + 2s + 2r − 2s) → B = (2s + 2s).(2r + 2r) → B = 2s + 1.2r + 1 → B = 2s + r + 2
При адаптации s и r в переменных m и k c S.T.M, Мы должны m > k вычитание 1 с обеих сторон у нас есть m − 1 > k − 1 при сравнении r > s, Мы должны r = m − 1 e s = k − 1, с этим у нас есть B = 2k − 1 + m − 1 + 2 → B = 2m + k − 2 + 2 → B = 2m + k, следовательно, уравнение;
F1: ⇒ (2m − 1 + 2k − 1)2 = 2m + k + (2m − 1 − 2k − 1)2
Если k равно 1, Так MDC(2m − 1 + 21 − 1, 2, 2m − 1 − 21 − 1) = MDC(2m − 1 + 20, 2, 2m − 1 − 20) = MDC(2m − 1 + 1, 2, 2m − 1 − 1) = 1, ∀m ∈ N*
Пример использования этого уравнения, в котором MDC=1, c m = 2, 3, 5, 6. ; м не может быть 1, потому что k был 1.
(22 − 1 + 1)2 = 22 + 1 + (22 − 1 − 1)2 → 32 = 23 + 12 → 9 = 8 + 1
(23 − 1 + 1)2 = 23 + 1 + (23 − 1 − 1)2 → 52 = 24 + 32 → 25 = 16 + 9
За m = 4
(24 − 1 + 1)2 = 24 + 1 + (24 − 1 − 1)2 → 92 = 25 + 72 → 34 = 25 + 72 → 81 = 32 + 49
За m = 5
(25 − 1 + 1)2 = 25 + 1 + (25 − 1 − 1)2 → 172 = 26 + 152 → 289 = 64 + 225
За m = 6
(26 − 1 + 1)2 = 26 + 1 + (26 − 1 − 1)2 → 332 = 27 + 312 → 1089 = 128 + 961
Если k > 1, Так MDC(2m − 1 + 2k − 1, 2, 2m − 1 − 2k − 1) = 2, ∀m, k ∈ N*, где m > k
Пример, если m = 5, Так k варьируется между 2 до 4.
(2m − 1 + 2k − 1)2 =2m + k + (2m − 1 − 2k − 1)2→ (25 − 1 + 2k − 1)2 =25 + k + (25 − 1 − 2k − 1)2→ (24 +2k − 1)2 =25 + k + (24 − 2k − 1)2
За k = 2
(24 + 22 − 1)2 = 25 + 2 + (24 − 22 − 1)2 → (24 + 21)2 = 27 + (24 − 21)2
→ 182 = 27 + 142 → 324 = 128 + 196
За k = 3
(24 + 23 − 1)2 = 25 + 3 + (24 − 23 − 1)2 → (24 + 22)2 = 28 + (24 − 22)2
→ 202 = 28 + 122 → 400 = 256 + 144
За k = 4
(24 + 24 − 1)2 = 25 + 4 + (24 − 24 − 1)2 → (24 + 23)2 = 29 + (24 − 23)2
→ 242 = 29 + 82 → 242 = 29 + 26 → 576 = 512 + 64
F2: Быть (2s.kr + k)2 = B + (2s.kr − k)2 ⇒ B = (2s.kr + k)2 − (2s.kr − k)2, c B, k, r, s ∈ ℕ где
r > s, r и s переменные в настоящее время не определены.
B = (2s.kr + k)2 − (2s.kr − k)2 → B = (2s.kr + k − 2s.kr + k).(2s.kr + k + 2s.kr − k) → B = (2k).(2s + 1.kr) → B = 2k.2s + 1.kr → B = 2s + 2.kr + 1, Для чего B быть написанным как мощность достаточно s + 2 = r + 1, Оказывается, что B = (2k)r + 1 или же B = (2k)s + 2, Однако, чтобы это было правдой, оно должно быть больше s r > s.
Гипотеза s + 2 = r + 1 ⇒ s = r − 1 и диссертация r > s
Мы должны s + 1 > s добавляя 1 с обеих сторон s + 2 > s + 1 ⇒ r + 1 = s + 2 > s + 1 > s ⇒ r + 1 > s в свою очередь r + 1 > r следовательноr > s, понять, что при использовании Гипотезы, где s = r − 1 ⇒ r = s + 1 и заменить в r > s неравенство выполнено s + 1 > s.
Следовательно B = (2k)r + 1 = (2k)s + 2 = (2k)r + 1, тогда уравнение;
(2r − 1.kr + k)2 = (2k)r + 1 + (2r − 1.kr − k)2, так что все основано на одной и той же переменной m, просто r будет равно m, то есть r = m. С этим у нас уже есть другое уравнение;
F2: ⇒ (2m − 1.km + k)2 = (2k)m + 1 + (2m − 1.km − k)2
Если k Это 1, это само уравнение F1 из MDC=1;
(2m − 1.1m + 1)2 = (2.1)m + 1 + (2m − 1.1m − 1)2 → (2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
Если k > 1 Имеет как MDC = k
MDC(2m − 1.km + k, 2k, 2m − 1.km − k) = k, ∀m, k ∈ N*.
(2m − 1.km + k)2 = (2k)m + 1 + (2m − 1.km − k)2
(2m − 1.2m + 2)2 = (4)m + 1 + (2m − 1.2m − 2)2
(22m − 1 + 2)2 = 4m + 1 + (22m − 1 − 2)2
(22.1 − 1 + 2)2 = 41 + 1 + (22.1 − 1 − 2)2 → 42 = 42 + 02 → 16 = 16
Se m = 2
(22.2 − 1 + 2)2 = 42 + 1 + (22.2 − 1 − 2)2 → (23 + 2)2 = 43 + (23 − 2)2 → 102 = 43 + 62 → 100 = 64 + 36
(22.3 − 1 + 2)2 = 43 + 1 + (22.3 − 1 − 2)2 → (25 + 2)2 = 44 + (25 − 2)2 → 342 = 44 + 302 → 1156 = 256 + 900
*
*
*
И так далее …
За k = 3
(2m − 1.km + k)2 = (2k)m + 1 + (2m − 1.km − k)2
(2m − 1.3m + 3)2 = 6m + 1 + (2m − 1.3m − 3)2
(21 − 1.31 + 3)2 = 61 + 1 + (21 − 1.31 − 3)2
(20.3 + 3)2 = 62 + (20.3 − 3)2 → 62 = 62 + 02
(22 − 1.32 + 3)2 = 62 + 1 + (22 − 1.32 − 3)2
(21.9 + 3)2 = 63 + (21.9 − 3)2 → 212 = 63 + 152 → 441 = 216 + 225
(23 − 1.33 + 3)2 = 63 + 1 + (23 − 1.33 − 3)2Nn
(22.27 + 3)2 = 64 + (22.27 − 3)2 → 1112 = 64 + 1052 → 12321 = 1296 + 11025
*
*
*
И так далее …
F3: Быть (2s + kr)2 = B + (2s − kr)2 ⇒ B = (2s + kr)2 − (2s − kr)2, c B, r, s ∈ ℕ где r > s, r и s переменные, которые в настоящее время не определены.
B = (2s + kr)2 − (2s − kr)2 → B = (2s + kr − 2s + kr).(2s + kr + 2s − kr) → B = 2.kr.2s + 1 → B = 2s + 2.kr, в этом случае для того, чтобы B был достаточно мощным r = s + 2. На самом деле r > s, потому что s s 2 > r s s 1 > s ⇒ r > s при размещении экспонента в качестве функции m, просто s й m это дает нам r q й 2.
Логотип B = 2s + 2.kr = (2k)r = (2k)m + 2.
Итак, новое уравнение:
F3: ⇒ (2m + km + 2)2 = (2k)m + 2 + (2m − km + 2)2, c k ∈ N* и m ≥ 0.
Если k составляет 1 для ∀м ∈ НЗ MDC No 1 или Если м составляет от 0 до ∀k ∈ N* и также MDC = 1.
Если ни один из этих случаев не возникает F3 Оно имеет MDC = 2α ≥ 2, ∀α ∈ N*
Логика такая же для G1,«Так как она генерал»;
Потому что при выполнении B = (ar + 2s.tr )2 − (ar − 2s.tr)2 → B = (ar + 2s.tr − ar + 2s.tr).(ar + 2s.tr + ar- 2s.tr) →
Проще говоря, s + 2 = r или s = r – 2, поскольку r – это m, выполняющее преобразование, мы имеем s = m – 2, то есть;
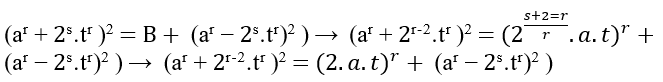 G1: ⇒ (am + 2m − 2.tm)2 = (2.a.t)m + (am − 2m − 2.tm)2
G1: ⇒ (am + 2m − 2.tm)2 = (2.a.t)m + (am − 2m − 2.tm)2
Игральная кость:
C = am + 2m − 2.tm, B = 2.a.t e A = |am − 2m − 2.tm|
( i ) Если a нечетное и m > 2 o MDC(C,b,A)=1, ∀t ∈ N*.
( ii ) Если нечетным с м No 2 и т чет, MDC (C,b,A)=1
( iii ) Если нечетные с м й 2 и т нечетным, MDC (C, b, A) 2 “≥ 2 с α ∈ N*.
( iv ) Если пара и м > 2 MDC(C, b, A) = 2α ≥ 2, ∀t, α ∈ N*.
( v ) Если a в паре с m No 2 и t нечетным MDC (C, b, A) = 1, t ∈ N*.
( vi ) Если a в паре с м й 2 и т пара MDC (C, b, A) = 2α ≥ 2, t, α ∈ N*.
4. ФОРМУЛЫ, ГЕНЕРИРУЕМЫЕ Т.M E S.T.M С РЕШЕНИЯМИ В НАТУРАЛЬНОМ
Основные данные; a,b,c,x,y,z,A,B,C,α e k ∈ N
Формула 1 : Cz = Cxyk + 1 = By+ Ax, mdc(x,y,z)=1
( by + ax )xyk + 1 = [ b( by + ax)xk]y + [ a( by + ax )yk]x
Игральная кость:
C =by+ ax, B =b(by+ ax)xk e A = a( by+ ax )yk, MDC(C, B, A) = C.
Формула 2 : Cz = Cxk + 1 = Bx+ Ax, или же Cz = Cyk + 1 = By+ Ay, mdc(z,x)= mdc(z,x) = 1
( bx + ax )xk + 1 = [ b( bx + ax )k ]x + [ a( bx + ax )k ]x
ИЛИ ЖЕ
( by + ay )yk + 1 = [ b( by + ay )k]y + [ a( by + ay )k ]y
Игральная кость:
C =bx+ ax, B =b(bx+ ax)k e A = a(bx+ ax )k, MDC(C, B, A) = C.
ИЛИ ЖЕ
C =by+ ay, B =b(by+ ay)k e A = a( by+ ay )k, MDC(C, B, A) = C.
[ c( cxk− ax )α]xk = ( cxk− ax )xkα+1 +[ a(cxk−ax)kα]x
ИЛИ ЖЕ
[ c( cyk− by )α]yk = [ b( cyk− by )kα]y + ( cyk− by )ykα+1
Игральная кость:
C = c(cxk − ax), B = cxk − ax e A = a.(cxk −ax), MDC(C,B,A)= B.
ИЛИ ЖЕ
C = c(cyk − by), B = b(cyk − by) e A = cyk − by, MDC(C,B,A)= A.
ИЛИ ЖЕ
(2n+1 − 2)n = (2n − 1)n + 1 + (2n − 1)n
Игральная кость:
a = 2.(2n − 1), B = (2n − 1)n + 1 e c = 2n − 1, MDC(a B,c)=MDC(2.(2n − 1), (2n − 1)n + 1, 2n − 1) = 2n − 1 = c
Формула 5: G1: ⇒ (am + 2m − 2.tm)2 = (2.a.t)m + (am − 2m − 2.tm)2
Игральная кость:
C = am + 2m − 2.tm, B = 2.a.t e A = |am − 2m − 2.tm|, c t ≠ 2.a
( i ) Если a нечетное и m > 2 o MDC(C,b,A)=1, ∀t ∈ N*.
( ii ) Если нечетным с m = 2 и t пара, MDC(C,b,A)=1 .
( iii ) Если нечетные с м й 2 и т нечетным, MDC(C, b, A) = 2α ≥ 2 c α ∈ N*.
( iv ) Если пара и м > 2 MDC(C, b, A) = 2α ≥ 2, ∀t, α ∈ N*.
( v ) Если a в паре с m = 2 и t нечетным MDC(C, b, A) = 1, t ∈ N*.
( vi ) Если a в паре с м й 2 и т пара MDC(C, b, A) = 2α ≥ 2, t, α ∈ N*.
В частности
c2 = 2m + 1 + b2, MDC(a,b,c)=1
(2m−1+1)2=2m+1+(2m−1−1)2
c=2m−1+1, b=2 и a=2m−1−1, MDC(a,b,c)=1
5. T.G.M ИЛИ ГЕНЕРАЛ ТЕОРЕМА МАСЕНА
Учитывая любое действительное уравнение положительных центнеров в виде власти, или порожденных Т.М или С.T.M при умножении на дежавю, где dα является адекватной основой преобразования в сумму двух сил, и α является нескольким положительным показателем показателей других баз или mmc экспонентов, умноженных на t*, таким образом, приводит к власти, написанной в сумме двух других полномочий с общим фактором d или кратным d.
, при B> A и m ≥ n ≥ 2, где α=mmc(1,m,n).t, t ϵ N*
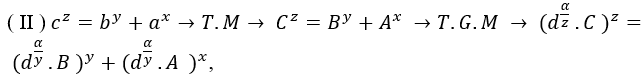 , где α=mmc(z,y,x).t, t ϵ N*
, где α=mmc(z,y,x).t, t ϵ N*
![]() , где α=mmc(n,1,n).t, t ϵ N*
, где α=mmc(n,1,n).t, t ϵ N*
( IV ) C2=B+A2→ Geralpor S.T.M→ ( am + 2m − 2.tm )2 = ( 2.a.t )m + ( am − 2m − 2.tm )2→T.G.М →![]()
, где α =mmc(2,m,2).β, β ϵ N*
При этом у нас всегда есть общий фактор в формате гипотезы, если экспоненты x,y,z≥3, независимо от уравнения адресовано.
“За исключением ( IV ), который будет иметь класс 2 всегда по крайней мере на одной из баз”.
5.1 ДОКАЗАТЕЛЬСТВО Т.G.M
Чтобы доказать эту теорему, необходимо доказать элементы. ( I ), ( II ), ( III ) и ( IV ).
Доказательство предмета ( I ) Есть ли какое-либо уравнение типа ![]()
, c B,
умножив на степень
, d на данный момент не определено, однако
![]() ,
,
То есть dm.n.t , скоро у нас есть;
![]() поскольку d не определено, достаточно быть равным
поскольку d не определено, достаточно быть равным
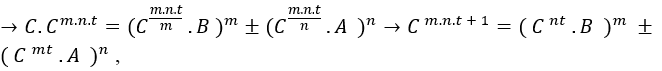 , где C – общий множитель уравнения,
, где C – общий множитель уравнения,
![]()
Пример в цифрах;
C1 = Bm+Am→ 29 =33 + 22, по теореме d=C1=29 eα= mmc(1,3,2).t = 6t, →296t+1 = 33 . 296t + 22. 296t
296t+1 =( 3.292t )3 + ( 2.293t )2 , если t=1 у нас есть 297=25233+487782, mdc( 29 , 2523 , 48778 ) = 29 ,если t = 2 у нас есть 2913=21218433+11896466422, mdc(29, 2121843 , 1189646642 ) = 29 и так далее с t ≥3
C2 = Bm-An→ 23 =33-22, по теореме d=C2=23eα=mmc(1,3,2).t = 6t,→236t+1 =33.236t-22.236t→
236t+1 =(3.232t)3 – (2.233t)2→, если t=1 у нас есть 237=15873-243342,mdc( 23 , 1587 , 24334 ) = 23,если t = 2 у нас есть 2313=8395233-2960717782, mdc(23, 839523 , 296071778 ) = 23 и так далее с t ≥3.
Доказательство предмета ( II ) Есть ли какое-либо уравнение типа cz=by+ax с решениями в натуральных числах, Т.М мы придем к эквивалентному уравнению со следующими основаниями;
C =by+ax, B =b(by+ax )xk e A =a( by+ax )yk, с уравнением Cxyk+1=By+Ax→Cz=By+Ax
При умножении на степень dα , d на данный момент не определено, однако
α=mmc(z,y,x).t , tϵN*, То есть dzyx.t , скоро у нас есть;
dzyx.t .Cz= dzyx.t.By+dzyx.t .Ax→(dyx.t .C )z= (dzx.t .B )y+(dzy.t .A )x→ Como mdc( C , B , A ) = C então
MDC[(dyx.t .C ),(dzx.t .B ),(dzy.t .A ) ] ≥ dt .C ,в частности, если d = C у нас есть Cz(yxt+1)= (Czx.t .B )y+(Czy.t .A )x
MDC[ C , (Czx.t .B ), (Czy.t .A ) ] = C. Расширение с использованием всех данных уравнение;
{ dyx.t . by+ax }z= {dzx.t .b( by+ax )xk}y+{dzy.t .a( by+ax )yk}x
подобно z= xyk + 1
{dyx.t .( by+ax ) }xyk+1= {d(xyk+1)x.t .b(by+ax )xk}y+{d(xyk+1)y.t .a( by+ax )yk}x
Пример в цифрах
x=y=2, t=k=1 e b=a=3 e d=5
{54 .( 32+32 ) }5= {510 .3( 32+32 )2}2+{510 .3( 32+32 )2}2
{54 .18 }5= {510 .3.182}2+{510 .3.182}2
112505=94921875002+94921875002
MDC(11250 ,9492187500,9492187500)=11250
Доказательство пункта (III). Имеет ли какое-либо уравнение типа cn=B+an,с положительными целочисленными решениями, согласно S.T.M, у нас есть огромное количество уравнений, но B всегда ![]() ,умножив уравнение на степень dα, d, не определенную в данный момент, с α = mmc (n, 1, n) .t, t ϵ N *, получим
,умножив уравнение на степень dα, d, не определенную в данный момент, с α = mmc (n, 1, n) .t, t ϵ N *, получим
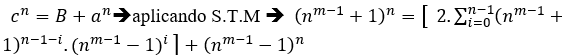
у нас есть;
![]()
→ Поскольку d не определено, просто d = B то есть;
Примеры;
(1)
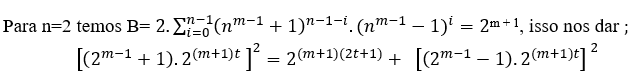
Без = 2, у нас есть→ (3.23t )2=23(2t+1)+ 26t, ∀ t ∈N, MDC[(3.23t),2,2]=2
Без = 3, у нас есть→(5.24t )2=24(2t+1)+(3.24t)2, ∀ t ∈N, MDC[(5.24t),2,(5.24t)]=2
[…]
( 2 )
Если m = 3, имеем →{10.488t} 3=4883t+1+ {8.488t }3, ∀ t ∈N,MDC[(10.488t),488,8.488t] = 488
[…]
( 4 )
( 5 )
∀ m > 1, t ∈ N, MDC[Das Bases] = 2.6m. (64m-4 + 20. 62m-3 +1)
( 7 )
И так далее
.
.
.
( … )
ПРИМЕЧАНИЕ: До сих пор элементы ( I ), ( II ) и ( III ) остается только ( IV )
Доказательство пункта ( IV ) Будьте любое уравнение типа c2=B+a2, с решениями в положительных цен, используя средства S.T.М, у нас есть;
C2=B+C2→Генерал S.T.M→( am + 2m − 2.tm )2 = ( 2.a.t )m + ( am − 2m − 2.tm )2, умножив на мощность dα, c d на данный момент не определено, однако α = mdc(2,m,2).β , β ϵ N*, на этот раз он использует β, потому что в уравнении уже есть t, которое, как сказано, есть;
dα.(am + 2m − 2.tm )2 = dα.( 2.a.t )m + dα.( am − 2m − 2.tm )2
[dmβ.( am + 2m − 2.tm )]2 = [d2β.( 2.a.t )]m + [dmβ( am − 2m − 2.tm )]2 [dmβ .( am + 2m − 2.tm )]2 = [2at.d2β ]m + [dmβ ( am − 2m − 2.tm )]2
В этом случае d может быть любое число, принадлежащее к положительным ценителям, за исключением нуля, (dϵN*).
Пример в цифрах;
a=2, d=5et=m=β = 3
[59 .( 23 + 21.33)]2 = [12.56]3 + [59 .( 23 - 21.33)]2
[ 59 .( 62 )]2 = [12.56]3 + [59 .( -46)]2
[121093750]2 = [187500]3 + [ -89843750 ]2
1210937502 = 1875003 + (- 89843750 )2
MDC[121093750 ,187500 ,| – 89843750 |] = 31250
ПРИМЕЧАНИЕ: MDC(Базы) ≥ dβ, тот 31250 = 2.d2β>dβ
Идея та же для любого уравнения с суммой 2 власти.
Значит, ты доказываешь Т.G.M
Любопытство: ( 1.0 )
5 = 3 + 2 → умноженный на базу 3 → 5.3 = 32 + 2.3 → нравиться 3 = 5 – 2 → заменяет в первом члене 5(5 – 2)=32 + 2.3 → 52 – 2.5 = 32 + 2.3 → изоляция 52 = 32 + 2.( 3 + 5 ) →
52 = 32 + 2.( 8 ) → 52 = 32 + 2.( 23 ) → 52 = 32 + 24.
( 1.1 )
53 = 53 → 53 = 5.52 → мы можем написать 5 = 22 + 1, вставив второй член→
53 = (22 + 1).52 → 53 = 22.52 + 52 → 53= 102 + 52.
“ПРИМЕЧАНИЕ: Это любопытство еще одна статья, которую я буду публиковать в будущем, ABC Гипотеза”
6. ДОКАЗАТЕЛЬСТВО ГИПОТЕЗЫ BEAL
(1-е условие) Учитывая уравнение cz = by + ax с решениями в положительных integers, с { z , y, x ≥ 3 / c, b , a ≠ 0 }, то, b и c имеют общий премьер-фактор, который означает, что a, b и c делится на одно и то же простое число.
Или
(2-е условие) Уравнение a x + b y = c z не имеет решения для положительных интеграторов с x,y,z ≥ 3 и mdc (a,b,c)
Начало теста
A (2-ое Условие ) Невозможно получить номера в положительных integers с mdc(a,b,c) = 1, и exponents x,y,z ≥ 3, по двум причинам, уже показаны:
Первый — Было показано, что Фермат-Каталонская гипотеза имеет только конечное количество решений, в настоящее время Есть только 10 уравнений найдено, в котором, б, и с являются положительными целые без общих основных факторов и х, у, и z являются положительными целом удовлетворяющих , потому ч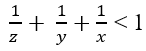
,то все решения будут иметь 2 в качестве одного из экспонентов, это уже придерживается гипотезы mdc (a ,b,c) No1, и экспоненты x,y,z ≥ 3.
НАЙДЕНЫ 10; Изображение взято с сайта Википедии.

2ª — Если вы голосуете за часть С.T.M обратите внимание, что там, где уравнения имеют mdc (базы) No 1, он всегда имеет показатель 2, даже различные другие экспоненты, и как S.T.M было доказано, так же, как гипотеза Фермат – каталонские государства по крайней мере один из экспонентов должно быть 2, а затем придерживается гипотезы по простой причине содержания экспонента 2 в одной из баз.
Так что осталось доказать только одно условие.
(1-е условие) уже возможно через Т.M, S.T.M e T.G.M, все имеют общие факторы в обеих базах только для того, чтобы показать, что он имеет общий премьер-фактор, который делит обе базы с экспонентами х, y, z ≥ 3.
ДОКАЗАТЕЛЬСТВО:
Игральная кость;
Пусть p – простое число и Fp = pu общий простой фактор p, и pi ≠pi+1, i индекс, отличные кузены и показатели Ui ≥ Ui+1≥0, i индекс, разные показатели степени или нет, то C можно ввести натуральное число как;
C = Fp = pu, ou C = p1u1.p2u2 ou C = p1u1.p2u2. p3u3 .p4u4 …piui .pi+1ui+1… Общие простые множители, такие как cz = by + ax, и каким-то способом T.M, S.T.M e T.G.M, получается Cz = By + Ax, Так;
Cz =(Fp )z = pz.u↔By + Ax = pz.u, ou Cz =( p1u1 ) .p2u2 )z =p1z.u1 .p2z.u2 ↔By + Ax = p1z.u1 .p2z.u2 или же
Cz =(p1u1.p2u2. p3u3 .p4u4 … piui.pi+1ui+1…)z =p1z.u1 .p2z.u2. p3z.u3.p4z.u4… piz.ui.pi+1z.ui+1…= By + Ax
ЗДАНИЕ Cz → Cz ИЗ Cn.
На самом деле 1 и 1, потому что 1 является нейтральным элементом умножения сказал, что это c ϵ N* при умножении с обеих сторон у нас есть 1.c = 1.c→c = c, когда умножается снова с у нас есть c.c =c.c→c2 = c2→ если этот процесс продолжается в течение n раз у нас есть → cn = cn, обратите внимание, если n > z, у нас есть cn>cz.
Таким образом, cn = cn может быть вписан как cn = cz.cn – z, гипотеза гипотезы заключается в том, что cz= by+ ax, имеет общий главный фактор, который разделяет основания c,b и a, с z,y,x ≥ 3, с этим у нас есть;
cn = cz.cn – z→cn = ( by+ ax).cn – z→cn = by. cn – z + ax.cn – z, то если cz= by+ ax имеет разрешения в положительных integers, с экспонентами большле чем или равно до 3, в действительности cn q мимо. cn = by. cn – z + ax.cn – z, имеет фактор который разделяет оба потому что mdc (cn, by. cn – z, ax.cn – z) – cn> 1.
Перевод показывает, что cz= by+ ax имеет такие решения, так что на самом деле это подтверждает гипотезу, и это тезис. Но чтобы добраться до этого заявления, мы должны доказать равенство, но это уже было показано теоремами Т.M, S.T.M e T.G.M, однако, условия экспонентов были больше, чем или равны 3 не были включены, ни условия основных факторов, так что заключение это доказано Beal гипотезы.
Использование Т.M у нас есть это уравнение cz= by+ ax, стали;
(by+ax)xyk+1=[b.(by+ax)xk ]y+[a.(by+ax)yk]x, где z = xyk + 1, C = by+ax ,
B= b.(by+ax)xk и A = a.(by+ax)yk , То есть Cz = By + Ax, c mdc (C,B,A) = C >1, за x,y,z> 2 ou x,y,(xyk+1) > 2.
Так что, если у Cz = By + Ax есть решения в положительных интеграторах, то cz = cxyk+1 = by + ax, по топору, просто потому, что он имеет тот же формат или структуру. Тем не менее, осталось показать cn, что такое; cn = by. cn – z + ax.cn – z , адаптация под базы C, B и A у нас есть;
C n = By. C n – z + Ax.Cn – z
(by+ax)n=[b.(by+ax)xk ]y.(by+ax)(n-z)+[a.(by+ax)(yk )]x.(by+ax)(n-z)
(by+ax)n=by.(by+ax)xyk + n- z+ax.(by+ax)xyk + n- z , как z = xyk+1,
(by+ax)n=by.(by+ax)xyk + n- xyk-1 +ax.(by+ax)xyk + n- xyk-1
(by+ax)n=by.(by+ax)n-1+ax.(by+ax)n-1
«Это уравнение в функциях показателей n, x, y, основанное на ранее показанных теоремах, у нас есть (n – 1) кратно x, y, это n – 1 =
xyt или же n = xy.t + 1, o t просто чтобы отличить от k, уже используя ”
(by+ax)xy.t+1=by.(by+ax)xyt +ax.(by+ax) xyt
(by+ax)xy.t+1=[b.(by+ax)xt ]y+[a.(by+ax)yt]x
Takим образом Cn>Cz→Cn-Cz> 0 → (by+ax )xy.t+1-(by+ax )(xy.k+1)>0→ деление на (by+ax ), temos→(by+ax )xy.t-(by+ax )(xy.k)>0→dividindo (by+ax )xy, temos →
(by+ax )t-(by+ax )k>0→(by+ax )t>(by+ax )k→t > k, ∀ t,k ∈N
Тогда уравнение со всеми переменными можно записать следующим образом;
( EQ1 )(by+ax)xy(t+k)+1=[b.(by+ax)x(t+k) ]y+[a.(by+ax)(y(t+k) )]x
ИЛИ ЖЕ
( EQ2 ) (by+ax)xy( t – k )+1)=[b.(by+ax)x( t – k ) ]y+[a.(by+ax)y(t – k) ]x
Как и другие формулы, генерируемые Т.M и некоторые также из S.T.M e T.G.M, который имеет формат Cz = By +Ax, по QX, имеет такое же поведение, как ( EQ1)и( EQ2), то, показывая условия основных факторов, как в начале этого теста буквально доказывает все условия Гипотеза Beal для утвердительного случая, то есть (1-е состояние ).
(#) Для случая общего премьер-фактора в ( E’1)e ( E’2), это Cz= By + Ax = pz.u ;
Таким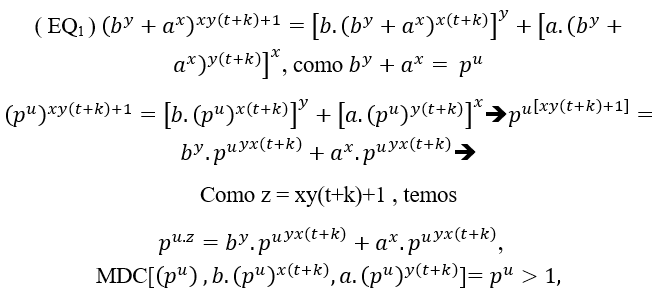 образом, общий главный фактор р, потому что равенство удовлетворяется, если она прод
образом, общий главный фактор р, потому что равенство удовлетворяется, если она прод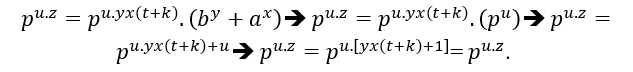 олжается,
олжается,
Аналогично ( EQ1 ) будет иметь тот же результ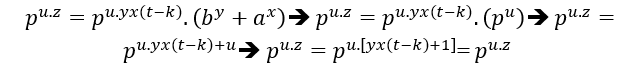 ат
ат
(##) В случае 2 распространенных основных факторов в (EQ1)e(EQ2)![]() э
э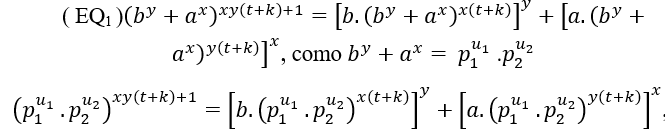 то
то
, на самом деле mdc будет продуктом двух полномочий различных премьер, это![]()
Проверка равенства, например, z = xy(t+k)+1, у нас ес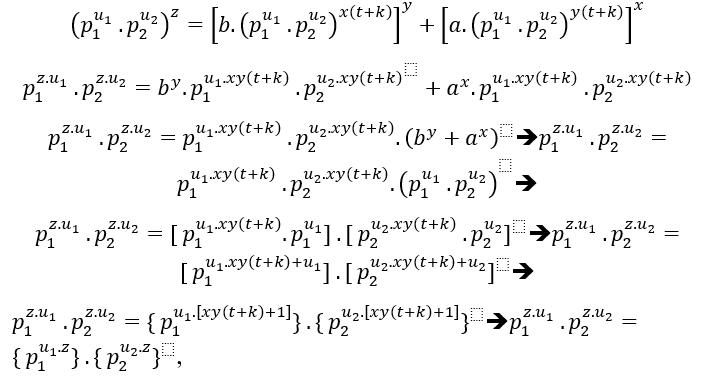 ть;
ть;
при разделении на любой из общих основных факторов попадает в состояние (я).
Аналогично (EQ2);
( #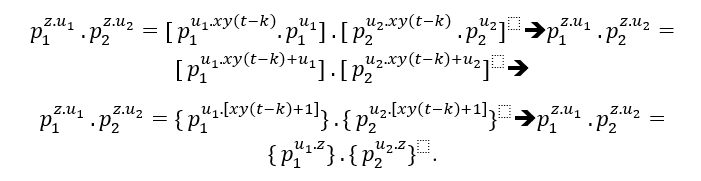 ## ) В случае общего основных факторов (EQ1) и (EQ2) это;
## ) В случае общего основных факторов (EQ1) и (EQ2) это;
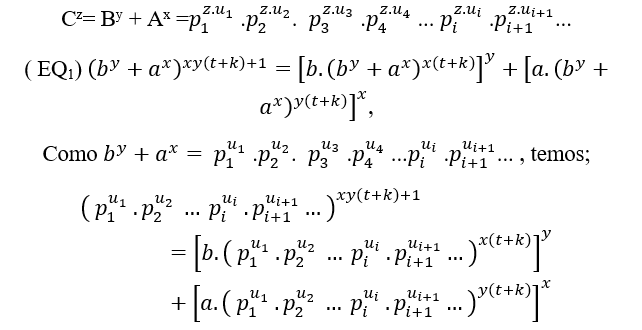
На самом деле мы будем иметь MDC с несколькими общими премьер-факторов, или с 3 года, полномочия различных премьер друг от друга, эт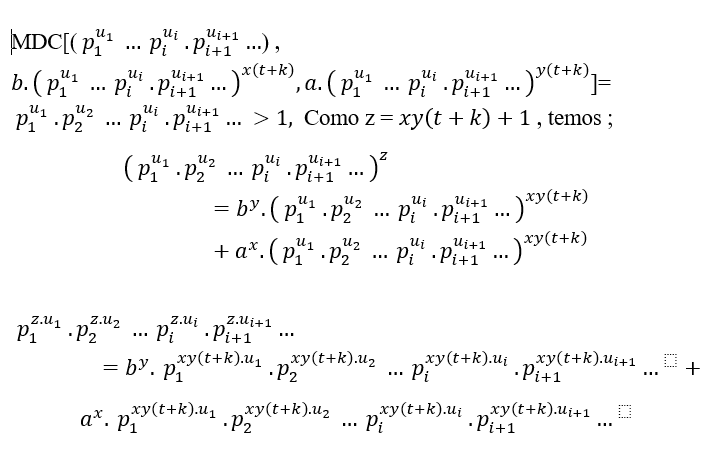 о
о
_________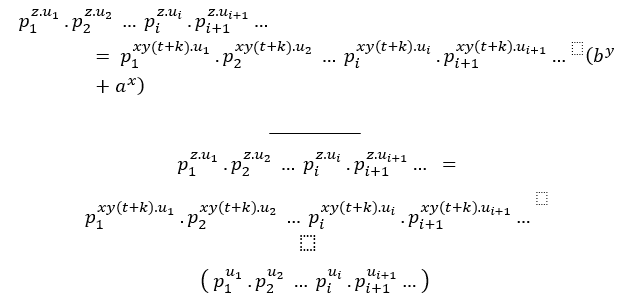
_________
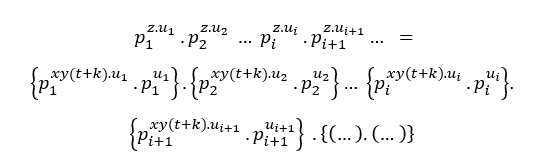
Так же, как условие ( ## ), у нас есть;
Каж дый раз, когда он делится на общий премьер-фактор они будут уменьшаться, пока она не станет лишь общим основным фактором.
Аналогично (EQ2), он также удовлетворен;
7. ЗАКЛЮЧИТЕЛЬНЫЕ СООБРАЖЕНИЯ
Эта статья была предложена в качестве общего объективного доказательства – там Beal гипотезы, при использовании теоремы T.M, S.T.M e T.G.M в сочетании с приложениями в теории числа было на самом деле можно продемонстрировать, однако не удалось найти Con – например, при использовании средств в ходе разработки, должно быть, заметили, что каждый шаг имеет важное значение для других в любом случае по отношению к теоремам, представленным без Т.M не мог использовать Т.G.M, sem o T.G.M o S.T.M не может быть использован для гипотезы Beal, если у него нет Т.M o S.T.M e T.G.M было бы что-то очень расплывчато, другими словами, не поддерживает демонстрацию такой гипотезы.
В лучшем случае без других теорем, таких как Теорема Пифагора, Последняя теорема Фермата, Теорема Себе и гипотеза Фермата – каталонский Т.M было бы что-то очень расплывчато и займет гораздо больше времени, чтобы быть доказано, просто обладая такими теоремами Т.M является продолжением и в то же время то, что поддержка теоремы цитируется, другими словами Т.M был недостающий кусок для завершения.
8. РЕКОМЕНДАЦИИ
BEAL, Andrew. Site: Wiki de Poker. 2008. Disponível em:<https://poker.fandom.com/wiki/Andrew_Beal> Acesso em: 03 de Junho de 2018.
FERMAT, biografias de Matemáticos. Site: Só Matemática. 1998-2019. Disponível em: <https://www.somatematica.com.br/biograf/fermat.php> Acesso em: 18 de Maio de 2018.
KILHIAN, (Sebastião Vieira do Nascimento, “Sebá”). A Conjectura de Beal – Casos Particulares. Site: O baricentro da Mente. 28/04/2012. Disponível em: <https://www.obaricentrodamente.com/2014/11/a-conjectura-de-beal-casos-particulares.html> Acesso em: 27 de Maio de 2018.
TANIYAMA e SHIMURA, Teorema de Shimura-taniyama-Wil. Editada pela última vez em 5 de setembro de 2017 Site: Wikipédia. Disponível em:<https://pt.wikipedia.org/wiki/Teorema_de_Shimura-Taniyama-Weil> Acesso em: 16 de Junho de 2018.
WILES, Biografia de matemáticos. Site: Só Matemática. 1998-2019. Disponível em: <https://www.somatematica.com.br/biograf/andrew.php > Acesso em: 15 de Maio de 2018.
9. ПОИСК ИСТОЧНИКОВ
Site: O Baricentro da Mente. Título: A conjectura de Beal casos particulares. URL: <https://www.obaricentrodamente.com/2014/11/a-conjectura-de-beal-casos-particulares.html> Acesso em: 05 de Maio de 2018.
Site: O Baricentro da Mente. Título: Método de resolução das equações de Sebá. URL: <https://www.obaricentrodamente.com/2012/04/metodo-de-resolucao-das-equacoes-de.html> Acesso em: 05 de Maio de 2018.
Site: Folha de São Paulo. Título: Livro narra solução de teorema que confundiu teóricos por 358 anos. URL: <https://www1.folha.uol.com.br/fsp/ciencia/fe25109801.htm> Acesso em: 10 de Maio de 2018.
Site: Wikipedia. Título: Conjectura de Beal. URL:
<https://pt.wikipedia.org/wiki/Conjectura_de_Beal> Acesso em: 24 de Maio de 2018.
Site: ICM. Título: Detalhes do Autor “Sebastião Vieira do nascimento ( Sebá )”. URL:
<https://www.lcm.com.br/site/livros/detalhesAutor?id=A01644> Acesso em: 27 de Setembro de 2019.
Site: Morfismo. Título: Conjectura de Beal. URL:
<https://morfismo.wordpress.com/2013/11/25/conjectura-de-beal/> Acesso em: 28 de Julho de 2018.
Site: DocSity. Título: Fermat, Notas de estudos de Física. URL:
<https://www.docsity.com/pt/fermat-6-1/4705276/> Acesso em: 01 de Setembro de 2019.
Site: Wikipedia. Título: Conjectura de Fermat-Catalan. URL:
<https://pt.wikipedia.org/wiki/Conjectura_de_Fermat-Catalan> Acesso em: 23 de Setembro de 2019.
[1] Выпускной в математике.
Представлено: август 2019 года.
Утверждено: ноябрь 2019 года.