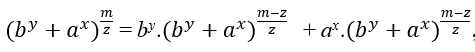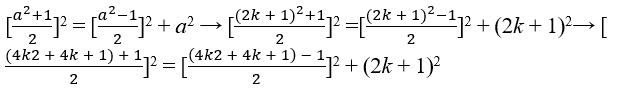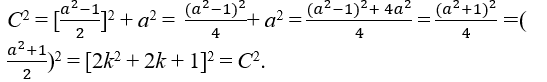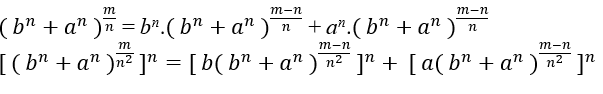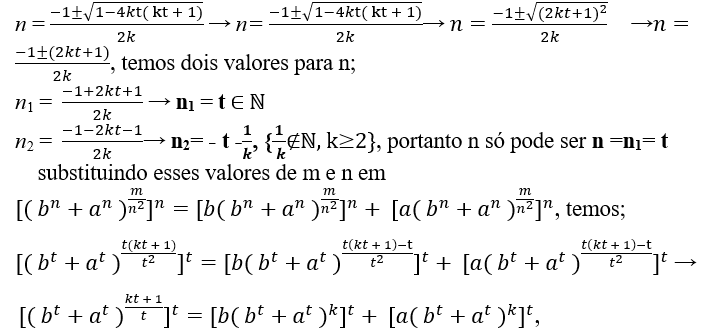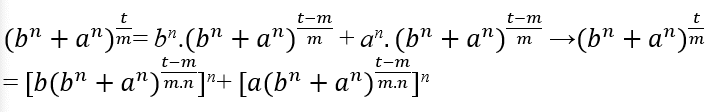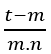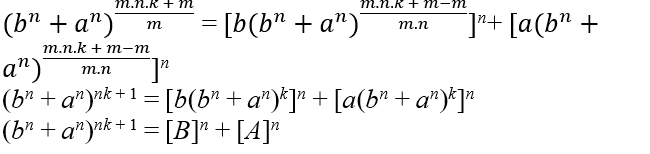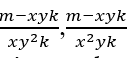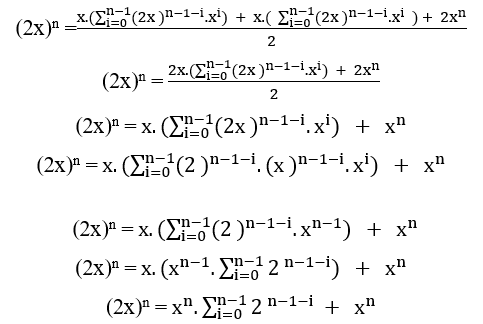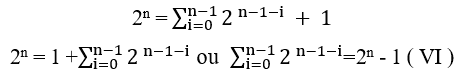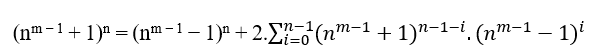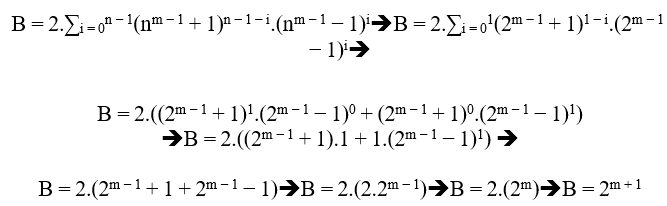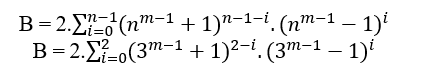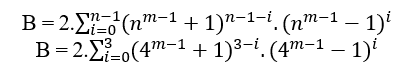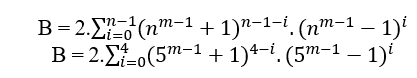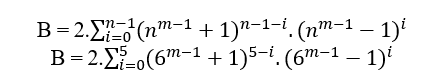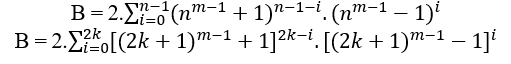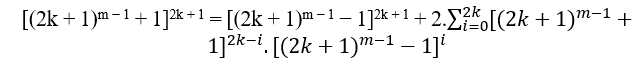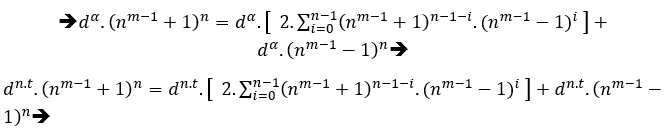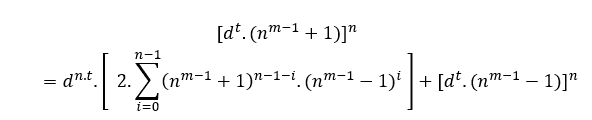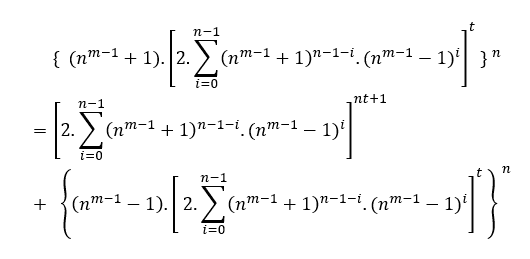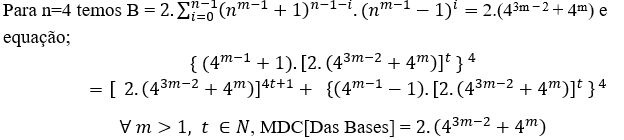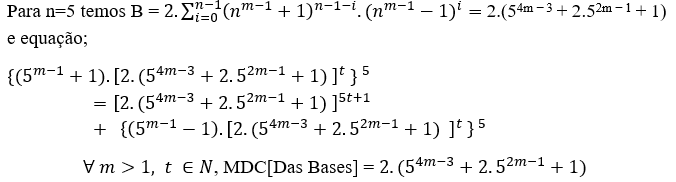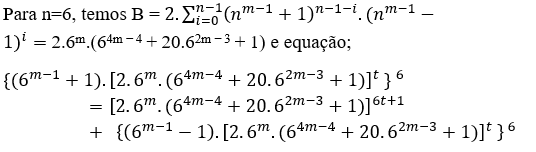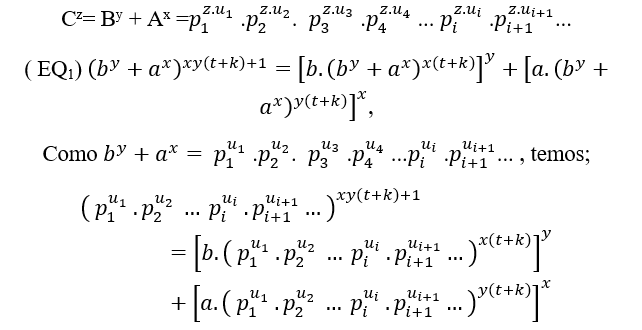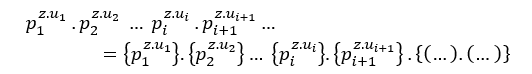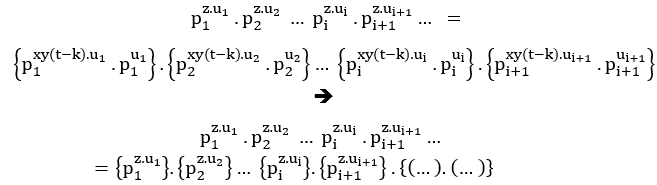ORIGINALER ARTIKEL
SOUSA, Francisco Rafael Macena de [1]
SOUSA, Francisco Rafael Macena de. Demonstration der Beal-Vermutung. Revista Científica Multidisciplinar Núcleo do Conhecimento. 04-Jahr, Ed. 11, Vol. 05, S. 132-173. November 2019. ISSN: 2448-0959, Zugriffsverbindung: https://www.nucleodoconhecimento.com.br/mathematischen-olympiaden/demonstration-der-beal
STATEMENT DER KONJEKTURE
Wenn ax + by = cz , wobei a, b, c, x, y und z positive ganze Zahlen und x, y, z ≥ 3 sind, dann haben a, b und c einen gemeinsamen Primfaktor, was bedeutet, dass a, b und c durch dieselbe Primzahl teilbar sind. Oder die Gleichung ax + by = cz hat keine Lösung für positive ganze Zahlen mit x, y, z ≥ 3 und mdc (a, b, c) = 1.
ZUSAMMENFASSUNG
Dieser Artikel enthält Demonstrationen mit Prinzipien der Algebra und Zahlentheorie, in Bezug auf die Vermutung wurde von Andrew Beal ein Banker und Enthusiast der Zahlentheorie angekündigt schlug eine Herausforderung für diejenigen, die beweisen oder präsentieren Gegenbeispiel zu einem solchen Problem, dass verallgemeinert fermat es Last Theorem, cn = bn + an, mit n ≥ 3, dies wurde von der englischen Mathematiker Andrew Wiles als Grundlage einer Vermutung von Mathematiker Yutaka Taniyama und Goro Shimu demonstriert , diese Demonstration von Wiles nur wenige Mathematiker werden durch das hohe Niveau oder Komplexität zu verstehen, wird auch verwendet werden, die Sebé Theorem, “Sebastio Vieira do Nascimento (Sebé)”, graduierte in Wirtschaftswissenschaften von UFPB, Master in Ingenieurwesen der gleichen, ordentliche Professor der UFCG, seine bewährte Theorem basiert auf, dass cm = bn + an, mit m und n prime unter sich, dies ist mdc , die Vermutung wurde von Beal selbst im Jahr 1993 vorgeschlagen, aber es war nur gut bekannt, auch von der mathematischen Gemeinschaft im Jahr 1997, nachdem R. D. Mauldin veröffentlicht den Artikel a Generalization of Fermat es Last Theorem: The Beal Conjecture and Prize Problem in the Journal Noticesofthe American Mathematical Society.
Schlüsselwörter: Vermutung, Andrew Beal, Fermats letzter Satz.
1. EINFÜHRUNG
Dieser Artikel zielt darauf ab, die Vermutung von Beal zu beweisen, vorgeschlagen von Andrew Beal ein Banker, Unternehmer, Investor, Pokerspieler und Amateur-Mathematiker, der Faszination in zahlentheorie hat, forderte er jeden Mathematiker in der Welt zu beweisen oder geben ein Gegenbeispiel zu seiner Vermutung, die von 1993 bis heute vorgeschlagen wurde, wurde keine Demonstration präsentiert, die die Vermutung einschließlich fermat es Last Theorem verallgemeinert , enthält dieser Artikel mathematisches Wissen, dass jeder, der kam, um die zweite Klasse der High School abgeschlossen zu haben und hat Leichtigkeit in mathematischen Eigenschaften ist möglich, die ersten Demonstrationen zu verstehen, bereits für diejenigen, die eine höhere Ausbildung in genauund darüber hinaus haben, wird leicht von Anfang bis Ende zu verstehen sein, die Vermutung basiert auf positiven ganzen Zahlen oder Lösungen in natürlichen Zahlen mit den größeren Exponenten gleich 3 (drei) und ihre Basen größer oder gleich 1 (ein) , wenn ja, wird nachgewiesen, dass tatsächlich die mdc (c, b , a) = C > 1, wobei dieses C der gemeinsame Primfaktor ist, der a, b und c teilt, mit dem ≤ b oder einem ≥ b, so dass es möglich ist, als Gleichung cz = by + ax, x, y, z ≥ 3, Exponenten, widersprüchlichen Fall als mdc (c, b , a ) = 1 e x, y, z ≥ 3, und x, y, z ≥ 3, dies ist der einzige Wert, der c, b, a ist 1 (a) teilt, mit anderen Worten a,b und c sind Primierungen untereinander.
Um zur Demonstration zu gelangen, war es notwendig, neue Theoreme zu erstellen, aber damit der Satz tatsächlich gültig ist, sowie die Vermutung muss im Laufe der Theoreme aus Prinzipien und Eigenschaften in der Zahlentheorie erstellt werden, die größte Herausforderung in diesem Artikel, wie jeder andere, der Primzahlen beinhaltet jene Zahlen, die nur zwei Teiler in den natürlichen haben, die 1 (eins) und sich selbst (Primzahl) , weil es immer noch etwas ist, dass die Theorie der Zahlen noch nicht in der Lage war, einen schnelleren Weg zu finden, um riesige Zahlen zu faktorisieren, aber in der Zahlentheorie haben wir als Hypothese und auch bewiesen, dass jedes X eine zusammengesetzte Zahl schreiben kann – es X als Einprodukt verschiedener Kräfte gleicher oder unterschiedlicher Primzahlen, einschließlich, wenn es Exponenten 0 (Null) oder 1 (eins) hat. Die Idee dieser Vermutung ist einfach, die Begegnung von Primus zu erleichtern.
2. KURZE GESCHICHTE ZU CONJECTURA
2.1 FERMAT UND SEIN SATZ
Es beginnt mit Pierre Fermat, der im 18. Jahrhundert Frankreich lebte, ein Beamter in der französischen Stadt Toulouse, Mathematik für ihn war sein Lieblingszeitvertreib, die interessante Sache ist, dass Fermat hatte größeren Ruhm aufgrund seiner Bräuche der Präsentation zu anderen Mathematiker Probleme, die die größten Köpfe der Zeit herausgefordert, wo sie oft seine Zeitgenossen ratlos in einem Versuch, sie zu lösen verlassen. Fermat hatte die Idee, einen Satz ähnlich dem berühmten Pythagoras-Theorem zu schaffen, der heute in diesem Jahrhundert bekannt ist, aber keine Lösungen in der Natur hatte, dieser Satz ging über seine Zeit hinaus und erlangte Ruhm im Laufe des Jahrhunderts, weil er keine Lösung oder ein Gegenbeispiel fand, weil dieser seinen Namen gewann und weil er seine letzte Herausforderung hatte als sein Name der letzte Theorem von Fermat , die Gleichung seines Ruhms ist cn = bn + an, wo a, b, c und n ∈ N, mit n ≥ 3, nach ihm hatte die Demonstration, starb, ohne dass jemand wusste, was seine angebliche Antwort war, weil dies als sein letzter Satz bekannt wurde. Das Verdienst der Entdeckung dieses Satzes verdankt e.B. seinem Erstgeborenen, er sah mehrere Notizen von Fermat in einem bestimmten Buch der Aritmetik, die dazugehörten, denn sein Vater hatte die Angewohnheit, Entwürfe oder Anmerkungen in Büchern zu machen. Nach dem Fund des Sohnes wurden die Notizen oder Entdeckungen in einem Buch Arithmetica de Diofanto veröffentlicht, das Beobachtungen des Vaters enthielt, 1670 enthielt das Buch 48 Beobachtungen, aber auf dem Weg gaben Generationen von Mathematikern und Physikern Lösungen für ihre Herausforderungen, hatten jedoch eine, die die meisten für die letzte hielten, weil dies einen so herausfordernden Namen hatte. In seinem Buch enthielt er folgende Aussage: “Ich habe eine wunderbare Demonstration dieses Satzes entdeckt, die jedoch nicht in den Rand dieses Buches passt” (FERMAT. 1607 – 1665)2.
2.2 YUTAKA TANIYAMA, GORO SHIMURA UND ANDREW WILES
1954 wurden Yutaka Taniyama und Goro Shimura, junge japanische Mathematiker, Freunde, weil sie sich für dasselbe Buch, denselben Artikel und die gleichen Berechnungen interessierten, diese Taniyama-Shimura-Vermutung ermöglichte es Wiles, den Traum seines Jungen zu verwirklichen, indem er eine intellektuelle Anstrengung und Entschlossenheit einsetzte, die einem Menschen schwer zu glauben war. Die Vermutung, die die beiden präsentierten, diente als Weg zu ihrer endgültigen Lösung des Problems, aber Mathematiker Yutaka Taniyama nahm sich 1958 das Leben, so dass er die Entwicklung der Lösung weiter verzögerte, auf die Entwicklung der Vermutung, ob es nicht absichtlich gemacht wurde, Fermats letztes Theorem zu lösen, aber es war, was wirklich später geschah Wiles erkannte, dass eine solche Grundlage, die den Beweis half – definitiv dort dieser Theorem , denn wer könnte sich vorstellen, dass die Arbeit von zwei Studenten des späten zwanzigsten Jahrhunderts könnte in etwas verwendet werden, die eines der größten Geheimnisse in der Geschichte der Mathematik gelöst. Aber es war Andrew Wiles, der am Ende Fermats letzten Satz demonstrierte, Wiles ist ein Princeton-Universitätsprofessor, der sein Interesse an dem Problem begann, als ein Kind in seiner Heimatstadt eine öffentliche Bibliothek hatte, aber erst 1986 begann er wirklich, seine Arbeit zur Lösung des Satzes seiner Träume zu beginnen, so Wiles, dass seine Forschung unter völliger Geheimhaltung durchgeführt wurde. , denn in seinem Wesen wusste er, dass er die Lösung finden würde, aber es war nicht an der Zeit, so etwas gegenüber der akademischen Gemeinschaft zu bestätigen, Intuition ist alles für eine leidenschaftliche Zahlentheorie, aber die Intuition zeigt den Weg, aber zu beweisen, ob es richtig oder falsch ist, braucht Zeit und Hingabe, vielleicht aus Angst vor dem Druck, der angesichts eines so berühmten Problems leiden würde und schwierige Lösung war zu riskant, um eine solche mögliche Ausgangslösung zu bestätigen , bei der Analyse der Vermutung der beiden Japaner, Andrew Wiles bemerkte, dass ein solcher Satz könnte ein Weg zu lösen sein, aber die Vermutung musste zuerst bewiesen werden, bevor zu zeigen, was er so viel gesucht hatte, seit er ein Kind war, in seinem Kopf war es so klar, dass Wiles von der Lösung des Satzes alle auf den Beweis der Vermutung der beiden Studenten träumen konnte , aber Wiles hat nicht Fermats letztes Theorem gezeigt, sondern die Taniyama-Shimura-Vermutung, die Beweise implizieren wird – dort.
Schließlich, am 23. Juni 1993, auf einer Konferenz am Sir Isaac Newton Institute for Mathematical Sciences in Cambridge, Andrew Wiles, 356 Jahre nach der Präsentation des Satzes, machte seine Ankündigung seiner Demonstration, aber enthielt einen kleinen Fehler in seiner Lösung, Wiles zieht sich für ein Jahr zurück, um einen solchen Fehler zu korrigieren und seine neue Neufassung Demonstration präsentieren , nach der Korrektur und Überprüfung des gleichen Fehlers entdeckt, dauerte es ein paar Monate, um seine Lösung zu bewerten, seine Demonstration hatte 200 Seiten, und nach einer langen Zeit der Angst, seine Entdeckung oder Demonstration wurde schließlich akzeptiert, aber so komplex, dass nur wenige Menschen weltweit in der Lage waren, es zu verstehen, und Wiles (nach Erhalt eines Preises im Wert von 50.000,00 Pfund von der Wolfskehl Stiftung) , tritt er als der Mathematiker, der die faszinierendsten und herausforderndsten Satz in der Geschichte der Mathematik demonstriert, und damit schließt eines der größten Probleme nicht begegnet oder demonstriert, die große Mathematiker vor und während herausgefordert, so Fermat es Letzten Satz hat keine Lösungen mit positiven ganzheitlichen Zahlen mit n ≥ 33.
2.3 ANDREW BEAL UND SEINE KONJEKTURE, DIE SEINEN NAMEN ERHALTEN HAT
Andrew Beal (* 29. November 1952), Bankier, Unternehmer, Investor, Pokerspieler und Amateurmathematiker und Enthusiast eines der besten Bereiche, das ist Zahlentheorie. Beal ist auch für Beals Vermutung bekannt, während er Verallgemeinerungen von Fermats letztem Satz untersucht, von 1993 bis 1997 bot Beal einen Geldpreis für einen von Experten begutachteten Beweis für diese Vermutung oder ein Gegenbeispiel an, da es 1993 einen Wert von 5.000 US-Dollar hatte, den Wert des Preises mehrmals erhöhte und derzeit 1.000.000,00 US-Dollar für die Person beträgt, die dies beweist oder ein widersprüchliches Beispiel für diejenigen darstellt, die Fermats letzter Satz. Nach den eigenen Aussagen des Bankiers, in einer American Mathmatical Society Presseanzeige, ist das Ziel der Millionär Wert ist es, “junge Köpfe zu inspirieren, über das Thema zu reflektieren und machen sie mehr und mehr interesse an der Studie der Mathematik” 4.
3. ENTWICKLUNG ZUR KONJEKTURE VON BEAL
Um dies zu demonstrieren, werden drei neue Theoreme (T.M, S.T.M e T.G.M), da Sebés Theorem ein besonderer Fall von Beals Vermutung ist, wird dies auch später gezeigt werden.
3.1 MACENA ODER T.M
Unter Zwei Gleichungen Eq1:cz = by + ax e Eq2:cm = cm mit positiven Gesamtlösungen und hat als gemeinsame Basis c ≠ 0, mit c, b, a, z, y, x und m ∈ N, m > z ist es möglich, eine neue Gleichung Eq3 zu bestimmen, die sowohl das Format von Eq1 als auch Eq2 hat. Das bedeutet, wenn Eq3 Eq1 nicht erfüllt, hat es nicht ganze positive Lösungen. Beispie1 ist die Gleichung Eq1 → c2 = b2 + a2 e Eq2 → cm = cm com c ≠ 0 e m ∈ ℕ, wir wissen, dass Eq1 ganze Lösungen hat, weil es pythagoheran eigener Satz ist, überprüfen Sie einfach mit den pythagorischen Triples, so wie Eq2 auch ganze Lösungen hat, wird dies vor sich gehen. Das heißt, dann ist es möglich, eine Eq3-Gleichung zu bestimmen, die sowohl das Eq1– als auch das Eq2-Format hat. Verwenden Sie als c ≠ 0 die folgenden Schritte in Eq1 → c2 = b2 + a2 → 1 = c− 2.(b2 + a2)(I) Eq1 → c2 = b2 + a2 → c=(b2+a2)1/2(II)
Eq2, weil wir schreiben können Eq2 diesen Weg cm = cm.1 beim Ersetzen von (I) haben wir cm = cm.c−2.(b2 + a2) → cm = cm−2.(b2 + a2) → cm = b2.cm−2 + a2.cm−2(III) Einsetzen von (II) in (III);
= b2.
+ a2.
→
=
.
Sei m – 2 ein Vielfaches von 4, dh m – 2 = 4.n, mit n ∈ ℕ, dann haben wir m = 4.n + 2, wenn wir ersetzen; (b2 + a2)2.n + 1 = [b(b2 + a2)n]2 +[a(b2+a2)n]2
(b2 + a2)2n + 1 = [B]2 + [A]2 Jetzt müssen wir nur noch prüfen, ob (b2 + a2)2n + 1 es ist wie C2,durch die pythagoreischen Dreiergruppen ist diese Gleichheit bald erfüllt (b2 + a2)2.n + 1 = (c2)2.n + 1 = c2.(2.n + 1) = [c2.n + 1]2 = [C]2
Deshalb C2 = [B]2 + [A]2 das gleiche Format Eq1 zu schließen muss Eigentum von haben
Eq2C2 = [B]2 + [A]2 → (b2 + a2)2n + 1 = [b(b2 + a2)n]2 + [a(b2 + a2)n]2 → (c2)2n + 1 = [b(c2)n]2 + [a(c2)n]2 →
c4n + 2 = [b.c2n]2 + [a.c2n]2 → c4n + 2 = b2c4n + a2c4n → c4n + 2 = c4n.(b2 + a2) → c4n+2=c4n.(c2) → c4n+2=c4n+2 →cm=cm . Dann wurde verifiziert, dass es möglich ist, eine Gleichung Eq3 zu finden, die beide Eigenschaften hat, so dass Gleichung Eq3 für diese beiden Gleichungen ist; → (b2+a2)2n+1=[b(b2+a2)n]2+[a(b2+a2)n]2
3.1.1 TASTING T.M
Sein Eq1: cz = by + ax e Eq2: cm = cm, com m > z, a, b, c, x, y, z , m ∈ ℕ e c ≠ 0.
Beweisen Eq2:
In der Tat 1 = 1, Multiplikation beider Seiten mit c ∈ N* haben wir 1.c = 1.c, wenn wir wieder mit dem gleichen c multiplizieren, haben wir c2 = c2, logisch multiplizieren dimiert mit m Mal, die wir haben werden;
cm = c{(11 + 12 + 13 + … + 1m − 1 + 1m) = m} = cm. Daher zu Eq2 angezeigt.
Als c ≠ 0 können wir folgende Geräte verwenden:
cz = by + ax → 1 = c − z.(by + ax)( I ) neutrales Element der Multiplikation
cz = by + ax → c =(by+ax)1/z( II )
Das Eq2 kann wie folgt geschrieben werden cm = cm.1 , Wenn (I) in dieser Gleichung ersetzt wird, erhält man:
cm = cm.1 → cm = cm.c − z.(by + ax) → cm = cm − z.(by + ax) → cm = by.cm − z + ax.cm − z
Das Ersetzen von (II) führt zu;
, wobei die y- und x-Exponenten als Beweis dienen
Für was
∈ ℕ die MMC (zy, zx) = zxy, also muss m – z ein Vielfaches von zxy sein, also m – z = zxy.k, mit k ∈ ℕ. Das Isolieren von m und das Ersetzen in der Gleichung ergeben:
(by + ax)xyk + 1 = [b.(by + ax)xk]y + [a.(by + ax)yk]x
Das ist also die neue Gleichung;
Eq3:(by + ax)xyk + 1 = [b.(by + ax)xk]y + [a.(by + ax)yk]x → Cxyk + 1 = By + Ax
Nach dem Prinzip des Vergleichs oder Formats Cxyk + 1 = By + Ax es ist äquivalent zu cz = by + ax, es ist genau die Struktur von Beals Vermutung.
Bald befriedigte es die Eq1 Mangel zeigt, dass es auch das Format von hat Eq2: cm = cm
(by + ax)xyk + 1 = [b.(by + ax)xk]y + [a.(by + ax)yk]x, mögen cz = by + ax wir haben;
(cz)xyk + 1 = [b.(cz)xk]y + [a.(cz)yk]x → cz.(xyk + 1) = [b.cz.xk]y + [a.cz.yk]x → czxyk + z = by.czxyk + ax.czxyk → mögen
m = zxyk + z
cm = by.czxyk + ax.czxyk → cm = czxyk.(by + ax) → cm = czxyk.(cz) → cm = czxyk + z = cm.
Daher bewährt, da Eq3 zufrieden Eq1 und Eq2.
Mögen:
CZ = By + Ax
C = by + ax, B = b.(by + ax)xk, A = a.(by + ax)yk e Z = xyk + 1
MDC(C, B, A) = MDC(by + ax, b.(by + ax)xk, a.(by + ax)yk) = by + ax = cz = C.
MDC(Z, y, x) = MDC(xyk + 1, y, x) = 1
OBS:
Wenn k Null ist, haben wir;
(by + ax)xyk + 1 = [b.(by + ax)xk]y + [a.(by + ax)yk]x → (by + ax)1 = [b.(by + ax)0]y + [a.(by + ax)0]x, mögen by + ax = cz ≠ 0 deshalb (by + ax)0 = 1
(by + ax)1 = [b.1]y + [a.1]x → by + ax = by + ax
Wenn m gleich z wäre, wäre die Gleichung Eq1 und Eq2 swäre gleich, wäre wiederum gleich Eq3
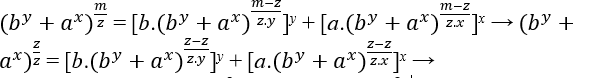
(by + ax)1 = [b.(by+ax)0]y + [a.(by+ax)0]x → by + ax = [b.1]y + [a.1]x.
Wenn Fall x=y=k=1 haben wir ein perfektes Quadrat
(durch + ax)xy[b.(by + ax)xk]k + [a.(by + ax)yk]1 = y + x → (b1 + a1)1[b.(b1 + a1)1] + 1[a.(b1 + a1)1] = 1 + 1 →
(b + [b.(b + a)]a)2[a.(b + a)] = + → (b + a)2 = b.(b + a) + a.(b + a) = b2 + ba + ab + a2 + b2 + 2ab + a2 = (b + a)2
Beispiel2 Überprüfung mit Zahlen die Gleichung Eq3, be b=3, a=2 und n=1 haben wir;
(b2 + a2)2n +[b(b2 + a2)n] 1 =[a(b2 + a2)n] 2 + 2 → (32 + 22)2.1 + [3(32 + 22)1]1 = [2(32 + 22)1]2 + 2 →
(9 + 4)3[3(9 + 4)] = 2[2(9 + 4)] + 2 → 133[3.13] = 2[2.13] + 2 → 133 = 392 + 262 → 2187 = 1521 + 676 → 2187 = 2187
3.2 JEDEN FALL PER T.M
Um die Gültigkeit dieses Satzes zu zeigen, ist es auch notwendig, die Möglichkeiten oder möglichen Werte von z, y, x und m ∈ N zu zeigen, wenn er keinem Theorem widerspricht, der bereits von Mathematikern wie (Pythagoras theorem ” von mehreren Mathematikern, Sebs Theorem ” von Sebastian ” und fermat es Last Theorem ” von Andrew Wiles ” und so on) gezeigt wurde.M ist gültig und wird ein Werkzeug sein, um die Beal-Vermutung zu beweisen.
3.2.1 PYTHAGORAS THEME
Dies ist, wenn z=y=x=2
Angenommen, Eq1 → c2 = b2 + a2, hat ganze Lösungen, für c, a, b, m ∈ N, c ≠ 0 und Eq2 → cm ist es möglich, einen Eq3 zu finden, der die beiden vorherigen Gleichungen erfüllt, wenn dies bald auftritt Eq1 → c=√(b2+a2 )∈ ℕ.
Diese Demonstration wurde bereits in Beispiel1 gezeigt, es ist nur notwendig zu zeigen, dass die Bedingung c=√(b2+a2) ∈ ℕ tatsächlich mit dem pythagorischen Triple erfüllt ist.
Hypothese ist c2 = b2 + a2 These C2 = C2.
Mit Hypothese c2 = b2 + a2 Addieren auf beiden Seiten durch 2b + 1 ∈ N, wird ein perfektes Quadrat auf einer Seite erhalten, c2 + 2b + 1 = b2 + 2b + 1 + a2 → c2 + 2b + 1 = (b + 1)2 + a2, wir wissen, dass in einem rechten Dreieck die Hypotenuse größer ist als jede der Kateten, insbesondere c > b > a, dann gibt es die Möglichkeit von c = + b 1 , erkennen Sie, dass dies eine geeignete Lösung ist, um Gleichung c2 + 2b + 1 = (b + 1)2 + a2 → c2 + 2b + 1 = c2 + a2 → 2b + 1 = a2 zu lösen, wenn b isoliert wird, erhalten wird und als
erkenne
, dass sowohl b als auch c eine ganze Zahl ausreichen (a) ungerade sein, weil ungerade Zeiten ungerade zeiten bleibt, daher a = 2k + 1 Bedingung, um mit ungeraden k ∈ ℕ, so haben wir;
→ 2 [2k2 + 2k + 1]= 2 [2k2 + 2k]+ (2k + 1)2, also haben wir C = 2k2 + 2k + 1, B = 2k2 + 2k und A = 2k + 1 ∈ N, sind die pythagorean Triples (2k2 + 2k + 1, 2k2 + 2k, 2k + 1), Überprüfung der These
3.2.2 FÜR DEN FALL VON FERMAT’S LAST THEOREM
Dies ist, wenn z=y=x=n
Angenommen, Eq1 → cn = bn + an, hat eine Lösung für n≥3, mit c, a, b, m ∈ N, c ≠ 0 und Eq2 → cm = cm ist es möglich, einen Eq3 zu finden, der die beiden vorherigen Gleichungen erfüllt, wenn dies bald Auftritt Eq1 → c = n√bn+an ∈ ℕ.
Als c ≠ 0 können wir Gleichung Eq1 wie folgt schreiben;
Eq1 → cn = bn + an → 1 = c − n.(bn + an)(I) neutrales Element der Multiplikation
Eq1 → cn = bn + an → c = ( bn+an )1/n(II)
Überprüfen Sie, ob Gleichung Eq2 wie folgt geschrieben werden kann, ohne ihre Werte zu ändern cm = cm.1, beim Ersetzen von (I) in Eq2, wir haben;
cm = cm.c − n.(bn + an) → cm = cm − n.(bn + an) → cm = bn.cm − n + an.cm − n(III)
Ersetzt (II) in (III)
Beachten Sie, dass das Format das gleiche wie in Gleichung Eq1 ist. Überprüfen Sie einfach, ob m – n ein Vielfaches von ist n2, Wenn ja, dann können wir schreiben m − n = n2.k mit k ∈ ℕ, isolieren m haben wir m = n2.k + n Dies ist eine Gleichung von 2. klasse;
m = n2.k + n ⇒ kn2 + n − m = 0, damit können wir Werte für m und n von Bhaskara finden.
, so dass n notwendigerweise natürlich ist
-1±√1-4km muss ein Vielfaches von sein 2k, damit;
-1±√1-4km = 2k.t, mit t ∈ ℕ
-1±√1-4km = 2k.t → ±√1-4km= 2k.t + 1 Erhöhen Sie beide auf das Quartal, das wir haben 1 + 4km = (2k.t + 1)2 → 4km = (2k.t + 1)2 − 1 erkenne, dass es dann die Differenz zweier Quadrate ist;
4km = (2k.t + 1 − 1).(2k.t + 1 + 1) → 4km = (2k.t).(2k.t + 2) → 4km = 4.(k.t).(k.t + 1) → km = k.t.(k.t + 1) →
m = t( kt + 1), dann Ersetzen dieses Wertes von m in n = -1±√1-4km wir haben;
demnächst (bt + at)kt + 1 = Bt + At, realisieren kt + 1 ist kein Vielfaches von t, weil mdc ( kt + 1 , t ) = 1, das ist “kt + 1” und “t” sind Cousins dazwischen, und von Andrew Wiles ist es unmöglich bt + at = ct (Fermats letzter Satz), für t > 2.
Da kt + 1 ≠ t.α, mit 2 < α ∈ ℕ, daher Eq1 nicht erfüllt, hat Eq1 keine Lösungen, wie es in T heißt.M.
Jedoch C =kt+1√Bt+At ∈ ℕ, EQSebá, Sebas Theorem zur Überprüfung der Gleichheit;
C = kt+1√Bt+A → C = kt+1√[b (bt+at )k]t+ [a( bt+at )k]t →C = kt+1√bt( bt+at )kt + at ( bt+at )kt → kt+1√( bt+at )kt.( bt+at ) → C = kt+1√( bt+at )kt+1 → C = bt + at.
3.2.3 SEB-THEME
cm = bn+ an, mit mdc(m,n)=1
Demonstration von Sebastiéo Vieira do Nascimento (Seba)
Satz: Die Gleichung Cm = An + Bn lässt natürliche Lösungen für m und n Primungen einander zu.
Beweis:
Sei die Gleichung;
( 1 )cm = bn + an, sein a, b, c, n und m positive Ganze Zahlen. Multiplizieren Sie beide Glieder der Gleichung ( 1 ) por (bn + an)m
du kriegst:
( 2 )cm*(bn + an)m = (bn + an)*(bn + an)m, Ersetzen des Wertes von da (1) im (2), du kriegst:
(bn + an)m + 1 = (bn + an)*(bn + an)m
oder
( 3 )(bn + an)m + 1 = bn(bn + an)m + an(bn + an)m
Wenn wir Werte für a und b so wählen, dass a ≤ b oder a ≥ b ist, und in (3) ersetzen, werden positive ganzzahlige Werte für A, B und C erhalten.
Beispiel: Teilen Sie ein Quadrat auf verschiedene Weise in zwei Würfel auf. Die Gleichung sei:
( 4 )C2 = B3 + A3, Betrachten Sie die Gleichung:
c2 = b3 + a3, Multiplizieren Sie beide Elemente der obigen Gleichung mit (b3 + a3)m, wo m und n ∈ ℕ, wir haben:
c2(b3 + a3)m = (b3 + a3)(b3 + a3)m
( 5 )(b3 + a3)m + 1 = b3(b3 + a3)m + a3(b3 + a3)m
Wenn wir Gleichung (5) mit Gleichung (4) vergleichen, müssen wir m in Potenzen von 3 und m + 1 in Potenzen von 2 zerlegen. Dies ist nur möglich, wenn m und m + 1 jeweils Vielfache von 3 und 2 sind. Demnächst:
m = 6k – 3 e m + 1 = 6k – 2, Somit lautet Gleichung (5):
(b3 + a3)6k − 2 = b3(b3 + a3)6k − 3 + a3(b3 + a3)6k − 3
[(b3 + a3)3k − 1]2 = [b(b3 + a3)2k − 1]3 + [a(b3 + a3)2k − 1]3, Daher werden die Lösungen für die gegebene Gleichung erhalten durch:
C = (b3 + a3)3k − 1, B = b(b3 + a3)2k − 1 und A = a(b3 + a3)2k − 1, wo k ∈ N*, a und b ∈ ℕ.
Beweisen mit dem T.M das ist wenn z=m und y=x=n
Nehme an, dass Eq1 → cm = bn + an, hat Lösung für m und n Primzahl zueinander dies ist
mdc(m,n)=1, mit c, a, b, t, m und n ∈ ℕ, c ≠ 0 und Eq2 → ct = ct Sie können einen finden
Eq3 das erfüllt die beiden vorhergehenden Gleichungen, wenn dies bald auftritt Eq1 → c =m√bn+an ∈ ℕ.
Als c ≠ 0 können wir die folgenden Methoden verwenden;
cm = bn + an → 1 = c − m*(bn + an), (I) neutrales Element der Multiplikation
cm = bn + an → c = (bn+an)1/m, (II)
Wir können schreiben Eq2 diesen weg ct = ct.1, ersetzen ( I ) im Eq2 wir haben;
ct = ct.c − m.(bn + an) → ct = ct − m.(bn + an) → ct = bnct − m + anct − m, beim Ersetzen von (II) haben wir;
Para que
sei natürlich t – m muss ein Vielfaches von n und m sein, also t – m = m.n.k, mit k ∈ ℕ, Wenn wir t isolieren, haben wir t = m.n.k + m, wenn wir es in der Gleichung ersetzen, erhalten wir es;
Es bleibt zu zeigen, dass nk + 1 ist ein Vielfaches von m, wenn ja, hat es die Form nk + 1 = m.α, mit α ∈ ℕ oder bn + an = Cm
Wenn einer dieser beiden Fälle auftritt, haben wir Cm = Bn + An dann wird gezeigt, dass Gleichung Eq1 eine Lösung hat.
Wir müssen t – m = m.n.k teilen beide durch m, es wird erha
-1 = n.k Hinzufügen von 1 auf beiden Seiten
= n.k + 1, da t ist vielfache m, so
∈ N, mit diesem können wir die folgenden Schritte verwenden;
Als
= n.k + 1 und nk + 1 = m.α ist dies
= m.α → α =
, wenn α natürlich ist
dann sollte es natürlich sein, wenn nur, wenn t auch ein Vielfaches von m2 ist, aber t nicht vielfachem m2 ist, da es von der Form t = m.n.k + m ist, auch wenn k gleich m wäre, wäre es von der Form t = n.m2 + m = m.(nk + 1) ≠ m2.(nk + 1), also ist NK+1 nicht vielfaches von T, also mdc (NK+1,T)=1, sind Primierungen zwischen einander.
Es bleibt nur zu prüfen, bn + an =Cm.
Sabemos que nk + 1 não é múltiplo de n, pois o mdc(nk + 1, n) = 1 e como a igualdade da equação (bn + an)nk + 1 = [b(bn + an)k]n + [a(bn + an)k]n ist bereits früher in zufrieden EQSebá, nach dem Format oder Vergleichsprinzip müssen wir:
Cnk + 1 = Bn + An equivale a cm = bn + an, demnächst;
(bn + an)nk + 1 = Bn + An → (cm)nk + 1 = cm.(nk + 1) = [cnk + 1]m = Cm = Bn + An
Wenn Gleichung Eq1 erfüllt ist, muss noch Gleichung Eq2 → ct = ct, gezeigt werden. Beachten Sie Folgendes:
(bn + an)nk + 1 = Bn + An → (bn + an)nk + 1 = [b(bn + an)k]n + [a(bn + an)k]n →
(cm)nk + 1 = [b(cm)k]n + [a(cm)k]n → cm.(nk + 1) = [b(cm)k]n + [a(cm)k]n
como t= m.( nk + 1 );
ct = bn(cm)nk + an(cm)nk → ct = (cm)nk(bn + an) → ct = (cm)nk(cm) → ct = (cm)nk + 1 → ct = cm.(nk + 1) = ct, Dies ist bewiesen, weil Gleichung Eq3 Eigenschaften sowohl von Gleichung Eq1 als auch von Gleichung Eq2. hat.
3.2.4 IN CASE THEY ARE MULTIPLE BY T.M
Fall (1): für mehrere y x ist dies y = xk mit k ∈ N
Seien Sie Eq1: cz = bxk + ax e Eq2 :cm = cm, mit m > z und c ≠ 0 finden Sie eine neue Gleichung Eq3, die Eigenschaften von Eq1 und Eq2 hat, wenn Eq3 keine Eigenschaft des Eq1 demnächst Eq1 besitzt, keine gesamtlösungen hat.
Als c ≠ 0 haben wir;
cz = bxk + ax → 1 = c − z.(bxk + ax), (I) neutrales Element der Multiplikation
cz = bxk + ax → c = (bxk+ax)1/z, (II)
Wir können Gleichung Eq2 wie folgt schreiben: ( I );
cm = cm.c − z.(bxk + ax) → cm = cm − z.(bxk + ax) → cm = bxk.cm − z + ax.cm − z, beim Ersetzen von (II) haben wir;
Setzen Sie die xk und x in Beweise, die wir haben;
Beachten Sie, dass mmc (zxk, zx) und damit
∈ ℕ, notwendigerweise muss z – m ein Vielfaches von zxk sein, das ist m – z = zxk.α mit α ∈ ℕ, womit wir haben;
(bxk + ax)xk.α + 1 = [b.(bxk + ax)α]xk + [a.(bxk + ax)k.α]x, Beachten Sie, dass diese Gleichung wie folgt geschrieben werden kann;
(bxk + ax)xk.α + 1 = [bk.(bxk + ax)k.α]x + [a.(bxk + ax)k.α]x, das ist Sebas Theorem, das schon bald bewiesen wurde Cxk.α + 1 = Bxk + Ax gleichwertig Cm = Bx + Ax weil MDC(xk.α + 1 , xk )=MDC(xk.α + 1 , x)= MDC(m,x)=1, daher Cousin zueinander, gleichwertig
Eq1.
Überprüfung Eq2 was ist cm = cm
(bxk + ax)xk.α + 1 = [b.(bxk + ax)α]xk + [a.(bxk + ax)k.α]x, als bxk + ax = cz wir haben; (cz)xk.α + 1 = [b.(cz)α]xk + [a.(cz)k.α]x → czxk.α + z = [b.czα]xk + [a.czk.α]x als m = zxk.α + z
cm = bxk.cxzkα + ax.cxzk.α → cm = cxzkα(bxk + ax) → cm = cxzkα(cz) → cm = cxzkα + z = cm.
Bald zufrieden Eq1 und Eq2, daher bewiesen.
Fall (2): für x Vielfaches von y das ist x = yk mit k ∈ ℕ
Diese Demonstration ist analog zum Fall (1), wird das ankommen Eq3 es ist;
(by + ayk)yk.α + 1 = [b.(by + ayk)k.α]y + [a.(by + ayk)α]yk →
(by + ayk)yk.α + 1 = [b.(by + ayk)k.α]y + [a.(by + ayk)kα]y → Cyk.α + 1 = By + Ay äquivalent
Cm = By + Ay Äquivalent wiederum Eq1: cz = by + ayk mit k, α ∈ ℕ .
Fall (3): für mehrere z von x ist dies z = xk und MDC(z,x,y)=1, mit k ∈ N
Be Eq1: cxk = by + ax, wir können Eq1 des folgenden Formats Eq1 schreiben: by = cxk − ax, und Eq2 wird auf der Grundlage von b statt c, mit b ≠ 0 und c > a, Logo Eq2: bm = bm, mit m > y, so ist es möglich, Dass Eq3, das sowohl Eq1 als auch Eq2 Eigenschaft hat, wenn es Eq1 nicht erfüllt, dann hat Eq1 keine vollständigen positiven Lösungen.
Als b ≠ 0 wir haben;
by = cxk − ax → 1 = b − y(cxk − ax), (I) neutrales Element der Multiplikation
by = cxk − ax → b = (cxk-ax)1/y, (II)
Eq2 kann wie folgt geschrieben werden bm = bm.1, ersetzt (I) im Eq2 wir haben;
bm = bm.b − y(cxk − ax) → bm = bm − y(cxk − ax) → bm = cxk.bm − y − ax.bm − y, ersetzen (II) wir haben;
, xk und x isolieren, die wir haben;
MMC( xyk , x )= xyk, für was
∈ ℕ, m – y muss ein Vielfaches von sein xyk, das ist m − y = xyk.α, mit α ∈ ℕ, mit diesen daten haben wir;
(cxk − ax)xkα + 1 = [c.(cxk − ax)α]xk − [a.(cxk − ax)k.α]x, Beachten Sie, dass wir wie folgt organisieren können:
(cxk − ax)xkα + 1 = [c.(cxk − ax)α]xk − [a.(cxk − ax)k.α]x → [c.(cxk − ax)α]xk = (cxk − ax)xkα + 1 + [a.(cxk − ax)k.α]x, daher kann z ein Vielfaches von x sein, und sein MDC( z , x , y ) = 1
Als z = xk, wir haben;
[c.(cz − ax)α]z = (cz − ax)zα + 1 + [a.(cz − ax)k.α]x, damit haben wir;
C = c.(cz − ax)α, B = cz − ax e A = a.(c1 − ax)k.α, demnächst Cz = Bzα + 1 + Ax, als z=xk, das ist äquivalent zu Eq1, bleibt zu zeigen, dass es auch ist Eq2: bm = bm.
[c.(cz − ax)α]z = (cz − ax)zα + 1 + [a.(cz − ax)k.α]x, als by = cz − axez = xk, wir haben;
[c.(by)α]xk = (by)xkα + 1 + [a.(by)k.α]x → cxk.(by)xkα = bxykα + y + ax.(by)xk.α, als m = xykα + y, wir haben;
cxk.bxykα = bm + ax.bxyk.α → cxk.bxykα − ax.bxyk.α = bm → bxykα.(cxk − ax) = bm → bxykα.(by) = bm → bxykα + y = bm
→ bm = bm
Also wie Eq3 zufrieden Eq1 und Eq2, demnächst Eq1 hat Lösungen für positive ganze Zahlen.
Fall (4) für multiple z von y ist dies z = yk mit k ∈ N
Diese Demonstration ist analog in Bezug auf Fall (3), sie erreichen das gleiche Format wie Gleichung Eq3, aber mit b anstelle von a, und y anstelle von x;
[c.(cyk − by)α]yk = [b.(cyk − by)k.α]y + (cyk − bx)ykα + 1, mit α ∈ ℕ.
Fall (5): für mehrere z von x und y ist dies z = xyk mit MDC(z, x, y) = MDC(x, y)≥1 und k ∈ N
Seien Sie Eq1: cxyk = by + ax e Eq2: cm = cm, mit c ≠ 0 und k ∈ N, finden Sie eine neue Gleichung Eq3, die Eigenschaften von Eq1 und Eq2 hat, wenn Eq3 keine Eigenschaft des Eq1-Logos hat, hat Eq1 keine gesamtlösungen.
Als c ≠ 0 wir haben;
cxyk = by + ax → 1 = c − xyk*(by + ax), (I) neutrales Element der Multiplikation
Possamos escrever Eq2 da seguinte maneira usando ( I );
cm = cm.c − xyk.(by + ax) → cm = cm − xyk.(by + ax) → cm = by.cm − xyk + ax.cm − xyk , beim Ersetzen von (II) haben wir;
, Setzen von y- und x-Beweisen, die wir haben;
Die MMC(xy2k , x2yk )=x2y2k, für was
∈ ℕ, obligatorisch m – xyk muss ein Vielfaches von sein x2y2k das ist m − xyk = x2y2k.α, mit α ∈ ℕ, bald haben wir;
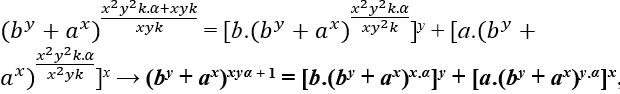Veja que xyα + 1 não é múltiplo de xy, pois MDC(xy.α + 1 , xy ) = 1, demnächst Eq1 nicht hat positive ganzzahlige Lösungen für z Vielfache von x und y.
Denn durch by + ax durch das vorher gezeigte Vergleichsprinzip entspricht cxyk + 1 = by + ax und als z = xyk haben wir cz + 1 = by + ax. Daher ist z +1 nicht vielfaches von x und y, so dass Eq1 keine Lösung in positiven Ganzzahlen hat.
Caso ( 6 ): für z mehrere von x, und y mehrere von x es ist z = xk e y = xt, mit k ≥ t und MDC(z,x,y)=x , e k, t ∈ ℕ
Sein Eq1: cxk = bxt + ax und Eq2: cm = cm, mit c ≠ 0 e k, t ∈ ℕ, Es ist möglich, eine neue Gleichung zu finden Eq3, das hat Eigenschaften von Eq1 und Eq2 fall Eq3 hat kein Eigentum an Eq1 demnächst Eq1 Es gibt keine vollständigen Lösungen.
Als c ≠ 0 wir haben;
cxk = bxt + ax → 1 = c − xk*(bxt + ax), , (I) neutrales Element der Multiplikation
cxk = bxt + ax → c = (bxt + ax)1/xk (II)
Wir können schreiben Eq2 wie folgt mit ( I );
cm = cm.c − xk.(bxt + ax) → cm = cm − xk.(bxt + ax) → cm = bxt.cm − xk + ax.cm − xk, beim ersetzen von (II) wir haben;
, xt und x zu isolieren, die wir haben;
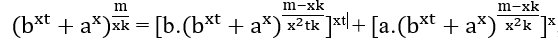, MMC(x2tk,x2k)=x2tk, für haben
∈ ℕ es ist nötig dass m – xk sei ein Vielfaches von x2tk, das ist m − xk = x2tk.α, mit α ∈ ℕ, Ersetzen dieser Werte wird erhalten;
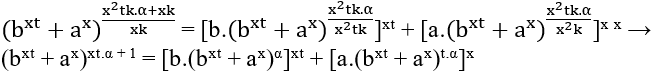Als xt.α + 1 ist kein Vielfaches von x, bleibt zu sehen bxt + ax, realisiere das zunächst Eq1 es ist cxk = bxt + ax → (ck)x = (bt)x + ax Fermats letzter Satz.
Da Eq3 Eq1 nicht satisfie Eq1 satisfie hat, hat Eq1 daher keine positive Gesamtlösung, wenn z ein Vielfaches von x und y Vielfaches von x ist.
Fall ( 7 ): für z mehrere von y, und x mehrere von y é z = yk e x = yt, mit k ≥ t und MDC(z,x,y)=y , und k, t ∈ ℕ
Diese Demonstration ist analog zu Fall (6), da sie in Fermats letzten Satz fällt.
Fall ( 8 ): für z Vielfaches von y und x, x oder y Vielfaches voneinander ist dies z = xyk und x = yt oder z = xyk und y = xt, mit k ≥ t und MDC(z,x,y)=y oder MDC(z,x,y)=x , und k, t ∈ ℕ
Diese Demonstration ist analog zu Fall (6) und (7), da sie in Fermats letzten Satz fällt.
Obs: cxyk = bxt + ax → (cyk)x = (bt)x + ax e cxyk = by + ayt → (cxk)y = by + (at)y, beide Fermats letzter Satz.
Schlussfolgerung für den Fall, dass die Exponenten mehrere sind:
Es gibt keine Lösung für positive ganze Zahlen, in Fällen (5), ( 6 ), ( 7 ) und ( 8 )
3.3 ACCORDING ZU MACENA ODER S.T.M
Bei n ≥ 2 ist es immer möglich, einen B=(nm − 1 + 1)n−(nm − 1 − 1)n, zu bestimmen, und wenn MDC(a, B, c) = 1 dann n gerade Grad hat, wenn die MDC(a, B, c) = 2.t ≥ 2 dann ist der n Grad ungerade, in beiden Fällen erfüllen sie ein an = B + cn, insbesondere für alle geraden oder ungeraden n haben wir die MDC(a,B,c) = c, wobei c von der Form 2n − 1.
Um diesen Satz zu beweisen, müssen Sie ein Tool finden, bevor Sie es beweisen.
Werkzeug:
Um das Werkzeug zuerst zu finden, müssen wir analysieren, wie sich das Binomial von Newton ab Grad 2 verhält.
(x + y)2 = 1.x2 + 2.x.y + 1.y2, das ist 1 2 1.
(x + y)3 = 1.x3 + 3.x2.y + 3.x.y2 + 1.y3, das ist 1 33 1.
(x + y)4 = 1.x4 + 4.x3.y + 6.x2.y2 + 4.x.y3 + 1.y4, das ist1 4 6 4 1.
(x + y)5 = 1.x5 + 5.x4.y + 10.x3.y2 + 10.x2.y3 + 5.x.y4 + 1.y5, das ist 15101051.
*
*
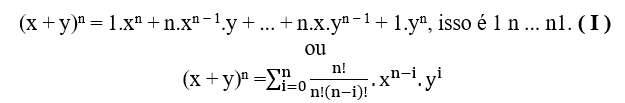
Jetzt subtrahieren xn oder yn auf beiden Seiten von (I) wird es erhalten;
(x + y)n − xn = n.xn − 1.y + … + n.x.yn − 1 + yn( I I)
oder
(x + y)n − yn = 1.xn + n.xn − 1.y + … + n.x.yn bei 1( I I)
Durch die Differenz von zwei Kräften des gleichen Grades können wir schreiben (x + y)n xn, wie folgt;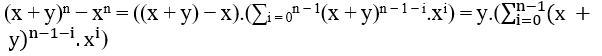
Ebenso können wir auch schreiben (x + y)n – yn, wie folgt;
Damit haben wir zwei neue Gleichungen, die sich nur in x und y unterscheiden.
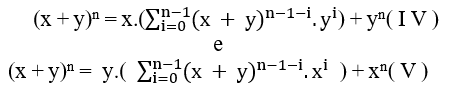
Hinzufügen ( I V ) und ( V ) haben wir;
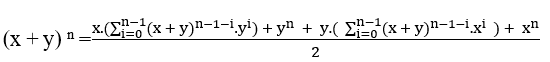
Damit es
durch 2 teilbar ist, ist nur y gleich x dies ist y = x oder x = y, mit dem wir
Dividiert durchden gemeinsamen Faktor, der xn ist, haben wir;
Das Element ( VI ) ist das Werkzeug, das verwendet wird, um den Satz zu beweisen.
Beweisen, dass n ungerade oder gerade ist:
Sein m ≥ 2, Es ist möglich, Gleichungen des Formats zu erhalten cn = B + an, wo der MDC(c,B,a) = 1 wenn Grad n gerade ist, und MDC(c, B, a) = 2.t ≥ 2, mit t ∈ N*, wenn der Grad n ungerade ist.
Methode, wenn die Basis 2 ist, wird sie für das Vervollständigen von Quadraten verwendet, wenn es 3 ist, wird es Würfel vervollständigen, und so weiter, bis die Basis n die Umpisth-Leistung verwendet.
Seien Sie b eine Basis, mit b ∈ N*, so dass Initiative, die wir haben;
Für b = 2 haben wir;
2m = 2m in der Tat ist dies gültig, können wir wie folgt schreiben 2m = 2m.1, erkennen, dass die folgende Gleichheit gültig ist.
2m = 2m.(2 − 1) → 2m = 2m + 1 − 2m → 2.2m − 1 = 2m + 1 − 2.2m − 1, Um das Quadrat des ersten Elements zu vervollständigen, fügen Sie einfach auf beiden Seiten hinzu 22(m − 1) + 1, das führt zu;
2.2m − 1 + 22(m − 1) + 1 = 2m + 1 − 2.2m − 1 + 22(m − 1) + 1 → (22(m − 1) + 2.2m − 1 + 1) = 2m + 1 + (22(m − 1) − 2.2m − 1 + 1) , wir haben also zwei perfekte Quadrate und damit eine neue Gleichung;
(2 m – 1+ 1 )2 = 2 m + 1+ (2 m – 1– 1 )2( 1 )
Ilhre MDC(2m − 1 + 1, 2, 2m − 1 − 1) = 1
Sehen Sie, dass es nur in Fall m von einer Variablen abhängt, siehe die Beispiele unter Verwendung der Zahlen.
Für m = 2
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
(21 + 1)2 = 23 + (21 − 1)2
(2 + 1)2 = 23 + (2 − 1)2
32 = 23 + 12
9 = 8 + 1
Für m = 3
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
(22 + 1)2 = 24 + (22 − 1)2
(4 + 1)2 = 24 + (4 − 1)2
52 = 24 + 32
52 = 42 + 32
25 = 16 + 9
Für m = 4
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
(23 + 1)2 = 25 + (23 − 1)2
(8 + 1)2 = 25 + (8 − 1)2
92 = 25 + 72
(32)2 = 25 + 72
34 = 25 + 72
81 = 32 + 49
Für m = 5
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
(24 + 1)2 = 26 + (24 − 1)2
(16 + 1)2 = 26 + (16 − 1)2
172 = 26 + 152
289 = 64 + 225
Für m = 6
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
(25 + 1)2 = 27 + (25 − 1)2
(32 + 1)2 = 27 + (32 − 1)2
332 = 27 + 312
1089 = 128 + 961
Und so weiter.
Für b = 3 haben wir;
3m = 3m in der Tat ist dies gültig, können wir wie folgt schreiben 3m = 3m.1 erkennen, dass die folgende Gleichheit gültig ist.
3m = 3m.1 → 3m = 3m.(3 − 2) → 3m = 3m + 1 − 2.3m → 3.3m − 1 = 3m + 1 − 3.2.3m − 1, Um den Würfel auf der ersten Seite der Gleichheit zu vervollständigen, fügen Sie einfach hinzu 33(m − 1) + 3.32(m − 1) + 1em ambos os lados, com isso resulta em;
3.3m − 1 + 33(m − 1) + 3.32(m − 1) + 1 = 3m + 1 − 2.3m + 33(m − 1) + 3.32(m − 1) + 1 → (33(m − 1) + 3.32(m − 1) + 3.3m − 1 + 1) = 3m + 1 + 33(m − 1) + 3.32(m − 1) + − 3.2.3m − 1 + 1 → (3m − 1 + 1)3 = 3m + 1 + 33(m − 1) + 3.32(m − 1) − 2.3m + 1, es muss welche geben k ∈ ℕ, das addierte und subtrahierte, dass sie einen perfekten Würfel auf der zweiten Seite der Gleichheit erzeugen, so wie es im vorherigen Beispiel passiert ist, also haben wir;
(3m − 1 + 1)3 = [3m + 1 + 33(m − 1) + 3.32(m − 1) − 2.3m + 1 + k] − k, bestimmen k, genug 3m + 1 + 33(m − 1) + 3.32(m − 1) − 2.3m + 1 + k = (3m − 1 − 1)3;
3m + 1 + 33(m − 1) + 3.32(m − 1) − 2.3m + 1 + k = 33(m − 1) − 3.32(m − 1) + 3.3m − 1 − 1
3m + 1 + 3.32(m − 1) − 2.3m + 1 + k = − 3.32(m − 1) + 3.3m − 1 − 1
k = − 3m + 1 − 3.32(m − 1) − 3.32(m − 1) + 3.3m − 1 + 2.3m − 1 − 1
k = − 3m + 1 − 6.32(m − 1) + 3.3m − 1 + 2.3m − 2
k = − 3m + 1 − 2.3.32(m − 1) + 3m + 2.3m − 2
k = − 3m + 1 − 2.32(m − 1) + 1 + 3.3m − 2
k = − 3m + 1 − 2.32m − 1 + 3.3m − 2
k = − 3m + 1 − 2.(32m − 1 + 1) + 3.3m
k = − 3m + 1 − 2.(32m − 1 + 1) + 3m + 1
k = − 2.(32m − 1 + 1)
Demnächst
− k = 2.(32m − 1 + 1)
Damit haben wir eine andere Gleichung
(3m − 1 + 1)3 = [3m + 1 + 33(m − 1) + 3.32(m − 1) − 2.3m + 1 + k] − k
(3m − 1 + 1)3 = (3m − 1 − 1)3 + 2.(32m − 1 + 1)
(3m − 1 + 1)3 = 2.(32m − 1 + 1) + (3m − 1 − 1)3( 2 )
Als 3m − 1 + 1 , 2.(32m − 1 + 1) e 3m − 1 − 1, Sie sind Paare, weil die Potenz von 3 immer ungerade ist, wenn man 1 addiert oder 1 von dieser Potenz subtrahiert, um uns ein Paar zu geben.
Deshalb der MDC(3m − 1 + 1, 2.(32m − 1 + 1), 3m − 1 − 1) = 2.t ≥ 2, mit t ∈ N*. Beispiel in Zahlen:
Für m = 2 wir haben;
(3m − 1 + 1)3 = 2.(32m − 1 + 1) + (3m − 1 − 1)3
(31 + 1)3 = 2.(33 + 1) + (31 − 1)3
(4)3 = 2.(28) + (2)3
43 = 2.28 + 23, MDC( 4 , 2.28 , 2 ) = 2
64 = 56 + 8
Für m = 3 wir haben;
(3m − 1 + 1)3 = 2.(32m − 1 + 1) + (3m − 1 − 1)3
(32 + 1)3 = 2.(35 + 1) + (32 − 1)3
(10)3 = 2.(244) + (8)3
103 = 2.244 + 83
1000 = 488 + 512
Und so weiter.
Die schnellste Methode, um diese Gleichungen zu finden, ist die Verwendung cn =B +an wo c = nm − 1+1 und a = nm − 1−1, das ist;
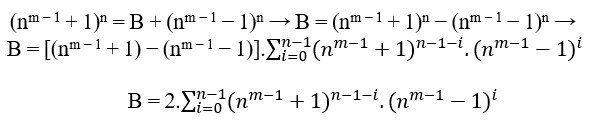
Die allgemeine Gleichung lautet also:
Wenn n klasse 2 ist, haben wir;
Deshalb;
(nm − 1 + 1)n = B + (nm − 1 − 1)n
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2( 1 )
MDC(2m − 1 + 1, 2, 2m − 1 − 1) = 1, com m ≥ 2.
Wenn n von Klasse 3 ist, haben wir;
B = 2.((3m − 1 + 1)2.(3m − 1 − 1)0 + (3m − 1 + 1)1.(3m − 1 − 1)1 + (3m − 1 + 1)0.(3m − 1 − 1)2)
B = 2.((3m − 1 + 1)2 + (3m − 1 + 1).(3m − 1 − 1) + (3m − 1 − 1)2)
B = 2.((32(m − 1) + 2.3m − 1 + 1) + 32(m − 1) − 1 + (32(m − 1) − 2.3m − 1 + 1))
B = 2.(2.32(m − 1) + 1 + 32(m − 1))
B = 2.(32(m − 1)(2 + 1) + 1)
B = 2.(32(m − 1)(3) + 1)
B = 2.(32(m − 1) + 1 + 1)
B = 2.(32m − 1 + 1)
Deshalb;
(nm − 1 + 1)n = B + (nm − 1 − 1)n
(3m − 1 + 1)3 = 2.(32m − 1 + 1) + (3m − 1 − 1)3( 2 )
MDC(3m − 1 + 1, 2.(32m − 1 + 1), 3m − 1 − 1) = 2.t ≥ 2, com t ∈ N* e m ≥ 2
Wenn n von Klasse 3 ist, haben wir;
B = 2.((4m − 1 + 1)3.(4m − 1 − 1)0 + 4m − 1 + 1)2.(4m − 1 − 1)1 + 4m − 1 + 1)1.(4m − 1 − 1)2 + 4m − 1 + 1)0.(4m − 1 − 1)3)
B = 2.(43m − 2 + 4m) ou B = 22m + 1.(24(m − 1) + 1) ou B = 26m − 3 + 22m + 1 ou B = 82m − 1 + 22m + 1
Die Berechnungen korrekt durchgeführt;
B = 2.(43m − 2 + 4m) ou B = 22m + 1.(24(m − 1) + 1) ou B = 26m − 3 + 22m + 1 ou B = 82m − 1 + 22m + 1
Also haben wir;
(nm − 1 + 1)n = B + (nm − 1 − 1)n
(4m − 1 + 1)4 = 2.(43m − 2 + 4m) + (4m − 1 − 1)4( 3 )
O MDC(4m − 1 + 1, 2.(43m − 2 + 4m), 4m − 1 − 1) = 1, com m ≥ 2
oder
(22(m − 1) + 1)4 = 22m + 1.(24(m − 1) + 1) + (22(m − 1) − 1)4
O MDC(22(m − 1) + 1, 22m + 1.(24(m − 1) + 1), 22(m − 1) − 1) = 1, com m ≥ 2
oder
(22(m − 1) + 1)4 = 26m − 3 + 22m + 1 + (22(m − 1) − 1)4
O MDC(22(m − 1) + 1, 26m − 3, 22m + 1, 22(m − 1) − 1) = 1, mit m ≥ 2
Wenn n Grad 5 ist, haben wir;
B = 2((5m − 1 + 1)4 − 0.(5m − 1 − 1)0 + (5m − 1 + 1)4 − 1.(5m − 1 − 1)1 + (5m − 1 + 1)4 − 2.(5m − 1 − 1)2 + (5m − 1 + 1)4 − 3.(5m − 1 − 1)3 + (5m − 1 + 1)4 − 4.(5m − 1 − 1)4)
B = 2((5m − 1 + 1)4 + (5m − 1 + 1)3.(5m − 1 − 1) + (5m − 1 + 1)2.(5m − 1 − 1)2 + (5m − 1 + 1).(5m − 1 − 1)3 + (5m − 1 − 1)4)
Wenn Sie die Berechnungen durchführen, wird sich herausstellen, dass B wert ist.
B = 2.(54m − 3 + 2.52m − 1 + 1)
Die Gleichung für Klasse 5 lautet also:
(5m − 1 + 1)5 = 2.(54m − 3 + 2.52m − 1 + 1) + (5m − 1 − 1)5( 4 )
MDC(5m − 1 + 1, 2.(54m − 3 + 2.52m − 1 + 1), 5m − 1 − 1) = 2.t ≥ 2, com t ∈ N* e m ≥ 2.
Wenn n von Klasse 6 ist, haben wir;
B = 2.((6m − 1 + 1)5 − 0.(6m − 1 − 1)0 + (6m − 1 + 1)5 − 1.(6m − 1 − 1)1 + (6m − 1 + 1)5 − 2.(6m − 1 − 1)2 + (6m − 1 + 1)5 − 3.(6m − 1 − 1)3 + (6m − 1 + 1)5 − 4.(6m − 1 − 1)4 + (6m − 1 + 1)5 − 5.(6m − 1 − 1)5)
B = 2.((6m − 1 + 1)5 + (6m − 1 + 1)4.(6m − 1 − 1) + (6m − 1 + 1)3.(6m − 1 − 1)2 + (6m − 1 + 1)2.(6m − 1 − 1)3 + (6m − 1 + 1).(6m − 1 − 1)4 + (6m − 1 − 1)5)
Wenn Sie die Berechnungen korrekt ausführen, erhalten Sie Folgendes:
B = 2.(65m − 4 + 20.63m − 3 + 6m), ou B = 2.6m.(64m − 4 + 20.62m − 3 + 1) und die Gleichung ist;
(6m − 1 + 1)6 = 2.6m.(64m − 4 + 20.62m − 3 + 1) + (6m − 1 − 1)6( 5 )
Mit MDC(6m − 1 + 1, 2.6m.(64m − 4 + 20.62m − 3 + 1), 6m − 1 − 1) = 1, mit m ≥ 2
Beachten Sie dann, dass die Bedingungen von (1) bis (5) für die Fälle erfüllt sind, in denen n gerade und n ungerade ist.
Um diese Gleichung zu beweisen, müssen wir für den allgemeinen Fall nicht nur von (1) bis ( 5 ), sondern von (1) bis (n) zeigen.
Für n Paar:
Seien Sie n =2k mit k ∈ N*, durch die vorherigen Beispiele wird die MDC(a,B,c)=1, die ersetzt in B erhalten;
Durch die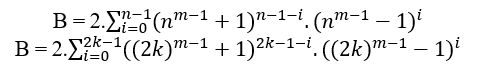 
Definition von Pair ist das B bereits ein Paar, dann ist es durch 2 teilbar, es bleibt c und a zu überprüfen. Wenn c und a Odd sind, dann ist der MDC (c,B,a) 1, wenn c und b ist Gerade dann ist die MDC(c,B,a) ist 2.t ≥ 2, mit t ∈ N*.
Als c = nm nm 1 + 1 und a = nm – 1 – 1 der Gleichung cn = B + ein beim Ersetzen der Werte von n und B haben wi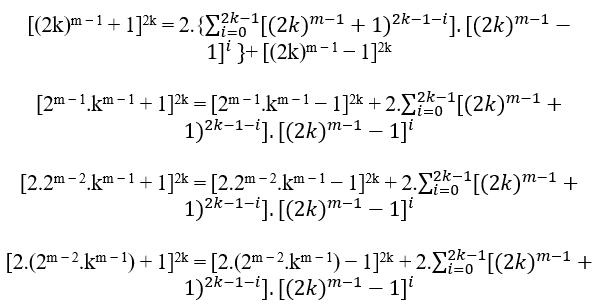
r;
Also 2. (2m n 2.km 1) + 1 als 2. (2m – 2.km 1) 1, sind ungerade, also a und c sind ungerade, wobei dies der einzige Wert ist, der a, B und c teilt, 1 ist.
Für n Impar:
Ob n = 2k + 1 mit k ∈ N*, durch die vorherigen Beispiele die MDC(a,B,c)=1, wird die ersetzt in B erhalten;
Durch das Festlegen des Paares ist das B bereits ein Paar, dann ist es durch 2 teilbar, es bleibt c und a zu überprüfen. Wenn c und a ungerade sind, dann ist die MDC(c,B,a) 1, wenn c und b gerade dann ist, dann ist die MDC(c,B,a) 2.t ≥ 2, mit t ∈ N*.
Als c = nm − 1 + 1 und a = nm − 1 − 1 der Gleichung cn = B + an wenn wir die Werte von n und B ersetzen, haben wir;
Als 2k + 1 ist seltsam, wenn wir quadrieren, ist es auch seltsam:
(2k + 1)2 = 4k2 + 4k + 1 = 2.(2k2 + 2k) + 1
Wenn wir auf beiden Seiten 1 addieren oder 1 subtrahieren, ist das ein Paar?
(2k + 1)2 + 1 = 2.(2k2 + 2k) + 2 = 2.[2k2 + 2k + 1] é um par, e (2k + 1)2 − 1 = 2.(2k2 + 2k) − 2 = 2.[2k2 + 2k − 1] es ist ein Paar.
Als 2k + 1 ist seltsam, wenn wir uns zum Würfel erheben, ist auch seltsam:
(2k + 1)3 = 8k3 + 12k2 + 6k + 1 = 2.(4k3 + 6k2 + 3k) + 1
Wenn wir auf beiden Seiten 1 addieren oder 1 subtrahieren, ist das ein Paar?
(2k + 1)3 + 1 = 2.(4k3 + 6k2 + 3k) + 2 = 2.[4k3 + 6k2 + 3k + 1] é um par, e (2k + 1)3 − 1 = 2.(4k3 + 6k2 + 3k) − 2 = 2.[4k3 + 6k2 + 3k − 1] es ist ein Paar.
Als 2k + 1 ist ungerade, wenn wir die vierte Potenz erhöhen, ist auch ungerade:
(2k + 1)4 = 16k4 + 32k3 + 6k + 1 = 2.(8k4 + 16k3 + 3k2) + 1
Wenn wir auf beiden Seiten 1 addieren oder 1 subtrahieren, ist das ein Paar?
(2k + 1)4 + 1 = 2.(8k4 + 16k3 + 3k2) + 2 = 2.[8k4 + 16k3 + 3k2 + 1] es ist ein Paar und
(2k + 1)4 − 1 = 2.(8k4 + 16k3 + 3k2) − 2 = 2.[8k4 + 16k3 + 3k2 − 1] es ist ein Paar.
Wenn es so weitergeht, wird es immer ein Paar sein (2k + 1)m − 1 + 1 und (2k + 1)m − 1 − 1 ist gerade und wie B gerade ist, so ist der kleinste Wert, der c, B und a teilt, 2, also
MDC(a, B, c) = 2.t ≥ 2, mit t ∈ N*
Wir haben also die beiden Hauptgleichungen:
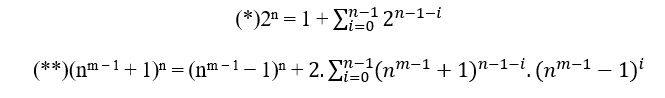
3.3.1 TASTING S.T.M
Um zu probieren ST.M bleibt nur noch zu zeigen, dass unabhängig davon, ob es gerade oder ungerade ist, wir MDC(a,B,c) = c haben, wobei c wo c = 2n − 1 bereits gezeigt wurde, dass (**) andere MDC hat, wenn n gerade und n gerade ist. Mas se usarmos a ferramenta (*) que foi gerada a partir do binômio de Newton, ao fazer x = y foi reduzido para a seguinte equação;
Als
durch Isolieren
wir haben;
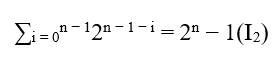
Durch Ersetzen von (I2) und (I1) wird es erhalten;
(2x)n = xn.(2n − 1) + xn
Damit die erste Seite der Gleichung als die Summe zweier Potenzen der zweiten Seite der Gleichung und als gemeinsamer Faktor geschrieben wird xn, jedoch als Wert von
x, so genug x geschrieben werden als 2n − 1, das heißt, die Gleichung wird nur vom Grad n abhängen, also haben wir;
(2x)n = xn.(2n − 1) + xn
(2.(2n − 1))n = (2n − 1)n.(2n − 1) + (2n − 1)n
Also eine andere Gleichung, die nur von einer Variablen abhängt.
(2.(2n − 1))n = (2n − 1)n + 1 + (2n − 1)n
Daten für diese neue Gleichung;
a = 2.(2n − 1), B = (2n − 1)n + 1 e c = 2n − 1
MDC(a,B,c)=MDC(2.(2n − 1), (2n − 1)n + 1, 2n − 1) = 2n − 1 = c
für n paar
Das ist n=2k mit k ∈ N*
MDC(2.(22k − 1), (22k − 1)2k + 1, 22k − 1) = 22k − 1 = c
Für n seltsam
das ist n= 2k + 1 mit k ∈ N*
MDC(2.(22k + 1 − 1), (22k + 1 − 1)2k + 2, 22k + 1 − 1) = 22k + 1 − 1 = c
Tatsächlich wurde nachgewiesen, dass alle vom S.T.M. vorgeschlagenen Aussagen beantwortet wurden.
Test mit Zahlen;
Für n = 2 wir haben;
(2.(2n − 1))n = (2n − 1)n + 1 + (2n − 1)n
(2.(22 − 1))2 = (22 − 1)2 + 1 + (22 − 1)2
(2.(3))2 = 33 + 32
62 = 33 + 32
36 = 27 + 9
Für n = 3 wir haben;
(2.(2n − 1))n = (2n − 1)n + 1 + (2n − 1)n
(2.(23 − 1))3 = (23 − 1)3 + 1 + (22 − 1)3
(2.(7))3 = 74 + 73
143 = 74 + 73
2744 = 2401 + 343
Im Moment hat S.T.M. anscheinend zwei Gleichungen, aber nur eine ist im Vermutungsformat, das es ist;
(2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
MDC(2m − 1 + 1, 2, 2m − 1 − 1) = 1, com m ≥ 2. “Dies ist nicht der Fall, da es 2 als Exponenten enthält”
und
(2.(2n − 1))n = (2n − 1)n + 1 + (2n − 1)n
MDC(2.(2n − 1), 2n − 1, 2n − 1) = 2n − 1, mit n ≥ 2. ” wenn n>2 dann zu Beal Conjecture gehört”
3.4 ANDERE GLEICHUNGEN GENERATED VON DER METHODE VON S.T.M.
F1: ⇒ (2m − 1 + 2k − 1)2 = 2k(m + 1) + (2m − 1 − 2k − 1)2
Es ist der General ( 1 ).
MDC(2m − 1 + 2k − 1, 2, 2m − 1 − 2k − 1) = 1, mit k = 1 und m ≥ 2.
oder
MDC(2m − 1 + 2k − 1, 2, 2m − 1 − 2k − 1) = 2, mit m ≥ 2 und m > k > 1.
Geben Sie ein, wenn m = 4, dann kann k 3.2 und 1 sein.
F2: ⇒ (2m − 1.km + k)2 = (2k)m + 1 + (2m − 1.km − k)2
Dies ist die allgemeine Gleichung der vorherigen.
MDC(2m − 1.km + k, 2k, 2m − 1.km − k) = k, com m ≥ 2 e k ∈ N*.
F3: ⇒ (2m + km + 2)2 = (2k)m + 2 + (2m − km + 2)2
oder
(2m + km + 2)2 = (2k)m + 2 + (km + 2 − 2m)2
Wenn m = 0 und k Für ein Paar haben wir; MDC(1 + k2, 2k, |1 − k2|) = 1, mit k ∈ N*.
Wenn m = 0 und k ist seltsam, was wir haben; MDC(1 + k2, 2k, |1 − k2|) = 2α ≥ 2, mit k, α ∈ N*.
Wenn k ist seltsam, was wir haben MDC(2m + km + 2, 2k, |2m − km + 2|) = 1, mit m ≥ 1 und k ∈ N*.
Ween k für Paar haben wir; MDC(2m + km + 2, 2k, |2m − km + 2|) = 2α ≥ 2, mit m ≥ 1 e k, α ∈ N*.
Allgemeine Formatformel C2 = B + A2 ⇒ C2 = bm + A2
G1: ⇒ (am + 2m − 2.tm)2 = (2.a.t)m + (am − 2m − 2.tm)2
Würfel:
C = am + 2m − 2.tm, b = 2.a.t und A = |am − 2m − 2.tm|
( i ) Wenn das ungerade ist und > 2 der MDC(C,b,A)=1, ∀t ∈ N*.
( ii ) Wenn a mit m = 2 und t a Even ungerade ist, ist der MDC(C,b,A)=1 .
( iii ) Wenn a mit m = 2 und t ein Odd ungerade ist, ist MDC(C, b, A) = 2α ≥ 2 com α ∈ N*.
( iv ) Wenn a paar und m > 2 ist, ist MDC(C, b, A) = 2α ≥ 2, ∀t, α ∈ N*.
( v ) Wenn a mit m = 2 und t an Odd gekoppelt ist, ist MDC(C, b, A) = 1, t ∈ N*.
( vi ) Wenn a mit m = 2 und t a paart wird, wird der MDC(C, b, A) = 2α ≥ 2, t, α ∈ N*.
Wie jede Formel oder Gleichung zustande kam:
Die Idee entstand aufgrund der Fermat-Katalanischen Vermutung, denn wenn man Cz = By + Ax hat, hat es nur eine begrenzte Menge an Lösungen, bei denen A, B und C positive Ganze rinniert sind, ohne gemeinsame Primfaktoren und x, y und z sind positive ganze Zahlen befriedigend ()/() < 1, weil alle Lösungen 2 als exponenten haben. Aus diesem Grund wäre es möglich, dass die Festsetzung von Exponenten 2 im quadratischen Unterschied zufriedenstellende Ergebnisse im Format der Vermutung hätte? Bei Verwendung der gleichen Methode von S.T.M, foi surgindo novas equações com soluções nos inteiros positivos.
F1: Seja (2r + 2s)2 = B + (2r − 2s)2 ⇒ B = (2r + 2s)2 − (2r − 2s)2, com B, r, s ∈ ℕ onde r > s, r e s variáveis não definidas no momento.
B = (2r + 2s)2 − (2r − 2s)2 → B = (2r + 2s − 2r + 2s).(2r + 2s + 2r − 2s) → B = (2s + 2s).(2r + 2r) → B = 2s + 1.2r + 1 → B = 2s + r + 2
Ao adaptar s e r nas variáveis m e k como S.T.M, temos que m > k subtraindo 1 em ambos os lados temos m − 1 > k − 1 ao compara r > s, temos que r = m − 1 e s = k − 1, com isso temos B = 2k − 1 + m − 1 + 2 → B = 2m + k − 2 + 2 → B = 2m + k, portanto a equação é;
F1: ⇒ (2m − 1 + 2k − 1)2 = 2m + k + (2m − 1 − 2k − 1)2
Ween k ist 1, damit MDC(2m − 1 + 21 − 1, 2, 2m − 1 − 21 − 1) = MDC(2m − 1 + 20, 2, 2m − 1 − 20) = MDC(2m − 1 + 1, 2, 2m − 1 − 1) = 1, ∀m ∈ N*
Beispiel bei Verwendung dieser Gleichung, die hat MDC=1, mit m = 2, 3, 5, 6. ; m kann nicht 1 sein, weil k 1 war.
Für m = 2
(22 − 1 + 1)2 = 22 + 1 + (22 − 1 − 1)2 → 32 = 23 + 12 → 9 = 8 + 1
Für m = 3
(23 − 1 + 1)2 = 23 + 1 + (23 − 1 − 1)2 → 52 = 24 + 32 → 25 = 16 + 9
Für m = 4
(24 − 1 + 1)2 = 24 + 1 + (24 − 1 − 1)2 → 92 = 25 + 72 → 34 = 25 + 72 → 81 = 32 + 49
Für m = 5
(25 − 1 + 1)2 = 25 + 1 + (25 − 1 − 1)2 → 172 = 26 + 152 → 289 = 64 + 225
Für m = 6
(26 − 1 + 1)2 = 26 + 1 + (26 − 1 − 1)2 → 332 = 27 + 312 → 1089 = 128 + 961
Wenn k > 1, damit MDC(2m − 1 + 2k − 1, 2, 2m − 1 − 2k − 1) = 2, ∀m, k ∈ N*, wo m > k
Beispiel wenn m = 5, damit k variiert zwischen 2 bis zu 4.
(2m − 1 + 2k − 1)2 =2m + k + (2m − 1 − 2k − 1)2→ (25 − 1 + 2k − 1)2 =25 + k + (25 − 1 − 2k − 1)2→ (24 +2k − 1)2 =25 + k + (24 − 2k − 1)2
Für k = 2
(24 + 22 − 1)2 = 25 + 2 + (24 − 22 − 1)2 → (24 + 21)2 = 27 + (24 − 21)2
→ 182 = 27 + 142 → 324 = 128 + 196
Für k = 3
(24 + 23 − 1)2 = 25 + 3 + (24 − 23 − 1)2 → (24 + 22)2 = 28 + (24 − 22)2
→ 202 = 28 + 122 → 400 = 256 + 144
Für k = 4
(24 + 24 − 1)2 = 25 + 4 + (24 − 24 − 1)2 → (24 + 23)2 = 29 + (24 − 23)2
→ 242 = 29 + 82 → 242 = 29 + 26 → 576 = 512 + 64
F2: Sein (2s.kr + k)2 = B + (2s.kr − k)2 ⇒ B = (2s.kr + k)2 − (2s.kr − k)2, mit B, k, r, s ∈ ℕ wo r > s, r und s Variablen, die derzeit nicht definiert sind.
B = (2s.kr + k)2 − (2s.kr − k)2 → B = (2s.kr + k − 2s.kr + k).(2s.kr + k + 2s.kr − k) → B = (2k).(2s + 1.kr) → B = 2k.2s + 1.kr → B = 2s + 2.kr + 1, Damit B als Potenz genug geschrieben wird s + 2 = r + 1, es stellt sich heraus, dass B = (2k)r + 1 oder B = (2k)s + 2, Damit dies jedoch zutrifft, muss es größer als s sein r > s.
Hypothese s + 2 = r + 1 ⇒ s = r − 1 und these r > s
Wir müssen s + 1 > s 1 auf beiden Seiten hinzufügen s + 2 > s + 1 ⇒ r + 1 = s + 2 > s + 1 > s ⇒ r + 1 > s seinerseits r + 1 > r deshalb r > s, erkennen, dass bei Verwendung der Hypothese wo s = r − 1 ⇒ r = s + 1 und ersetzen in r > s Ungleichheit ist erfüllt s + 1 > s.
Deshalb B = (2k)r + 1 = (2k)s + 2 = (2k)r + 1, dann ist die Gleichung;
(2r − 1.kr + k)2 = (2k)r + 1 + (2r − 1.kr − k)2, so dass alles auf der gleichen Variablen m basiert, nur r gleich m ist, das heißt r = m. Damit haben wir bereits eine andere Gleichung;
F2: ⇒ (2m − 1.km + k)2 = (2k)m + 1 + (2m − 1.km − k)2
Wenn k es ist 1, Dies ist die Gleichung selbst F1 von MDC=1;
(2m − 1.1m + 1)2 = (2.1)m + 1 + (2m − 1.1m − 1)2 → (2m − 1 + 1)2 = 2m + 1 + (2m − 1 − 1)2
Wenn k > 1 hat als MDC = k
MDC(2m − 1.km + k, 2k, 2m − 1.km − k) = k, ∀m, k ∈ N*.
Für k = 2
(2m − 1.km + k)2 = (2k)m + 1 + (2m − 1.km − k)2
(2m − 1.2m + 2)2 = (4)m + 1 + (2m − 1.2m − 2)2
(22m − 1 + 2)2 = 4m + 1 + (22m − 1 − 2)2
Se m = 1
(22.1 − 1 + 2)2 = 41 + 1 + (22.1 − 1 − 2)2 → 42 = 42 + 02 → 16 = 16
Se m = 2
(22.2 − 1 + 2)2 = 42 + 1 + (22.2 − 1 − 2)2 → (23 + 2)2 = 43 + (23 − 2)2 → 102 = 43 + 62 → 100 = 64 + 36
Se m = 3
(22.3 − 1 + 2)2 = 43 + 1 + (22.3 − 1 − 2)2 → (25 + 2)2 = 44 + (25 − 2)2 → 342 = 44 + 302 → 1156 = 256 + 900
*
*
*
Und so weiter …
Für k = 3
(2m − 1.km + k)2 = (2k)m + 1 + (2m − 1.km − k)2
(2m − 1.3m + 3)2 = 6m + 1 + (2m − 1.3m − 3)2
Se m = 1
(21 − 1.31 + 3)2 = 61 + 1 + (21 − 1.31 − 3)2
(20.3 + 3)2 = 62 + (20.3 − 3)2 → 62 = 62 + 02
Se m = 2
(22 − 1.32 + 3)2 = 62 + 1 + (22 − 1.32 − 3)2
(21.9 + 3)2 = 63 + (21.9 − 3)2 → 212 = 63 + 152 → 441 = 216 + 225
Se m = 3
(23 − 1.33 + 3)2 = 63 + 1 + (23 − 1.33 − 3)2Nn
(22.27 + 3)2 = 64 + (22.27 − 3)2 → 1112 = 64 + 1052 → 12321 = 1296 + 11025
*
*
*
Und so weiter …
F3: Seja (2s + kr)2 = B + (2s − kr)2 ⇒ B = (2s + kr)2 − (2s − kr)2, mit B, r, s ∈ ℕ wo r > s, r und s Variablen, die derzeit nicht definiert sind.
B = (2s + kr)2 − (2s − kr)2 → B = (2s + kr − 2s + kr).(2s + kr + 2s − kr) → B = 2.kr.2s + 1 → B = 2s + 2.kr, in diesem Fall ist B eine Leistung genug r = s + 2. In der Tat r > s, weil s + 2 > r = s + 1 > s ⇒ r > s bei der Platzierung des Exponenten als Funktion von m, nur s = m dies uns r = m + 2 gibt.
Damnäschst B = 2s + 2.kr = (2k)r = (2k)m + 2.
Die neue Gleichung lautet also:
F3: ⇒ (2m + km + 2)2 = (2k)m + 2 + (2m − km + 2)2, mit k ∈ N* und m ≥ 0.
Wenn k 1 für ∀m ∈ N* ist, ist mDC = 1 oder wenn m 0 bis ∀k ∈ N* auch der MDC = 1 ist.
Wenn keiner dieser Fälle auftritt F3 Es hat MDC = 2α ≥ 2, ∀α ∈ N*
Die Logik ist dieselbe für G1, “Da es das Allgemeine ist”;
Denn indem man B = macht (ar + 2s.tr )2 − (ar − 2s.tr)2 → B = (ar + 2s.tr − ar + 2s.tr).(ar + 2s.tr + ar- 2s.tr) →
.
Einfach s + 2 = r oder s = r – 2, mit r es ist m Wir machen die Konvertierung, die wir haben s = m – 2, das ist;
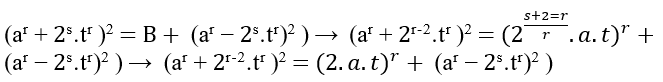G1: ⇒ (am + 2m − 2.tm)2 = (2.a.t)m + (am − 2m − 2.tm)2
Würfel:
C = am + 2m − 2.tm, B = 2.a.t e A = |am − 2m − 2.tm|
( i ) Wenn das ungerade ist und m > 2 ist der MDC(C,b,A)=1, ∀t ∈ N*.
( ii ) Wenn a mit m = 2 und t a Even ungerade ist, ist der MDC(C,b,A)=1 .
( iii ) Wenn a mit m = 2 und t ein Odd ungerade ist, ist mDC(C, b, A) = 2″ ≥ 2 mit α ∈ N*.
( iv ) Wenn a paar und m > 2 ist, ist MDC (C, b, A) = 2′ ≥ 2, ∀t, α ∈ N*.
( v ) Wenn a mit m = 2 und t an Odd gekoppelt ist, ist mDC(C, b, A) = 1, t ∈ N*. ( vi ) Wenn a mit m = 2 und t a paart wird, wird der MDC (C, b, A) = 2, ≥ 2, t, α ∈ N*.
4. FORMELN GENERATED VON T.M E S.T.M MIT LÖSUNGEN IN NATURAL
Grundinformation: a,b,c,x,y,z,A,B,C,α e k ∈ N
Formel1: Cz = Cxyk + 1 = By+ Ax, mdc(x,y,z)=1
( by + ax )xyk + 1 = [ b( by + ax)xk]y + [ a( by + ax )yk]x
Würfel:
C =by+ ax, B =b(by+ ax)xk e A = a( by+ ax )yk, MDC(C, B, A) = C.
Formel2: Cz = Cxk + 1 = Bx+ Ax, ouCz = Cyk + 1 = By+ Ay, mdc(z,x)= mdc(z,x) = 1
( bx + ax )xk + 1 = [ b( bx + ax )k ]x + [ a( bx + ax )k ]x
ODER
( by + ay )yk + 1 = [ b( by + ay )k]y + [ a( by + ay )k ]y
Würfel:
C =bx+ ax, B =b(bx+ ax)k e A = a(bx+ ax )k, MDC(C, B, A) = C.
ODER
C =by+ ay, B =b(by+ ay)k e A = a( by+ ay )k, MDC(C, B, A) = C.
Formel: Cz = Cxk = Bxkα+ 1+Ax, ouCz=Cyk = Bykα+ 1+Ay, mdc( z, y , x ) = 1
[ c( cxk− ax )α]xk = ( cxk− ax )xkα+1 +[ a(cxk−ax)kα]x
ODER
[ c( cyk− by )α]yk = [ b( cyk− by )kα]y + ( cyk− by )ykα+1
Würfel:
C = c(cxk − ax), B = cxk − ax e A = a.(cxk −ax), MDC(C,B,A)= B.
ODER
C = c(cyk − by), B = b(cyk − by) e A = cyk − by, MDC(C,B,A)= A.
Formel4:
(2.(2n − 1))n = (2n − 1)n + 1 + (2n − 1)n
ODER
(2n+1 − 2)n = (2n − 1)n + 1 + (2n − 1)n
Würfel;
a = 2.(2n − 1), B = (2n − 1)n + 1 e c = 2n − 1, MDC(a B,c)=MDC(2.(2n − 1), (2n − 1)n + 1, 2n − 1) = 2n − 1 = c
Formel5:
G1: ⇒ (am + 2m − 2.tm)2 = (2.a.t)m + (am − 2m − 2.tm)2
Würfel:
C = am + 2m − 2.tm, B = 2.a.t e A = |am − 2m − 2.tm|, Com t ≠ 2.a
( i ) Wenn das ungerade ist und m > 2 ist der MDC(C,b,A)=1, ∀t ∈ N*.
( ii ) Wenn a mit m = 2 und t a Even ungerade ist, ist der MDC(C,b,A)=1 .
( iii ) Wenn a mit m = 2 und t ein Odd ungerade ist, ist MDC(C, b, A) = 2″ ≥ 2 mit α ∈ N*.
( iv ) Wenn a paar und m > 2 ist, ist mDC (C, b, A) = 2′ ≥ 2, ∀t, α ∈ N*.
( v ) Wenn a mit m = 2 und t an Odd gekoppelt ist, ist mDC(C, b, A) = 1, t ∈ N*. ( vi ) Wenn a mit m = 2 und t a paart wird, wird der MDC (C, b, A) = 2, ≥ 2, t, α ∈ N*.
Speziell
c2 = 2m + 1 + b2, MDC(a,b,c)=1
(2m−1+1)2=2m+1+(2m−1−1)2
c=2m−1+1, b=2 e a=2m−1−1, MDC(a,b,c)=1
5. T.G.M ODER ALLGEMEINETHEMACENA
Gegeben jede gültige Gleichung der positiven ganzen Zahlen in Form von Macht, oder erzeugt durch T.M oder S.T.M bei multipliziert mit d’ einer Macht, wobei d eine angemessene Grundlage für die Umwandlung in die Summe von zwei Kräften ist, und α ein mehrfachpositiver Ganzzahlexponent der Exponenten der anderen Basen oder mmc der Exponenten multipliziert mit t * ist, ergibt sich also eine Macht, die in der Summe von zwei anderen Kräften mit einem gemeinsamen Faktor d oder einem Vielfachen von d geschrieben ist.
Beispiel:
, mit B>A e m ≥ n ≥ 2, wo α=mmc(1,m,n).t, t ϵ N*
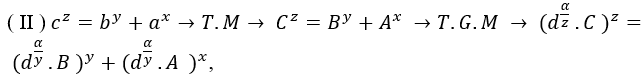, , , , wo α=mmc(z,y,x).t, t ϵ N*
, wo α=mmc(n,1,n).t, t ϵ N*
( IV ) C2=B+A2→ Geralpor S.T.M→ ( am + 2m − 2.tm )2 = ( 2.a.t )m + ( am − 2m − 2.tm )2→T.G.M →
, wobei α =mmc(2,m,2).β, β ε N*
Damit haben wir immer einen gemeinsamen Faktor im Format der Vermutung, wenn die Exponenten x,y,z≥3, unabhängig von der angesprochenen Gleichung.
“Mit Ausnahme von ( IV ), die Note 2 immer mindestens auf einer der Basen haben wird”.
5.1 PROVING T.G.M
Um diesen Satz zu beweisen, ist es notwendig, die Gegenstände zu beweisen. ( I ), ( II ), ( III ) und ( IV ).
Der Beweispunkt (I) gibt eine Gleichung des Typs an
, mit B,
durch Multiplikation mit einer Potenz
, d derzeit jedoch nicht definiert
, das ist dm.n.t , demnächst haben wir;
mit d ist nicht definiert, nur gleich dem zu sein
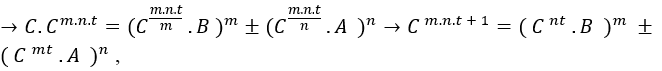, wo C ist der gemeinsame Faktor der Gleichung,
Beispiel in Zahlen;
C1 = Bm+Am→ 29 =33 + 22, nach dem Satz d=C1=29 eα= mmc(1,3,2).t = 6t, →296t+1 = 33 . 296t + 22. 296t
296t+1 =( 3.292t )3 + ( 2.293t )2 , wenn t=1 temos 297=25233+487782, mdc( 29 , 2523 , 48778 ) = 29 ,wenn t = 2 wir haben 2913=21218433+11896466422, mdc(29, 2121843 , 1189646642 ) = 29 und so weiter mit t ≥3
C2 = Bm-An→ 23 =33-22, nach dem Satz d=C2=23eα=mmc(1,3,2).t = 6t,→236t+1 =33.236t-22.236t→
236t+1 =(3.232t)3 – (2.233t)2→, wenn t=1 wir haben 237=15873-243342,mdc( 23 , 1587 , 24334 ) = 23,wenn t = 2 wir haben 2313=8395233-2960717782, mdc(23, 839523 , 296071778 ) = 23 und so weiter mit t ≥3.
Beweisgegenstand( II ) Ob irgendeine Gleichung des Typs cz=by+ax Mit Lösungen für positive ganze Zahlen kommen wir nach T.M. zu einer äquivalenten Gleichung mit den folgenden Grundlagen.
C =by+ax, B =b(by+ax )xk e A =a( by+ax )yk, mit gleichung Cxyk+1=By+Ax→Cz=By+Ax
Beim Multiplizieren mit einer Potenz dα , d im Moment jedoch nicht definiert
α=mmc(z,y,x).t , tϵN*, das ist dzyx.t , demnächst haben wir;
dzyx.t .Cz= dzyx.t.By+dzyx.t .Ax→(dyx.t .C )z= (dzx.t .B )y+(dzy.t .A )x→ Mit mdc( C , B , A ) = C damit
MDC[(dyx.t .C ),(dzx.t .B ),(dzy.t .A ) ] ≥ dt .C , insbesondere wenn d = C haben wir Cz(yxt+1)= (Czx.t .B )y+(Czy.t .A )x
MDC[ C , (Czx.t .B ), (Czy.t .A ) ] = C. Erweitern mit allen Daten die Gleichung ist;
Dyx.t . by+ax }z= {dzx.t .b( by+ax )xk}y+{dzy.t .a( by+ax )yk}x
Mit z= xyk + 1
{dyx.t .( by+ax ) }xyk+1= {d(xyk+1)x.t .b(by+ax )xk}y+{d(xyk+1)y.t .a( by+ax )yk}x
Beispiel in Zahlen
x=y=2, t=k=1 e b=a=3 e d=5
{54 .( 32+32 ) }5= {510 .3( 32+32 )2}2+{510 .3( 32+32 )2}2
{54 .18 }5= {510 .3.182}2+{510 .3.182}2
112505=94921875002+94921875002
MDC(11250 ,9492187500,9492187500)=11250
Beweisgegenstand ( III ) Ob irgendeine Gleichung des Typs cn=B+an,Mit Lösungen für positive ganze Zahlen von S.T.M. haben wir jedoch eine Vielzahl von Gleichungen B es ist je 
, durch Multiplizieren der Gleichung mit der Potenz dα, d im Moment nicht definiert, mit α = mmc(n,1,n).t, t ϵ N*, wir haben
Mit
haben wir;
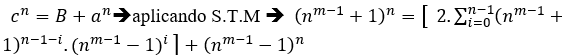
→Da d nicht definiert ist, ist d = B ausreichend;
Oder
Beispiele;
( 1 )
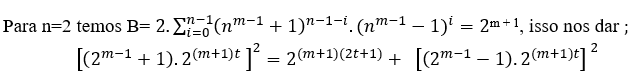
Wenn m = 2, haben wir → (3.23t )2=23(2t+1)+ 26t, ∀ t ∈N, MDC[(3.23t),2,2]=2
Wenn m = 3, haben wir →(5.24t )2=24(2t+1)+(3.24t)2, ∀ t ∈N, MDC[(5.24t),2,(5.24t)]=2
[…]
( 2 )
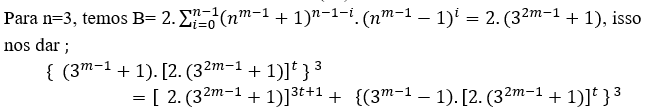Wenn m = 2, haben wir →{4.56t}3=563t+1+ {2.56t } 3, ∀ t ∈N, MDC[(4.56t),56,2.56t]= 56
Wenn m=3, haben wir →{10.488t} 3=4883t+1+ {8.488t }3, ∀ t ∈N,MDC[(10.488t),488,8.488t] = 488
[…]
( 4 )
( 5 )
( 6 )
∀ m > 1, t ∈ N, MDC[Das Bases] = 2.6m. (64m-4 + 20. 62m-3 +1)
( 7 )
Und so weiter
.
.
.
( … )
ANMERKUNG: Bisher bleiben nur die Punkte ( I ), ( II ) und ( III ) übrig ( IV )
Prüfpunkt ( IV ) Seien Sie eine beliebige Gleichung vom Typ c2=B+a2, mit Lösungen in den positiven ganzzahlen, mit den Mitteln von S.T.M, das haben wir;
C2=B+C2→General von S.T.M→( am + 2m − 2.tm )2 = ( 2.a.t )m + ( am − 2m − 2.tm )2, durch Multiplikation mit der Kraft dα, mit d im Moment jedoch nicht definiert α = mdc(2,m,2).β , β ϵ N*, diesmal verwenden β weil die Gleichung bereits t hat, heißt das, dass wir haben;
dα.(am + 2m − 2.tm )2 = dα.( 2.a.t )m + dα.( am − 2m − 2.tm )2
[dmβ.( am + 2m − 2.tm )]2 = [d2β.( 2.a.t )]m + [dmβ( am − 2m − 2.tm )]2 [dmβ .( am + 2m − 2.tm )]2 = [2at.d2β ]m + [dmβ ( am − 2m − 2.tm )]2
In diesem Fall kann d eine beliebige Zahl sein, die zu den positiven Ganzzahlen mit Ausnahme von Null (d’N*) gehört.
Beispiel in Zahlen;
a=2, d=5et=m=β = 3
[59 .( 23 + 21.33)]2 = [12.56]3 + [59 .( 23 - 21.33)]2
[ 59 .( 62 )]2 = [12.56]3 + [59 .( -46)]2
[121093750]2 = [187500]3 + [ -89843750 ]2
1210937502 = 1875003 + (- 89843750 )2
MDC[121093750 ,187500 ,| – 89843750 |] = 31250
HINWEIS: Das MDC(Das Bases ) ≥ dβ, das 31250 = 2.d2β>dβ
Die Idee ist die gleiche für jede Gleichung mit der Summe von 2 Leistung.
Sie beweisen also T.G.M
Neugier: ( 1.0 )
5 = 3 + 2 → multipliziert mit der Basis 3 → 5.3 = 32 + 2.3 → mit 3 = 5 – 2 → ersetzt im ersten Mitglied 5(5 – 2)=32 + 2.3 → 52 – 2.5 = 32 + 2.3 → isolieren 52 = 32 + 2.( 3 + 5 ) →
52 = 32 + 2.( 8 ) → 52 = 32 + 2.( 23 ) → 52 = 32 + 24.
( 1.1 )
53 = 53 → 53 = 5.52 → wir können schreiben 5 = 22 + 1, das zweite Mitglied einsetzen→
53 = (22 + 1).52 → 53 = 22.52 + 52 → 53= 102 + 52.
“HINWEIS: Diese Neugier ist ein weiterer Artikel, den ich in Zukunft veröffentlichen werde, ABC-Vermutung”
6. PROVING THE BEAL CONJECTURE
(1. Bedingung) Gegeben die Gleichung cz = by + ax, mit Lösungen in den positiven ganzen Zahlen, mit { z , y, x ≥ 3 / c, b , a ≠ 0 } , dann a, b und c haben einen gemeinsamen Primfaktor, was bedeutet, dass a, b und c durch die gleiche Primzahl teilbar sind.
Oder
(2. Zustand) Gleichung a x + b y = c z hat keine Lösung für positive ganze Zahlen mit x,y,z ≥ 3 und mdc(a,b,c)=1
Starten des Tests
A (2. Bedingung ) Aus zwei bereits gezeigten Gründen ist es unmöglich, Zahlen in den positiven Ganzzahlen mit mdc(a,b,c) =1 und den Exponenten x,y,z ≥ 3 zu erhalten:
1. — Es hat sich gezeigt, dass die Fermat-Katalanische Vermutung nur eine begrenzte Menge an Lösungen hat, derzeit gibt es nur 10 Gleichungen gefunden, in denen a, b und c positive ganze Zahlen ohne gemeinsame Primfaktoren sind und x, y und z sind positive Ganze befriedigend
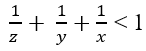
, weil alle Lösungen 2 als einen der Exponenten haben werden, dies bleibt bereits bei der Hypothese von mdc(a ,b,c) =1 und die Exponenten x,y,z ≥ 3.
DIE 10 GEFUNDENEN SIND; Bild von Wikipedia-Website genommen.
2. — Wenn Sie für Teil S.T.M beachten Sie, dass, wenn die Gleichungen die mdc(bases)=1 haben, es immer einen Exponenten 2 hat, sogar die anderen Exponenten variiert, und als S.T.M hat sich bewährt, genau wie die Fermat-Vermutung – Katalanisch besagt, dass mindestens einer der Exponenten 2 sein sollte, und dann die Hypothese aus dem einfachen Grund, einen Exponenten 2 in einer der Basen zu enthalten, klebt.
Es gibt also nur noch eine andere Bedingung, die bewiesen werden muss.
Der (1. Zustand) ist bereits über T.M, S.T.M e T.G.M, alle haben gemeinsame Faktoren in beiden Basen nur um zu zeigen, dass es einen gemeinsamen Primfaktor hat, der beide Basen mit den Exponenten x,y,z ≥ 3 teilt.
BEWEIS:
Würfel;
Sei p eine Primzahl und Fp = pu ein gemeinsamer Primfaktor p, und pi ≠pi+1, i Index, verschiedene Cousins und Exponenten Ui ≥ Ui+1≥0, i Index, verschiedene Exponenten oder nicht, dann kann C eine natürliche Zahl eingegeben werden als;
C = Fp = pu, ou C = p1u1.p2u2 ou C = p1u1.p2u2. p3u3 .p4u4 …piui .pi+1ui+1… Gemeinsame Primfaktoren wie cz = by + ax, und durch eine Methode von T.M, S.T.M und T.G.M, erhalten wird Cz = By + Ax, damit;
Cz =(Fp )z = pz.u↔By + Ax = pz.u, ou Cz =( p1u1 ) .p2u2 )z =p1z.u1 .p2z.u2 ↔By + Ax = p1z.u1 .p2z.u2 oder
Cz =(p1u1.p2u2. p3u3 .p4u4 … piui.pi+1ui+1…)z =p1z.u1 .p2z.u2. p3z.u3.p4z.u4… piz.ui.pi+1z.ui+1…= By + Ax
GEBÄUDE Cz → Cz VON Cn.
In der Tat 1 = 1, weil 1 ein neutrales Element der Multiplikation ist, das c ε N* ist, haben wir, wenn auf beiden Seiten multipliziert, 1.c = 1.c→c = c, wenn wir wieder mit c multipliziert haben c.c =c.c→c2 = c2→ wenn dieser Prozess für n Mal fortgesetzt wird, haben wir → cn = cn, beachten Sie, wenn n > z, haben wir cn>cz.
So kann cn = cn als cn = cz.cn – z eingeschrieben werden, die Hypothese der Vermutung ist, dass cz= by+ ax, einen gemeinsamen Primfaktor hat, der die Basen c,b und a, mit z,y,x ≥ 3 teilt, mit diesem haben wir;
cn = cz.cn – z→cn = ( by+ ax).cn – z→cn = by. cn – z + ax.cn – z,wenn cz= by+ ax Lösungen in den positiven ganzen Zahlen hat, mit Exponenten größer oder gleich 3, in der Tat cn = by. cn – z + ax.cn – z, hat einen Faktor, der sich sowohl trennt, weil die mdc(cn, by. cn – z, ax.cn – z) = cn> 1.
Das Übersetzen wird gezeigt, dass cz= by+ ax solche Lösungen hat, also bestätigt es in der Tat die Hypothese und dies ist eine These. Aber um zu dieser Aussage zu gelangen, müssen wir Gleichheit beweisen, aber das haben die T-Theoreten bereits bewiesen.M, S.T.M e T.G.M, jedoch waren die Bedingungen der Exponenten größer oder gleich 3 wurden nicht enthalten, noch die Bedingungen der wichtigsten Faktoren so schlussfolgesam die Beal Vermutung nachgewiesen.
Verwenden von T.M temos que a equação cz= by+ ax, tornasse;
(by+ax)xyk+1=[b.(by+ax)xk ]y+[a.(by+ax)yk]x, wo z = xyk + 1, C = by+ax ,
B= b.(by+ax)xk und A = a.(by+ax)yk , das ist Cz = By + Ax, mit mdc (C,B,A) = C >1, für
x,y,z> 2 ou x,y,(xyk+1) > 2.
Wenn also Cz = By + Ax Lösungen in den positiven ganzen Zahlen hat, dann cz = cxyk+1 = by + ax, einfach weil es das gleiche Format oder die gleiche Struktur hat. Das heißt, es bleibt zu zeigen cn, was ist;
cn = by. cn – z + ax.cn – z , Anpassung an die Basen C, B und A, die wir haben;
C n = By. C n – z + Ax.Cn – z
(by+ax)n=[b.(by+ax)xk ]y.(by+ax)(n-z)+[a.(by+ax)(yk )]x.(by+ax)(n-z)
(by+ax)n=by.(by+ax)xyk + n- z+ax.(by+ax)xyk + n- z , mit z = xyk+1,
(by+ax)n=by.(by+ax)xyk + n- xyk-1 +ax.(by+ax)xyk + n- xyk-1
(by+ax)n=by.(by+ax)n-1+ax.(by+ax)n-1
“Dies ist die Gleichung in Funktionen der Exponenten n, x, y, basierend auf den zuvor gezeigten Theoremen, die wir haben ( n – 1) ist ein Vielfaches von x,y, das ist n – 1 =
xyt oder n = xy.t + 1, der t es ist nur um von k zu unterscheiden, die bereits verwendet werden ”
(by+ax)xy.t+1=by.(by+ax)xyt +ax.(by+ax) xyt
(by+ax)xy.t+1=[b.(by+ax)xt ]y+[a.(by+ax)yt]x
Sp wie Cn>Cz→Cn-Cz> 0 → (by+ax )xy.t+1-(by+ax )(xy.k+1)>0→Teilen durch (by+ax ), wir haben→(by+ax )xy.t-(by+ax )(xy.k)>0→Teilen (by+ax )xy, wir haben →
(by+ax )t-(by+ax )k>0→(by+ax )t>(by+ax )k→t > k, ∀ t,k ∈N
Dann kann die Gleichung mit allen Variablen wie folgt geschrieben werden:
( EQ1 )(by+ax)xy(t+k)+1=[b.(by+ax)x(t+k) ]y+[a.(by+ax)(y(t+k) )]x
ODER
( EQ2 ) (by+ax)xy( t – k )+1)=[b.(by+ax)x( t – k ) ]y+[a.(by+ax)y(t – k) ]x
Um zu diesen beiden Formeln zu gelangen, verwenden Sie einfach T.M, mit n-z=xyt→n= xyt + z, und als z=xyt haben wir n = xy (t +k), und wie gezeigt wurde, dass t > k, auch gültig ist n = xy( t – k ) ∈N*
Wie die anderen Formeln, die von T generiert werden.M und einige auch von S.T.M e T.G.M, das das Format Cz = By +Ax hat, hat das gleiche Verhalten wie ( EQ1)e ( EQ2), dann zeigt die Bedingungen der Primfaktoren, wie zu Beginn dieses Tests buchstäblich beweisen alle Bedingungen der Beal Vermutung für den positiven Fall, das ist (1. Bedingung ).
(#) Für den Fall eines gemeinsamen Primfaktors in ( EQ1)e ( EQ2) ist dies Cz= By + Ax = pz.u ;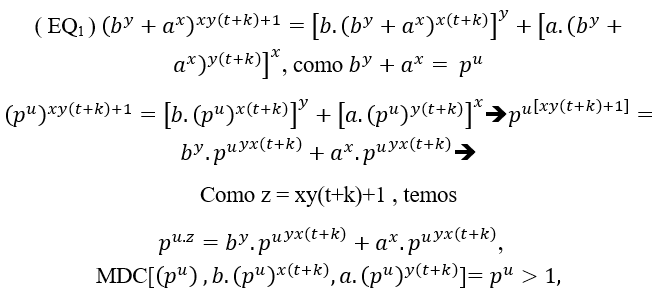
Daher ein gemeinsamer Primfaktor p, weil die Gleichheit befriedigt wird, wenn sie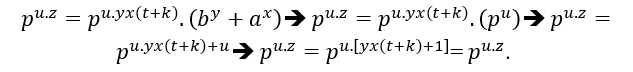 
anhält,
Analog zu ( EQ1 ) wird das gleiche Ergebnis
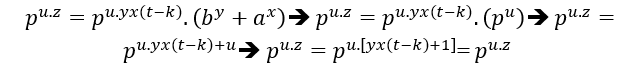(##) Bei 2 gemeinsamen Primfaktoren in (EQ1) und (EQ2) ist dies
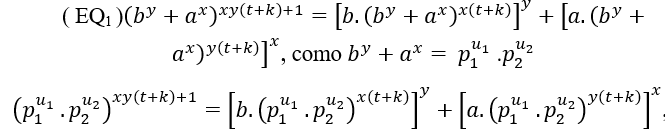, in der tat wird die mdc das Produkt von zwei Mächten unterschiedlicher Primierungen sein,
Überprüfung der Gleichheit, wie z = xy(t+k)+1, haben wir;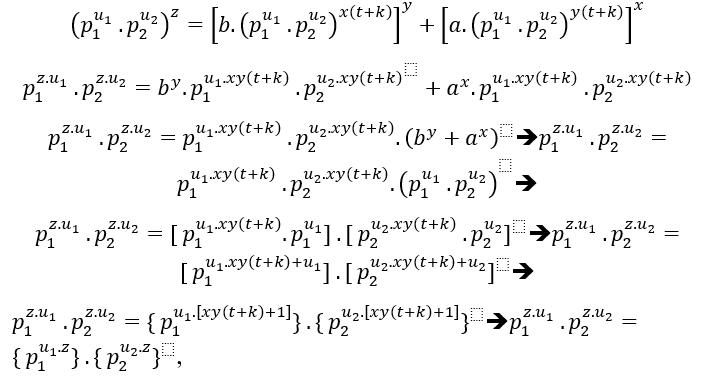
wenn die Division durch einen der üblichen Primfaktoren in den Zustand fällt ( # ).
Analog zu (EQ2);
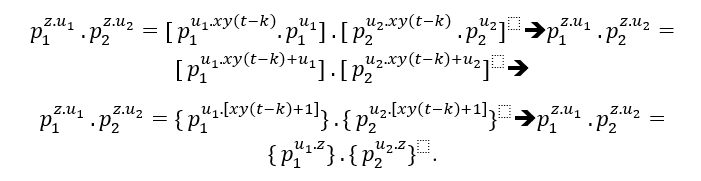( ### ) Bei einem gemeinsamen Primfaktor in (EQ1) und (EQ2) ist dies der Fall;
In der Tat werden wir ein MDC mit mehreren gemeinsamen Primfaktoren haben, oder ab 3 Jahren, Kräfte unterschiedlicher Primierungen voneinander, das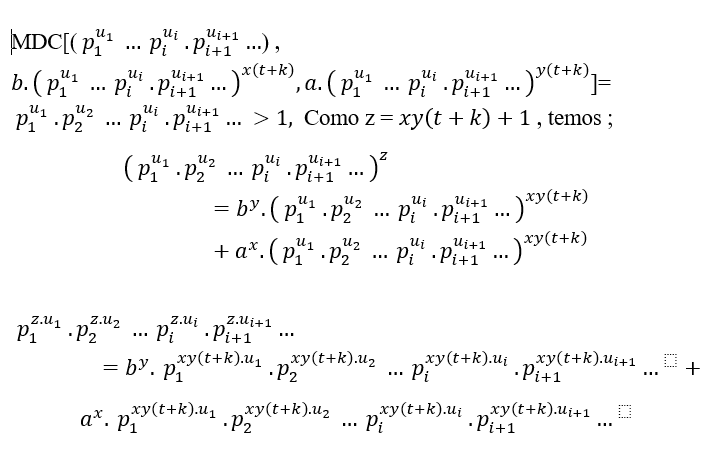
ist
________
_
_________
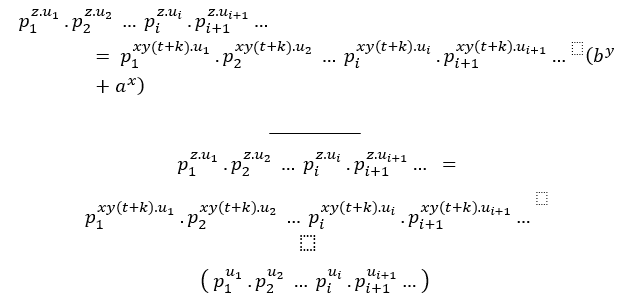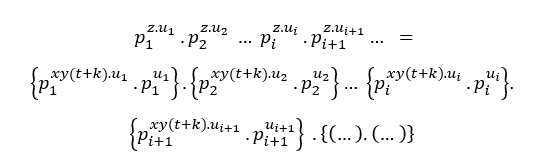
Genau wie die Bedingung ( ## ) haben wir;
Jedes Mal, wenn es durch einen gemeinsamen Primfaktor dividiert, werden sie reduzieren, bis es nur ein gemeinsamer Primfaktor wird.
Analog zu (EQ2) ist es auch zufrieden;
Daher bewährte Vermutung!
7. ABSCHLIEßENDE ÜBERLEGUNGEN
Dieser Artikel wurde als allgemeiner objektiver Beweis vorgeschlagen – dort die Beal-Vermutung, bei der Verwendung der T-Theoreme.M, S.T.M e T.G.M in Kombination mit Anwendungen in der Zahlentheorie war es tatsächlich möglich, zu zeigen, aber es war nicht möglich, ein Con -Beispiel zu finden, aber bei der Verwendung der Mittel im Laufe der Entwicklung muss festgestellt haben, dass jeder Schritt für den anderen sowieso in Bezug auf die Theoreme ohne das T präsentiert wesentlich war.M konnte T nicht verwenden.G.M, sem o T.G.M o S.T.M konnte nicht für die Beal-Vermutung verwendet werden, wenn sie nicht über T.M o S.T.M e T.G.M wäre etwas sehr vage, mit anderen Worten, würde die Demonstration solcher Vermutungen nicht unterstützen.
Bestenfalls ohne die anderen Theoreme wie Pythagoras Theorem, Fermats Letztes Theorem, Sebés Theorem und Fermats Vermutung – Katalanisch das T.M wäre etwas sehr vage und würde viel länger dauern, um bewiesen zu werden, nur durch den Besitz solcher Theoreme das T.M ist eine Erweiterung und gleichzeitig, welche Unterstützung die zitierten Sätze, mit anderen Worten T.M war das fehlende Stück für die Fertigstellung.
8. VERWEISE
BEAL, Andrew. Site: Wiki de Poker. 2008. Disponível em:<https://poker.fandom.com/wiki/Andrew_Beal> Acesso em: 03 de Junho de 2018.
FERMAT, biografias de Matemáticos. Site: Só Matemática. 1998-2019. Disponível em: <https://www.somatematica.com.br/biograf/fermat.php> Acesso em: 18 de Maio de 2018.
KILHIAN, (Sebastião Vieira do Nascimento, “Sebá”). A Conjectura de Beal – Casos Particulares. Site: O baricentro da Mente. 28/04/2012. Disponível em: <https://www.obaricentrodamente.com/2014/11/a-conjectura-de-beal-casos-particulares.html> Acesso em: 27 de Maio de 2018.
TANIYAMA e SHIMURA, Teorema de Shimura-taniyama-Wil. Editada pela última vez em 5 de setembro de 2017 Site: Wikipédia. Disponível em:<https://pt.wikipedia.org/wiki/Teorema_de_Shimura-Taniyama-Weil> Acesso em: 16 de Junho de 2018.
WILES, Biografia de matemáticos. Site: Só Matemática. 1998-2019. Disponível em: <https://www.somatematica.com.br/biograf/andrew.php > Acesso em: 15 de Maio de 2018.
9. SUCHQUELLEN
Site: O Baricentro da Mente. Título: A conjectura de Beal casos particulares. URL: <https://www.obaricentrodamente.com/2014/11/a-conjectura-de-beal-casos-particulares.html> Acesso em: 05 de Maio de 2018.
Site: O Baricentro da Mente. Título: Método de resolução das equações de Sebá. URL: <https://www.obaricentrodamente.com/2012/04/metodo-de-resolucao-das-equacoes-de.html> Acesso em: 05 de Maio de 2018.
Site: Folha de São Paulo. Título: Livro narra solução de teorema que confundiu teóricos por 358 anos. URL: <https://www1.folha.uol.com.br/fsp/ciencia/fe25109801.htm> Acesso em: 10 de Maio de 2018.
Site: Wikipedia. Título: Conjectura de Beal. URL:
<https://pt.wikipedia.org/wiki/Conjectura_de_Beal> Acesso em: 24 de Maio de 2018.
Site: ICM. Título: Detalhes do Autor “Sebastião Vieira do nascimento ( Sebá )”. URL:
<https://www.lcm.com.br/site/livros/detalhesAutor?id=A01644> Acesso em: 27 de Setembro de 2019.
Site: Morfismo. Título: Conjectura de Beal. URL:
<https://morfismo.wordpress.com/2013/11/25/conjectura-de-beal/> Acesso em: 28 de Julho de 2018.
Site: DocSity. Título: Fermat, Notas de estudos de Física. URL:
<https://www.docsity.com/pt/fermat-6-1/4705276/> Acesso em: 01 de Setembro de 2019.
Site: Wikipedia. Título: Conjectura de Fermat-Catalan. URL:
<https://pt.wikipedia.org/wiki/Conjectura_de_Fermat-Catalan> Acesso em: 23 de Setembro de 2019.
[1] Abschluss in Mathematik.
Eingereicht: August 2019.
Genehmigt: November 2019.
