FREIRE, Amanda Freitas [1], RODRIGUES, Fabiana Soares [2], AQUINO, Maria Rosane Souza [3], SOARES, Maria Vanessa [4], GOIS, David Denis Pires de [5], VIANA, José Damião [6]
FREIRE, Amanda Freitas; et.al. Die Verwendung von Geobrett im Geometrieunterricht: Berechnung von Fläche und Umfang. Multidisziplinäre Kern Fachzeitschrift des Wissens. 03-Jahr, Ed. 06, Jg. 03, s. 119-135, Juni 2018. ISSN:2448-0959
Zusammenfassung
Diese Forschung bringt als das zentrale Thema die Lehre zur Berechnung der Fläche und den Umfang der Figuren in der Ebenen Geometrie, Nutzung als Ressource das Geobrett. Wehrt sich, in diesem Artikel die Idee, dass durch den Einsatz von manipulierbaren Materialien möglich, die Lehr-/Lerninhalte erleichtern, ebenso die Argumentation und das Interesse der Studenten an der Problemlösung zu entwickeln. In diesem Artikel vorgestellt werden mit einem Feld von qualitativen Charakter, entstanden in der letzten Reihe der Grundschule, in der achten Klasse "C" staatliche Schule Journalist Edson Régis, in São Cristóvão Nachbarschaft in der Stadt Arcoverde-PE, statt einer Workshop statt durch die institutionelle Programm Einleitung zu unterrichten (PIBID). Während des Workshops wurde eine effektive Teilnahme an Klasse und auch eine Verbesserung der Schülerleistungen.
Stichwörter: Didaktik in der Mathematik, Planimetrie, Geobrett.
Einführung
Heute leben wir in einer Art dieses konzentrierte sich zunehmend auf technologische Fortschritte, und das Treffen ist erforderlich für die verschiedenen menschlichen Aktionen von einfachen zu komplexen Dingen. Mathematische Wissen ist von größter Bedeutung für das Individuum bezieht sich auf die Gesellschaft und der Umwelt, in der er lebt. Dieses wissen heute stellen im täglichen Leben vieler Studierender durch Schwierigkeiten beim Aufbau von Beziehungen, als es mit alltäglichen Situationen erfahren. BNCC (nationale gemeinsame Curriculum Base) berichtet über diese Verbindung, die die Teilnehmer sollen mit täglichen Veranstaltungen gewonnenen Erkenntnisse zu etablieren, und beschreibt die folgenden:
Es ist wichtig hervorzuheben, dass diese Verbindung zwischen der physischen Welt, die uns umgibt und die unbekannte Welt der Mathematik ein Doppelzimmer bezogen werden kann. Zum Beispiel, während ein Parallelogramm Rechteck als ein abstraktes Modell für den Schuhkarton physisches Objekt, an das abstrakte Modell des räumlichen geometrischen Figur Kugel fungiert, können wir das Objekt der physischen Welt des Fußballs (Brasilien, 2015) verbinden .
Das Ziel dieser Forschung ist es, die Bedeutung des Einsatzes von Unterrichtsmaterial Mathematik lernen und Lehren der Ebenen Geometrie, insbesondere die Berechnung der Fläche und Umfang. So werden in der physischen Welt oder immateriellen Mathematik ist in alles um uns herum, so dass es wichtig, Ihr Wissen ist. In der Klasse der Komplexität in der assoziierten Mathematik mit den Tag zu Tag wird es mehr vorhanden ist, sobald die Probleme und Fragen nicht in einer Weise vertreten sind, in denen die Schüler berühren und posieren mit etwas körperliches. Diese Fragen sind in einer Weise nur imaginäre präsentiert. Also wenn jede Funktion gibt, die den Lehrer erlaubt in eurer physischen Form der Sackgasse aussetzen kann und die Fragen der Lehre wird attraktiver und leicht verständlich für den Schüler.
Verlassen diese Schwierigkeiten ergeben sich einige Fragen: wie man mathematische Bildung für Studenten attraktiver machen? Die Verwendung von das Geobrett als Lernwerkzeug erleichtern würde das Lernen der Schüler? Wie können wir als Erzieher die Lehren/Lernen vielseitiger gestalten? Es ist wichtig, dass Lehrer machen Gebrauch von dem wissen, dass der Student bereits besitzt und verlassen diesen Punkt, die Verbindungen mit Mathematik bekannt erzielt werden. Nichts ist nützlicher, befolgen die Anweisungen in der Gesellschaft auftretende Probleme gelernt. Mit diesem entwickelten wir diese Forschung durch die institutionelle Programm Einleitung zu unterrich[7]ten (PIBID) der Gemeinde von Superior Bildung der Arcoverde (EFSA), um den Studenten ein in Handarbeit mit Unterrichtsmaterial Mathematik vorstellen. Wir empfehlen das Geobrett als Werkzeug für Lehr/Lern Berechnung Fläche und Umfang der Ebene Figuren, für Studenten der Finalserie der Grundschule II, speziell im 8. Jahr Journalist Edson Régis im Arcoverde-PE gelegen und. Da wir mit diesem Feature wie Grundbegriffe der Ebenen Geometrie oder nicht-euklidischen Geometrie erkunden können: Punkt, Linie und Fläche.
Die erste geometrischen Ideen entstanden mit der menschlichen Fähigkeit, Alternativen zu suchen, praktische Probleme zu lösen:
Suche nach der Herkunft der Entwicklung der Geometrie in den frühen Tagen mit der primitive Mensch, wir können uns vorstellen, dass Wissen Raum Konfigurationen, Formen und Größen, möglicherweise mit der menschlichen Fähigkeit entstanden zu beobachten und darüber nachzudenken, die Verschiebungen, mit dem Bau von Strategien für die Jagd und Nahrung zuschneiden, mit der Erstellung von Werkzeugen und Utensilien, um ihre Grundbedürfnisse zu befriedigen. Gehäuse mit der Arbeitsteilung zu sichern wurden andere Bedürfnisse entstehen und die Produktion von geometrischen Kenntnisse zu erweitern. Die Notwendigkeit für den Bau, begrenzen das Land führte zu der Vorstellung von Zahlen und Kurven und Positionen als vertikal, senkrecht, parallel (GH, 2008, s. 7).
Methodik
Es ist eine Forschung mit qualitativen Ansatz, die eine Technik der Feldforschung diente. Als Instrument der Datenerhebung waren verwendeten Fragebögen, Interviews und Beobachtungen.
Auf der Suche nach Antworten auf die Fragen, die in der Einleitung präsentiert führen wir verschiedene Aktivitäten wie Interviews mit Lehrern und Schülern und einem Workshop mit dem Geobrett. At, wurde interviewt die Regents Professor achten Klasse "C", und bald nach der Serie, die vorausgeht, ein Fragebogen wurde erstellt mit fünf Fragen: Weißt du, das Geobrett? Sie verwenden irgendeine Art von Ressourcen für den Unterricht in Geometrie? Was sind die Schwierigkeiten, die während dieser Klassen? Während des Kurses haben Sie die wichtigsten flachen geometrischen Figuren vorgestellt? Wie bringen Sie die Berechnung der Flächen und Umfänge.
Im Hinblick auf Schüler, ein Fragebogen auf 30 Studenten mit fünf Fragen angewendet wurde, einige von ihnen sind: Kennst du das Geobrett? Geometrie Klasse der Lehrer verwendet, irgendeine Art von verwertbares Material? Sie wissen, was der Umfang ist? Und Umgebung? Sie wissen, wie man den Umfang und die Fläche dieser Zahlen zu berechnen?
Um die Antworten zu analysieren, erkennt man die große Schwierigkeit in den Inhalt der Nachfrist das Geobrett und ein paar flachen Figuren zugeschnitten. Basierend auf den Antworten einen Workshop mit der Geobrett, Adressierung der Berechnung von Fläche und Umfang.
Nach dem Workshop interview mit Studenten zur Bewertung der Leistung, mit drei Fragen: könnte das Geobrett in der Geometrie verwendet werden? Dieses Feature erleichtert die Berechnung von Fläche und Umfang? Gab es Schwierigkeiten im Umgang mit dem Geobrett?
Diese Studie zielt darauf ab, finden Antworten auf die Fragen dargelegt und die Bedeutung der das Geobrett als Vermittler von Lehr-Lern-Prozess der Berechnung Flächeninhalt und Umfang zu überprüfen.
Didaktik der Mathematik
Zukünftige Lehrer in Mathematik werden mit Situationen der Besorgnis in der Lehr-Lern-Prozess konfrontiert. Im Unterricht der Lehrer sollte Lehren eine große Menge von Inhalten in kurzer Zeit, dieses wissen, das hat hunderte von Jahren in ein paar Stunden Unterricht, wird diese übergeben die meiste Zeit in einer Weise übermitteln abrupte und schwer zu abstrahieren und verursachen Blockaden in das Verständnis der Schüler.
Vergessen Sie auch dieses Ziel des Lernprozesses ist, dass Studenten können die größte Nutzung möglich, aber dieses Ziel ist noch lange erreicht, weil viele Lehrer beschäftigen sich mehr mit der Menge an Inhalten als die Menge dieses angewendet Wissen ist von den Studierenden offen.
Der Bau des mathematischen Wissens hängt stark von der Art und Weise, in der sie sich richten, die Konzepte müssen in einer Art und Weise näher an die physische Realität, Beispiele des täglichen Lebens zu bringen, und auch die Kenntnisse von Schülern außerhalb übertragen werden Feld Schule. Die Lehrer wäre die Verantwortung für Ihren Unterricht im Voraus planen, basierend auf den Bedürfnissen und Schwierigkeiten Ihrer Schüler, in dem Ihr Ziel ist es, den Mangel an Ihre Schüler zu liefern.
Saint Junior (2011), heißt es:
Der Mathematikunterricht muss als einen weiteren Prozess der Konstruktion, vorstellen in denen es notwendig, einen Plan für die Bewältigung der Probleme, zu haben ist und es ist möglich, die vorgeschlagenen Ziele der mechanisch.
Mathematik in den Nachrichten
Es ist bekannt, dass Mathematik aus dem Moment, die der Mensch benötigt entstanden zu zählen. Seitdem der Mensch Strategien schuf zu zählen, um die erste mathematische Symbole im Laufe der Zeit erstellen zu können, waren die Mengen vertreten durch Ausdrücke, Gesten, Worte und Symbole, jeder von denen Menschen hatte Ihren Weg Darstellung.
Mathematik im Laufe der Geschichte leidet seit verschiedene Entwicklungen, was wir heute kennen zu lernen. Derzeit dieser Disziplin spielt eine wesentliche Rolle im Leben des Mannes, Ihre Nutzung und die Kenntnisse in diesem Bereich bietet das Individuum die Möglichkeit zum Aufbau einer Zukunft deutlich besser. Die Unkenntnis dieser schränkt Menschen um Probleme des Alltags, geben Sie auf dem Arbeitsmarkt zu lösen und um neues Wissen in verschiedenen Bereichen zu erwerben, das Mathematik als eine Disziplin verwendet ist unverzichtbar.
Diesem Zusammenhang ermöglicht es uns, diese Disziplin in vielen Aspekten, ins Klassenzimmer bringen analysieren, prüfen wir die Schwierigkeiten beim Lernen von einigen Studenten gestoßen.
In diesem Bereich gibt es unterschiedliche Inhalte, in denen sie mehrere Lernschwächen gefunden werden, eine der Disziplinen der Mathematik, in denen gibt es große Schwierigkeiten, ist die Geometrie.
Ebene Geometrie oder nicht-euklidischen Geometrie
Euclid in Ihrem Buch "Das Element" in 13 Bänden geteilt, wenn 10, dass er sich Ihre Kreation und 03 Zahlentheorie widmete erwirkt werden auf drei geometrische, sie sind:
- Der Punkt (ist, dass Sie nicht Teile)
- Der geraden (Länge ohne Dicke)
- Der Plan (ist alles, was die Länge und Breite hat)
Diese werden als keine Definition übernommen, weil sie primitiven Worte sind.

Im Rahmen der Ebenen Geometrie untersuchen wir die Polygone und flachen Figuren, wie Rechteck, Quadrat, Parallelogramm, Dreieck, Trapez, unter anderem.
Polygon ist ein begrenzter Plan für geraden Segmenten, so dass es, so finden wir zwei Arten: regelmäßige, mit Seiten und Winkel kongruent und unregelmäßig, mit Seiten und Winkel kongruent, in dieser Studie finden wir primitiven Konzepte der Geometrie flach, die Berechnung der Fläche und den Umfang, die Berechnung des Umfangs der Ebene Figuren wird durch die Summe seiner Teile gemacht. Wir wissen, dass ein Quadrat hat vier Seiten Messen ?, bald haben wir den folgenden Ausdruck:, wo ist der Umfang und ? ist die Seite des Platzes, der Umfang ist der Umriss einer gegebenen Fläche, sei es regelmäßig, oder nicht.
Die Fläche eines Polygons ist schon ein bisschen komplizierter, weil es wird nicht die Umrisse der Figur, aber die Nummer, die sie in den Plan, das Gebiet besetzt ist in der Regel durch den Buchstaben gegeben ermittelt werden, mit einem Ausdruck, der entsprechend der Abbildung geht, die es darstellt , mal sehen, einige Bilder und wie ihre jeweiligen Bereiche und Umfänge zu berechnen.
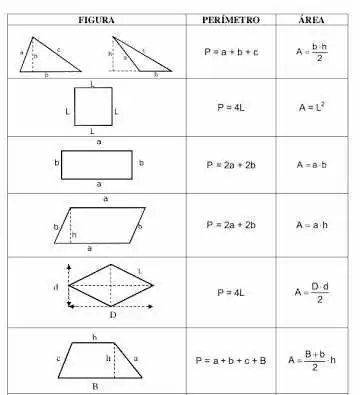
Beispiele:
Berechnen Sie die Bereiche der folgenden Abbildungen:
Ab diesem Punkt können wir sehen, dass die Realität des Schülers voll ist von flachen geometrischen Figuren, dann, dass Schüler wird Probleme verschiedener Komplexität, so dass das geometrische wissen wichtig, die intellektuelle Ausbildung wird der Student wird weil es Sie mit Fertigkeiten versieht und Fähigkeiten, die Ihnen hilft bekommen gelegen und lösen bestimmter Probleme in der Umgebung in die It eingefügt.
Nach dem nationalen Lehrplan Parameter – PCN (Brasilien, 1998) sind die geometrische Konzepte ein wichtiger Teil des Lehrplans der Mathematik in der Mittelschule, weil dadurch der Student eine besondere Art des Denkens entwickelt, das Ihnen ermöglicht verstehen und darstellen der Welt, in der er lebt. Wenn dies von der physischen Welt gearbeitet, können Schüler, Verbindungen zwischen Mathematik und anderen Bereichen des Wissens zu machen.
Es ist verständlich, die laut NKS lernt Geometrie ist von größter Bedeutung in allen Ebenen des Bildungssystems. Allerdings kümmern sich die Lehrer aus mehreren Gründen nicht über die Lehre der Geometrie und so wenig in Suchfunktionen, die den Lehr-und Lernprozess zu erleichtern und zu machen, dass Lernen mehr Dynamik, ohne aus dem Kontext. Beobachten, dass einige Autoren ihre Lehrbücher zu entwickeln, dass der Inhalt in den letzten Kapiteln, die Einhaltung der Hub durch Pädagogen setzen.
GEOBRETT
Der Name kommt von der gemeinsamen Geo Geobrett Bedeutung Geometrie und Plan, d.h. flache Oberfläche daher Geobrett. Wort ist, dass es zuerst 1961 von Professor Caleb Gattegno, des Institute of Education, University of London (KNIJNIK, BASSO verwendet wurde; KLÜSENER, 1996; Menezes, 2008).

Das Geobrett ist ein Stück Fläche Holz mit Nägeln den gleichen Abstand voneinander erschlossen. Es gibt einige Arten von Geobrett: Square, Rundschreiben, das Trelissado und das Oval Office. Der Platz ist die am weitesten verbreitete, hölzerne Oberfläche zusammengesetzte Split so kariert Square von Äquidistanten Nägel. Es ist eine einfache Konfektion, wodurch ihre Schwierigkeiten überwinden und gleichzeitig lernen, sie zu manipulieren, es kann auch verwendet werden, als ein mathematisches Spiel, das Verständnis des Schülers in spielerische Beziehung erleichtert. Diese Funktion ermöglicht es den Studierenden, neue Erfahrungen zu erwerben und auch ermöglicht eurer physischen Form, so abstrakt, imaginäre Modus durch den Bau der Figuren zu verlassen und haben ein zusätzliches Gimmick basierend auf Pin-Anzahl von links nach Recht, Zeilen und Spalten, innerhalb und außerhalb der förderlichen Arbeit dynamischer werden, denn im Gegensatz zu anderen spielen das Geobrett Flexibilität, hat also die Studenten können tun und jederzeit rückgängig machen mit Ihrem Lehrer.
Laut Sharma (2009, s. 8) weist darauf hin, dass:
Im Spiel, das können Sie Risiken eingehen, versuchen, versuchen, erfinden, kostenlos alle des Geistes eines strafenden Bewertung und Neutrum. Der Lehrer, der das Spiel nutzt hat die Aufgabe, zu organisieren und systematisieren diese Aktivitäten um die Studenten auf der Suche nach neuem Wissen (…) zu ermöglichen.
Jedoch merkt, dass mit der Einführung der Geobrett zur Förderung der Lehre der Ebenen Geometrie eine andere Art der Annäherung an und repräsentieren verschiedene Fitness-Inhalte, wie z. B.: Berechnung von Fläche und Umfang von Polygonen.
Feldforschung
Nach der Identifizierung der Geobrett als nutzbare Ressource und in der Lage waren, um sinnvolles lernen zu fördern drei Fragebögen, zwei für die Sammlung von Daten und ein weiteres für die Sammlung der Ergebnisse.
Nach den Fragebogen, den der aktuellen Lehrer, die nie verwendet antwortete didaktische Ressource manipuliert und ignoriert das Geobrett. Der Vorgängerserie in Ihrem Bericht-Staaten, die aus verwenden andere manipulierbar Materialien, einschließlich das Geobrett. Diese brachte umstritten, da nach dem Interview mit Studenten, sie seien nicht das Material kennen.
Den Inhalt arbeitete, wurden Berechnungen von Flächen und Umfänge der Figuren flach, bevor wir die Werkstatt übernehmen wir auch ein Interview mit der Klasse, wir erkannt eine große Schwierigkeit für das Geobrett zu erkennen, einige Polygone berechnen Flächen und Umfänge, wie in der folgenden Ergebnisse gezeigt.
1.) YOU KNOW das GEOBRETT?
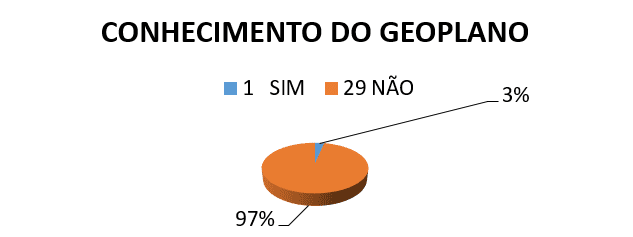
2.) Geometrie Klassen der PROFESSOR hat bereits verwendet einige Art VERWERTBARES MATERIAL?
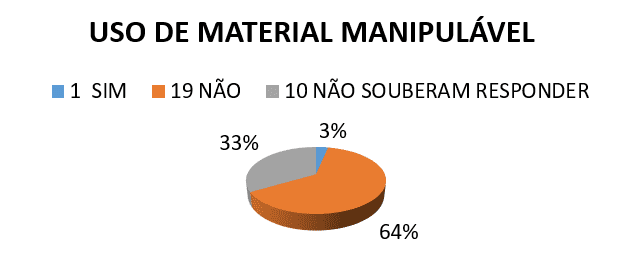
3.) Sie wissen, was Umfang und Fläche ist?

(4) welche Zahlen unten kennen SIE?
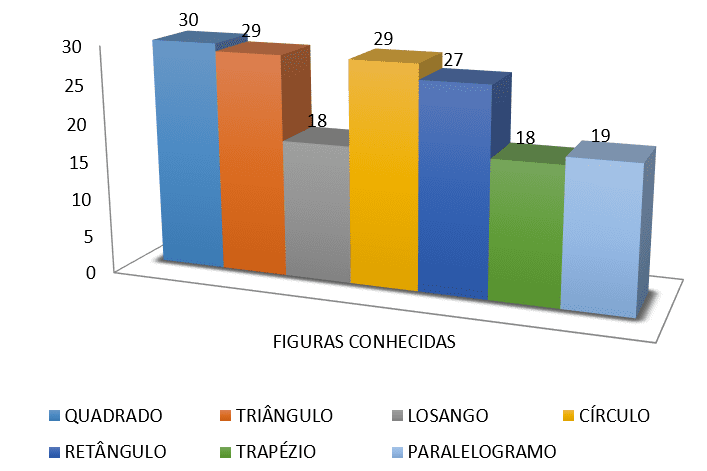
(5) Sie wissen berechnen, den Umfang oder den Bereich von einigen von diesen Zahlen?

Durch die Analyse der gewonnenen Daten, erkannte die Notwendigkeit, einen Workshop zu leiten, in denen das Geobrett sich als Ressource präsentierte für das Lehren und lernen. Durch diesen Workshop möchten wir zeigen so vielseitig wie der Umgang mit dieser Funktion.
Aufgeteilt in fünf Gruppen von sechs Schülern, wurde jede Gruppe zwei Geoplanos, ein Quadrat, einen Kreis und ein gewisses Maß an elastischen gegeben. In einem ersten Moment nach Auslieferung der Geoplanos Studenten, sie hatten eine Zeitlang die Freiheit zu behandeln und nach den Vorstellungen der einzelnen Figuren zu bauen.
Mit dem Einsatz von Folien gab es einen Ansatz zeigt die wichtigsten regelmäßigen Polygone. Bald, nachdem die Schüler auszuführenden Berechnungen Umfänge und Bereiche von verschiedenen Polygonen mit dem Geobrett und karierten Netz in Frage gestellt. Diese Herausforderung eine partizipative Bewegung seitens der Studenten, bei etwas anderes aus Ihrem Alltag gebracht. Das Geobrett wenn Reize verwendet, Interesse weckt und Vielseitigkeit Klasse zu bringen.
Smole, Diniz und Cândido hervorzuheben, die:
Einer der großen Vorteile des das geobrett ist, im Gegensatz zu dem Blatt, er hat Mobilität, ist "dynamisch", und die Flexibilität mit dem können sie tun und rückgängig machen Konstruktion ermöglicht das Kind gewöhnt sich Figuren in mehreren Positionen sehen, bemerken, wenn ein eine Chance, die ich für die Lösung eines Problems eignet und ggf. sofort korrigieren. (2003, s. 112).
Während des Workshops durch die Kommentare wurde festgestellt, dass gab es eine Verbesserung der Leistungen der Schüler, wenn die Berechnungen vorgeschlagen, auch eine effektive Teilnahme in der Klasse.



Wie lernen Bewertung gab es die Notwendigkeit einer anderen Fragebogen mit den Schülern für die Bestätigung der Ergebnisse wie in der Grafik dargestellt.
1.) das GEOBRETT genutzt werden in der Geometrie?

2.) diese Funktion erleichtert Fläche und Umfang berechnen?

(3.) RATE ihre Leistung im Umgang mit dem GEOBRETT?
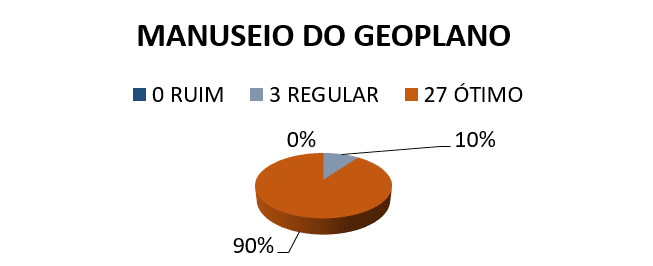
Nach den Ergebnissen, die durch die Umfrage mit den Schülern nach dem Workshop erhalten wurde festgestellt, dass eine wirksame seitens der Studenten für einige Ergebnisse Vereinbarung. Das erste und das zweite Diagramm zeigt, dass 100 % der Studenten stimmen mit dem Einsatz von Geobrett in der Geometrie, da diese Funktion berechnen Flächeninhalt und Umfang erleichtert. Noch Analyse der Ergebnisse ist es möglich, zu bemerken, dass diese Funktion einfach zu handhaben, weil die dritte Abbildung eine hohe Bewertung in Bezug auf die Leistung der Schüler beim Umgang mit dem Geobrett zeigt, 10 % der Studenten gefunden, Ihre regelmäßigen Handhabung und Leistung 90 % große.
Daher die lernen der Schüler war signifikant während der Ausführung des Workshops, zeigte die gleiche Begeisterung, Engagement, Neugier und Engagement, die Herausforderungen vorgeschlagen, mit dem Geobrett und karierten Netz lösen.
Abschließende Überlegungen
Die Ressourcen, wenn gut gestaltet, bieten den Studierenden den Bau des mathematischen Wissens, so diesen Job entschieden wir uns das Geobrett wählen, denn es wird aus der vorherigen Kenntnis dieses Werkzeug für die Erzieher, die anbieten, können für die Ausbildung von anders als Ihre kognitive Entwicklung, Bereitstellung systematisierte und konkrete Situationen zu erweitern.
Daher wird diese Funktion verwendet werden, als eine Lehrmethode in dem Studenten erleben Sie unterschiedliche Lernsituationen Symbole arbeiten können, lösen Probleme im Zusammenhang mit Umfang und Fläche von Polygonen, in denen sie eine echte Analyse durchführen können Was erlebt wird. Dabei ist das Geobrett, für solche passt perfekt in diese Aktivitäten gewählt, weil nach dem nationalen Lehrplan Parameter, die Spiele in einer Art und Weise in der Regel Träger einen relevanten Aspekt, das ist eine Herausforderung, die für den Schüler, d. h. führt, es eine große Weg, um ihn dazu ermutigen, neue Situationen zu bewältigen, wo sie ihre Erkenntnisse, verlieren Ihre Angst vor dem lernen Mathematik umsetzen können.
Laut Rego & Rego (2013).
… Durch Experimente mit Betonmaterial entwickelt die Schüler eine Vorliebe für die Freude der Entdeckung, Herausforderungen zu bewältigen und zu überwinden, Entwicklung von Gewohnheiten und Sitten, die später als Individuum und in der Lage zu handeln führen können.
Kann davon ausgegangen werden, dass durch Spiele, Lehrmittel und Werkzeuge Vermittler von Lehr-/Lernprozess ist möglich, dass Pädagogen Mathestunden vielseitiger, attraktiv für die Studierenden.
Referenzen
Brazilien. Ministerium für Bildung. Gemeinsamen Lehrplan: Mathematik: MEC, 2015, s. 116.
Brazilien. Abteilung der grundlegenden Bildung. Lehrplan: Mathematik-Parameter. Brasilia: MEC/SEF.1998.
GH, Claudia Maria. Geometrie: Raum und Form. Unochapecó: Chapecó; Koordination des Fernunterrichts, 2008.
MARKHAM, j. e. (Ed.). Wissen, interdisziplinäre und Lehrtätigkeit mit Mathe-Spiele: einen methodischen Vorschlag. Recife: UFRPE, 2008. (Mathematische Zusammenhang Serie)
REGO, R. G; REGO. R. M. Matematicativa. 4. Ed. View London 2013 (Lehrerausbildung) s. 25
SANTOS JUNIOR, V. B. D. Die Mobilisierung der mathematischen Inhalte in praktischen Tätigkeiten im Rahmen des Spiels mit Licenciandos für Mathematik. Dissertation (Master in Naturwissenschaften und Mathematik)-Trainee-Programm in Naturwissenschaften und Mathematik Bildung, Abteilung Bildung, ländliche Universidade Federal von Pernambuco. Recife, 2011. S. 22-36
SHARMA, Monica Menezes. Die spielerische Tätigkeit in Mathematik Klasse: Aktion und Reflexion. Erhältlich in <http: sbem.com.br/files/ix/enem/minicurso/trabalhos="">.</http:> Abgerufen am 20. Oktober 2009.
SMOLE, Kátia Cristina Stocco; DINIZ, Maria Ignez de Souza Vieira; Candide, Patricia Terezinha. Figuren und Formen. Porto Alegre: New Haven, 2003. (0 bis 6 mathematische Sammlung, V. (3).
[1] Abschluss im Laufe des Jahres-Abschluss in Mathematik von der CESA.
[2] Abschluss im Laufe des Jahres-Abschluss in Mathematik von der CESA.
[3] Abschluss im Laufe des Jahres-Abschluss in Mathematik von der CESA.
[4] Abschluss im Laufe des Jahres-Abschluss in Mathematik von der CESA.
[5] Abschluss im Laufe des Jahres-Abschluss in Mathematik von der CESA.
[6] Berater. Professor für CESA.
[7] Die PIBID ist ein Programm der Bundesregierung, die die Ausbildung von Lehrern in höhere Level für Grundbildung und der Förderung des Lehrerberufs fördern will. Zugriff auf mehr Informationen:<HTTP: www.capes.gov.br/educacao-basica/capespibid=""></HTTP:>