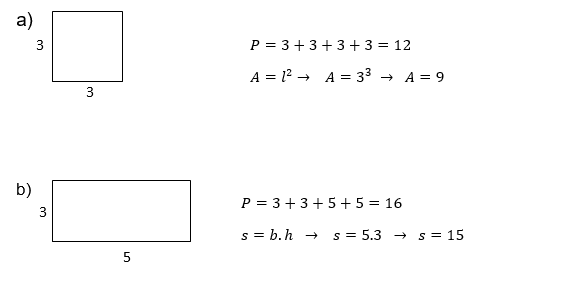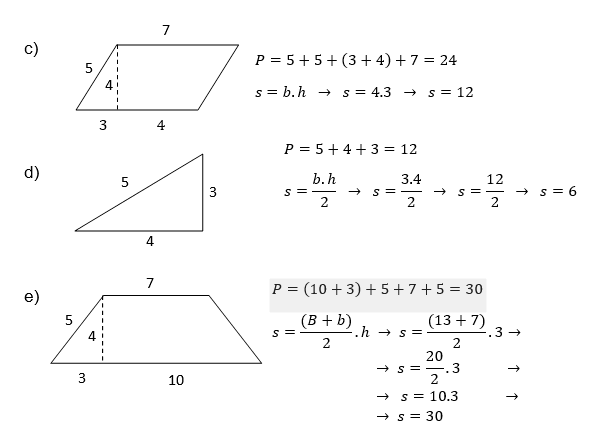FREIRE, Amanda Freitas [1], RODRIGUES, Fabiana Soares [2], AQUINO, Maria Rosane Souza [3], SOARES, Maria Vanessa [4], GOIS, David Denis Pires de [5], VIANA, José Damião [6]
FREIRE, Amanda Freitas; et.al. L'uso di battuto nell'insegnamento della geometria: calcolo area e perimetro. Rivista scientifica multidisciplinare di nucleo di conoscenza. anno 03, Ed. 06, vol. 03, pp. 119-135, giugno 2018. ISSN:2448-0959
Riepilogo
Questa ricerca porta come tema centrale l'insegnamento del calcolo area e perimetro di figure della geometria piana, utilizzando come risorsa il battuto. Si difende, in questo articolo, l'idea che attraverso l'uso di materiale manipolabile è possibile facilitare il contenuto di insegnamento/apprendimento, allo stesso modo sviluppare la motivazione e l'interesse degli studenti nella risoluzione di problemi. In questo articolo sarà presentato con un campo di carattere qualitativo, che si è verificato nella serie finale della scuola elementare, tenuto presso l'ottavo grado scuola statale "C" giornalista Edson Régis, nel quartiere di São Cristóvão alla città di Arcoverde-PE, un workshop tenuto attraverso il programma istituzionale dell'iniziazione all'insegnamento (PIBID). Durante il workshop è stato notato un'effettiva partecipazione in classe e anche un miglioramento delle prestazioni degli studenti.
Parole chiave: insegnamento della matematica, geometria piana, battuto.
Introduzione
Oggi, viviamo in una sorta di questo sempre più incentrata sui progressi tecnologici, e la riunione è necessaria per le varie azioni umane da semplice a cose complesse. La conoscenza matematica è della massima importanza per l'individuo si riferisce alla società e l'ambiente in cui vive. Questa conoscenza al giorno d'oggi non si presentano nella vita quotidiana di molti studenti, dalle difficoltà nell'instaurare relazioni quanto appreso con situazioni di giorno in giorno. BNCC (Base di Curriculum comune nazionale) relazioni su questa connessione che gli studenti dovranno stabilire le conoscenze acquisite con gli eventi quotidiani e viene descritto di seguito:
È importante sottolineare che questa associazione tra il mondo fisico che ci circonda e il mondo sconosciuto della matematica può essere correlata a una doppia. Ad esempio, mentre un parallelepipedo rettangolo funge da un modello astratto per la scatola di oggetto fisico, per il modello astratto della sfera di figura geometrica spaziale, possiamo associare l'oggetto di calcio mondo fisico (Brasile, 2015) .
L'obiettivo di questa ricerca è quello di evidenziare l'importanza dell'uso delle risorse nell'apprendimento della matematica per l'insegnamento e l'insegnamento della geometria piana, in particolare il calcolo dell'area e il perimetro. Così essere nel mondo fisico o immateriale matematica è presente in tutto intorno a noi, quindi è importante alla vostra conoscenza. In Aula la complessità matematica associato con il giorno per giorno, diventa più presente, una volta che i problemi e le domande presentate non sono rappresentate in un modo in cui lo studente può toccare e posa con qualcosa di fisico. Questi problemi sono presentati in un modo solo immaginario. Così quando c'è qualsiasi caratteristica che permette all'insegnante può esporre nella vostra forma fisica all'impasse e le questioni sollevate, l'insegnamento diventa più attraente e facile da capire per lo studente.
Lasciando queste difficoltà presentate derivano alcune domande: come fare educazione matematica più attraente per gli studenti? L'uso di battuto come strumento di insegnamento faciliterebbe l'apprendimento degli studenti? Come come educatori possiamo rendere l'insegnamento/apprendimento più versatile? È fondamentale che gli insegnanti fanno uso della conoscenza che lo studente già possiede e lasciando quel punto può essere fatto che noto connessioni con la matematica. Niente è più utile utilizzare le istruzioni apprese a problemi che sorgono sulla società. Con questo abbiamo sviluppato questa ricerca attraverso il programma istituzionale dell'iniziazione all'inseg[7]namento (PIBID) del comune di Superior formazione di Arcoverde (EFSA), al fine di introdurre lo studente ad un realizzato con risorse didattiche di matematica. Suggeriamo il battuto come strumento di insegnamento/apprendimento di calcolare l'area e il perimetro di figure piane, per gli studenti della serie finale della scuola elementare II, in particolare l'8 ° anno giornalista Edson Régis situate in Arcoverde-PE e. Poiché con questa caratteristica possiamo esplorare concetti di base della geometria piana o geometria non-euclidea come: punto, linea e piano.
Prime idee geometriche ha avuto origine con la capacità umana di cercare alternative per risolvere problemi pratici:
Cercando l'origine dello sviluppo della geometria nei primi giorni, con l'uomo primitivo, possiamo immaginare che le configurazioni di conoscenza dello spazio, forme e dimensioni hanno avuto origine, possibilmente con la capacità umana di osservare e riflettere spostamenti, con la costruzione di strategie per la caccia e cibo raccolto, con la creazione di strumenti e utensili, al fine di soddisfare i loro bisogni di base. Per garantire la custodia, con la divisione del lavoro, stavano emergendo altre esigenze e la produzione di allargare la conoscenza geometrica. La necessità per la costruzione, delimitare la terra parallelo condotto alla nozione di figure e curve e posizioni come verticale, perpendicolare, (GH, 2008, pag. 7).
Metodologia
È una ricerca con un approccio qualitativo, che è stata utilizzata una tecnica di ricerca sul campo. Come strumento di raccolta dei dati sono stati utilizzati questionari, interviste e osservazione.
In cerca di risposte alle domande presentate nell'introduzione, eseguiamo diverse attività quali interviste con insegnanti e studenti e un workshop con il battuto. At in primo luogo, è stato intervistato il professor del reggente di ottavo grado "C" e subito dopo la serie che precede, un questionario è stato elaborato contenente cinque domande: sai il battuto? Utilizzare un certo tipo di risorsa per l'insegnamento della geometria? Quali sono le difficoltà incontrate durante queste lezioni? Durante le lezioni, avete presentato le principali figure piatta geometriche? Come si insegna il calcolo di aree e perimetri.
Per quanto riguarda gli studenti, un questionario è stato applicato a trenta studenti con cinque domande, alcuni di loro sono: sai il battuto? Geometria classe l'insegnante utilizzata una sorta di materiale utilizzabile? Sai che cos'è il perimetro? E zona? Sapete come calcolare il perimetro e l'area di queste figure?
Per analizzare le risposte, si realizza la grande difficoltà nel contenuto, il periodo di tolleranza per soddisfare il battuto e alcune figure piane. Sulla base delle risposte ha tenute un workshop con il battuto, affrontare il calcolo di area e perimetro.
Dopo il workshop, intervista con gli studenti per valutare le prestazioni, contenente tre domande: il battuto potrebbe essere utilizzato in geometria? Questa caratteristica ha facilitato il calcolo dell'area e il perimetro? C'era difficoltà nel maneggiare il battuto?
Questo studio mira a trovare le risposte alle domande indicate e verificare l'importanza del battuto come facilitatore del processo di insegnamento-apprendimento del calcolo area e perimetro.
Insegnamento della matematica
Futuri insegnanti di matematica si trovano ad affrontare situazioni di preoccupazione nel processo di insegnamento-apprendimento. In classe l'insegnante dovrebbe insegnare una grande quantità di contenuti in tempi brevi, deve trasmettere questa conoscenza che ha preso centinaia di anni in poche ore di classe, essendo questi passò la maggior parte del tempo in modo brusco e difficilmente astratto e causare blocchi nella comprensione degli studenti.
Dimenticate che anche tale obiettivo del processo educativo è che gli studenti possono avere l'utilizzazione più grande possibile, ma questo obiettivo è lungi dall'essere raggiunto, perché molti insegnanti sono più preoccupati con la quantità di contenuti che la quantità applicata questo la conoscenza è ricettiva dallo studente.
La costruzione della conoscenza matematica dipende molto il modo in cui si rivolgono, i concetti devono essere trasferiti in un modo più vicino alla realtà fisica, portando esempi di vita quotidiana e anche utilizzando le conoscenze acquisite dagli studenti di fuori il campo scuola. Gli insegnanti sarebbe la responsabilità della tua lezione di pianificazione in anticipo, basato sulle esigenze e le difficoltà del tuo allievo, in cui il vostro scopo è di fornire la mancanza dei vostri studenti.
Saint Junior (2011), afferma che:
L'insegnamento della matematica deve essere pensato come un più ampio processo di costruzione, in cui è necessario disporre di un piano per affrontare i problemi presentati, ed è possibile raggiungere gli obiettivi proposti di modo meccanico.
Matematica nelle notizie
È noto che la matematica è emerso dal momento che l'uomo aveva bisogno di contare. Da quel momento l'uomo stava creando strategie per contare per essere in grado di creare i primi simboli matematici con il passare del tempo, sono state rappresentate le quantità di espressioni, gesti, parole e simboli, ciascuno dei quali persone ha avuto il tuo modo rappresentazione.
Matematica nel corso della storia ha subito varie evoluzioni per arrivare a quello che conosciamo oggi. Attualmente questa disciplina svolge un ruolo essenziale nella vita dell'uomo, è l'uso e la conoscenza in questo settore offre all'individuo la possibilità di costruire un futuro significativamente migliore. La mancanza di questa conoscenza limita gli esseri umani per risolvere i problemi della vita quotidiana, per entrare nel mercato del lavoro e per acquisire nuove conoscenze in vari settori che utilizza la matematica come disciplina è indispensabile.
Questo contesto ci permette di analizzare questa disciplina in molti aspetti, portando in aula, esamineremo le difficoltà di apprendimento incontrate da alcuni studenti.
All'interno di questo campo non ci sono contenuti diversi in cui si trovano parecchie difficoltà di apprendimento, una delle discipline di matematica in cui ci sono grandi difficoltà è la geometria.
Geometria piana o geometria non-euclidea
Euclide nel suo libro "The Element" diviso in 13 volumi, dove 10 che si dedicò alla vostra creazione e teoria dei numeri 03, cercato su tre quelli geometrici, che sono:
- Il punto (è che non avete parti)
- Il rettilineo (lunghezza senza spessore)
- Il piano (è tutto quello che ha lunghezza e larghezza)
Questi ultimi sono presi come nessuna definizione perché sono parole primitivi.

Nel contesto della geometria piana, studieremo i poligoni e figure piane, come ad esempio rettangolo, quadrato, parallelogramma, triangolo, trapezio, tra gli altri.
Poligono è un limitato piano per segmenti retti, lasciandola, troviamo due tipi: normale, con lati e angoli congruenti e irregolari, con lati e angoli congruenti, in questo studio possiamo trovare concetti primitivi della geometria piatto, che è il calcolo area e perimetro, calcolare il perimetro di figure piane è fatta dalla somma delle sue parti. Sappiamo che un quadrato ha quattro lati misurano ?, presto abbiamo la seguente espressione:, dove è il perimetro e ? è il lato della piazza, il perimetro è il contorno di una data superficie, sia esso regolare o non.
L'area di un poligono è già un po' più complicata, perché non sarà il contorno della figura, ma il numero che occupa nel piano, la zona è di solito dato dalla lettera può essere determinata con un'espressione che va secondo la figura che rappresenta , vediamo alcune immagini e come calcolare le loro rispettive aree e perimetri.
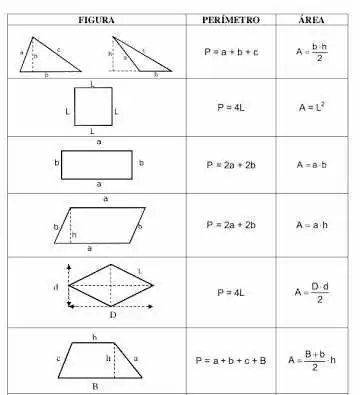
Esempi:
Calcolare le aree delle figure qui sotto:
A partire da questo punto che possiamo vedere che la realtà dello studente è piena di figure geometriche piatta, quindi che lo studente si incontra problemi di varia complessità, così la conoscenza geometrica diventa importante per la formazione intellettuale lo studente perché vi fornirà le competenze e le abilità che ti aiuterà a ottenere situate e risolvere alcuni problemi nell'ambiente in cui esso è inserito.
Secondo il national curriculum parametri – PCN (Brasile, 1998), i concetti geometrici sono una parte importante del curriculum di matematica nella scuola media, perché attraverso questo lo studente sviluppa un particolare tipo di pensiero che ti permette di comprendere e rappresentare il mondo in cui vive. Se questo ha funzionato dal mondo fisico, permette agli studenti di fare collegamenti tra matematica e altre aree di conoscenza.
È comprensibile che, secondo i PCN di apprendimento di geometria è di fondamentale importanza in tutti i livelli dell'istruzione. Tuttavia gli insegnanti per diversi motivi non si preoccupano l'insegnamento della geometria e così poco nella funzionalità di ricerca che facilitano l'insegnamento-apprendimento e per fare che l'apprendimento più dinamico, senza allontanarsi dal contesto. Osservando che alcuni autori a sviluppare i loro libri di testo messo quel contenuto negli ultimi capitoli, rendendo la conformità con il colpo di educatori.
BATTUTO
Il nome deriva dal comune Geo, battuto significato geometria e piano, il che significa superficie piana quindi battuto. Parola è che è stato usato in primo luogo nel 1961, dal professor Caleb Gattegno, dell'Istituto di formazione, Università di Londra (KNIJNIK, BASSO; KLÜSENER, 1996; Menezes, 2008).

Il battuto è che un pezzo di legno superficie piana con Chiodi filettati alla stessa distanza uno da altro. Ci sono alcuni tipi di battuto: quadrate, circolari, il Trelissado e l'ufficio ovale. La piazza è il più usato, in legno superficie Spalato composto così a scacchi Piazza dai chiodi equidistanti. È una confezione semplice, che aiuta gli studenti a superare le loro difficoltà e allo stesso tempo imparare a manipolarla, può anche essere utilizzato come un gioco matematico che facilita la comprensione dello studente in rapporto giocoso. Questa caratteristica permette agli studenti di acquisire nuove esperienze e inoltre rende possibile la tua forma fisica, lasciando così astratto, immaginario modalità attraverso la costruzione di figure e hanno un ulteriore espediente basato sul numero di pin da sinistra a diritto, righe e colonne, dentro e fuori il lavoro di abilitazione più dinamico, perché a differenza di altri giochi il battuto ha flessibilità, così gli studenti possono fare e annullare in qualsiasi momento con il tuo insegnante.
Secondo Sharma (2009, p. 8) sottolinea che:
Nel gioco può rischiare, provare, provare, inventare, il tutto gratuitamente il fantasma di una valutazione punitivo e neutro. L'insegnante che utilizza il gioco ha il ruolo di organizzare e sistematizzare queste attività per consentire agli studenti di raggiungere a piedi in cerca di nuove conoscenze (…).
Tuttavia si rende conto che con l'introduzione del battuto, può promuovere l'insegnamento della geometria piana un diverso modo di approcciare e rappresentano vari contenuti di fitness, come: calcolo area e perimetro di poligoni.
Ricerca sul campo
Dopo aver identificato il battuto come una risorsa usabile e in grado di promuovere l'apprendimento significativo, tre questionari, due erano per la raccolta dei dati e l'altro per la raccolta di risultati.
Secondo il questionario che l'attuale insegnante ha risposto che mai usato qualsiasi risorsa didattica manipolato e non riconosce il battuto. La serie precedente nella vostra relazione si afferma che ha fatto uso di altri materiali manipolabili, compreso il battuto. Queste portate controverso perché secondo l'intervista con gli studenti, hanno sostenuto di non conoscere il materiale.
Il contenuto ha lavorato, erano i calcoli delle aree e perimetri di figure piane, prima applichiamo il workshop abbiamo anche un'intervista con la classe, abbiamo rilevato una grande difficoltà per loro di riconoscere il battuto, pochi poligoni, calcolare aree e perimetri, come mostrato nei seguenti risultati.
1) YOU KNOW il battuto?
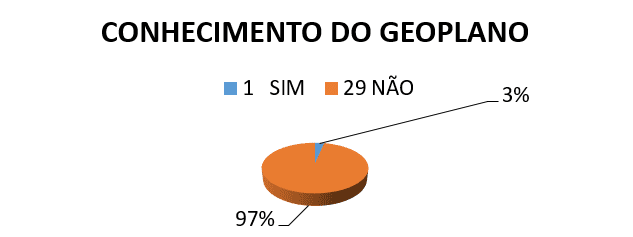
2) geometria classi il professore ha già usato qualche sorta di materiale utilizzabile?
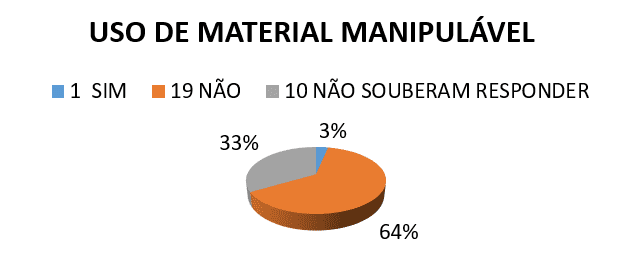
3rd) Sai che cosa è perimetrale o zona?

4) quali figure sotto lo sai?
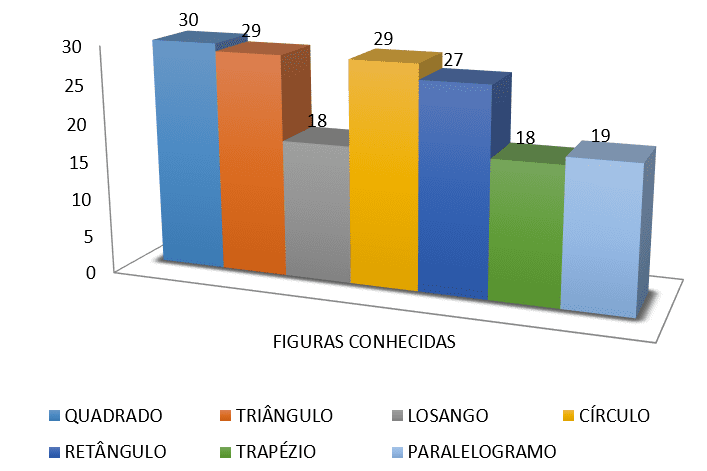
5) Sai calcolare il perimetro o l'area di alcune di queste figure?

Analizzando i dati ottenuti, si capì la necessità di condurre un workshop, in cui il battuto è stato presentato come una risorsa per l'insegnamento e l'apprendimento. Attraverso questo workshop cerchiamo Visualizza così versatile come questa funzionalità di gestione.
Diviso in cinque gruppi di sei studenti, ogni gruppo è stato dato due Geoplanos, un quadrato, un cerchio e una certa quantità di elastico. In un primo momento dopo recapitati gli studenti Geoplanos, hanno avuto per un po' la libertà di gestire e costruire figure secondo la fantasia di ciascuno.
Con l'uso di diapositive, c'era un approccio mostrando i principali poligoni regolari. Poco dopo, ha sfidato gli studenti per eseguire calcoli di perimetri e aree di vari poligoni utilizzando il battuto e la maglia a scacchi. Questa sfida ha portato un movimento partecipativo da parte di studenti, nel caso di qualcosa di diverso dalla tua vita quotidiana. Il battuto quando utilizzato charms, suscita interesse e portare versatilità alla classe.
Smole, Diniz e Cândido evidenziare che:
Uno dei grandi vantaggi del battuto è, a differenza del foglio di carta, che ha la mobilità, è "dinamico", e la flessibilità con cui si può fare e disfare la costruzione permette il bambino si abitua a vedere figure in diverse posizioni, notare se una dato una possibilita ' che ho fatto per la soluzione di un problema è adatto e correggerla subito se necessario. (2003, p. 112).
Durante il workshop attraverso i commenti, è stato notato che c'era un miglioramento delle prestazioni degli studenti quando eseguendo i calcoli proposti, anche un'effettiva partecipazione in classe.



Come valutazione di apprendimento c'era la necessità di eseguire un altro questionario con gli studenti per la conferma dei risultati ottenuti come mostrato nella grafica.
1a) il battuto potrebbe essere utilizzato in geometria?

2) questa funzione facilitato calcolo area e perimetro?

3) Tasso di rendimento loro nel maneggiare il battuto?
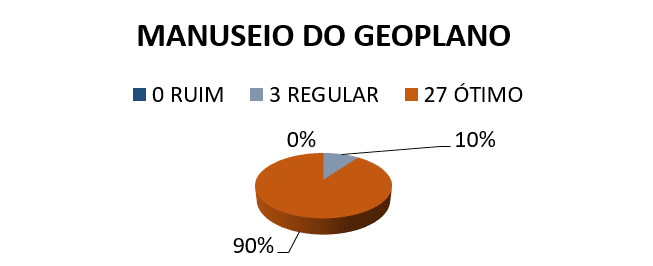
Secondo i risultati ottenuti attraverso l'indagine condotta con gli studenti dopo il workshop, si è notato che c'era un accordo efficace da parte di studenti per alcuni risultati. Il primo e il secondo grafico mostra che 100% degli studenti sono d'accordo con l'uso di battuto in geometria, poiché questa funzione facilitato calcolo area e perimetro. Ancora analizzando i risultati, che è possibile notare che questa caratteristica è facile da gestire, perché il terzo grafico presenta un rating elevato in relazione allo svolgimento degli studenti quando si maneggia il battuto, 10% degli studenti trova la regolare gestione e prestazioni Ottimo il 90%.
Pertanto l'apprendimento degli studenti è stato significativo durante l'esecuzione del workshop, la stessa ha mostrato entusiasmo, impegno, curiosità e dedizione, risolvere le sfide proposte utilizzando il battuto e la maglia a scacchi.
Considerazioni finali
Le risorse, quando ben progettati, offrono agli studenti la costruzione di conoscenze matematiche, così questo lavoro abbiamo deciso di scegliere il battuto, perché sarà da una conoscenza preliminare di questo strumento per l'educatore che può offrire per educare un modo diverso per espandere il vostro sviluppo cognitivo, fornendo situazioni sistematizzati e concrete.
Pertanto, questa funzionalità verrà utilizzata come un metodo di insegnamento in cui gli studenti possono sperimentare situazioni di apprendimento diversi simboli di lavoro, risolvere problemi che coinvolgono il perimetro e area dei poligoni, in cui saranno in grado di fare un'analisi reale Che cosa è essere sperimentato. In tal modo, il battuto, scelto per tale si inserisce perfettamente in queste attività, perché secondo il national curriculum parametri, i giochi in un modo generalmente sono portatori di un aspetto rilevante, che è una sfida che conduce allo studente, vale a dire, è un grande modo per incoraggiarlo ad affrontare nuove situazioni dove possono mettere in pratica loro apprendimenti, perdere la paura di imparare la matematica.
Secondo Rego & Rego (2013).
… Attraverso esperimenti con materiale concreto, lo studente sviluppa un gusto per il piacere della scoperta, per affrontare sfide e superarle, lo sviluppo di abitudini e costumi che possono portare più tardi di essere un individuo e in grado di agire.
Si può concludere che, attraverso giochi, risorse didattiche e facilitatori di strumenti di insegnamento/apprendimento è possibile che gli educatori fare lezioni di matematica più versatile, attraenti per gli studenti.
Riferimenti
Brasile. Ministero della pubblica istruzione. Piano di studi comune: Matematica: MEC, 2015, p. 116.
Brasile. Dipartimento di fondamentale formazione. Curriculum Nazionale: Parametro di matematica. Brasilia: MEC/SEF.1998.
GH, Claudia Maria. Geometria: spazio e forma. UNOCHAPECÓ: Chapecó; Coordinamento della formazione a distanza, 2008.
MARKHAM, j. e. (ed.). Conoscenza, interdisciplinare e attività didattiche con giochi di matematica: una proposta metodologica. Recife: UFRPE, 2008. (Contesto matematico serie)
REGO, R. G; REGONDI. R. M. Matematicativa. 4. Ed. Visualizzazione. Londra 2013 (formazione degli insegnanti) p. 25
SANTOS JUNIOR, V. B. D. La mobilitazione del soddisfare matematico in attività pratiche nel contesto del gioco con Licenciandos di matematica. Tesi di laurea (master in educazione scientifica e matematica)-corso di laurea in scienza e matematica istruzione, dipartimento dell'educazione, Università federale rurale di Pernambuco. Recife, 2011. P. 22-36
SHARMA, Monica Menezes. L'attività ludica in aula di matematica: azione e riflessione. Disponibili in <http: sbem.com.br/files/ix/enem/minicurso/trabalhos="">.</http:> Acceduto a sopra 20 ottobre 2009.
SMOLE, Kátia Cristina Stocco; DINIZ, Maria Ignez de Souza Vieira; Candide, Patricia Terezinha. Figure e forme. Porto Alegre: New Haven, 2003. (collezione matematica 0-6, v. 3).
[1] Laurea nel corso di laurea in matematica il Cesa.
[2] Laurea nel corso di laurea in matematica il Cesa.
[3] Laurea nel corso di laurea in matematica il Cesa.
[4] Laurea nel corso di laurea in matematica il Cesa.
[5] Laurea nel corso di laurea in matematica il Cesa.
[6] Advisor. Professore di CESA.
[7] Il PIBID è un programma del governo federale che vuole incoraggiare la formazione degli insegnanti nel livello superiore per l'istruzione di base, contribuendo al miglioramento della professione docente. Più accesso alle informazioni:<HTTP: www.capes.gov.br/educacao-basica/capespibid=""></HTTP:>